Abstract
Principal component analysis (PCA) is well established as a powerful statistical technique in the realm of yield curve modeling. PCA based term structure models typically provide accurate fit to observed yields and explain most of the cross-sectional variation of yields. Although principal components are building blocks of modern term structure models, the approach has been less explored for the purpose of risk modelling—such as Value-at-Risk and Expected Shortfall. Interest rate risk models are generally challenging to specify and estimate, due to the regime switching behavior of yields and yield volatilities. In this paper, we contribute to the literature by combining estimates of conditional principal component volatilities in a quantile regression (QREG) framework to infer distributional yield estimates. The proposed PCA-QREG model offers predictions that are of high accuracy for most maturities while retaining simplicity in application and interpretability.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Interest rate risk is pervasive in the balance sheet of banks. Financial assets; such as loans, fixed income portfolios and derivatives books—and liabilities; such as deposits, commercial paper and bonds, are all exposed to interest rates with different time to maturity—collectively referred to as the yield curve. While managing interest rate risk is of crucial importance for banks, this is a complex task for several reasons. Firstly, the number of financial assets and liabilities exposed to interest rate risk is typically high. As a consequence, separate modeling of each financial instrument is infeasible. Secondly, the time to maturity of the financial instruments carrying interest rate risk ranges from one day and up to 30 years. Hence, multivariate models are required to capture the dynamics of the yield curve. However, multivariate modeling in the context of interest rate risk has proven very challenging, due to parameter proliferation and estimation convergence issues. Thirdly, interest rate risk models are generally difficult to specify and estimate from a statistical point of view, caused by regime switching behavior and time-varying dynamics of the yields.
To accommodate these constraints, financial institutions typically aggregate interest rate risk. In the cross-sectional dimension, long and short exposures are combined to form net positions. In the time-to-maturity dimension, exposures of adjacent maturities are mapped into predefined time buckets.Footnote 1 Although this alleviates the complexity of the underlying portfolio risk composition, banks are still faced with the challenging problem of constructing a model which appropriately captures the risk level under prevailing market conditions. In lack of readily available models which can be implemented without demanding data requirements or complex optimization routines,Footnote 2 historical simulationFootnote 3 and stress testingFootnote 4 are frequently applied for this purpose.
In this paper we propose a model which aims to resolve some practical limitations for banks in relation to interest rate risk management. The proposed model is based on principal component analysis (PCA), which is well established as a powerful statistical technique in the realm of yield curve modeling. Litterman and Scheinkman (1991) were the first to document the ability of the first three principal components to explain most of the cross-sectional variation in yields, and to assign meaningful economic interpretations as level, slope and curvature factors, respectively, to the first three principal components. PCA based term structure models typically provide accurate fit to observed yields and explain most of the cross-sectional variation of yields. Although principal components (PCs) are building blocks of modern term structure models, the approach has been less explored for density estimation and the purpose of risk modelling—such as Value-at-Risk (VaR) and Expected Shortfall (ES). The novelty is on combining estimates of conditional principal component volatilities in a quantile regression (QREG) framework to infer distributional yield estimates—which we call PCA-QREG model. Quantile regression, introduced by Koenker and Bassett Jr. (1978), has found several applications in finance, due to its flexible and semi-parametric nature. The latter is of particular importance for the purpose of this paper, in light of the complex stylized facts of yields (Deguillaume et al., 2013). The PCA-QREG model is parsimonious, accurate for most maturities and does not require data beyond the time-series of yields. We also show that it fits well into the typical mapping of interest rate risk performed by banks and is relatively easy to estimate. As such, the PCA-QREG model can readily be applied by banks and other practitioners.Footnote 5
The remainder of the article is organized as follows. Section 2 presents a comprehensive literature review within both subjects: term structure modeling and quantile regression. Section 3 describes the data, while Sect. 4 explains the methodology proposed. Section 5 shows the results from the empirical investigation. Finally, Sect. 6 discusses the contribution of the paper and concludes.
2 Literature review
2.1 Term structure modeling
The yield curve is an important economic object and has been extensively studied by researchers in macroeconomics and finance. As noted by Jacobs Jr. (2017), modeling the term structure of interest rates is critical in two domains of finance; the pricing of bonds and interest rate derivatives under the risk-neutral measure \({\mathbb {Q}}\), and the management of interest rate risk under the physical measure \({\mathbb {P}}.\)Footnote 6 This paper contributes to the latter class of models.
The no-arbitrage class of models (Heath et al., 1992; Hull & White, 1990; Jamshidian, 1997) focus on perfectly fitting the term structure at a point in time to ensure that no arbitrage possibilities exist, which is of crucial importance for replicating interest rate derivatives. These \({\mathbb {Q}}\)-measure models are not constructed to describe a realistic evolution of different components of the term structure, and has little to say about dynamics or forecasting. In the realm of derivatives pricing, the market consensus has been to assume a log-normal distribution for forward rates, as implied by the Black model (Black, 1976).Footnote 7 This is strongly motivated by the analytical tractability of the models, albeit slightly at odds with statistical analysis, which has revealed complex behaviour of interest rate volatility.
The first study to compare the empirical performance of single factor short-rate models in a unified generalized method of moments framework is Chan et al. (1992). They carry out a parametric estimation of some of the drivers of the short-rate process, and find constant elasticity of variance models to perform best. Stanton (1997) discovers strong evidence for non-linearity in the short-rate drift. Statistically complex behaviour of short-rates is further supported by Ait-Sahalia (1996), who argues that the short rate should be close to a random walk in the middle of its historical range but strongly mean-reverting outside this range. In a similar fashion, Bekaert and Ang (1998) and Bansal and Zhou (2002) find that a switch behaviour, with a reversion level and reversion speed for each regime, should be appropriate for the short-rate. The multifactor affine equilibrium term structure models, first introduced by Duffie and Kan (1996) and Duffee (2002), are concerned with the dynamics of the full yield curve, as opposed to the typical short-rate focus of the single-factor model. The multifactor models have gained attention, due to their affine structure and ability to model yields of all maturities under various assumptions about the risk premium. A shortcoming of these models, however, is a common assumption of stationary state variables. As for most financial variables, yields have time-varying covariances, but this stylized fact cannot yet be accommodated by the affine multifactor term structure models.
Gray (1996) investigates the dynamics of the short-term interest rate and concludes that a model of time-varying mean reversion and time-varying GARCH effects is appropriate. Similarly, Dayioğlu (2012) and Hassani et al. (2020) implement GARCH models and find that asymmetric models with skewed error distributions are better than symmetric models. Ang and Bekaert (2002), Dai et al. (2007) and Bansal and Zhou (2002) focus on regime-switches in the parameters characterizing the mean, the mean-reversion speed and the volatility of the short rate process and generally find support for the presence of two volatility states. Deguillaume et al. (2013) take a slightly different approach. Instead of focusing on heteroscedasticity or time-varying model parameters, they use data from several currencies and find that the observed dependence of the magnitude of rate changes on the level of rates is a function with three regimes; approximate log-normal behaviour for high and low rates and normal at the intermediate level. Similarly, Meucci and Loregian (2016) assumes two level-dependent regimes for interest rates; where high rates are normally distributed and low rates are log-normally distributed.
As for the cross-sectional variation of yields, Litterman and Scheinkman (1991) were the first to point out that eigenvectors and eigenvalues convey interest summary information about the underlying yield curve dynamics, and introduced the interpretation of the first three principal components as level, slope and curvature factors, respectively. Since the seminal contribution of Ang and Piazzesi (2003), PCA has been the building blocks of discrete time term structure models (Adrian et al., 2013; Bauer & Rudebusch, 2016; Cochrane & Piazzesi, 2008; Hamilton & Wu, 2012; Joslin et al., 2011).Footnote 8 Although these models have proved to be relatively successful for predicting yields and are able to disentangle risk-neutral yields and term premia, estimating interest rate distributions is not their primary purpose. Estimating interest rate distributions through risk factor simulation, such as PCA, is relatively unexplored. Hagenbjörk and Blomvall (2019), who use a Copula-GARCH approach to simulate yields, is a notable exception. Their focus, however, is to investigate the accuracy of alternative methods for interpolating forward rates, which is a different topic than what is covered in this paper.
To model the conditional dynamics of the entire yield curve, multifactor volatility models are needed. Multivariate stochastic volatility models (Harvey et al., 1994), which specify that the conditional variance matrix depends on some unobserved or latent process rather than on past observations, have gain limited attraction in practice due to the complexity of estimation. Multivariate GARCH models jointly estimate the univariate heteroscedastic process of the risk factors and their correlations. Bauwens et al. (2006) and Boudt et al. (2019) survey this class of models, and classify them into three categories; direct generalizations of the univariate GARCH model (Bollerslev et al., 1988), linear combinations of univariate GARCH models (Van der Weide, 2002) and non-linear combinations of univariate GARCH models (Bollerslev, 1990; Colacito et al., 2011; Engle, 2002; Tse & Tsui, 2002).
2.2 Quantile regression
Quantile regression, introduced by Koenker and Bassett Jr. (1978), has found a number of applications within risk management. Taylor (1999) finds that a quantile regression approach delivers a better fit to multi-period data when forecasting volatility compared to variations of the GARCH(1,1) model. In a comparable setting, Taylor (2000) finds that an artificial neural network yields better results when estimating the tails of the distribution compared to a linear quantile regression model. The Conditional Autoregressive Value at Risk (CAViaR) approach developed by Engle and Manganelli (2004) models VaR as an autoregressive process and involve an explicit modeling of the dynamics of the conditional quantile. Huang et al. (2011) use quantile regression to forecast foreign exchange rate volatility. Their proposed model performs better in-sample than a number of benchmark models in a nineteen year sample of daily data on nine currency pairs. Chen et al. (2012) forecast VaR using the intraday range of stock market indices and exchange rates in a nonlinear quantile regression model. Haugom et al. (2016) propose a parsimonious quantile regression model to forecast day-ahead value-at-risk across asset classes which performs comparably well to the more complicated CAViaR model. Pradeepkumar and Ravi (2017) analyze a set of machine learning algorithms with the purpose of forecasting volatility of financial variables using quantile regression. They use foreign exchange rate data, among other financial variables, and find that a Particle Swarm Optimization (PSO)-trained Quantile Regression Neural Network performs best. Christou and Grabchak (2019) estimate a non-iterative quantile regression model on five US stock market indices. Taylor (2019) jointly estimates VaR and ES in a CAViaR-framework using maximum likelihood. Ghysels et al. (2016) incorporate quantile regression in the MIDAS framework.
3 Data
For the empirical investigation, we use a dataset recently developed by Liu and Wu (2021).Footnote 9 The authors provide U.S. Treasuries zero coupon yields with maturities ranging from 1 month to 30 years, from 1961 to 2020. They report smaller pricing errors in the short end of the curve, compared to the frequently analysed GSW-dataset (Gürkaynak et al., 2007). Due to missing observations in the long end of the curve, we start our sample in 1985.
Zero coupon yields as reported by Liu and Wu (2021), 1985/01–2019/12
The descriptive statistics in Table 1 and a visual inspection of Fig. 1 confirm the stylized facts typically observed for yields: level, slope and curvature is time-varying; yields are correlated and highly persistent; short-term rates are more volatility than long-term rates. As evident from Fig. 1, yields have generally declined during this period. Bernanke (2013) assigns this long-run decline in yields to cyclical factors, including the slow pace of economic recovery, modest inflation rates, and accommodative monetary policy. Jotikasthira et al. (2015) points to lower term premia in long-term yields. Although yields of different maturities tend to move in the same direction, the slope of the yield curve has varied over time. The yield curve is typically upward sloping, but the slope has been negative at some occasions, such as during the global financial turbulence in 2008. These dynamics are consistent with an interpretation of the yield curve slope as a recession indicator.Footnote 10
The sample covers important economic events; such as the 1987 stock market crash, the Asian crisis, the dot.com asset pricing bubble in the beginning of this century, the global financial crisis initiated by the Lehman-brothers default, the euro sovereign and banking crises as well as the recent period of quantitative easing and unprecedentedly low rates.
4 Methodology
4.1 Conditional volatility of PCs as risk factors
The density of yields has complex statistical characteristics, with time-varying moments and regime switching behaviour. Still, due to high persistence and correlations, PCA typically explains most of the cross-sectional variation of yields.Footnote 11 Furthermore, low-dimensional PCA-based term structure models provide accurate fit to observed yields. Thus, PCs lend themselves to parsimonious risk model specifications.
To motivate our choice of risk factors backed out of PCs, we briefly sketch the main principles in the application of PCA to term structure modeling: the matrix X contains \(T \times n\) demeaned changes in yields, where T is the number of time points and n is the number of yield maturities. PCA is performed on V, the covariance matrix of X.The matrix X in the new referential of the PCs is given by
where W is the \(n \times n\) orthogonal matrix of eigenvectors of V. Note that W is ordered so that its first column is the eigenvector corresponding to the largest eigenvalue of V, and the last column corresponding to the smallest eigenvalue. Using only k principal components to represent the variability in X, we consider the \(T \times k\) matrix, P*, which is given by the first k columns of P.
The \(n \times n\) covariance matrix of yield log-changes X, with \(n(n+1)/2\) different elements, is obtained from k different conditional variance estimates. For instance, in the \(n=360\) dataset reported by Liu and Wu (2021), we only need to compute three conditional variances of principal components to obtain time varying estimates of more than several thousand covariances and variances.
Since the PCs are uncorrelated by construction, their unconditional covariance matrix is diagonal. This is however not necessarily the case for their conditional covariance matrix. Generally, multivariate conditional volatility models decompose the conditional covariance matrix of returns \({{\textbf {V}}}_t\) as
where \({{\textbf {D}}}_t\) is the diagonal matrix of conditional volatility standard deviations and \({{\textbf {C}}}_t\) is the correlation matrix.Footnote 12
Subsequent to the seminal contributions of Engle (1982) and Bollerslev (1986), the GARCH family of models have proven successful in capturing heteroscedasticity across asset classes. We apply the multivariate exponentially weighted moving average (EWMA) model, which is defined as
with individual elements of \({\hat{\Sigma }}_{t}\) given by
In the previous equations, \({\hat{\Sigma }}_{t} = [{\hat{\sigma }}_{t,ij}]_{i,j = 1, 2, \ldots, n}\) represents the estimate of the covariance matrix for period t, \(y_{t} = [y_{t,i}]_{i = 1, 2, \ldots, n} ^T\) is the vector of the yield log-changes for period t, and \(0< \lambda < 1\) is the decay factor. EWMA can be seen as a restricted iGARCH model, with \(\beta = \lambda\) and \(\alpha = 1-\lambda\). The main reasons for choosing EWMA over other more flexible alternatives are parsimony and ease of implementation.
4.2 Quantile regression
The Quantile Regression method originally introduced by Koenker and Bassett Jr. (1978), is particularly well suited for the purpose of our approach.Footnote 13 QREG does not require complex optimization routines, is relatively simple to estimate and can readily be applied by practitioners. Also, QREG has a parsimonious specification, which reduces the risk of overfitting and biased parameter estimates. Furthermore, the flexible nature of QREG does not require specific parametric assumptions on the explanatory variables themselves nor the residuals. Regression quantile estimates are known to be robust to outliers, a desirable feature in general and for application to financial data in particular.
In the general case, the simple linear quantile regression model is given by
where the distribution of \(\epsilon _{q}\) is left unspecified.Footnote 14 The expression for the conditional q quantile, with \(0< q < 1\), is defined as a solution to the minimization problem (Koenker & Bassett Jr., 1978),
where
The Least Absolute Error (the conditional mean) is a special case, but the quantile regression method explicitly allows one to model all relevant quantiles of the distribution of the dependent variable.
4.3 The PCA-QREG model
In our proposed model, the conditional quantile function \(\Delta {\hat{y}}_{\tau ,t+1,T\mid t}\) can be expressed as
where \(\Delta {\hat{y}}\) is the yield log-change, \(\tau\) is the quantile, t is calendar time and T is time to maturity of \(y\). A unique vector of regression parameters \([{\hat{\alpha }}_{\tau ,t}, {\hat{\beta }}_{\tau ,t}^{{\mathrm{PC}}_1}, {\hat{\beta }}_{\tau ,t}^{{\mathrm{PC}}_2}, {\hat{\beta }}_{\tau }^{{\mathrm{PC}}_3}]\) is obtained for each quantile of interest. Estimates of conditional PC volatilities, \(\sigma ^{{\mathrm{PC}}_i}_{t}\) with \(i=1, 2, 3\), are obtained from the EWMA model defined in Eq. (1). Hence the whole distribution of yield-changes can be found by using conditional volatilities of PCs as predictors in the estimated quantile regression model.
The PCA-QREG model accommodates the empirical findings of Deguillaume et al. (2013). They show that interest rate volatility is dependent on interest rate levels in certain regimes. For low rates, below 2%, and for high rates, above 6%, volatility increases proportionally to the interest rate level. In the intermediate 2–6% range, however, interest rate volatility does not seem to depend on the interest rate level. Although these findings of regime switching behaviour are interesting, we choose to model interest rate volatility separated from interest rate levels. If volatility is dependent on the current regime, a volatility model based on actual principal component changes will capture this behavior for these different regimes indirectly. This approach works regardless of the regime, even under negative interest rates. Furthermore, the inherent flexibility of the quantile regression specification, which does not make parametric assumptions about dependent or independent variables, is well adapted to the stylized facts reported by Deguillaume et al. (2013).
The PCA-QREG approach is computationally highly effective, due to the combination of PCA and EWMA as the basis for conditional risk estimates. Furthermore, the approach carries additional practical advantages: the number of principal components k can be changed to control approximations from the model, depending on the statistical characteristics of the specific yield curve under consideration - for instance, to reduce noise in conditional yield correlations. Moreover, since it is based on PCA, PCA-QREG quantifies how much risk is associated with each systematic risk factor. In term structures, the three first principal components have meaningful economic interpretation as systematic level, slope and curvature factors.Footnote 15 This can be an advantage for risk managers as their attention is directed towards the most important sources of risk.
5 Empirical investigation
In this section we test the empirical performance of the PCA-QREG model out-of-sample. First, we investigate the ability of the model to provide accurate univariate estimates for key maturities in the term structure. We proceed to illustrate the PCA-QREG’s practical applicability for Value-at-Risk (VaR) estimation and benchmark the model to historical simulation—which is the most frequently applied VaR-model by practitioners.
5.1 Risk factor modeling
PCA on zero coupon yields as reported by Liu and Wu (2021), 1985/01–2019/12. The left panel shows the shape of the eigenvectors of the first three PCs. The right panel shows the contribution of the first three PCs in explaining total cross-sectional yield variation
Figure 2 displays the results from PCA on log-changes of zero-coupon yields reported by Liu and Wu (2021) over the full sample period 1985/11–2019/12 and broadly concur to typical findings in the literature. The left panel shows eigenvectors of the first three components. The first principal component (PC1) impacts all rates more or less by the same magnitude and can thus be considered a level factor. PC2 switches sign as maturity increases and impact short rates differently than long rates, which supports the interpretation of the second PC as a slope factor. PC3, while having negative loading on intermediate rates, has positive loadings on short- and long term rates, which indicates that the third PC can be viewed as a curvature factor. The right panel shows that the first three PCs explain most of the cross-sectional variation of yields.
5.2 Out-of-sample testing
The estimation procedure at each t is as follows: For each i, with \(i=1,2,3\), we compute the principal components of yield log-changes, \(\text{PC}_{t-w:t}^{i}\). From this, we filter the principal component conditional volatilities, \({\sigma ^{{\mathrm{PC}}i}_{t-w:t}}\), over the estimation window using the multivariate EWMA specification. Quantile regression coefficients for all \(\tau\); \({\hat{\beta }}_{\tau ,t}^{{\mathrm{PC}}i}\) can then be estimated, by regressing conditional volatilities of PCs on yield log-changes. Finally, \(t+1\) distributional yield estimates are obtained from the PCA-QREG model defined in (4).
We use a moving estimation window w of 4000 observations. The first estimation window starts in 1985/11/25 and ends 2001/12/03, which implies that the first out-of-sample estimates are for 2001/12/04. We repeat the procedure until 2019/12/31, which leads to 4513 daily out-of-sample estimates in total.
To balance accuracy and bias, we use three PCs, \(\textit{k} = 3\). The EWMA persistence parameter, \(\lambda\), is fixed and set equal to 0.98.
5.2.1 Univariate tests of key maturities
The main purpose of the PCA-QREG model is to provide multivariate conditional density forecasts characterising the full yield curve, since this is a necessity in daily interest rate risk management. Still, the model should provide accurate univariate estimates for all points of the curve. To investigate this we use the standard approach for backtesting.Footnote 16 In our study this involves recording the number of occasions over the sample period where the realized return exceeds the quantile estimate from the PCA-QREG model, and comparing this number to the prespecified level.
According to Christoffersen (2011), a proper model should satisfy two conditions: (i) the number of exceedances should be as close as possible to the number implied by the quantile, and (ii) the exceedances should be randomly distributed across the sample, meaning that we observe no clustering of exceedances. In other words, we want to avoid that the model overestimates or underestimates the number of exceedances in certain periods. To test both conditions, we employ the unconditional test of Kupiec (1995) and the conditional coverage test of Christoffersen (1998).Footnote 17
Table 2 shows that PCA-QREG model performs well for most maturities and quantiles in terms of estimating the unconditional distribution, as the hit-% from the model is fairly close to the prescribed quantiles. This is confirmed in Table 3, which reports p-values for the Kupiec (1995) and Christoffersen (1998) coverage tests evaluated in the tails of the distributions. High p-values support the null-hypothesis of correctly specified models for most of the yields investigated, which implies that the PCA-QREG model is able to provide dynamically accurate distributional estimates. The exception is the 3 months yield, for which the PCA-QREG model appears to be misspecified. From the left panel of Fig. 3 it becomes evident that the model is only partly able to capture the dynamics of the short end of the yield curve. There are several likely explanations for this. First and foremost, the literature has well documented the difficulties of calibrating short-rate models, due to structural shifts and time varying stochasticity of the short rate. The EWMA conditional volatility model that we apply in this study might not be flexible enough. This is especially relevant when taking the fairly long out-of-sample period of nearly 20 years into account, since the sample most likely contains structural shifts which cannot be econometrically easily accommodated. Also, the 2009–2016 period, where short-rates were close to the zero lower bound, seems to be especially problematic. These unprecedentedly low levels might cause difficulties for any time-series based model. Also, at levels close to zero, even modest basispoint volatility will create high lognormal volatility.Footnote 18 Notably, as illustrated in the right panel of Fig. 3, the PCA-QREG model does not seem to suffer from the same problem at the long end of the curve—possibly due to the fact that long-term rates have been higher than the shortest rates.
5.2.2 Empirical application
In this section, we evaluate the accuracy of VaR estimates from the PCA-QREG model and compare to those from the historical simulation (HS) benchmark model. For this purpose, we analyze the daily returns on a portfolio equally invested in 3 months, 1 year, 5 years, 10 years and 30 years securities.
The relation between the yield \(y^{(n)}_{t}\) and log-price \(p^{(n)}_{t}\) of a n-year discount bond at time t is given by
The log holding period return from buying a n-year bond at time t and selling it as a \(n-1\) year bond at time \(t+1\) is
Hence, the return \(w_{t+1}\) on the equally weighted portfolio of j bonds with maturity \(n \in N\) is
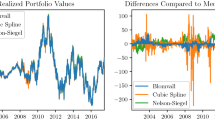
We estimate VaR for the assumed portfolio using the historical simulation method and the PCA-QREG model. Under historical simulation, the \(\text{VaR}_t^\tau\) estimate is the \(\tau\)-th quantile of the historical return distribution for the hypothetical portfolio over estimation period, covering \(w = 4000\) observations from time t. To estimate \(\text{VaR}_t^\tau\) from the PCA-QREG model, we start by estimating conditional yield estimates from Eq. (6). We then revalue the bond portfolio using Eq. (7) and compute daily returns from Eq. (9). The resulting VaR-estimates for the 5% quantile are displayed in Fig. 4. This figure reveals that the PCA-QREG model is significantly better at estimating the conditional dynamics of the bond portfolio then the HS model. The HS model is unable to capture the heteroscedasticity of yields, and the resulting VaR-estimates are consequently too stable. The PCA-QREG model on the other hand, is able to adapt to changing market conditions and adjust VaR-estimates correspondingly.
To statistically compare the HS and PCA-QREG models, we use the asymmetric loss function of González-Rivera et al. (2004):
where \(d_t^{\tau } = {\mathbbm {1}} (y_t<\text{VaR}_t^\tau )\) is the \(\tau\) quantile loss function and \({\mathbbm {1}}\) is the indicator function. We compute VaR losses using (10) for the HS and PCA-QREG models respectively. We then apply the modified Diebold–Mariano (DM) test (Diebold & Mariano, 1995; Harvey et al., 1997) to verify whether the PCA-QREG model provides significantly more precise VaR-estimates than the HS model, as measured by the VaR loss function in (10). Table 4 shows p-values for the DM-test of VaR estimates at different quantiles. The null hypothesis in the DM test is that the PCA-QREG and HS models have equal predictive ability. p-values from the DM-test support the alternative hypothesis—the PCA-QREG is the better performer.
6 Discussion and conclusion
Interest rate risk management is a core activity in the asset-liability management of banks. Banks have long and short exposures along all maturities, and there is a need to model and forecast possible future outcomes for the whole yield curve. This multivariate distributional forecast is very challenging due to complex yield curve dynamics, and there is no consensus with regards to consistent and appropriate risk modelling of interest rates. Hence, there is a need for parsimonious models which are able to capture time-varying market dynamics and provide accurate forecasts of yield distributions, while retaining interpretability and simplicity in application.
In this paper we combine principal component analysis and quantile regression and propose the PCA-QREG model, which alleviates some of these issues. We first model the main principal components of the yield curve, calculate their volatilities using exponential weighted moving averages and then let these be explanatory variables in a quantile regression model. The volatilities of the first three principal components have meaningful economic interpretations as they describe the variations of level-, slope,- and curvature factors, respectively. In this way, we have a risk model where risk factors can be explained and where stress testing/scenario analysis can be directly applied. Further, we document that the volatility of these principal components carry predictive information relevant for predicting yield curve distributions. Trough extensive out-of-sample testing over a sample period that covers multiple major global economic events, we show that the model is robust and generally provides accurate forecasts, most notably in the tails of the yield distributions—which are most important for risk management purposes. In sum, we propose a risk model for interest rates that contains economic intuition, transparency, is easy to implement and understand, and also displays excellent out of sample performance.
There are several directions for further research. One is to apply this framework to other financial markets, such as commodities. Consumers, producers and traders in these markets have great need for consistent modelling and forecasting of futures curves. These market participants need to predict the distributions of futures prices (hence risk) for all sets of maturities, mapping their long and short positions in these contracts. Here, higher order principal components (and their volatilities) might be included, to capture seasonality effects. The performance of our model for these markets remains an open question. Another direction is to adopt other methods for modelling the volatility of the principal components (e.g. use more advanced multivariate GARCH models) and establish more tests for out of sample distributions. Furthermore, non-linear quantile regression models might prove appropriate.
Data availability
The data analyzed in the current study is publicly available at https://sites.google.com/view/jingcynthiawu.
Notes
The granularity of the time buckets depends on preferences. In practice, quarterly frequency is often applied in the short end of the yield curve and annual thereafter.
A representative example of this class of models is the LIBOR Market Model (LMM) (Brace et al., 1997; Jamshidian, 1997). Although LMM is typically calibrated in the risk-neutral measure for the purpose of derivatives pricing, LMM can be calibrated in the empirical measure using Kalman-filtering. However, it has proven difficult to calibrate the model when yields are close to zero, which is currently the case in many currencies.
Among the financial institutions that disclose their methodology, 73% use historical simulation to estimate Value-at-Risk (Pérignon & Smith, 2010).
Stress testing is often advocated by regulators, see for example the Fundamental Review of the Trading Book (FRTB), newly issued by the Basel Committee: https://www.bis.org/bcbs/publ/d457.htm.
An implementation to estimate the PCA-QREG model and replicate the results in this paper can be found in this GitHub repository: https://github.com/MortenRisstad/PCAQREG.
The spanning problem—whether inclusion of explanatory variables beyond the PCs of the yield curve increase the predictability of yields—is still under academic debate (Bauer & Hamilton, 2018).
The dataset is publicly downloadable from the author’s website: https://sites.google.com/view/jingcynthiawu.
The Federal Bank of New York reports that the slope of the yield curve can predict US recessions and financial crises (Fed, 2021).
The same applies to other groups of financial variables, such as commodity term structures and volatility surfaces—see Alexander (2009a) for applications.
In the Constant Conditional Correlation model of Bollerslev (1990), \({{\textbf {C}}}_t\) is a historical (realized) correlation matrix. In the Dynamic Conditional Correlation model of Engle (2002), \({{\textbf {C}}}_t\) is an exponentially weighted moving average (EWMA) correlation matrix. In the GO-GARCH specification (Van der Weide, 2002), \({{\textbf {D}}}_t\) is the conditional volatility of principal components whereas \({{\textbf {C}}}_t\) is the identity matrix.
This is different than a standard error term because its distributional properties are not required to meet the same criteria as those in standard regression models.
Backtesting refers to testing the accuracy of a model over a historical period when the true outcome is known.
See Appendix for further details.
1 basispoint change in yields is relatively more at low rates than at high rates.
References
Adrian, T., Crump, R. K., & Moench, E. (2013). Pricing the term structure with linear regressions. Journal of Financial Economics, 110(1), 110–138.
Ait-Sahalia, Y. (1996). Testing continuous-time models of the spot interest rate. The Review of Financial Studies, 9(2), 385–426.
Alexander, C. (2009a). Market risk analysis, quantitative methods in finance (Vol. 1). Wiley.
Alexander, C. (2009b). Market risk analysis, value at risk models (Vol. 4). Wiley.
Ang, A., & Bekaert, G. (2002). Regime switches in interest rates. Journal of Business & Economic Statistics, 20(2), 163–182.
Ang, A., & Piazzesi, M. (2003). A no-arbitrage vector autoregression of term structure dynamics with macroeconomic and latent variables. Journal of Monetary economics, 50(4), 745–787.
Bansal, R., & Zhou, H. (2002). Term structure of interest rates with regime shifts. The Journal of Finance, 57(5), 1997–2043.
Bauer, M. D., & Hamilton, J. D. (2018). Robust bond risk premia. The Review of Financial Studies, 31(2), 399–448.
Bauer, M. D., & Rudebusch, G. D. (2016). Monetary policy expectations at the zero lower bound. Journal of Money, Credit and Banking, 48(7), 1439–1465.
Bauwens, L., Laurent, S., & Rombouts, J. V. (2006). Multivariate GARCH models: A survey. Journal of Applied Econometrics, 21(1), 79–109.
Bekaert, G., & Ang, A. (1998). Regime switches in interest rates. NBER Working Paper, (w6508).
Bernanke, B. (2013). Long-term interest rates: A speech at the annual monetary/macroeconomics conference: The past and future of monetary policy, sponsored by Federal Reserve Bank of San Francisco, San Francisco, California, March 1, 2013. Technical report, Board of Governors of the Federal Reserve System (US).
Bianchetti, M., &Morini, M. (2013). Interest rate modelling after the financial crisis. In M. Morini, & M. Bianchetti (Eds.) Risk books (Vol. 11).
Black, F. (1976). The pricing of commodity contracts. Journal of Financial Economics, 3(1–2), 167–179.
Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, 31(3), 307–327.
Bollerslev, T. (1990). Modelling the coherence in short-run nominal exchange rates: A multivariate generalized arch model. The Review of Economics and Statistics, 498–505.
Bollerslev, T., Engle, R. F., & Wooldridge, J. M. (1988). A capital asset pricing model with time-varying covariances. Journal of Political Economy, 96(1), 116–131.
Boudt, K., Galanos, A., Payseur, S., & Zivot, E. (2019). Multivariate GARCH models for large-scale applications: A survey. In Handbook of statistics (Vol. 41, pp. 193–242). Elsevier.
Brace, A., Gatarek, D., & Musiela, M. (1997). The market model of interest rate dynamics. Mathematical Finance, 7(2), 127–155.
Chan, K. C., Karolyi, G. A., Longstaff, F. A., & Sanders, A. B. (1992). An empirical comparison of alternative models of the short-term interest rate. The Journal of Finance, 47(3), 1209–1227.
Chen, C. W., Gerlach, R., Hwang, B. B., & McAleer, M. (2012). Forecasting value-at-risk using nonlinear regression quantiles and the intra-day range. International Journal of Forecasting, 28(3), 557–574.
Christoffersen, P. (2011). Elements of financial risk management. Academic Press.
Christoffersen, P. F. (1998). Evaluating interval forecasts. International Economic Review, 841–862.
Christou, E., & Grabchak, M. (2019). Estimation of value-at-risk using single index quantile regression. Journal of Applied Statistics, 46(13), 2418–2433.
Cochrane, J. H., & Piazzesi, M. (2008). Decomposing the yield curve. Unpublished working paper. University of Chicago.
Colacito, R., Engle, R. F., & Ghysels, E. (2011). A component model for dynamic correlations. Journal of Econometrics, 164(1), 45–59.
Dai, Q., Singleton, K. J., & Yang, W. (2007). Regime shifts in a dynamic term structure model of us treasury bond yields. The Review of Financial Studies, 20(5), 1669–1706.
Dayioğlu, T. (2012). Forecasting overnight interest rates volatility with asymmetric GARCH models. Journal of Applied Finance & Banking, 2(6), 151–162.
Deguillaume, N., Rebonato, R., & Pogudin, A. (2013). The nature of the dependence of the magnitude of rate moves on the rates levels: A universal relationship. Quantitative Finance, 13(3), 351–367.
Diebold, F., & Mariano, R. (1995). Comparing predictive accuracy. Journal of Forecasting, 13.
Diebold, F. X., & Rudebusch, G. D. (2013). Yield curve modeling and forecasting: The dynamic Nelson–Siegel approach. Princeton University Press.
Duffee, G. R. (2002). Term premia and interest rate forecasts in affine models. The Journal of Finance, 57(1), 405–443.
Duffie, D., & Kan, R. (1996). A yield-factor model of interest rates. Mathematical Finance, 6(4), 379–406.
Engle, R. (2002). Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business & Economic Statistics, 20(3), 339–350.
Engle, R. F. (1982). Autoregressive conditional heteroscedasticity with estimates of the variance of united kingdom inflation. Econometrica: Journal of the Econometric Society, 987–1007.
Engle, R. F., & Manganelli, S. (2004). CAViaR: Conditional autoregressive value at risk by regression quantiles. Journal of Business & Economic Statistics, 22(4), 367–381.
Fed, N. Y. (2021). The yield curve as a leading indicator.
Ghysels, E., Plazzi, A., & Valkanov, R. (2016). Why invest in emerging markets? The role of conditional return asymmetry. The Journal of Finance, 71(5), 2145–2192.
González-Rivera, G., Lee, T.-H., & Mishra, S. (2004). Forecasting volatility: A reality check based on option pricing, utility function, value-at-risk, and predictive likelihood. International Journal of Forecasting, 20(4), 629–645.
Gray, S. F. (1996). Modeling the conditional distribution of interest rates as a regime-switching process. Journal of Financial Economics, 42(1), 27–62.
Gürkaynak, R. S., Sack, B., & Wright, J. H. (2007). The us treasury yield curve: 1961 to the present. Journal of Monetary Economics, 54(8), 2291–2304.
Hagenbjörk, J., & Blomvall, J. (2019). Simulation and evaluation of the distribution of interest rate risk. Computational Management Science, 16(1), 297–327.
Hamilton, J. D., & Wu, J. C. (2012). Identification and estimation of Gaussian affine term structure models. Journal of Econometrics, 168(2), 315–331.
Harvey, A., Ruiz, E., & Shephard, N. (1994). Multivariate stochastic variance models. The Review of Economic Studies, 61(2), 247–264.
Harvey, D., Leybourne, S., & Newbold, P. (1997). Testing the equality of prediction mean squared errors. International Journal of Forecasting, 13(2), 281–291.
Hassani, H., Yeganegi, M. R., Cuñado, J., & Gupta, R. (2020). Forecasting interest rate volatility of the united kingdom: Evidence from over 150 years of data. Journal of Applied Statistics, 47(6), 1128–1143.
Haugom, E., Ray, R., Ullrich, C. J., Veka, S., & Westgaard, S. (2016). A parsimonious quantile regression model to forecast day-ahead value-at-risk. Finance Research Letters, 16, 196–207.
Heath, D., Jarrow, R., & Morton, A. (1992). Bond pricing and the term structure of interest rates: A new methodology for contingent claims valuation. Econometrica: Journal of the Econometric Society, 77–105.
Huang, A. Y., Peng, S.-P., Li, F., & Ke, C.-J. (2011). Volatility forecasting of exchange rate by quantile regression. International Review of Economics & Finance, 20(4), 591–606.
Hull, J., & White, A. (1990). Pricing interest-rate-derivative securities. The Review of Financial Studies, 3(4), 573–592.
Jacobs, M., Jr. (2017). A mixture of distributions model for the term structure of interest rates with an application to risk management. American Research Journal of Business and Management, 3, 1–17.
Jamshidian, F. (1997). Libor and swap market models and measures. Finance and Stochastics, 1(4), 293–330.
Joslin, S., Singleton, K. J., & Zhu, H. (2011). A new perspective on Gaussian dynamic term structure models. The Review of Financial Studies, 24(3), 926–970.
Jotikasthira, C., Le, A., & Lundblad, C. (2015). Why do term structures in different currencies co-move? Journal of Financial Economics, 115(1), 58–83.
Koenker, R. (2017). Quantile regression: 40 years on. Annual Review of Economics, 9, 155–176.
Koenker, R., & Bassett Jr., G. (1978). Regression quantiles. Econometrica: Journal of the Econometric Society, 33–50.
Koenker, R., & Hallock, K. F. (2001). Quantile regression. Journal of Economic Perspectives, 15(4), 143–156.
Kupiec, P. (1995). Techniques for verifying the accuracy of risk measurement models. The Journal of Derivatives, 3(2).
Litterman, R., & Scheinkman, J. (1991). Common factors affecting bond returns. Journal of Fixed Income, 1(1), 54–61.
Liu, Y., & Wu, J. C. (2021). Reconstructing the yield curve. Journal of Financial Economics.
Meucci, A., & Loregian, A. (2016). Neither “normal’’ nor “lognormal’’: Modeling interest rates across all regimes. Financial Analysts Journal, 72(3), 68–82.
Pérignon, C., & Smith, D. R. (2010). The level and quality of value-at-risk disclosure by commercial banks. Journal of Banking & Finance, 34(2), 362–377.
Pradeepkumar, D., & Ravi, V. (2017). Forecasting financial time series volatility using particle swarm optimization trained quantile regression neural network. Applied Soft Computing, 58, 35–52.
Rebonato, R. (2018). Bond pricing and yield curve modeling: A structural approach. Cambridge University Press.
Stanton, R. (1997). A nonparametric model of term structure dynamics and the market price of interest rate risk. The Journal of Finance, 52(5), 1973–2002.
Taylor, J. W. (1999). A quantile regression approach to estimating the distribution of multiperiod returns. The Journal of Derivatives, 7(1), 64–78.
Taylor, J. W. (2000). A quantile regression neural network approach to estimating the conditional density of multiperiod returns. Journal of Forecasting, 19(4), 299–311.
Taylor, J. W. (2019). Forecasting value at risk and expected shortfall using a semiparametric approach based on the asymmetric Laplace distribution. Journal of Business & Economic Statistics, 37(1), 121–133.
Tse, Y. K., & Tsui, A. K. C. (2002). A multivariate generalized autoregressive conditional heteroscedasticity model with time-varying correlations. Journal of Business & Economic Statistics, 20(3), 351–362.
Van der Weide, R. (2002). GO-GARCH: A multivariate generalized orthogonal GARCH model. Journal of Applied Econometrics, 17(5), 549–564.
Funding
Open access funding provided by NTNU Norwegian University of Science and Technology (incl St. Olavs Hospital - Trondheim University Hospital). The research presented in this paper is partly funded by Sparebank 1 Markets.
Author information
Authors and Affiliations
Contributions
The authors are grateful to Abhiroan Parashar, who in his Master’s thesis submitted to NTNU in 2021, initially explored the concepts developed in this paper. The thesis was jointly co-supervised by all authors. RP: methodology, validation, writing—reviewing and editing. MR: data curation, methodology, formal analysis, interpretation, implementation, writing—original draft. SW: conceptualization, methodology, validation.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Unconditional coverage test
The Kupiec (1995) test is a likelihood ratio test designed to reveal whether a VaR model provides the desirable unconditional coverage. For a long position, the daily VaR will be a negative number, and we define an indicator sequence as follows:
If the return is more negative than the long VaR estimate on a given day, we count an exceedance.
Under the null hypothesis that the number of exceedances is equal to the prespecified VaR, the test statistic is (Kupiec, 1995):
where \(n_{1}\) and \(n_{0}\) is the number of exceedances and non-exceedances, respectively. \(\pi _{{\mathrm{exp}}} = p\) is the expected proportion of exceedances, while \(\pi _{{\mathrm{obs}}} = n_{1}/(n_{0}+n_{1})\) represents the observed fraction of exceedances. The asymptotic distribution of \(-2\ln (\text{LR}_{\text{UC}})\) is \(\chi ^{2}\) with one degree of freedom.
1.2 Conditional coverage test
The unconditional test does not take into account whether several violations occur in rapid succession or if they tend to be isolated. Christoffersen (1998) extended the Kupiec test and proposed a joint test for correct coverage and for the detection of whether a quantile exceedance today has implications for the probability of a quantile exceedance tomorrow. Under the null hypothesis that the number of violations is equal to the prespecified VaR and the violations are randomly distributed, the test statistic is:
where \(n_{ij}\) denotes the number of times an indicator variable with value i is immediately followed by an indicator variable with value j. Further, \(\pi _{01} = n_{01}/(n_{00}+n_{01})\), \(\pi _{11} =n_{11}/(n_{10}+n_{11})\) and the rest of the notation is as described for the Kupiec test. The test statistic follows a \(\chi ^{2}\) distribution with two degrees of freedom. As a practical matter, one may incur samples where \(\pi _{11} = 0\). In this case, the test statistic is stated as Christoffersen (2011):
A drawback of the conditional coverage test of Christoffersen is that the test only takes into account one violation immediately followed by another, ignoring all other patterns of clustering.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pimentel, R., Risstad, M. & Westgaard, S. Predicting interest rate distributions using PCA & quantile regression. Digit Finance 4, 291–311 (2022). https://doi.org/10.1007/s42521-022-00057-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42521-022-00057-7