Adaptive weights clustering of research papers

Abstract

The JEL classification system is a standard way of assigning key topics to economic articles to make them more easily retrievable in the bulk of nowadays massive literature. Usually the JEL (Journal of Economic Literature) is picked by the author(s) bearing the risk of suboptimal assignment. Using the database of the Collaborative Research Center from Humboldt-Universität zu Berlin we employ a new adaptive clustering technique to identify interpretable JEL (sub)clusters. The proposed Adaptive Weights Clustering (AWC) is available on http://www.quantlet.de/ and is based on the idea of locally weighting each point (document, abstract) in terms of cluster membership. Comparison with $k$-means or CLUTO reveals excellent performance of AWC.

1 Introduction

“Words are the new numbers”. This quote (Thorsrud 2018) expresses the insights into the power of the spoken, written or tweeted message in a plethora of applications, social networks and academic discourse. The academic publication industry offers us a rich portfolio of research work in variety of outlets like journals, books or epub platforms. The mass of textual data requires pre-structuring in order to avoid the “needle in a haystack” problem that everybody seems to have when one looks for specific information, e.g. in a particular domain of a scientific discipline. This is one of the major reasons why abstracts as condensed information of a full research document are required and that is why, e.g. economic papers are classified according to JEL codes. The JEL classification system originated with the Journal of Economic Literature and is a standard method of classifying scholarly literature in the field of Economics (JEL Classification System 2011).

The assignment of such a classification code is done by authors manually and submitted together with a publication. This procedure bears risks. First, author(s) may not be aware of the “best fitting” JEL code in the sense of fast retrieval properties. Second, the spectrum of submitted codes may be too rich or too narrow. For the reasons described above we propose a clustering procedure that automatically assigns the JEL codes to submitted papers.

We analyze papers’ abstracts from the School of Business and Economics in Humboldt-Universität zu Berlin. Papers from 2005 to 2017 are stored on the CRC “Economic Risks” web page (Projects of the crc 649 2018) and have an open access. Besides the main information such as title, authors and date of issue, this web page stores for every paper its abstract and JEL codes given by the authors. By clustering this collection of documents in an unsupervised learning context we also identify the research directions and activity of economic research on certain topics. Comparing cluster sizes of certain topics will allow us to see whether research groups have biased activity relative to mainstream economic and digital finance research.

The topic distribution, its size and the origin of research group are particularly important in digital finance, where we observe a very dynamic development of new topics, erasing interest in older ones. Consequently the results presented here allow for efficient allocation of resources, especially in the research on digital finance.

Recently a non-parametric technique called Adaptive Weights Clustering (AWC) has emerged that showed a good performance on various artificial and real world examples (Efimov et al. 2019). How can we cluster texts? One needs to convert words into numbers. Examples of such numerization of texts into numbers abound, see e.g. Zhang et al. (2016) or Blei et al. (2003).

All the clustering methods will consider finding an accurate clustering structure as a demanding task, since all the documents belong to the economic risk domain. Off the shelf clustering technology is based on partitioning like the k-means (Hartigan and Wong 1979) and its variations. More advanced techniques include members of the CLUTO toolkit (Karypis 2002), but often require assumptions on data distribution or number of clusters. We propose and apply the AWC algorithm to cluster the abstracts of the papers and try to find a correlation between the resulting cluster structure and the JEL codes of the papers. In Efimov et al. (2019) a detailed comparison of AWC with the state-of-the-art algorithms [Spectral clustering with Normalized Cut (NCut) (Shi and Malik (2000)), Local Learning based Clustering Algorithm (LLCA) (Wu and Schölkopf (2007)), Clustering via Local Regression (CLOR) (Sun et al. (2008)), Regularized Local Reconstruction for Clustering (RLRC) (Sun et al. (2009)) and CLUTO toolkit (Karypis (2002))] is provided. AWC demonstrates a very good performance on a wide range of artificial and real life examples and outperforms the popular competitive procedures even after optimizing their tuning parameters.

In evaluating relative performance we compare AWC with the standard k-means clustering algorithm (Hartigan and Wong 1979) and the graph partitioning based algorithm from the CLUTO toolkit (Karypis 2002). Clustering via k-means is one of the most frequently used partitional clustering algorithms. The aim of the k-means algorithm is to divide M points in N dimensions into K clusters so that the sum of squares within clusters is minimized. It seeks a “local” optimal solution that no movement of a point from one cluster to another will reduce the within-cluster sum of squares (Hartigan and Wong 1979).

CLUTO (Karypis 2002) is a package for clustering low and high dimensional datasets. It provides different classes of algorithms based on partitional, agglomerative and graph-partitioning patterns. Agglomerative clustering is a bottom-up hierarchical clustering method which proceeds by starting with the individual instances and grouping the ones that have most similarities. It produces a sequence of partitions in which each partition is nested into the next partition in the sequence (Karypis et al. 1999).

As a result it constructs from the data a dendrogram, which displays the intermediate clustering assignments and the merging process. As a contrast to the agglomerative paradigm, graph partitioning algorithms perform a sequence of recursive splits until the desired number of clusters are found. CLUTO’s Metis graph partitioning based algorithms has been shown to produce high quality clustering results in high-dimensional datasets with low computational cost (Karypis and Kumar 1998). In comparing these mentioned cluster techniques we are able to show superior performance for AWC on our dataset.

This paper is organized as follows: Sect. 2 describes in details the Adaptive Weights Clustering algorithm and a heuristic for tuning of its parameter. In Sect. 3 the process of collecting documents and further preprocessing steps are carried out to prepare the data collection for cluster analysis. In Sect. 4 we choose clustering performance measures and define a true clustering structure for our data collection. The comparison of clustering methods and experimental results are shown in Sect. 5. Finally, a conclusion is given about the results of the papers main ideas. Some more details about numerical examples are postponed to Appendix.

2 Adaptive Weights Clustering

Adaptive Weights Clustering (AWC) is a non-parametric clustering technique based on separation via a likelihood ratio homogeneity detection test. Since a cluster is by definition a homogeneous region (without gaps). A direct advantage of this definition is that it does not require specifying number of clusters.

The clustering structure is conveniently described in terms of binary weights $w_{ij}$, where $w_{ij} =1$ indicates being points $X_i$ and $X_j$ in the same cluster, whereas $w_{ij} =0$ means that these points belong to different clusters. For each point $X_ i$, the associated cluster $C_{i}$ is given by the collection of positive weights $(w_{ij})$ over all $j$. The resulting symmetric matrix of weights $W$ consists of blocks of ones, where each block of ones describes one cluster.

AWC attempts to iteratively recover the weights $w_{ij}$ from the data. It starts with very local clustering structure $C_{i}^{(0)}$, that is, the starting positive weights $w_{ij}^{(0)}$ are limited to the closest neighbors $X_{j}$ of the point $X_{i}$ in terms of a distance $d(X_{i},X_{j})$. At each step $k \ge 1$, the weights $w_{ij}^{(k)}$ are recomputed by means of statistical “no gap” tests between $C_{i}^{(k-1)}$ and $C_{j}^{(k-1)}$, the local clusters on step $k-1$ for points $X_i$ and $X_j$ correspondingly. Only the neighbor pairs $X_{i}, X_{j}$ with $d(X_{i},X_{j}) \le h_{k}$ are checked, where the locality parameter $h_{k}$ and therefore the number of neighbors $X_{j}$ for each fixed point $X_{i}$ grow in each step. The resulting matrix of weights $W$ is used for the final clustering.

2.1 Clustering by adaptive weights

Let $\{X_{1},\ldots , X_{n}\} \subset {\mathbb {R}}^{p}$ be the set of all samples $X_{i}$, where the dimension $p$ can be very large or even growing. The proposed technique operates with a known distance or similarity matrix $\bigl ( d(X_{i},X_{j}) \bigr )_{i,j=1}^{n}$ only. Here the Euclidean norm is used: $d(X_{i},X_{j}) = \Vert X_{i} - X_{j} \Vert$, for $i,j=1,\ldots ,n$.

The procedure starts from a small scale and considers only points close to each other, then slowly increases the scale and finally considers all pairs of points. For each point $X_{i}$, weights $w_{ij}^{(k)}$ are computed using only points from the neighborhood of radius $h_{k}$ around $X_{i}$ and $X_{j}$. As the locality parameter $h_{k}$ increases with $k$, weights become more and more data driven during iterations.

A sequence of radii: A growing sequence of radii $h_{1} \le h_{2} \le \cdots \le h_{K}$ is fixed which determines how fast the algorithm will accelerate from very local structures to large scale objects. Each value $h_{k}$ can be viewed as a resolution (scale) of the method at step $k$. The average number of screened neighbors for each $X_{i}$ at step $k$ grows at most exponentially with $k \ge 1$.

Initialization of weights: On initialization each point is connected with its $n_0$ closest neighbors, where the proposed choice of $n_0 = 2 p+ 2$.

Updates at step k: Suppose that the first $k-1$ steps of AWC have been carried out. This results in collection of weights $\bigl \{ w_{ij}^{(k-1)}, \, {j=1,\ldots ,n} \bigr \}$ for each point $X_{i}$. These weights describe a local “cluster” associated with $X_{i}$. By construction, only those weights $w_{ij}^{(k-1)}$ can be positive for which $X_{j}$ belongs to the ball $B(X_{i},h_{k-1}) = \{ x :d(X_{i},x) \le h_{k-1} \}$. At the next step $k$ a larger radius $h_{k}$ is picked and the weights $w_{ij}^{(k)}$ are recomputed using the previous results.

The basic idea behind the definition of $w_{ij}^{(k)}$ is to check for each pair $i,j$ with $d(X_{i},X_{j}) \le h_{k}$ whether the related clusters are well separated or they can be aggregated into one homogeneous region. A test statistic $T_{ij}^{(k)}$ is computed to compare the data density in the union and overlap of two clusters for points $X_{i}$ and $X_{j}$ using the weights $w_{ij}^{(k-1)}$ from the preceding step. The formal definition involves the weighted empirical mass of the overlap and the weighted empirical mass of the union of two balls $B(X_{i}, h_{k-1})$ and $B(X_{j}, h_{k-1})$ shown on Fig. 1.

The empirical mass of the overlap $N_{i\wedge j}^{(k)}$ as shown in the second graph of Fig. 1 is:

$$\begin{aligned} N_{i\wedge j}^{(k)}= & {} \sum _{l\ne i,j} w_{il}^{(k-1)} w_{jl}^{(k-1)} , \end{aligned}$$

(1)

which is the number of points in the overlap of $B(X_{i}, h_{k-1})$ and $B(X_{j}, h_{k-1})$ except points $X_{i},X_{j}$.

Fig. 1

Test of “no gap between local clusters”. From left: Homogeneous case; $N_{i\wedge j}^{(k)}; \, N_{i\triangle j}^{(k)}; \, N_{i\vee j}^{(k)}$

Similarly, the mass of the complement (third graph in Fig. 1)

$$\begin{aligned} N_{i\triangle j}^{(k)}= & {} \sum _{l\ne i,j} \bigl \{ w_{il}^{(k-1)} \mathbb {1}\bigl ( X_{l} \not \in B(X_{j}, h_{k-1}) \bigr ) + w_{jl}^{(k-1)} \mathbb {1}\bigl ( X_{l} \not \in B(X_{i}, h_{k-1}) \bigr ) \bigr \} \quad \end{aligned}$$

(2)

$N_{i\triangle j}^{(k)}$ counts the number of points in $C_{i}^{(k-1)}$ and $C_{j}^{(k-1)}$ which do not belong to the overlap $B(X_{i}, h_{k-1}) \cap B(X_{j}, h_{k-1})$. Finally, mass of the union $N_{i\vee j}^{(k)}$ is defined via (1), (2) as the sum of the mass of the overlap and the mass of the complement:

$$\begin{aligned} N_{i\vee j}^{(k)}= & {} N_{i\wedge j}^{(k)} + N_{i\triangle j}^{(k)} \, . \end{aligned}$$

(3)

The gap between two regions is measured considering the ratio of these two masses (1, 3):

$$\begin{aligned} \tilde{\theta }_{ij}^{(k)}= & {} {N_{i\wedge j}^{(k)}} \, \big / \, {N_{i\vee j}^{(k)}} \ . \end{aligned}$$

(4)

The value (4) can be viewed as an estimate of $\theta _{ij}$ which measures the ratio of the averaged density in the overlap of two local regions $C_{i}$ and $C_{j}$ relative to the average density. (4) should be close to the ratio of the corresponding volumes for identical cluster membership also denoted as local homogeneity:

$$\begin{aligned} \tilde{\theta }_{ij}^{(k)}\approx & {} q_{ij}^{(k)} = \frac{V_{\cap }(d_{ij}, h_{k-1})}{2V(h_{k-1}) - V_{\cap }(d_{ij}, h_{k-1})}. \quad \end{aligned}$$

Where $V(h)$ is the volume of a ball with radius $h$ and $V_{\cap }(d_{ij}, h)$ is the volume of the intersection of two balls with radius $h$ and the distance between centers $d_{ij} = d(X_{i},X_{j})$.

The new value $w_{ij}^{(k)}$ can be viewed as a randomized test of the null hypothesis $H_{ij}$ of no gap between $X_{i}$ and $X_{j}$ against the alternative of a significant gap. The gap is significant if $\tilde{\theta }_{ij}^{(k)}$ is significantly smaller than $q_{ij}^{(k)}$. The construction is illustrated in Fig. 2 for the homogeneous situation (left) and for a situation with a gap (right).

Fig. 2

Left: Homogeneous case. Right: “Gap” case

To quantify the notion of significance, the statistical likelihood ratio test of “no gap” between two local clusters is considered, that is $\tilde{\theta }_{ij}^{(k)} > q_{ij}^{(k)}$ vs $\tilde{\theta }_{ij}^{(k)} \le q_{ij}^{(k)}$ :

$$\begin{aligned} T_{ij}^{(k)}= & {} N_{i\vee j}^{(k)} \,\, KL\bigl ( \tilde{\theta }_{ij}^{(k)},q_{ij}^{(k)} \bigr ) \, \bigl \{ \mathbb {1}( \tilde{\theta }_{ij}^{(k)} \le q_{ij}^{(k)}) - \mathbb {1}( \tilde{\theta }_{ij}^{(k)} > q_{ij}^{(k)}) \bigr \} . \end{aligned}$$

(5)

Here $KL(\theta ,\eta )$ is the Kullback–Leibler (KL) divergence between two Bernoulli laws with parameters $\theta$ and $\eta$:

$$\begin{aligned} KL(\theta ,\eta )= & {} \theta \log \frac{\theta }{\eta } + (1 - \theta ) \log \frac{1 - \theta }{1 - \eta }. \end{aligned}$$

(6)

Finally, the weights $w_{ij}^{(k)}$ are updated for all pairs of points $X_{i}$ and $X_{j}$ with distance $d_{ij} \le h_{k}$:

$$\begin{aligned} w_{ij}^{(k)}= & {} \mathbb {1}\left( d_{ij} \le {h_{k}}\right) \, \mathbb {1}\left( {T_{ij}^{(k)}} \le {\lambda }\right) \end{aligned}$$

where $\lambda$ is some hyperparameter controlling the size of the test (5).

Note that the first indicator function in (6) allows to recompute the $n \times n_{k}$ weights, where $n_{k}$ is the average number of neighbors in the $h_{k}$ neighborhood.

The tests $T_{ij}^{(k)}$ are scaled by a global constant $\lambda$ which is the only tuning parameter of the method. Large $\lambda$-values will lead to aggregation of in-homogeneous regions. On the contrary, small $\lambda$ increases the sensitivity of the methods to in-homogeneity, but may lead to artificial segmentation.

2.1.1 Parameter tuning

A heuristic choice of $\lambda$ (based on the effective cluster size) is as follows:

Let $w_{ij}^{K}(\lambda )$ be the collection of final AWC weights. Define

$$\begin{aligned} S(\lambda )= & {} \sum _{i,j=1}^{n} w_{ij}^{K}(\lambda ) . \end{aligned}$$

A natural way to pick $\lambda$-value is to check for a jump in $S(\lambda )$. This resembles the elbow criterion that is from PCA. In the case of a complex cluster structure, several jump points can be observed with the corresponding $\lambda$-value for each jump. In this situation all those $\lambda$-values should be tried and the appropriateness of the clustering should be checked.

3 Document collection and preprocessing

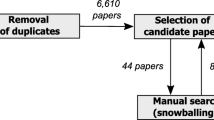
The research center web page (Projects of the crc 649 2018) provides an open access to the Discussion Papers from year 2005 to year 2017 from the School of Business and Economics in Humboldt-Universität zu Berlin. We scrape this web page and extract abstracts of the papers, which form our dataset. For evaluation purposes we also scrape from the website the JEL codes of each paper. The aim is to learn and possibly discover whether the resulting clusters carry information about the JEL code allocation of the overall 784 papers. The standard text preprocessing steps are performed to transform the collection of raw data to the vector space. First we split documents into words and transfer all the letters to small ones. Then we perform stemming, remove all punctuation, numbers, special characters, stopwords and words which occurred only once in the dataset. At this step we have a collection of preprocessed documents and the research areas of each document. For details about this information extraction we refer to Zhang et al. (2016). The most frequent terms in the collection were: “calibration”, “credit”, “density”, “expectation”, “inflation”, “labor”, “quantile”, “shocks”. One clearly sees that the documents/abstracts operate in a quantitative economic field, since besides clearly economic terms like “credit” one finds “density” at almost identical frequency.

The basic model for document clustering is the vector space model, therefore we convert the preprocessed documents into tf-idf vector space (Härdle et al. 2018). Here each document, $X_i$ is first presented as a term-frequency vector in the term-space: $X_{itf} = \{ tf_{ij} \}_{j=1}^d$, where $tf_{ij}$ is the frequency of the j-th term in the document i and d is the dimension of the term-space.

Then, each document is weighted via its inverse document frequency (IDF). This weighting factor ensures the frequent term across all documents in a dataset being discounted and considering as a non informative term. Hence, for each $i$th document, we obtain the following vector representation: $X_i = \{ x_{ij} \}_{j=1}^d$, where

$$\begin{aligned} x_{ij} = tf_{ij} \times idf_{j}, \quad idf_{j} = \log {\frac{1 + n}{1 + n_j}} + 1. \end{aligned}$$

Here $idf_{j}$ is the inverse document frequency, $n$ is the number of documents in a collection and $n_j$ is the number of documents which contain the term $j$. Hence, tf-idf of a word gives a product of how frequent this word is in the document multiplied by how unique the word is w.r.t. the entire corpus of documents. Words in the document with a high tf-idf score appear frequently in the document and are informative within specific document. The resulting matrix is used further for cluster analysis.

4 Evaluation criteria

In the experiments to measure the clustering quality we used Adjusted Rand Index ARI (Hubert and Arabie 1985), Normalized Mutual Information NMI (Strehl and Ghosh 2002) and F-score, which are considered as the most popular measures for cluster validation particularly for textual data. ARI, NMI and F-score measure the similarity between the defined true clusters and the estimated clusters.

Suppose that the true clustering structure is $C^* = \{C^*_m\}_{m=1}^M$ and the estimated clustering structure is $C = \{C_l\}_{l=1}^L$.

The ARI is defined in the following way:

$$\begin{aligned} \mathrm{{ARI}}(C, C^*) = \frac{\sum _{ml}\left( {\begin{array}{c}n_{ml}\\ 2\end{array}}\right) - \sum _{m}\left( {\begin{array}{c}n^*_{m}\\ 2\end{array}}\right) \sum _{l}\left( {\begin{array}{c}n_{l}\\ 2\end{array}}\right) / \left( {\begin{array}{c}n\\ 2\end{array}}\right) }{\frac{1}{2}\{\sum _{m}\left( {\begin{array}{c}n^*_{m}\\ 2\end{array}}\right) + \sum _{l}\left( {\begin{array}{c}n_{l}\\ 2\end{array}}\right) \} - \sum _{m}\left( {\begin{array}{c}n^*_{m}\\ 2\end{array}}\right) \sum _{l}\left( {\begin{array}{c}n_{l}\\ 2\end{array}}\right) / \left( {\begin{array}{c}n\\ 2\end{array}}\right) }, \end{aligned}$$

where $n_{ml} = |C^*_m \cap C_l|$, $n^*_{m} = |C^*_m|$, $n_{l} = |C_l|$.

For the NMI the same designations are used:

$$\begin{aligned} \mathrm{{NMI}}(C, C^{*}) = \frac{\sum _{ml} n_{ml} \log {\frac{n \, n_{ml}}{n_{m}^{*} \, n_{l}}}}{\sqrt{\sum _{m} n_{m}^{*} \log ( n_{m}^{*}/n) \, \, \sum _{l} n_{l} \log (n_{l}/n)}} . \end{aligned}$$

The F-score is the harmonic mean of precision and recall.

When defining the true clustering structure for the economic literature dataset, we assign to each document its first JEL code. This choice is based on the idea, that the first JEL code represents the primary topic of the document. For this note, the true partitioning and the corresponding matrix of weights are shown on Fig. 3. Here, on the left panel of the Fig. 3 we plotted the first two principal components of the true partitioning and colored each cluster by a different color. The right panel of the figure shows the corresponding matrix of weights where white and black colors represent weights being equal to 1 and 0, respectively.

There are overall $M = 17$ clusters. The biggest cluster consists of 399 documents and appears as the C JEL code which stands for Mathematical and Quantitative Methods; 65% of the documents contain the JEL code C. This may be explained by the fact that the majority of papers from this dataset includes ideas based on statistical methods, particularly econometrics. Interestingly though, there are two singleton clusters about Economics Teaching and History of Economic Thought.

Fig. 3

Left: true clustering structure $C^*$. Right: corresponding matrix of weights. https://github.com/QuantLet/q_awc

5 Experiments

In this section we cluster the research paper abstracts dataset using different methods and compare the produced clustering structures with the true clustering $C^*$. The clustering algorithms used in evaluation are AWC, standard $k$-means and the vcluster algorithm from the CLUTO toolkit. $k$-means and CLUTO both require as a parameter the number of true clusters $K$. While AWC has only parameter $\lambda$, which is tuned using the heuristics described in Sect. 2.1.1. CLUTO’s vcluster algorithm is a bisecting graph partitioning-based algorithm which is greedy in nature and therefore depends on the order of the input documents. The $k$-means algorithm also includes randomness in the clustering process. Thus we run both CLUTO and $k$-means 500 times with different random states and choose the best result for each $k : 2 \le k \le 25$. The results are shown in Figs. 4 and 5. On the left panel we show the clustering measures as a function of $k$, number of clusters. One can see that $k$-means and CLUTO show best performance for $k = 4$ and $k = 3$ correspondingly. As the results are acquired by choosing the best result from 500 iterations, on the right panel of Figs. 4 and 5 we display the ARI distribution as box plots. From these plots one can estimate the somewhat high fluctuation of the employed clustering methods.

For AWC we run the algorithm with different $\lambda$-values from $[-0.1, 1.4]$ and compute the sum of weights $S(\lambda )$. The choice of range interval is due to the fact that for $\lambda$ outside of this interval AWC either splits all points into separate clusters ($\lambda < -0.1$) or merges all points into one huge cluster ($\lambda > 1.4$). Here we also specify a starting neighborhood size $n_0 = 40$ which is similar to vcluster from CLUTO. Figure 6 displays $S(\lambda )$ as a black curve with three points before a visible jump. These points are denoted by A, B, C. We do not consider points with $\lambda > 0.4$ because $S(\lambda ) \ge 0.5$, indicating a situation when almost all points are placed in one-two huge clusters only. All three $\lambda$ “candidates” guarantee ARI being higher than 0.22, thus can be considered as good choices for $\lambda$. Moreover, ARI reaches its maximum value exactly in the second candidate point B (ARI $= 0.31$). Note though, that we can not identify point B as the best choice out of A, B, C only from the $S(\lambda )$ plot. On the other hand AWC actually provides only 3 (good in terms of the chosen measures) clustering answer to choose from which we consider as success compared to the situation of other algorithms which require the true number of clusters as input. In addition, we want to point out that we consider the best run of $k$-means and CLUTO out of 500 runs. To understand the quality of the chance to get a good cluster division, we added the corresponding box plots on Figs. 4 and 5. From these plots we may conclude that even if we provide the best $k$ for $k$-means, the answer in most cases might be questionable. For CLUTO the variation in quality is not so bad but if we provide any $k$ different from 3 the answer will have ARI $< 0.2$. For AWC to actually make the final choice we propose to look into each cluster structure corresponding to A, B, C and make the final choice depending on the quality of these clusters.

Fig. 4

$k$-means: Left: Best result for each measure from 500 runs for each $K$. Best result for $K = 4$. Right: Box plot displaying the full range of variation (from min to max) of the ARI measure from 500 runs for each $K$. https://github.com/QuantLet/q_awc

Fig. 5

Cluto: left: best result for each measure from 500 runs for each $K$. Best result for $K = 3$. Right: Box plot displaying the full range of variation (from min to max) of the ARI measure from 500 runs for each $K$

Fig. 6

AWC: choice of the $\lambda$ parameter based on the sum of weights heuristics

The results for point C are shifted to A.3. Let us look more carefully at point B. To interpret the detected clusters, we match them with its word cloud, Figs. 7, 8, 9, 10, 11, 12 and 13. For each word in the word cloud there are two characteristics: size and color. The size is proportional to the frequency of a word in the corresponding cluster: the more popular a word is inside a cluster, the larger size it has. The color corresponds to the idf value of a word in the whole dataset: the higher is the idf value of a word, the darker is its color and more important/informative it is in the dataset. Basically the cluster is formed around the simultaneously large and dark words.

It is also interesting how the detected clusters correspond to the JEL codes. For each cluster we have plotted a bar chart in the right panel of Figs. 7, 8, 9, 10, 11, 12 and 13. The blue bars represent the percentage of a JEL code inside a cluster, i.e they show which part of the documents is labelled by a JEL code inside one cluster. The orange bars indicate which part of the documents with a JEL code lies inside a cluster. For example, if for one cluster the blue and orange bars for JEL code $J$ are 50% and 100% correspondingly, that means half of the documents in that cluster has label $J$ and all documents in our dataset with code $J$ actually lie inside that cluster.

Fig. 7

Cluster 1: the Quantitative Finance $C + G$. Left: word cloud. Right: bar chart

Fig. 8

Cluster 2: the Law and Economics $K + N + R$. Left: word cloud. Right: bar chart

Fig. 9

Cluster 3: the Macro and Monetary E. Left: word cloud. Right: bar chart

Fig. 10

Cluster 4: the Labor J. Left: word cloud. Right: bar chart

Fig. 11

Cluster 5: the Industrial Organization L. Left: word cloud. Right: bar chart

Fig. 12

Cluster 6: the Microeconomics D. Left: word cloud. Right: bar chart

Fig. 13

Cluster 7: the Business, Marketing M. Left: word cloud. Right: bar chart

Let us investigate in details each cluster detected by AWC.

From the bar chart at the Fig. 7 one can see that more than 85% of the documents in the first detected cluster contain the JEL code C: Mathematical and Quantitative Methods, about 50% contain G: Financial Economics. In fact more than 60% of all the documents with JEL C and G are inside this cluster. As an additional information, the word cloud on the Fig. 7 indicates popular words such as forecast, estimator, distribution, volatility, etc. To this end, having a combination of C and G we can interpret this cluster as Quantitative Finance.

In the second cluster at the Fig. 8 we see a combination of K: Law and Economics, N: Economic History and R: Real Estate. This mixture indicates that this cluster is more of a social science type one and indeed it contains papers on Bayesian Networks and Sex-related Homicides (Stahlschmidt et al. 2011), also How does entry regulation influence entry into self-employment and occupational mobility? (Prantl and Spitz-Oener 2009). therefore we label this cluster as Social Science.

The third cluster shown on the Fig. 9 obviously covers E: Macroeconomics and Monetary Economics. One can see it from the bar chart where more than 70% of documents in the cluster contain E, as well as from the word cloud with keywords like monetary, inflation, policy, interest, rate, etc.

It is also clear that the fourth detected cluster on the Fig. 10 is about J: Labor and Demographic Economics. More than 85% of the documents within this cluster contain J and the word cloud points out wage, worker, employment, labor, occupation and so on. The fifth cluster on the Fig. 11 gathers papers from L: Industrial Organization. The word cloud summarizes keywords covered in the cluster: firm, innovation, manager, corporate, contract and so on. Therefore we refer to this cluster as Industrial Organization. Looking at the sixth cluster on the Fig. 12 one can clearly interpret it as Microeconomics. More than 85% of the documents within this cluster are from D: Microeconomics.

The seventh cluster on the Fig. 13 is also very informative. The word cloud indicates keywords like brand, customer, product, manufacturers, etc. Also the majority of papers within this cluster contain the JEL code M: Business Administration, Business Economics, Marketing, Accounting, Personnel Economics. Therefore we refer to this cluster as Business Economics and Marketing.

It is worth also noting that the majority of the documents contain C: Mathematical and Quantitative Methods and G: Financial Economics. This is due to the fact that the research center had a focus on Econometrics.

In summary we might claim that the resulting clusters show that AWC detects informative data divisions which correspond to JEL codes.

A similar analysis via k-means and CLUTO is provided in A.1 and A.2 in Appendix. In essence, CLUTO detects clusters only about Quantitative Finance and E: Macroeconomics and Monetary Economics, and k-means additionally finds J: Labor and Demographic Economics. Both methods aggregate all the documents with other JEL codes together in one cluster.

This indicates that both methods cannot provide the necessary granularity for identification of e.g. the JEL code groups. On the contrary, AWC provides an interpretable cluster structure and leads to machine learned identification of the papers’ research directions.

6 Conclusion

The JEL classification system is a fast way to retrieve research papers in economics. Based on the CRC649 research center database we present an innovative clustering. It is fully automatic, adaptive and leads to interpretable JEL clusters. The basic idea is based on locally weighting each document or abstract in terms of its cluster membership. The numerical implementation of AWC in Python is available at http://www.quantlet.de/. Simulation studies and empirical performance reveal an excellent performance of this clustering technique. We show that by clustering paper abstracts with AWC it is possible to automatically identify papers research directions and activity of economic research on certain topics.

A Appendix

1.1 A.1 Clusters found by k-means

Here we examine the clusters detected by k-means. Figures 14, 15, 16 and 17 show the best clustering structure from k-means in terms of maximum ARI measure. The first cluster on Fig. 14 is similar to the first cluster found by AWC. Around 90% of its documents contain the JEL code C: Mathematical and Quantitative Methods and 45% contain G: Financial Economics. Moreover, it contains around 60% of all the documents with JEL codes C and G. Since this cluster is a mixture of Quantitative Methods and Financial Economics, we interpret it as Quantitative Finance.

However, things are not that clear for the second cluster on the Fig. 15. It can be seen from the bar chart that k-means mixes documents from almost all JEL codes into this cluster. Also the word cloud is non-informative. As a result we get an uninterpretable cluster. The third k-means cluster on Fig. 16 is close to the third cluster found by AWC. It is clear from both, the bar chart and the word cloud, that this cluster represents E: Macroeconomics and Monetary policy.

There is also a clear similarity between the fourth k-means cluster shown on Fig. 17 and the fourth cluster from AWC on Figure 10. Here also the bar chart indicates the JEL code J and the word cloud points out words like wage, worker, employment, labor, occupation.Therefore, we refer to this cluster as J: Labor and Demographic Economics.

Fig. 14

k-means cluster 1: the Quantitative Finance. Left: word cloud. Right: bar chart

Fig. 15

k-means cluster 2: the Business, Micro, Macro. Left: word cloud. Right: bar chart

Fig. 16

k-means cluster 3: the Macro and Monetary Economics. Left: word cloud. Right: bar chart

Fig. 17

k-means cluster 4: the Labor Market. Left: word cloud. Right: bar chart

1.2 A.2 Clusters found by CLUTO

CLUTO reaches maximal ARI value for $k=3$. Figures 18, 19 and 20 show clusters found by the best run of CLUTO. Similar to AWC and k-means, the first cluster detected by CLUTO on Fig. 18 is a mixture of JEL codes C: Quantitative Methods and G: Financial Economics, therefore represents Quantitative Finance. Figure 19 shows that about 60% of all the documents in the second CLUTO cluster contain JEL code E: Macroeconomics and Monetary policy, also around 60% of all the documents with the code E are placed here. In addition it contains documents from C: Quantitative Methods, G: Financial Economics and F: International Economics. Taking into account also keywords from the word cloud such as shock, inflation, monetary, policy, etc, we label this cluster as Macroeconomics and Monetary policy. Though the first two clusters are clear, the third CLUTO cluster on Fig. 20 is an aggregation of almost all the JEL codes, therefore is not interpretable.

Fig. 18

CLUTO cluster 1: the Quantitative Finance. Left: word cloud. Right: bar chart

Fig. 19

CLUTO cluster 2: the Macro and Monetary Economics. Left: word cloud. Right: bar chart

Fig. 20

CLUTO cluster 3: the Economics. Left: word cloud. Right: bar chart

1.3 A.3 Clusters found by AWC at the point C

It is also interesting to investigate the cluster structure found by AWC with different $\lambda$ value. Figure 21 demonstrates the first cluster detected by AWC with $\lambda$ taken at the point C from Fig. 6. It represents again Quantitative Finance. Other clusters aggregate articles from research fields such as Macro and Monetary Economics, Labor Economics, Business Economics and Marketing, Statistical Learning and Microeconomics. These and clusters at finer granularity yield similar groupings as before. Hence, we see that the other choice of the $\lambda$ is apparently robust as AWC detects informative clusters corresponding to JEL codes of the papers.

Fig. 21

AWC (C) cluster 1: the Quantitative Finance. Left: word cloud. Right: bar chart