Simplicial and Minimal-Variance Distances in Multivariate Data Analysis

Abstract

In this paper, we study the behaviour of the so-called k-simplicial distances and k-minimal-variance distances between a point and a sample. The family of k-simplicial distances includes the Euclidean distance, the Mahalanobis distance, Oja’s simplex distance and many others. We give recommendations about the choice of parameters used to calculate the distances, including the size of the sub-sample of simplices used to improve computation time, if needed. We introduce a new family of distances which we call k-minimal-variance distances. Each of these distances is constructed using polynomials in the sample covariance matrix, with the aim of providing an alternative to the inverse covariance matrix, that is applicable when data is degenerate. We explore some applications of the considered distances, including outlier detection and clustering, and compare how the behaviour of the distances is affected for different parameter choices.

1 Introduction

The Mahalanobis distance is one of the most useful tools in multivariate data science, underpinning a huge variety of practical data analysis methods. This distance measures the proximity of a point $x \in \mathbb {R}^d$ to a d-dimensional set of points $X = \{x_{1}, \dots , x_{N}\} \subset \mathbb {R}^{d\times N}$. It was introduced in Mahalanobis [27]. The Mahalanobis distance corresponds to the Euclidean distance in the standardized space where variables are uncorrelated and have unit variance. It has applications in cluster analysis [16, 44], outlier detection [35], financial settings [40], text classification [39] and image processing [32, 45], to name a few.

The Mahalanobis distance requires the inversion of the $d\times d$ sample covariance matrix, which we denote by $W$. This covariance matrix is commonly singular (or very close to being singular) in high-dimensional settings [13], which often causes instability when computing the Mahalanobis distance and sometimes makes it practically unusable.

The Moore–Penrose pseudo-inverse $W^{-}$ is commonly used in cases where the covariance matrix is not invertible, see Wei et al. [41] and Lahav et al. [22], for example. This pseudo-inverse is constructed using the nonzero eigenvalues and corresponding eigenvectors of the covariance matrix $W$, and satisfies the four Moore–Penrose conditions [17]. However, by using all nonzero eigenvalues, it can be adversely affected by very small eigenvalues, creating discrepancies between $W^{-}$ and the true inverse, if it exists [6, 19]. The Moore–Penrose pseudo-inverse is unique, and so has no flexibility in these cases where eigenvalues close to zero can cause issues.

Knowing how to deal with high-dimensional data is extremely important, as our ability to collect and store large quantities of data continues to grow. Although there are benefits to having datasets with large amounts of information, analysing and understanding these datasets can present many challenges. For example, the concentration of points in high dimensions can cause distances between them to be (approximately) the same [5], yielding difficulties in determining whether points are ‘close’ or ‘far away’ to each other [1]. Given a high enough dimension, there will exist at least one subspace such that a significant number of points can be classified as being ‘close’ together [46]. Huge datasets create combinatorially intractable search spaces and extracting information or patterns may not be computationally possible. Such datasets also increase the probability of detecting spurious relations [38]. Existing rudimentary data processing algorithms do not scale to scenarios of degenerate data in big dimensions [2].

High-dimensional data is usually highly correlated [9, 33]. Measures of proximity that typically work well in low-dimensional settings, such as the Euclidean and Manhattan distance, do not take correlations into consideration when measuring the scatter of the data. Using a distance measure like the Mahalanobis distance accounts for these correlations and therefore produces more accurate and meaningful results in such settings. However, the correlated variables also result in an intrinsic dimensionality that is lower than the given dimensionality of the data [46], causing degeneracy. As such, it is important to have methods that can account for correlations, that can effectively deal with the possibility of singular covariance matrices, and that are not limited by the problems of the Moore–Penrose pseudo-inverse.

A common solution to some of the problems outlined is to use an estimator which produces an invertible sample covariance matrix, rather than using the sample covariance matrix produced by the maximum likelihood estimator (MLE). Examples include methods which shrink the MLE sample covariance matrix towards some other target matrix: Ledoit and Wolf [25] use the identity matrix as the target, whereas Schäfer and Strimmer [37] allow for a user-defined target matrix. However, it is hard to know what the ideal target matrix is [24]. Other methods include shrinking only the largest and smallest eigenvalues [43], tapering off-diagonal elements to zero [3, 15], applying $\ell _{1}$ penalties directly to covariance matrix entries [10] and many others. We recommend Fan et al. [12] and Lam [23] for detailed overviews of such methods.

Methods which estimate the inverse covariance matrix directly, such as neighbourhood selection [29], modified Cholesky decompositions [21] and $\ell _{1}$ regularization approaches [7, 14], prevent inversion errors and can improve computation time. However, these methods still suffer from the potentially impractical assumption that the inverse covariance matrix should be sparse.

Pronzato et al. [34] introduced a family of so-called k-simplicial distances which, according to the claim in that paper, resemble the squared Mahalanobis distance and could be used in situations where the data is degenerate or close to being degenerate. These k-simplicial distances are defined as averaged volumes of all possible $k$-dimensional simplices formed by x and all points from the set X, for a user-defined $k \in \{1, \dots , d\}$. The distances are raised to a user-defined power $\delta > 0$. For general $\delta >0$, the choice $k=1$ gives the $\ell _\delta$-distance in $\mathbb {R}^d$. For $\delta = 2$, the parameter choices $k = 1$ and $k = d$ give distances proportional to the squared Euclidean and Mahalanobis distances, respectively. The choice of parameter k indicates the dimension of the simplices used, and can be chosen in such a way as to avoid the problems of degeneracy and small eigenvalues, which cause issues in other methods, such as the Moore–Penrose pseudo-inverse. When $\delta = 2$, there is a more efficient method of finding the k-simplicial distance using a matrix polynomial in $W$, rather than through computation of volumes of simplices, which is outlined in Sect. 2. For other values of the parameter $\delta$, we demonstrate a sub-sampling method which improves computational speed, with very little observed change to the distances measured.

We also introduce a new distance, the k-minimal-variance distance, which constructs a matrix polynomial in $W$ of degree $k-1$. In this method, the constructed polynomial yields a squared distance with minimum variance. Like the k-simplicial distance, the k-minimal-variance distance can be used when $W$ is singular, and produces a distance measure which accounts for correlations in the dataset. We explore the choice of the parameter $k$, and show that $k$ can be relatively low to produce good results, making the k-minimal-variance distance a quick and viable alternative to the Mahalanobis distance. We will use examples to show how minimizing the variance of the distances can provide a more intuitive distance measure for use with correlated data.

We consider the performance of the k-minimal-variance distance and compare it to the $k$-simplicial distance, the Euclidean distance and the Mahalanobis distance. We also show in Sect. 5.2 that both distances proposed may produce more accurate results than the Euclidean and Mahalanobis distances when used for clustering applications.

The structure of this paper is as follows: Sect. 2 introduces and further studies the k-simplicial distance formulated in Pronzato et al. [34]. Section 3.1 explores the effects of the parameters $k$ and $\delta$ in the k-simplicial distance through numerical examples. Section 3.2 introduces the sub-sampling method which reduces computation time and allows us to consider large sample sizes. Section 3.3 uses outlier detection examples to produce parameter recommendations for the k-simplicial distance. Section 4 introduces the k-minimal-variance distance. We compare the k-simplicial and k-minimal-variance distances to each other in both their efficiency at minimizing variance in Sect. 5.1 and compare their performance at clustering some real-life datasets against the Mahalanobis and Euclidean distances in Sect. 5.2. We give our conclusions about the distance measures in Sect. 6.

2 $k$-Simplicial Distances

Assume we are given a set of $N$ points in d-dimensions $X = \{x_{1}, \dots , x_{N}\} \subset \mathbb {R}^{d\times N}$, with no assumptions on how this set of points has been generated. The sample mean and covariance matrix associated with X are defined, respectively, as follows:

$$\begin{aligned} {\mu } = \frac{1}{N} \sum _{j=1}^N x_j\, , \;\;\; {W}= \frac{1}{N} \sum _{j=1}^N (x_j- {\mu })(x_j- {\mu })^\top \,. \end{aligned}$$

(1)

The squared Euclidean distance between a point $x \in \mathbb {R}^{d}$ and the set X is

$$\begin{aligned} \rho _{E}^{2} (x,X)= (x- {\mu })^\top (x- {\mu })\, . \end{aligned}$$

The squared Mahalanobis distance between $x \in \mathbb {R}^{d}$ and X is defined by

$$\begin{aligned} \rho _M^2 (x,X)= (x- {\mu })^\top {W}^{-1} (x- {\mu })\, , \end{aligned}$$

(2)

where $W^{-1}$ is the inverse of the sample covariance matrix $W$. If the matrix ${W}$ is singular then its inverse does not exist, and so the Moore–Penrose pseudo-inverse $W^{-}$ is often used in place of ${W}^{-1}$ in (2). A pseudo-inverse is a type of generalized inverse, satisfying some but not necessarily of all the properties of an inverse matrix; the Moore–Penrose pseudo-inverse satisfies the four Moore–Penrose conditions [17]. When we use $W^{-}$ in the Mahalanobis distance we will call it the pseudo-Mahalanobis distance.

To compute the k-simplicial distance between $x \in \mathbb {R}^{d}$ and $X = \{x_{1}, \dots , x_{N}\} \subset \mathbb {R}^{d\times N}$, we calculate volumes of $k$-dimensional simplices raised to a given power $\delta >0$. Let $r \le d$ be the intrinsic dimension of the dataset X, which is the rank of X when $X$ is considered as a $d\times N$ matrix. The volumes of all k-dimensional simplices are zero for $k >r$ and so it makes no sense to use $k >r$.

Let $\mathscr {V}_{k}(x, z_{1}, \dots , z_{k})$ be the volume of a $k$-dimensional simplex with vertices x and $z_{1}, \dots z_{k} \in \mathbb {R}^{d}$. This volume can be computed by

$$\begin{aligned} \mathscr {V}_{k}(x, z_{1}, \dots , z_{k}) = \frac{1}{k!}\left| \text {det}(Z^{\top }Z)\right| ^{1/2}, \end{aligned}$$

where det(A) is the determinant of the matrix A and |a| is the absolute value of the scalar a [34]. Z is the $d \times k$ matrix with columns $[(z_{1} - x) \;(z_{2} - x)\; \dots \; (z_{k} - x)]$. Let

$$\begin{aligned} J= \left\{ (j_{1}, \dots , j_{k}) \in \{1, \dots , N\}^{k} \mid j_{1}< \dots < j_{k} \right\} \end{aligned}$$

(3)

be the set of all ordered $k$-combinations of the indices in $\{1, \dots , N\}$. Define

$$\begin{aligned} P_{k, \delta }(x, X) = \frac{1}{\left( {\begin{array}{c}N\\ k\end{array}}\right) }\sum _{(j_{1}, j_{2}, \dots , j_{k}) \in J}\mathscr {V}_{k}^{\delta }(x, x_{j_{1}}, \dots , x_{j_{k}})\, , \end{aligned}$$

(4)

which is the average volume of all k-dimensional simplices created by the query point x and points in X, raised to the power of a user-defined scalar $\delta > 0$. For given $\delta >0$ and $1 \le k \le r$, the centre of the set X (that is, the k-simplicial multidimensional median) is defined as

$$\begin{aligned} \overline{\mu }_{k, \delta } = \arg \min _x P_{k, \delta }(x, X)\, , \end{aligned}$$

which may not be uniquely defined for $\delta \le 1$. Recommendations for these parameters will be discussed in Sects. 3 and 5. We then define the k-simplicial outlyingness function by

$$\begin{aligned} O_{k, \delta }(x, X) = \frac{P_{k, \delta }(x, X)}{P_{k, \delta }(\overline{\mu }_{k, \delta }, X)} - 1\,. \end{aligned}$$

(5)

The function (5) is non-negative, has value 0 at the centre of the sample and is unitless; these are the required properties that an outlyingness function must possess, see Wilks [42]. For any $\delta >0$, we define the k-simplicial distance (here to the power of $\delta$) from the query point $x$ to the dataset $X$ by

$$\begin{aligned} \rho ^{\delta }_{k, \delta }(x, X) = c_{k, \delta } O_{k, \delta }(x, X) = c_{k, \delta }\left( \frac{P_{k, \delta }(x, X)}{P_{k, \delta }(\overline{\mu }_{k,\delta }, X)} - 1\right) , \end{aligned}$$

(6)

where the constant $c_{k, \delta }$ is chosen so that

$$\begin{aligned} \frac{1}{N} \sum _{j=1}^N \rho ^{2}_{k, \delta }(x_j, X)=1\, . \end{aligned}$$

(7)

The normalization (7) is introduced to ensure consistency of the k-simplicial distances for different k. In the next section we see that, for $\delta =2$ and all $k\le r$, this normalization constant is $c_{k, 2}=1/k$. For $\delta \ne 2$, we find constants $c_{k, \delta }$ numerically from (7).

As shown in [34, Theorem 5], for $\delta =2$ and any eligible k we get $\overline{\mu }_{k, \delta }= {\mu } ,$ the sample mean. Moreover, we obtain, similarly to [34, Sect. 3.1]

$$\begin{aligned} \frac{1}{N}\sum _{j=1}^N {P_{k, 2}(x_j, X)} =(k+1){P_{k, 2}( \mu , X)}\, . \end{aligned}$$

(8)

We then define the squared k-simplicial distance (of order $\delta = 2$) from $x$ to the dataset $X$ as

$$\begin{aligned} \rho ^{2}_{k, 2}(x, X) = \frac{1}{k} O_{k, 2}(x, X) =\frac{1}{k}\left( \frac{P_{k, 2}(x, X)}{P_{k, 2}( \mu , X)} - 1\right) \, . \end{aligned}$$

(9)

The difference between (9) and the corresponding definition in [34, Eq. 17] is the introduction of the normalizing constant 1/k, which provides consistency of the distances for different k in the sense that (7) holds for $\delta =2$ and all $k=1,2 \ldots , r$. The equality in (7) with $\delta =2$ directly follows from (8).

Direct evaluation of the distances given by (9), i.e. by empirical calculation of the volumes of all $\left( {\begin{array}{c}N\\ k\end{array}}\right)$ simplices, can be computationally time-consuming. Below, we consider an alternative method for the case with $\delta =2$, which is much faster and easier. Reducing this computational time when $\delta \ne 2$ is considered in Sect. 3.2.

Let $\Lambda = \{\lambda _{1}, \dots , \lambda _{d}\}$ be the set of eigenvalues of the sample covariance matrix $W$ defined in (1). The elementary symmetric function of degree $k \le d$ associated with the set $\Lambda$ is given by

$$\begin{aligned} e_{k}(\Lambda ) = \sum _{1\le i_{1}< i_{2}< \dots < i_{k} \le d} \lambda _{i_{1}}\dots \lambda _{i_{k}}\, , \end{aligned}$$

with $e_{0}(\Lambda )=1$. If $k>r= \mathrm{rank} (X)$ then $e_{k}(\Lambda )=0$ and the k-simplicial distance is always 0.

For $k \le r$, define the function

$$\begin{aligned} q_{k}(W) = \sum _{i=0}^{k-1}(-1)^{i}e_{k-i-1}(\Lambda )W^{i} \end{aligned}$$

(10)

and the associated matrix

$$\begin{aligned} S_{k} = \frac{q_{k}(W)}{e_{k}(\Lambda )}\, . \end{aligned}$$

As follows from [34, Sect. 3.2], for any $k \le r$,

$$\begin{aligned} \rho ^{2}_{k,2}(x, X) =\frac{1}{k} (x-\mu )^{\top }{S_{k}}(x-\mu )\, . \end{aligned}$$

(11)

Note that the matrices $S_{k}$, $k=1,\ldots ,r$, are polynomials in the covariance matrix $W$.

Since $S_1=I_d/ \mathrm{trace}(W)$, where $I_d$ is the identity $d\times d$ matrix, for $k = 1$ the squared distance (11) is equal to the squared Euclidean distance divided by the trace of the covariance matrix $W$:

$$\begin{aligned} \rho ^{2}_{1, 2}(x, X) = (x-\mu )^{\top } {S_{1}}(x-\mu ) = (x-\mu )^{\top }\frac{q_{1}(W)}{e_{1}(\Lambda )}(x-\mu ) = \frac{(x-\mu )^{\top }(x-\mu )}{\mathrm{trace}(W)}\, . \end{aligned}$$

When $k = d$ and $W$ is invertible, we have $S_d= W^{-1}$ and therefore the squared k-simplicial distance (11) is equal to the squared Mahalanobis distance multiplied by a factor $1/d$ (for details see [34, Sect. 3.1]):

$$\begin{aligned} \rho ^{2}_{d, 2}(x, X) = \frac{1}{d} (x-\mu )^{\top } {S_{d}}(x-\mu ) = \frac{1}{d} (x -\mu )^{\top }{W^{-1}}(x - \mu )\, . \end{aligned}$$

We prove the following theorem comparing the variance of the squared Euclidean distance, Mahalanobis distance and k-simplicial distance with $k = 2$ and $\delta = 2$.

Theorem 1

Assume $X = \{x_{1}, \dots , x_{N}\}$ is a set of $N$ normally distributed $d$-dimensional vectors (data points) with sample mean $\mu$ and sample covariance matrix $W$, as defined in (1). Let $\Lambda = \{\lambda _{1}, \dots , \lambda _{d}\}$ be the set of eigenvalues of the matrix $W$, and assume $\mathrm{rank}(X)=r \le d$. Then

$$\begin{aligned} \text {Var}\left( \rho _{r,2}^{2}(x, X)\right) \le \text {Var}\left( \rho _{2, 2}^{2}(x, X)\right) < \text {Var}\left( \rho _{1,2}^{2}(x, X)\right) , \end{aligned}$$

where $\rho _{k,2}^{2}(x,X)$ is the squared k-simplicial distance between the point x and set X as defined in (6) with $\delta =2$.

Proof

We can write the k-simplicial distance between a point x and set X with $k = 2,\, \delta =2$ as

$$\begin{aligned} \rho _{2, 2}^{2}(x, X) = (x - \mu )^{\top }\frac{S_{k}}{k}(x - \mu ) = (x - \mu )^{\top }\frac{S_{2}}{2}(x - \mu ) = (x - \mu )^{\top }\frac{q_{2}(W)}{2e_{2}(\Lambda )}(x - \mu ) \end{aligned}$$

with $q_{2}(W) = e_{1}(\Lambda )I_{d} - W$, from (10). From (24) in Appendix A, the variance of the k-simplicial distance with $k = 2, \delta =2$ may be written as

$$\begin{aligned} \mathrm{Var}\left( \rho _{2, 2}^{2}(x, X)\right) = 2\mathrm{trace}\left( \left( \frac{S_{2}}{2}W\right) ^{2}\right) = \frac{\mathrm{trace}\left( W^{2}(e_{1}(\Lambda )I_d - W)^{2}\right) }{2e_{2}(\Lambda )^{2}}. \end{aligned}$$

(12)

Let $\eta _{j} = \sum _{i \ne j}\lambda _{i} = \sum _{i=1}^{r}\lambda _{i} - \lambda _{j}=e_{1}(\Lambda )-\lambda _{j}$. Consider the second-order elementary symmetric polynomial:

$$\begin{aligned} e_{2}(\Lambda ) = \sum _{i < j}\lambda _{i}\lambda _{j} = \frac{1}{2}\sum _{i \ne j}\lambda _{i}\lambda _{j} = \frac{1}{2}\left( \sum _{i = 1}^{r}\sum _{j = 1}^{r}\lambda _{i}\lambda _{j} - \sum _{i = 1}^{r}\lambda _{i}^{2}\right) = \frac{1}{2}\sum _{j = 1}^{r}\lambda _{j}\eta _{j}\, . \end{aligned}$$

Then (12) can be rewritten as:

$$\begin{aligned}&\mathrm{Var}\left( \rho _{2, 2}^{2}(x, X)\right) = \frac{\mathrm{trace}\left( W^{2}(e_{1}(\Lambda )I_d - W)^{2}\right) }{2e_{2}(\Lambda )^{2}}\nonumber \\&= \frac{\sum _{j = 1}^{d}\lambda _{j}^{2}(e_{1}(\Lambda ) - \lambda _{j})^{2}}{2(\frac{1}{2}\sum _{j = 1}^{d}\lambda _{j}\eta _{j})^{2}} = \frac{2\sum _{j = 1}^{r}\lambda _{j}^{2}\eta _{j}^{2}}{(\sum _{j = 1}^{r}\lambda _{j}\eta _{j})^{2}} \end{aligned}$$

(13)

and similarly, using (25) from Appendix A, we may write

$$\begin{aligned} \mathrm{Var}\left( \rho _{1, 2}^{2}(x, X)\right) = \frac{2\sum _{j = 1}^{r}\lambda _{j}^{2}}{(\sum _{j = 1}^{r}\lambda _{j})^{2}}. \end{aligned}$$

(14)

Consider the denominator in (14). By the Cauchy–Schwartz inequality,

$$\begin{aligned} \left( \sum _{j = 1}^{r}\lambda _{j}\right) ^{2} = \left( \sum _{j = 1}^{r}1\cdot \lambda _{j}\right) ^{2} \le \sum _{j = 1}^{r}1^{2}\sum _{j = 1}^{r}\lambda _{j}^{2} = r\sum _{j = 1}^{r}\lambda _{j}^{2}, \end{aligned}$$

and so it follows that

$$\begin{aligned} \mathrm{Var}\left( \rho _{1, 2}^{2}(x, X)\right) = \frac{2\sum _{j = 1}^{r}\lambda _{j}^{2}}{(\sum _{j = 1}^{r}\lambda _{j})^{2}} \ge \frac{2\sum _{j = 1}^{r}\lambda _{j}^{2}}{r\sum _{j = 1}^{r}\lambda _{j}^{2}} = \frac{2}{r} = \mathrm{Var}\left( \rho _{r, 2}^{2}(x, X)\right) \, . \end{aligned}$$

Again using the Cauchy–Schwartz inequality for the denominator in (13), we have

$$\begin{aligned} \left( \sum _{j = 1}^{r}\lambda _{j}\eta _{j}\right) ^2 \le r\sum _{j=1}^{r}\lambda _{j}^{2}\eta _{j}^{2}, \end{aligned}$$

and so it follows

$$\begin{aligned} \mathrm{Var}\left( \rho _{2, 2}^{2}(x, X)\right) = \frac{2\sum _{j = 1}^{r}\lambda _{j}^{2}\eta _{j}^{2}}{(\sum _{j = 1}^{r}\lambda _{j}\eta _{j})^{2}} \ge \frac{2\sum _{j = 1}^{r}\lambda _{j}^{2}\eta _{j}^{2}}{r\sum _{j = 1}^{r}\lambda _{j}^{2}\eta _{j}^{2}} = \frac{2}{r} = \mathrm{Var}\left( \rho _{r, 2}^{2}(x, X)\right) . \end{aligned}$$

It remains to show that

$$\begin{aligned} \mathrm{Var}\left( \rho _{1, 2}^{2}(x, X)\right) = \frac{2\sum _{j = 1}^{r}\lambda _{j}^{2}}{\left( \sum _{j = 1}^{r}\lambda _{j}\right) ^{2}} \ge \frac{2\sum _{j = 1}^{r}\lambda _{j}^{2}\eta _{j}^{2}}{(\sum _{j = 1}^{r}\lambda _{j}\eta _{j})^{2}} = \mathrm{Var}\left( \rho _{2, 2}^{2}(x, X) \right) . \end{aligned}$$

(15)

The validity of the inequality in (15) does not depend on the change $\lambda _{i} \rightarrow c\lambda _{i}$ for all $i$ and for any constant $c > 0$. Therefore, we can choose $\lambda _{1}, \lambda _{2}, \dots , \lambda _{r}$ such that $\sum _{i = 1}^{r}\lambda _{i} = 1$ and express quantities in (15) as moments of a random variable $\xi$ concentrated on [0, 1] having values $\lambda _{i}$ with probabilities $\lambda _{i}$.

Let $\tau _{j} = E[\xi ^{j}]$. In this notation, we have the following properties:

$$\begin{aligned}&\sum _{j = 1}^{r}\lambda _{j} = E[\xi ^{0}] = 1, \\&\sum _{j = 1}^{r}\lambda _{j}^{2} = E[\xi ] = \tau _{1},\\&\sum _{j = 1}^{r}\lambda _{j}\eta _{j} = \sum _{j = 1}^{r}\lambda _{j}(1 - \lambda _{j}) = 1 - E[\xi ] = 1 - \tau _{1},\\&\begin{aligned}\sum _{j = 1}^{r}\lambda _{j}^{2}\eta _{j}^{2} = \sum _{j = 1}^{r}\lambda _{j}^{2}(1 - \lambda _{j})^{2}&= E[\xi ] - 2E[\xi ^{2}] + E[\xi ^{3}] = \tau _{1} - 2\tau _{2} + \tau _{3}.\end{aligned}\, \end{aligned}$$

Using these properties, the inequality in (15) has the form

$$\begin{aligned} \tau _{1} \ge \frac{\tau _{1} - 2\tau _{2} + \tau _{3}}{(1 - \tau _{1})^{2}}. \end{aligned}$$

Rearranging gives $\tau _{1}^{3} + 2\tau _{2} - 2\tau _{1}^{2} - \tau _{3} \ge 0$, which is true for all probability measures on [0, 1]. $\square$

3 Applying the k-Simplicial Distance

3.1 Choosing $k$ in the k-Simplicial Distance

The choice of the parameter $k$ is integral to the performance of the k-simplicial distance. In this section, we show how different choices of k affect the distance through experimental results. We use three examples, in each of which we generate $N = 500$ points from a d-dimensional multivariate normal distribution, with zero mean and diagonal covariance matrix. The value of d and the eigenvalues of the covariance matrix used to generate the points are given in Table 1. We use the sample covariance matrix when computing our distance measures, and so the true eigenvalues of the matrix will differ slightly from those in the table.

Table 1 Details of datasets generated to be used in examples

For given values of $k \le r = \text {rank}(X)$, we find the $k$-simplicial distances between all points in the dataset to the dataset $X$ itself, for both $\delta = 2$ and $\delta = 1$. Note that for distances using $\delta = 1$, sub-sampling is used to find the distance, using the method described in Sect. 3.2. We compare the empirical cumulative distribution functions (CDF) produced by the k-simplicial distances in Figs. 1, 2 and 3. For examples with $\delta = 2$ we also consider the squared pseudo-Mahalanobis distance multiplied by $1/r$, which is equal to the $k$-simplicial distance with $k = r$.

Fig. 1

CDFs of k-simplicial distances with eigenvalues $\Lambda =\Lambda _{A}$ a $\delta = 2$, b $\delta = 1$

Fig. 2

CDFs of k-simplicial distances with eigenvalues $\Lambda =\Lambda _{B}$ a $\delta = 2$, b $\delta = 1$

Fig. 3

CDFs of k-simplicial distances with eigenvalues $\Lambda =\Lambda _{C}$ a $\delta = 2$, b $\delta = 1$

Example 1 Eigenvalues $\Lambda =\Lambda _{A}$. The CDFs for the distances measured for Dataset A using the k-simplicial distance with $\delta = 2$ are given in Fig. 1a and indicate that the squared Euclidean distance (proportional to the k-simplicial distance with $k = 1, \delta = 2$) produces a large range of distances with high variance, when compared to the distances produced when using other values of $k$. We see, in the $\delta = 2$ case, low values of $k$ (compared to the rank $r = 9$) begin to converge away from the squared Euclidean distance, and towards the squared pseudo-Mahalanobis distance quickly. Figure 1b shows a similar pattern for the distance with $\delta = 1$.

Example 2 Eigenvalues $\Lambda =\Lambda _{B}$. The CDFs for the k-simplicial distances using $\delta = 2$ on Dataset B are given in Fig. 2a. For relatively low values of $k$ (compared to the rank $r = 40$), such as $k = 10$, we see the distances converging to those produced when $k = r$, i.e. the pseudo-Mahalanobis distance in the case where $\delta =2$. A similar profile is observed for $\delta = 1$ in Fig. 2b, with CDFs of distances converging towards the CDF with $k = r = 40$ as $k$ increases.

Example 3 Eigenvalues $\Lambda =\Lambda _{C}$. The CDFs for the distances with $\delta = 2$ are given in Fig. 3a. Again, we see for relatively low values of $k$ (compared to rank $r = 22$) the distance measure converges towards the distance where $k = r$. Note that for the $k$-simplicial distances with $\delta = 1$, $k = 10$ in Fig. 3b, the CDF lies underneath that of $k = 22$, as the distances produced are so similar.

Figures 1, 2 and 3 all demonstrate that the $k$-simplicial distance transitions from the squared Euclidean distance multiplied by $1/\text {trace}(W)$ to the squared Mahalanobis distance multiplied by $1/r$ for $\delta = 2$ as k increases. A similar monotonic behaviour is shown for $\delta = 1$. The eigenvalues of the covariance matrix have an effect on what an appropriate choice of $k$ may be. It is important to ensure the most influential dimensions (that is, those with the largest eigenvalues) are all considered, by taking k larger than the number of large eigenvalues.

For example, consider Fig. 3. The two large eigenvalues in $\Lambda _{C}$ result in $k = 2$ behaving similarly to $k = 1$, particularly in the $\delta = 2$ case, whereas in Fig. 1, the CDF produced using the distance with $k = 2$ is very different to the CDF where $k = 1$, as there is only one large eigenvalue.

In general, we recommend using a value of $k$ that is larger than the number of ‘large’ eigenvalues the covariance matrix $W$ has, relative to the size of the other eigenvalues. This is easier to see when there is a clear elbow or ‘drop-off’ in the value of the eigenvalues. Otherwise, it can be appropriate to find the k-simplicial distances with several values of k and measure the best value according to some metric appropriate to the task. This is a common method for choosing a parameter value in many parameter-dependent tasks, such as K-means clustering.

Not much performance gain is made by choosing a value of $k$ that also encompasses the smaller eigenvalues. As an example of this, see Fig. 2, where there are seven ‘large’ eigenvalues, 33 ‘small’ eigenvalues and 10 zero eigenvalues. Using $k = 10$ does not give a huge improvement in performance compared to using $k = 5$ (where performance is measured here by the minimizing of variance) but it is computationally more expensive.

3.2 Numerical Computation of k-Simplicial Distances Using Sub-Sampling

When $\delta \ne 2$, the k-simplicial distance is calculated by averaging the volumes of all $\left( {\begin{array}{c}N\\ k\end{array}}\right)$ simplices formed with x and X. This can be computationally intensive, particularly for large N and d. To circumvent this problem, we can sample a subset of the simplices to reduce computation time to milliseconds. The size of the sub-sample of simplices depends on the user’s wish for precision. This size does not have to be large to achieve practically accurate approximations, which will be demonstrated in the examples that follow, where we use less than $0.05\%$ of all possible simplices when we use $k = 3$, and less than $0.0004\%$ when using $k = 4$.

Let $J$ be as defined in (3). To compute the k-simplicial distances, we have to compute the values of $P_{k, \delta }(x, X)$ defined in (4). The procedure to approximate these values is as follows. For any sampling proportion $\gamma \in [0, 1]$, we form $J^{(\gamma )}$, a subset of $J$ of size $|J^{(\gamma )}| = \left\lceil {\gamma \times \left( {\begin{array}{c}N\\ k\end{array}}\right) }\right\rceil$ and approximate (4) with

$$\begin{aligned} P_{k, \delta , \gamma }(x, X) = \frac{1}{|J^{(\gamma )}|}\sum _{(j_{1}, \dots , j_{k}) \in J^{(\gamma )}}\mathscr {V}_{k}^{\delta }(x, x_{j_{1}}, \dots , x_{j_{k}}). \end{aligned}$$

A simple but efficient way of constructing $J^{(\gamma )}$ consists of taking random samples of size k without replacement from the set $\{1,2, \ldots , N\}$, see Blom [4]. This reduces computation time dramatically, and in examples that follow we see such sub-sampling is highly effective in producing results extremely close to those of the ‘full’ distance measure, in which we average the volumes over all available simplices.

In the following examples we revisit the sets of eigenvalues given in Table 1 and calculate the distances from all points in a dataset to the dataset itself, using the full sample (where possible) and then a smaller sample using 10,000 simplices. We generate data according to the procedure outlined in the beginning of Sect. 3.1. We compare the effect that different sampling sizes have on the distribution of distances calculated though investigating histograms and moments of these distances. Our analysis in Sect. 3.1 indicates that using low values of $k$ gives good performance, and is less computationally intensive than using higher values, so we will use $k = 3$ and $k = 4$ in the sub-sampling examples that follow.

Example 1 Eigenvalues $\Lambda =\Lambda _{A}$. Figure 4a shows histograms of the distances between all points of dataset A to the dataset itself, as produced by the $k$-simplicial distance with $\delta = 2,\, k = 3$. The blue solid histogram shows the ‘full’ distances with no sub-sampling (using polynomials), and the orange dotted histogram shows the sub-sampled distance with 10,000 simplices. This is repeated for other parameters in the rest of Fig. 4, as detailed in the captions.

These histograms show that the distribution of distances produced using a small sample of simplices is extremely similar to the distribution of distances produced using the full sample of simplices available. For the examples using $\delta = 1$, we cannot produce the full distance directly as it requires the computation of the volume of $\left( {\begin{array}{c}500\\ k\end{array}}\right)$ simplices, so we compare the distances produced using a sub-sample of 10,000 simplices to the distances when using a larger sub-sample of simplices (1% of the total amount of simplices in the $k = 3$ case, 0.01% in the $k = 4$ case). In both cases, the distribution of the larger sample and the 10,000 simplex sample remain very similar. Table 2a and b also demonstrate this, with the summary statistics remaining close even for small samples.

Fig. 4

Histograms to compare the distribution of the k-simplicial distances from all points to the mean for eigenvalues $\Lambda _{A}$ with different parameters k and $\delta$ for different sampling amounts. Blue, solid histograms show the distances produced using the full sample of simplices when $k = 3$, and a larger sample when $k = 4$. The orange dotted histograms show the distances produced when using a sample of 10,000 simplices.

Table 2 Summary statistics of the distances when (a) $k = 3$, (b) $k = 4$ with eigenvalues $\Lambda _{A}$

Example 2 Eigenvalues $\Lambda =\Lambda _{B}$. We again see in Fig.  5 and Table 3a and b that using a low number of simplices (compared to the full amount of simplices available, or a large sample) produces distances that are mostly the same as the full distance measure. This example illustrates that the sampling method is effective even in cases with a lot of small and zero eigenvalues.

Fig. 5

Histograms to compare the distribution of the k-simplicial distances from all points to the mean for eigenvalues $\Lambda _{B}$ with different parameters k and $\delta$ for different sampling amounts. Blue, solid histograms show the distances produced using the full sample of simplices when $k = 3$, and a larger sample when $k = 4$. The orange dotted histograms show the distances produced when using a sample of 10,000 simplices.

Table 3 Summary statistics of the distances when (a) $k = 3$, (b) $k = 4$ with eigenvalues $\Lambda _{B}$

Example 3 Eigenvalues $\Lambda =\Lambda _{C}$. Figure 6 and Table 4a and b show that the number of small or zero eigenvalues does not influence the performance of the sub-sampling. Overall, we see sub-sampling is an effective way to drastically reduce computation time while maintaining the same results as the full k-simplicial distance. This means that using the distance with $\delta \ne 2$ is much more accessible than it otherwise would be.

Fig. 6

Histograms to compare the distribution of the k-simplicial distances from all points to the mean for eigenvalues $\Lambda _{C}$ with different parameters k and $\delta$ for different sampling amounts. Blue, solid histograms show the distances produced using the full sample of simplices when $k = 3$, and a larger sample when $k = 4$. The orange dotted histograms show the distances produced when using a sample of 10,000 simplices.

Table 4 Summary statistics of the distances when (a) $k = 3$, (b) $k = 4$ with eigenvalues $\Lambda _{C}$

3.3 Outlier Labelling Example

In this section, we illustrate one potential application of the k-simplicial distance measure. The $k$-simplicial distance could be a useful tool in identifying outlying points in high-dimensional degenerate datasets, where the Euclidean distance struggles to measure distance meaningfully due to the sparse and correlated nature of the data, and the Mahalanobis relies on the inversion of a matrix possessing many small (and potentially zero) eigenvalues. We investigate how different values of the parameter $k$ and the scalar power $\delta$ perform in identifying outliers.

We perform the following experiments. We consider three 10-dimensional examples, each with different sets of data. Each dataset $D_{i}, \, i = \{I, II, III\}$, is made up of two clusters: $D_{i} = D_{i, 1} + D_{i, 2}$. The first cluster $D_{i, 1}$ has 450 points, mean $\mu _{1}$ as specified in Table 5 and covariance matrix produced by a matrix with eigenvalues as specified in the table, rotated by a rotation matrix. The second cluster $D_{i, 2}$ has 50 points, a different mean $\mu _{2}$ but the same covariance matrix as $D_{i, 1}$. By doing this, we test the robustness of the distances against rotations and correlations in the data, as well as its ability to tell two similar but separate clusters apart.

Table 5 Datasets to be used in outlier labelling

We measure the distance of all points in the dataset $D_{i}$ to the largest cluster, $D_{i, 1}$. We label the furthest 50 points from this cluster $D_{i, 1}$ as outliers for each dataset $i$. We consider how many of the points the $k$-simplicial distances correctly label as outliers from $D_{i, 1}$ for different values of $k$ and $\delta$. If it were to incorrectly label all the outlying points as inliers, we would have a minimum value of 400. If the distance correctly labels all points, we will get a value of 500. Table 6 contains the number of points correctly labelled by the distance measures using different values of $k$ and $\delta$ for the k-simplicial distances. In Table 7, we provide the Area Under the Receiver Operating Characteristic Curve (AUC) score for the labels produced by the distances, for different values of $k$ and $\delta$. The AUC score measures the overall performance of a binary classifier, where a score of 1 indicates a perfect labelling and 0.5 is the minimum score [18].

Table 6 Number of points correctly labelled by the distance measures using different values of $k$ for the k-simplicial distances

Table 7 AUC scores for outlier detection when using the k-simplicial distance with different values of $k$ and $\delta$

Considering the $k$-simplicial distance with $\delta = 2$, we see that the values of $k$ which perform best are those slightly larger than the number of ‘large’ eigenvalues. For Dataset I, we have 4 ‘large’ eigenvalues and values of $k = 5, 6$ perform best when using $\delta = 2$. Similar results are shown in Datasets II and III. Larger values of $k$ begin to break down when $\delta = 2$ as they require the use of the smaller eigenvalues when forming the simplices. This indicates that lower values of $k$ outperform the squared pseudo-Mahalanobis distance multiplied by $1/r$.

Distances using $\delta = 1$ are more robust to the effect of degeneracy. The performance improves as $k$ increases, but unlike the $\delta = 2$ case, there is no breakdown in success once $k$ encompasses the smaller eigenvalues too, making it less sensitive to the choice of $k$ than the distance with $\delta = 2$. These distances were computed using very low sub-sampling amounts, and so there is not considerable computational time disadvantage in using $\delta = 1$ over $\delta = 2$. Overall, this example illustrates that using $\delta = 1$, even with sub-sampling, can give a more stable distance measure than using $\delta = 2$ as $k$ increases, particularly for outlier detection applications.

4 k-Minimal-Variance Distances

Assume that $X$ is a normally distributed $d$-dimensional dataset, with sample mean $\mu$ and sample covariance matrix $W$. We now introduce a family of generalized squared distances from a point $x$ to the set $X$, in the form

$$\begin{aligned} \rho _{A}^{2}(x, X) = (x - \mu )^{\top }A(x-\mu ), \end{aligned}$$

(16)

where $A$ is a matrix polynomial in $W$ of user-defined degree $k-1 \le r$, where $r = \mathrm{rank}(X)$. From the moments of a quadratic form (see (23) in Appendix A), we have

$$\begin{aligned} E\left( \rho _{A}^{2}(x, X)\right)&= \text {trace}(AW),\,\,\, \text {Var}\left( \rho _{A}^{2}(x, X)\right) = 2\text {trace}\left( (AW)^{2}\right) . \end{aligned}$$

For given $k \le r$, we wish to find the matrix $A$ such that $\text {trace}(AW) = d$ holds and $\text {Var}\left( \rho _{A}^{2}(x, X)\right)$ is minimized. The condition $\text {trace}(AW) = d$ ensures the identifiability of a solution from the minimization of the Lagrange function (20) and weights the solution towards $W^{-1}$ (if $W^{-1}$ exists).

We can motivate minimizing the variance of the distances by considering the CDFs in Figs. 1, 2 and 3. The Mahalanobis distance has the smallest variance out of all distances considered, and can be written as a $(d-1)$-degree polynomial when the covariance matrix is non-singular. We aim to replicate the minimization of the variance of the distances produced through lower degree polynomials that also work in the case of a singular covariance matrix, making for a quicker and more versatile method.

Let $A$ be a polynomial in $W$, expressed as

$$\begin{aligned} A = \sum _{i = 0}^{k-1}\theta _{i}W^{i}. \end{aligned}$$

(17)

The first moment of the distance (16) is $E\left( \rho _{A}^{2}(x, X)\right) = \sum _{i = 0}^{k-1}\theta _{i}\text {trace}(W^{i + 1}).$ Note that $\mathrm{trace}(W^{i}) = \sum _{j = 1}^{d}\lambda _{j}^{i}$, where $\lambda _{1}, \dots , \lambda _{d}$ are the eigenvalues of $W$. Then let $\theta = \left( \theta _{0}, \theta _{1}, \dots , \theta _{k-1}\right) ^{\top }$, and define the matrix

$$\begin{aligned} Y = \left( y_{ji}\right) _{j = 1, \dots , d, \, i = 0, \dots , k-1}=\left( \lambda _{j}^{i + 1}\right) _{j = 1, \dots , d, \, i = 0, \dots , k-1}. \end{aligned}$$

Using this notation, the variance of the distance (16) can be written using (23) from Appendix A as

$$\begin{aligned} \text {Var}\left( \rho _{A}^{2}(x, X)\right) = 2\theta ^{\top }Y^{\top }Y\theta . \end{aligned}$$

(18)

Proposition 1

For given $k \le r$, let $\mathcal {A}_{k-1}$ be the set of matrices $A$ of the form (17) satisfying the condition $\mathrm{trace}(AW) = d$. The solution to the optimization problem

$$\begin{aligned} A^{*} = {{\,\mathrm{arg\,min}\,}}_{A \in \mathcal {A}_{k-1}}{\text {Var}}\left( \rho _{A}^{2}(x, X)\right) = \sum _{i = 0}^{k-1}\theta _{i}^{*}W^{i} \end{aligned}$$

is given by the set of coefficients

$$\begin{aligned} \theta ^{*} = \frac{d}{S^{\top }(Y^{\top }Y)^{-}S}(Y^{\top }Y)^{-}S, \end{aligned}$$

where

$$\begin{aligned} S^{\top } = \left( \mathrm{trace}(W^{i+1})\right) _{i = 0}^{k-1} = \left( \mathrm{trace}(W), \mathrm{trace}(W^{2}), \dots , \mathrm{trace}(W^{k})\right) . \end{aligned}$$

For the matrix $A^{*}$, the variance of the distance (16) is given by

$$\begin{aligned} \text {Var}(\rho _{A^{*}}^{2}(x, X)) = 2d^{2}/\left( S^{\top }(Y^{\top }Y)^{-}S\right) . \end{aligned}$$

(19)

If the matrix $Y^{\top }Y$ is non-degenerate, then $(Y^{\top }Y)^{-}$ becomes $(Y^{\top }Y)^{-1}$.

Proof

The Lagrange function used to minimize the variance (18) with the constraint $\text {trace}(AW) = \sum _{i = 0}^{k-1}\theta _{i}\text {trace}(W^{i + 1}) = d$ is

$$\begin{aligned} \mathcal {L}(\theta , \omega ) = \frac{1}{2}\theta ^{\top }Y^{\top }Y\theta - \omega (\theta ^{\top }S - d). \end{aligned}$$

(20)

Note that $\theta ^{\top }S= \text {trace}(AW)$.

Differentiating the Lagrange function with respect to $\theta$ and setting the result equal to 0, we get $Y^{\top }Y\theta = \omega S$, which gives: $\theta ^{*} = \omega (Y^{\top }Y)^{-}S.$ The required value of $\omega$ is found from the unbiasedness condition $\text {trace}(AW) = d$, giving $\omega = {d}/{S^{\top }(Y^{\top }Y)^{-}S}.$ Substituting $\theta ^{*}$ into (18) gives the variance of the distance as in (19). $\square$

5 Experimental Analysis

5.1 Efficiency of k-Minimal-Variance Distances Compared to k-Simplicial Distances

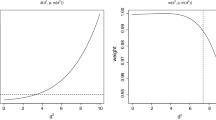
We consider the efficiency of the k-minimal-variance distances (16) with $A=A^{*}$ as derived in Theorem 1 and k-simplicial distances (11) with $\delta =2$ relative to the (sometimes pseudo-)Mahalanobis distance. As we consider the Mahalanobis distance multiplied by $1/r$ to align with the $k$-simplicial distance, we must also consider the $k$-minimal-variance distance multiplied by $1/d$ for comparability.

We define the efficiency of the k-minimal-variance distances as

$$\begin{aligned} \mathrm{eff}_{MV}^{(k)}=\frac{\mathrm{Var}\left( \rho _{A^{*}/d}^{2}(x, X)\right) }{\mathrm{Var}\left( \rho _{r, 2}^{2}(x, X)\right) }=\frac{2/\left( S^{\top }(Y^{\top }Y)^{-}S\right) }{2/r}\, , \end{aligned}$$

(21)

with $\mathrm{Var}\left( \rho _{A^{*}}^{2}(x, X)\right)$ derived in (19). We define the efficiency of the k-simplicial distances with $\delta =2$ as

$$\begin{aligned} \mathrm{eff}_{simp}^{(k)}=\frac{\mathrm{Var}\left( \rho _{k,2}^{2}(x, X)\right) }{\mathrm{Var}\left( \rho _{r, 2}^{2}(x, X)\right) }=\frac{({2}/{k^{2}})\mathrm{trace}\left( (S_{k}W)^{2}\right) }{2/r}, \end{aligned}$$

(22)

with $\mathrm{Var}\left( \rho _{k,2}^{2}(x, X)\right)$ stated in (24) in Appendix A.

We generate $N = 500$ points $X = \{x_{1}, \dots , x_{N}\} \subset \mathbb {R}^{d\times N}$ from a d-dimensional multivariate normal distribution with zero mean and diagonal covariance matrix $W$ with eigenvalues $\Lambda =\{\lambda _{1}, \dots , \lambda _{d}\}$. We take the eigenvalues to be:

$$\begin{aligned} \Lambda _{1}= & {} (10, 7, 6, 5, 4, 3, 2, 1, 1, 1)\, ,\\ \Lambda _{2}= & {} (10, 4, 3, 2, 1, 1, 1, 1, 1, 1)\, ,\\ \Lambda _{3}= & {} (10, 5, 3, 2, 1, 1, 1, 1, 1, 0)\, . \end{aligned}$$

Table 8 demonstrates the high-efficiency of the k-minimal-variance distances even for small k. Note that $k-1$ is the order of the polynomial in $W$ minimizing (18); in this example, linear and quadratic polynomials perform well. The efficiency of the k-simplicial distances improves as k gets larger but also has variance tolerably close to that of the Mahalanobis distance even for k significantly smaller than r.

Table 8 Efficiencies (21) and (22) for different k, with three different sets of eigenvalues of the covariance matrix $W$ given by $\Lambda _{i}$, $i=1,2,3$.

For larger dimensions, with covariance matrices possessing a number of zero eigenvalues, the examples are more striking. Table 9 gives the results of performing the same exercise on the datasets described in Sect. 3.1, with eigenvalues given in Table 1. Table 9 shows that the k-minimal-variance distances start to have similar variance to the squared (pseudo-)Mahalanobis distance using much lower values of $k$ than in the $k$-simplicial distance with $\delta = 2$. For values as low as $k = 2$, we see the variance of the k-minimal-variance distance is much closer to that of the Mahalanobis distance than the k-simplicial distances.

We note little performance gain when choosing $k > 3$ in these examples, indicating that $A^*$ even with small $k$ is often a good enough approximation to the inverse of the covariance matrix from the viewpoint of the distance generated by this matrix. From an efficiency perspective, the k-minimal-variance produces better results at a lower computational cost than the k-simplicial distance.

Table 9 Efficiencies (21) and (22) for different k, with three different sets of eigenvalues of the covariance matrix $W$ as given in Table 1 in Sect. 3.1.

5.2 Comparison of Performances of the $K$-Means Clustering Algorithm with Different Distances

We compare the performance of the $K$-Means clustering algorithm [26] when applied using the Euclidean distance, the Mahalanobis distance, the k-minimal-variance distance and the k-simplicial distance (with $\delta = 2$). We do this by applying $K$-Means to 5 real datasets, obtained from the UCI Machine Learning Repository [11], with the exception of the ‘Digits’ dataset, which was obtained through the Python package sklearn’s data loading functions [31]. The details of these datasets are given in Table 10.

Each dataset was appropriately preprocessed: rows with missing values were removed, and the data was normalized such that each variable has values in range [0, 1]. It is important to note that the $K$ used in the $K$-Means clustering algorithm is used to indicate how many clusters we seek, and is different to the $k$ used in our distance measures. For each dataset, the choice of $K$ in the $K$-Means algorithm is used as the ‘true’ number of clusters, given in Table 10, as these datasets are all fully labelled.

Table 10 Real datasets used to evaluate performance of distances when used with $K$-Means clustering

The $K$-Means algorithm is classically applied using the Euclidean distance, but research has shown success in applying the algorithm with the Mahalanobis distance to exploit the covariance structure of a dataset (see Gnanadesikan et al. [16], or more recently [30]). The method of applying $K$-Means with the Mahalanobis, k-minimal-variance or k-simplicial distances is given in Algorithm 1, following the algorithm given in Melnykov and Melnykov [8]. These distance measures require the covariance matrix of each cluster; and as such we require initial estimates of the clusters. We obtain these initial estimates by performing a few iterations of the $K$-Means algorithm using the Euclidean distance. Clearly, this initial estimate can have a large influence on the resulting clusters found by the other distances, and so we run the $K$-Means algorithm 1000 times for each distance.

As this is a supervised task, we can compare the labels given by $K$-Means to the ‘true’ labels to assess the performance of the clustering algorithm. We do this using two external evaluation methods, namely the adjusted rand (AR) score [20, 31] and the purity score [28]. We use these two different evaluation methods to corroborate the results. The adjusted rand score is calculated as follows.

Let $L_{T}$ be the vector of true labels, and let $L_{P}$ be the labels assigned by the $K$-Means clustering. Define $a$ as the number of pairs of points in the same set in $L_{T}$ and in the same set in $L_{P}$, i.e. the number of points whose labels are the same in $L_{T}$ and $L_{P}$. Define $b$ as the number of pairs of points in different sets in $L_{T}$ and in different sets in $L_{P}$, i.e. the number of points whose labels are different in $L_{T}$ and $L_{P}$. The unadjusted rand score is given by

$$\begin{aligned} R = \frac{a + b}{\nu }, \end{aligned}$$

where $\nu$ is the total number of possible pairs in the dataset, without ordering. The unadjusted rand score does not account for the possibility that random label assignments can perform well, so we discount the expected rand score $E[R]$ of random labellings by defining the adjusted rand score as

$$\begin{aligned} AR = \frac{R - E[R]}{\text {max}(R) - E[R]}. \end{aligned}$$

Fig. 7

Adjusted rand scores and purity scores of the clusterings produced by $K$-Means when using different distance measures. ED: Euclidean distance, MD: Mahalanobis distance, MV-k: Minimal-variance distance with parameter $k$, SD-k: Simplicial distance with parameter $k$

The adjusted rand score takes values in [-1, 1], where 1 indicates a perfect matching between $L_{T}$ and $L_{P}$.

To find the purity score, we proceed as follows: let $T = \{t_{1}, t_{2}, \dots , t_{m}\}$ be the set of ‘true’ clusters in the data, and let $P = \{p_{1}, p_{2}, \dots , p_{K}\}$ be the set of predicted clusters. The purity score measures the extent to which a predicted cluster $p_{i}$ only contains points from a single ‘true’ cluster $t_{j}$:

$$\begin{aligned} \mathcal {P}(T, P) = \frac{1}{N}\sum _{i = 1}^{K}\max _{j}|p_{i}\cap t_{j}|, \end{aligned}$$

where $N$ is the total number of points. That is, for each predicted cluster $p_{i}$, we count the highest number of points from a single true cluster $t_{j}$ predicted to be in $p_{i}$. These counts are summed and divided by the total number of observations. The purity score takes values in [0, 1], with 1 being a perfect clustering.

Figure 7 gives the AR and purity scores for the $K$-Means clustering of each dataset using the varying distance measures being considered. For the k-minimal-variance and k-simplicial distances, we show the distances with values of $k$ which produced the highest scores. Note that the pseudo-Mahalanobis distance is used in cases where the data is degenerate. The eigenvalues for each of the datasets in Table 10 can be found in Appendix B. The influence of these eigenvalues on the performance of the different distance measures is important, particularly when choosing values of k. When we discuss eigenvalues being ‘close to zero’, this is in relation to the largest eigenvalue of the dataset. There is no specific threshold for being ‘close to zero’, but the examples should give some intuition about choosing the parameter k.

Tables 11, 12 and 13 give the median AR score for each dataset by each method of clustering, and the standard deviation of these scores, with bold values denoting the highest score(s) out of all methods used. Although the AR score and the purity score measure distinct aspects of the success of a clustering, Fig. 7 shows that the same patterns emerge for both evaluation methods, and so we only consider the AR score in the tables.

Table 11 Iris dataset: Median AR scores (and standard deviations) for each given distance

Iris is a 4-dimensional dataset, with no extreme small eigenvalues in comparison to its largest eigenvalue. Figures 7a, b and Table 11 show that the Mahalanobis distance performs best, joint with the k-simplicial and k-minimal-variance distances when $k = 4$ (recall that these distances are equal to the Mahalanobis distance when $k = d$). The Iris dataset is low-dimensional and full-rank, and hence the Mahalanobis distance can use the true inverse of the covariance matrix. This example illustrates the performance gains that can be made in cluster analysis by taking the correlations in the data into consideration. Even when we use $k=3$ in the k-simplicial and k-minimal-variance distances, we achieve better results than the Euclidean distance.

Table 12 Median AR scores (and standard deviations) for each given dataset and distance

Figures 7a, b and Table 12a consider the Wine dataset, and show that the Mahalanobis, k-minimal-variance and k-simplicial distances outperforms the Euclidean distance, again highlighting the importance of accounting for correlation. The Wine dataset has some very small eigenvalues compared to its largest eigenvalue, and as such the Moore–Penrose pseudo-inverse is likely to have been adversely impacted [19]. Choosing the k-minimal-variance or k-simplicial distance avoids this impact, and as such produces better clustering results. This example also highlights that the k-minimal-variance distance performs very well with lower values of k, whereas the k-simplicial distance requires a higher value of k to achieve its best results, as seen before in the efficiency evaluations in Sect. 5.1. This gives better computational-time for the best results when using the k-minimal-variance distance, but does make the distance more sensitive to a too-high choice of k, as seen by the decrease in AR scores in Table 12a.

The Image Segmentation dataset has a number of very large eigenvalues, some eigenvalues very close to zero, and five zero eigenvalues. Figures 7a and b shows that the Mahalanobis distance performs worse than the Euclidean distance, perhaps due to the effect of very small eigenvalues on the Moore–Penrose pseudo-inverse. The k-minimal-variance and k-simplicial distance outperform the Mahalanobis distance here, as they are less likely to be adversely affected by these small eigenvalues. Table 12b shows that the k-minimal-variance distance attains the highest AR score out of all the distances, but does not improve greatly on the Euclidean distance.

Table 13 Median AR scores (and standard deviations) for each given dataset and distance

The Digits and Protein datasets (Table 13a, and b, respectively) both have a substantial number of small and zero eigenvalues (see Appendix B), indicating why our distances perform better than the pseudo-Mahalanobis distance. The Mahalanobis distance does not add much performance gain compared to the Euclidean distance in these examples, but the correct choice of k in the k-minimal-variance or k-simplicial distances provides improvement.

In these examples, we see that K-Means with the k-minimal-variance distance reaches its best adjusted rand score with relatively low k, whereas the k-simplicial distance needs higher values of k to reach this. However, the k-simplicial distance is less likely to breakdown for too-high a choice of k, as we see in Tables 12a and 13a with the k-minimal-variance. For the k-simplicial distance, the values of k that produce the best adjusted rand score roughly match with the number of ‘larger’ eigenvalues in the datasets.

6 Conclusion

In this paper, we have continued the work done by Pronzato et al. [34] in researching the k-simplicial distance. This distance considers the covariance structure of the data, but is less adversely affected by the presence of small eigenvalues than the Mahalanobis distance.

We have studied the choice of the parameter k in detail, through the use of numerical examples, illustrating that too low a choice of k does not give much improvement on the Euclidean distance, and too high a choice of k doesn’t give much performance benefit over lower values, but does increase computational complexity. We recommend a choice of k influenced by the number of ‘large’ eigenvalues present, with respect to the other eigenvalues of the sample covariance matrix. We also discuss the benefits and limitations of different choices of the parameter $\delta$: $\delta = 1$ is more robust, and well suited to applications such as outlier detection, but does not have a fast method of full computation. If $\delta = 2$, we have a significantly faster and easier method of producing the distance, but this is more likely to be influenced by the presence of outliers. We discuss the implementation of sub-sampling simplices, which greatly improves computation time when we are using the distance with $\delta = 1$ with minimal changes to the results of the distance.

We have also introduced a new measure of distance, namely the k-minimal-variance distance. Again, this distance is less affected by the presence of small eigenvalues than the Euclidean and Mahalanobis distances (for appropriate choices of the parameter k) but is highly influenced by the choice of the parameter k which needs to be chosen carefully to ensure good performance of the distance.

Overall, we show that the k-minimal-variance distance is more efficient at minimizing the variance of the distances for lower choices of k (and therefore has better computation time) than the k-simplicial distance, but that the k-simplicial distance is less likely to be negatively affected by too-high a choice of k. We have given several examples where the k-minimal-variance and/or the k-simplicial distances outperform the multivariate distances commonly used. Namely, these proposed distances perform well where other classical distances often fail: when data is correlated, degenerate and has small eigenvalues, as well as possibly zero-valued eigenvalues.

Appendices

Appendix A: Moments and Distributions of Distances

From Rencher and Schaalje [36], let $y$ be a random vector with mean $\mu$ and covariance matrix $W$, and let $A$ be a symmetric matrix of constants, then

$$\begin{aligned} E\left( y^{\top }Ay\right) = \text {trace}(AW) + \mu ^{\top }A\mu . \end{aligned}$$

If $y$ is normally distributed with sample mean $\mu$ and sample covariance matrix $W$, then

$$\begin{aligned} \text {Var}\left( y^{\top }Ay\right) = 2\text {trace}\left( (AW)^{2}\right) + 4\mu ^{\top }AWA\mu . \end{aligned}$$

Our distances considered in this paper are generalized squared distances of the form

$$\begin{aligned} \rho _{A}^{2}(x, X) = (x - \mu )^{\top }A(x - \mu ), \end{aligned}$$

where $x$ is normally distributed with sample mean $\mu$ and sample covariance matrix $W$. Therefore we replace $y$ with $(x - \mu )$, which is normally distributed with zero mean, giving:

$$\begin{aligned} E\left( \rho _{A}^{2}(x, X)\right) = \text {trace}(AW),\,\,\, \text {Var}\left( \rho _{A}^{2}(x, X)\right) = 2\text {trace}\left( (AW)^{2}\right) . \end{aligned}$$

(23)

1.1 A1: Moments of the $k$-Simplicial Distance When ($\delta$ = 2)

For a point $x \in X$, where $X$ is normally distributed with sample mean $\mu$ and sample covariance matrix $W$, consider $\rho ^{2}_{k, 2}(x, X) = (x - \mu )^{\top } \frac{S_{k}}{k} (x- \mu )$, i.e. the squared $k$-simplicial distance from the sample mean $\mu$ to a point $x$. We have

$$\begin{aligned} E\left( \rho ^{2}_{k, 2}(x, X)\right) = \frac{1}{k}\text {trace}(S_{k}W),\,\,\, \text {Var}\left( \rho ^{2}_{k, 2}(x, X)\right) = \frac{2}{k^{2}}\text {trace}\left( (S_{k}W)^{2}\right) . \end{aligned}$$

(24)

1.2 A2: Moments of the Squared Euclidean Distance Divided by Trace($W$)

Applying the formulae for the moments of quadratic forms to the squared Euclidean distance divided by trace($W)$, where we take $A = \frac{I_{d}}{\text {trace}(W)}$, we have

$$\begin{aligned} E\left( \rho ^{2}_{1, 2}(x, X)\right) = \text {trace}\left( \frac{W}{\text {trace}(W)}\right) = \frac{\text {trace}(W)}{\text {trace}(W)} = 1, \end{aligned}$$

$$\begin{aligned} \text {Var}\left( \rho ^{2}_{1, 2}(x, X)\right) = 2\text {trace}\left( \frac{W^{2}}{\text {trace}(W)^{2}}\right) = \frac{2\text {trace}(W^{2})}{\text {trace}(W)^{2}} = \frac{2\sum _{i = 1}^{d}\lambda _{i}^{2}}{(\sum _{i = 1}^{d}\lambda _{i})^{2}}. \end{aligned}$$

(25)

Appendix B: Eigenvalues of the Five Real-Life Datasets

Below are the eigenvalues of the real datasets used in the $K$-Means clustering examples in Sect. 5.2.

Iris: [4.2, 0.24, 0.08, 0.02]

Wine: [99201.8, 172.5, 9.4, 5.0, 1.2, 0.84, 0.28, 0.15, 0.11, 0.07, 0.04, 0.02, 0.008]

Image Seg.: [11393.8, 9183.6, 5479.5, 2300.1, 217.2, 161.7, 55.7, 14.4, 3.6, 1.2, 0.2, 0.02, 0.001, 0.001, 0, 0, 0, 0, 0]

Digits: [179.0, 163.7, 141.8, 101.1, 69.5, 59.1, 51.9, 44.0, 40.3, 37.0, 28.5, 27.3, 21.9, 21.3, 17.6, 16.9, 15.9, 15.0, 12.2, 10.9, 10.7, 9.6, 9.2, 8.7, 8.4, 7.2, 6.9, 6.2, 5.9, 5.2, 4.5, 4.2, 4.0, 3.9, 3.7, 3.5, 3.1, 2.7, 2.7, 2.5, 2.3, 1.9, 1.8, 1.7, 1.4, 1.3, 1.3, 0.93, 0.67, 0.49, 0.25, 0.09, 0.06, 0.06, 0.04, 0.02, 0.008, 0.004, 0.001, 0.001, 0, 0, 0, 0]

Protein: [2.4, 1.6, 0.5, 0.3, 0.2, 0.1, 0.08, 0.07, 0.06, 0.05, 0.04, 0.03, 0.03, 0.03, 0.02, 0.02, 0.01, 0.01, 0.01, 0.008, 0.008, 0.006, 0.006, 0.005, 0.005, 0.004, 0.004, 0.003, 0.003, 0.003, 0.002, 0.002, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.0]