Extension of Marginal Complementary Log–Log Model and Separations of Marginal Homogeneity for Ordinal Categorical Data

Abstract

The present paper considers a model that indicates the structure of inhomogeneity for marginal distributions for ordinal categorical data. The model is based on the complementary log–log transformation of marginal cumulative probability. A theorem that the marginal homogeneity model holds if and only if the proposed model and the marginal mean and variance equality model holds is given. Also, a model based on the conditional marginal distribution is considered under certain condition.

1 Introduction

Table 1 Occupational status for Japanese father–son pairs; from Tominaga [19, p. 131]

Two-way contingency tables with the same row and column categories occur frequently in, for example, panel studies, occupational studies and longitudinal studies. The data in Table 1 illustrate occupational status for Japanese father–son pairs, which is taken directly from Tominaga [19, p. 131]. Each observation pairs father’s occupation with son’s occupation. These variables have four levels with ordinal categories. The smaller category number means higher status. For the data in Table 1, many observations concentrate on main-diagonal cells. Therefore, the independence between two variables does not hold in the contingency table which is constructed from matched-pairs data. Then, we are interested in considering various symmetry (or asymmetry) instead of independence. This paper treats methods for analyzing square tables.

For a $r \times r$ square contingency table with ordered categories, let X and Y be the row and column random variables, respectively. Also, let $p_{ij}$ denotes the probability that an observation will fall in the ith row and jth column of the table for $i = 1, \ldots ,r; j = 1, \ldots ,r$. We assume $p_{ij}>0$ for all i and j. Bowker [4] considered the symmetry model defined by $p_{ij}=p_{ji}$ for $i<j$. The marginal homogeneity (MH) model is defined by

$$\begin{aligned} p_{i\cdot } = p_{\cdot i} \quad (i = 1, \ldots , r), \end{aligned}$$

where $p_{i\cdot } = \sum ^r_{t=1}p_{it}$ and $p_{\cdot i} = \sum ^r_{s=1}p_{si}$ (Stuart [15]). This model indicates the structure that satisfies the identity of marginal distributions of row and column. Also, Caussinus [5] showed the theorem that the symmetry model holds if and only if both the quasi-symmetry model, which indicates a symmetric structure for odds ratios, and the MH model holds. We shall refer this theorem as separation of symmetry. For the details of method for joint distribution, please see Bishop et al. [3] and Agresti [2].

Let $F^X_i$ and $F^Y_i$ denote the marginal cumulative probabilities of X and Y, respectively, namely $F^X_i = \sum ^i_{s=1}p_{s\cdot }$ and $F^Y_i = \sum ^i_{t=1}p_{\cdot t}$ for $i = 1, \ldots , r-1$. The MH model may also be expressed as

$$\begin{aligned} F^X_i = F^Y_i \quad (i= 1,\ldots , r-1). \end{aligned}$$

When the MH model fits poorly for a real data set, we are interested in applying some extension of the MH model. Indeed, the MH model fits the data in Table 1 poorly (see Sect. 6.1). McCullagh [11] considered the marginal cumulative logistic (ML) model defined as follows:

$$\begin{aligned} L_i^X=\varDelta +L_i^Y\quad (i=1,\ldots ,r-1), \end{aligned}$$

where $L_i^X$ and $L_i^Y$ denote the logit transformations of $F_i^X$ and $F_i^Y$, respectively. That is,

$$\begin{aligned} L_i^X=\log \frac{F_i^X}{1-F_i^X}, \quad L_i^Y=\log \frac{F_i^Y}{1-F_i^Y}. \end{aligned}$$

Also, see Agresti [1, p. 205]. The ML model with $\varDelta =0$ is the MH model, namely the ML model is the extension of the MH model. Moreover, Miyamoto et al. [12] proposed the conditional ML (CML) model, and Saigusa et al. [13] proposed the marginal complementary log–log (MCLL) model. The ML (CML) model states that one (conditional) marginal distribution is a location shift of the other (conditional) marginal distribution on a logistic scale. The MCLL model states that one marginal distribution is a location shift of the other marginal distribution in terms of a function $1-\exp (-\exp (x))$. In this paper, we consider a model that is more relaxed than these models. The extensions of the ML and CML models exist (Kurakami et al. [9]). Therefore, an extension of the MCLL model is proposed in Sect. 2.

Caussinus [5] gave the separation of symmetry. The separation may be useful to see a reason for the poor fit of the symmetry model when the symmetry model fits the data poorly. Thus, we are interested in considering a necessary and sufficient condition of the MH model. We give the separaton of marginal homogeneity in Sect. 3.

This paper is organized as follows. Section 2 proposes an extension of the MCLL model. Section 3 shows two theorems. Section 4 extends the proposed model into multi-way contingency table. Section 5 discusses the goodness-of-fit test. Section 6 gives examples. Section 7 concludes this paper.

2 Extension of MCLL

Let $C^X_i$ and $C^Y_i$ denote the marginal cumulative complementary log–log transforms of $F_i^X$ and $F_i^Y$, respectively. That is,

$$\begin{aligned} C^X_i = \log \left( -\log \left( 1 - F^X_i \right) \right) , \quad C^Y_i = \log \left( -\log \left( 1 - F^Y_i \right) \right) \quad (i=1,\ldots ,r-1). \end{aligned}$$

The extended MCLL (EMCLL) model is defined by

$$\begin{aligned} C^X_i = C^Y_i + i\log ( \varDelta _1 ) + \log ( \varDelta _2 ) \quad (i=1,\dots ,r-1). \end{aligned}$$

(1)

The EMCLL model is an extension of the MCLL model. We would like to note that (i) the EMCLL model with $\varDelta _{1}=\varDelta _{2}=1$ is reduced to the MH model and (ii) the EMCLL model with $\varDelta _{1}=1$ is reduced to the MCLL model. This model indicates that the probability that X is $i+1$ or above, is equal to the probability that Y is $i+1$ or above to the power of $\varDelta ^i_1 \varDelta _2$, for $i=1,\ldots ,r-1$, namely,

$$\begin{aligned} (1-F^X_i) = (1-F^Y_i)^{\varDelta ^i_1 \varDelta _2} \quad (i=1,\ldots , r-1). \end{aligned}$$

Also, in Eq. (1), $i\log (\varDelta _{1})+\log (\varDelta _{2})$ is the difference between the two random variables on complementary log–log scale, namely (i) the MCLL model (i.e., $\varDelta _{1}=1$) indicates that one marginal distribution is a location shift of the other marginal distribution, and (ii) the EMCLL model indicates that the difference between two marginal distributions depends on the value of category i.

The Gumbel (minimum) distribution function is

$$\begin{aligned} G(x) = 1 - \exp \left( - \exp \left( \frac{x-\alpha }{\beta } \right) \right) , \quad -\infty< x < \infty \end{aligned}$$

where $\alpha$ is the location parameter and $\beta$ ($>0$) is the scale parameter. Let $G^{{\tilde{X}}}(x)$ be the Gumbel distribution function with parameter $(\alpha _{1},\beta _{1})$ and $G^{{\tilde{Y}}}(x)$ be the Gumbel distribution function with parameter $(\alpha _{2},\beta _{2})$. Then, the difference between two complementary log–log transforms of $G^{{\tilde{X}}}(x)$ and $G^{{\tilde{Y}}}(x)$ is expressed as

$$\begin{aligned} \log \left( -\log \left( 1 - G^{{\tilde{X}}}(x) \right) \right) - \log \left( -\log \left( 1 - G^{{\tilde{Y}}}(x) \right) \right) = \left( \frac{1}{\beta _{1}} - \frac{1}{\beta _{2}}\right) x + \frac{\alpha _{2}}{\beta _{2}} - \frac{\alpha _{1}}{\beta _{1}}. \end{aligned}$$

This structure is similar to the EMCLL model. If we set $\beta _{1} = \beta _{2} = 1$ without loss of generality, then

$$\begin{aligned} \log \left( -\log \left( 1 - G^{{\tilde{X}}}(x) \right) \right) - \log \left( -\log \left( 1 - G^{{\tilde{Y}}}(x) \right) \right) = \alpha _{2} - \alpha _{1}. \end{aligned}$$

This is similar to the Eq. (1) with $\varDelta _{1}=1$, that is, the location shift model. Also, if we set $\alpha _{1} = \alpha _{2} =0$ without loss of generality, then

$$\begin{aligned} \log \left( -\log \left( 1 - G^{{\tilde{X}}}(x) \right) \right) - \log \left( -\log \left( 1 - G^{{\tilde{Y}}}(x) \right) \right) = \left( \frac{1}{\beta _{1}} - \frac{1}{\beta _{2}}\right) x. \end{aligned}$$

The difference depends only on the scale parameter. This is similar to the Eq. (1) with $\varDelta _{2}=1$. For ordinal categorical data, if it is reasonable to assume an underlying Gumbel distribution, then the proposed model may be appropriate for the square contingency tables.

Miyamoto et al. [12], Tahata et al. [18], and Shinoda et al. [14] considered the models depending on the conditional marginal cumulative probability. These models indicate the structure of marginal inhomogeneity on the condition that an observation will fall in one of off-diagonal cells of the table.

Let $F^{X(c)}_i$ and $F^{Y(c)}_i$ denote the conditional marginal cumulative probabilities of X and Y, respectively, given that $X \ne Y$. That is, for $i=1, \dots ,r-1$,

$$\begin{aligned} F^{X(c)}_i = \hbox {Pr}(X \le i|X \ne Y) = \sum ^i_{k=1} p^{c}_{k\cdot }, \\ F^{Y(c)}_i = \hbox {Pr}(Y \le i|X \ne Y) = \sum ^i_{k=1} p^{c}_{\cdot k}, \end{aligned}$$

where

$$\begin{aligned} p^c_{ i\cdot }= & \frac{ p_{i\cdot } - p_{ii} }{ \delta } = \Pr (X=i|X\ne Y), \\ p^c_{ \cdot i }= & \frac{ p_{\cdot i} - p_{ii} }{ \delta } = \Pr (Y=i|X\ne Y), \end{aligned}$$

with $\delta = \sum \sum _{s \ne t} p_{st} = \Pr (X \ne Y)$.

We shall consider the conditional EMCLL (CEMCLL) model which is defined by

$$\begin{aligned} C^{X(c)}_i = C^{Y(c)}_i + i\log ( \varDelta ^*_1 ) + \log ( \varDelta ^*_2 ) \quad (i=1,\ldots , r-1), \end{aligned}$$

where

$$\begin{aligned} C^{X(c)}_i = \log \left( - \log \left( 1 - F^{X(c)}_i \right) \right) , \quad C^{Y(c)}_i = \log \left( - \log \left( 1 - F^{Y(c)}_i \right) \right) . \end{aligned}$$

Similarly, (i) the CEMCLL model with $\varDelta _{1}^*=1$ reduces to the conditional MCLL (CMCLL) model proposed by Shinoda et al. [14]. The CMCLL model indicates that one conditional marginal distribution is a location shift of the other conditional marginal distribution. The CEMCLL model indicates that the difference between two conditional marginal distributions depends on the value of category i. In a similar manner to the EMCLL model, the CEMCLL model may be appropriate if it is reasonable to assume underlying Gumbel distribution for the conditional marginal distribution.

Both the EMCLL and CEMCLL models show the inhomogeneity of two marginal distributions. The EMCLL model shows the difference between the complementary log–log transformation of the row and column marginal distribution function is linear with respect to category i. On the other hand, the CEMCLL model shows that of row and column conditional marginal distribution function is linear with respect to category i.

3 A Necessary and Sufficient Condition for the MH

The MH model does not fit for a given dataset because the MH model is very restrictive. Marginal inhomogeneity models such as the ML and MCLL models were proposed. We are interested in detecting the probabilistic structure for the poor fit of the MH model. When the MH model can be separated into two or more models, analyzing these models may be helpful to elucidate the reason for the poor fit of the MH model.

Consider a model defined by

$$\begin{aligned} E(X) = E(Y), \end{aligned}$$

where $E(X)=\sum _{i} i p_{i \cdot }$ and $E(Y) = \sum _{i} i p_{\cdot i}$. We shall refer to the model as the mean equality (ME) model. Also, we consider a model defined by

$$\begin{aligned} E(X) = E(Y) \quad \hbox {and} \quad E(X^{2}) = E(Y^{2}), \end{aligned}$$

(2)

where $E(X^2)=\sum _{i} i^2 p_{i \cdot }$ and $E(Y^2) = \sum _{i} i^2 p_{\cdot i}$. We would like to note that Eq. (2) is equivalent to

$$\begin{aligned} E(X) = E(Y) \quad \hbox {and} \quad V(X) = V(Y), \end{aligned}$$

(3)

where $V(X)=E(X^{2})-E(X)^{2}$ and $V(Y)=E(Y^{2})-E(Y)^{2}$. Thus, we shall refer to the Eq. (3) as the mean and variance equality (MVE) model.

We give the following lemma.

Lemma 1

The MVE model is equivalent to the following restrictions:

$$\begin{aligned} \sum ^{r-1}_{i=1}( F_{i}^{X} -F_{i}^{Y} ) =0 \quad \hbox {and} \quad \sum ^{r-1}_{i=1}i( F_{i}^{X} -F_{i}^{Y} ) =0. \end{aligned}$$

(4)

Proof

We can see that

$$\begin{aligned} \sum ^r_{i=1}i^t (p_{i\cdot }-p_{\cdot i}) = \sum ^r_{i=1}i^t \left\{ \left( F^X_i - F^Y_i \right) - \left( F^X_{i-1} - F^Y_{i-1} \right) \right\} \quad (t=1,2), \end{aligned}$$

because $p_{i \cdot } = F^X_i - F^X_{i-1}$ and $p_{\cdot i}=F^Y_i - F^Y_{i-1}$ with $F_{0}^{X}=F_{0}^{Y}=0$ and $F_{r}^{X}=F_{r}^{Y}=1$. Since the right-hand side in the above equation is expressed as

$$\begin{aligned} \sum ^{r-1}_{i=1}i^t (F^X_i - F^Y_{i}) - \sum ^r_{i=2}((i-1)+1)^t (F^X_{i-1} - F^Y_{i-1}), \end{aligned}$$

we can obtain

$$\begin{aligned} \sum ^r_{i=1}i^t (p_{i\cdot }-p_{\cdot i}) = \sum ^{r-1}_{i=1}\left\{ i^t - (i+1)^t \right\} (F^X_i - F^Y_{i}) \quad (t=1,2). \end{aligned}$$

(5)

If the MVE model holds, then

$$\begin{aligned} \sum ^r_{i=1}i^t (p_{i\cdot }-p_{\cdot i}) = 0 \quad (t=1,2) \end{aligned}$$

(6)

from Eq. (2). Thus, we can obtain Eq. (4) from Eq. (5).

Conversely, if Eq. (4) holds, then we can obtain Eq. (6) from Eq. (5), namely the MVE model holds. The proof is completed. $\square$

We obtain the following theorem.

Theorem 1

The MH model holds if and only if both the EMCLL and MVE models hold.

Proof

If the MH model holds, then (i) the EMCLL model with $\varDelta _{1}=\varDelta _{2}=1$ holds and (ii) the MVE model holds because

$$\begin{aligned} \sum ^r_{i=1}i^t (p_{i\cdot }-p_{\cdot i}) = \sum ^r_{i=1}i^t (p_{i\cdot }-p_{i \cdot }) = 0 \quad (t=1,2). \end{aligned}$$

Next, we assume that both the EMCLL and MVE models hold, and then we show that the MH model holds. If the MVE model holds, then

$$\begin{aligned} \sum ^{r-1}_{i=1}( F_{i}^{X} -F_{i}^{Y} ) =0 \quad \hbox {and} \quad \sum ^{r-1}_{i=1}i( F_{i}^{X} -F_{i}^{Y} ) =0, \end{aligned}$$

from Lemma 1. So, we have

$$\begin{aligned} \sum ^{r-1}_{i=1}(i\log (\varDelta _1) + \log (\varDelta _2))( F_{i}^{X} -F_{i}^{Y}) =0. \end{aligned}$$

(7)

Also, if the EMCLL model holds, we have

$$\begin{aligned} C^{X}_i - C^{Y}_i = i\log (\varDelta _1) + \log (\varDelta _2) \quad (i=1,\ldots , r-1) . \end{aligned}$$

(8)

Equations (7) and (8) lead to

$$\begin{aligned} \sum ^{r-1}_{i=1}(C^{X}_i - C^{Y}_i)( F_{i}^{X} -F_{i}^{Y} ) =0. \end{aligned}$$

As complementary log–log function increases monotonically, we see

$$\begin{aligned} (C^{X}_i - C^{Y}_i)(F_{i}^{X} -F_{i}^{Y}) \ge 0 \quad (i=1,\ldots ,r-1). \end{aligned}$$

Thus, we can obtain

$$\begin{aligned} F_i^X=F_i^Y \quad (i=1,\ldots ,r-1). \end{aligned}$$

This is the MH model. The proof is completed. $\square$

The MVE model can be expressed as

$$\begin{aligned} \sum ^{r-1}_{i=1}( F_{i}^{X(c)} -F_{i}^{Y(c)} ) =0 \quad \hbox {and} \quad \sum ^{r-1}_{i=1}i( F_{i}^{X(c)} -F_{i}^{Y(c)} ) =0. \end{aligned}$$

In a similar manner to proof of Theorem 1, this leads to the equation

$$\begin{aligned} \sum ^{r-1}_{i=1}(C^{X(c)}_i - C^{Y(c)}_i)( F_{i}^{X(c)} -F_{i}^{Y(c)} ) =0. \end{aligned}$$

Thus, we can obtain

$$\begin{aligned} F_{i}^{X(c)} =F_{i}^{Y(c)} \quad (i=1,\dots ,r-1). \end{aligned}$$

This is the MH model. Therefore, we can obtain the following theorem.

Theorem 2

The MH model holds if and only if both the CEMCLL and MVE models hold.

From Theorems 1 and 2, we can obtain the following corollary.

Corollary 1

If the MVE model holds, then the EMCLL model holds if and only if the CEMCLL model holds.

Saigusa et al. [13] and Shinoda et al. [14] gave the separation of marginal homogeneity. We would like to note that Theorems 1 and 2 include these results.

4 Extension for Multi-Way Table

Consider a multi-way $r^T$ contingency table of same classification having ordered categories. Let $X_t$ denotes the t-th random variable for $t=1,\ldots ,T$, and let $\Pr (X_1=i_1,\ldots ,X_T=i_T)=p_{i_1\cdots i_T}$ for $i_t=1,\ldots ,r$. The MH[T] model is defined by

$$\begin{aligned} p^{(1)}_{i}=\cdots =p^{(T)}_{i}\quad (i=1,\ldots ,r), \end{aligned}$$

where

$$\begin{aligned} p^{(t)}_i = \Pr (X_t = i). \end{aligned}$$

Let $F^{X_t}_i$ denotes the marginal cumulative probability of $X_t$, namely, $F^{X_t}_i=\sum ^i_{s=1} p^{(t)}_s$ for $i=1,\ldots ,r-1$, and let $C^{X_t}_i$ denotes the complementary log–log transform of $F^{X_t}_i$. The EMCLL[T] model is defined by

$$\begin{aligned} C^{X_1}_i = C^{X_t}_i + i\log (\varDelta _{1t}) + \log (\varDelta _{2t}) \quad (i=1,\ldots ,r-1;t=2,\ldots ,T). \end{aligned}$$

Also, the ME[T] model is defined by

$$\begin{aligned} E(X_1)=\cdots =E(X_T), \end{aligned}$$

and the MVE[T] model is defined by

$$\begin{aligned} E(X_1)=\cdots =E(X_T) \quad \hbox {and} \quad V(X_1)=\cdots =V(X_T). \end{aligned}$$

We obtain the following theorem.

Theorem 3

The MH[T] model holds if and only if both the EMCLL[T] and the MVE[T] models hold.

Proof

If the MH[T] model holds, then the EMCLL[T] and MVE[T] models hold.

Next, we assume that both the EMCLL[T] and MVE[T] models hold, and then we show that the MH[T] model holds. In a similar manner to the proof of Theorem 1, if both the EMCLL[T] and MVE[T] models hold, for any $t=2,\ldots ,T$,

$$\begin{aligned} \sum ^{r-1}_{i=1}(C^{X_1}_i - C^{X_t}_i)( F^{X_1}_i -F^{X_t}_i ) =0. \end{aligned}$$

We can obtain

$$\begin{aligned} F^{X_1}_i=F^{X_t}_i \quad (i=1,\ldots ,r-1;t=2,\ldots ,T), \end{aligned}$$

because the complementary log–log function is a strictly monotonically increasing function. This is the MH[T] model. The proof is completed. $\square$

Let $F^{X_t(c)}_i$ denotes the conditional marginal cumulative probability of $X_t$, given that there is at least one set of unequal random variables. That is, for $i=1, \dots ,r-1$; $t=1, \dots , T$,

$$\begin{aligned} F^{X_t(c)}_i = \hbox {Pr}(X_t \le i|(X_1, \ldots , X_T)\ne (s,\ldots ,s),s=1,\ldots ,r) = \sum ^i_{k=1} p^{(t)_c}_{k}, \end{aligned}$$

where

$$\begin{aligned} p^{(t)_c}_{i}= & \frac{ p^{(t)}_{i} - p_{i \cdots i} }{ \delta _T } = \Pr (X_t=i|(X_1, \ldots , X_T)\ne (s,\ldots ,s),s=1,\ldots ,r), \end{aligned}$$

with

$$\begin{aligned} \delta _T = 1-\sum ^r_{i=1} p_{i\cdots i} = \Pr ((X_1, \ldots , X_T)\ne (s,\ldots ,s),s=1,\ldots ,r). \end{aligned}$$

The CEMCLL[T] model is defined by,

$$\begin{aligned} C^{X_1(c)}_i = C^{X_t(c)}_i + i\log ( \varDelta ^*_{1t} ) + \log ( \varDelta ^*_{2t} ) \quad (i=1,\ldots , r-1;t=2,\ldots ,T), \end{aligned}$$

where

$$\begin{aligned} C^{X_l(c)}_i = \log \left( - \log \left( 1 - F^{X_l(c)}_i \right) \right) . \end{aligned}$$

We would like to note that the MVE[T] model can be expressed as

$$\begin{aligned} \sum ^{r-1}_{i=1}( F^{X_1(c)}_i -F^{X_t(c)}_i ) =0 \quad \hbox {and} \quad \sum ^{r-1}_{i=1}i( F^{X_1(c)}_i -F^{X_t(c)}_i ) =0 \quad (t=2,\dots ,T). \end{aligned}$$

Then, we can obtain the following theorem.

Theorem 4

The MH[T] model holds if and only if both the CEMCLL[T] and MVE[T] models hold.

From Theorems 3 and 4, we can obtain the following corollary.

Corollary 2

If the MVE[T] model holds, then the EMCLL[T] model holds if and only if the CEMCLL[T] model holds.

5 Goodness-of-Fit Test

Let $n_{i_1 \cdots i_T}$ denote the observed frequency in the ($i_1,\ldots ,i_T$) cell of the $r^T$ table with $n = \sum \cdots \sum n_{i_1\cdots i_T}$, and let $m_{i_1 \cdots i_T}$ denote the corresponding expected frequency, that is, $m_{i_1 \cdots i_T}=np_{i_1 \cdots i_T}$. We assume that a multinomial distribution applies to the table. The maximum likelihood estimates (MLEs) of expected frequencies under each model can be obtained using the Newton–Raphson method in the log-likelihood equation. The likelihood ratio chi-squared statistic for testing the goodness-of-fit of model M is given by

$$\begin{aligned} G^2(M) = 2\sum ^r_{i_1=1}\cdots \sum ^r_{i_T=1} n_{i_1 \cdots i_T} \log \left( \frac{n_{i_1 \cdots i_T}}{{\hat{m}}_{i_1 \cdots i_T}} \right) , \end{aligned}$$

where ${\hat{m}}_{i_1 \cdots i_T}$ are the MLE of $m_{i_1 \cdots i_T}$ under the model. If zero cells occur, it may be desirable to aggregate a table. On the other hand, Goodman [6] and Grizzle et al. [8] recommended replacing $n_{ij}$ by $n_{ij}+(1/2)$ and $n_{ij}+(1/r^{2})$, respectively, when zero cells occur. Both suggestions are used in practice.

The MH[T] model has $(T-1)(r-1)$ restrictions. This implies the number of degrees of freedom (df) of statistic for testing the goodness-of-fit of the MH[T] model, namely the df for the MH[T] model is $(T-1)(r-1)$. Similarly, the df for the ME[T] model is $T-1$ and that for the MVE[T] model is $2(T-1)$. The MCLL[T] (CMCLL[T]) and EMCLL[T] (CEMCLL[T]) models have $T-1$ and $2(T-1)$ additional parameters than the MH[T] model, respectively. Then, those for testing the goodness-of-fit of the MCLL[T] (CMCLL[T]) and EMCLL[T] (CEMCLL[T]) models are $(T-1)(r-2)$ and $(T-1)(r-3)$, respectively, because $(T-1)(r-1)-(T-1)=(T-1)(r-2)$ and $(T-1)(r-1)-2(T-1)=(T-1)(r-3)$. We would like to note that the df for the MH[T] model is equal to the sum of the df for the EMCLL[T] (CEMCLL[T]) model and the MVE[T] model.

Consider two models, say $M_1$ and $M_2,$ such that if model $M_1$ holds, then model $M_2$ holds. For testing the goodness-of-fit of model $M_1$ assuming that model $M_2$ holds, the conditional likelihood ratio statistic is given by $G^2(M_1 | M_2) = G^2(M_1) - G^2(M_2)$. The number of df for the conditional test is the difference between the numbers of df for models $M_1$ and $M_2$. The conditional test statistics are more powerful because they are based on fewer degrees of freedom.

As an example, we consider the MLEs of the expected frequencies $\{ m_{ij}\}$ under the CEMCLL model for a square contingency table. Those under the EMCLL, MCLL (CMCLL), MH, ME, and MVE models can be obtained in a similar manner to this case, although those are omitted here. To obtain the MLEs under the CEMCLL model, we must maximize the Lagrangian

$$\begin{aligned} L= & \sum ^r_{i=1} \sum ^r_{j=1} n_{ij} \log p_{ij} - \lambda \left( \sum ^r_{i=1} \sum ^r_{j=1} p_{ij} -1 \right) \\&\quad - \sum ^{r-1}_{i=1} \mu _i \left( \log \left( 1 - F^{X(c)}_i \right) - \varDelta ^{*i}_1 \varDelta ^*_2 \log \left( 1 - F^{Y(c)}_i \right) \right) , \end{aligned}$$

with respect to $\{p_{ij}\}, \lambda , \{ \mu _{i} \}$, $\varDelta ^*_1$ and $\varDelta ^*_2$. Setting the partial derivatives of L equal to zero, we obtain the equations

$$\begin{aligned} p_{ij} = n_{ij} \left[ n +I_{( i\ne j)} \sum ^{r-1}_{k=1} \frac{\mu _k}{\delta } \left\{ \frac{F^{X(c)}_k - I_{(k\ge i)}}{1-F^{X(c)}_k} - \varDelta ^{*i}_1 \varDelta ^{*}_2 \frac{F^{Y(c)}_k - I_{(k\ge j)}}{1-F^{Y(c)}_k}\right\} \right] ^{-1} \end{aligned}$$

for $i=1,\ldots ,r;j=1,\ldots ,r$, as well as

$$\begin{aligned} 1-F^{X(c)}_i= & \left( 1-F^{Y(c)}_i \right) ^{\varDelta ^{*i}_1 \varDelta ^{*}_2}\quad (i = 1, \ldots , r-1), \\&\sum ^{r-1}_{i=1} \mu _i \log \left( 1-F^{Y(c)}_i \right) ^{i\varDelta ^{*(i-1)}_1\varDelta ^*_2} = 0 \quad \hbox {and} \quad \\&\sum ^{r-1}_{i=1} \mu _i \log \left( 1-F^{Y(c)}_i \right) ^{\varDelta ^{*i}_1} = 0, \end{aligned}$$

where $I_{(\cdot )}$ is the indicator function. Using the Newton–Raphson method, we can solve the equations with respect to $\{ p_{ij} \}, \{ \mu _i \}$, $\varDelta ^*_1$ and $\varDelta ^*_2$. Therefore, we can obtain the MLEs of $\{ m_{ij} \}$, $\varDelta ^*_1$ and $\varDelta ^*_2$ under the CEMCLL model.

6 Examples

6.1 Occupational Status for Japaneses

Consider the data in Table 1 taken from Tominaga [19, p. 131] again. Table 2 gives the values of likelihood ratio chi-square statistic $G^2$ for testing the goodness-of-fit of models. We analyze the data using the new model and the properties of the MH model.

Table 2 Likelihood ratio chi-square values $G^2$ for models to the data in Table 1

First, we want to see whether the marginal distribution of father’s status is equal to that of his son. Since the MH model fits poorly from Table 2, we can infer that the marginal distribution of father’s status is different from that of his son. Then, the extended models (i.e., the MCLL and EMCLL models) are applied to the data, and neither fit well.

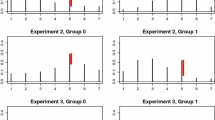
Second, we want to see whether the conditional marginal distribution of father’s status is equal to that of his son on the condition that his status is different from that of his son. Then, we shall apply the extended models (i.e., the CMCLL and CEMCLL models) based on the conditional marginal cumulative distributions. The CEMCLL model only fits well. Under the CEMCLL model, the MLEs of $\varDelta ^*_1$ and $\varDelta ^*_2$ are ${\hat{\varDelta }}^*_1 = 1.59$ and ${\hat{\varDelta }}^*_2 = 0.75$ with the standard errors 0.099 and 0.127, respectively. We want to see whether $\varDelta _{1}^*=1$ and $\varDelta _{2}^*=1$. Consider the hypothesis that the MH model holds under the assumption that the CEMCLL model holds. According to the test based on the difference between $G^{2}$ values for the MH and CEMCLL models, this hypothesis is rejected at the 0.05 significance level because $203.55-1.67=201.88$ with 2 df. Therefore, the CEMCLL model may be preferable to the MH model. Hence, under the CEMCLL model, the probability that the son’s status in a pair is $i+1$ or above, is estimated to be equal to the probability that his father’s status in a pair is $i+1$ or above to the power of $0.75\times 1.59^i$, for $i=1,2,3$, on condition that the father’s status is different from his son’s status. Since ${\hat{\varDelta }}^{*i}_1 {\hat{\varDelta }}^*_2 > 1$ for $i=1,2,3$ under the CEMCLL model, ${\hat{F}}_i^{X(c)} > {\hat{F}}_i^{Y(c)}$ and that difference tends to be greater as i increases, where ${\hat{F}}_i^{X(c)}$ and ${\hat{F}}_i^{Y(c)}$ are MLEs of the conditional marginal cumulative probabilities of X and Y for $i=1,2,3$. Therefore, the occupational distribution for son is stochastically lower than the occupational distribution for father on the condition that father’s status is different from his son’s status. The difference becomes greater as the status category number increases. Please see Fig. 1.

Fig. 1

Observed and estimated conditional marginal distribution functions (cmF): the solid line is for son’s status and the dashed line is for father’s status where the estimated cmF is red and the observed cmF is black

Last, according to Theorem 2, we can see that the poor fit of the MH model is caused by the influence of the lack of structure of the MVE model rather than the CEMCLL model.

6.2 Occupational Status for British

Table 3 is taken directly from Agresti [2, p. 448]. The table relates father’s and son’s occupational status category for a British sample. Social mobility data in Britain have been analyzed many authors, for example, Bishop et al. [3], Goodman [7], Agresti [1], Xie [20], Lang and Scott [10], Sobel et al. [16], and Tahata [17]. These articles mainly focused on the structure of joint distributions. On the other hand, we focus on the structure of marginal distributions.

Table 3 Occupational status for British father–son pairs; from Agresti [2, p. 448]

A cursory glance at the data reveals that the MH model is inappropriate. Indeed, $G^{2}(MH)=32.80$ for testing its fit, with $\hbox {df}=4$. For the population represented by this sample, we analyze whether the (conditional) occupational distribution for sons differs from the (conditional) occupational distribution for fathers.

First, we apply the MCLL and EMCLL models to compare two marginal distributions. These models fit well, having $G^{2}(MCLL)=4.26$ ($\hbox {df}=3$) and $G^{2}(EMCLL)=3.04$ ($\hbox {df}=2$), respectively. Their parameter estimates are ${\hat{\varDelta }}_{2}=0.88$ with the standard error 0.020 under the MCLL model and ${\hat{\varDelta }}_{1}=0.98$ and ${\hat{\varDelta }}_{2}=0.96$ with the standard errors 0.022 and 0.079, respectively, under the EMCLL model. Consider the hypothesis that the MCLL model holds under the assumption that the EMCLL model holds, that is, $\varDelta _{1}=1$. According to the test based on the difference between $G^{2}$ values for the MCLL and EMCLL models, this hypothesis is accepted at the 0.05 significance level because $4.26-3.04=1.22$ with 1 df. Therefore, the MCLL model may be preferable to the EMCLL model. The occupational distribution for son is stochastically higher than the occupational distribution for father. As the reference, we give the observed and estimated marginal distribution functions in Fig. 2.

Fig. 2

Observed and estimated marginal distribution functions (mF): the solid line is for son’s status and the dashed line is for father’s status where the estimated mF is red and the observed mF is black

Last, we apply the CMCLL and CEMCLL models to compare two conditional marginal distributions on the condition that father’s status is different from his son’s status. These models fit well, having $G^{2}(CMCLL)=5.35$ ($\hbox {df}=3$) and $G^{2}(CEMCLL)=3.53$ ($\hbox {df}=2$), respectively. Their parameter estimates are ${\hat{\varDelta }}^{*}_{2}=0.82$ with the standard error 0.031 under the CMCLL model and ${\hat{\varDelta }}^{*}_{1}=0.95$ and ${\hat{\varDelta }}^{*}_{2}=0.97$ with the standard errors 0.035 and 0.130, respectively, under the CEMCLL model. Consider the hypothesis that the CMCLL model holds under the assumption that the CEMCLL model holds, that is, $\varDelta ^{*}_{1}=1$. According to the test based on the difference between $G^{2}$ values for the CMCLL and CEMCLL models, this hypothesis is accepted at the 0.05 significance level because $5.35-3.53=1.82$ with 1 df. Therefore, the CMCLL model may be preferable to the CEMCLL model. The occupational distribution for son is stochastically higher than the occupational distribution for father on the condition that father’s status is different from his son’s status. As the reference, we give the observed and estimated conditional marginal distribution functions in Fig. 3.

Fig. 3

Observed and estimated conditional marginal distribution functions (cmF): the solid line is for son’s status and the dashed line is for father’s status where the estimated cmF is red and the observed cmF is black

7 Concluding Remarks

In this paper, the EMCLL[T] and CEMCLL[T] models have been proposed for $T\ge 2$. The EMCLL[T] model should be applied when we want to see the inhomogeneity between cumulative marginal distributions. On the other hand, the CEMCLL[T] model should be applied when we want to see the inhomogeneity between conditional cumulative marginal distributions on the condition that there is at least one variable unequal to others. As described in Sect. 2, if it is reasonable to assume an underlying Gumbel distribution with the location parameter and the scale parameter, then the proposed models may be appropriate for the square contingency tables with ordinal categories. We would like to note that these models should not apply to the data with nominal categories.

In comparison with the MCLL[T] (CMCLL[T]) model, additional parameters $\varDelta _{1t}$ ($\varDelta ^*_{1t}$) for $t=2,\ldots ,T$ allow us to consider degrees of inhomogeneity proportional to category number as it shown in Sect. 6. The conditional test statistics are more powerful because they are based on fewer degrees of freedom. Thus, the proposed models enable more detailed analysis for the contingency tables with the same ordinal categories.

Theorems 1, 2, 3, and 4 have been shown in this paper. These results may be useful to see the reason why the poor fit of the MH[T] model when the MH[T] model fits poorly for the real dataset. If the MCLL[T] model and the EMCLL[T] model (or the CMCLL[T] model and the CEMCLL[T] model) both fit well,

$$\begin{aligned} G^2(MCLL[T]|EMCLL[T]) = G^2(MCLL[T]) - G^2(EMCLL[T]) \end{aligned}$$

or

$$\begin{aligned} G^2(CMCLL[T]|CEMCLL[T]) = G^2 (CMCLL[T]) - G^2(CEMCLL[T]) \end{aligned}$$

with $(T-1)$df is useful to test the hypothesis that $\varDelta _{1t} = 1$ (or $\varDelta ^{*}_{1t} = 1$) for $t=2,\ldots ,T$ under the assumption that the EMCLL[T] (CEMCLL[T]) model holds. Indeed, we have used these properties for the occupational status of British father–son pairs.