1 Introduction

Compressible flows over curved surfaces are ubiquitous in the aerospace field, both in external (e.g., aircraft wings) and internal (e.g., turbomachinery) configurations. The dynamics of these flows involves complex phenomena, such as shock wave/boundary layer interactions, non-uniform pressure gradients and centrifugal instabilities. Common feature of these phenomena is the generation of a highly unsteady flow field. Besides requiring further fundamental research, these phenomena make it challenging to predict turbulence intensities, skin friction, wall pressure fluctuations and heat transfer. Concerning technology applications, mispredicted flow instabilities can be detrimental to structural integrity and aerodynamic performance. A key tool in this context is the direct numerical simulation (DNS), whose predictive capabilities can aid both fundamental research and technological development. However, numerical algorithms for compressible flows simulations are less standardized then those for incompressible flows [1]. The hyperbolic nature of compressible Navier–Stokes equations allows for the presence of propagating disturbances and discontinuities, which interact with the underlying turbulence. Accurate simulations of such problems are challenging due to the contradictory requirements of numerical methods suited for turbulence, which must minimize any numerical dissipation that would otherwise overwhelm the small scales, and shock-capturing schemes, which must introduce numerical dissipation to stabilize the solution across discontinuites [2].

Further complications arise from geometric complexities. These are typically addressed using local mesh refinement in Cartesian frameworks or unstructured meshes, which, in turn, causes high computational cost or decreased accuracy, respectively [3]. In recent years, the immersed boundary method (IBM) has gained popularity and it has been successfully used in conjunction with turbulence models to simulate high-Reynolds-number flows [4]. Within DNS, though, the IBM struggles to provide a sufficiently accurate description of the boundary layer, especially in presence of separated flow [5]. A different approach to deal with complex geometries relies on the use of body-fitted meshes in a generalized curvilinear coordinate framework. This technique ensures most accurate simulation of the fluid dynamics near the wall and straightforward implementation of high-order finite-difference (FD) schemes.

Among FD approximations, central schemes are preferable as they do not introduce any artificial dissipation, but require special care for their susceptibility to numerical instability. This non-linear instability is due to the accumulation of aliasing errors resulting from discrete evaluation of the convective terms [6]. To address this problem, Pirozzoli [7] proposed an energy-preserving formulation of convective terms, based on fully splitting the derivatives of triple products through the product rule. This technique allows to capture the whole range of turbulence scales without needing any additional stabilization, such as artificial diffusivity [8], explicit filtering of physical variables [9] or relying solely on WENO schemes for convective terms discretization [10]. For years these stabilization strategies have set the standards for DNS of compressible flows, especially in the case of body-fitted grids, as most of the existing energy-preserving schemes are only formulated in Cartesian coordinates [11]. Another appealing property of energy-preserving formulations is that they can be efficiently combined with shock-capturing methods, yielding hybrid schemes that currently represent an optimal strategy for the computation of shocked flows [12].

Within this framework, we developed the high-fidelity solver FLEW, tailored for DNS of turbulent compressible flows over complex geometries. The solver relies on a third-order Runge–Kutta scheme for time integration and high-order FD methods for spatial discretization. Using generalized curvilinear coordinates, a body-fitted grid is transformed from the physical space, where its cells are skewed, to the computational space, where it appears as a regular hexahedron with cubic cells. This process allows to approximate spatial derivatives with FD methods originally developed for Cartesian frameworks. The switch between physical and computational space is carried out through the metric terms, which are computed by numerically deriving the physical mesh coordinates. FLEW employs message passing interface (MPI) parallelization and supports graphics processing unit (GPU) architectures, essential requirements to access the latest generation of high-performance computing (HPC) clusters. This paper is organized as follows. In Sect. 2 we describe the key points of the implemented algorithms, providing a thorough explanation of how energy-preserving schemes are tailored to a curvilinear framework in a computationally efficient manner. In Sect. 3 we present an extensive validation of the code, demonstrating its capabilities in a wide range of flow regimes and configurations. Results of the inviscid Taylor–Green vortex, turbulent curved channel flow, transonic laminar airfoil flow and supersonic turbulent ramp flow are discussed.

2 Methodology

2.1 Balance Equations

FLEW solves the compressible Navier–Stokes equations for a perfect gas written in generalized curvilinear coordinates. The Cartesian coordinates \((x_i)\) of a body-fitted grid are transformed into boundary-conforming curvilinear coordinates \((\xi _j)\) through the mapping \(x_i(\xi _j)\), with \(i,j=1,2,3\). Thus, the boundary surface is composed of segments of coordinate surfaces \(\xi _j=\text {const}\). In such a framework, assuming a stationary grid, the Navier–Stokes equations read

$$\begin{aligned} \frac{1}{J} \frac{\partial {\textbf{Q}}}{\partial t} +\frac{\partial }{\partial \xi _j} \left( \hat{\textbf{F}}_j - \hat{\textbf{F}}_j^{\textbf{v}}\right) =0, \qquad j=1,2,3. \end{aligned}$$
(1)

Here and throughout the paper the repeated index convention is used to indicate summation. The vectors of conservative variables, convective and viscous fluxes are

$$\begin{aligned}{} & {} {\textbf{Q}}= \left[ \begin{array}{c} \rho \\ \rho u_i\\ \rho E \end{array}\right] ,\qquad \hat{\textbf{F}}_j=\left[ \begin{array}{c} \rho \hat{u}_j \\ \rho u_i \hat{u}_j + p\hat{J}_{ji} \\ \rho \hat{u}_j H \end{array}\right] ,\nonumber \\{} & {} \quad \hat{\textbf{F}}^{\textbf{v}}_j=\left[ \begin{array}{c} 0 \\ \sigma _{ik} \hat{J}_{jk}\\ \left( \sigma _{ik}u_k-q_i\right) \hat{J}_{ji} \end{array}\right] , \end{aligned}$$
(2)

where \(E=c_vT+u_iu_i/2\) is the total energy, \(H=E+p/\rho\) the total enthalpy, \(u_i\) the velocity component in the \(i^{th}\) Cartesian direction, \(\hat{u}_j=u_i\hat{J}_{ji}\) the velocity component (normalized by J) in the \(j^{th}\) curvilinear direction, with \(\hat{J}_{ji}=J_{ji}/J\), being \(J_{ji}=\partial \xi _j / \partial x_i\) the Jacobian matrix of the transformation \(\xi _j(x_i)\), and J its determinant. The constitutive equations defining the viscous stress tensor and heat flux vector are

$$\begin{aligned} \sigma _{i k}=\mu \left( \frac{\partial u_i}{\partial x_k} +\frac{\partial u_k}{\partial x_i}-\frac{2}{3} \frac{\partial u_{\ell }}{\partial x_{\ell }} \delta _{i k}\right) , \qquad q_i = -\kappa \frac{\partial T}{\partial x_i}, \end{aligned}$$
(3)

where \(\mu\) is the dynamic viscosity and \(\kappa =c_p\mu /Pr\) the thermal conductivity. Due to the perfect gas assumption, the Prandtl number is constant and fixed to \(Pr=0.72\). The system is completed by the equation of state \(p=\rho RT\). For the viscosity–temperature relationship, both the power law and Sutherland’s law are available. The Navier–Stokes equations are solved in non-dimensional form. From the minimal set of four independent reference variables, \(\rho _0, T_0, l_0, R\), the other reference quantities are derived as \(p_0=\rho _0 R T_0,~u_0=\sqrt{RT_0},~\mu _0=\rho _0 u_0 l_0,~t_0=l_0/u_0\), where \(l_0\) and \(t_0\) are the reference length and time.

2.2 Spatial Discretization

FLEW relies on high-order FD schemes designed for uniform stencils. By recasting the governing equations from Cartesian into curvilinear form (1), skewed input cells are stretched into cubic uniform cells, allowing the application of standard FD schemes. In the following, we will refer to the Cartesian system \((x_i)\) as ‘physical space’ and to the curvilinear one \((\xi _j)\) as ‘computational space’.

2.2.1 Convective Terms

The convective derivative in the \(j^{th}\) direction (temporarily omitting pressure forces) can be expressed as

$$\begin{aligned} \frac{\partial \rho \hat{u}_j \varphi }{\partial \xi _j}, \qquad j=1,2,3, \end{aligned}$$
(4)

where \(\varphi\) is the transported scalar quantity, i.e., 1 for the continuity equation, \(u_i\) for the momentum equation, H for the energy equation. Convective derivatives are manipulated according to the work of Pirozzoli [13] who, after assessing several energy-preserving types of splitting, proposed the following as the most robust:

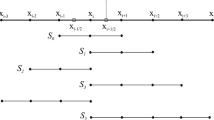
$$\begin{aligned} \frac{\partial \rho \hat{u}_j \varphi }{\partial \xi _j}= & {} \frac{1}{4} \frac{\partial \rho \hat{u}_j \varphi }{\partial \xi _j} +\frac{1}{4}\left( \rho \frac{\partial \hat{u}_j \varphi }{\partial \xi _j} +\hat{u}_j \frac{\partial \rho \varphi }{\partial \xi _j} +\varphi \frac{\partial \rho \hat{u}_j}{\partial \xi _j}\right) \nonumber \\{} & {} \quad +\frac{1}{4}\left( \rho \hat{u}_j \frac{\partial \varphi }{\partial \xi _j} +\rho \varphi \frac{\partial \hat{u}_j}{\partial \xi _j} +\hat{u}_j \varphi \frac{\partial \rho }{\partial \xi _j}\right) . \end{aligned}$$
(5)

The numerical discretization relies on identifying a numerical flux at the intermediate nodes, such that

$$\begin{aligned} \left( \frac{\partial \rho \hat{u}_j \varphi }{\partial \xi _j}\right) _{\mathcal {N}} \approx \left( \hat{f}_{j ; 1 / 2}-\hat{f}_{j ;-1 / 2}\right) _{\mathcal {N}}. \end{aligned}$$
(6)

An approximation of convective derivatives that is locally conservative (and computationally efficient) is based on the following expression for the numerical flux:

$$\begin{aligned} \left( \hat{\textbf{f}}_{j ; 1 / 2}\right) _{\mathcal {N}}= 2 \sum _{\ell =1}^L a_{\ell } \sum _{m=0}^{\ell -1} \left[ \begin{array}{c} \left( \widetilde{\rho , \hat{u}_j, 1}\right) _{j ;-m, \ell } \\[.3cm] \left( \widetilde{\rho , \hat{u}_j, u_i}\right) _{j ;-m, \ell } +\left( \widetilde{p, \hat{J}_{j i}, 1}\right) _{j ;-m, \ell } \\[.3cm] \left( \widetilde{\rho , \hat{u}_j, H}\right) _{j ;-m, \ell } \end{array} \right] _{\mathcal {N}}, \end{aligned}$$
(7)

where

$$\begin{aligned} (\widetilde{f, g, h})_{j ; n, \ell }= \frac{1}{8}\left( f_{j ; n}+f_{j ; n+\ell }\right) \left( g_{j ; n}+g_{j ; n+\ell }\right) \left( h_{j ; n}+h_{j ; n+\ell }\right) \end{aligned}$$
(8)

is the two-point, three-variable discrete averaging operator, \(a_{\ell }\) are the standard coefficients for central approximations of the first derivative, and 2L is the order of accuracy, which can be set by the user from second to eighth. The scaling of the order of accuracy was verified by Pirozzoli [13], who performed a grid sensitivity study using the same numerical scheme employed here.

2.2.2 Metric Terms

The metric terms are the elements of the Jacobian matrix, \(J_{ji} = \partial \xi _j / \partial x_i\), of the coordinate transformation \(\xi _j(x_i)\). Being generally unknown, \(J_{ji}\) is obtained by inverting the Jacobian matrix of the inverse transformation \(x_i(\xi _j)\). That is

$$\begin{aligned} \left[ \begin{array}{ccc} \xi _x &{} \xi _y &{} \xi _z\\ \eta _x &{} \eta _y &{} \eta _z\\ \zeta _x &{} \zeta _y&{} \zeta _z \end{array}\right] = \left[ \begin{array}{ccc} x_{\xi } &{} x_\eta &{} x_\zeta \\ y_{\xi } &{} y_\eta &{} y_\zeta \\ z_\xi &{} z_\eta &{} z_\zeta \end{array}\right] ^{-1}. \end{aligned}$$
(9)

For the present purposes, we assume that the coordinate transformation is locally invertible and does not depend on time. The inverse matrix \(\partial x_i / \partial \xi _j\) is computed by numerically deriving the Cartesian coordinates of the mesh along each \(\xi _j\) direction. A crucial aspect in evaluating metrics is to preserve the freestream. To address this problem, we use the same approximations as employed for the convective terms. Thus, metric terms are evaluated at each node \(\mathcal {N}\) as

$$\begin{aligned} \left( \frac{\partial x_i}{\partial \xi _j}\right) _{\mathcal {N}} = \left( \hat{{f}}_{j;1/2}-\hat{{f}}_{j;-1/2}\right) _{\mathcal {N}}, \qquad i=1,2,3, \end{aligned}$$
(10)

where \((x_i)_{\mathcal {N}}\) are the Cartesian coordinates of the grid node \(\mathcal {N}\), and \(\hat{{f}}_{j;1/2}\) is the numerical flux taken at the intermediate node. The subscript j; 1/2 denotes a shift by 1/2 about \(\mathcal {N}\) in the positive \(j^{th}\) direction. Spacings in the computational space are set to be all unity, thus grid nodes correspond to integer values of \(\xi _j\). The numerical flux is computed as

$$\begin{aligned} \left( \hat{f}_{j;1/2}\right) _{\mathcal {N}}= 2 \sum _{\ell =1}^L a_{\ell } \sum _{m=0}^{\ell -1} \left[ \left( \widetilde{x_i, 1, 1}\right) _{j;-m, \ell } \right] _{\mathcal {N}}, \qquad i=1,2,3, \end{aligned}$$
(11)

where the accuracy order must match that of convective derivatives. Using these scheme, the following metric identities are numerically satisfied:

$$\begin{aligned} \frac{\partial \hat{J}_{ij}}{\partial \xi _i}=0, \qquad i=1,2,3, \end{aligned}$$
(12)

which is necessary and sufficient condition to ensure freestream preservation [9].

2.2.3 Shock Capturing

The locally conservative formulation (7) allows straightforward hybridization of central approximations with shock-capturing methods, based in FLEW on Lax–Friedrichs flux vector splitting and weighted essentially non-oscillatory (WENO) reconstruction. To implement such schemes, the characteristic form of the Euler equations must be expressed in the curvilinear system \(\xi _j\). This is possible by introducing a metric normalization such that the physical velocity components projected along \(\xi _j\) appear in the vectors of convective fluxes. That is

$$\begin{aligned} \tilde{\textbf{F}}_j=\left[ \begin{array}{c} \rho \tilde{u}_j \\ \rho u_i \tilde{u}_j+p \tilde{J}_{j i} \\ \rho \tilde{u}_j H \end{array}\right] , \qquad i=1,2,3, \end{aligned}$$
(13)

where \(\tilde{J}_{ji}\) are the metric terms normalized by \(m_j\) (e.g., \(\tilde{J}_{1i}=J_{1i}/m_1\)), defined as

$$\begin{aligned} m_{1}=\left| \frac{\partial \xi }{\partial x_i}\right| ,\qquad m_{2}=\left| \frac{\partial \eta }{\partial x_i}\right| ,\qquad m_{3}=\left| \frac{\partial \zeta }{\partial x_i}\right| . \end{aligned}$$
(14)

With such normalization, \(\tilde{u}_j=u_i \tilde{J}_{j i}\) is the \(j^{th}\) component of the contravariant velocity, i.e., the projection of the velocity vector along \(\xi _j\). The Jacobian matrix of the normalized flux vector can be diagonalized as \({\partial \tilde{\textbf{F}}_j}/{\partial \textbf{Q}}= \textbf{R}_j\mathbf {\Lambda }_j\textbf{L}_j\), where \(\textbf{R}_j\) and \(\textbf{L}_j\) are the right and left eigenvectors matrices, and \(\mathbf {\Lambda }_j\) is the diagonal matrix of the eigenvalues. For each \(j^{th}\) direction, left and right eigenvectors are evaluated at the interface (denoted by the subscript j; 1/2), using the Roe’s average for flow variables and the arithmetic mean for metric terms. Positive and negative flux components are projected along the characteristic directions using a local Lax–Friedrichs flux splitting:

$$\begin{aligned} \left( \tilde{\textbf{g}}_{j ; 1 / 2}^{ \pm }\right) _{\mathcal {N}}= \frac{1}{2}\left[ \textbf{L}_{j ; 1 / 2} \left( \tilde{\textbf{F}}_j \pm \left| \lambda _{\max }\right| \textbf{Q}\right) \right] _{\mathcal {N}}, \end{aligned}$$
(15)

where \(\left| \lambda _{\max }\right|\) is the maximum eigenvalue over the entire stencil. First, the characteristic fluxes are consistently normalized as

$$\begin{aligned} \hat{\textbf{g}}_{1}^{\pm }=\frac{m_1}{J}\tilde{\textbf{g}}_{1}^{\pm },\qquad \hat{\textbf{g}}_{2}^{\pm }=\frac{m_2}{J}\tilde{\textbf{g}}_{2}^{\pm },\qquad \hat{\textbf{g}}_{3}^{\pm }=\frac{m_3}{J}\tilde{\textbf{g}}_{3}^{\pm }. \end{aligned}$$
(16)

Then, the \(\hat{\textbf{g}}_{j}^{\pm }\) are reconstructed by non-linearly combining the interpolation polynomials on WENO sub-stencils. Finally, the WENO reconstructions \(\hat{\textbf{g}}_{j}^{\textrm{WENO}\pm }\) are projected back into physical space, obtaining the numerical flux at the interface:

$$\begin{aligned} \left( \hat{\textbf{f}}_{j ; 1 / 2}\right) _{\mathcal {N}} =\left[ \textbf{R}_{j ; 1 / 2} \left( \hat{\textbf{g}}_{j ; 1 / 2}^{\textrm{WENO}+} +\hat{\textbf{g}}_{j ; 1 / 2}^{\textrm{WENO}-}\right) \right] _{\mathcal {N}}. \end{aligned}$$
(17)

The accuracy of WENO schemes reaches up to seventh order. The transition between energy-preserving and shock-capturing discretization is controlled by an improved version of the Ducros shock sensor [14]:

$$\begin{aligned} \theta =\max \left( \frac{-\partial u_i / \partial x_i}{\sqrt{(\partial u_i / \partial x_i)^2 +\omega _i \omega _i +u_0^2}}, \; 0\right) , \qquad i=1,2,3, \end{aligned}$$
(18)

where \(\omega _i\) is the vorticity and \(u_0\) is the reference velocity. The sensor is designed to be \(\theta \approx 0\) in smooth flow regions and \(\theta \approx 1\) in the presence of shock waves. Fixed a customized threshold \(\theta _0\), the shock-capturing scheme is locally activated if \(\theta >\theta _0\).

2.2.4 Viscous Terms

Spatial derivatives of viscous terms are approximated using central schemes, which are applied in the computational space. Our goal is to find the analytic relation to reconstruct derivatives from the computational into physical space. First, let us consider the viscous terms in Cartesian coordinates and expand them to Laplacian form,

$$\begin{aligned} \frac{\partial \sigma _{i j}}{\partial x_j}= & {} \mu \left[ \frac{\partial ^2 u_i}{\partial x_j \partial x_j} +\frac{1}{3} \frac{\partial }{\partial x_i} \left( \frac{\partial u_k}{\partial x_k}\right) \delta _{ij}\right] \nonumber \\{} & {} \quad +\left( \frac{\partial u_i}{\partial x_j} +\frac{\partial u_j}{\partial x_i} -\frac{2}{3} \frac{\partial u_k}{\partial x_k} \delta _{i j}\right) \frac{\partial \mu }{\partial x_j}, \end{aligned}$$
(19)

to avoid odd–even decoupling phenomena. As for the energy equation

$$\begin{aligned} \frac{\partial \left( \sigma _{i j} u_i-q_j\right) }{\partial x_j}= u_i\frac{\partial \sigma _{i j}}{\partial x_j} +\sigma _{i j} \frac{\partial u_i}{\partial x_j} +\frac{c_p}{Pr}\left( \mu \frac{\partial ^2 T}{\partial x_j \partial x_j} +\frac{\partial \mu }{\partial x_j} \frac{\partial T}{\partial x_j}\right) . \end{aligned}$$
(20)

The relationship between the first derivative of a generic variable \(\varphi\) expressed in physical (\(x_i\)) and computational (\(\xi _j\)) space is obtained applying the chain-rule:

$$\begin{aligned} \frac{\partial \varphi }{\partial x_i} = \frac{\partial \xi _j}{\partial x_i} \frac{\partial \varphi }{\partial \xi _j}, \qquad j=1,2,3, \end{aligned}$$
(21)

while the Laplacian, assuming that the \(\zeta\) axis is normal to the surface, is written as

$$\begin{aligned} \begin{aligned} \frac{\partial ^2 \varphi }{\partial x_i \partial x_i}&= J\left( \frac{\partial \hat{g}_{11}}{\partial \xi } \frac{\partial \varphi }{\partial \xi } +\hat{g}_{11}\frac{\partial ^2 \varphi }{\partial \xi ^2} \right. \\&\quad \left. +\frac{\partial \hat{g}_{12}}{\partial \xi } \frac{\partial \varphi }{\partial \eta } +\hat{g}_{12}\frac{\partial ^2 \varphi }{\partial \xi \partial \eta } +\frac{\partial \hat{g}_{21}}{\partial \eta } \frac{\partial \varphi }{\partial \xi }+\right. \\&\quad \left. +\hat{g}_{21}\frac{\partial ^2 \varphi }{\partial \eta \partial \xi } +\frac{\partial \hat{g}_{22}}{\partial \eta } \frac{\partial \varphi }{\partial \eta } +\hat{g}_{22}\frac{\partial ^2 \varphi }{\partial \eta ^2}\right) \\&\quad +\zeta _z^2\left( \frac{\partial ^2 \varphi }{\partial \zeta ^2} -\zeta _z \frac{\partial \varphi }{\partial \zeta } \frac{\partial ^2 z}{\partial \zeta ^2}\right) , \end{aligned} \end{aligned}$$
(22)

where

$$\begin{aligned}{} & {} \hat{g}_{11}=\frac{\xi _x^2+\xi _y^2}{J}, \quad \hat{g}_{22}=\frac{\eta _x^2+\eta _y^2}{J}, \nonumber \\{} & {} \quad \hat{g}_{12}=\hat{g}_{21}=\frac{\xi _x \eta _x+\xi _y \eta _y}{J}. \end{aligned}$$
(23)

Equations (21) and (22) allow us to reconstruct in physical space derivatives that are approximated in computational space, where central schemes can be applied. First and second derivatives in the \(j^{th}\) direction are computed at the node \(\mathcal {N}\) as

$$\begin{aligned}{} & {} \left( \frac{\partial \varphi }{\partial \xi _j}\right) _{\mathcal {N}} \approx \sum _{\ell =-L}^L a_{\ell } \left( \varphi _{j;\ell }\right) _{\mathcal {N}}, \nonumber \\{} & {} \quad \left( \frac{\partial ^2\varphi }{\partial \xi _j^2}\right) _{\mathcal {N}} \approx \sum _{\ell =-L}^L b_{\ell } \left( \varphi _{j;\ell }\right) _{\mathcal {N}}, \end{aligned}$$
(24)

where \(b_{\ell }\) are the coefficients for second derivatives. The accuracy order ranges from second to eighth.

2.3 Characteristic Boundary Conditions

In addition to physical boundary conditions, FLEW features dynamic conditions based on characteristic wave relations [15], namely non-reflecting for far-field boundaries and reflecting for no-slip walls. Considering the boundaries at the coordinate surface \(\xi =\textrm{const}\), the convective derivative in the \(\xi\) direction reads

$$\begin{aligned} \frac{\partial \hat{\textbf{F}}_1}{\partial \xi } = \frac{\partial }{\partial \xi }\left( \hat{J}_{1i} \textbf{F}_i\right) , \qquad {\textbf{F}}_i=\left[ \begin{array}{c} \rho {u}_i \\ \rho u_i {u}_j+p \delta _{ij} \\ \rho {u}_i H \end{array}\right] , \qquad i=1,2,3, \end{aligned}$$
(25)

where we split the contribution of the convective flux in Cartesian coordinates, \({\textbf{F}}_i\), from that of the metric terms, \(\hat{J}_{1i}\), associated to the \(\xi\) direction. Expanding the product derivative, we get

$$\begin{aligned} \frac{\partial \hat{\textbf{F}}_1}{\partial \xi } = \hat{J}_{1i} \frac{\partial \textbf{F}_i}{\partial \xi } +\textbf{F}_i \frac{\partial \hat{J}_{1i}}{\partial \xi }. \end{aligned}$$
(26)

The first term of the right-hand side can be recast as

$$\begin{aligned} \hat{J}_{1i} \frac{\partial \textbf{F}_i}{\partial \xi } =\frac{m_{1}}{J} \frac{\partial \tilde{\textbf{F}}_1}{\partial \xi } =\frac{m_{1}}{J}\textbf{R}_{1}\mathbf {\Lambda }_{1}\textbf{L}_{1} \frac{\partial \textbf{Q}}{\partial \xi }, \end{aligned}$$
(27)

where the Jacobian matrix of the flux, \({\partial \tilde{\textbf{F}}_1}/{\partial \textbf{Q}}\), has been diagonalized as outlined in paragraph 2.2.3. Exploiting the local one-dimensional approximation, the conservative variables are updated at the boundary according to the following equation:

$$\begin{aligned} \frac{1}{J} \frac{\partial {\textbf{Q}}}{\partial t}+ \frac{m_{1}}{J} \textbf{R}_{1} \mathcal {L}_{1} \frac{\partial \textbf{Q}}{\partial \xi } +\textbf{F}_i \frac{\partial \hat{J}_{1i}}{\partial \xi }=0, \end{aligned}$$
(28)

where \(\mathcal {L}_{1}=\mathbf {\Lambda }_{1}\textbf{L}_{1} {\partial \textbf{Q}}/{\partial \xi }\) has the physical interpretation of wave amplitudes associated with the characteristic field. Analogous considerations can be made for boundaries at the surface \(\eta =\textrm{const}.\)

2.4 Time Integration

Spatial discretization leads to a semi-discrete system of ordinary differential equations:

$$\begin{aligned} \frac{1}{J}\frac{\textrm{d} \textbf{Q}}{\textrm{d} t}=\textbf{R}(\textbf{Q}), \end{aligned}$$
(29)

where \(\textbf{R}\) is the vector of the residuals. The system is advanced in time using a three-stage, third-order Runge–Kutta scheme [16]:

$$\begin{aligned} \textbf{Q}^{(\ell )}=\textbf{Q}^{(\ell -1)} +\alpha _{\ell } \Delta t \textbf{R}^{(\ell -1)} +\beta _{\ell } \Delta t \textbf{R}^{(\ell )}, \qquad \ell =1,2,3, \end{aligned}$$
(30)

where \(\textbf{Q}^{(0)}=\textbf{Q}^n\) and \(\textbf{Q}^{(3)}=\textbf{Q}^{n+1}\) are the solution vectors at the time-step n and \(n+1\), respectively. The integration coefficients are \(\alpha _{\ell }=(0,17 / 60,-5 / 12)\) and \(\beta _{\ell }=(8 / 15,5 / 12,3 / 4)\). The time-step \(\Delta t\), which is updated at each iteration by default, is chosen as the minimum value among the convective, viscous and thermal limitation:

$$\begin{aligned} \Delta t = \text {CFL} \cdot \min \left( \Delta t_{\text {conv}},\, \Delta t_{\text {visc}}, \,\Delta t_{\text {thrm}} \right) , \end{aligned}$$
(31)

which are computed, in turn, as the minimum value among all cells. Respectively

$$\begin{aligned} \begin{aligned}&\Delta t_{\text {conv}}=\min _{\text {cells}}\left( \frac{1}{|\tilde{u}_j|+m_j c}\right) ,\; \Delta t_{\text {visc}}=\min _{\text {cells}}\left( \frac{1}{m_j^2 \nu }\right) , \;\\&\Delta t_{\text {thrm}}=\min _{\text {cells}}\left( \frac{1}{m_j^2 \alpha }\right) , \end{aligned} \end{aligned}$$
(32)

where \(j=1,2,3\) is the curvilinear direction, c is the speed of sound, \(\nu =\mu /\rho\) is the kinematic viscosity, \(\alpha = \kappa /\rho\) is the molecular conductivity. The Courant–Friedrichs–Lewy \((\textrm{CFL})\) number can be set by the user (a value close to unity is usually optimal).

3 Validation

FLEW is designed to perform DNS for various flow configurations, including the curved channel, compression ramp and wing airfoil. In this section, we validate the solver for these configurations by comparing the results to experimental and numerical data available in the literature. In addition, we use the inviscid Taylor–Green vortex on a wavy mesh as a benchmark.

3.1 Inviscid Taylor–Green Vortex

The energy-preserving properties of the solver are tested using the inviscid Taylor–Green flow, proposed by Duponcheel et al. [17] as time-reversibility test. The solution is computed in a triply periodic domain consisting of a wavy two-dimensional mesh, depicted in Fig. 1, which is extruded in the third dimension. The mesh is generated according to the following mapping [8]:

$$\begin{aligned} \begin{aligned}&x(\xi , \eta )=\frac{\xi -1}{N_{\xi }-1} L_x+ 0.4 \sin \left( 2 \pi \frac{\eta -1}{N_\eta -1}\right) , \\&y(\xi , \eta )=\frac{\eta -1}{N_\eta -1} L_y+ 0.2 \sin \left( 4 \pi \frac{\xi -1}{N_{\xi }-1}\right) , \\&z(\zeta )=\frac{\zeta -1}{N_\zeta -1} L_z, \end{aligned} \end{aligned}$$
(33)

where \(L_x=L_y=L_z=2\pi\) and \(N_x=N_y=N_z=32\). The flow is initialized as follows:

$$\begin{aligned} \begin{aligned}&\rho =\rho _0 \\&u=u_0 \sin (x) \cos (y) \cos (z) \\&v=-u_0 \cos (x) \sin (y) \cos (z) \\&w=0 \\&p=p_0+u_0^2[\cos (2 x)+\cos (2 y)][\cos (2 z)+2] / 16 \end{aligned} \end{aligned}$$
(34)

where \(u_0=M_0c_0\) is the reference velocity (the Mach number is \(M_0=0.01\)) and \(c_0,~p_0,~\rho _0\) are the reference speed of sound, pressure and density.

Fig. 1
figure 1

Cross section on the x, y plane of the wavy domain for the Taylor–Green vortex simulation

Full size image

Due to the lack of viscosity, from the ordered initial conditions small-scale turbulence structures are rapidly formed with incurred growth of vorticity. The solution is advanced up to time \(t/t_0 = 8\), at which the velocity field is reversed, and then further advanced up to \(t/t_0 = 16\) (the reference time and length are \(t_0=l_0/u_0\) and \(l_0=1\)). Based on the time-reversibility property of the Euler equations, the initial conditions should be exactly recovered.

Fig. 2
figure 2

Flow visualization of the inviscid Taylor–Green vortex using one isosurface of Q-criterion. The snapshots are taken at time \(t/t_0=0.0\) (a), \(t/t_0=3.2\) (b), \(t/t_0=6.4\) (c), \(t/t_0=9.6\) (d), \(t/t_0=12.8\) (e), \(t/t_0=16.0\) (f)

Full size image

In Fig. 2, we display a sequence of snapshots of the flow field, which qualitatively show that the initial coherent structures are faithfully reproduced at the end of the simulation. Simulation results are depicted in Fig. 3, where we report the time evolution of total kinetic energy and enstrophy. The kinetic energy is perfectly conserved over time, showing that no numerical dissipation is introduced. The total enstrophy grows markedly up to the reversal time (\(t/t_0 = 8\)), at which it begins to decrease following a symmetrical trend, with exact recovery of the initial condition at the final time (\(t/t_0 = 16\)).

Fig. 3
figure 3

Results of the Taylor–Green vortex simulation: time evolution of the total kinetic energy (\(K/K_0\), red line), and enstrophy (\(\Omega /\Omega _0\), blue line)

Full size image

3.2 Turbulent Curved Channel Flow

We focused on validating FLEW in the presence of pressure gradients due to surface curvature. For this purpose, we considered the classical study by Moser & Moin [18], where pressure-driven flow in a mildly-curved channel was simulated. The same flow configuration was recently used by Brethouwer [19] as benchmark.

Fig. 4
figure 4

Scale drawing of the computational domain of the turbulent curved channel flow. The radius of curvature, \(r_c\), is measured at the centreline

Full size image

The computational domain is bounded by sectors of concentric cylinders (a scale drawing appears in Fig 4). The curvature parameter is \(\delta /r_c=1/79\), where \(\delta\) is the channel half-width and \(r_c\) is the radius of curvature measured at the centreline. The domain has a length of \({4}\pi \delta /3\) in the spanwise (z) direction and subtends an angle of \(0.16~\textrm{rad}\) in the azimuthal (\(\theta\)) direction, which yields a length of \(12.64\delta\) along the centreline. An imposed mean-pressure gradient in the azimuthal direction drives the flow. No-slip isothermal conditions are imposed at the walls, while periodic boundary conditions are enforced in the azimuthal and spanwise directions, so that the simulated flow is the fully evolved turbulent flow in a curved channel. The bulk Reynolds number is \(\textrm{Re}_b=\rho _b u_b \delta / \mu _0 = 2600\) and the bulk Mach number is \(M_b=u_b/c_0=0.1\), where \(\mu _0\) and \(c_0\) are the viscosity and speed of sound at the wall temperature. The bulk density and velocity are defined as

$$\begin{aligned} \rho _b=\frac{1}{\mathcal {V}} \int _{\mathcal {V}} \rho ~\textrm{d}\mathcal {V}, \quad u_b=\frac{1}{\rho _b \mathcal {V}} \int _{\mathcal {V}} \rho u ~\textrm{d} \mathcal {V}, \end{aligned}$$
(35)

where \(\mathcal {V}\) is the domain volume. The computation is carried out with \(N_{\theta }\times N_{r}\times N_{z}=216\times 72\times 144\), leading to grid spacings of \(\Delta z^+=5\), \(r_{\textrm{c}}^{+} \Delta \theta =10\), \(\Delta r^+=0.2\) at the wall. The mesh in the redial direction is staggered such that the wall coincides with an intermediate node, where the convective fluxes are identically zero. This approach guarantees correct telescoping of the numerical fluxes and exact conservation of the total mass, with the further benefit of doubling the time-step [20].

Table 1 Comparison of local and global values of friction Reynolds number
Full size table

The surface curvature generates centrifugal instability, which breaks the symmetry in wall-normal direction. Specifically, the convex curvature of the inner wall has a stabilizing effect, leading to turbulence attenuation and smaller wall shear stress. Conversely, the concave curvature of the outer wall has a destabilizing effect, leading to turbulence amplification and larger wall shear stress. This trend is confirmed by the local values of friction Reynolds number, which resulted \(\textrm{Re}_{\tau ,i}=155\) at the convex (inner) wall and \(\textrm{Re}_{\tau ,{o}}=179\) at the concave (outer) wall. The local friction velocities are computed as

$$\begin{aligned} u_{\tau ,{i}}^2=\nu \frac{\partial \overline{u}_\theta }{\partial r}\bigg |_{r_i}, \qquad u_{\tau ,{o}}^2=\nu \frac{\partial \overline{u}_\theta }{\partial r}\bigg |_{r_o}, \end{aligned}$$
(36)

where \(\overline{u}_\theta\) is the mean streamwise velocity. A global friction velocity can be defined as follows. The mean pressure gradient in the curved channel is \((\textrm{d} P / \textrm{d} \theta ) / r\), which must be equal to \(-\rho u_{\tau }^2 / \delta\). From the streamwise momentum balance we obtain \(\textrm{d} P / \textrm{d} \theta = -\rho \left( r_i^2 u_{\tau ,i}^2+r_o^2 u_{\tau ,o}^2\right) /\left( 2 r_c \delta \right)\), hence

$$\begin{aligned} u_{\tau ,g}^2= \frac{r_{i}^2 u_{\tau ,i}^2+r_o^2 u_{\tau ,o}^2}{2 r_{c}^2}. \end{aligned}$$
(37)

A comparison with the results of Moser & Moin and Brethouwer’s is shown in Table 1, where we report the local and global values of friction Reynolds number. The flow can be visualized in Fig. 5. The instantaneous field of velocity magnitude (5a) is depicted alongside two wall-parallel slices (5b), revealing a predominance of high-speed streaks near the concave wall and of low-speed streaks near the convex one.

Fig. 5
figure 5

Instantaneous field of the velocity magnitude normalized by the bulk velocity \((u/u_b)\) for the turbulent curved channel flow (a). Wall-parallel slices of \(u/u_b\) at \(y^+=15\), locally computed from the concave (b, top) and convex wall (b, bottom)

Full size image

One-point statistics are shown in Fig. 6, where we report the mean velocity profile in local wall units and turbulence intensities. The mean velocity in the log-law region is higher at the convex wall (black line in Fig. 6a) due to normalization with the local friction velocity, which is lower at the convex wall (i.e., lower wall shear stress). Velocity fluctuations, especially in the azimuthal direction (red line in Fig. 6b), highlight amplification of turbulence near the concave wall due to centrifugal instability. In general, we can appreciate the excellent agreement of the results.

Fig. 6
figure 6

One-point statistics for the turbulent cuved channel flow. Mean velocity profile in local wall units (a): black line refers to the convex wall, blue line to the concave one. Root mean square of velocity fluctuations (Instantaneous field of the velocity magnitude normalized by the bulk velocity ): red line refers to \(u_{\theta ,\text {rms}}\), blue line to \(u_{r,\text {rms}}\), black line to \(u_{z,\text {rms}}\)

Full size image

3.3 Transonic Laminar Airfoil Flow

Laminar flows over an airfoil are commonly employed to assess accuracy, stability and convergence of solution algorithms for the Navier–Stokes equations. In recent years, these flows have also served as test cases for high-order numerical schemes, as in the study by Swanson [21], which we reference. Our investigation involves a two-dimensional laminar flow over a NACA 0012 airfoil at free-stream Mach number \(M_{\infty }=0.8\), Reynolds number \(\textrm{Re}=500\) (based on the chord length, c) and angle of attack \(\alpha =10^{\circ }\). The fore part of the domain has a radius of curvature 20c, and the outlet is positioned 20c downstream of the trailing edge. Four different grid densities are considered to analyze grid sensitivity. In all cases, structured meshes with C-type topology are generated using the open-source program Construct2D [22]. The finest mesh consists of \(N_x \times N_y = 1280\times 512\) grid points, with 768 cells on the airfoil clustered near the leading and trailing edges. The number of grid points was successively halved in both coordinate directions, to the coarsest mesh consisting of \(N_x \times N_y = 160\times 64\). Figure 7 shows the near-field region of the \(320\times 128\) grid.

Fig. 7
figure 7

Near field view of the \(320\times 128\) grid for laminar flow over a NACA 0012 airfoil

Full size image

No-slip adiabatic conditions are applied at the airfoil surface, while non-reflective boundary conditions are employed at the far field. The C-mesh closure generates a computational boundary in the wake region. Wake boundary conditions are handled by acting only on the ghost nodes, in which the solution of the corresponding internal nodes is set. This approach ensures that the boundary cutting through the domain in the wake region remains perfectly transparent to the flow.

Fig. 8
figure 8

Mach contours and streamlines for the laminar flow over a NACA 0012 airfoil (\(1280\times 512\) grid)

Full size image

Inflow conditions are such that the flow accelerates sufficiently to create a small supersonic region, without forming a shock wave. The supersonic zone of the flow is revealed in the Mach contours displayed in Fig. 8, where streamline patterns around the airfoil are also presented. We observe two recirculation regions with large extent both on the suction side of the airfoil and in the wake.

Table 2 Comparison of the aerodynamic coefficients for the laminar flow over a NACA 0012 airfoil
Full size table
Fig. 9
figure 9

Distribution of pressure coefficient (a) and skin-friction coefficient (b) for the laminar flow over a NACA 0012 airfoil

Full size image

The comparison of the aerodynamic coefficients (Table 2), as well as the distribution of surface pressure and skin-friction (Fig. 9), reveals a very close agreement between our results and Swanson’s. These results also indicate that reasonably good estimates of the \(C_L\) and \(C_D\) can be achieved on fairly coarse grids.

3.4 Supersonic Turbulent Ramp Flow

A canonical configuration to study shock wave/boundary layer interactions is the compression ramp. Supersonic turbulent flows over a ramp has been extensively investigated through wind-tunnel experiments, whereas only a few DNS are available in the literature for this configuration.

Fig. 10
figure 10

Scale drawing of the computational domain for the turbulent ramp flow

Full size image

One of the most relevant computational study is by Wu & Martin [23], who performed a DNS of supersonic turbulent flow over a \(24^{\circ }\) compression ramp. Our results are compared to their study, as well as to the experimental work of Bookey et al. [24] for the same configuration. A scale drawing of the computational domain is presented in Fig. 10. Dimensions are \(29\delta\) upstream and \(18\delta\) downstream of the corner in the streamwise direction, \(2.2\delta\) in the spanwise direction and \(6\delta\) in the wall-normal direction, where \(\delta\) is the \(99\%\) thickness of the incoming boundary layer. The mesh is generated analitically following the procedure used by Martin et al. [25], who provides full details of the mapping in the relevant work. The grid is clustered near the wall in the wall-normal direction, and a corner singularity is avoided by prescribing a finite curvature at the ramp corner. The DNS is performed with \(N_{x}\times N_y\times N_{z}=2432\times 256\times 160\) points, leading to grid spacings of \(\Delta x^+ \simeq 5\), \(\Delta z^+ \simeq 3\) and \(\Delta y^+ = 0.5\) at the wall. The incoming flow conditions are \(M_{\infty }=2.9\) and \(\textrm{Re}_{\delta }=31,500\). A recycling–rescaling method is applied to feed the inflow turbulence [26], with the recycling station located \(15\delta\) downstream of the inlet. Non-reflecting boundary conditions are used at the outlet and top boundary, while at the wall is enforced a no-slip isothermal condition with reflecting treatment based on characteristic wave relations.

Fig. 11
figure 11

Cross-stream visualization of turbulent ramp flow in terms of instantaneous numerical Schlieren. Downstream of the corner gradients are steeper, showing turbulence amplification due to the interaction with the shock

Full size image

The approaching turbulent boundary layer is deflected at the corner, where the shock system originates. Turbulence intensity amplifies as the flow crosses the shock, resulting in large density and pressure fluctuations. This interaction is depicted in Fig. 11, where we present an instantaneous field of numerical Schlieren. The coherent flow structures, visible in Fig. 11, indicate the presence of an extended region of separated flow.

Table 3 Comparison of separation and reattachment points for the ramp flow (the corner is located at the origin)
Full size table
Fig. 12
figure 12

One-point statistics for the turbulent ramp flow: mean wall-pressure distribution (a) and mean velocity profiles (b) located in the incoming boundary layer (black line) and \(4\delta\) downstream of the corner (blue line)

Full size image

Flow separation and reattachment can be precisely located as the points at which the mean friction coefficient changes sign. In our DNS, they are respectively predicted at \(x_s=-3.2\delta\) and \(x_r=1.3\delta\) (the ramp corner is located at \(x=0\)). A comparison with the results of Wu & Martin and Bookey et al. is shown in Table 3. To asses the accuracy of our simulation, we compare the wall pressure distribution and mean velocity profile across the interaction. Mean wall-pressure distribution (Fig. 12a) is predicted within the experimental uncertainty of \(5\%\) [24]. Two velocity profiles are shown in Fig. 12b, one in the incoming boundary layer and the other \(4\delta\) downstream of the corner. In both cases, the agreement is within \(5\%\).

4 Conclusions

We presented FLEW, a high-fidelity solver for DNS of compressible flows over complex geometries. The code is HPC-oriented thanks to MPI parallelization and the ability to run on multi-GPU architectures. Various aspects of extending the energy-preserving schemes proposed by Pirozzoli [13] to simulate flows over curvilinear meshes are presented. In Sect. 2, we describe a locally conservative approximation of convective derivatives suitable for generalized curvilinear coordinates. We also discuss how shock waves, viscous terms and characteristic boundary conditions are treated. Special attention is devoted to the metric terms, which are computed with the same scheme used for convective derivatives, ensuring the freestream preservation.

Demonstrative examples of the efficacy of the implemented algorithms are provided in Sect. 3. We started our assessment from the time-reversibility benchmark of the inviscid Taylor–Green vortex, aiming to to test the energy-preserving capability of our solver on curvilinear meshes. The results demonstrate that the solver can perfectly recover the initial conditions, indicating the absence of any artificial dissipation. Various viscous test cases, including the curved channel flow, airfoil flow and ramp flow, further substantiate the accuracy and robustness of our solver across a wide range of flow regimes, spanning from low-subsonic, through transonic to supersonic conditions. Comparison of the results with experimental and numerical data available in the literature revealed excellent agreement for all tested configurations.

While employing the generalized curvilinear coordinates in two directions already allows us to address numerous significant problems, our next goal is to remove the constraint that the third axis be normal to the surface. This extension will enable the code to handle fully arbitrary geometries.