Modelling the Wall Pressure Fluctuations on the VEGA-C Launcher in Supersonic Conditions

Abstract

The prediction of pressure fluctuations generated over the external surface of aerospace launchers during the atmospheric flight remains a challenging task due to the complexity of the geometry and the effects of compressibility at high supersonic Mach numbers. An experimental database is here analysed to the scope of providing a procedure to model and predict the relevant statistics of the wall pressure fluctuations generated by a supersonic flow overflowing the VEGA-C Launcher Vehicle. Data have been obtained in an extensive Wind Tunnel test campaign carried out in the trisonic wind tunnel of the National Institute for Aerospace Research (INCAS) in Bucharest. Wall-mounted pressure transducers allowed for the computation of the pressure Auto- and Cross-spectra over the fourth (the payload region) and third stages of the launcher model. Coherence functions are modelled through exponential-like analytical functions following the approaches usually adopted in canonical boundary layer flows, whereas the auto-spectra models are based on polynomial fits. The approach adopted for the achievement of proper non-dimensional quantities as well as the procedure implemented for the full-scale extrapolation is presented and discussed.

1 Introduction

Pressure fluctuations induced by a compressible flow overflowing aerospace vehicles during the ascent in the dense atmosphere may induce vibrations in the interior and cause costly damages to the payload. Furthermore, the random pressure load acting on the surface panels may accelerate possible structural damages due to fatigue effects. For these reasons, several research studies in the past have targeted the analysis, in a statistical sense, of the pressure fluctuations acting on the external surface of aerospace vehicles as well as the development of proper analytical and semi-empirical predictive models (see, e.g. [1,2,3] for extensive reviews). However, most of the studies carried out so far were focused on the buffeting phenomenon occurring mainly at transonic flow conditions (see, e.g. [4,5,6,7,8]); whereas, cases at supersonic flow conditions have been less studied, few data are available in the literature and they are mainly referred to equilibrium boundary layers overflowing simple geometries (see, e.g. [9, 10] and [11]).

In the present approach, the investigation is aimed at developing an appropriate procedure to set up predictive models of relevant statistical quantities of the wall pressure fluctuations acting on the surface of an aerospace launcher at supersonic flow conditions. The transonic situation is not considered therein since the strong dependency of the flow physics (e.g. shock waves, expansion waves, flow separations and recirculations) upon both the Mach number and the position along the launcher renders less effective the modelling attempt.

The database analysed therein has been obtained during an extensive experimental measurement campaign aimed at the aerodynamic and aeroacoustic characterisation of the VEGA-C launcher [12]. A 1:30 scaled model has been installed within the test section of the trisonic wind tunnel available at INCAS, the National Institute for Aerospace Research of Romania. The flow conditions analysed spanned from low subsonic (M = 0.5) to high supersonic (M = 2.7). The transonic conditions, of interest for the buffeting phenomenon, were analysed in Camussi et al. [12]; whereas, the present paper is focalised on the high supersonic cases corresponding to M ≥ 2. In the same paper [12], the acoustic qualification of the INCAS trisonic wind tunnel was reported, demonstrating the good acoustic quality of the facility. More details on the experimental setup are given in Sec. 2; whereas, the approach adopted for the analytical modelling is reported in Sec. 3 along with a brief description of the procedure to be adopted for the full-scale extrapolation. The main results achieved are presented in Sec. 4; they include flow visualisations that are very useful for a qualitative description of the flow behaviours. The conclusions are eventually given in Sec. 5.

2 Experimental Set-Up

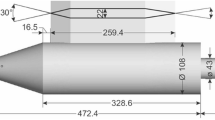
Experiments have been carried out in the trisonic wind tunnel available at INCAS, a blow-down-type tunnel that provides air for a short period of time depending on the specified test condition [13]. The tunnel is capable of testing in three speed regimes: subsonic, transonic and supersonic covering a Mach range between 0.4 and 3.5. This Mach number range is achieved using two separate test sections. The wind tunnel test section has dimensions of 1.2 × 1.2 m2 with an interchangeable porous transonic test section with variable porosity from 0.01% to 9%. The transonic test section with porous walls operates in the Mach number range between 0.4 and 1.2. A solid wall test section is instead installed to achieve the higher Mach numbers, of interest for the present investigation. A 1:30 VEGA-C scaled model is installed in the test section through a rigid sting connected to the rear side of the model and properly motorised to regulate the angle of attack (AoA). 24 Kulite transducers, type XCQ-062-25PSID, are flush mounted at the external surface of the model and distributed on the ogive, the Boat-tail, and the fourth stage, as sketched in Fig. 1. It is noted that the transducers distribution includes three clusters where spanwise positions are present. These arrays are useful for the analysis and modelling of the cross-spectra and coherence functions. Four additional transducers are installed at the wall of the WT, their signals having been used for tonal background noise decontamination [11].

Fig. 1

A sketch of the VEGA-C model indicating the location of the Kulite pressure transducers (red dots)

The flow conditions analysed are summarised in Table 1. The fluctuating pressure data were acquired with a sampling frequency (f_s) of 100 kHz for 4 s. A bandpass filter was set to select a frequency range of interest from 10 Hz to 50 kHz to avoid aliasing problems and filter out low-frequency spurious effects due to standing waves generated within the wind tunnel.

Table 1 The main parameters settled for the supersonic test campaign

The wind tunnel is equipped with a pair of 750 mm diameter optical glass windows that can be installed in the side walls of the test section for Schlieren visualisations. The configuration of this system is the conventional “Z” arrangement with 30” diameter parabolic mirrors and additional plane mirrors to fold the system and to enable it to fit with the ground position for the digital camera and light source units. The images are recorded through a Photron SA4 fast camera setting the frame rate at 250fps, a good compromise between time resolution and illumination.

3 Modelling and Full-Scale Extrapolation

In this section, the procedure adopted to model the fluctuating pressure field acting on the external surface of the scaled model is presented. The discussion will cover a preliminary dimensional analysis and a brief clarification of the approach adopted to model both the auto- and the cross-spectra. We refer to the literature for a review of existing models [1,2,3].

3.1 Models of Auto- and Cross-Spectra

To the extent of the auto-spectrum, several models were proposed in the past also taking into account the effect of the Mach number (see, e.g. [14] and [15]). In the earliest and most used model proposed by Corcos [16], a simple representation consisted of assuming a constant value of the spectrum up to a certain transitional frequency and then a decay law with a fixed exponent. In the present approach, to better account for the spectra shape and its variation along the launcher model, a polynomial approximation of third and fifth orders is instead preferred. This approximation will be used to reproduce the auto-spectra in non-dimensional form.

To the extent of the cross-spectra modelling, the approach proposed by Corcos [16] seems to be the most appropriate as well. This model has been demonstrated to be very robust and reliable also for supersonic boundary layers [11, 17, 18]. Under the assumptions of a fully developed turbulent boundary layer, the pressure field is expressed by a cross-correlation function that decays with space separation and time and is convected with the mean flow. The main assumption of the model is the use of the separation of variables approach to represent the correlation function dependence upon the streamwise separation ξ and the crosswise separation η.

In summary, the cross-spectrum is represented as follows:

$$S_{{pp^{\prime}}} \left( {x_{i} , \xi ,\eta ,\omega } \right) = S_{pp} \left( {x_{i} , \omega } \right) \Gamma \left( {x_{i} , \xi ,\eta ,\omega } \right) = S_{pp} \left( {x_{i} , \omega } \right) \gamma \left( {\xi ,\eta ,\omega } \right)e^{{j\frac{\omega \xi }{{U_{c} \left( {x_{i} } \right)}}}} ,$$

where the quantity Γ is defined as the product of the coherence function, denoted as $\gamma \left(\xi ,\eta ,\omega \right)$, by an oscillating function ${e}^{j\phi \left(\xi ,\omega \right)}$ (where $j=\sqrt{-1}$). Here, $\phi \left(\xi ,\omega \right)$ is the phase which depends only upon ξ and is defined from the convection velocity of the flow ${U}_{c}({x}_{i})$ by:

$$\varphi \left( { \xi ,\omega } \right) = \frac{\omega \xi }{{U_{c} \left( {x_{i} } \right)}}.$$

As pointed out in [17], the convection velocity U_c is computed from the peak of the cross-correlation function determined from adjacent transducers or it is taken as a fraction of the local external velocity $Ue.$

The coherence function $\gamma \left(\xi ,\eta ,\omega \right)$ is represented through a separation of variables approach that leads to the following expression:

$$\gamma \left( {\xi ,\eta ,\omega } \right) = A\left( {\xi ,\omega } \right)B\left( {\eta ,\omega } \right).$$

The Corcos’ model suggests expressing A and B as exponential decaying forms:

$$A\left( {\xi ,\omega } \right) = e^{{\frac{ - \left| \xi \right|}{{L_{\xi } \left( \omega \right)}}}} {\text{and }}B\left( {\eta ,\omega } \right) = e^{{\frac{ - \left| \eta \right|}{{L_{\eta } \left( \omega \right)}}}} ,$$

where ${L}_{\xi }\left(\omega \right)$ and ${L}_{\eta }\left(\omega \right)$ are the so-called coherence lengths in the streamwise and transverse direction respectively. It must be pointed out that most of the models proposed after the Corcos’ outcome, continued to follow its original philosophy. The common feature among those models is the separation of variables approach used to represent the correlation function dependence upon the streamwise and crossflow separation, this being the so-called ‘multiplication hypothesis’.

The main distinction among different models is the way the exponential coefficients ${L}_{\xi }\left(\omega \right)$ and ${L}_{\eta }\left(\omega \right)$ are represented in terms of the angular frequency. In the original Corcos’ modelling, they take the following simple forms:

$$L_{\xi } \left( \omega \right) = \frac{{U_{C} \left( {z_{i} ,\omega } \right)}}{{\alpha_{C} \omega }}\quad L_{\eta } \left( \omega \right) = \frac{{U_{C} \left( {z_{i} ,\omega } \right)}}{{\beta_{C} \omega }},$$

where α_C and β_C are constant parameters to be determined by a fit of the experimental results.

In view of the Corcos’ type assumptions, the auto-spectrum modelling is independent of the coherence function modelling. This approach substantially implies that the shape of the cross-spectrum is determined by the auto-spectrum, while the exponential functions determine the way such a shape evolves in streamwise and spanwise directions.

It should be pointed out that the Corcos’ model was based on a proper fitting of the data provided by Willmarth & Woldridge [19], and it has been proposed and validated in incompressible flow conditions. However, it has been shown that even at high supersonic M (e.g. [11]), the separation of variables approach is still valid whereas compressibility only affects the amplitude of the coefficients α_C and β_C.

The present approach follows the path of the literature, and the cross-spectrum will be represented in terms of coherence lengths to be determined through proper fits of the coherence functions. The cross-spectra will be computed in correspondence with the transducer clusters highlighted in Fig. 1, where measurements comprising both streamwise and crosswise separations are available.

3.2 Non-dimensional Representation

The dimensional analysis permits the representation of the original problem in terms of independent, significant dimensionless parameters. This procedure is crucial for the extrapolation to full scale of the results obtained on the scaled model from the Wind Tunnel tests.

Two characteristic velocity length scales should be considered. The first one is related to the free stream flow, U_∞, while the second one characterises the TBL propagation effects, and it is the local convection velocity U_c. It is obvious that when the auto-spectrum alone is considered, the best choice is to consider U_∞; whereas for the cross-spectrum, the best choice is U_c.

The typical length scale to be adopted to normalise the streamwise spatial independent variable x is the reference length scale of the launcher Λ. On the other hand, the turbulent boundary layer displacement thickness δ₁ is used to normalise the frequency and the spectra amplitude. This parameter is not measured experimentally but has been determined numerically through dedicated RANS simulations.

The tests have been carried out at different angles of incidence, spanning from  – 10° to + 10°, which, therefore, is another independent dimensionless parameter. Finally, also the Mach number is taken into account even though only two values are considered in the supersonic range (see Table 1).

Following a dimensional Buckingham-like analysis, the non-dimensional representation of the auto-spectrum is given by:

$$S_{pp}^{*} = \frac{{S_{pp} }}{{q^{2} }}\frac{{U_{\infty } }}{{\delta_{1} }}_{{}}^{{}} ,$$

where q is the dynamic pressure of the mean stream.

The auto-spectrum is a function of the following dimensionless parameters:

$$M_{\infty } , St, x^{*} , \alpha ,$$

where the Strouhal number is defined as:

$$St = \frac{{f\delta_{1} }}{{U_{\infty } }}{\text{and }}x^{*} = \frac{x}{\Lambda }.$$

According to the separation of variables approach, the non-dimensional spectrum can be represented as follows:

$$S_{pp}^{*} = H\left( {St} \right){ }H\left( {x^{*} } \right){ }F_{1} \left( \alpha \right)F_{2} \left( {M_{\infty } } \right)_{{}}^{{}} .$$

$H(St)$ is the key quantity that, having unitary integral, provides the energy of the pressure fluctuations as a function of the non-dimensional frequency. As already anticipated, $H(St)$ will be approximated by a polynomial fit. It must be taken into account that $H\left(St\right)$ is obtained by a proper fit of the non-dimensional spectra obtained from transducers belonging to the region where the shape of the auto-spectra remains approximately the same. This averaging process provides also an estimation of the uncertainty that is determined from the standard deviation of the mean spectrum.

$H\left({x}^{*}\right)$ is the integral of the non-dimensional spectrum whereas the functions ${F}_{1}(\alpha )$ and ${F}_{2}({M}_{\infty })$ provide the dependence upon AoA and Mach number.

In the case of the cross-spectra, the following three new independent dimensionless groups have to be taken into account:

$U^{*} = \frac{{U_{c} }}{{U_{\infty } }}$: velocity scale ratio;

$\Delta x^{*} = \frac{\left| \xi \right|}{{\delta_{1} }}:$ normalised longitudinal separation;

$\Delta y^{*} = \frac{\left| \eta \right|}{{\delta_{1} }}$: normalised azimuthal separation.

According to the Corcos’ model, the cross-spectra are determined as a product of the non-dimensional coherence function by the auto-spectrum leading to the following expression of the non-dimensional cross-spectrum:

$$S_{{pp^{\prime}}}^{*} = S_{pp}^{*} \left( {x_{{}}^{*} , St, M_{\infty } , \alpha } \right) \gamma \left( {St,U^{*} ,\Delta x_{{}}^{*} ,\Delta y_{{}}^{*} } \right)e^{{j\frac{{2\pi St \Delta x_{{}}^{*} }}{{U^{*} }}}}$$

and the coherence function assumes the following form:

$$\gamma \left( {St,U^{*} ,\Delta x_{{}}^{*} ,\Delta y_{{}}^{*} } \right) = e^{{ - \alpha_{c} \frac{{2\pi St \left| {\Delta x^{*} } \right|}}{{U^{*} }}}} e^{{ - \beta_{c} \frac{{2\pi St \left| {\Delta y^{*} } \right|}}{{U^{*} }}}} .$$

In account of the definitions of St, U*, $\Delta {x}^{*}$ and $\Delta {y}^{*}$, the coefficients of the exponential functions read as follows:

$$\gamma \left( {St,U^{*} ,\Delta x_{{}}^{*} ,\Delta y_{{}}^{*} } \right) = e^{{ - \alpha_{c} \frac{{2\pi f\delta_{1} }}{{U_{\infty } }}\frac{\left| \xi \right|}{{\delta_{1} }}\frac{{U_{\infty } }}{{U_{c} }}}} e^{{ - \beta_{c} \frac{{2\pi f\delta_{1} }}{{U_{\infty } }}\frac{\left| \eta \right|}{{\delta_{1} }}\frac{{U_{\infty } }}{{U_{c} }}}} = e^{{ - \alpha_{c} \frac{2\pi f}{{U_{c} }}\left| \xi \right|}} e^{{ - \beta_{c} \frac{2\pi f}{{U_{c} }}\left| \eta \right|}} .$$

Therefore, it is possible to introduce two new non-dimensional frequencies (see also the early papers [18] and [19]):

$$St_{\xi } = \frac{2\pi f}{{U_{c} }}\left| \xi \right|{\text{and }}St_{\eta } = \frac{2\pi f}{{U_{c} }}\left| \eta \right|,$$

that can be adopted for the graphical representation of the coherence functions as well as for their fit.

In the present investigation, the exponents α_c and β_c are dependent upon the position along the launcher; whereas, their dependency upon the Mach number and the AoA is weak.

4 Results

An overall, even though qualitative, characterisation of the flow behaviour along the launcher has been achieved through flow visualisations carried out using the Schlieren technique.

Figure 2 reports the result achieved at the two supersonic Mach numbers and α = 0°. The trace of the bow shock as well as of other Mach waves is well visible in both cases. As expected, shock waves are formed at the end of the boat-tail and at the interstage 3–4 and are accompanied by expansion waves. The two cases differ only by the inclination of the Mach waves and of the oblique shocks that are more inclined at the higher M. Apart from this, it is clear that the flow behaviour is very similar and, as expected, the dependency upon the Mach number is not relevant.

Fig. 2

Schlieren visualisations obtained at α = 0° for M = 2 (a) and M = 2.75 (b)

The effect of the angle of incidence is reported in Fig. 3 for the case at M = 2. Similar results are obtained at M = 2.75 and are not reported for brevity. It is shown that no separations occur at the highest angle of attach and the overall flow evolution along the launcher does not change significantly. It should be pointed out that the black lines originated from the model surface correspond to localised density variations due to oblique shocks and Mach Waves. Indeed, they are originated form locations along the launcher corresponding to variations of the surface inclination.

Fig. 3

Schlieren visualisations obtained at M = 2 for α = 5° (a) and α = 10° (b)

In summary, the Schlieren visualisations confirm the expected flow patterns along the launcher and provide a clear indication that the effect of both M and $\alpha$ is very weak. This outcome has been confirmed also by the analysis of the pressure spectra (these results are not reported here for the sake of conciseness) and, thus, the functions ${{F}_{1}(\alpha )}$ and ${{ F}_{2}({M}_{\infty })}$ of the auto-spectrum model will be assumed to be constant.

Examples of results obtained in the auto-spectra analysis are given in Fig. 4. The reported plots are the functions $H(St)$ and the corresponding uncertainties estimated from the averaging process that is carried out to obtain the mean spectrum. The four subplots correspond to the four regions of the launcher where the shape of the spectra remains similar.

Fig. 4

Averaged spectra (black dotted lines) and approximating functions (black line) reported with their uncertainty range (red lines). The examples correspond to M = 2 and $\alpha$ = 0°

It is shown that, except for the very high frequencies, that are not of interest for the full-scale reconstruction, there is a very good agreement between the approximating function and the reference spectra. Similar results are obtained at M = 2.75 and are not reported here for brevity. It should be pointed out that the discrepancy at very high frequencies is due to the fact that the approximating functions are limited to a maximum St corresponding to log10(St) = 2.5. This is due to the fact that at higher frequencies, the spectra are not reliable and are affected by background electronic noise.

The analytical approximation, also reported in Fig. 4, is given by a polynomial fit of the 5th order that is applied to the spectra in the bi-logarithmic scale. Therefore, the analytical form of the model has the following expression:

$$log_{10} \left[ {H\left( {St} \right)} \right] = A\left[ {log_{10} \left( {St} \right)} \right]^{5} + B\left[ {log_{10} \left( {St} \right)} \right]^{4} + C\left[ {log_{10} \left( {St} \right)} \right]^{3} + D\left[ {log_{10} \left( {St} \right)} \right]^{2} + E\left[ {log_{10} \left( {St} \right)} \right]^{{}} + F.$$

The coefficients are not reported therein since they depend on the position along the launcher. Of course, they have to be taken into account in the extrapolation of the spectra at full scale.

Examples of streamwise coherence functions determined on different positions along the launcher are given in Fig. 5. The cases reported correspond to M = 2 and $\alpha$ = 0° but similar results have been obtained at the other AoAs and M. Even though with different decay amplitudes, it is shown that the pure exponential decay approximation applies for all cases. Therefore, the Corcos’ approach can be considered valid and the only parameter to be adjusted in the model is the coefficient ${\alpha }_{c}$.

Fig. 5

Examples of streamwise coherence functions computed between consecutive transducers located on the ogive (red line), the boat-tail (black line), the cylinder (green line). The dashed straight lines are the exponential approximations. This example corresponds to M = 2 and $\alpha$ = 0°

Analogous results obtained considering radial separations are given in Fig. 6. The results refer to the three microphone clusters reported in Fig. 1 where transducers are separated in the spanwise direction. It is shown that again the exponential decay can be considered a valid approximation and the shape of the coherence functions is less dependent upon the position along the launcher. In this case, a unique value of the exponential coefficient ${\beta }_{c}$ can be considered in the model.

Fig. 6

Examples of spanwise coherence functions computed between consecutive transducers (separated in the radial direction) located on the ogive (red line), the boat-tail close to the ogive (black line), the boat-tail close to the interstage (green line) (see transducers clusters in Fig. 1). The dashed straight line is the exponential approximation valid for all the considered cases. This example corresponds to M = 2 and $\alpha$ = 0°

The reconstruction at model or full scale is performed using the non-dimensional representation of the auto- and cross-spectra. The data processing described above provides the functions $H\left(St\right)$ (through the coefficients of the fits and the Strouhal axis) and $H({x}^{*})$. The effect of $\alpha$ and ${M}_{\infty }$ is not modelled since it has been shown above that the dependency upon those parameters is weak.

From the flight data, it is possible to recover the free stream velocity and the dynamic pressure at the desired Mach number, that corresponds to a certain altitude of the actual launcher trajectory. On the other hand, the displacement thickness must be provided by the numerical simulations of the full-scale launcher at a location that, when scaled by factor 1:30, corresponds to the location of one of the available transducers or lies within one of the regions where the model applies.

An example is reported in the following for a supersonic case, at M = 2 and $\alpha$=5°. According to the flight data, the free stream velocity and the dynamic pressure are, respectively, ${U}_{\infty FS}=800m/s$ and ${q}_{\infty FS}=23200Pa$, where the subscript FS stands for full scale. The boundary layer displacement thickness ${\delta }_{1FS}\left(x\right)$ is taken from the numerical results at full scale and the function H(St) is reconstructed from the coefficients of the polynomial approximation.

The dimensional spectrum at the location $x$ is eventually reconstructed according to the following expression:

$$S_{pp} = H\left( {St} \right) H\left( {x^{*} } \right)\frac{{q_{\infty FS}^{2} \delta_{1FS} \left( x \right)}}{{U_{\infty FS} }}.$$

Similarly, the dimensional frequency is given by the following formula:

$$f = \frac{{St \delta_{1FS} }}{{U_{\infty FS} }}.$$

An example of a full-scale reconstructed spectrum, corresponding to one sensor on the Fairing, is presented in Fig. 7 together with the uncertainty range.

Fig. 7

Normalised full-scale auto-spectrum on the Fairing at M = 2 and $\alpha$=5°. The dotted lines represent the bounds of the uncertainty interval also reconstructed at full scale

To the extent of the cross-spectra, the extrapolation at full scale is straightforward once the auto-spectra are reconstructed. Indeed, according to the Corcos’s approach adopted in the present modelling procedure, the cross-spectra are given by the product of the auto-spectra and the non-dimensional coherence function that, as shown above, is approximated by a pure exponentially decaying function.

5 Conclusions

A procedure for modelling the wall pressure auto- and cross- spectra generated on the surface of the VEGA-C launcher in highly supersonic flow conditions has been presented. The analysis is based on the post-processing of an experimental database obtained from wind tunnel measurements at M = 2 and 2.75 on a 1:30 scaled launcher model.

The spectral modelling relies on the Corcos’ assumption that usually is considered valid only for fully developed turbulent boundary layers in equilibrium conditions. A Buckingham-like analysis allows for the representation of the auto- and cross-spectra in non-dimensional form and a separation of variable approach is adopted to account for the influence of the main governing non-dimensional parameters.

Schlieren visualisations provided useful overall pictures of the flow behaviour and confirmed that both the Mach number and the AoA weakly influence the flow physics.

It is shown that the non-dimensional auto-spectra can be approximated by 5th-order polynomial functions whereas an exponential approximation is valid for the coherence functions. Except for the transverse coherence, both the coefficients of the polynomial fit and the exponent of the decay law depend upon the position along the launcher.

Taking into account the conditions at full scale as well as RANS results providing the boundary layer thickness along the launcher (at model and full scale), a simple procedure to extrapolate the results at full scale is presented.

Further investigations are surely needed to extend the modelling approach presented therein to a broader range of flow conditions, in particular in terms of the Mach number. Considering the relevant costs and difficulties in performing wind tunnel tests at supersonic flow conditions, this task remains a challenge for future research activities.