1 Introduction

Laminated composite structures have been employed in several engineering fields, e.g., aerospace, naval, and automotive industries. Even though they permit reducing the structural weight and optimizing performance, composite structures may induce complex structural phenomena due to the inhomogeneity of material properties. Among them, the free-edge effects arise at the interfaces between dissimilar layers near geometrical or mechanical discontinuities in the component and may lead to the onset of damage.

This paper adopts 2D structural models to analyze free-edge effects. Thorough reviews on these models can be found in Reddy [1] and Carrera [2]. The Kirchhoff–Love theory [3, 4] was the first 2D model. Classical Lamination Theory (CLT) is the extension of this theory for the laminated structures; see Reissner [5]. CLT has several drawbacks, as it neglects transverse shear and thickness stretching. The First-Order Shear Deformation Theory (FSDT), based on the papers of Reissner [6] and Mindlin [7], improves CLT by considering constant transverse shear deformations.

Several refined theories have been developed in recent decades to overcome the limitations of CLT and FSDT [8]. Carrera [2, 9,10,11,12] proposed models based on Reissner’s Mixed Variational Theorem (RMVT) and the Principle of Virtual Displacements (PVD) within the context of the Carrera Unified Formulation (CUF).

The Layer-Wise approach (LW) has emerged to improve the results of Equivalent Single-Layer methods (ESL). LW is particularly beneficial for detecting local phenomena and complex through-the-thickness distributions of transverse stresses [13,14,15,16,17]. A third approach is the Variable Kinematics (VK) one, where the structural theory can vary point-wise. By employing this approach, computational costs can be significantly reduced [18,19,20]. Botshekanan Dehkordi et al. [21] proposed a VK approach to analyze sandwich plates. RMVT was adopted with the CUF to assess axial and transverse stress components. Furthermore, the grouping of plies approach has been previously introduced within the framework of CUF for 2D composite structures [22,23,24]. In the present paper, the VK approach is employed on plate and shell models, with the adoption of Lagrange polynomials.

Seminal works on free-edge phenomena are those by Hayashi [25] and Puppo and Evensen [26]. Then, in 1970, Pipes and Pagano [27] provided the first approximation of the three-dimensional (3D) stress fields at the free edges. Mittelstedt and Becker [28] provided an excellent review. Several closed-form solutions were provided for the free-edge analysis. For instance, Pipes and Pagano [29] proposed an approximate elasticity solution by employing a Fourier series to represent the displacements. Then, Pagano [30] studied normal stresses in symmetric composite laminates by adopting a modified version of the higher-order theory provided by Whitney and Sun [31].

Numerical approaches have also been used to study free edges in composites; e.g., the finite difference method was used in Pipes, and Pagano [27] for symmetric laminates. Wang and Crossman [32] used three-node finite elements with a finer mesh near the free-edge zone. Whitcomb et al. [33] used eight-node elements to analyze stress singularities. Raju and Crews [34] adopted 3D solid elements. Robbins and Reddy [35] used a higher-order LW plate element. Vidal et al. [36] used the proper generalized method where eight-node elements discretized the reference mid-plane, while a refined LW fourth-order expansion was adopted in the thickness direction. De Miguel et al. [37, 38] used advanced beam models in the framework of CUF for several loading conditions and failure evaluations near the free-edge zone. Stapleton et al. [39] used CUF for the stress analysis of adhesively bonded double-lap joints.

This work analyzes free-edge effects using two approaches to compute transverse stresses: Hooke’s law and the integration of the indefinite equilibrium equations of 3D elasticity [40]. The latter is commonly called the stress recovery technique and has been widely utilized in previous studies. For instance, Patni et al. [41] investigated shear stresses in the CUF framework using the beam formulation and Lagrange serendipity expansions over the cross-section. Carrera [2] compared Taylor-like and Legendre expansions with the stress recovery technique for plate and shell structures. Petrolo et al. [42] recently examined beams, plates, and shells within the CUF framework. Additionally, Park et al. [43] proposed a nonlinear predictor–corrector procedure to accurately recover stresses in laminated plates.

This paper is organized as follows: Section 2 provides a brief introduction to the unified formulation within a finite element method framework. Section 3 explains the three modeling approaches adopted in this work. In Sect. 4, the three-dimensional indefinite equilibrium equations are introduced. Section 5 presents the results for plates and shells using several CUF-based models. Conclusions of this paper and the possible developments are drawn in Sect. 6.

2 Unified Formulation

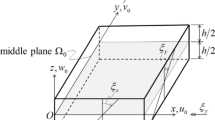
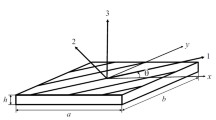
Two generic laminated structures, namely a plate and a shell, are shown in Fig. 1.

Fig. 1
figure 1

Plate and shell models. A Cartesian reference system is used for the plate model (x, y, z), while a curvilinear system (\(\alpha\), \(\beta\), z) is adopted for the shell model

Full size image

In particular, the plate model uses the z coordinate for the thickness direction, and the plane x–y lays on the mid-surface \(\Omega _0\). The shell adopts a curvilinear reference frame (\(\alpha\), \(\beta\), z) to account for the curvatures, R\(_{\alpha }\) and R\(_{\beta }\), where \(\alpha\) and \(\beta\) are the two in-plane directions. The displacement vectors for the multilayered plates and shells are introduced as follows:

$$\begin{aligned} \varvec{\textbf{u}}^k(x,y,z) = \left\{ \begin{array}{ccc} u^k_{x}&u^k_{y}&u^k_{z} \end{array}\right\} ^{T}, {\;} \varvec{\textbf{u}}^k(\alpha ,\beta ,z) = \left\{ \begin{array}{ccc} u^k_{\alpha }&u^k_{\beta }&u^k_{z} \end{array}\right\} ^{T}, \end{aligned}$$
(1)

where the superscript \((\bullet )^k\) indicates a layer. The stress, \({\mathbf {\sigma }}^k\), and strain, \({\mathbf {\epsilon }}^k\), components are indicated in the vectorial form:

$$\begin{aligned} \begin{aligned} \varvec{\sigma }^k&= \left\{ \begin{array}{cccccc} \sigma _{xx}^k&\sigma _{yy}^k&\sigma _{zz}^k&\sigma _{xz}^k&\sigma _{yz}^k&\sigma _{xy}^k \end{array}\right\} ^{T},\\ \varvec{\epsilon }^k&= \left\{ \begin{array}{cccccc} \epsilon _{xx}^k&\epsilon _{yy}^k&\epsilon _{zz}^k&\epsilon _{xz}^k&\epsilon _{yz}^k&\epsilon _{xy}^k \end{array}\right\} ^{T}\\ \varvec{\sigma }^k&= \left\{ \begin{array}{cccccc} \sigma _{\alpha \alpha }^k&\sigma _{\beta \beta }^k&\sigma _{zz}^k&\sigma _{\alpha z}^k&\sigma _{\beta z}^k&\sigma _{\alpha \beta }^k \end{array}\right\} ^{T}, \\ \varvec{\epsilon }^k&= \left\{ \begin{array}{cccccc} \epsilon _{\alpha \alpha }^k&\epsilon _{\beta \beta }^k&\epsilon _{zz}^k&\epsilon _{\alpha z}^k&\epsilon _{\beta z}^k&\epsilon _{\alpha \beta }^k \end{array}\right\} ^{T}. \end{aligned} \end{aligned}$$
(2)

The displacement–strain relation is given in the following:

$$\begin{array}{*{20}l} {\epsilon ^{k} = {\mathbf{b}}^{k}{\mathbf{u}}^{k} ,} \hfill \\ \end{array} {\text{ }}$$
(3)

where \(\varvec{\textbf{b}}\) is the matrix of differential operators. The components of this matrix change depending on whether plate or shell models are adopted. Further details are provided in [44]. In this work, linear elastic orthotropic materials are considered. Therefore, the constitutive relation can be expressed as follows:

$$\sigma ^{k} = \mathbf{C}^{k} \mathbf{\epsilon} ^{k}$$
(4)

where \({\varvec{\textbf{C}}}^k\) is the material elastic matrix, whose explicit form can be found in [45, 46].

In the Carrera Unified Formulation (CUF), the 3D displacement field of the plate (i.e., \(\varvec{\textbf{u}}^k(x,y,z)\)) and shell models (i.e., \(\varvec{\textbf{u}}^k(\alpha ,\beta ,z)\)) can be expressed as a general expansion of the primary unknowns, as shown in Table 1.

Table 1 CUF Expansions of the primary unknowns. \(\tau\) and s are repeated indexes with \(\tau\) = 1,2,....,M and s = 1,2,....,M, while M denotes the number of the expansion functions
Full size table

F\(_{\tau }\) and F\(_{s}\) are the expansion functions of the generalized displacements and variations, \(\varvec{\textbf{u}}^k_{\tau }\) and \(\delta \varvec{\textbf{u}}^k_{s}\), respectively. The Einstein convention is applied with repeated indices \(\tau\) and s. M is the number of the expansion functions, and \(\delta\) indicates the variations of the displacements [44].

This paper uses Lagrange expansions. The 3D displacement field is obtained by interpolating the displacements evaluated at the Lagrange Points (LP), see [47]. The cubic interpolation is given as an example. The four points are equally spaced. \(\zeta _1=-1\), \(\zeta _2=-1/3\), \(\zeta _3=+1/3\) and \(\zeta _4=+1\), and the following expansions can be obtained:

$$\begin{aligned} \begin{aligned} F_1&=-\frac{9}{16}\left( \zeta +\frac{1}{3}\right) \left( \zeta -\frac{1}{3}\right) \left( \zeta -1\right) ,\\ F_2&=+\frac{27}{16}\left( \zeta +1\right) \left( \zeta -\frac{1}{3}\right) \left( \zeta -1\right) ,\\ F_3&=-\frac{27}{16}\left( \zeta +1\right) \left( \zeta +\frac{1}{3}\right) \left( \zeta -1\right) ,\\ F_4&=+\frac{9}{16}\left( \zeta +\frac{1}{3}\right) \left( \zeta -\frac{1}{3}\right) \left( \zeta +1\right) . \end{aligned} \end{aligned}$$
(5)

2.1 Finite Elements

The Finite Element Method (FEM) can be employed within the CUF framework as shown in Table 2.

Table 2 FEM and CUF modeling of the primary unknowns. i and j are repeated indexes with i = 1,2,....,N\(_{n}\) and j = 1,2,....,N\(_{n}\), N\(_{n}\) is the number of the FE nodes per element
Full size table

N\(_{i}\) and N\(_{j}\) are the shape functions, while the repeated subscripts i and j indicate summation. N\(_{n}\) is the number of Finite Element (FE) nodes per element. Additionally, \(\varvec{\textbf{q}}^k_{\tau i}\) and \(\varvec{\textbf{q}}^k_{s j}\) are the vectors of FE nodal unknowns and variations:

$$\begin{aligned} \begin{aligned} \begin{array}{cccccc} \varvec{\textbf{q}}^k_{\tau i} &{} =&{} \left\{ q^k_{x_{\tau i}} \; q^k_{y_{\tau i}} \; q^k_{z_{\tau i}} \right\} ^{T}, &{} \varvec{\textbf{q}}^k_{\tau i} &{} =&{} \left\{ q^k_{\alpha _{\tau i}} \; q^k_{\beta _{\tau i}} \; q^k_{z_{\tau i}} \right\} ^{T}, \\ \\ \delta \varvec{\textbf{q}}^k_{s j} &{} =&{} \left\{ \delta q^k_{x_{s j}} \; \delta q^k_{y_{s j}} \; \delta q^k_{z_{s j}} \right\} ^{T}, &{}\delta \varvec{\textbf{q}}^k_{s j} &{} =&{} \left\{ \delta q^k_{\alpha _{s j}} \; \delta q^k_{\beta _{s j}} \; \delta q^k_{z_{s j}} \right\} ^{T}. \end{array} \end{aligned} \end{aligned}$$
(6)

Lagrange polynomials are used as the shape functions [45]. In the present paper, classical 2D nine-node bi-quadratic finite elements will be employed for both plate and shell formulations.

2.2 Governing Equations

The principle of virtual displacements is used,

$$\begin{aligned} \begin{array}{lll} \displaystyle \int _{V_k}(\delta {\mathbf {\epsilon }}^{kT}{\mathbf {\sigma }}^{k})\textrm{d}V_k= {} \delta L_{e}, \end{array} \end{aligned}$$
(7)

where V\(_k\) is the volume considered the integration domain, and the left-hand side of the equation represents the variation of the internal work. In contrast, the right-hand side is the variation of the external work. By substituting the geometrical relations (Eq. (3)), the constitutive equation (Eq. (4)), and applying the CUF and the FEM approximations (Table 2), the governing equations can be obtained:

$$\begin{aligned} \begin{array}{lll} \delta \varvec{\textbf{q}}_{s j}^{kT}:\; \varvec{\textbf{k}}^{k}_{i j \tau s} \; \varvec{\textbf{q}}_{\tau i}^{k} = \varvec{\textbf{p}}_{s j}^{k}, \end{array} \end{aligned}$$
(8)

where \(\varvec{\textbf{k}}^{k}_{i j \tau s}\) represents a 3 \(\times\) 3 matrix, called the Fundamental Nucleus (FN) of the mechanical stiffness matrix. The explicit form of the nine FN elements depends on the selected formulation. The explicit expressions of the FN components can be found in [44]. FN is expanded with respect to the indexes \(\tau\) and s to obtain the stiffness matrix of each layer k. Subsequently, the matrices of each layer are assembled at the multi-layer level depending on the considered approach (ESL, LW, or VK). For a detailed discussion on the assembly of the FN, please refer to [44].

3 Modeling Approaches

This work compares Equivalent Single-Layer (ESL), Layer-Wise (LW), and Variable Kinematics (VK) approaches. In this section, a brief overview of the three approaches is provided. See Pagani et al. [47] for details on the assembly procedure for each approach.

In ESL models, the kinematic assumptions are uniform throughout the structure’s thickness. The variables are independent of the number of layers; see Fig. 2(a). In this approach, the stiffness matrices of each layer are homogenized by summing the contributions from all the layers.

In the case of LW models, different sets of variables are assumed for each layer, and the continuity of displacements is imposed at the layer interfaces. The LW approach allows for accurately capturing the discontinuous behavior of the derivatives of the primary unknowns, as illustrated in Fig. 2(b).

VK involves using different sets of expansion functions to develop combined ESL/LW models. Figure 2(c) illustrates how this method can effectively incorporate a non-local LW approach.

Fig. 2
figure 2

Equivalent single-layer (a), layer-wise (b) and variable kinematics (c) modeling of the displacement field along the thickness of a structure

Full size image

4 Integration of the 3D Indefinite Equilibrium Equations

Fig. 3
figure 3

Pattern of points for the integration of 3D equilibrium equations in a four-layer structure

Full size image

The approach is based on integrating the in-plane stresses derived from the constitutive laws in the thickness directions. Figure 3 shows a schematic representation of the numerical integration along a four-layer structure.

Plate In the static case, assuming no volume forces, the equilibrium equations of 3D elasticity for a plate can be expressed as follows:

$$\begin{aligned} \begin{aligned} \delta u_x&: \sigma _{xx,x}+\sigma _{xy,y}+\sigma _{xz,z}=0,\\ \delta u_y&: \sigma _{yx,x}+\sigma _{yy,y}+\sigma _{yz,z}=0,\\ \delta u_z&: \sigma _{zx,x}+\sigma _{zy,y}+\sigma _{zz,z}=0. \end{aligned} \end{aligned}$$
(9)

By integrating the equilibrium equations from \(z^{i-1}\) to \(z^{i}\) for each layer the equations can be written as:

$$\begin{aligned} \begin{aligned} \sigma _{xz}^{i}&=\sigma _{xz}^{i-1}-\int _{i-1}^{i}\left( \sigma _{xx,x}+\sigma _{xy,y}\right) dz,\\ \sigma _{yz}^{i}&=\sigma _{yz}^{i-1}-\int _{i-1}^{i}\left( \sigma _{yx,x}+\sigma _{yy,y}\right) dz,\\ \sigma _{zz}^{i}&=\sigma _{zz}^{i-1}-\int _{i-1}^{i}\left( \sigma _{zx,x}+\sigma _{zy,y}\right) dz. \end{aligned} \end{aligned}$$
(10)

Shell In the static case, the indefinite equilibrium equations of 3D elasticity for shell structures can be expressed as follows:

$$\begin{aligned} \begin{aligned} \delta u_{\alpha }&:\frac{\partial \sigma _{\alpha z}}{\partial z}+\sigma _{\alpha z}\left( \frac{2}{R_{\alpha }\;H_{\alpha }}+\frac{1}{R_{\beta }\;H_{\beta }}\right) \\&\quad +\frac{1}{H_{\alpha }}\frac{\partial \sigma _{\alpha \alpha }}{\partial \alpha }+\frac{1}{H_{\beta }}\frac{\partial \sigma _{\alpha \beta }}{\partial \beta }=0,\\ \delta u_{\beta }&:\frac{\partial \sigma _{\beta z}}{\partial z}+\sigma _{\beta z}\left( \frac{1}{R_{\alpha }\;H_{\alpha }}+\frac{2}{R_{\beta }\;H_{\beta }}\right) \\&\quad +\frac{1}{H_{\beta }}\frac{\partial \sigma _{\beta \beta }}{\partial \beta }+\frac{1}{H_{\alpha }}\frac{\partial \sigma _{\alpha \beta }}{\partial \alpha }=0, \end{aligned} \end{aligned}$$
(11)

with

$$\begin{aligned} H_{\alpha }=1+\frac{z}{R_{\alpha }},\qquad H_{\beta }=1+\frac{z}{R_{\beta }}. \end{aligned}$$
(12)

If only cylindrical shells are considered, where the curvature in the \(\alpha\) direction (i.e., R\(_{\alpha }\)) tends to infinity, the equilibrium equations can be modified:

$$\begin{aligned} \begin{aligned} \delta u_{\alpha }&:\frac{\partial \sigma _{\alpha z}}{\partial z}+\sigma _{\alpha z}\left( \frac{1}{R_{\beta }\;H_{\beta }}\right) =-\frac{\partial \sigma _{\alpha \alpha }}{\partial \alpha }-\frac{1}{H_{\beta }}\frac{\partial \sigma _{\alpha \beta }}{\partial \beta },\\ \delta u_{\beta }&:\frac{\partial \sigma _{\beta z}}{\partial z}+\sigma _{\beta z}\left( \frac{2}{R_{\beta }\;H_{\beta }}\right) =-\frac{1}{H_{\beta }}\frac{\partial \sigma _{\beta \beta }}{\partial \beta }-\frac{\partial \sigma _{\alpha \beta }}{\partial \alpha }, \end{aligned} \end{aligned}$$
(13)

with

$$\begin{aligned} H_{\alpha }=&1,\qquad H_{\beta }=1+\frac{z}{R_{\beta }}. \end{aligned}$$
(14)

Due to the left-hand side of the previous equations, a numerical method is necessary to solve them. In this paper, the trapezoidal rule is used for the integration. Therefore, the integrals can be written as follows,

$$\begin{aligned} \begin{aligned} \sigma _{\alpha z}^{i}&=\left( \sigma _{\alpha z}^{i-1}\left( 1+\frac{z^i-z^{i-1}}{2 H_{\beta } R_{\beta }}\right) \right. \\&\quad \left. +\int _{i-1}^{i}\left( -\frac{\partial \sigma _{\alpha \alpha }}{\partial \alpha }-\frac{1}{H_{\beta }}\frac{\partial \sigma _{\alpha \beta }}{\partial \beta }\right) \textrm{d}z \right) /\left( 1+\frac{z^i-z^{i-1}}{2 H_{\beta } R_{\beta }}\right) \\ \sigma _{\beta z}^{i}&=\left( \sigma _{\beta z}^{i-1}\left( 1+\frac{z^i-z^{i-1}}{H_{\beta } R_{\beta }}\right) \right. \\&\quad \left. +\int _{i-1}^{i}\left( -\frac{1}{H_{\beta }}\frac{\partial \sigma _{\beta \beta }}{\partial \beta }-\frac{\partial \sigma _{\alpha \beta }}{\partial \alpha }\right) \textrm{d}z \right) /\left( 1+\frac{z^i-z^{i-1}}{H_{\beta } R_{\beta }}\right) . \end{aligned} \end{aligned}$$
(15)

5 Numerical Results

In this section, the evaluation of out-of-plane stresses is carried out for two study cases and considers the presence of free-edge phenomena. The first case focuses on composite plates, where two symmetric stacking sequences are investigated. The second case involves the analysis of a shell composite structure consisting of four layers. Results from the open literature are taken as reference solutions when available. If no literature results exist, the LW models are the reference solutions.

The theories adopted will be displayed using the following notation: LN is the Lagrange expansion with N points used. For instance, L7 stands for a seven-node expansion; H indicates the use of Hooke’s law, and I stands for the stress recovery method.

5.1 Composite Plates

Fig. 4
figure 4

Finite element mesh over the x–y plane for the composite plates

Full size image

A composite symmetric plate is analyzed as the first example. Two different stacking sequences are considered. The surface of the plate is rectangular with sides L=40 mm, b=20 mm, and the height is h=5 mm. The material properties are defined as follows: E\(_{1}\)= 137.9 GPa, E\(_{2}\)= E\(_{3}\)= 14.5 GPa, \(\nu _{12}\)= \(\nu _{13}\)= \(\nu _{23}\)= 0.21, G\(_{12}\)= G\(_{13}\)= G\(_{23}\)= 5.9 GPa. Pagano [48] originally proposed the analysis. A uniform axial strain \(\epsilon _{0}\) is applied along the x-axis by prescribing an end-displacement u\(_x\) = \({\mp }\) 1 mm at x = ± L/2. The uniform traction load induces a constant strain state along the x-axis in the central region of the plate, provided the length L is sufficiently larger than the perturbed regions next to the pulled edges. Transverse normal, \(\sigma _{zz}\), and shear, \(\sigma _{xz}\), stresses are evaluated. The results are reported in a scaled form as follows:

$$\begin{aligned} {\overline{\sigma }}_{zz} =\frac{\sigma _{zz}}{\epsilon _{0}}, \qquad {\overline{\sigma }}_{xz} =\frac{\sigma _{xz}}{\epsilon _{0}}. \end{aligned}$$
(16)

The FEM is employed for the discretization, using a non-uniform mesh with a size of 16\(\times\)18 elements, as depicted in Fig. 4. The mesh is finer near the free edge to capture the localized effects accurately. Although a convergence analysis has been conducted, the details are not presented for brevity.

5.1.1 Four-Layer Plate

In the first configuration, a four-layer plate is analyzed. Figure 5 describes the geometric and loading conditions. The stacking sequence is [45\(^\circ\)/-45\(^\circ\)]\(_s\). Results are compared with several literature models. Wang and Crossman [32] used a finite element model for generalized plane strain; D’Ottavio et al. [49] adopted the RMVT with fourth-order Legendre polynomials.

A preliminary convergence analysis is conducted for choosing the LW theories. Figure 6 illustrates the discretization in the y-z plane for the LW case; along z, one LW expansion per layer is used. In Fig. 7, shear stresses, \(\sigma _{xz}\), via Hooke’s Law are evaluated. In Fig. 7 (a), the stresses are calculated at the interface between the 45\(^\circ\) and -45\(^\circ\) layers (z=-h/4) along the y-axis and x=0. Figure 7 (b) shows the stress along the thickness evaluated at x=0 and near the free edge (y/b=0.998). The seven-node Lagrange expansion provides the best results.

Fig. 8 shows the theories adopted and the related Degrees of Freedom (DOF). Seven-node Lagrange expansions are always used along the thickness. Case A adopts the LW approach, Case B uses the ESL approach, whereas Case C and Case D are VK models in which two and three sets of L7 expansions are used, respectively.

Shear stress, \({\sigma }_{xz}\), is evaluated along the y-axis in Fig. 9 via Hooke’s law (H) and the integration (I). Through-the-thickness distributions at x=0 are shown in Figs. 10 and 11, at y/b=0.998 and y/b=0.78, respectively. Table 3 shows shear stresses in [0,y/b=0.78,-h/4] and [0,y/b=0.998,-h/4].

Fig. 5
figure 5

Geometry and loads of the four-layer composite plate

Full size image
Fig. 6
figure 6

Mesh over the y–z plane for the four-layer composite plates. LW approach

Full size image
Fig. 7
figure 7

Convergence analysis for the [45\(^\circ\)/-45\(^\circ\)]\(_s\) plate. Evaluation of the shear stresses with the Hooke’s law

Full size image
Fig. 8
figure 8

Theories adopted for the four-layer composite plate

Full size image
Fig. 9
figure 9

Shear stresses along y for the [45\(^\circ\)/-45\(^\circ\)]\(_s\) plate, z =-h/4

Full size image
Fig. 10
figure 10

Shear stresses along z for the [45\(^\circ\)/-45\(^\circ\)]\(_s\) plate, y/b=0.998

Full size image
Fig. 11
figure 11

Shear stresses along z for the [45\(^\circ\)/-45\(^\circ\)]\(_s\) plate, y/b=0.78

Full size image
Table 3 [45\(^\circ\)/-45\(^\circ\)]\(_s\) plate. Shear stresses, \({\overline{\sigma }}_{xz}\), with Hooke’s Law, H, and the stress recovery method, I, evaluated in [0,b,-h/4]
Full size table

The results suggest the following:

  • When stresses are calculated along the y-axis, Case A and Case D are close to the literature solution. The Hooke’s Law and stress recovery method yield similar results.

  • Considering the stresses at the free edge, the a posteriori integration of the stresses improves the results for Cases B, C, and D. At the same time, Case A-H and Case A-I yield similar results. The ESL model, namely Case B, is the least refined theory and is far from the reference solutions. Table 3 shows significant differences in the peaks between the two techniques.

  • When shear stresses are calculated at y/b=0.78, the ESL model and Case C approach the LW model. For instance, the difference with Case A-H is 5.51 % for the Case C-H, whereas for Case C-I is 2.22 %.

  • VK theories can detect the local phenomena, where an LW-like description is adopted. In particular, Case D is as accurate as Case A for the two layers at the bottom, whereas it is similar to Case C for the other two layers.

5.1.2 Eight-Layer Plate

The geometric and loading conditions of the second configuration are shown in Fig. 12. The stacking sequence is [90\(^\circ\)/0\(^\circ\)/45\(^\circ\)/-45\(^\circ\)]\(_s\). Results are compared with two reference solutions; Gaudenzi et al. [50] used a model with the displacements variables expanded in power series, and D’Ottavio et al. [49] adopted the same approach introduced for the first case above.

A convergence analysis for the choice of the LW theory is performed. Figure 13 shows the discretization employed in the y–z plane for the LW case; along z, one LW expansion per layer is used. Figure 14 presents the convergence analysis and considers transverse axial and shear stresses at y/b=0.998 and x=0. For this case, four-node Lagrange expansions are chosen for the LW approach. Figure 15 shows the models adopted and their DOF. Case A adopts the LW approach with an L4 for each layer. Case B uses the ESL approach with an L7 for the entire thickness. Cases C and D are VK models with local L4 and L7 expansions. L7 expansions were used as in the ESL case; higher-order models are needed to detect the complex stress distribution.

Transverse axial stress, \({\sigma }_{zz}\), is shown in Fig. 16, y/b=0.998, and Fig. 17, y/b=0.78. Similarly, shear stresses, \({\sigma }_{xz}\), are shown in Figs. 18 and 19. Table 4 shows shear stress values at [0,y/b=0.78,-h/8] and [0,y/b=0.998,-h/8].

Fig. 12
figure 12

Geometry and loads for the eight-layer composite plate

Full size image
Fig. 13
figure 13

Mesh over the y–z plane for the eight-layer composite plates. LW approach

Full size image
Fig. 14
figure 14

Convergence analysis for the [90\(^\circ\)/0\(^\circ\)/45\(^\circ\)/-45\(^\circ\)]\(_s\) plate. Evaluation of the transverse axial (a) and shear (b) stresses along z at y/b=0.998 with the Hooke’s Law

Full size image
Fig. 15
figure 15

Theories adopted for the eight-layer composite plate

Full size image
Fig. 16
figure 16

Transverse axial stresses along z for the [90\(^\circ\)/0\(^\circ\)/45\(^\circ\)/-45\(^\circ\)]\(_s\) plate at y/b=0.998

Full size image
Fig. 17
figure 17

Transverse axial stresses along z for the [90\(^\circ\)/0\(^\circ\)/45\(^\circ\)/-45\(^\circ\)]\(_s\) plate at y/b=0.78

Full size image
Fig. 18
figure 18

Shear stresses along z for the [90\(^\circ\)/0\(^\circ\)/45\(^\circ\)/-45\(^\circ\)]\(_s\) plate at y/b=0.998

Full size image
Fig. 19
figure 19

Shear stresses along z for the [90\(^\circ\)/0\(^\circ\)/45\(^\circ\)/-45\(^\circ\)]\(_s\) plate at y/b=0.78

Full size image
Table 4 [90\(^\circ\)/0\(^\circ\)/45\(^\circ\)/-45\(^\circ\)]\(_s\) plate. Shear stresses, \({\overline{\sigma }}_{xz}\), with Hooke’s Law, H, and the stress recovery method, I, evaluated at [0,b,-h/8]
Full size table

The results suggest that

  • The LW model results match those from the literature.

  • Both stress evaluation approaches provide similar results when LW is used. Differences are larger in the other cases and when peak values are considered.

  • When stresses are evaluated far from the free edge, all models are closer to LW.

  • The local use of LW in a VK approach effectively improves accuracy. In other words, where LW is used, the accuracy improves significantly independent of the model used elsewhere.

5.2 Composite Shell

Fig. 20
figure 20

Geometry and loads for the four-layer composite shell

Full size image
Fig. 21
figure 21

Theories adopted for the four-layer composite shell

Full size image

A composite symmetric cylindrical shell is considered with stacking sequence [45\(^\circ\)/-45\(^\circ\)]\(_s\). The geometry and loading conditions are described in Fig. 20 with the following dimensions: L=40 mm, R\(_{\beta }\)=20 mm, b=\(\frac{2\pi R_{\beta }}{6}\) and h=5 mm. The material properties and loads are the same as in the previous sections. Shear stresses are scaled according as follows:

$$\begin{aligned} {\overline{\sigma }}_{\alpha z} =\frac{\sigma _{\alpha z}}{\epsilon _{0}}. \end{aligned}$$
(17)

The same, non-uniform, 16 \(\times\) 18 mesh is used as in the previous cases. Figure 21 shows the theories adopted and their DOF.

Shear stresses, \({\sigma }_{\alpha z}\), are evaluated at the interface between the 45\(^\circ\) and -45\(^\circ\) layers (z=-h/4) along the \(\beta\)-axis, \(\alpha\) =0, see Fig. 22. \({\sigma }_{\alpha z}\) are calculated along the thickness of the structure, \(\alpha\) =0. Figures 23 and 24 show the results near the free edge (\(\beta\)/b=0.998) and at \(\beta\)/b=0.78, respectively. Table 5 shows shear stresses at [0,\(\beta\)/b=0.78,-h/4] and [0,\(\beta\)/b=0.998,-h/4].

Fig. 22
figure 22

Shear stresses along y for the [45\(^\circ\)/-45\(^\circ\)]\(_s\) shell at z=-h/4

Full size image
Fig. 23
figure 23

Shear stresses along z for the [45\(^\circ\)/-45\(^\circ\)]\(_s\) shell at \(\beta\)/b=0.998

Full size image
Fig. 24
figure 24

Shear stresses along z for the [45\(^\circ\)/-45\(^\circ\)]\(_s\) shell at \(\beta\)/b=0.78

Full size image
Table 5 [45\(^\circ\)/-45\(^\circ\)]\(_s\) laminate shell. Shear stresses, \({\overline{\sigma }}_{\alpha z}\), with Hooke’s Law, H, and the stress recovery method, I, evaluated at [0,b,-h/4]
Full size table

The results suggest that:

  • Considering the stresses evaluated along the y-axis, Hooke’s Law and stress recovery method results do not present significant differences.

  • As in previous cases, using LW and the stress recovery technique may improve the accuracy near the free edge.

  • When shear stresses are calculated far from the free edge, less refined models are sufficient, as illustrated in Table 5.

  • VK theories can calculate the stresses accurately where a local refinement is adopted.

6 Conclusions

This paper presents results concerning free-edge effects in composite plates and shells. Lagrange-based polynomials are used along the thickness in the Carrera Unified Formulation (CUF) framework. Three modeling approaches are used: the equivalent single layer, the layer-wise, and the variable kinematics approach. The latter leads to local refinement of the structural theory to reduce the computational costs. Furthermore, the constitutive equations and the stress recovery method evaluate the out-of-plane stresses. The results are compared with literature solutions whenever available. The following final remarks can be made:

  • The stresses calculated at the free edge are well evaluated only if LW models are adopted.

  • The stress recovery technique can improve the accuracy of stresses from equivalent single-layer models.

  • The local use of VK leads to an accuracy comparable to full LW models. In other words, independent of the modeling approach used elsewhere, VK improves the accuracy locally with significantly reduced computational costs.

In future works, beam and doubly curved shells could be considered. Furthermore, geometrical and material nonlinear applications could be investigated.