1 Introduction

Free-flying robots have been recently developed to operate on-board the International Space Station (ISS) as semi-autonomous robotic assistants [18]. SPHERES [13], Int-Ball and CIMON are projects of free-flyers already employed in the ISS, and designed as modular base for the integration of a wide range of hardware and software as monitoring and maintenance tools of ISS systems. Thus, free-flyers are the ideal platform for manual observation of the ISS from ground control, autonomous sensor readings and surveying of ISS conditions, and human–robot interactions during long duration human missions. The NASA Astrobee project, described in [3, 16], consists in the realization of 3 high capable robots able to moving and operate inside the ISS for long periods of time without crew supervision or intervention. In particular, in the top-aft bay, the Astrobee is equipped with a perching arm to grasp ISS handrails and objects. The robotic arm is designed as two-joints two-links robotic arm, and when not in use, it is stowed in the top payload bay, while the joints allow the arm deployment and motion for grasping.Please confirm the section headings are correctly identified.I do, the section headings are correctly identified.

The coordinated control of attitude and manipulator is a topic discussed in several researches about aerial and space manipulators, as reported in [10, 12], where the disturbances introduced by the manipulator are computed, and robust control strategies are proposed to stabilize the system. As well, the Astrobee can be considered as a small satellite floating in the micro-gravity environment of the ISS, and the reduced mass turns the robot to be more sensitive to external disturbances, while the actuators have more limitation due to the their small dimensions, as it is in [6, 14]. Thus, it is important to estimate correctly the possible disturbance introduced by the robotic arm, and to design an attitude controller able to stabilize the system in every possible scenario. Therefore, the objective of this research is to realize an accurate mathematical model of the Astrobee robot, coupling the attitude dynamics with the robotic arm dynamics, to design an effective attitude controller. Robust attitude controllers have been taken into account, to achieve reactivity and stability to parameters variation. In particular, the twisting sliding mode controller (TW-SMC) has been proposed for precise attitude control since, as it is in [4, 17], sliding mode controllers (SMC) are characterized as low complexity, and low computational cost control methods, making the TW-SMC a suitable approach for the Astrobee attitude control. For the same reason, a first-order SMC is designed for the arm manipulator. TW-SMC is compared with a backstepping controller, already employed in [5] with an aerial manipulator, considering several scenarios in Matlab/Simulink simulations where the controllers performance, in terms of manipulator motion stabilization and robustness, are analyzed. Moreover, the ability of the controller to preserve the desired attitude has been verified through combined simulations between Simulink and the NASA Astrobee simulator.

The paper is organized as follows. The Astrobee attitude dynamics is presented in “NASA Astrobee: Mathematical Model”, including the arm manipulator model. “Controllers Design” describes the sliding mode controllers for both manipulator and main body, and the design process of the backstepping controller. Simulation results are shown in “Simulation Results”. Finally, some concluding remarks are described in “Conclusion and Future Works”.

2 NASA Astrobee: Mathematical Model

In this section the kinematics and dynamics model of the Astrobee is introduced. The system orientation has been described trough the quaternions formulation for its compactness, low computational cost and lack of singularity [9]. Thus, the kinematics can be expressed as the quaternions variation in time:

$$\begin{aligned} \begin{Bmatrix} {\dot{q}}_0\\ {\dot{q}}_1\\ {\dot{q}}_2\\ {\dot{q}}_3 \end{Bmatrix} =\frac{1}{2} \begin{bmatrix} 0 &{} -\omega _x &{} -\omega _y &{} -\omega _z\\ \omega _x &{} 0 &{} -\omega _z &{} \omega _y\\ \omega _y &{} \omega _z &{} 0 &{} -\omega _x\\ \omega _z &{} -\omega _y &{} \omega _x &{} 0 \end{bmatrix} \begin{Bmatrix} q_0\\ q_1\\ q_2\\ q_3 \end{Bmatrix} \end{aligned}$$
(1)

where \(\omega =\{\omega _x,\omega _y,\omega _z\}^T \in {\mathbb {R}}^3\) is the angular velocity, expressed in the body reference frame, and \(q=\{q_0,q_v\}^T\) are the quaternions, in which \(q_0\) is the scalar component and \(q_v \in {\mathbb {R}}^3\) is the vector part. The attitude dynamics is defined by a modified version of the Euler equation, where terms related to the manipulator motion are included. In fact, considering the center of mass (CoM) of the robot fixed in the CoM of the main body, the overall moment of inertia is expressed as

$$\begin{aligned} J=J_{body}+J_{arm,0} \end{aligned}$$
(2)

where \(J_{body} \in {\mathbb {R}}^{3,3}\) is the inertia matrix of the main body, and \(J_{arm,0} \in {\mathbb {R}}^{3,3}\) is the inertia matrix of the manipulator referred to the CoM, which is a variable value in function of the manipulator configuration, finally, \(J \in {\mathbb {R}}^{3,3}\) is the total moment of inertia. Following the approach used in [5] for an aerial manipulator, the attitude dynamics equation can be derived from the angular momentum conservation expressed in the body reference frame

$$\begin{aligned} {\dot{h}}=T-\omega \times h \end{aligned}$$
(3)

where \(h \in {\mathbb {R}}^3\) is the robot angular momentum and \(T \in {\mathbb {R}}^3\) is the resultant external torque acting on the body. Exploiting the angular momentum h as the combination of the manipulator and the overall system motion, the attitude dynamics can be expressed as

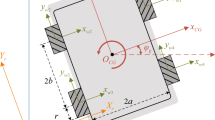
$$\begin{aligned}&{\dot{J}}\omega +J{\dot{\omega }}+({\dot{J}}_a\omega _a)_b+(J_a{\dot{\omega }}_a)_b\nonumber \\&\quad =T-\omega \times \left[ J\omega + (J_a\omega _a)_b \right] \end{aligned}$$
(4)

where each term related to the manipulator is expressed in the body reference frame. In particular, the manipulator can be modeled as two-links two-joints robotic arm, as shown in Fig. 1, and its dynamics can be expressed through the joints rotation

$$\begin{aligned} \ddot{\theta _a}=J_{a}^{-1}M \end{aligned}$$
(5)

where \(\theta _a\in {\mathbb {R}}^2\) are the joints angle, \(M\in {\mathbb {R}}^2\) is the torque applied in each joint, and \(J_a\in {\mathbb {R}}^{2,2}\) is a diagonal matrix, where \(J_{a,ii}\) is the moment inertia of the rotating manipulator part around the i-th joint. According to its configuration, each term of the manipulator dynamics included in the attitude dynamics can be computed in the the body reference frame through a rotational matrix expressed as function of the joints angles. In particular, \({\dot{J}}_a\) is related only to the rotation of the second joint that causes variations in \(J_{11}\), but considering the limitations in the second joint rotation it can be considered as negligible. On the other hand, the terms \((J_a{\dot{\omega }}_a)_b\) and \((J_a\omega _a)_b\) of Eq. (4) matches the robotic arm control input \(u_a\in {\mathbb {R}}^3\) and angular momentum \(h_a\in {\mathbb {R}}^3\), both expressed in the body reference frame. Thus, the final formulation of the attitude dynamics has been rewritten as

$$\begin{aligned} {\dot{\omega }}=J^{-1}\left[ (T-u_{a})-\omega \times (J\omega +h_{a})-{\dot{J}}\omega \right] \end{aligned}$$
(6)

where \(T = u_c+u_{ext}\), in which \(u_c\in {\mathbb {R}}^3\) is the control input of the body and \(u_{ext}\in {\mathbb {R}}^3\) is the external disturbances. The arm manipulator influences the system dynamics including disturbance torques, and modifying the overall inertia. The system dynamics can be combined with attitude and manipulator controllers, as showed in Fig. 2, to realize a complete mathematical model of the Astrobee system.

Fig. 1
figure 1

Robotic arm model

Full size image
Fig. 2
figure 2

Astrobee model scheme

Full size image

3 Controllers Design

In this section, the sliding mode controllers are described for both manipulator and main body. The overall system needs two controllers, one to handle the manipulator motion and one to achieve attitude control and stabilization, as shown in Fig. 2. Both the controllers have been designed considering sliding mode control strategies, since SMCs are characterized as low complexity, low computational burden, and robust control methods [15]. For the attitude control, it has been compared with a backstepping controller, which include an iterative algorithm to define an adaptive control to faster stabilize the disturbances.

3.1 First-Order SMC

The robotic arm controller has been designed as first-order SMC. In particular, SMC consists in the definition of a sliding surface \(\sigma\), which has to be reached by the system. Thus, the control forces lead the system on \(\sigma\), and let it slide on the surface [17]. The sliding surface is usually defined by a linear combination of the tracking error derivatives

$$\begin{aligned} \sigma =k_\gamma e_y^{(\gamma )} + k_{\gamma -1} e_y^{(\gamma -1)}+...+k_1e_y , \end{aligned}$$
(7)

where \(k_\gamma >0\) is a constant parameter, and \(e_y^{(\gamma )}\) is the \(\gamma\)-th derivative of the tracking error that is defined as

$$\begin{aligned} e_y=y_{ref}-y \end{aligned}$$
(8)

where \(y\in {\mathbb {R}}^n\) and \(y_{ref}\in {\mathbb {R}}^n\) are the system output and the desired value. The convergence of the methods is assured if terms \(k_\gamma\) lead to negative real part roots in the polynomial P(x), defined as

$$\begin{aligned} P(x)=k_\gamma x^{(\gamma )} + k_{\gamma -1} x^{(\gamma -1)}+...+k_1x \end{aligned}$$
(9)

In this way, when the trajectory is confined on the sliding surface, the tracking error will reach 0 in an exponential way, according to the roots of P(x) [15]. Thus, the control law has to be chosen so that the sliding surface is both invariant and attractive, so a discontinuous term is needed in its definition. The ideal control law is expressed through the \(sign(\cdot )\) function

$$\begin{aligned} u=-ksign(\sigma ). \end{aligned}$$
(10)

The manipulator controller has been realized according to the first-order sliding mode control strategy. The sliding surface has been designed through the joints angles and the angular velocity errors, defined as

$$\begin{aligned} {\left\{ \begin{array}{ll} \theta _{a,e}=\theta _{a,ref}-\theta _a\\ \omega _{a,e}=\omega _{a,ref}-\omega _{a} \end{array}\right. } \end{aligned}$$
(11)

where \(\theta _{a,e},\omega _{a,e}\in {\mathbb {R}}^2\) are the the joints angle and angular velocity errors, \(\theta _{a,ref},\omega _{a,ref}\in {\mathbb {R}}^2\) are the desired values, and \(\theta _a,\omega _a\in {\mathbb {R}}^2\) are the real time values. Thus, the sliding surface has been defined as

$$\begin{aligned} \sigma =\lambda \theta _{a,e}+\omega _{a,e} \end{aligned}$$
(12)

where \(\lambda >0\) is constant. However, the discontinuous term in the control law brings a high frequency oscillation around the sliding surface. Thus, to overcome this problem, defined chattering effect, the hyperbolic tangent formulation has been employed

$$\begin{aligned} u_{arm}=-k\tanh {(\eta \sigma )} \end{aligned}$$
(13)

where \(\eta >0\) is constant.

3.2 Second-Order TW-SMC

As attitude controller an higher-order sliding mode is proposed for its feature of improved accuracy under heavy uncertainty conditions, and chattering effect reduction [1, 7]. The rth-order sliding mode is characterized by continuous \(r-1\) number of derivatives of \(\sigma\) in the vicinity of the sliding surface. Hence, the rth-order sliding mode is determined by

$$\begin{aligned} \sigma =\sigma ^{(1)}=...=\sigma ^{(r-1)}=0 \end{aligned}$$
(14)

In particular, the TW-SMC is a second-order SMC that takes advantage of the first-order sliding surface derivative in the control law to improve the controller performance and to reduce the chattering effect

$$\begin{aligned} u=-k_1sign(\sigma )-k_2sign({\dot{\sigma }}) \end{aligned}$$
(15)

According to [8], let’s consider a general definition of the second-order derivative of the sliding surface

$$\begin{aligned} \ddot{\sigma }=h(t,x)+g(t,x)u \qquad g(t,x)\ne 0 \end{aligned}$$
(16)

where the bounds of functions h(t, x) and g(t, x) can be defined as

$$\begin{aligned} h(x,t)<C \qquad K_m<g(t,x)<K_M \end{aligned}$$
(17)

For the attitude controller, the sliding surface has been designed through the quaternions and angular velocity errors, defined as

$$\begin{aligned} {\left\{ \begin{array}{ll} q_e=q_{ref}^{-1}\otimes q\\ \omega _e=\omega _{ref}-\omega \end{array}\right. } \end{aligned}$$
(18)

where \(q_{ref}\) and \(\omega _{ref}\) identify the desired states. As in [4], the sliding surface \(\sigma\) can be expressed as

$$\begin{aligned} \sigma =\lambda q_e+\omega _e \end{aligned}$$
(19)

where \(\lambda >0\) is constant. The second-order derivative of \(\sigma\) can be computed replacing the derivatives of \(q_e\) and \(\omega _e\) with Eqs. (1) and (6), and it has been linearized to reach the formulation

$$\begin{aligned} \ddot{\sigma }=(\ddot{\sigma })_{u=0}+\left( \frac{\partial \ddot{\sigma }}{\partial u}\right) _{u=0}u \end{aligned}$$
(20)

Thus, it is possible to estimate the bounds of functions h(t, x) and g(t, x) analyzing the variation of \(\ddot{\sigma }\), since

$$\begin{aligned} h(t,x)=(\ddot{\sigma })_{u=0} \qquad g(t,x)=\left( \frac{\partial \ddot{\sigma }}{\partial u}\right) _{u=0} \end{aligned}$$
(21)

According to [8], to achieve accuracy and stability of the proposed control method, controller parameters \(k_1\) and \(k_2\) have been chosen to satisfy the condition

$$\begin{aligned} {\left\{ \begin{array}{ll} K_m(k_1+k_2)-C>K_M(k_1-k_2)+C\\ K_m(k_1-k_2)>C \end{array}\right. } \end{aligned}$$
(22)

The control law has been defined using the hyperbolic tangent formulation to further reduce the chattering effect, as in [2]

$$\begin{aligned} u_{c}=-k_1\tanh {(\eta \sigma })-k_2\tanh {(\eta {\dot{\sigma }})} \end{aligned}$$
(23)

where \(\eta >0\) is constant, and \(k_1,k_2>0\) are constant parameters that satisfy the condition expressed in Eq. (22).

3.3 Backstepping Controller

The backstepping controller is included in this research to compare its performance with the TW-SMC, since it has been already employed in similar applications for aerial manipulators. It consists in an adaptive controller based on Lyapunov function. In control theory, a Lyapunov function V(x) is continuously differentiable function, positive definite, and such that

$$\begin{aligned} \forall x \ne 0,\ \exists u \rightarrow {\dot{V}}(x,u)<0 \end{aligned}$$
(24)

where the last condition stands that for each state x exists a control u able to drive V(x) to zero, bringing the system to an equilibrium stable state. The backstepping controller has been designed following a procedure similar to [5], employed for an aerial manipulator. The definition of two Lyapunov function is needed, and they are computed using the system kinematics and dynamics. Considering the vectorial part of the quaternions error, its variation can be expressed as

$$\begin{aligned} \dot{\tilde{q}}_v=\frac{1}{2}(\tilde{q}_0I+[\tilde{q}_v\times ]){\tilde{\omega }} \end{aligned}$$
(25)

where \(q_e=\{\tilde{q}_0,\tilde{q}_v\}\), and \(\tilde{q}_v\in {\mathbb {R}}^3\) has been chosen as the backstepping variable. Defining \(\omega _c\) as the backstepping virtual control variable, Eq. (25) has been rewritten as

$$\begin{aligned} \dot{\tilde{q}}_v=\frac{1}{2}(q_0I+[q_v\times ])(\omega _c + {\tilde{\omega }}-R(q_e)\omega _d) \end{aligned}$$
(26)

where \(R(q)\in {\mathbb {R}}^{3,3}\) is the rotational matrix. The first Lyapunov function candidate has been defined as

$$\begin{aligned} V_1=\tilde{q}_v^T\tilde{q}_v+(1-\tilde{q}_0)^2 \end{aligned}$$
(27)

and its derivative is

$$\begin{aligned} {\dot{V}}_1=2\tilde{q}_v^T\dot{\tilde{q}}_v+2(1-\tilde{q}_0)\dot{\tilde{q}}_0 \end{aligned}$$
(28)

Defining the control variable \(\omega _c\) as

$$\begin{aligned} \omega _c=-K_1\tilde{q}_v+R(q_e)\omega _d \end{aligned}$$
(29)

Equation (28) can be rewritten as

$$\begin{aligned} {\dot{V}}_1=-\tilde{q}_v K_1 \tilde{q}_v^T + \tilde{q}_v{\tilde{\omega }}^T \end{aligned}$$
(30)

that is negative definite when \({\tilde{\omega }}=0\). The second Lyapunov function candidate has been defined as

$$\begin{aligned} V_2=V_1+\frac{1}{2}{\tilde{\omega }}^T J {\tilde{\omega }} \end{aligned}$$
(31)

and its derivative is

$$\begin{aligned} {\dot{V}}_2=-\tilde{q}_v K_1 \tilde{q}_v^T + \tilde{q}_v{\tilde{\omega }}^T+{\tilde{\omega }}^T J \dot{{\tilde{\omega }}}+\frac{1}{2}{\tilde{\omega }}^T {\dot{J}} {\tilde{\omega }} \end{aligned}$$
(32)

Considering the system dynamics Eq. (32) can be rewritten as

$$\begin{aligned} {\dot{V}}_2= & {} -\tilde{q}_v^TK_1\tilde{q}_v+\tilde{q}_v^T{\tilde{\omega }}\nonumber \\&+{\tilde{\omega }}^T(\varSigma \times {\tilde{\omega }}-\omega _c\times J{\tilde{\omega }}+\gamma +T-\frac{1}{2}{\dot{J}}{\tilde{\omega }}) \end{aligned}$$
(33)

where \(\varSigma\) and \(\gamma\) are defined as

$$\begin{aligned} {\left\{ \begin{array}{ll} \varSigma =J{\tilde{\omega }}+J\omega _c\\ \gamma =J\omega _c\times \omega _c-J{\dot{\omega }}_c-{\dot{J}}\omega _c \end{array}\right. } \end{aligned}$$
(34)

Defining the control law as

$$\begin{aligned} u_c=-K_2{\tilde{\omega }}-\tilde{q_v}-u_a-\gamma +\omega _c\times J{\tilde{\omega }}+\frac{1}{2}{\dot{J}}{\tilde{\omega }} \end{aligned}$$
(35)

Equation (33) can be rewritten as

$$\begin{aligned} {\dot{V}}_2=-\tilde{q_v}^TK_1\tilde{q_v}-{\tilde{\omega }}^TK_2{\tilde{\omega }} \end{aligned}$$
(36)

which is a negative definite function. Thus, both \(V_1\) and \(V_2\) have been verified as Lyapunov functions, and the proposed control law, expressed by Eq. (35), can compute a torque taking into account the attitude error, the arm torque and motion, and the inertia variation, leading the Astrobee to track the desired attitude.

4 Simulation Results

Fig. 3
figure 3

Astrobee model

Full size image

In this section, TW-SMC performance in terms of attitude control and stabilization are analyzed running Matlab Simulink simulations. As introduced with the attitude dynamics, Eq. (6), the manipulator motion leads to disturbances that have to be stabilized.

The Astrobee system is modeled as a 32 cm-on-a-side cube-shaped robot, and equipped with a two-links two-joints robotic arm. In particular, the Astrobee’s main body is characterized by a mass of \(m_b=9.4\ \text {kg}\) and an inertia of \(J_b=\text {diag}([0.17\ 0.16\ 0.19])\ \text {kgm}^2\), while the robotic arm is connected on the body edge, as shown in Fig. 3, and its links have, respectively, a length of \(l_1= 0.15\ \text {m}\) and \(l_2= 0.10\ \text {m}\) and a mass of \(m_1=0.162\ \text {kg}\) and \(m_2=0.103\ \text {kg}\).

Since the geometrical parameters are subjected to uncertainties the proposed controllers have been tested in different scenarios where the Astrobee’s parameters are changed. The initial conditions see the Astrobee in the desired configuration, with \(q_0=[1\ 0\ 0\ 0]^T\), \(\omega _0=[0\ 0\ 0]^T\), and the manipulator stowed \(\theta _{a,0}=(180^\circ , 0^\circ )\). All the simulations are characterized by the same manipulator motion request, and it consists in manipulator deploying \(\theta _a=(0^\circ , 0^\circ )\), a rotation around the second joint to \(\theta _a=(0^\circ , 30^\circ )\), a second rotation around the second joint to \(\theta _a=(0^\circ , -30^\circ )\), and manipulator stowing \(\theta _a=(180^\circ , 0^\circ )\).

The first scenario considers the manipulator motion stabilization with different manipulator deploying and stowing speed. Different manipulator rotation speed leads to different disturbances in terms of manipulator control torque and gyroscopic torque. Figure 4 shows the simulation results in terms of Euler Angles. The TW-SMC is able to stabilize the disturbances introduced by the manipulator motion recovering the desired configuration in acceptable time. The backstepping controller shows better performance in terms of orientation error, since its control law, Eq. (35), contains the manipulator control input \(u_a\), thus,it is able to react faster to the disturbance. Changing the angular speed request does not create a significant variation in the controller performance, despite the increasing of the disturbances.

Fig. 4
figure 4

Manipulator stabilization

Full size image
Fig. 5
figure 5

Manipulator stabilization with different body mass

Full size image
Fig. 6
figure 6

Manipulator stabilization with different links masses

Full size image

The second scenario considers different values of the Astrobee body mass and inertia, and the arm rotational speed of \(\omega _a=2\ \text {rad/s}\). Figure 5 shows simulation results in term of Euler Angles. Changing the Astrobee inertia leads to different sensitiveness to disturbances, but the variation of this parameter does not change the controllers performance.

The third and forth scenarios aim to test the controllers with different disturbances, considering different links masses and a possible object gripped with the arm rotational speed of \(\omega _a=2\ \text {rad/s}\). Figure 6 shows simulation results in term of Euler Angles. Considering different values of manipulator’s links masses, with arm rotational speed \(\omega _a=2\ \text {rad/s}\), leads to different disturbances. The reduced dimension of the links makes impossible to consider relevant changes in the links masses, leading to insignificant changes in both controllers performance. However, these effects are amplified considering a gripped object, modeled as a point mass in the end-effector position, as reported in Fig. 7. However, moving the arm while a small object is gripped is still a possible operation and the controllers are able to handle the disturbances introduced by this kind of scenario despite an increase of the orientation error.

Fig. 7
figure 7

Manipulator stabilization with a gripped object

Full size image

4.1 NASA Astrobee Simulator

The Astrobee attitude model has been compared with the 3D model in the NASA Astrobee simulator [11], shown in Fig. 8. It consist in an open source software realized in ROS Gazebo to simulate the Astrobee flight inside the ISS environment. To verify the goodness of results, NASA Astrobee simulator software has been used combined with Matlab Simulink that is able to communicate and exchange information with ROS Gazebo through the ROStoolbox block set. In this way, it is possible to test the controller in a more realistic scenario, where the system dynamics is expressed by the Astrobee ROS 3D model floating in the micro-gravity environment of the ISS, and the attitude controller, implemented in Simulink, reads the information about orientation and angular velocity to compute and apply the desired torque directly on the 3D model. Since the manipulator is managed by manual commands in the simulator, it is impossible to collect precise comparable results. Moreover, the high computational cost of the combined simulation, leads to imperfections and delays in the communication of the two software, leading to delays and errors in the control torque application. Figure 9 shows simulation results in term of Euler Angles for an arm motion request that consist in deploying and stowing. The results are not comparable with numerical simulations since the delay in the application of torque, due to synchronization error between Simulink and ROS, leads to higher orientation errors. However, despite the communication delays and errors, also in this scenario the TW-SMC is able to restore the desired orientation in acceptable time.

Fig. 8
figure 8

NASA Astrobee simulator [11]

Full size image
Fig. 9
figure 9

Manipulator stabilization in NASA Astrobee simulator

Full size image

5 Conclusion and Future Works

The objective of this research is to realize an accurate mathematical model for the NASA Astrobee free-flyer attitude dynamics and to propose an attitude controller able to stabilize the disturbances introduced by the robotic arm motion. The system dynamics has been defined combining the overall attitude dynamics and the robotic arm dynamics in the angular momentum conservation. The controller has been designed as a robust attitude controller able to overcome uncertainties in parameters and disturbances. Thus, sliding mode controllers have been taken into account for their properties of robustness and low computational cost. In particular, for precise attitude control and stabilization a TW-SMC has been designed, and compared with a backstepping controller, already employed in similar application for aerial manipulators. Despite the reduced mass of the Astrobee that turns the robot to be more sensitive to the disturbances, and the actuators limitation due to their small dimension, the simulations show that the controller is able to operate in several scenarios, and to always track the desired attitude. Thus, the robustness of the proposed control method has been tested considering simulations with parameters variation, and the results obtained make the TW-SMC a good control strategies able to fulfill several space manipulators tasks. However, the comparison with the backstepping controller shows the limitation of the constant parameters that define the TW-SMC control law, while the adaptation and the inclusion of the robotic arm control input in the backstepping controller control law results to be more effective. The NASA Astrobee simulator has been used in co-simulation with Simulink to test the proposed controller in a more real scenario. The results obtained confirm the goodness of the mathematical model and the performance of the TW-SMC. Possible future works are the implementation of the actuators model to evaluate more accurate performance of the designed controller, and the combination of attitude and position control to test the system in more challenging missions and scenarios.