1 Introduction

The Galilean moons are the four largest moons of Jupiter. They have many interesting peculiarities, in particular, Io is the closest to Jupiter and it is the most volcanically active body in the solar system due to its strong tidal interaction with the gas giant [1]. Europa has been under the spotlight since Hubble Space Telescope and successively a re-analysis of Galileo mission data detected water vapor plumes coming from its surface [2], an additional evidence of the existence of a liquid ocean under its icy crust. This discovery and the presence of a strong tidal dissipation within the moon makes Europa one of the most promising environments to look for life in the solar system. Ganymede is the biggest moon in our Solar System, even bigger than planet Mercury. It is the only satellite and—besides Mercury and the Earth—one of only three solid bodies in the Solar System that are known to generate a magnetic dipole field [3]. Lastly, Callisto, the farthest Galilean moon with respect to Jupiter, has the oldest and most heavily cratered surface in the Solar System [4] and due to the presence of an induced magnetic field detected by Galileo spacecraft it is also believed to contain a large liquid reservoir below the outer icy shell [5]. Moreover, the three innermost Galilean moons (Io, Europa and Ganymede) follow a very interesting periodic orbital pattern, the so-called Laplace resonance [6]:

$$\begin{aligned} n_\mathrm{Io}-3n_\mathrm{Europa}+2n_\mathrm{Ganymede} = 0, \end{aligned}$$
(1)

where n represents the mean motion of the moon. Therefore, they are in a 4:2:1 orbit period ratio that implies a strong correlation in their dynamics. To this day, it is still not explained the origin of such resonance and it is not clear whether it is stable and how long will it last. One of the consequences of the Laplace resonance is the persistence of the tidal dissipation of the moons, in particular of Io [7]. In fact, the dissipation on the planet interior is due to the orbital eccentricity of the moons around Jupiter, causing a periodic oscillation of the huge Jupiter’s gravitational potential they feel, going from a maximum when the moons are at the pericenter to a minimum when they are at the apocenter. This causes the tidal bulge on the moons, generated by the tidal potential exerted by Jupiter, to change its altitude and, as a consequence, to dissipate energy in the satellite interior as heat. However, the energy dissipation tends to circularize the orbits of the moons undergoing this phenomena, but thanks to the presence of the Laplace resonance, which acts as an eccentricity forcer, this dissipation is not keen to diminish in the short period [8].

So, due to the strong tidal potential that Jupiter exerts on the moons and the presence of the resonance that maintains the orbital eccentricity, this dissipation is not keen to diminish in the short period [8].

Assessing the influence of the tides on the orbital motions of the satellites is complex because the satellite orbits are perturbed by mutual gravitational attraction with other satellites, as well as by the non-spherical shape of the parent-planet [9]. Consequently, the determination of the tides requires accurate numerical models that account for the many dynamical perturbations expected over long duration observations, to decorrelate the various dynamical effects (long periods with secular effects due to the tides) [9].

Up to now, the several solutions of the Galilean satellites motion disagree both about the amount of dissipation and the direction of the dynamical evolution of the moons. For example, according to Layney et al. [10], the accelerations due to the tides have induced a cumulative shift in the satellite orbital positions of 55 km, −125 km and −365 km for Io, Europa, and Ganymede, respectively, over the past 116 years. Therefore, this suggest that Io’s orbit is contracting, while the orbits of Europa and Ganymede are expanding [10]. These results show that the Galilean moons could eventually escape from the Laplace resonance, with consequences on the tidal dissipation in Io and Europa, and so on their potential habitability.

On the contrary, Lari [11] showed that on a long timescale, the tidal dissipation results in an outward migration for all the satellites, Io included. After about 4 Myr, Io stops its inward migration and starts migrating outwards. According to these results, since the eccentricity of Io decreases, dissipation in Jupiter gains importance against the one within Io. This provides more energy to the orbit of Io and makes all three semi-major axes increase [11]. This surprising behavior of the Galilean satellites may conceal some clues about the origin of the Laplace resonance and could indicate that the Laplace resonance is quite new since it has not yet reached an equilibrium configuration [11]. More probably, this transition could be due to cyclic variations of the dissipation parameters, periodically forcing the Laplace resonance to slightly resettle at the new equilibrium configuration [11].

2 JUICE Mission

A good opportunity to clarify the problem is the future JUICE mission. JUICE, also known as the JUpiter ICy moons Explorer, is a European Space Agency mission intended to explore Jupiter and three of its icy moons: Europa, Callisto and Ganymede [12]. It will be launched approximately in June 2022 (according to CReMA 3.2 [12]) and it will enter in orbit around Jupiter at the end of 2029. Then, it will perform a Jupiter tour with many flybys of the Galilean moons, with the exception of Io, and a 9-month Ganymede orbital phase.

JUICE is provided by a number of scientific instruments, the one we will focus for the sake of this dissertation is 3GM.

Gravity and Geophysics of Jupiter and the Galilean Moons (3GM) addresses JUICE scientific objectives related to gravity, geophysics and atmospheric science exploiting the radio link between the spacecraft and the Earth. Radiometric data, in combination with altimetry and other measurements, will provide information on the static gravity fields of Ganymede, Callisto and Europa, on the rotational state and tidal deformation of Ganymede and Callisto, on the presence of density variations within the ice shell of Ganymede, and on dissipation within the Jovian interior [11].

During the Jupiter tour and Ganymede orbital phase we will have the opportunity to retrieve data about the gravity field of the moons, together with their tidal parameters like the Love number k in both its real and imaginary part, which are fundamental to assess the amount of dissipation undergoing inside the moons [13]. This information will be obtained as part of the JUICE spacecraft orbit reconstruction, relying on very accurate range and range-rate measurements provided by the 3GM Ka-band Transponder (KaT) and the fixed 2.5 m High Gain Antenna (HGA) [14].

3 Orbit Determination

The orbit determination (OD) problem is the process that reconstructs the trajectory of a body in space. It is an iterative procedure based on the comparison between the “observed observables” and the received observational data (for example, radiometric data such as range and range-rate measurements) with the so-called “computed observables”, obtained by an orbit determination program. In this work, we used the JPL’s OD software MONTE (Mission-analysis, Operations and Navigation Tool-kit Environment) [15], which is an astrodynamic computing platform developed by JPL that has been employed for over a decade on NASA’s most demanding deep space missions. The computed observables are obtained from a mathematical dynamical model of the system in study that include all the relevant forces that influence the motion of the satellites and of the spacecraft. Of course, the knowledge of the system is not perfect and the difference between the real observed and the computed observables forms the residuals. In simulation environment, we are only interested in the uncertainties that could be obtain with the mission; therefore, the difference between observed observables and computed observables is a random noise that we chose accordingly with the amount of noise we expect from the measurements. These residuals enable an adjustment to some model parameters thanks to a least-squares estimation filter, in which the optimal solution is defined to be the set of parameter values that minimizes the weighted sum of squares of residuals [16]. We can define the cost function to be minimized as

$$\begin{aligned} J = \sum _{i=1}^{m} \left( \frac{{{\varvec{\xi }}}_{\mathbf {i}}}{{\varvec{\sigma }}_{\mathbf {i}}}\right) ^2 = \xi ^\mathrm{T} W \xi = (\mathbf {z}-\hat{\mathbf {z}})^\mathrm{T} W (\mathbf {z} - \hat{\mathbf {z}}), \end{aligned}$$
(2)

where \({{\varvec{\xi }}}\) are the residuals, \(\mathbf {z}\) is the vector of the observed observables, \(\hat{\mathbf {z}}\) the computed observables, m is the dimension of the observables vectors, \(\sigma _i\) are the uncertainties associated with the measurements and W is the weight matrix assumed to be the inverse of the covariance matrix of the measurement noise.

The goal of the estimation process is to minimize the cost function J, in particular, we search for the state that minimizes the derivative J with respect the state vector. The problem is nonlinear because of the dependence of A and \(\hat{\mathbf {z}}\) on the state vector, but we can neglect this higher order terms with good approximation [16].

The correction to the state vector that minimize J is represented by

$$\begin{aligned} \hat{\mathbf {x}}_{k+1} = \hat{\mathbf {x}}_k - (A_k^\mathrm{T} W A_k + P_0^{-1})^{-1}(A_k^\mathrm{T} W (\mathbf {z}-\hat{\mathbf {z}}(\hat{\mathbf {x}}_k))+P_0^{-1}\mathbf {x_0}) \end{aligned}$$
(3)

where \(\hat{\mathbf {x}}_{k+1}\) is the estimated state vector at the end of the \(k+1\) iteration, \(A_k\) is the matrix of the partial derivatives computed at the kth iteration, \(P_0\) the a priori covariance matrix and \(\mathbf {x_0}\) is the a priori state vector.

The covariance matrix of the estimation is

$$\begin{aligned} P= (A_k^\mathrm{T} W A_k + P_0^{-1})^{-1}. \end{aligned}$$
(4)

3.1 Multi-arc Approach

The dynamical model of the spacecraft (S/C) is not completely deterministic, due to the fact that our probe is small enough to be significantly affected by complex non-gravitational interactions [17]. Given that gravity radio science investigations, usually, use data from different flybys that are separated in time by weeks or months, we have to use an approach that overcomes the non-deterministic nature of the orbit determination problem. A widely adopted method is called multi-arc approach [18,19,20]. In this approach, the entire time span of the observations is decomposed in short non-overlapping and non-contiguous intervals, each one with its own set of observables and its initial conditions. In the multi-arc approach, we make a distinction in the parameters that forms our state: the vector of all fit parameters \({\mathbf {x}}\)=[\({\mathbf {g}}\);\({\mathbf {l}}\)] is split into a vector \(\mathbf {g}\) of global fit parameters and a vector \(\mathbf {l}\) of local fit parameters. The global parameters are common to all arcs, while the local parameters are different for each arc. This method results in over-parameterization, with the additional initial conditions being able to absorb the dynamical model uncertainties [21]. Through the multi-arc approach we obtain an improved estimate of the global parameters with respect to a single-arc approach, simply because we estimate all the arcs simultaneously [22].

4 Numerical Simulations

The success of a gravity science experiment relies on the accuracy of the parameters that we can estimate with the mission data. To do so, it is useful to perform numerical simulations that are a covariance analysis of the parameters we want to study. This means that the generation of the simulated observables and of the computed measurements are obtained using the same dynamical models. This allows to obtain the formal uncertainties of the estimated parameters under different assumptions and scenarios.

The gravity field of the bodies in study is expressed in terms of series expansion of spherical harmonics functions:

$$\begin{aligned}&{\mathcal {U}}(\mathbf {r},\phi ,\lambda ) = \frac{\mu }{r}\left\{ 1+ \sum _{l=2}^{\infty }\sum _{m=0}^{l}P_{lm}\mathrm{sin}(\phi )\left( \frac{r_\mathrm{ref}}{r}\right) ^l[C_{lm}cosm\lambda \nonumber \right. \\&\quad \left. +S_{lm}\mathrm{sin}m\lambda ]\right\} , \end{aligned}$$
(5)

where

  • \(r_\mathrm{ref}\) the equatorial radius of the body in study;

  • \(\mathbf {r}\), \(\phi \) and \(\lambda \) the radial position, latitude and longitude, respectively;

  • \(P_{lm}\) (sin\(\phi \)) the associated Legendre polynomials of degree l and order m;

  • \(C_{lm}\),\(S_{lm}\) coefficients of the gravity harmonics determined experimentally.

The cyclic variation of the gravity field due to the tidal potential exerted from the central body (in our case Jupiter) to one of its moons (the Galilean moons in our case) can be expressed as [23]:

$$\begin{aligned} \varDelta {\mathcal {U}}^\mathrm{sat} =\sum _{l=2}^{\infty }k_l\left( \frac{r_\mathrm{ref}}{r}\right) ^{l+1}{\mathcal {U}}^\mathrm{cen}_{l}, \end{aligned}$$
(6)

where \({\mathcal {U}}^\mathrm{sat}\) is the gravity potential of the moon, \({\mathcal {U}}^\mathrm{cen}\) the central body potential and \(k_l\) represent the degree l Love number, which is linked to the tidal response of the perturbed body.

Through numerical simulations, we want to assess the accuracy of some of the fundamental parameters useful to understand dissipation in the Jovian system. Consequently, the orbital evolution of the system, given the flybys available for JUICE mission, in particular the gravitational parameters of Europa, Ganymede and Callisto, the Love numbers of the latter two moons and the main gravitational parameter of Jupiter, use only range and range-rate measurements.

4.1 JUICE Trajectory

For our analysis, we assumed the JUICE reference trajectory defined by CReMa 3.2 [12], considering an arc length of 48 h around the closest approach (C/A). Some of the Ganymede’s flybys available from CReMA 3.2 have been neglected because of the large distance with respect to Jupiter. The maximum altitude considered was 2544 km (G06 flyby). In particular, we considered

  • 2 flybys of Europa

  • 6 flybys of Ganymede

  • 12 flybys of Callisto

In Figures 1, 2 and 3, we can see the ground tracks of JUICE during the considered flybys of Ganymede, Callisto, and Europa. The ground tracks are very useful to understand which parameter of the gravity field we will be able to estimate: an equatorial flyby will be more sensitive to \(C_{22}\) (C coefficient of Eq. (5), of order and degree 2) coefficient, while, alone, not sensitive to \(J_2\) (= \(-C_{20}\): C coefficient of Eq. (5) of order 2 and degree 0). Given that \(J_2\) coefficient is defined as the mass distribution along the equator and it is axial symmetric, a polar flyby is the optimal approach to measure it. While \(C_{22}\) represents the mass distribution in longitude, a equatorial flyby would be the best configuration to measure its effect on the spacecraft dynamic.

Fig. 1
figure 1

Ground tracks of the flybys performed by JUICE over Ganymede

Full size image
Fig. 2
figure 2

Ground tracks of the flybys performed by JUICE over Callisto

Full size image
Fig. 3
figure 3

Ground tracks of the flybys performed by JUICE over Europa

Full size image

Therefore, as we can see from Figures 1, 2 and 3 we have a good coverage of Ganymede and Callisto, allowing to estimate both \(J_2\) and \(C_{22}\) independently and, potentially, also the higher order harmonics. On the other side, for Europa we have only two flybys, with a medium coverage, enabling the estimation of only the degree-2 gravity field.

4.2 Data Selection and Weights

To perform simulations, we need to define the weight to assign to our data, i.e. the amount of noise. Therefore, we computed the expected noise using empirical relations based on Cassini’s data analysis [24, 25].

Fig. 4
figure 4

Plot of the expected range-rate noise during JUICE mission at integration time 60 s, at different bands. The colored regions represent the different phases of the JUICE mission. The vertical dashed lines represent the time of the moons’ flybys. In this work, as reference noise for Ka-band, we adopted \(4\times 10^{-14}\) ADEV (12 \(\upmu \)m/s), represented by the dotted green line

Full size image

In Fig. 4, we can see the plot of the expected range-rate noise during the Juice mission up to Callisto flyby number 12 (C12), the last flyby considered in this work, referred to 60 s integration time. We assumed to calibrate the path delay induced by Earth’s troposphere using water vapour radiometers. Looking at the lines plotted, we have different colours here too:

  • In red is plotted the expected noise of the X/X band.

  • In blue is plotted the expected noise of the Ka/Ka band.

  • In black is plotted the expected noise of combination of X/X and Ka/Ka bands.

  • In green is plotted the expected noise of the combination of X/X, X/Ka and Ka/Ka bands.

As we can see each band and combination is affected differently from noise, for example, the three simultaneous links (X/X, X/Ka, and Ka/Ka) will permit full cancellation of dispersive noises sources [26, 27], mainly the interplanetary plasma and the Earth ionosphere. In fact, as we can see in the plot, there are two zones in which the noise makes a sort of spike, those are the points in which we have a conjunction between Earth, Sun and the probe (Sun–Earth–probe (SEP) angle close to 0) and, therefore, the noise due to the solar plasma is at its maximum [28]. Only the triple link plotted in green is invariant to this conjunction.

In our simulation, we considered only a constant reference noise represented by the dotted green horizontal line corresponding to the average noise level of the triple link that is 12 \(\upmu \)m/s. The dotted red line is an average value of the X/X noise to see the difference between the two. Therefore, for this analysis, we considered an Allan deviation (ADEV) of \(4\times 10^{-14}\), corresponding to Doppler measurements having an accuracy of 12 \(\upmu \)m/s at 60 s integration time. The range data have been simulated every 60 s with a conservative noise of 20 cm two-way [29].

Regarding the configuration of the ground antennas, we considered the ESTRACK Deep Space Network. Up to now, only ESA’s Deep Space Antenna 3 (Malargue) is capable of transmitting and receiving at both X and Ka bands. However, we assumed that for the time the JUICE mission will arrive at Jupiter, all three stations will support both X and Ka bands. Moreover, Water vapour radiometers for tropospheric path delay calibration at ESTRACK stations are currently in development. In the simulation of the observables, a minimum spacecraft elevation angle of 15 has been adopted to account for errors that might affect low-elevation calibration data for Earth’s troposphere. In addition, we considered the occultation of the radio link by Jupiter and the Galilean moons.

4.3 Simulation Setup

In this analysis, we performed a global integration of the satellites during the entire time span of the mission. This allows to potentially improve the ephemerides of the system using the data acquired during the different JUICE flybys of the moons, keeping into account the correlation between different satellites.

The filter solved for:

  • State of JUICE at the beginning of each arc: The state vector of the JUICE S/C is estimated at the beginning of each arc, approximately 24 h prior to the C/A. We used a conservative approach to set the a priori uncertainties, using a diagonal covariance matrix with \(1-\sigma \) of 100 km in position and 0.001 km/s in velocity.

  • Initial state of the satellites: The reference epoch was chosen at the halfway point of the mission, to reduce the numerical errors. The a priori values of the state vector of Europa, Ganymede and Callisto were retrieved from the last Jupiter ephemerides set released by the JPL, JUP310. The a priori uncertainties were also set using a conservative approach, 10 km for the position and \(1\times 10^{-4}\) m/s for the velocity.

  • Europa’s gravity field: we estimated the Europa gravity field up to second degree and order harmonics. We took conservative a priori uncertainties of the gravity field. Values can be seen in Table 1.

  • Ganymede’s gravity field: we estimated up to fourth degree and order harmonics. The a priori uncertainties of the gravity field can be seen in Table 2. Up to second degree and order harmonics we used a priori uncertainties coming from the results of the analysis of Galileo mission [30] multiplied by a large safety factor (100), for higher degrees we considered values we computed of a synthetic gravity field using Kaula’s rule [31] multiplied by a factor 5.

  • Callisto’s gravity field: the estimation went up to degree order 7 harmonics. The a priori uncertainties of the gravity field can be seen in Table 3. As for Ganymede, we used values coming from the results of the analysis of Galileo mission [32] for the degree-2 harmonics multiplied by a large safety factor (100), for higher degree we considered values we computed of a synthetic gravity field using Kaula’s rule [31] multiplied by a factor 5.

  • Ganymede and Callisto gravity tides: given the limited number of flybys to the moons we estimated only the real part of second degree Love number \(k_2\). This represents the primary effect of the tidal interaction. In fact, it expresses an equatorial distortion of the satellite in the direction of the perturbing body. We assumed \(k_2 = k_{20} = k_{21} = k_{22}\), meaning that the body’s deformation due to the tidal distortion is the same in every direction. This is a good assumption for terrestrial bodies [21]. The a priori uncertainty was set to 1.

  • Second-degree harmonics static components: For Ganymede and Callisto, the estimated \(J_2\) and \(C_{22}\) coefficients include a permanent tidal contribution [19]. The a priori uncertainties of the gravity field can be seen in Table 2 for Ganymede and Table 3 for Callisto.

  • GM of the Jupiter system: The GM of Jupiter’s planetary system (where G is the Gravitational Constant and M is the mass) is retrieved from the JUP310 ephemerides set, estimated, mainly, by the study of the orbit evolution of the Galilean satellites, with a large a priori uncertainty of 2.8 km\(^3\)/s\(^2\) [21].

  • Jupiter gravity field coefficients: we included only the \(J_2\) gravity coefficient because with a conservative a priori uncertainty (see Table 4).

  • Jupiter pole position at J2000: The pole position, right ascension and declination, has been estimated at a reference epoch (J2000).

  • Jupiter tidal response: we estimated both real and imaginary part of second degree Love number at the frequency of Io. The a priori uncertainties used can be seen in Table 4. We took the a priori uncertainty of the real part of the \(k_2\) Love number from [33], because with our setup we are not able to have a good estimate of the parameter and we want to constrain its value. For the imaginary part our a priori uncertainty is approximately 10 times our solution uncertainty, so that we do not constrain our solution.

  • Scale factor for the solar radiation pressure: JUICE’s solar radiation pressure scaling factor was set to 1.0 with an uncertainty of the 20\(\%\).

  • SRA bias: Possible systematic instrumental effects (such as electronic delays) are estimated. The a priori uncertainty considered was 15 m.

5 Results

5.1 Europa Gravity

In the following, we show the results of our analysis for Europa gravity parameters:

Table 1 Europa a priori and expected uncertainties (\(1-\sigma \))
Full size table

In Table 1, the expected uncertainties in the Europa-related parameters are reported. We compared our solution with the one obtained from the analysis of the data of four flybys of Europa (E4, E6, E11, and E12) by the Galileo spacecraft performed by Anderson et al. [34]. They combined the Doppler data from all four encounters, along with ground-based astrometric data on the positions of the four Galilean satellites and optical navigational data from the Voyager and Galileo missions to Jupiter, to obtain models of Europa’s interior structure. All the flybys were almost equatorial; therefore, the estimation of the \(J_2\) gravity coefficient could not be performed precisely. For this reason, in the analysis, they assumed the hydrostatic equilibrium condition for Europa, hence constraining the value of \(J_2\) to be 10/3 of \(C_{22}\) value (see, e.g. [35]). The \(J_2\) uncertainty coming from their results is, therefore, not realistic, being constrained by \(C_{22}\). With JUICE we expect to obtain an improvement on all the listed parameters, in particular by a factor 8 for \(C_{22}\) and 5 for \(J_2\), even though we are considering only 2 flybys instead of 4. The most probable reason for this improvement is the larger noise on Galileo Doppler data, about 1.0 mm/s at 60 s, due to the use of a S-band link. In fact, a problem in the deployment of the High-Gain Antenna (HGA) during the mission limited the accuracy capabilities with respect the initial configuration that included also the more accurate X-band link [36].

5.2 Ganymede Gravity

Below we show the results of our analysis for Ganymede gravity parameters:

Table 2 Ganymede a priori and expected uncertainties (\(1-\sigma \))
Full size table

We compared our results with the solution obtained from the analysis of the radiometric data of two flybys of Ganymede by the Galileo spacecraft, happened, respectively, on 27 June and 6 September 1996 [30]. The two encounters were intentionally targeted to optimize gravity field measurements; the first was a near-equatorial pass at an altitude of 835 km, while the second was a near-polar pass at an altitude of 261 km [30]. The first encounter was more sensitive to \(C_{22}\), while the second to \(J_2\). For both encounters, an a priori hydrostatic equilibrium constrain was imposed. As we can see from the right column, JUICE is expected to improve Galileo’s uncertainties on the gravitation parameters of Ganymede, in particular by a factor 4 the uncertainty on \(J_2\) and by a factor 7 \(C_{22}\). However, we should remind that we did not take into account the Ganymede circular orbit (GCO) phase in our analysis. This latter phase is expected to give the most important scientific return of the mission [37] so our Ganymede’s results could be greatly improved in a complete JUICE mission analysis.

5.3 Callisto Gravity

In the following, the results of our analysis for Callisto gravity parameters are shown:

Table 3 Callisto a priori and expected uncertainties (\(1-\sigma \))
Full size table

Again we compared our results with the solution obtained from the analysis of the radiometric data of five flybys of Callisto by the Galileo spacecraft [32]. JUICE is expected to improve all Callisto’s parameters as we can see in the right column of Table 3, in particular we highlight a factor 10 improvement for \(C_{22}\) and 2 for \(J_{2}\). Regarding the Love number \(k_2\), different levels of uncertainty can be obtained, from 0.073 to 0.1, depending on different assumptions on the strength of Callisto gravity field. It has to be taken in account that in our analysis, we are only considering two radiometric observables: Range and Doppler, but a more extensive analysis including other observables like optical, DDOR and stellar occultation would surely improve the uncertainty. In addition, it is important to highlight that the detection of tides relies on sampling the gravity field at different mean anomalies. In fact, the Love number \(k_2\) represents the response of the gravity filed of a body to the tidal forcing during the orbital period due to orbital eccentricity; therefore, measuring the gravity field at well distributed mean anomalies of the orbit is the optimal approach to study the \(k_2\) of a body [38]. However, in our case, as we can see in Fig. 5 (a plot showing the position of Callisto with respect to Jupiter during JUICE’s Callisto flybys), the mean anomalies of Callisto with respect to Jupiter during Callisto’s flybys are not well distributed at different angles. The accuracy on the Callisto Love number could be improved with a different mission design.

Fig. 5
figure 5

Position of Callisto with respect to Jupiter during JUICE flybys

Full size image

Moreover, as said before, we are analysing only the Jovian orbital phase; hence, we are not considering the Ganymede circular orbit phase that is expected to give a contribution to the accuracies on the parameters of other Galilean moons too, even if marginal.

5.4 Jupiter Gravity

In the following we show the results of our analysis for Jupiter gravity parameters:

Table 4 Jupiter a priori and expected uncertainties (\(1-\sigma \))
Full size table

In Table 4, the expected uncertainties in the Jupiter-related parameters are reported. To assess the goodness of the obtained results we compare them with the values obtained from the analysis of the radiometric data of 17 perijove passes of the JUNO mission [33]. As expected, our analysis gives much larger uncertainties associated with \(J_2\) coefficient. This is because JUNO mission is focused on the study of Jupiter and it performed several polar orbits around it [39], thus allowing a precise and direct estimation of the second-degree gravity harmonics; the JUICE mission, instead, will retrieve Jupiter coefficient from a better constraint of the Galilean moon ephemerides, which of course influences the estimation of the gravity harmonics of Jupiter, but it is an indirect, and less accurate, measure. For the same reason, the uncertainty of Jupiter \(Re(k_2)\) is constrained to the a priori value.

Another comparison can be done with the result obtained by Lainey et al. [10]. In their analysis, it was used a completely different set of data: an extensive set of astrometric ground observations that started in 1891, with heliometer measurements and the first photos, and continued until 2007, with the most recent observations from the FASTT survey [40], including also observations of the mutual events from 1973 to 2003. Lainey et al. obtained an uncertainty of 0.203e−05 for the imaginary part of the Love number of Jupiter at the frequency of Io, almost two order of magnitude more accurate than our simulation result. The reason is that the imaginary part of the Love number produces a cumulative effect on the satellite orbit evolution, quadratic with time in longitude and linear in semi-major axis. Hence, even if astrometric data are less accurate than radiometric data, because of the much larger time coverage, a better estimation of Im\((k_2)\) can be obtained. It has to be specified that in our analysis the Jupiter’s Im\((k_2)\) is considered only at the frequency of Io. This is because Io is the most important tidal perturber of Jupiter and dominates the orbital evolution of the Galilean moons [11]. This allows to keep our model simpler and still obtain reasonable results. In Lainey et al.’s study, the Jupiter’s Im\((k_2)\) takes into account the tidal bulges raised by all moons using a constant Jupiter quality factor.

5.5 Satellite Ephemerides

Fig. 6
figure 6

Uncertainties on Europa’s position wrt Jupiter plotted for the duration of the JUICE mission. Black vertical dotted lines represent the Ganymede’s flybys, magenta represent Europa’s flybys and orange represent Callisto’s flybys

Full size image

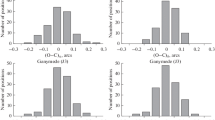
An important insight into the effectiveness of the estimation is the analysis of the uncertainties in the ephemerides of all the Galilean moons, in the radial (R), normal (N) and transverse (T) directions. As can be seen from Figs. 8, 7, 6 and 9, the time evolution of the uncertainty in the R, T and N directions differs from one component to the other. As expected, the R and T direction are coupled, and given that we are more sensitive to changes in radial direction, those two components usually show the best accuracy, while we are less sensitive to N direction changes [38].

Regarding Europa (Fig. 6), the first thing we can notice is an improvement in all three directions’ uncertainty near the two Europa’s flybys with respect the rest of the mission, especially in normal and transverse direction. The minimum uncertainties are in the order of 1 m in radial direction and 20 m for normal and transverse during the 2 flybys, while the maximum values are approximately 10 m, 200 m, 500 m, for R, T and N directions, respectively.

Fig. 7
figure 7

Uncertainties on Ganymede’s position wrt Jupiter plotted for the duration of the JUICE mission

Full size image

The position uncertainties for Ganymede (Fig. 7) look more homogeneous over the mission time span with respect to Europa. As expected, we have a more precise estimation in the beginning of the mission where we have the 6 Ganymede’s flybys with uncertainties of \(\sim \) 50 m for N direction, 10 m for T and 1 m for radial direction. In the second half part of the mission, the uncertainties grow, reaching 200 m and 50–100 m, respectively, for normal and transverse, while R uncertainty remains almost unchanged.

Callisto (Fig. 8) shows results comparable with Ganymede. The accuracy slightly improves in the second half of the mission, where the 12 Callisto’s flybys are located, but overall the uncertainties are around 1 m, 10 m and 100 m, respectively, for R, T and N directions.

Fig. 8
figure 8

Uncertainties on Callisto’s position wrt Jupiter plotted for the duration of the JUICE mission

Full size image

Lastly, we added in the estimation filter the ephemerides of Io to see how the estimation of the other three Galilean moons could constrain the uncertainty on Io’s position. In general, we saw that estimating the ephemerides of Io during the duration of the JUICE mission mainly influences the uncertainty of the position and velocity of Europa, while the other two moons are almost unperturbed. Future work will investigate better this relationship. As we can see from Fig. 9, we obtained uncertainties in the order of 5 km for normal direction and 100 m for radial direction. Transverse direction uncertainties varies more with respect to the other direction, we can see that they reach a minimum of approximately 1 km. Looking at Figs. 6 and 9, we can notice that the improvement on Io transverse position uncertainty reaches its minimum in the neighborhood of the Europa’s flybys, exactly where the accuracy on Europa’s position improved, confirming the bond between the two moons due to the Laplace Resonance.

Fig. 9
figure 9

Uncertainties on Io’s position wrt Jupiter plotted for the duration of the JUICE mission

Full size image

6 Conclusions

The main focus of this work was to study how the future JUICE space mission radiometric data can improve the knowledge on the ephemerides and gravity fields of Europa, Ganymede and Callisto, including the tidal dissipation between Jupiter and Io.

The expected uncertainties in the scientific parameters of interest were obtained by performing numerical simulations. Comparing our results with the analysis of the past Galileo mission, we can conclude that JUICE is expected to greatly improve the accuracies in all the main gravitational parameters of the moons in study.

Of the different parameters, the Love number \(k_2\) of Callisto is particularly interesting, because it allows to constrain the thickness of the ice shell, if present. In this work, we obtained an expected uncertainty between 0.073 and 0.1, depending on the assumption about the strength of the gravity field. Improvements are expected using more observables like optical and VLBI and with an improvement in the tour design, and in particular with a better distribution of true anomalies of Callisto during JUICE flybys.

In addition, the imaginary part of the Jovian Love number \(k_2\) is a key parameter to evaluate the orbital evolution of the Galilean moons and the Laplace Resonance stability. In our simulations, we considered Jupiter’s Im\((k_2)\) only at Io’s frequency, because it dominates the orbital evolution of the Galilean moons, obtaining an uncertainty of \(6.1\times 10^{-4}\), two orders of magnitude larger than the current value quoted in [10]. This is in line with expectations since the time span of observation was more than 100 years in Lainey et al. 2009, while we only considered 2 years of mission.

Adopting reasonable values for the measurements accuracy and for the a priori uncertainties, the standard deviation on Europa, Ganymede, Callisto and Io positions in the radial, transverse and normal directions were estimated. The radial direction reached a minimum of about 1 m for the three satellites. For the transverse component, a minimum uncertainty of 50 m, 10 m, 8 m for Europa, Ganymede and Callisto was reached, respectively. Lastly, the normal reached a minimum of 20 m, 50 m and 70 m, respectively, for Europa, Ganymede and Callisto.

Subsequently, we added in the estimation filter the ephemerides of Io to see how the other three Galilean moons could constrain the orbit of Io, obtaining a minimum uncertainty of 100 m, 900 m and 5 km for radial, transverse and normal direction, respectively. We are able to estimate the orbit of Io, even if the JUICE mission is not performing any flyby of the moon, due to the Laplace resonance that strongly correlates the three innermost Galilean moons. For the same reason, adding Io’s state in the estimation filter greatly influences the uncertainty on the position of Europa.

Future work will include the GCO phase and other type of observables that were not considered in this dissertation, like optical and DDOR observation, that could greatly improve the solution accuracies.