1 Introduction

Position determination and time transfer in GNSS rely on a simple model. Consider four synchronized clocks located at positions \({\mathbf {r}}_j\), \(j = 1,2,3,4\). The satellites transmit electromagnetic pulses at times \(t_j\) respectively. Suppose that these four signals are received at position \({\mathbf {r}}\) at instant t. The receiver records the reception event happening at \(t+ \delta t\) where \(\delta t\) is the offset of the receiver clock with respect to the satellite system time. From the principle of the constancy of the speed of light c we have [1]:

$$\begin{aligned} c\left( t + \delta t-t_{j}\right) =\left| {\mathbf {r}}-{\mathbf {r}}_{j}\right| , \quad j=1,2,3,4 \end{aligned}$$
(1)

Having four independent equations, one can solve for the four unknowns \({\mathbf {r}}, \delta t\). Such a solution is also called a “navigation solution”. In principle the solution can be computed with information from any number of satellites greater than or equal to four. Timing errors of 1 ns will lead to positioning errors in the order of 30 cm. It is obvious that in order to minimize the estimation error, accurate knowledge of \({\mathbf {r}}_j\) and \(t_j\) is needed. The former parameter is nowadays broadcast to final users with an accuracy between few dm and a meter thanks to accurate orbit determination techniques, a topic not addressed in this work. The estimation accuracy of the latter parameter depends on the stability of the satellite clocks and on their synchronization with respect to a common time scale (system time). In current GNSS processing schemes is tightly coupled with the orbit determination problem. Currently, inter-satellite clock offsets and orbits are retrieved in a complex joint estimation process that requires a large ground network. The accuracy of the service provided at space segment level is usually characterized in terms of Signal-in-Space Range Error (SiSRE), a parameter that factors in both orbit determination offsets and satellite clock errors and indicates the expected satellite-to-user range error. This error characterizes the maximum ranging accuracy achievable by the system, which is then subsequently further impaired by propagation (atmospheric) and user local effects (e.g. multipath and receiver biases). Typical SiSRE values in modern GNSSs are in the order of a few tens of centimeters. The DLR Institute of Communication and Navigation is currently working on a next generation satellite system (with codename Kepler) based on optical inter-satellite links (OISLs) providing autonomous synchronization with offsets below 1 ps [5, 6]. OISLs allow for a better separation of space (orbits) and time (synchronization), leading to a much higher level of synchronization across the whole constellation than what is achievable in current architectures, which in turn largely enhances precise orbit determination. The SiSRE can potentially be reduced to below one cm [9, 10], offering a highly accurate navigation service to final users.

The key to autonomous synchronization in space is the capability of remotely comparing satellite clock readings via OISLs. Two-Way Time Transfer techniques can be applied to retrieve relative clock offsets, but a careful modelling of spurious effects introducing estimation biases is necessary. To the targeted level of inter-satellite synchronization of 1 ps, relativistic biases play a major role. These effects include second order Doppler shifts of clocks due to their velocity, gravitational shifts, and other relativistic delays on the propagation of light through spacetime. If such effects are not properly accounted for, the benefit of operating stable clocks and having a mean for accurate synchronization via OISLs will be masked [1]. Synchronization schemes for picosecond-level accuracy need to be addressed in a relativistic framework and this is the goal of this work.

The first objective in this paper is to present a synchronization method based on time transfer techniques. Satellites will exchange electromagnetic signals containing information about times of emission and reception of reference bits which are taken in their proper time scale. The method presented will allow us to synchronize satellites pair-wise with respect to a defined coordinate time. The whole system can be synchronized via consecutive synchronizations between satellite couples.

The second objective is the characterization of the magnitude of the relativistic effects in order for the time transfer scheme to reach picosecond-level accuracy. Since this level of accuracy is rather high, higher-order relativistic effects need to be considered. This means studying the effect of inclusion of Earth’s geopotential harmonics beyond the \(J_2\) moment, and analysing the influence of additional celestial bodies. An analysis is carried out to obtain a model precise enough to satisfy the requirement of picosecond synchronization. For future use, this analysis also provides models for femtosecond-level synchronization and beyond.

Finally, the third goal is to define the requirements on satellite orbit accuracy for correct relativistic modelling with target performance of picosecond accuracy in synchronization. This is done by analysing the magnitude of relativistic model errors induced by satellite orbit errors (sensitivity analysis).

2 Simultaneity

The notion of synchronization is closely connected with the notion of simultaneity. Indeed, synchronized clocks must simultaneously produce the same time markers. The Newtonian theory of gravitation postulates the existence of absolute space and time, independent from each other. In the theory of relativity the refusal of the notions of absolute and independent space and time results in different time rates in different Reference Systems (RSs). As a consequence the notion of simultaneity loses its absolute and unique meaning [7].

To address a problem in the framework of relativity it is first necessary to introduce some concepts, such as the concepts of proper and coordinate quantities [16]:

  • Proper quantities are the direct results of observation without involving any information that is dependent on the choice of a spacetime reference frame. In our analysis the most fundamental quantity is proper time, which is the time measured by an observer in a frame of reference that is attached to the observer itself (proper to that observer).

  • Coordinate quantities are dependent on choices of a spacetime coordinate system. An example is the coordinate time difference between two events (the difference between the time coordinates of these events) or the rate of a clock with respect to the coordinate time of some spacetime reference system, which are both dependent on the chosen reference system.

For analysis of any process in the framework of relativity one must introduce four-dimensional RSs. Consider a time scale \(\tau\) (denoting the proper time of an observer) and three space coordinates \({\mathbf {r}} = (x,y,z)\). In the relativistic context there are different proper time rates in different reference systems. The relativistic synchronization framework in this work follows the concepts presented in [7]. Consider the following events:

  • Event E1 in RS1: \((\tau _{1_0}, {\mathbf {r}}_1)\)

  • Event E2 in RS2: \((\tau _{2_0}, {\mathbf {r}}_2)\)

In most cases, two different RSs refer to two different time scales \(\tau _1 \ne \tau _2\). This implies that we cannot say anything about the simultaneity of the events E1 and E2. In order to determine if the two events are simultaneous we need to use the concept of coordinate time.

Consider a third reference frame RS3 with proper time t and position coordinates \({\tilde{\mathbf {r}}}\). For the other reference systems RS1 and RS2, this third reference frame can be used to define simultaneity.

The events E1 and E2 can be expressed in coordinates of this third common RS as:

  • Event E1 in RS3: \((t_{1_0}, {\tilde{\mathbf {r}}}_1)\)

  • Event E2 in RS3: \((t_{2_0}, {\tilde{\mathbf {r}}}_2)\)

We say E1 and E2 are simultaneous if the condition \({t_{1_0}=t_{2_0}}\) is satisfied in this common reference frame. This third reference frame can be chosen freely, its choice depends on convenience and any RS can be used to define coordinate time. Luckily, in most cases we can find a transformation that relates the proper time of an RS to the coordinate time. The coordinate scale t can be expressed as a function of the proper time scale \(\tau\) of the RS of interest, i.e., \(t=t(\tau )\).

Using this notion, we can say that E1 and E2 are simultaneous if the condition \(t(\tau _{1_0}) = t(\tau _{2_0})\) is satisfied in the RS where coordinate time is defined. This concept is what we define as coordinate simultaneity.

The key point is to find the relation linking the time scales \(\tau _1\) and \(\tau _2\) to the coordinate time scale t. If this relation is found it is possible to syntonize or, with an additional step, synchronize the clocks of two different reference systems with respect to the coordinate time. These two concepts need to be defined [20]:

  • Coordinate syntonization: align the rate of clocks such that both run at same frequency. In the relativistic context to syntonize means to find the rate of a clock in an RS with respect to another clock in a different RS. Syntonizing a clock with proper time \(\tau\) with respect to the coordinate time t means finding the relation:

    $$\begin{aligned} \left( \frac{\text {d} \tau }{\text {d} t}\right) = f(t,{\mathbf {r}}(t),{\mathbf {v}}(t)) \end{aligned}$$
    (2)

    where f is a function that depends on the coordinate time t, the position \({\mathbf {r}}(t)\) and the velocity \({\mathbf {v}}(t)\) of the clock.

  • Coordinate synchronization: this entails establishing a one-to-one transformation between coordinate time events t and proper time events \(\tau\). By knowing the function f and assigning an initial condition \(\tau (t_0) = \tau _{0}\) relating the coordinate instant \(t_0\) to the proper time instant \(\tau _0\), we can then unambiguously solve the differential Eq. (2) for the proper time instant \(\tau (t)\):

    $$\begin{aligned} \tau (t) = \tau _0 + \int \limits _{t_0}^{t} f(t,{\mathbf {r}}(t),{\mathbf {v}}(t))\text {d}t \end{aligned}$$
    (3)

Equation (3) can also be reversed: the coordinate time t can be expressed as a function of the proper time \(\tau\) as \(t = t(\tau )\) fixing a value for \(\tau\). To have a solution we need to ascribe a coordinate instant \(t_0\) to some proper instant \(\tau _0\) and solve Eq. (3) for \(t(\tau )\).

In the present work, we consider two coordinate time scales t and \(t'\) to be different even if they differ only by a constant term: \(t' = t + const\). Consider two satellites A and B with proper times \(\tau _A\) and \(\tau _B\).

  • Setting an initial condition \(\tau _A(t_{0}) = \tau _{A_{0}}\) and using Eq. (3) for the specific case of A, it is possible to transform the readings of clock A to some coordinate time t.

  • In an analogous way it is possible to transform the readings of clock B to some coordinate time \(t'\) using Eq. (3) for B and setting an initial condition \(\tau _B(t_{0}') = \tau _{B_{0}}\).

The coordinate time scale \(t'\) differs from t due to the fact that the initial conditions are arbitrary and generally different. The two coordinate time scales t and \(t'\) are related via \(t = t' + \varDelta _{AB}\) where \(\varDelta _{AB}\) is a constant term that describes the coordinate time offset between the two clocks.

To synchronize clocks A and B is to find a suitable initial value \(\tau _B(t_{0}) = \tau _{B_{0}}\) for clock B enabling us to transform the readings of B to the same coordinate time scale t as the one that A transforms to, i.e. \(\varDelta _{AB} = 0\) and \(t' = t\). A visual representation of these concepts is presented in Fig. 1.

The initial conditions that allow for synchronization can be found with time transfer methods. The event that allows us to ascribe \(t_{0}\) to \(\tau _{B_{0}}\) is called “the synchronizing event”.

Fig. 1
figure 1

Coordinate time offset. Both clocks transform their time events to the coordinate scale. Given two arbitrary initial conditions the two clocks transform the time of the event to two different scales, one shifted by \(\varDelta _{AB}\) with respect to the other. We can see that the same observed event “Ev” is not simultaneous in the coordinate time scale. Synchronizing the clocks means choosing well one of the initial conditions such that \(\varDelta _{AB} = 0\) or such that \(\varDelta _{AB}\) is accurately known and can be removed in post-processing

Full size image

2.1 Choice of Coordinate Time

In general relativity every frame is equivalent so any RS can be chosen to be the coordinate RS. Almost all users of GNSS are at fixed locations on the rotating Earth, or else are moving very slowly over Earth’s surface and the clocks are ticking according to a terrestrial time scale, typically UTC. This leads to the natural idea of using an Earth-centered, Earth-fixed, reference frame (ECEF frame) as a coordinate RS. In this model the Earth rotates about a fixed axis with a rotation rate of about \(\omega _E = 7.3 \times 10^{-5}\) rad/s. Typically this reference frame is the World Geodetic System (WGS-84) [1]. The fact that this frame is rotating implies directly that the frame is non-inertial. However if the purpose is coordinate synchronization of multiple clocks the choice of the coordinate frame must be addressed carefully. In fact when a non-inertial RS is chosen to define coordinate time there is an absence of transitivity: if clock A is synchronized with clock B, and B with C, then A is not necessarily synchronized with C. This gives rise to fundamental problems in the synchronization of a GNSS. In order to overcome this difficulty one must construct in the neighbourhood of the Earth a local inertial RS, in which the gravitational field of external bodies can be represented in the form of tidal terms only [7]. For GNSS it means that synchronization of the entire system of ground-based and orbiting clocks is performed in the local inertial frame, or Earth Center Inertial (ECI) coordinate system [2]. The coordinate time t of the ECI frame is defined at infinity, outside Earth’s gravity well [1]. If we synchronize with respect to \(t = t_{\mathrm {ECI}}\), we are synchronizing with respect to the coordinate time of an inertial RS, so that the validity of transitivity can be assumed.

3 The Proper Time Rate

The relationship between the proper time \(\tau\) of a clock in the vicinity of Earth and some coordinate time t is defined by the spacetime metric, which is derived from the metric tensor, the solution of the Einstein Field Equation. The metric tensor completely characterizes the spacetime metric which describes the relation between spatial and time coordinates. When Earth is modelled as a non-rotating spherical mass, the solution of such an equation leads to the Schwarzschild metric. The Schwarzschild metric describes the region surrounding a non-rotating spherical mass [17, 19].

The Schwarzschild metric in isotropic coordinates (\(r, \theta , \phi\)) is [11]:

$$- \mathrm {d}s^2= -\left( \frac{1- \frac{GM_E}{2 rc^2}}{1+\frac{GM_E}{2 rc^2}}\right) ^{2}c^2\mathrm {d}t^2 +\left( 1+ \frac{GM_E}{2 rc^2} \right) ^{4} \left( \mathrm {d}r^2+r^2\mathrm {d}\phi ^2+r^2\sin ^2\theta \mathrm {d}\theta ^2 \right)$$
(4)

Expanding the parentheses and keeping only \(c^{-2}\) terms we get:

$$\begin{aligned} \mathrm {d} s^{2} \approx \left( 1+\frac{V}{c^2}-\frac{v^2}{2c^2}\right) ^2 c^2 \mathrm {d}t^2 \end{aligned}$$
(5)

where \(V(r) = - \frac{GM_E}{r}\) is the Earth’s monopole potential and \(v^2 := \frac{ \mathrm {d}r^2+r^2 \mathrm {d}\phi ^2+r^2\sin ^2\theta \mathrm {d}\theta ^2}{\mathrm {d}t^2}\) is the square of the velocity of the clock.

The spacetime metric is related to the proper time \(\tau\) of a clock via:

$$\begin{aligned} \mathrm {d} s = c \mathrm {d}\tau \end{aligned}$$
(6)

With this, we can obtain the proper time rate of a clock with respect to ECI coordinate time as:

$$\begin{aligned} \frac{\mathrm {d}\tau }{\mathrm {d}t } = \left( 1+\frac{V}{c^2}-\frac{v^2}{2c^2}\right) . \end{aligned}$$
(7)

The proper time rate in Eq. (7) is expressed with respect to coordinate time \(t= t_{\mathrm {ECI}}\).

The rate of coordinate time used in GNSS, however, is closely related to International Atomic Time (TAI), defined as the coordinate time at a surface of a constant effective gravitational equipotential at mean sea level in the ECEF.

It is advantageous to exploit the fact that all clocks on the reference surface tick at the same rate to redefine the rate of coordinate time by standard clocks at rest on Earth’s geoid. This is done by adopting the following coordinate change:

$$\begin{aligned} \mathrm {d}t_{\mathrm {Geoid}} = \left( 1 + \frac{\varPhi _0}{c^2}\right) \mathrm {d}t_{\mathrm {ECI}} \end{aligned}$$
(8)

where \(t_{\mathrm {Geoid}}\) is the new coordinate time for clocks at rest on Earth’s geoid and \(\varPhi _0\) is the effective gravitational potential at the surface of the geoid (that also includes the Doppler term due to its rotation ) [2]. When this time scale change is made, the proper time rate of Eq. (7) becomes:

$$\begin{aligned} \frac{\mathrm {d}\tau }{\mathrm {d}t_{\mathrm {Geoid}}} = \left( 1+\frac{V-\varPhi _0}{c^2} -\frac{v^2}{2c^2} \right) . \end{aligned}$$
(9)

We should remark here that in Eq. (9) we are comparing the rate of a clock in the vicinity of Earth with respect to the time of a clock at rest on the surface of the geoid but with the understanding that synchronization is established in an underlying, locally inertial, reference frame (the ECI frame) [2]. The numerical value of the parameters and quantities presented in the preceding sections are given in Table 1.

Table 1 Values of used parameters [15]
Full size table

4 Autonomous Synchronization

Some natural event, as an observation of occultation of a star by a planet for instance, may be considered as a synchronizing event. Both observers may chose an arbitrary initial condition linking their proper time to the coordinate time, transform their proper time readings of observation of the natural event into coordinate times \(t_{Ev}\) and \(t_{Ev}'\) and then determine the coordinate offset \(\varDelta _{AB}\). A faster and more reliable manner of synchronization is the artificial creation of a synchronizing event on the world line of the observer B via exchange of signals. This method of synchronization is called “autonomous” or “independent” synchronization. In the system that we are considering, optical communication enables the exchange of data with timestamps. This allows for time transfer between remote references [7].

4.1 Two-Way Synchronization

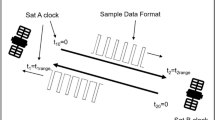
Let’s consider a Two-Way Time Transfer (TWTT) scheme as presented in [7]: satellite A, located at \({\mathbf {r}}_A\), transmits at coordinate time \(t_{0}\) a message with proper time stamp \(\tau _{A_0}\). Satellite B receives it at coordinate time \(t_{1}\), stamps it with proper time stamp \(\tau _{B_1}\). After a delay satellite B re-transmits it back stamping it with the proper time of re-transmission \(\tau _{B_2}\). The signal is finally received at coordinate time \(t_{3}\) from Satellite A that stamps it at \(\tau _{A_3}\). The coordinate propagation times for the round trip are respectively \(T_{AB} = t_1 - t_0\) and \(T_{BA} = t_3 - t_2\). Assume that we have additional delays \(\delta _N^{R}\) and \(\delta _N^{T}\) which denote the hardware delays relative to the reception (R) and transmission (T), with \(N = A,B\). Figure 2 shows a model of this two-way exchange.

Fig. 2
figure 2

Timing events: depicted are the trajectories of Satellite A and Satellite B with corresponding proper and coordinate times at signal transmission and reception in both directions of the communication

Full size image

Suppose we have an initial condition \(\tau _A(t_{0}) = \tau _{A_0}\). Clock A can transform its reading of any event happening at \(\tau _A\) solving the following equation for the corresponding coordinate time \(t(\tau _A)\):

$$\begin{aligned} \tau _{A} - \tau _{A_0} = \int \limits _{t_{0}}^{t(\tau _A)} \left( 1+\frac{V({\mathbf {r}}_A(t')) -\varPhi _0}{c^2}-\frac{v_A(t')^2}{2c^2} \right) \text {d}t' \end{aligned}$$
(10)

Satellite A is thus able to transform its proper time of reception \(\tau _{A_3}\) into the coordinate time instant \(t_3\). If the trajectories of A and B are known with high accuracy, it is possible to determine the parameters \({\mathbf {r}}_A(t),v_A(t)\) and \({\mathbf {r}}_B(t),v_B(t)\) in the form of functions of the coordinate time scale t. Our goal is to retrieve the coordinate time of reception \(t_1\) so that we are able to ascribe it to the reading \(\tau _{B_1}\). The coordinate instant \(t_1\) can be retrieved with the following iterative method [7]:

$$\begin{aligned} t_{1}^{(0)}&= t_0 + \frac{1}{2}\left( t_3 - t_{0}- \delta _{Int} \right) + \delta _{Prop}^{(0)} + \delta _{hw} \end{aligned}$$
(11)
$$\begin{aligned} t_{1}^{(n)}&=t_0 + \frac{1}{2}\left( t_3 - t_{0} - \delta _{Int}\right) + \delta _{Prop}^{(n-1)} +\delta _{hw}\end{aligned}$$
(12)
$$\begin{aligned} t_1&= \lim \limits _{n \rightarrow \infty } t_1^{(n)}, \quad n =1,2,3, \ldots \end{aligned}$$
(13)

where:

$$\begin{aligned} \delta _{Int}&= \int \limits _{\tau _{B_1}}^{\tau _{B_2}} \left( 1-\frac{V({\mathbf {r}}_B(\tau )) -\varPhi _0}{c^2}+\frac{v_B(\tau )^2}{2c^2} \right) \mathrm {d}\tau \end{aligned}$$
(14)
$$\begin{aligned} \delta _{Prop}^{(n)}&=\frac{1}{2}\left( T_{AB}^{(n)} -T_{BA}^{(n)}\right) \end{aligned}$$
(15)
$$\begin{aligned} T_{AB}^{(n)}&= \frac{R_{AB}^{(n)}}{c}, \quad T_{BA}^{(n)} = \frac{R_{BA}^{(n)}}{c} \end{aligned}$$
(16)
$$\begin{aligned} R^{(n)}_{AB}&=\Vert {\mathbf {r}}_B(t_1^{(n)}) -{\mathbf {r}}_A(t_0)\Vert \end{aligned}$$
(17)
$$\begin{aligned} R^{(n)}_{BA}&=\Vert {\mathbf {r}}_A(t_3) -{\mathbf {r}}_B(t_1^{(n)}+\delta _{Int})\Vert \end{aligned}$$
(18)
$$\begin{aligned} \delta _{hw}&= \frac{1}{2}\left( \delta ^T_A -\delta ^R_A\right) +\frac{1}{2}\left( \delta ^R_B - \delta ^T_B \right) \end{aligned}$$
(19)

Here, \(\delta _{Int}\) is the integral of the proper time rate over the path of clock B between reception from A and transmission from B, which in coordinate time corresponds to \(t_2 - t_1\). The term \(\delta _{Prop}\) is the half difference of propagation time during the round trip between A and B (expressed with \(T_{AB}\) and \(T_{BA}\) respectively). The initial \(\delta _{Prop}^{(0)}\) can be estimated thanks to the approximate knowledge of the positions of the satellites. Finally, \(\delta _{hw}\) identifies the residual hardware delay in a TWTT exchange. This may be largely mitigated if the transmit and receive delays at either side of the communication are similar. Satellite B observes the signal reception happening at \(\tau _{B_1}\). Thus, we can ascribe the calculated moment \(t_1\) to the observed moment \(\tau _{B_1}\) and, thereby synchronize clock B with clock A. We found the initial condition \(\tau _B(t_{1}) = \tau _{B_1}\) that allows clock B to transform all events seen in its timescale \(\tau _B\) to the same coordinate time t as the one that clock A transforms to.

4.2 Comparison with a One-Way Synchronization

For completeness, we could consider a One-Way Time Transfer (OWTT), where we have a unidirectional exchange of signals from Satellite A to Satellite B. In Fig. 2 the communication would end at the signal reception from Satellite B at coordinate time instant \(t_1\). In this case \(t_1\) can be determined with the following iterative method:

$$\begin{aligned} t_{1}^{(0)}&= t_{0} + T_{AB}^{(0)} \end{aligned}$$
(20)
$$\begin{aligned} t_{1}^{(n)}&= t_{0} + T_{AB}^{(n-1)}\end{aligned}$$
(21)
$$\begin{aligned} t_1&= \lim \limits _{n \rightarrow \infty } t_1^{(n)}, \quad n =1,2,3, \ldots \end{aligned}$$
(22)

where:

$$T_{AB}^{(n)}= \frac{R_{AB}^{(n)}}{c} + \frac{\varPhi _0}{c^2}\frac{R_{AB}^{(n)}}{c} + \frac{2GM_{E}}{c^3} \ln \left( \frac{\Vert {\mathbf {r}}_{A}(t_0)\Vert +\Vert {\mathbf {r}}_{B}(t_1^{(n)})\Vert + R_{AB} }{\Vert {\mathbf {r}}_{A}(t_0)\Vert + \Vert {\mathbf {r}}_{B}(t_1^{(n)})\Vert -R_{AB}} \right)$$
(23)

Here, \(T_{AB}^{(0)}\) is the roughly estimated propagation time that can be computed thanks to the approximate knowledge of the positions of the satellites.

The first term on the right-hand side of Eq. (23) is the classical Euclidean time that light takes to go from point A to point B. The second and third terms are delays resulting from the time dilation experienced by light when travelling through a gravitational field and are purely relativistic effects. The third term is called the Shapiro delay. This expression for the propagation of light can be found by setting the spacetime element \(\text {d}s = 0\), solving for \(\text {d}t\) and integrating it on the path from A to B. The two relativistic terms are of the order of tens of picoseconds and therefore have to be taken into account to achieve picosecond-level synchronization with an OWTT. Note also that reception event \(t_1\) is determined with the knowledge of the trajectories \({\mathbf {r}}_{A}(t), {\mathbf {r}}_{B}(t)\). In an OWTT, inaccurate knowledge of the positions and trajectories would directly result in an offset due to errors in the calculation of \(T_{AB}\). This is one of the main limitations of this method: before synchronization, even assuming that the satellite positions are known with cm accuracy, the resulting modelling errors are in the order of hundreds of picoseconds in the determination of \(t_1\) (and thus in a corresponding synchronization offset). Moreover, in an OWTT we can only achieve clock synchronization if spurious terms, such as hardware delays in the optical terminals used to establish the link, can be modelled and removed. This may prove difficult: a characterisation of these delays in a relevant operational environment would be difficult to achieve for picosecond-level accuracy.

Due to the quasi-symmetry of the communication, a TWTT is preferred because it mitigates all the problems of the OWTT mentioned above. Positioning errors, hardware delays and additional relativistic offsets mitigate or cancel out in the expressions for determining \(t_1\). Indeed, in a TWTT we are interested in characterizing the difference of propagation times during the round trip and not their absolute magnitude. If we compute Eq. (15) using the expression for the one-way propagation times (23) we can see that the difference of the additional relativistic terms is of the order of femtoseconds and is therefore negligible. In fact in Eq. (16) the expression for the propagation time is simpler and only includes the Euclidean term. It will be shown in a dedicated section (Sect. 6.2.2) that positioning errors are also mitigated in a TWTT.

4.3 System Synchronization

One can synchronize any arbitrary number of other satellites using a cascaded approach, i.e. Satellite A gets synchronized with B via a time transfer, B gets synchronized with C and so on until all satellites are synchronized to the same coordinate scale. However, this implies that at least one clock exchanges signals with a clock keeping the coordinate time. In a GNSS this last clock would be on Earth. Essentially, only one ground station would be sufficient to guarantee the link with the terrestrial time scale. The presented synchronization method allows for a significant degree of autonomy of the satellite system. In the extreme case, lacking even the ground station, the satellite clocks realize a “space clock” whose time scale definition is not affected by the poor knowledge of the geopotential on the surface of Earth [20]. Such a clock, moving in an unperturbed orbit and well-defined coordinate system, would bring significant value and new capabilities to time and frequency transfer worldwide, to precision geodesy and terrestrial reference frames, to earth-environmental science and to navigation systems [3].

5 Picosecond Synchronization Models

In both time transfer methods presented, in order to reach picosecond precision it is necessary to have precise models of the proper time rate \(\left( \frac{\text {d} \tau }{\text {d}t}\right)\) and of the propagation time \(T_{AB}\) (or the difference of propagation times in a TWTT).

5.1 The proper Time Integral

We recall here the expression of the proper time rate of a clock in Earth’s vicinity with respect to TAI coordinate time t:

$$\begin{aligned} \frac{\mathrm {d}\tau (t)}{\mathrm {d}t } = \left( 1+\frac{V({\mathbf {r}}(t)) -\varPhi _0}{c^2}-\frac{v(t)^2}{2c^2}\right) \end{aligned}$$
(24)

Integrating Eq. (24) it is possible to transform any reading of the clock \(\tau\) to events of coordinate time scale t. This integral has to be solved analytically or numerically in order to relate instants of the two scales. The complexity of finding a solution depends on the model of the potential. The gravitational potential V in Eq. (24) is the sum of the Earth’s gravitational potential \(V_E\) and the one created by the cumulative contribute of other celestial planets, \(V_{SC}\).

The Earth’s gravitational potential \(V_E\) is defined through a summation of spherical harmonics [14]:

$$V_{E}(r,\alpha ,\beta )= -\frac{GM_{E}}{r} \Bigg [ 1 + \sum _{n=2}^{n_{ \mathrm {max}}} \sum _{m=0}^{n} \left( \frac{a_{\oplus }}{r}\right) ^n {\bar{P}}_{nm}(\sin \beta ) \times \left( {\bar{C}}_{nm}\cos (m\alpha ) + {\bar{S}}_{nm}\sin (m\alpha ) \right) \Bigg ] $$
(25)

where:

  • \(a_{\oplus }\) is the semi-major axis of the WGS 84 Ellipsoid;

  • \({\bar{C}}_{nm}\) and \({\bar{S}}_{nm}\) are the normalized gravitational coefficients contained in EGM2008;Footnote 1

  • \({\bar{P}}_{nm}\) is the normalized associated Legendre function of degree n and order m;

  • \(\alpha\) and \(\beta\) are respectively the longitude and latitude of the satellite position in an ECEF frame.

Not all terms in the summation are significant: the model should only retain \(n_{max}\) terms, sufficient to guarantee that the model inaccuracies remain below ps-level. The term \(V_{SC}\) is the gravitational contribution of body C (mass \(M_C\)) situated at \(\mathbf {r_{C}}\) on satellite S situated at \({\mathbf {r}}\). This is expressed as [20]:

$$\begin{aligned} V_{SC} = -G M_{C}\left[ \frac{1}{r_{S C}}-\frac{1}{r_{C}}-\frac{\mathbf {r_{C}} \cdot {\mathbf {r}}}{r_{C}^{3}} \right] \end{aligned}$$
(26)

where \(\mathbf {r_{SC}} =\mathbf {r_{C}}-{\mathbf {r}}\) and \(r = \Vert {\mathbf {r}}\Vert\).

The relation between the rate of a clock in the near Earth region (proper time \(\tau\)) with respect to coordinate time on Earth’s geoid becomes:

$$\begin{aligned} \begin{aligned} \left( \frac{\mathrm {d}\tau }{\mathrm {d}t}\right) \approx 1 +\frac{V_E}{c^2} - \frac{\varPhi _0}{c^2} - \frac{v^2}{2c^2} +\sum _{C \ne E} \frac{V_{SC}}{c^2} \\ \end{aligned} \end{aligned}$$
(27)

5.2 Evaluation of Proper Time Rate Terms for Kepler Satellites

In this section, we are interested in determining the number of terms to be included in the proper time rate expression \(\left( \frac{\mathrm {d} \tau }{\mathrm {d}t}\right)\) to be integrated in order for the integral terms to meet the requirement of picosecond-level accuracy. We need to characterize which effects play a role within the time of a signal exchange, which in the case of typical GNSS satellites in Medium Earth Orbit (MEO) is always within a second. The Kepler constellation consists of two segments: a set of navigation satellites in MEO, assigned approximately to the same orbital slots of the current Galileo constellation, and a smaller set of satellites in upper Low Earth Orbit (LEO). The relevant orbital parameters are summarized in Table 2.

Table 2 Summary of main Kepler parameters
Full size table

The satellites of both segments are homogeneously distributed over their orbital planes, i.e. \(45^{\circ }\) difference in mean anomaly for MEO and \(60^{\circ }\) for LEO neighbour satellites. The planes are also homogeneously distributed around the globe with a \(120^{\circ }\) separation in the right ascension of the ascending node (RAAN) for MEO planes and \(90^{\circ }\) for LEO planes. The argument of perigee is \(0^{\circ }\) for both segments. Since the communication time is always shorter than 1 s we can directly look for terms in the proper time rate that are smaller than the threshold of \(10^{-12}\) s/s. For completeness and future use we evaluate all terms of the proper time rate for different satellites against 3 thresholds: \(10^{-12}\), \(10^{-15}\) and \(10^{-18}\) s/s. The satellites’ orbits are simulated using the open source software General Mission Analysis Tool (GMAT), available from NASA [12]. The simulation interval is chosen to be the 10 days and the integration step to propagate the orbits is 30 s.

We have presented in Eq. (27) the terms to consider for a full model of the proper time rate for a clock located at \({\mathbf {r}}(t)\) in the vicinity of the Earth with respect to TAI coordinate time. As presented in Eq. (25), the “geopotential” \(V_E\) (gravitational potential of Earth) is defined through a summation of spherical harmonics. We name each term of the geopotential \(V_n\).

Figure 3 shows the maximal contribution of the single geopotential terms \(\frac{ V_{n}}{c^2}\) of degree n manifested during the simulated 10 days.

Fig. 3
figure 3

Maximum contribution of Earth’s potential harmonic terms of degree n on MEO and LEO satellites proper time rates

Full size image

We can see in Fig. 3 that only two terms (quadrupole formulation of the potential) are sufficient to describe the proper time rate of satellites in both constellations at the order of \(10^{-12}\). From the third term the information apported can be considered negligible. In any case it is clearly visible that the geopotential term of order \(n = 2\) for LEO satellites is very close to this threshold. In order to keep some margin it is advisable to consider a potential expansion with \(n_{max}=3\) for the LEO constellation. As expected more terms in the potential expansion are needed for stricter thresholds. A summary of the results is presented in Table 3.

Table 3 Number of geopotential harmonic terms to take into account in the proper time rate for different thresholds
Full size table

Using the orbital simulation data from GMAT each term of Eq. (27) for every single satellite has been computed and the maximal contribution of each term has been recorded. The orbital parameters of the sun, moon and other planets have been artificially modified to simulate the case where every other body considered is at its closest approach during the whole simulation. This is an extreme case that is very unlikely to happen but it gives an upper bound to the shift caused by each one of those bodies.

Fig. 4
figure 4

Maximum value of terms in the proper time rate expression for LEO and MEO satellites during the simulated 10 days

Full size image

Figure 4 shows the magnitude of the maximal contributions of the terms in Eq. (27) for MEO and LEO satellites in the constellation. For picosecond accuracy only the geopotential term and the second order Doppler term need to be considered. Gravitational effects of external bodies need to be taken into account for the stricter thresholds of \(10^{-15}\) s/s (Moon influence on MEO satellites) and \(10^{-18}\) s/s (Moon and Sun for both MEO and LEO satellites). Table 4 summarizes all the terms to be taken into account for a given constellation and threshold.

Table 4 Terms to take into account in the proper time rate for different thresholds
Full size table

6 Impact of Orbit Parameter Errors

We are now interested in the sensitivity of the derived models to orbit parameter errors. To analyse it we evaluate the resulting errors in proper time rate and in the difference of propagation times arising from errors in position, range and velocity. In fact we want to determine the permitted error on those parameters that leads to:

$$\begin{aligned}&\left. \frac{\mathrm {d} \tau }{\mathrm {d} t} \right| _{\text {w/Error}}-\left. \frac{\mathrm {d} \tau }{\mathrm {d} t} \right| _{\text {w/o Error}}=H~[s/s] \end{aligned}$$
(28)
$$\begin{aligned}&\left. \delta _{Prop}\right| _{\text {w/Error}}-\left. \delta _{Prop}\right| _{\text {w/o Error}}=H~[s]\nonumber \\&\text {where } H = {\left\{ \begin{array}{ll} 10^{-12}\\ 10^{-15}\\ 10^{-18} \end{array}\right. }. \end{aligned}$$
(29)

6.1 Velocity Error Margin

An error in the velocity of the satellites would impact the determination of the proper time rate, affecting the second-order Doppler term. Consider \((v_0 + \epsilon )\) the velocity of the satellite with error and \(v_0\) the velocity without error:

$$\begin{aligned} \left. \frac{\mathrm {d} \tau }{\mathrm {d} t} \right| _{\text {w/Error}}-\left. \frac{\mathrm {d} \tau }{\mathrm {d} t} \right| _{\text {w/o Error}}= \frac{(v_0 + \epsilon )^2}{2c^2} - \frac{v_0^2}{2c^2} = H \end{aligned}$$
(30)

which leads to:

$$\begin{aligned} \epsilon =\sqrt{v_{0}^{2}+2H c^{2}} - v_0 \end{aligned}$$
(31)

Assuming circular orbits, the orbital velocity of a body is \(v_0=\sqrt{\frac{G M}{a}}\) where a is the orbit radius. Table 5 summarizes the results for all thresholds H and both types of satellites considered for the Kepler constellation. It is noticeable how the requirement for the uncertainty in the velocity is technologically not hard to meet (at least for the \(10^{-12}\) case). The velocity can be determined with a higher level of precision without major difficulties.

Table 5 Allowed velocity error to remain below a proper time rate error threshold H
Full size table

6.2 Position Error Margin

6.2.1 Impact of Position Errors on the Proper Time Rate

Satellite position errors impact the determination of the proper time rate because of the dependence of the Earth’s geopotential on position. Particularly affected is the uniform geopotential term, which is the dominant term in the expansion and depends on the norm of the position vector \({\mathbf {r}}(t)\). Consider \((r_0 + \epsilon )\) the norm of the position vector of the satellite with error and \(r_0\) the same quantity without error:

$$\begin{aligned} \begin{aligned} \left. \frac{V}{c^2}\right| _{\text {w/Error}} -\left. \frac{V}{c^2}\right| _{\text {w/o Error}} = H \end{aligned} \end{aligned}$$
(32)

Using the assumption of uniform gravity \(V(r) = - \frac{ G M_E}{r}\):

$$\begin{aligned} \frac{G M_E}{c^{2}}\left( -\frac{1}{r_{o}+\epsilon }+\frac{1}{r_{o}}\right) = H\end{aligned}$$
(33)

which leads to:

$$\begin{aligned} \epsilon = \left( -\frac{H c^2}{GM_E} + \frac{1}{r_0}\right) ^{-1} - r_0 \end{aligned}$$
(34)

Table 6 summarizes the results for all thresholds H evaluating Eq. (34) for both types of satellites of the Kepler constellation. It can be seen again how the requirement for the uncertainty in the positioning is very loose (for the \(10^{-12}\) s/s case). There is no difficulty in knowing the radial position with such precision.

Table 6 Permitted radial position error to remain below a proper time rate error threshold H
Full size table

6.2.2 Impact of Position Errors on the Propagation Time

The real impact of satellite position errors manifests itself in the calculation of the difference in propagation times, rather than on the proper time rate. Assume that the real positions \({\mathbf {r}}_A(t)\) and \({\mathbf {r}}_B(t)\) are affected by positioning errors (in vectorial form) expressed respectively as \(\mathbf {\delta r}_A(t)\) and \(\mathbf {\delta r}_B(t)\) due to uncertainties in the orbit determination. The difference in propagation times is then:

$$\left. \delta _{Prop}\right| _{\text {w/Error}}= \frac{\Vert {\mathbf {R}}_{AB} + \mathbf {\delta r}_B(t_1) - \mathbf {\delta r}_A(t_0)\Vert }{2c} \nonumber - \frac{\Vert {\mathbf {R}}_{BA} + \mathbf {\delta r}_A(t_3) - \mathbf {\delta r}_B(t_2)\Vert }{2c} $$
(35)

As a first approximation we can assume that the position errors remain basically constant during the communication period which is expected to last a few hundreds of ms, i.e. \(\mathbf {\delta r}_A :=\mathbf {\delta r}_A(t_0) \approx \mathbf {\delta r}_A(t_3) \approx\) const. and \(\mathbf {\delta r}_B:=\mathbf {\delta r}_B(t_1) \approx \mathbf {\delta r}_B(t_2) \approx\) const. We have that \(\Vert \mathbf {\delta r}_B - \mathbf {\delta r}_A \Vert \ll \Vert {\mathbf {R}}_{AB}\Vert\) so we can use the Taylor expansion of Eq. (35).

Thus:

$$\begin{aligned} \left. \delta _{Prop}\right| _{\text {w/Error}}&\approx \left( \frac{R_{AB}}{c} - \frac{R_{BA}}{c}\right) \nonumber + \frac{\left( {\mathbf {N}}_{AB} + {\mathbf {N}}_{BA} \right) ^{\scriptscriptstyle {\mathrm {T}}}\left( \mathbf {\delta r}_B - \mathbf {\delta r}_A\right) }{2c}\end{aligned}$$
(36)
$$\begin{aligned}&=: \left. \delta _{Prop}\right| _{\text {w/o Error}} + H \end{aligned}$$
(37)

where H corresponds to the last term on the right hand side of Eq. (36), \({\mathbf {N}}_{AB} = \frac{{\mathbf {R}}_{AB}}{\Vert {\mathbf {R}}_{AB}\Vert }\) and \({\mathbf {N}}_{BA} = \frac{{\mathbf {R}}_{BA}}{\Vert {\mathbf {R}}_{BA}\Vert }\).

We identify here a synchronization offset H due to uncertainty in orbital position determination, expressed as:

$$\begin{aligned} H = \frac{\left( {\mathbf {N}}_{AB} + {\mathbf {N}}_{BA} \right) ^{\scriptscriptstyle {\mathrm {T}}}\left( \mathbf {\delta r}_B - \mathbf {\delta r}_A\right) }{2c} \end{aligned}$$
(38)

The offset is minimal when \({\mathbf {N}}_{AB} \approx - {\mathbf {N}}_{BA}\). This is the case for an approximately simultaneous exchange of signals, where \(t_0 \approx t_2\). In practice, since the clocks will be roughly synchronized, both Satellite A and Satellite B will send a signal at proper times \(\tau _{A0}\) and \(\tau _{B2}\) which they can approximately relate to coordinate times \(t_0 \approx t_2\).

The worst case scenario is when \(\mathbf {\delta r}_A = - \mathbf {\delta r}_B\) and both uncertainties are parallel to \({\mathbf {N}}_{AB} + {\mathbf {N}}_{BA}\). Preliminary analysis of Precise Orbit Determination (POD) for the Kepler constellation shows that by considering a simultaneous application of a large number of modelling errors (without using error reduction techniques), satellite 3D position errors are expected to be smaller than 70 cm. In the mentioned case, POD is performed by a single ground station with the support of the LEO segment, without any assumption of prior synchronization or use of ISLs [9]. In an operational scenario, satellites would infer their position from the broadcast ephemerides based on predicted orbits. The accuracy of the predicted orbits is expected to be lower than the one of POD orbits but it is nevertheless expected to be much better than 1 meter. To remain conservative, we assume here that the positions of all communicating Kepler satellites are known with a relatively large uncertainty \(\Vert \mathbf {\delta r}_A\Vert =\Vert \mathbf {\delta r}_B\Vert = 4\) m. A simulation has been performed by injecting orbital errors at this level and the results are given in Table 7. In the simulation different types of transmission delays \(t_2 - t_0\) are evaluated. In the first case optical signals are transmitted simultaneously, i.e. \(t_0 = t_2\). In the other cases Satellite B transmits after delay \(t_2 - t_0\) with respect to the moment of transmission \(t_0\) from Satellite A. We can see from the results that even when a large uncertainty in the positions of the satellites is considered and the communication is very asymmetric (\(t_2 > t_0\)), we can still model relativistic effects to within 1 ps accuracy. This means that with the current orbit determination capabilities we can accurately model relativistic effects to below 1 ps.

Table 7 Clock offsets resulting from 4 m positioning errors in TWTT assuming that those errors remain constants during the whole signal exchange process
Full size table

7 Technological State of the Art

So far, time transfer has been presented in abstract form through a mathematical description of the process. The goal of this section is to provide an overview of the technology required to make the presented synchronization methods a reality. Two-way time transfer at ps-level is possible via communication systems based on lasers, already space-qualified and operative for commercial satellite data relay applications [5]. Early ground-to-space tests of time transfer via non-coherent optical links have already demonstrated accuracies in the range of hundreds picoseconds. Examples of such tests are the Laser Time Transfer technology validated at 300 ps-level on Beidou satellites [8] and the Time Transfer by Laser Link (T2L2), which demonstrated time transfer between a number of International Laser Ranging Service (ILRS) stations and the Jason-2 satellite below the 100 ps-level [4]. These methods use non-coherent links. By exploiting laser-based coherent links, a network of two or more frequency references synchronized at sub-ps level can be established. A DLR laboratory demonstrator of coherent links is being developed to verify optical range, time transfer, and data transmission. The demonstrator consists of two terminals, running a bidirectional free-space optical link in the laboratory, with single-mode fiber coupling in the receivers at both sites. The optical carrier is modulated by a fast ranging sequence and a slower data stream. The coherent transceivers enable time-stamping received reference bits with sub-ps precision, enabling the exchange of measured time-of-arrival information between the paired satellites, which in turns enable two-way time transfer to retrieve clock offsets and perform inter-satellite ranging at sub-mm level [18]. Such optical transceivers could be integrated in existing optical communication terminals, such as those employed in the SpaceDataHighway operated in space since a few years in the framework of the Copernicus program to optically link LEO and GEO satellites. This integration is the focus of a DLR mission named COMPASSO, initiated in 2021, aiming at testing a coherent optical link for time/frequency transfer, ranging and data exchange between a terminal on the international space station and an optical ground station in Europe. The mission will hopefully pave the way to further validation missions aimed at testing autonomous accurate synchronization between satellites in higher orbits, and future utilization in GNSS constellations to augment navigation solution accuracy, system operability and robustness of operations.

8 Conclusion and Future Perspectives

This work focused on analysing how to accurately model relativistic effects to enable ps-accurate time transfer between satellites in MEO and LEO orbits. In Sects. 2 and 3 we have defined simultaneity and coordinate synchronization in the relativistic domain. A synchronization method based on a Two-Way Time Transfer was presented in Sect. 4. Then the relativistic effects to be taken into account for a time transfer with the necessary degree of accuracy have been studied, and Sect. 5 shows that the gravitational influence of other celestial bodies can be neglected and only the Earth geopotential has to be taken into account. The Earth’s geopotential needs to be characterised with a higher degree of accuracy than in current GNSS systems, considering harmonics beyond the \(J_2\) moment. For a correct relativistic modelling with the goal of picosecond-level synchronization accuracy, there is a need to keep the errors on orbits below a certain threshold. These thresholds have been calculated and presented in Sect. 6. It was discussed how a Two-Way Time Transfer picosecond synchronization is not only fundamentally feasible, but can also be implemented in practice.

A relativistic analysis is a fundamental step in the definition of the GNSS processing architecture, since in this framework synchronization offsets derive from fundamental characteristics of nature. The feasibility of relativistic synchronization with OISLs confirms the possibility of separating space and time in the error estimation process, resulting in a much higher level of synchronization across the constellation than is achievable in current architectures. This has the potential to greatly improve accurate orbit determination and consequently the navigation service for end users. Furthermore, the significant degree of autonomy in synchronization enabled by the proposed TWTT scheme has a potentially large impact on infrastructure and operational costs. The feasibility of an innovative concept of a fully autonomous ’space clock’ was also addressed. The idea of such a clock could be further investigated and has the potential to strongly impact the the field of time metrology, with the definition of a spatial time scale less affected by various terrestrial phenomena.