Abstract
A computational tool able to perform a fast analysis of hybrid rocket engines is presented, describing briefly the mathematical and physical models used. Validation of the code is also shown: 16 different static firing tests available in the open literature are used to compare measured operational parameters such as chamber pressure, thrust, and specific impulse with the code’s output. The purpose of the program is to perform rapid evaluation and assessment on a possible first design of hybrid rockets, without relying on computationally expensive simulations or onerous experimental tests. The validated program considers as benchmark and study case the design of a liquid-oxygen/paraffin hybrid rocket engine to be used as the upper stage of a small launcher derived from VEGA building blocks. A full-factorial parametric analysis is performed for both pressure-fed and pump-fed systems to find a configuration that delivers the equivalent total impulse of a VEGA-like launcher third and fourth stage as a first evaluation. This parametric analysis is also useful to highlight how the oxidizer injection system, the fuel grain design, and the nozzle features affect the performance of the rocket.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
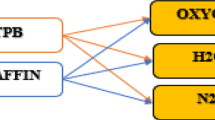
The distinctive feature of Hybrid Rocket Engines (HREs) is the physical separation of propellants, stored in different phases. Usually, the fuel is stored as a solid in the combustion chamber while the oxidizer is stored in a pressurized tank as a liquid or a gas, fed into the combustion chamber through a suitable injection system (Fig. 1) [21]. This particular method of propellant storage may entail some benefits with respect to both Liquid Rocket Engines (LREs) and Solid Rocket Motors (SRMs), such as safety, thrust modulation, and simplicity. The propellants used for hybrid propulsion are considered environmentally friendly and offer a remarkable specific impulse, generally in between the values achieved by liquid and solid propulsion [15].
Typical layout of a hybrid rocket [18]
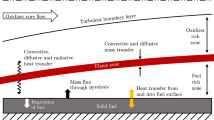
The main drawback of using HREs is that the conventional polymeric fuels used (also called pyrolyzing), such as Hydroxyl-Terminated PolyButadiene (HTPB) and High-Density PolyEthylene (HDPE), have a low regression rate that could lead to design problems when high thrust is required. With respect to SRMs, for HREs, delivering given thrust with a lower regression rate requires a larger burning surface or some kind of regression rate enhancement method, leading, respectively, to a worse volumetric loading factor or an increase in the system complexity. On the other hand, the class of fuels called liquefying presents a peculiar combustion phenomenology that allows to reach a much higher regression rate. Specifically, these fuels form a melted layer above the grain surface which, if some conditions are satisfied, can become hydrodynamically unstable because of the shear stress exerted by the core flow. The detachment and entrainment of fuel droplets from the unstable melted layer behave as a spray over the entire grain, yielding a higher mass transfer and ultimately increasing the regression rate [12, 13].
In the last decade, researches on liquefying fuels revived the interest of the scientific community which is currently focusing on paraffin-wax, a valuable candidate as a propellant thanks to its many benefits such as availability, safety, cost-effectiveness, and ballistic properties. Paraffin-based hybrid propulsion capabilities have been proven by many demonstrators, sounding rocket launches, and test facilities [8, 17]; therefore, there is a great interest in using HREs in place of the commonly employed solid-propellant and liquid-propellant engines for specific applications, like main engines in suborbital vehicles [3] or upper stages of small rockets [6].
The detailed design and analysis of a hybrid propulsion system rely mainly upon onerous numerical and experimental instruments such as Computational Fluid Dynamics (CFD) and test benches. Therefore, in an early phase of evaluation, the need for a tool capable of performing a quick evaluation of the performance of HREs is thus apparent. In this paper, a code based on zero-dimensional models is briefly presented with the aim to make the design of hybrid rockets easier and cheaper. The code is used in the framework of a full-factorial parametric analysis intended to design a third hybrid stage of a small launcher and to highlight the interactions between the performance delivered by the system and its operational parameters. The reference case is considered a HRE, candidate as substitute of a VEGA-like launcher third and fourth stage.
2 Code Description
This code is conceived as a tool able to quickly predict HRE performance using suitable 0-D models available in the open literature. It can be used in many ways, for example, to reproduce firing tests, to study the performance of a specific motor configuration, or to iterate on possible designs of defined hybrid rocket stage configurations, starting from some assigned high-level requirements.
2.1 Ballistic Model
The fuel grain shape is assumed single-port cylindrical to avoid complex and inefficient geometries, such as the multi-perforated grain, or complexity in the propellant grain production (e.g. complex 2D grains). Its dimensions, specifically external diameter \(D_\text {c}\) (equal to the chamber diameter), initial port diameter \(D_\text {p,0}\) and length \(L_\text {g}\), are treated as inputs. Once these parameters have been specified, the grain geometry and the total fuel mass available are uniquely fixed:
To take into account the highest possible total pressure losses due to the one-dimensional flow along the combustion chamber, a simple relation between the head-end pressure and chamber pressure is assumed [4]:
where \(\Gamma =\sqrt{\gamma \bigl (\frac{2}{\gamma +1}\bigr )^{\frac{\gamma +1}{\gamma -1}}}\) and \(J={A_\text {t}}/{A_\text {p}}\). The value of the throat-to-port area ratio at ignition is forced to be smaller than 0.5 to achieve a low Mach flow (at least \(M<0.3\)) in the combustion chamber. Fulfilling this condition guarantees small pressure losses and greater validity of a 0-D quasi-steady model.
Regression rate is assumed uniform along the motor axis, neglecting the contributions of the lateral ends. Its value is mainly dependent on the oxidizer mass flow rate injected and on the geometry of the grain, in the classical form:
where \(\dot{r}\) is expressed in \(\hbox {mm/s}\) and \(G_\text {ox}={\dot{m}_\text {ox}}/{A_\text {p}}\) in \({\text{kg}}/{{({\text{m}}}^{\text{2}}}{\text{s}})\) [11]. The fuel mass flow rate coming from the grain can, therefore, be evaluated as
Two alternative oxidizer feed systems are taken into account: i) a pump-fed system that provides a constant mass flow rate, and ii) a pressure-fed system, where the oxidizer mass flow rate varies over time, as it depends on the difference between the tank pressure \(P_\text {tk}\) and the chamber head-end pressure \(P_\text {h}\) by means of the hydraulic resistance Z in the oxidizer flow path:
In this case, the oxidizer flow is assumed to be both incompressible and turbulent [5]. Once the oxidizer and fuel mass flow rates are known at any time, the mixture ratio \({O}/{F}={\dot{m}_\text {ox}}/{\dot{m}_\text {fu}}\) and total mass flow rate \(\dot{m}_\text {tot}=\dot{m}_\text {ox}+\dot{m}_\text {fu}\) are computed. Assuming an isentropic expansion in the nozzle, the chamber pressure is obtained as
Propellant data on characteristic velocity and specific heat ratio are gathered from the NASA chemical equilibrium software CEA [10], assuming a frozen flow in the combustion chamber (this conservative assumption underestimates actual performance by 1–4% [4]). Data are interpolated with a shape-preserving piecewise cubic function of chamber pressure and oxidizer-to-fuel ratio:
Rocket efficiencies are taken into account assuming a \(c^*\)-efficiency (\(\eta _{c^*}\)) and a thrust efficiency (\(\eta _{C_F}\)). Performance parameters can be evaluated as follows:
Thrust coefficient is computed assuming a 1-D isentropic expansion to the exit pressure \(P_\text {e}\) with a constant heat ratio \(\gamma \) in a vacuum environment (\(P_\text {a}=0\)).
Throat erosion is taken into account correcting a reference value \(\dot{s}_\text {ref}\) through Bartz’s method:
where \(P_\text {ref}\) is 10 bar, \(D_\text {ref}\) is 50.8 mm and the reference erosion value \(\dot{s}_\text {ref}\) is chosen according to [2]. Since \(\dot{s}_\text {ref}\) is measured at stoichiometric conditions and the erosion rate model used does not consider mixture ratio variations, \(\dot{s}\) will be often overestimated in the computations, which can be considered as a conservative assumption.
Karabeyoglku et al. [11] rebuilding. Tests a 4L-05, b 4L-09, c 4P-01, and d 4P-03
These computations are performed at each time step, updating port and throat dimensions according to regression and erosion rate. Iterations stop once the available fuel mass is consumed or, for specific cases, when other conditions on the performance of the engine are met (for example once a target total impulse has been delivered). Engine dimensions are bounded by a maximum diameter \(D_{\text {max}}\). Structural mass and size of the different subsystems (combustion chamber, nozzle, oxidizer tank, pressurization system, feeding system and support structures) are taken into account according to [5, 9, 14, 20]. Performance, size and structural mass of the hybrid rocket can then be uniquely evaluated, for a specified feed system, from a set of 6 input parameters:
where \(L_\text {g}\), \(D_\text {p,0}\) and \(D_\text {c}\) define the geometrical dimensions of the grain, \(D_\text {t}\) and \(\varepsilon \) the nozzle, and \(\dot{m}_\text {ox,0}\) the initial oxidizer mass flow rate.
2.2 Code Validation
The capabilities of the code have been evaluated through the performance parameters rebuilding of 16 different static firing tests available in the open literature:
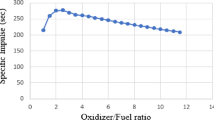
a Thrust and b specific impulse rebuilding from Lestrade et al. [16]
-
Karabeyoglu et al. [11] - Medium-scale motor burning gaseous oxygen/paraffin-wax. The aim of the research was to use large grains and mass fluxes (grain length is 1.148 m, while the oxidizer mass flux is between 100 and 1000 \({\text{kg}}/{{({\text{m}}}^{\text{2}}}{\text{s}})\) to investigate the effects of motor’s scale on operational parameters. The code’s chamber pressure plot, shown in Fig. 2, is in good agreement with the experimental data. Tests reproduced are 4L-05 (2a), 4L-09 (2b), 4P-01 (2c), and 4P-03 (2d).
-
Di Martino et al. [7] - Experimental test burning gaseous oxygen/paraffin-wax. This study was intended to assess the effects of the axial injection configuration on the regression rate. The average experimental thrust and pressure of the 200 N engine described in the research are compared with the values returned by the program. As shown in Tab. 1, the software output agrees well with the experimental data. The average error is 4.76 N on thrust and 0.46 bar on chamber pressure, with respective relative errors of 4.36% and 4.18%.
-
Paccagnella et al. [19] - Lab-scale experimental tests burning hydrogen peroxide/paraffin-wax. The distinctive feature of this experimental campaign is the long burning time (up to 80 seconds). The aim of the research was to assess the thermal resistance capabilities of a paraffin grain. Code’s results, shown in Fig. 3, are well in agreement with the experimental data. Rebuilding has been performed on tests A (3a), B (3b), and C (3c).
-
Lestrade et al. [16] - Lab-scale experiment burning nitrous oxide/paraffin-wax (reference test). This study was intended to assess the reliability of a 1-D code developed by the authors. Code’s results agree perfectly with the experimental data for chamber pressure (Fig. 3d), thrust (Fig. 4a), and specific impulse (Fig. 4b).
To summarize, every experimental test has been rebuilt with acceptable accuracy. Each test is characterized by different operational parameters such as propellants, grain dimensions, burning time, and average chamber pressure, ensuring the reliability of the code over a wide range of circumstances.
3 Parametric Analysis
The model is at last used to perform a full-factorial parametric analysis to study the effects of motor design on performance, in particular the interaction between fuel grain geometry, oxidizer feeding system, and throat diameter. The most performing configurations will then be evaluated for a first analysis of the possible substitution of a Vega-like launcher third and fourth stage with a HRE architecture, as study case. Due to the throttling capabilities of hybrid rocket engines, this stage is ideal to both propel the launcher during the final section of the ascent trajectory and perform the orbit insertion maneuvers, ideally replacing both the solid third stage Zefiro 9 (Z9) and the liquid fourth stage Attitude and Vernier Upper Module (AVUM) of the actual Vega launcher (data on performance, mass and dimensions of Z9 and AVUM are gathered from [1]).
Liquid oxygen/paraffin-wax (highly performing in terms of specific impulse) is chosen as propellant combination, assuming a 96% combustion efficiency and 98% nozzle efficiency (typical of this class of HRE in the literature [4]). According to [11], the coefficients a and n for the regression rate model in Eq. (4) are, respectively, 0.117 and 0.62, while the reference erosion rate \(\dot{s}_\text {ref}\) in Eq. (11) is 0.1 mm/s according to [2]. The program evaluates performance, structural mass and size of every configuration of the engine available, with input parameters in the range:
Each rocket configuration is required to deliver a 33000 kNs total impulse, which is approximately of the same order of magnitude of the combined total impulse delivered by Zefiro 9 and AVUM (in this case the grain’s external diameter is returned by the code as output so that the engine can host exactly the fuel needed to reach that target). This represents a very simplified assumption of the study without the need of more complex trajectory studies to derive high-level requirements for the HRE architecture. The maximum stage diameter is set to 1.9 m in the computations to respect the geometrical constraints of Vega. CEA data for the characteristic velocity of the propellant combination is shown in Fig. 5.
Two different oxidizer delivery systems are evaluated:
-
A pressure-fed injection system is coupled with an evaporated-propellant tank pressurization. In this configuration, the oxidizer mass flow rate is determined by the difference between tank and head-end pressure in Eq. (6). The value of the hydraulic resistance Z is chosen to get \(\dot{m}_\text {ox}=\dot{m}_\text {ox,0}\) at \(t=0\). The oxidizer tank pressure, set to \(p_\text {tk}=3.5p_\text {h,0}\) to have \(p_\text {tk}>1.2p_\text {h}\) at any time, is kept constant using the oxidizer itself at a gaseous state (evaporated thanks to a heater).
-
A pump-fed injection system is coupled with an evaporated non-propellant tank pressurization. In this configuration the oxidizer mass flow rate is kept constant and equal to \(\dot{m}_\text {ox,0}\) thanks to an electrically driven pump [5]. The oxidizer tank pressure, set to \(p_\text {tk}=4.5 \ \hbox {bar}\) to avoid pump cavitation, is kept constant using Helium, stored in a separate tank in a liquid state.
The specific impulse contour plots shown in Fig. 6 give insight into the relationship between fuel grain design, oxidizer mass flow rate and performance. In fact, the overall performance of a propulsion system in terms of specific impulse depends mainly on the mixture ratio which must preferably be as close as possible to the optimal value. In hybrid rockets, mixture ratio is determined entirely by the injection system (\(\dot{m}_\text {ox}\)) and by the grain design (\(L_\text {g}\) and \(D_\text {p}\)). Combining Eq. (2) and (4) in fact one can obtain
It is, therefore, clear how varying these three parameters the overall specific impulse of the rocket can be affected.
Another performance index that must be looked into is thrust, which is essential since it affects gravitational losses (not taken into account by the code) and mission constraints. As shown in Fig. 7a, thrust is entirely affected by the oxidizer feeding system. Although burning surface variations affect its value, their effect is negligible if compared to \(\dot{m}_\text {ox}.\)
At last, it is important to assess how the design of the rocket influences its propellant and structural mass. If a lower specific impulse is achieved, more propellant is needed to reach the required total impulse which, as a consequence, leads to a larger tank mass and pressurizing gas mass. At the same time though, increasing the specific impulse by means of chamber pressure is related to a higher structural mass since a larger wall thickness is required. Therefore, there must be an optimal configuration that guarantees the lowest propellant plus structural mass needed to deliver the total impulse required. However, it must be underlined that it is preferable to modify the specific impulse through the mixture ratio, since its influence (if compared to pressure) is much more relevant. The effect of chamber pressure on the structural mass can be seen in Fig. 7b. It is clear how a higher mass flow rate or a smaller throat diameter, related to a larger chamber pressure, leads to a weight increase.
In the end, once the thrust range needed to satisfy the mission’s constraints and to guarantee low gravitational losses is known (basically fixing \(\dot{m}_\text {ox,0}\)), the optimal hybrid stage (in terms of total impulse delivered) is the one that guarantees the highest specific impulse (driven by the grain design parameters \(L_\text {g}\) and \(D_\text {p,0}\)) with the lowest structural mass possible (associated with the nozzle design \(\varepsilon \) and, mostly, \(D_\text {t}\)). As previously mentioned, a full-factorial parametric analysis has been performed for both a pressure-fed system and a pump-fed system to identify possible architecture candidates. Results are shown in Tab. 2.
Both configurations seem promising. Since the oxidizer tank pressure is not related to chamber pressure in a pump-fed system, a much higher thrust and specific impulse can be achieved at the cost of complexity and stage length. A pressure-fed system on the other hand, despite allowing for a much simpler design, is forced to use a lower chamber pressure (through a lower oxidizer mass flow rate and larger throat diameter) to contain the structural mass, affecting both thrust and specific impulse. If compared to the Vega layout implementing the solid rocket Zefiro 9 and liquid engine AVUM as the third and fourth stage, the hybrid configurations save, respectively, 790 (6%) and 1320 (10%) kg of propellant and structural mass to deliver a total impulse of the same order of magnitude. The specific mission requirements will then affect the resulting increase in payload mass. Besides that, a hybrid third stage performing both the last section of the ascent trajectory and the orbit insertion maneuvers is related to a much lower system complexity. It is worth mentioning, anyhow, that this first assessment does not consider a deepened analysis of the whole achievable missions for the VEGA launch vehicle (multiple re-ignition for multi-payload configuration). Moreover, additional details and investigations on the oxidizer feeding system could improve the results. At last, it must be underlined that the hybrid stage configurations display a much greater length than Z9 and AVUM (16-18.5 m against about 6 m for the combined solid and liquid stages), outside the canonical length-to-diameter ratios commonly used for this class of launchers. This feature, caused by the employment of a liquid tank that leads to an increase in the overall length of the rocket especially when large propellant volumes are required, can be considered a downside of the HRE architectures resulting from the analysis. To limit this quantity, further constraints need to be introduced and their effect on the overall performance must be evaluated.
4 Conclusion
A fast computational approach able to evaluate hybrid rocket engines performance is presented, briefly discussing the main characteristics of the ballistic model implemented. The model can aid the design of hybrid rockets. Validation of the approach is provided through the rebuilding of chamber pressure, thrust and specific impulse of 16 different static firing tests from the literature. Experimental data and code output are in close agreement, ensuring its reliability over a wide range of operational parameters. At last, a full-factorial parametric analysis has been employed to identify the relationships between performance, grain design, nozzle features, and injection system, and to perform as case study an analysis of a HRE architecture of a VEGA-like launcher third stage. The hybrid configuration, thanks to its throttling capabilities, is required to perform both the final section of the ascent trajectory and the orbit insertion maneuvers, ideally replacing both the solid third stage Zefiro 9 and liquid fourth stage AVUM of the Vega launcher. The optimal designs found provide a total impulse of the same order of magnitude of Z9 and AVUM combined, with some potential saving of mass for both the pressure-fed or pump-fed system from a first analysis. Although the effect on performance of a constrained overall stage length as well as detailed aspects of the HRE candidate architectures need a deepened analysis, the program has proven itself to be a powerful instrument for the analysis and design of hybrid rockets, returning satisfactory preliminary results. Despite its good predictive capabilities, this software has plenty of room for improvements, in particular: (i) the program assumes a single-port cylindrical grain, and its versatility could be improved if it could handle any shape; (ii) predictive capabilities can be further improved with more accurate regression rate and erosion rate models; (iii) a transient model could be used instead of a quasi-steady model; (iv) instead of using interpolated propellant data, the CEA software could be used as a subroutine in the code to obtain them during runtime; v) the effect of mixture ratio on total pressure losses along the combustion chamber should be taken into account to get more accurate predictions of the HRE internal ballistics.
Change history
15 September 2021
A Correction to this paper has been published: https://doi.org/10.1007/s42496-021-00097-z
Abbreviations
- \( {C}_{F} \) :
-
Thrust coefficient
- J :
-
Throat-to-port area ratio
- M :
-
Mach number
- n :
-
Mass flux coefficient
- O/F :
-
Mixture ratio
- \({\gamma} \) :
-
Specific heat ratio
- \({\Gamma}\) :
-
Modified specific heat ratio
- \({\varepsilon} \) :
-
Nozzle area ratio
- \({\eta} \) :
-
Efficiency
- a :
-
Regression rate factor \(\text{mm}/\text{s} \cdot {{({\text{m}}}^2}{\text{s}}/{\text{kg}})^n\)
- A :
-
Area \({{\text{m}}^2}\)
- \({c^*}\) :
-
Characteristic velocity \(\text{m}/\text{s}\)
- D :
-
Diameter \({\mathrm {m}}\)
- F :
-
Thrust \({\mathrm {N}}\)
- G :
-
Mass flux \({\text{kg}}/{{({\text{m}}}^{\text{2}}}{\text{s}})\)
- \({I_{\text{sp}}}\) :
-
Specific impulse \({\text {s}}\)
- L :
-
Length \({\text {m}}\)
- m :
-
Mass \({\text {kg}}\)
- p :
-
Pressure \({\text {bar}}\)
- t :
-
Time \({\text {s}}\)
- Z :
-
Hydraulic resistance \({\text{bar}/\text{(kg}/\text{s}})^2\)
- \(\rho \) :
-
Density \({\text{kg}/\text{m}^{3}}\)
- \({\dot{m}}\) :
-
Mass flow rate \({\mathrm {kg/s}}\)
- \({\dot{r}}\) :
-
Regression rate \({\mathrm {mm/s}}\)
- \({\dot{s}}\) :
-
Erosion rate \({\mathrm {mm/s}}\)
- \({\text {a}}\) :
-
Ambient
- \({\text {c}}\) :
-
Chamber
- \({\text {code}}\) :
-
Code output
- \({\text {e}}\) :
-
Exit
- \({\text {exp}}\) :
-
Experimental
- \({\text {fu}}\) :
-
Fuel
- \({\text {g}}\) :
-
Grain
- \({\text {h}}\) :
-
Head
- \({\text {max}}\) :
-
Maximum
- \({\text {ox}}\) :
-
Oxidizer
- \({\text {p}}\) :
-
Port
- \({\text {ref}}\) :
-
Reference
- \({\text {t}}\) :
-
Throat
- \({\text {tk}}\) :
-
Tank
- \({\text {tot}}\) :
-
Total
- \({\text {0}}\) :
-
Initial
- AVUM:
-
Attitude and Vernier Upper Module
- CEA:
-
Chemical Equilibrim with Applications
- CFD:
-
Computational Fluid Dynamic
- HDPE:
-
High-Density PolyEthylene
- HRE:
-
Hybrid Rocket Engine
- HTPB:
-
Hydroxyl-Terminated PolyButadiene
- LRE:
-
Liquid Rocket Engine
- SRM:
-
Solid Rocket Motor
- Z9:
-
Zefiro 9
References
Avio online webpage. https://avio.com. Accessed 5 Mar 2021
Bianchi, D., Nasuti, F.: Numerical analysis of nozzle material thermochemical erosion in hybrid rocket engines. J. Propuls. Power 29(3), 547–558 (2013). https://doi.org/10.2514/1.B34813
Cai, G., Zhu, H., Rao, D., Tian, H.: Optimal design of hybrid rocket motor powered vehicle for suborbital flight. Aerosp. Sci. Technol. 25(1), 114–124 (2013). https://doi.org/10.1016/j.ast.2011.12.014
Casalino, L., Masseni, F., Pastrone, D.: Uncertainty analysis and robust design for a hybrid rocket upper stage. J. Spacecr. Rockets 56(5), 1424–1431 (2019). https://doi.org/10.2514/1.A34422
Casalino, L., Masseni, F., Pastrone, D.: Viability of an electrically driven pump-fed hybrid rocket for small launcher upper stages. Aerospace 6(3), 36 (2019). https://doi.org/10.3390/aerospace6030036
Casalino, L., Pastrone, D.: A straightforward approach for robust design of hybrid rocket engine upper stage. In: 51st AIAA/SAE/ASEE Joint Propulsion Conference, p. 4202. AIAA, Orlando, FL (2015). https://doi.org/10.2514/6.2015-4202
Di Martino, G.D., Mungiguerra, S., Carmicino, C., Savino, R., Cardillo, D., Battista, F., Invigorito, M., Elia, G.: Two-hundred-newton laboratory-scale hybrid rocket testing for paraffin fuel-performance characterization. J. Propuls. Power 35(1), 224–235 (2019). https://doi.org/10.2514/1.B37017
Faenza, M., Boiron, A.J., Haemmerli, B., Verberne, C.J.: The nammo nucleus launch: Norwegian hybrid sounding rocket over 100km. In: AIAA Propulsion and Energy 2019 Forum, p. 4049. AIAA, Indianapolis, IN (2019). https://doi.org/10.2514/6.2019-4049
Frank, C.P., Pinon-Fischer, O.J., Mavris, D.N., Tyl, C.M.: Design methodology for the performance, weight, and economic assessment of chemical rocket engines. J. Aerosp. Eng. 300(1), 04016071 (2017). https://doi.org/10.1061/(ASCE)AS.1943-5525.0000668
Gordon, S., McBride, B.J.: Computer program for calculation of complex chemical equilibrium compositions and applications. (1994)
Karabeyoglu, A., Zilliac, G., Cantwell, B.J., DeZilwa, S., Castellucci, P.: Scale-up tests of high regression rate paraffin-based hybrid rocket fuels. J. Propuls. Power 20(6), 1037–1045 (2004). https://doi.org/10.2514/1.3340
Karabeyoglu, M.A., Altman, D., Cantwell, B.J.: Combustion of liquefying hybrid propellants: Part 1, general theory. J. Propuls. Power 18(3), 610–620 (2002). https://doi.org/10.2514/2.5975
Karabeyoglu, M.A., Cantwell, B.J.: Combustion of liquefying hybrid propellants: Part 2, stability of liquid films. J. Propuls. Power 18(3), 621–630 (2002). https://doi.org/10.2514/2.5976
Larson, W.J., Henry, G.N., Humble, R.W.: Space propulsion analysis and design. McGraw-Hill, New York (1995)
Leccese, G., Cavallini, E., Pizzarelli, M.: State of art and current challenges of the paraffin-based hybrid rocket technology. In: AIAA Propulsion and Energy 2019 Forum, p. 4010. AIAA, Indianapolis, IN (2019). https://doi.org/10.2514/6.2019-4010
Lestrade, J.Y., Anthoine, J., Lavergne, G.: Liquefying fuel regression rate modeling in hybrid propulsion. Aerosp. Sci. Technol. 4(2), 80–87 (2015). https://doi.org/10.1016/j.ast.2014.11.015
Messinger, T., Hill, C., Quinn, D., Stannard, D., Doerksen, G., Johansen, C.T.: Development and test flight of the atlantis i nitrous oxide/paraffin-based hybrid rocket. In: AIAA Propulsion and Energy 2019 Forum, p. 4011. AIAA, Indianapolis, IN (2019). https://doi.org/10.2514/6.2019-4011
Paccagnella, E., Barato, F., Gelain, R., Pavarin, D.: Cfd simulations of self-pressurized nitrous oxide hybrid rocket motors. In: 2018 Joint Propulsion Conference, p. 4534. AIAA, Cincinnati, Ohio (2018). https://doi.org/10.2514/6.2018-4534
Paccagnella, E., Santi, M., Ruffin, A., Barato, F., Pavarin, D., Misté, G.A., Venturelli, G., Bellomo, N.: Testing of a long-burning-time paraffin-based hybrid rocket motor. J. Propuls. Power 35(2), 432–442 (2019). https://doi.org/10.2514/1.B37144
Saunders, D.J.: A method of calculating the weight and dimensions of a turbo pump for rocket propellants. Tech. rep, Royal Aircraft Establishment Farnborough (UK) (1949)
Sutton, G.P., Biblarz, O.: Rocket Propulsion Elements. John Wiley and Sons Inc, New York (2001)
Acknowledgements
This work has been carried out within a master’s thesis and is part of a wider research framework on hybrid rocket propulsion, funded by the Italian Space Agency under contract ASI N. 2019-5-I.0. On behalf of all authors, the corresponding author states that there is no conflict of interest.
Funding
Open access funding provided by Università degli Studi di Roma La Sapienza within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: Assignment of affiliations was not correct.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zolla, P.M., Migliorino, M.T., Bianchi, D. et al. A Computational Tool for the Design of Hybrid Rockets. Aerotec. Missili Spaz. 100, 253–262 (2021). https://doi.org/10.1007/s42496-021-00085-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42496-021-00085-3