1 Introduction

Applications for user-generated spatial web content have steadily grown ever since they were introduced as Volunteered Geographic Information (VGI) by Goodchild (2007). They support a wide range of services like environmental monitoring (Young et al. 2019), movement analysis (Boss et al. 2018), and disaster management (Crooks et al. 2013). Focusing on urban environments, examples of VGI applications are traffic monitoring (Das and Purves 2020), route choice behavior (Scott et al. 2021), decision-making (Giuffrida et al. 2019), and city perception (Bahrehdar et al. 2020).

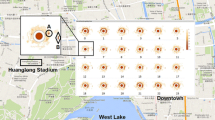
VGI data are often generated as point data and represent a sample of the underlying population of interest. The combination of these two characteristic features of VGI often causes problems for data exploration and interpretation when urban data are presented on maps. While the representativeness, and therefore the fitness for use of a VGI data sample in a particular application has to be assessed based on the data itself (Senaratne et al. 2017; Zhang and Zhu 2018), even representative VGI data could lead to overcrowded point clouds in very populated places when a large amount of points is georeferenced to a small area. For example, in the recent work of Knura et al. (2021), the information on moving and parked bicycles in the city of Dresden was retrieved utilizing an object detection algorithm on social media images. While outside of the central city areas, one can easily identify each point feature that represents the location of the photo on which bicycles were detected, this is not possible in the central city areas, where point symbolization significantly overlaps (Fig. 1). This effect, known as display clutter (Rosenholtz et al. 2007), makes it hard to read and impossible to visually count the number of points on a map.

Fig. 1
figure 1

Location of Flickr images on which bicycles were detected (quantitative aggregation is included through color; overlapping circles in the city center significantly affect data exploration and readability of the map)

Full size image

A potential solution to eliminate display clutter is to replace the individual point symbols with a representation for the point density at each location. For VGI applications in urban environments, cumulative and statistical values for distinguished areas of interest are often more important than the individual elements of the dataset (Hasan and Ukkusuri 2014). Therefore, it can be useful to visualize point datasets by directly linking the point density information to urban geometry objects, such as roads or pedestrian zones, instead of visualizing them as an overlying layer. The most straightforward method would be to relate each point to the nearest geometry object and count all points per object. A major drawback of this approach is that local clusters could disappear when assigned to larger objects, e.g., long roads or large squares. In this paper, we introduce new visualization approaches based on relating the density information of a point dataset to the underlying geometry objects by dividing roads and pedestrian zones into smaller units using point density information. Our intention is to:

  • resolve the problem of overlay between points and geometry layers to identify underlying geometry features more easily

  • resolve the problem of point counting and density range identification in highly cluttered areas

We start with an overview of point density visualization methods in Sect. 2. In Sect. 3, we introduce our new methods of relating density information to urban geometry. In Sect. 4, we apply these methods to the bicycle detection dataset, discuss the results in Sect. 5, and make a conclusion in Sect. 6.

2 Density Visualization

Considering that VGI often contains large numbers of point data, there is a high likelihood of visualizing overcrowded or dense point clouds, which bears certain drawbacks for interpretation (Li et al. 2014). The exploration of the dataset can be demanding, even when varying sizes or colors of points are used as a way of aggregation and abstraction (Opach et al. 2019). The cartographic solution to overcome display clutter is point generalization, where different operations like selection and displacement can be performed to reduce clutter and the overall number of points on the map (Slocum et al. 2009). If the point density of a certain area or the whole map is of interest, the generalization process should be guided by respective constraints that preserve local and global density characteristics (Knura and Schiewe 2022).

While the generalization operation of aggregation also reduces the number of points on the map Burigat and Chittaro (2008), it could be used in the same way to represent quantitative data—and therefore also point density—through point symbolization (Brewer and Campbell 1998). An approach that tackled the drawback of overlapping VGI points in this way was by arranging micro-diagrams in a regular grid on a map (Gröbe and Burghardt 2020). This approach achieved high diagram readability and a high-level overview of the data spread because of avoided overlaps. However, the interpretation of the data in relation to the basemap still stayed highly dependent on the current zoom level and estimating where the exact grid boundaries are. The same can be said for word clouds, which were recognized in visualizing spatial information as a promising approach that contains text georeferenced to a point location (Bertone and Burghardt 2017). This can be used in urban planning to better understand the common usage of urban areas, e.g., by visualizing the locations of keywords contained in georeferenced social media data (Dunkel 2015) or diaries of activities in urban areas (Li and Zhou 2017). Here, the keyword’s font size communicates the occurrence of that word on a specific location or urban area. However, it can still bring ambiguity in interpretation because it is not intuitively clear how large the buffer zones are to which the keywords relate. Additionally, the basemap is again visually covered by the layer that contains keywords visualizations.

A common, but completely different example of density visualization are heatmaps as a type of isarithmic maps that use color to represent zones of same values. In their most simple form, point density is measured by a form of zoning and counting the number of points in each zone, while kernel density procedures are the most common way to create heatmaps (De Smith et al. 2007). On standard visualizations which use heatmaps, the layer displaying the densities is usually an overlay above the basemap, e.g., in Fisher (2007). These overlays are semi- or non-transparent layers which can easily decrease the overall map readability and make the process of relating the density information to urban geometry more difficult and an exploratory process. A juxtaposed visualization of basemap and heatmap makes it harder to precisely identify units of urban geometry, because it is first necessary to identify a density area of interest, and then visually relate the information conveyed by it to a street, square, or park in the adjacent map (Lobo et al. 2015). Manually relating the density information to urban geometry can be done, e.g., by turning on and off the density visualization layer in an interactive map (especially in the case of non-transparent density visualization), or by trying to identify the geometry features on the basemap through a semi-transparent density visualization layer. Generally, these tasks can easily become time-consuming and require an increased cognitive effort while suffering from problems of split attention.

Some solutions for visual exploration of densities related to urban areas are designed as interactive dashboards. Already Hotta and Hagiwara (2009) recognized the importance of the efforts to provide interactive maps. In their work, the authors focused on developing a method for a faster generation of heatmaps from big data. Recently, Zhu et al. (2019) designed a dashboard that displays additional information in side views upon selecting an area or a point on the map. Similar tasks allow also Li et al. (2018) in their dashboard with the difference that it uses semi-transparent points that are classified by colors.

3 Relating Points to Geometry Features

Considering the drawbacks of existing approaches—such as overlapping of layers, dense point or word clutters, or spatial imprecision—we have identified the need to develop a density visualization approach that would ease and allow more precise identification of basemap features in relation to the density visualization. In this section, we present density visualization approaches that we developed with the intention of minimizing these drawbacks.

Because VGI data are often obtained within urban environments, our aim is to relate point density information to the existing geometry in urban areas—to which we further refer as urban geometry. For convenience and simplification purposes, the urban geometry on which we focus in this paper are roads, squares, and other pedestrian zones. We therefore only use line objects of roads and polygon objects of squares and pedestrian zones. We are aware that for many VGI applications, this subset of urban geometry is not sufficient, but the approaches shown in this section can be expanded to more heterogeneous datasets. As a second simplification, we removed all road parts that spatially overlap with polygons of squares and pedestrian zones to guarantee a consistent visualization.

We start this section with a short introduction into kernel density estimation, which provides an overlaying estimation of point density at each location. We then present a contrary concept of density visualization by relating each point to its nearest urban geometry object. In the last part of this section, we introduce two new approaches that extend the first two density visualizations.

3.1 Deriving Point Density Surfaces Using Kernel Density Estimation

Kernel density estimation (KDE) is an important method to visualize the spatial pattern of point events over a given location and is applied to numerous fields, such as criminology (Hart and Zandbergen 2014), epidemiology (Shi et al. 2021), or ecology (Péron 2019). The idea of KDE is to estimate densities of specified features at a location using a window (i.e., kernel) of its surrounding area with a specified bandwidth or radius and can be determined as (adapted from Silverman (1986)):

$$\begin{aligned} {\hat{f}} \left( x,y \right) = \frac{1}{nh^{2}}\sum _{i = 1}^{n}K\left( \frac{d_{i,(x,y)}}{h} \right) \, , \end{aligned}$$
(1)

where \(\hat{f}\) is the estimated density at a location with spatial coordinates (x, y), n is the total number of points under concern (e.g., images with bicycle detections), h is the kernel bandwidth (i.e., the search radius from (x, y)), \(d_{\mathrm{i,(x,y)}}\) is the distance between location i (where i are the number of points under concern) and location (x, y), and K is the kernel shape, a function used to measure the distance decay effect of the points. While there are several other kernel shape functions available—such as Gaussian, uniform, triangle, and Epanechnikov—we used a weighted quartic function to create heatmap zones in this paper. This function can be represented as:

$$\begin{aligned} K\left( \frac{d}{h} \right) = {\left\{ \begin{array}{ll} W \tfrac{15}{16}\left( 1-d^{2} \right) ^{2}\ &{} \quad \text {if} \quad 0< \left( \tfrac{d}{h} \right) \le 1 \, , \\ \quad 0 &{} \quad \text {otherwise} \, , \end{array}\right. } \end{aligned}$$
(2)

where W is the weight, e.g., the number of detected bicycles on the image. It is generally accepted that the selection of the kernel shape is not critical, while the bandwidth has a major impact on the KDE’s outcome (Shi 2010). A small bandwidth maintains local patterns better, while a larger bandwidth provides a smoother estimate.

3.2 Classifying Geometry Features Based on the Number of Associated Points

One solution to overcome the issues of overlying point and density information is to directly classify the urban geometry features according to the number of points in their immediate neighborhood. Therefore, we first created a model that assigns each georeferenced point to the nearest urban geometry feature as shown in Fig. 2. If not already located within a polygon feature, each point is assigned to the local Voronoi area, which we created for each line using a create-points-on-line operation and joining the respective areas for each polyline. Then, each feature was classified based on the number of points assigned to it. This approach resolves the issue of overlaps and overlying layers and allows to easily identify the numerical range of assigned points for the different urban geometry features. As it can be noted on the schematic representation of this approach (Fig. 2), the model classifies geometry features in their full geometry, no matter how large the polygon or how long the polyline is.

Fig. 2
figure 2

Workflow for classification of geometry features by assigning points to the nearest geometry object

Full size image

3.3 Dividing Geometry Features Into Units Based on Point Density Information

While the aforementioned approach uses the whole geometry of an object, more elaborate approaches should account for the actual spatial spread of point density within the objects. Therefore, we created two GIS models which first relate point detections to density polygons and then use these polygons to divide urban geometry features into smaller units. With this approach, the models provide a better overview of the exact point density spread over longer roads or larger squares and pedestrian zones.

3.3.1 Intersecting Point Clouds with Urban Geometry Using a Grid

In the first model, the whole urban area is first divided into smaller units using a grid, and then the number of points in each grid cell is counted. In the next step, the grid cells are classified according to the number of points within them, following a manually defined classification. Then, adjacent cells within the same classes are merged. After this, exterior boundaries of the newly created areas are used to divide the geometry features into smaller units and, finally, to visualize the classified urban geometry units. Figure 3 schematically visualizes this workflow. Compared to the approach in Sect. 3.2, geometry features are divided into subgeometry units of lower and higher point density and can be classified according to the underlying grid cells classes. The intermediate classification of the grid cells has an influence on the actual shape of the joined grid cells, and therefore the result of the process. For that reason, it is meaningful to choose a classification that is appropriate for used dataset, user task, and intended visualization purpose.

Fig. 3
figure 3

Workflow for subdivision and classification of geometry features using grid cells

Full size image

3.3.2 Intersecting Point Clouds with Basemap Geometry Using Contour Lines of a Heatmap

In the second model, estimated point density information is derived from a heatmap to be assigned to the urban geometry features. First, a heatmap is created from the input point data as described in Sect. 3.1. Based on the heatmap, respective contour lines that follow the edges of zones with different density values are generated. These contour lines are then intersected with the urban geometry features in the same way as in the grid-based approach. The result is, again, subdivided urban geometry units, which are then classified according to the corresponding heatmap area—i.e., based on the values which are separated through the contour lines. The workflow is shown in Fig. 4. The defined distance between the contour lines influences the actual shape of the resulting contour lines—and, therefore, the derived geometry objects—and should be chosen according to the used dataset, user task, and intended visualization purpose.

Fig. 4
figure 4

Workflow for subdivision and classification of geometry features using contour lines derived from a heatmap

Full size image

4 Application of Visualization Methods

In this section, we apply the density visualization approaches described in Sect. 3 to compare them with the common heatmap and pointmap approaches. We implemented the approaches as QGIS models and created the respective maps using VGI data from the social media platform Flickr and geometry data from the City of Dresden and Open Street Map (OSM). In the following subsections, we first give a short introduction to the data and parameter settings used for creating the maps before we present the respective visualizations that resulted from the developed GIS models.

4.1 Data and Visualization Settings

VGI data As reference VGI data, we use the dataset from Knura et al. (2021), where images containing bicycle detections in the area of Dresden, Germany, were retrieved from the Flickr YFCC100M dataset. The latter dataset was published under Creative Commons and contains 100 million user posts geolocated all over the world as photos or videos and related textual descriptions, covering the time span between 2004 and 2014. From this dataset, Knura et al. (2021) selected all posts georeferenced in Dresden and containing images and ran on them an object detection algorithm to identify bicycles. The detected bicycles were then classified as either stationary or moving and the case study showed that the geographical spread of the retrieved dataset over the city is typical for VGI data—as previously shown by (Jiang et al. 2016)—and can be seen as in-the-wild sensing of the city (Zhu et al. 2013). However, for this article, we do not differentiate between moving and stationary bicycles but use all images with bicycle detections as shown in Fig. 1.

Urban geometry data The urban geometry features that we work with in this paper are roads and pedestrian zones. The vector data of the road network in Dresden have been made openly available by the City of Dresden (State Capital Dresden 2021). In the dataset, roads are modeled as single lines that represent road lanes of both driving directions, as well as sidewalks. The dataset also includes several road categories that are not applicable for bicycles, such as railroad lines, so we removed these entries before running the models. For pedestrian zones in Dresden that include squares and other pedestrian areas, we used OSM polygons because these were not included in the former Dresden dataset.

Visualization settings To ensure comparability of results between different approaches, we used comparable parameter settings for the operational steps within our models. Table 1 provides an overview of the parameters used. Before deciding on these specific values, we analyzed the effects of various parameter combinations and decided on the latter because they provided a suitable visual representation of our VGI dataset considering the map scales in this paper. We based the parameters in each approach on the value of 50 m because lower values resulted in patterns that were too small to be well visible on maps showing wider Altstadt—the city center of Dresden—and because too many points would not be assigned to any urban feature (e.g., a significant number of grid cells smaller than 50 m \(\times\) 50 m did not intersect any road or square object in the grid-based approach). Greater values resulted in visualizations where the point hotspots were spreading over large areas (e.g., over whole squares), providing an overly generalized result. As the roads are modeled as polylines, to make them comparable with pedestrian zones that are polygons, we used average road width of 10 m in the process of normalizing density values.

To make the visualizations reflect the results of the models presented in this paper in a meaningful way, we implemented a classification that considers the characteristics of the social media dataset used. In the dataset, more than half of images with bicycle detections contain only one bicycle, while merely 6.7 percent contain more than five (Knura et al. 2021). Considering also that in the latter paper most of the 100 m \(\times\) 100 m grid cells contained up to 35 parked bicycle detections on photos posted within the cells, we expected a similar pattern for bicycle detections in general. Therefore, we decided to use an incremental classification that starts with five bicycle detections and doubles the value of the previous class in each next class. That way, we defined seven classes of bicycle detections from posted photos: 0, 1–5, 6–15, 16–35, 36–75, 76–155, and more than 155 bicycles; which resulted in a good distinction between urban geometry units in different classes. This classification visually distinguishes well the classes with a smaller, middle, and higher number of points. A common classification on all maps helped to compare the results of different approaches throughout the maps. All visualizations were created using QGIS Desktop, version 3.16.1 Hannover.

Table 1 Parameter values used for implementing visualization approaches
Full size table

4.2 Visualizations

4.2.1 Pointmap and Heatmap

Compared to the pointmap, a heatmap could provide more clarity in areas where numerous points overlap. For example, by eyeing a point clutter on a pointmap, only points at the top can be interpreted unambiguously, while the quality and quantity of underlying points are largely occluded (Fig. 1)—which negatively affects the overall readability of the map. In contrast, a heatmap like on Fig. 5, which was created using the Heatmap (Kernel Density Estimation) tool in QGIS, provides the cumulative point density estimation for each map pixel, so there is no cluttering and overlapping of points. Still, the density visualization is here as well a separate layer that overlays geometry features, significantly occluding parts of the layers below it. Because of the overlay, identifying urban geometry features below the areas that would display probability of very high density would, due to much darker shades, requires a comparison with a map that is not occluded and, therefore, would require also a higher cognitive effort. As it can be seen in Fig. 5, it is easy to find hotspots where images with bicycle detections are expected, but the readability and contrast of the underlying layers are significantly reduced.

Fig. 5
figure 5

Heatmap showing interpolated bicycle density information based on bicycle detections on photos posted on Flickr

Full size image

4.2.2 Density-Geometry Map Using Nearest Neighbor Relation

One of the possible solutions to relate points to urban geometry—a straightforward approach where each point is assigned to the nearest or underlying urban geometry object—was described in Sect. 3.2. The implementation of this approach is presented in Fig. 6. The map shows urban geometry objects classified based on the number of detected bicycles located on or in close proximity of the object. A map created using this approach allows the user to easily identify roads and pedestrian zones where a high number of point features were located (in this case, image posts with bicycle detections). For example, there are more than ten road segments with more than 75 bicycle detections from images. Among squares, three with the highest values are classified into the middle class of 36–75 bicycle detections. However, in the case of larger pedestrian zones (like the one that is a combination of the Neumarkt and An der Frauenkirche squares), or elongated ones (like Brühlsche Terrasse that is around 300 m long), classifying the whole object into one single class seems too general for specific purposes, providing too little details about the spatial pattern spread.

Fig. 6
figure 6

Points of photos with bicycle detections related to original urban geometry (without further subdivision to smaller units)

Full size image

4.2.3 Density-Geometry Map Using a Grid

Figure 7 visualizes the result of implementing the grid-based approach (Sect. 3.3.1). Large polygons and long roads are here divided into smaller, classified subgeometry units. The underlying grid structure is visible on most of the polygons. This differentiation reveals a unique pattern for each of the three largest squares in the center of the map. None of them has an evenly spread point distribution. In the North, both Schlossplatz and Neumarkt and An der Frauenkirche (considered together as one larger pedestrian zone) have most of the photos with bicycle detections in their north-western part, while Altmarkt in the central part of the map has the majority in its center. All the more, Brühlsche Terrasse is here divided into six zones, while in Fig. 6, it is one. In the same fashion, more details can also be identified on roads because smaller road sections at which the photos with bicycle detections occurred are now highlighted instead of having the whole original road segment classified in one class. This effect is nicely visible on most of the roads, e.g., on Lennéstrasse in the lower right corner.

Fig. 7
figure 7

Subdivision of streets, roads, and pedestrian zones based on their intersection with classified grid cells

Full size image

4.2.4 Density-Geometry Map Using a Heatmap

As a result of applying the approach that subdivides the geometry objects based on heatmap contour lines (Sect. 3.3.2), there are much fewer subgeometry units classified into the class of zero-values than in the grid-based approach, which can be observed in Fig. 8. While this is the consequence of assigning the heatmap density estimation values to the respective subgeometry units, small patterns of local extreme values are less visible and highlighted here. Besides that, within squares, very much the same patterns as in the grid-based approach appear, but here have rounded shapes. For example, at Altmarkt, in the center of the map, two hot spots within the square are visible, and it can be identified that the majority of image posts with bicycle detections should appear at the upper center of the square. In comparison to the grid-based approach, on linear objects, this visualization possibly provides fewer details by differentiating a lower number of segments. The difference becomes even more obvious on the shorter streets southern of Altmarkt. These geometry units largely kept their original length here but were classified differently than in the baseline-based approach. In general, this approach provides a very smooth visual appearance of density zones and provides a more accurate precision representation in respect to the uncertainties of geocoding and localization in VGI, but with the cost of eliminating potentially critical micro-locations.

Fig. 8
figure 8

Subdivision of streets, roads, and pedestrian zones based on intersection with contour lines derived from the heatmap

Full size image

5 Discussion

5.1 Resolving the Problem of Density Information as an Overlying Layer

Compared to the map with point clouds in Fig. 1, maps in Figs.  5, 6, 7, and 8 all provide a density overview of points with less display clutter and therefore much higher readability of the map. Still, there is another major difference between the heatmap in Fig. 5 and the following three maps: The surfaces of the density estimation are on the heatmap noticeably overlaying the basemap and urban geometry, making it rather inconvenient to relate spatial patterns of point density to exact local infrastructure. A possible method to solve this problem is to lower the opacity of the density estimation layer.

While this allows establishing a relation between the density pattern and the underlying layers, significantly lowering the opacity also results in a lower contrast between the point density estimation surfaces and underlying layers, which again decreases the readability of the density values. The maps in Figs. 6, 7, and 8 address this problem by relating the point density information directly to the urban geometry features. These features can, as a result, then be clearly and quickly identified as they directly provide the information about the (estimated) number of points—i.e., georeferenced images with bicycles detections—related to each urban geometry object. Visualizing an overlying layer with point density information above the urban geometry layer and relating the point density information between layers is, in this case, no longer needed.

Furthermore, heatmaps still require a visual exploration, while our methods allow also other ways of handling the data because the density-related information becomes an attribute appended to the geometry features dataset. This information can then be filtered, searched, further processed, or presented in additional ways (e.g., as a tabular list of subgeometry objects ordered by density values). Additionally, storing the density-related information in such a manner allows the visualizations to more easily be recreated; which provides a better time efficiency knowing that not all of the heatmap production methods can in GIS software be stored as permanent layers. In other words, the heatmap-creating tool would usually need to be re-run to re-create visualizations, which makes it more time-consuming and requires more effort.

5.2 Resolving the Problem of Point Density Identification

The approach presented in Sect. 3.2 has a major advantage: maintaining the original geometries. Technically, the numbers of geometry objects and object edges stay the same compared to the input dataset, which can, in some cases, be limiting in the exploration of spatial patterns. Despite this advantage, the approach does not offer the possibility to separately detect important pattern-related micro-locations within objects. This is, for small or short objects, not necessarily a significant issue, but can be limiting for larger or longer objects whose parts may be differently classified according to the number of corresponding points features. As a result, no meaningful spatial patterns can be identified on those objects other than the general conclusion: the closer to the city center (or the more popular place), the higher the number of points. This can be the case even for a dataset like a road network used in this paper, which consists of road segments segmented using road intersection points. Even with segmented roads, critical to visualize are segments within the city center where there is a large fluctuation of people and, thus, multiple micro-locations exist where important points clusters (e.g., georeferenced posts) could occur. Not even normalizing the number of point detections over the polygon’s area or length results in more helpful information: It only shows how frequented the urban geometry object in general is and does not allow a precise detection of all the important micro-locations.

In contrast, the approaches presented in Sect. 3.3subdivide these geometry features, leading to a higher number of map objects and respective edges. By implementing subdivision, they generally provide a higher level of details regarding the identification of spatial patterns within geometries, which is especially meaningful for investigating large or elongated geometry objects. Using the models described in Sect. 3.3, we were able to differentiate density hotspots on all geometry objects. The major advantage of these approaches is that the point density patterns are well visible on polygonal objects like squares and pedestrian zones—an effect that can be well observed in Fig. 9. The grid-based approach appears to be useful for the subdivision and classification of roads and other linear objects, providing a comprehensive subgeometry classification. It also allows visualizations of micro-locations for areas like squares or pedestrian zones (Fig. 9b). The advantage of the approach based on contour lines is that the point density patterns are very well visible on polygonal objects. The patterns receive a smoother shape on larger areas, which may be more intuitive to interpret than the grid cells because of high similarity to the zones of a heatmap (Fig. 9c). A drawback of the contour-line-based model in comparison to the grid-based is that on shorter linear objects, it tends to provide fewer details, meaning it results in a smaller number of subgeometry units.

Fig. 9
figure 9

Comparison of data visualization approaches on an urban micro-location in Dresden: a classification with Voronoi areas (per 2500 m2); b grid-based subdivision (\(50\, \mathrm {m} \times 50 \, \mathrm {m}\,\)grid cells); c contour-lines-based subdivision (heatmap radius 50 m)

Full size image

5.3 Influence of Input Data and Parameter Values on Visualizations

As a matter of course, the level of resulting details for each of the visualization approaches is influenced by the input data and respective parameter values. Using a dataset where the urban geometry is modeled differently than in the dataset used in this paper could have a major impact on spatial precision and granularity of visualized patterns: e.g., using road data from OSM, where driving lanes of opposite directions on wider roads are modeled separately, would be especially meaningful when there is a larger distance between road lanes, like a green area or a tram line between them. Thereby, increasing the level of granularity of the input data—i.e., having more objects and a higher cumulative object area—will lower the density values for some of the urban geometries when using the nearest neighbor relation. By contrast, an advantage of both approaches presented in Sect. 3.3 is that the local density is calculated independently from the urban geometry, and therefore the visualized density pattern is not affected when changing the input data.

For all but the nearest neighbor approach, the parameter value selection has a crucial effect on the resulting map and has to be a task-related decision. When using the grid-based approach, the grid cell size, as well as the classification on which the cells get aggregated, influence the final result. The smaller the grid cell is, the more detailed the spatial pattern within the urban geometries will be. However, if the cell size is too small, a significant number of the grid cells could not contain any points, which could lead to the point spread pattern getting underrepresented on the urban geometry features because intersections of empty cells with urban geometry units will be more common. The result of the second step in Fig. 3 would then be comparable to a heat map created using the uniform kernel function with a very small bandwidth. As described in Sect. 3.1, the bandwidth selection is crucial for KDE. For the approach that uses contour lines, the equidistance between the contour lines is the second important parameter. The larger the distance between the contour lines is, the less will the spatial pattern be visible in the resulting visualization.

5.4 Introduction of Uncertainties

In this paper, we aggregated point data to improve the usability of the map, but this generalization step also introduced uncertainty to our approaches. For the grid-based approach, we discussed the influence of the grid cell size on the result in the section before. Besides the size of the cells, their initial positioning could also have a major impact on the resulting spatial patterns displayed on the map. For example, it could be interesting to research the effects of shifting the cells for 50% of their size into different directions. Our assumption is that, in some locations, the resulting density pattern could change significantly. Another approach could also be to design an algorithm that automatically places the cells in a fashion that takes into account the constellation of the densest point clusters. Then, the cells would not be distributed within a bounding box that surrounds the dataset strictly from border to border starting from one side but would be distributed independently on a perfect fit within the bounding box in a way that best covers most populated locations.

In general, placing grid cells without taking into account the positions of dense point clusters potentially highlights density borders as much more certain than they actually are—especially because edges are an important factor in the cognitive map reading process. When intersected with urban geometry objects, these uncertainties could increase even more. To reduce this edge-related bias, possible solutions (other than the one mentioned in the paragraph before) would be to rotate the grid cells according to the major orientation of the road network in a city, or to use other shapes for grid cells, such as diamond or hexagon shapes, to see if they suit better to the urban geometry. Another solution for the edge-related bias—implementing softer border shapes—is already implemented in the approach based on the contour lines of a heat map because the kernel shapes prevent hard edges through the distance decay effect.

5.5 Influence of Scale and Data Privacy

When searching for the best parameter values, the targeted map scale and its impact on the visualization also have to be considered. First, as we use point density to divide urban geometries, the size of the input geometries must be suitable for the targeted map scale, even after being divided into several smaller units. At this point, legibility constraints from map generalization could help to decide if the input geometries are suitable (Stigmar and Harrie 2011). Second, the cell size of the grid-based approach, as well as the equidistance between the contour lines in the approach based on heatmap zones, has to be selected accordingly to the map scale and dependently on the task.

In this paper, we used an input dataset where each point represents the location of a social media post, which could possibly corrupt its contributor’s privacy due to georeferencing. Using privacy-sensitive data like social media data—and VGI in general—needs to guarantee contributors’ privacy even when the data are not directly linked to the original dataset that contains information on the contributors. In this regard, the resulting dataset of our approaches provides data privacy because the information on single points is lost by being aggregated within density surfaces that are assigned to the geometry objects. We also foresee the possibility of adapting the models of our approaches for processing privacy-aware data format proposed by Dunkel et al. (2020) as long as the spatial precision is applicable to the used geometry.

6 Conclusion

The presentation of VGI point data on maps tends to generate dense point clutters in highly populated places when a large amount of data are georeferenced to a small area. A common way to visualize the point density information of overlapping objects is to create a heatmap using kernel density estimation. While this solves the problem of cluttered point symbols, heatmaps have significant shortages for user tasks where density information has to be related to underlying geometry features. In this article, we tackled this problem and introduced two new approaches of visualizing point density using grid cells and heatmap contour lines, respectively. We showed that both approaches provide a way to visually differentiate micro-patterns within smaller and larger geometry objects, and by this in a detailed way and without overlaying and occluding the geometry features reveal characteristics of the dataset such as a specific spatial spread. Our approach based on a grid exactly highlights areas of high point density within squares and pedestrian zones and points out the parts of roads where points occur. In contrast to it, the approach based on contour lines generates a dataset representation in rounded shapes due to the edge-smoothing effect of the heatmap’s contour lines.

An aspect to which we want to focus on in future work is the optimization of the underlying grid regarding cell positioning, shape, and orientation. The other main focus of our future work will be to integrate our geometry subdivision and classification approaches into a dashboard for urban planning. In it, the used dataset of bicycle detections on social media images can be combined with other relevant data sources, e.g., existing bicycle parking stations, which could help to identify locations in a city that have a high need of bicycle-related infrastructure.

To further evaluate the usability of our approaches in a working environment, a user study needs to be conducted with experts facing similar density visualization and exploration tasks, such as urban planners. This will provide us better insights in the usability of our approaches when solving practical tasks, and reveal other datasets and applications that could benefit from approaches of visualizing point density as an urban geometry attribute, as presented in this paper. Possible applications we can anticipate are analyzing the return areas of e-scooters, bicycle or car-sharing systems, identifying locations of frequent traffic accidents, or deducing the best bird-observing spots based on historical bird-observation data.