Abstract
An essential purpose of choropleth maps is the visual perception of spatial patterns (such as the detection of hot spots or extreme values). This requires an effective and as intuitive as possible comparison of color values between different regions. Accordingly, a number of design requirements must be considered. Due to the lack of empirical evidence regarding some elementary design aspects, an online study with 260 participants was conducted. Three closely related effects were examined: the “dark-is-more bias” (i.e., the intuitive ranking of color lightness), the “area-size bias” (i.e., the neglect of small areas, since these are less dominant in perception than larger ones) and the “data-classification effect” (i.e., attention to data classification when interpreting spatial patterns). For each hypothesis, one or more maps in connection with single or multiple choice questions were presented. Users should detect extreme values, central tendencies or homogeneities of values as well as comment on their task solving certainty. In general, the hypotheses regarding the mentioned effects could be confirmed by statistical analysis. The results are used to derive conclusions and topics for future research. In particular, further comparative empirical studies are recommended to determine the best possible map types for given applications, also considering alternatives to choropleth maps.
Zusammenfassung
Ein wesentlicher Zweck von Choroplethenkarten ist die visuelle Wahrnehmung von räumlichen Muster (wie die Detektion von Hot Spots oder Extremwerten). Dies erfordert einen effektiven und möglichst intuitiven Vergleich von Farbwerten zwischen unterschiedlichen Regionen. Dementsprechend muss eine Reihe von Design-Anforderungen berücksichtigt werden. Aufgrund des bisherigen Mangels an empirischen Beweisen bezüglich einiger elementarer Design-Aspekte wurde eine Online-Studie mit 260 Teilnehmern durchgeführt. Diese untersuchte drei eng miteinander verwandte Effekte: Der „Dunkel-ist-mehr-Effekt“ (d.h., die intuitive Rangfolge der Farbhelligkeit), der „Flächengrößen-Effekt“ (d.h., die Vernachlässigung kleiner Flächen bei der Wahrnehmung, da diese im Vergleich weniger dominant wirken) und der „Datenklassifikations-Effekt“ (d.h., die Berücksichtigung der Datenklassifikation beim Vergleich von räumlichen Mustern). Für jede Hypothese wurden eine oder mehrere Karten mit single oder multiple choice-Fragen präsentiert. Die Nutzer sollten Extremwerte sowie zentrale Tendenzen und Homogenitäten der Werte erkennen und ihre Sicherheit bei der Aufgabenlösung bewerten. Im Allgemeinen konnten die Hypothesen bezüglich der genannten Effekte durch statistische Analysen bestätigt werden. Aus den Ergebnissen werden Schlussfolgerungen und Themen für die zukünftige Forschungsarbeiten abgeleitet. Insbesondere werden weitere vergleichende empirische Studien empfohlen, um bestmögliche Visualisierungsformen für gegebene Anwendungsfälle zu bestimmen, dies berücksichtigt auch Alternativen zu Choroplethenkarten.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Choropleth maps are used to visualize area-related, standardized data on a cardinal or ordinal scale with different colors or hatching (Slocum et al. 2009). While it is also possible to determine numerical values or value intervals at particular locations, the main objective of choropleth maps is the visual communication of spatial distributions (Monmonier 1974; Mersey 1990)—this includes
detection of global or local extreme values,
comparison of values of two or more regions,
estimation of hot/cold spots,
assessment of global or local homogeneity or heterogeneity,
estimation of central tendency (according to mean value),
estimation of global patterns (e.g., north–south divide), or
comparison of patterns in two maps.
Regardless of the specific task, one can distinguish between questions that require quantitative processing and outputs (e.g., “What is the maximum population density value?”), and those that require qualitative outputs on the basis of the visual perception only (e.g., “Which federal state has a higher population density—Hamburg or Bavaria?”). Visual perception is here understood as the organization, identification and interpretation of sensory information (Ward et al. 2015: 73).
For the visual perception based on maps, many applications (such as watching media maps) demand for as little usage of legends as possible. Instead, together with the imagination of spatial properties such as spatial homogeneity or hot spots, the tasks are primarily solved by comparing colors between given enumeration units. Accordingly, a couple of design requirements have to be taken into account to support these operations. Because the aspect of differentiation of colors—including the consideration of color vision deficiencies or the effect of lightness contrast—has been thoroughly investigated in previous work (see also Sect. 2), it is not in the scope of this study. Instead, the following research questions will be examined:
Is there an intuitive ranking or association of color lightness with attribute values (so-called “dark-is-more bias”)?
How strong is the effect of neglecting small areas because those are visually less dominant compared to larger areas or are simply overseen (so-called “area-size bias”)?
Is there a sufficient consideration of data classification during the comparison of spatial patterns (so-called “data-classification bias”)?
For answering these questions, an online study with 260 participants was conducted together with the German news agency dpa infografik and the news website SPIEGEL ONLINE (Sect. 3). Statistical testing is applied to verify the underlying hypotheses and to evaluate possible correlations with user groups. Finally, the results of the study will lead to general design and application recommendations for the overall goal of this research, which is concerned with an effective and efficient visual perception of spatial and thematic information in choropleth maps by focusing on the aforementioned biases (Sect. 4).
2 Previous Work
The overall idea of this article is to contribute to effective and efficient task solutions with the help of choropleth maps. Many years ago, several authors already defined necessary task classifications and catalogs (e.g., Monmonier 1974; Robinson et al. 1984). Mersey (1990) defined three types of choropleth map use functions—extracting values at locations, conveying an impression of spatial distribution, and comparing patterns between two or more maps. A more operational view was proposed in our own work (Schiewe 2016), which was based on a general scheme of tasks defined by Andrienko and Andrienko (2006) and decomposed the processes into necessary inputs, detailed operations and outputs. The remainder of this paper does not focus on specific map use tasks, but deals with design issues that support the underlying visual perception.
A key design issue is the choice of a suitable color scheme—with the focus on the distinctiveness of colors (hatching is neglected in the following because of its decreasing importance). There are some rules and recommendations in the literature that mainly depend on the type of data to be displayed (e.g., Brewer 1994; Slocum et al. 2009). For example, for unipolar data, it is recommended to use a sequential color scheme (one hue, varying lightness or saturation) to reflect a value order. There are tools such as ColorBrewer (Harrower and Brewer 2003) that support map makers with corresponding pre-defined color schemes.
In addition, there are other aspects such as esthetics, color associations, color vision problems or intended use for choosing an appropriate scheme (Slocum et al. 2009). With respect to the last item, Mersey (1990) compared color schemes for direct acquisition versus recall or recognition tasks, or Brewer et al. (1997) for sequential versus divergent attribute value displays. However, these and other studies show some inconsistent results. On the other hand, Brychtova and Coltekin (2015), based on eye tracking analysis, confirmed the hypothesis that large color differences increase the reading accuracy. For a good differentiability of six or more classes, a distance of ΔE00 = 10 or more was recommended (ΔE00 being the Euclidian color distance in the color space CIEDE 2000 of the International Commission of Illumination, CIE).
Closely related to the distinctiveness of colors, the intuitive ranking of colors is required for visual comparison purposes in choropleth maps. This is normally achieved by varying the intensity or saturation (single- or multi-hued). In textbooks (such as Robinson et al. 1984), the assignment of light colors to small values and dark colors to high values was recommended (so-called dark-is-more bias). However, there is little or outdated empirical work on this recommendation. For example, McGranaghan (1996) confirmed this bias using monochrome displays only. Because the intuitive dark-is-more bias is crucial for further interpretation tasks, it will be treated in this article.
Some studies also addressed the influence of background, contrast and opacity (e.g., McGranaghan 1989; Schloss et al. 2019), which may lead to a reduction of the dark-is-more bias. But again, studies could not reveal unique or transferable results. One step further, an adjustment of color distances to value differences is hardly considered (Weninger 2015). This may be of particular interest if a strong deviation from equidistant data classification occurs, which is then not translated into non-linear color value distances.
Choropleth maps have the problem that larger regions receive a higher visual weight than smaller regions (so-called area-size bias). This overemphasis is mentioned in the literature (e.g., Dent 1999; Speckmann and Verbeek 2010), in most cases with identifying alternatives to avoid this effect. For example, equal-area cartograms as grid or hexagon tile maps, either as single- or multi-element approximations, can be applied (Slocum et al. 2009). However, this leads to shape and topology distortions that are counterproductive to visually perceiving spatial patterns (see also Sect. 4). Thus, Wood and Dykes (2008) suggested equal-area cartograms that can interactively be switched forth and back (and eventually also morphed) with choropleth maps to display correct geographical and topological relationships. However, this approach is not feasible for a quick and easy perception in static (and for example, media) maps.
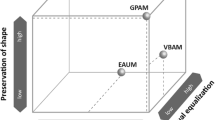
Alternatively to the idea of area equalization, areas can be resized according to the attribute values that they represent (area-by-value cartograms; Dent 1999)—examples are the well-known Worldmapper maps (Dorling et al. 2006). But again, localization is hampered and spatial patterns are disturbed. Roth et al. (2010) favored value-by-alpha maps that use translucency for visual equalization of each enumeration unit. Other ideas, like necklace maps that use additional symbols that surrounds the map regions (Speckmann and Verbeek 2010), avoid the area-size bias; however, localization occurs only in an indirect manner and spatial patterns are difficult to derive. To compare the different properties of cartograms, Johnson (2008) introduced the cube representation Cartogram3 that places map types along the axes topology preservation, shape preservation and visual equalization.
The topic of data classification is comprehensively treated in literature—here reference is made to the reviews by Cromley and Cromley (1996) or Coulsen (1987). Several empirical studies were also concerned with the comparison of such methods for answering typical map use tasks (e.g., Goldsberry and Battersby 2009; Brewer and Pickle 2002). A couple of non-spatial measures (such as within-class homogeneity or between-class heterogeneity) were defined to describe the resulting statistical uncertainty due to the classification process (Jenks and Caspall 1971; Dent 1999; Schiewe 2018). On the other hand, the influence of different classification methods and results on the visual perception is hardly investigated. Schiewe (2018) proposed some measures (global visual balance, within-class visual imbalance) for this purpose. However, empirical linkage of such measures to actual visual perception is still missing.
3 Empirical Study
3.1 Hypotheses
The first block of the study dealt with the dark-is-more bias, i.e., the intuitive association of color lightness with attribute values. To test the intuitiveness, maps were first shown without legends. The following hypotheses were under investigation:
(H1.1): Even without a legend, the darkest color hue is associated with the largest data value (and lightest hue with smallest value).
(H1.2): Providing a legend, the correct association of dark (light) color values to large (small) data values is further improved.
The second block was concerned with the area-size bias (also “Russia–Andorra effect”), i.e., the neglect of small areas in extreme value detection:
(H2.1): Without a legend very small areas with global extreme values are often missed.
(H2.2): Providing a legend very small areas with global extreme values are still (but less frequently) missed.
Finally, the data-classification bias was investigated, i.e., the consideration of data classification along with the comparison of spatial patterns:
(H3.1): Without a legend, spatial patterns (here: central tendency, homogeneity) are primarily classified according to the related color intensities—without questioning the underlying data classification.
(H3.2): Even with a legend, spatial patterns are primarily classified according to the related color intensities—without questioning the underlying data classification.
3.2 General Organization
To receive statistically reliable quantitative results, the study was designed as online study (created with Google Forms). It was advertised through the general communication channels of our project partners dpa infografik and SPIEGEL ONLINE, including calls for participation placed directly at the bottom of news maps on SPIEGEL ONLINE. The survey was online for about 8 weeks. The study was in German language only. In total, 260 participants took part.
3.3 Materials
3.3.1 Framework
After a short introduction into the survey, some questions related to cartographic skills (distinction of expert, school knowledge, layman), role (designer only, user only, both), and used display device (desktop monitor, smartphone, tablet, others) were asked.
For each hypothesis, one or more maps in connection with single or multiple choice questions were presented. In total, 14 maps were used, all of them having the States of the Unites States of America as geographical reference. On purpose, the map topics were not mentioned. The default data classification used six classes as a typical application case. Different color schemes with specific color hues (red, green, blue) were used for different tasks, all designed according to ColorBrewer scheme (Harrower and Brewer 2003). To avoid learning effects, all maps without legends were displayed first (referring to hypotheses x.1), followed by all maps with legends (hypotheses x.2).
After each block of hypotheses, the users were asked how safe they felt with their answers (single choice question, 5 classes).
3.3.2 Tasks Related to Hypotheses
For the first block, dealing with the dark-is-more bias, the task was to intuitively detect the minimum value in one, and the maximum value in another map (Fig. 1). The correct answers are based on common cartographic understanding that largest values are displayed with darkest color. In the first round, maps did not inherit a legend, in the second round they did.
With respect to the area-size bias, the task was to intuitively detect two minimum values in one map (Fig. 2), and two maximum values in another one. In both cases, the correct units were characterized by very different area sizes. Again, first round maps did not show any legend, while second round maps did. To consider the influence of the number of classes, different variations (4, 6, and 10 classes) were also used for the “with legend” case.
Concerning the data-classification bias in the realm of comparing spatial patterns, the tasks were to intuitively compare central tendency and homogeneity of data values in two side-by-side maps. For the case of a missing legend, the strict answer was not possible due to missing information about the underlying data classification. For the case of a given legend (Fig. 3), the example showed different class limits for the two maps so that an (at least fast and efficient) comparison was also not possible. If one would assume the same classification for both maps, one would have found larger central tendency (average) for the left and larger homogeneity of values for the right map in Fig. 3 due to the overall lightness impressions. Again, three different variations (4, 6, and 10 classes) were used to investigate the influence of the number of classes.
3.4 Analysis Method
In a first step, the answers were counted—in total, but also in subgroups by taking the user and usage characteristics (cartographic skills, roles, display devices) into account. Because in all cases the type of answers were either at nominal or ordinal scale, χ2 or Fisher tests (depending on the number of entries in the contingency tables) were conducted to evaluate differences between tasks or groups. A level of significance of α = 5% is applied. In addition, the overall degree of certainty was calculated as weighted mean of the five options (with 1 = “very certain”, etc.).
3.5 Results
3.5.1 User Data
With respect to cartographic skills, the majority of participants grouped themselves into the class of school knowledge (52%), followed by experts (43%) and laymen (5%).
Most of the participants saw themselves in the role of a user (69%), 7% as a producer only and the remaining 24% as producer and user.
Nearly half of the participants used a desktop monitor as display device (49%), followed by smartphones (37%), tablets (12%), and others (2%).
3.5.2 Test of Hypotheses
Detailed results of the study are documented in the “Appendix”. In the following, a summarized view is given for each hypothesis.
3.5.2.1 Dark-Is-More Bias
As Fig. 4 indicates, 92.6% correct answers were given for the first task (identification of maximum value), and 85.4% for the second one (minimum value)—in both cases without showing a legend. Surprisingly, a significant difference between these tasks occurred with the group of experts (p = 0.006/χ2), having the worst rate of 82.9% for the second task. It seems that many persons in this group were just too fast—smallest values in the eastern part were detected, while the absolute minimum in the west was missed quite often. Another reason for this could be a too optimistic self-assessment of “experts”. For all other combinations of groups and tasks, no significant differences could be observed.
The overall grade of certainty was 1.92 (close to 2 = “certain”). Only 7.7% of all participants were either not certain or very uncertain with their answers—this corresponds very well to the overall error rate. Here, layman showed the largest rate (3/14); however, due to the small number of people in this group, this is not statistically significant compared to the rest of the participants.
All in all, (H1.1) can be verified based on the rate of correct answers of about 90%.
Introducing a legend improved the level of correctness for finding the minimum value to 95.4%. Compared to the same scenario without legend (85.4%), this corresponds to a significant difference (p < 0.001/χ2). Laymen showed the best rate (100%); however, significant differences to the other two groups could not be detected. The overall grade of certainty increased from 1.92 to 1.33 (with only 1.5% being not certain or very uncertain)
Even if a certain learning effect is taken into consideration, (H1.2) can be verified based on these results.
3.5.2.2 Area-Size Bias
Correct answers for the detection of multiple extreme values—without legends—were 66.5% (for finding maximum values) and 55.8% (for minimum values; Fig. 5). As with the detection of just one extreme value before, the detection of minimum values was again worse than that of maximum values (with p = 0.011/χ2). In both cases, the large areas with extreme values were well detected—with success rates of 91.5% (maximum values) and 91.9% (minimum)—this is comparable to the rates observed before with the dark-is-more bias. On the other hand, the smaller areas had detection rates of only 71.5% (maximum) and 60.0% (minimum)—which in both cases is significantly different to the large areas (p < 0.001/χ2). Surprisingly, the overall certainty rate of users slightly improved from 1.92 (H1.1) to 1.89. Now only 5.4% of the persons were either “uncertain” or “very uncertain”.
With that, (H2.1)—the area-size bias—could be verified: small areas were missed by approximately 30–40% of map users, which is definitively too much.
Providing a legend led to an increase in the detection rate of extreme values within small areas (Fig. 5). However, in all cases, there was still a significant difference in large area detection (p < 0.001/χ2). It seems that there was a learning effect: Table 1 shows the chronological sequence of experiments, with an increase in the small area detection from 66.5 to 81.9%.
On the other hand, variations within the large area detection rates based on legends were getting slightly worse as the number of classes increased from 4 over 6 to 10 (96.2%, 93.8%, and 92.7%). However, this effect is statistically not strongly significant (change from 4 to 10 classes: p = 0.085/χ2).
The overall level of subjective certainty increased from 1.89 (H2.1) to 1.46 (H2.2).
Summarizing these results, one can verify (H2.2): there was an increase in the detection of small areas; however this error around 15% to 25% was probably also due to a learning effect and was still clearly larger than the one for large areas (5–10%).
3.5.2.3 Data-Classification Bias
For comparing the central tendency (“identify map with larger values on average”), first no legends were given. Taking the theoretical case of different classifications into account, the correct answer should be “don’t know”. However, only 3.8% took this choice. The majority (93.1%) selected that map that showed an overall darker appearance (Fig. 6). Also for comparing the homogeneity (“identify map with more homogeneous values”), the strict correct answer should be “don’t know”. Only 6.2% chose this option, while 65.8% took the one according to the more homogeneous color impression.
The overall certainty index of 2.22 (with only 8.9% in the “not certain” or “very uncertain” group) confirms that pattern interpretation is a more challenging task compared to the ones before.
Hypothesis (H3.1) could be confirmed. The underlying, actual data classification is not questioned by about 95% of the participants. If one neglects this aspect (and assumes identical class limits), the interpretation of central tendency based on the global distribution of related color intensities was performed mainly correct. However, error rates for homogeneity detection were significantly worse.
In the case of providing a legend, it has to be considered that different classifications were used for the left and right map. Consequently, a comparison of central tendency is hardly possible. For the three examples (with 4, 6, and 10 classes), only 15.2%, 8.9%, and 16.7% of the participants selected the strictly correct answer “don’t know”. The majority (43.6%, 50.6%, 47. 9%) still relied on the dominant color lightness, neglecting the different class limits.
A similar result was obtained for the homogeneity comparison (10 classes): only 17.9% voted for “don’t know”, while 46.7% made their choice according to the perception of homogeneous lightness. Experts realized the problem of different class limits more often than the other groups.
Obviously, these pattern interpretation tasks were the most difficult ones, including the additional (and eventually also confusing) effect of different class limits. Accordingly, the overall certainty level was only 2.79.
All in all, hypothesis (H3.2) could be verified. The majority of the map readers (including experts) ignored the data-classification bias and relied on the color lightness distribution only.
3.5.3 Free Comments
Most of the free comments were concerned with the missing legend for some of the tasks (which actually were left out by purpose) and the choice of colors. 5 out of the 260 users mentioned that the used color differences were not well detectable on their display devices. Consequently, a multi-hue instead of the single-hue color scheme was explicitly requested by two participants.
4 Discussion and Conclusions
4.1 Dark-Is-More Bias
Concerning the dark-is-more bias, a high intuitive and successful interpretation of extreme values for approximately 90% of all cases could be observed. With that the underlying hypotheses (H1.1) and (H1.2)—high values are associated with dark colors—could be verified. Surprisingly, maximum detection was significantly better than minimum detection—this effect might be due to the fact the maximum detection is required more often; however, this should be further investigated.
Despite this high success rates, a legend is still recommended for further optimization, even if an exact value determination is not required. To improve color distinctiveness, multi-hue schemes are helpful; however, it is expected that the intuitive ranking based on the overall lightness becomes more difficult. It is worth examining this aspect in more detail.
4.2 Area-Size Bias
Concerning the area-size bias, it was observed that the detection of small areas with global extreme values is significantly worse than those of large areas. Providing a legend improved these results; however, an inacceptable error rate of 15% to 25% remained. With that, hypotheses (H2.1) and (H2.2) could be verified.
As pointed out in Sect. 2, in the past a couple of alternatives to choropleth maps have been discussed to tackle this bias (e.g., equal-area, area-by-value, or value-by-alpha cartograms). However, from a theoretical point of view, there is no “perfect” solution as localization is hampered and/or topology and/or shape are disturbed so that spatial patterns cannot be determined with necessary accuracy (Fig. 7).
Much more comparative empirical research is needed to find (sub-)optimal solutions. Independent variables will be, aside from alternative map types, different base map geometries (such as number of islands, number of polygons, or interval of areas sizes), and different class numbers. Dependent variables are the effectiveness and efficiency for typical tasks such as localization of spatial units and detection of spatial patterns.
At this point, another dilemma occurs: on the one hand, empirical research can lead to the determination of a case-dependent optimum and on the other hand this flexibility does not increase intuition (for layman user in particular), because repetitive learning and experience are not supported through recurring map type displays.
4.3 Data-Classification Bias
Also the data-classification bias could be confirmed: while there is a good intuition during the global interpretation based on lightness differences, this takes place without questioning the underlying data classification by more than 90% of users (without legend) and 80% (with legend). Interpreting global homogeneity based on lightness impression only was obviously a much more challenging task compared to evaluating central tendency.
The data-classification bias is closely linked to an appropriate visualization, in particular, the distinctiveness of color intensities. As there are still problems for certain display devices, the number of classes should be kept as small as possible, in particular when (small) monitor displays are used. Defining a universal upper limit (e.g., 5 or 6 classes) is of course rather difficult due to the variety and huge number of available displays.
The perception of spatial distributions assumes that respective patterns such as local extreme values, large values differences between polygons, or hot spots are not disturbed through the data classification step. However, conventional classification methods do not consider spatial properties and do not guarantee their preservation. Hence, it is recommended to apply advanced methods that explicitly consider spatial context and show improved preservation rates (Chang and Schiewe 2018).
4.4 Overall Evaluation
All in all, the central hypotheses could be verified with this empirical study. Interestingly, in nearly all tasks, there was no significance for the groups with different cartographic skills. Of course, the within-subjects design of the survey together with no random task order facilitated some learning effects. However, the given sequence avoided confusion about the different tasks. Although some learning effects are assumed (in particular, when varying the number of classes), this did not disturb the overall trend of the results.
Although no major surprises occurred, the study now delivered a so far missing empirical evidence for key aspects in the context of visual perception of spatial distributions in choropleth maps. A couple of detailed study topics as mentioned earlier are still needed to further optimize the respective design. In addition, also the impact of different class numbers on successfully detecting spatial patterns needs to be further investigated.
References
Andrienko N, Andrienko G (2006) Exploratory analysis of spatial and temporal data: a systematic approach. Springer, Berlin
Brewer CA (1994) Color use guidelines for mapping and visualization. In: MacEachren AM, Taylor DRF (eds) Visualization in modern cartography. Elsevier Science, Tarrytown, NY, pp 123–147
Brewer CA, Pickle L (2002) Evaluation of methods for classifying epidemiological data on choropleth maps in series. Ann Assoc Am Geogr 92(4):662–681
Brewer CA, MacEachren AM, Pickle L, Herrmann D (1997) mapping mortality: evaluating color schemes for choropleth maps. Ann Assoc Am Geogr 87(3):411–438
Brychtova A, Coltekin A (2015) An empirical user study for measuring the influence of color distance and font size in map reading using eye tracking. Cartogr J. https://doi.org/10.1179/1743277414y.0000000101
Chang J, Schiewe J (2018) An open source tool for preserving local extreme values and hot/coldspots in choropleth maps. Kartogr Nachr 68(6):307–309
Coulsen MRC (1987) In the matter of class intervals for choropleth maps: with particular reference to the work of George Jenks. Cartographica 24(2):16–39
Cromley EK, Cromley RG (1996) An analysis of alternative classification scheme for medical atlas mapping. Eur J Cancer 32A(9):1551–1559
Dent BD (1999) Cartography: thematic map design, 5th edn. McGraw-Hill, Boston
Dorling D, Barford A, Newman M (2006) Worldmapper: the world as you’ve never seen it before. IEEE Trans Visual Comput Graph 12(5):757–764
Goldsberry K, Battersby S (2009) Issues of change detection in animated choropleth maps. Cartographica 44(3):201–215
Harrower M, Brewer CA (2003) ColorBrewer.org: an online tool for selecting colour schemes for maps. Cartogr J 40(1):27–37
Jenks G, Caspall F (1971) Error on choroplethic maps: definition, measurement, reduction. Ann Assoc Am Geogr 61:217–224
Johnson ZF (2008) Cartograms for political cartography. A question of design. Department of Geography, University of Wisconsin-Madison, Madison
McGranaghan M (1989) Ordering choropleth maps symbols: the effect of background. Am Cartogr 16(4):279–285
McGranaghan M (1996) An experiment with choropleth maps on a monochrome LCD panel. In: Wood CH, Keller CP (eds) Cartographic design: theoretical and practical perspectives. Wiley, Chichester, pp 177–190
Mersey JE (1990) Choropleth map design—a map user study. Cartographica 27(3):33–50
Monmonier M (1974) Measures of pattern complexity for choroplethic maps. Am Cartogr 1(2):159–169
Robinson AH, Sale RD, Morrison JL, Muehrcke PC (1984) Elements of cartography, 5th edn. Wiley, Toronto
Roth R, Woodruff AW, Johnson ZF (2010) Value-by-alpha maps: an alternative technique to the cartogram. Cartogr J 47(2):130–140. https://doi.org/10.1179/000870409X12488753453372
Schiewe J (2016) Preserving attribute value differences of neighboring regions in classified choropleth maps. Int J Cartogr 2(1):6–19. https://doi.org/10.1080/23729333.2016.1184555
Schiewe J (2018) Development and comparison of uncertainty measures in the framework of a data classification. Int Arch Photogramm Remote Sens Spat Inf Sci XLII-4:551–558
Schloss KB, Gramazio CC, Silverman AT, Wang AS (2019) Mapping color to meaning in colormap data visualizations. IEEE Trans Visual Comput Graph 25(1):810–819. https://doi.org/10.1109/TVCG.2018.2865147
Slocum TA, McMaster RB, Kessler FC, Howard HH (2009) Thematic cartography and geovisualization, 3rd edn. Prentice Hall, Upper Saddle River
Speckmann B, Verbeek K (2010) Necklace maps. IEEE Trans Visual Comput Graph 16(6):881–889
Ward MO, Grinsteim G, Keim D (2015) Interactive data visualization. Foundations, techniques, and applications, 2nd edn. A K Peters/CRC Press, Boca raton
Weninger B (2015) Lärmkarten zur Öffentlichkeitsbeteiligung—Analyse und Verbesserung der kartografischen Gestaltung. Ph.D. thesis, HafenCity University Hamburg, Germany
Wood J, Dykes J (2008) Spatially ordered treemaps. IEEE Trans Visual Comput Graph 14(6):1348–1355
Acknowledgements
The author thanks the project colleagues of SPIEGEL ONLINE (Marcel Pauly, Patrick Stotz, Achim Tack) and dpa infografik (Raimar Heber), as well as colleagues of the Lab for Geoinformatics and Geovisualization (g2lab) at HafenCity University Hamburg (in particular, Vanessa Forkert).
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Numerical Results of Empirical Study
Hypothesis (H1.1): Dark-is-more bias—without legend (6 classes)
Group | Detection of one maximum value | Detection of one minimum value | ||||
|---|---|---|---|---|---|---|
Correct (abs.) | Wrong (abs.) | Correct (%) | Correct (abs.) | Wrong (abs.) | Correct (%) | |
Laymen | 11 | 3 | 78.6 | 13 | 1 | 92.9 |
School knowledge | 125 | 10 | 92.6 | 117 | 18 | 86.7 |
Expert | 105 | 6 | 94.6 | 92 | 19 | 82.9 |
Designer | 17 | 1 | 94.4 | 15 | 3 | 83.3 |
User | 166 | 14 | 92.2 | 155 | 25 | 86.1 |
Both | 58 | 4 | 93.5 | 52 | 10 | 83.9 |
Desktop | 120 | 6 | 95.2 | 112 | 14 | 88.9 |
Tablet | 30 | 2 | 93.8 | 27 | 5 | 84.4 |
Smartphone | 85 | 10 | 89.5 | 77 | 18 | 81.1 |
Etc. | 6 | 1 | 85.7 | 6 | 1 | 85.7 |
Total | 241 | 19 | 92.7 | 222 | 38 | 85.4 |
Decision certainty | Very certain | Certain | Medium | Uncertain | Very uncertain | Overall grade |
|---|---|---|---|---|---|---|
Total | 101 | 105 | 34 | 14 | 6 | 1.92 |
Hypothesis (H1.2): Dark-is-more bias—with legend (6 classes)
Group | Detection of one minimum value | ||
|---|---|---|---|
Correct (abs.) | Wrong (abs.) | Correct (%) | |
Laymen | 14 | 0 | 100.0 |
School knowledge | 126 | 9 | 93.3 |
Expert | 108 | 3 | 97.3 |
Designer | 18 | 0 | 100.0 |
User | 169 | 11 | 93.9 |
Both | 61 | 1 | 98.4 |
Desktop | 126 | 0 | 100.0 |
Tablet | 27 | 5 | 84.4 |
Smartphone | 89 | 6 | 93.7 |
Etc. | 6 | 1 | 85.7 |
Total | 248 | 12 | 95.4 |
Decision certainty | Very certain | Certain | Medium | Uncertain | Very uncertain | Overall grade |
|---|---|---|---|---|---|---|
Total | 192 | 55 | 9 | 3 | 1 | 1.33 |
Hypothesis (H2.1)—Area-size bias—without legend (6 classes)
Group | Detection of two maximum values | Detection of two minimum values | ||||
|---|---|---|---|---|---|---|
Correct (abs.) | Wrong (abs.) | Correct (%) | Correct (abs.) | Wrong (abs.) | Correct (%) | |
Laymen | 8 | 6 | 57.1 | 8 | 6 | 57.1 |
School knowledge | 89 | 46 | 65.9 | 69 | 66 | 51.1 |
Expert | 76 | 35 | 68.5 | 68 | 43 | 61.3 |
Designer | 12 | 6 | 66.7 | 8 | 10 | 44.4 |
User | 118 | 62 | 65.6 | 95 | 85 | 52.8 |
Both | 43 | 19 | 69.4 | 42 | 20 | 67.7 |
Desktop | 89 | 37 | 70.6 | 76 | 50 | 60.3 |
Tablet | 19 | 13 | 59.4 | 14 | 18 | 43.8 |
Smartphone | 60 | 35 | 63.2 | 50 | 45 | 52.6 |
Etc. | 5 | 2 | 71.4 | 5 | 2 | 71.4 |
Total | 173 | 87 | 66.5 | 145 | 115 | 55.8 |
Decision certainty | Very certain | Certain | Medium | Uncertain | Very uncertain | Overall grade |
|---|---|---|---|---|---|---|
Total | 98 | 113 | 35 | 8 | 6 | 1.89 |
Hypotheses (H2.2)—Area-size bias—with legend (varying number of classes)
Group | Detection of two maximum values of 6 classes | Detection of two maximum values of 4 classes | Detection of two maximum values of 10 classes | ||||||
|---|---|---|---|---|---|---|---|---|---|
Correct (abs.) | Wrong (abs.) | Correct (%) | Correct (abs.) | Wrong (abs.) | Correct (%) | Correct (abs.) | Wrong (abs.) | Correct (%) | |
Laymen | 7 | 7 | 50.0 | 7 | 7 | 50.0 | 11 | 3 | 78.6 |
School knowledge | 96 | 39 | 71.1 | 103 | 32 | 76.3 | 108 | 27 | 80.0 |
Expert | 82 | 29 | 73.9 | 89 | 22 | 80.2 | 94 | 17 | 84.7 |
Designer | 12 | 6 | 66.7 | 12 | 6 | 66.7 | 12 | 6 | 66.7 |
User | 124 | 56 | 68.9 | 140 | 40 | 77.8 | 149 | 31 | 82.8 |
Both | 49 | 13 | 79.0 | 47 | 15 | 75.8 | 52 | 10 | 83.9 |
Desktop | 88 | 38 | 69.8 | 97 | 29 | 77.0 | 107 | 19 | 84.9 |
Tablet | 22 | 10 | 68.8 | 22 | 10 | 68.8 | 24 | 8 | 75.0 |
Smartphone | 69 | 26 | 72.6 | 73 | 22 | 76.8 | 76 | 19 | 80.0 |
Etc. | 6 | 1 | 85.7 | 7 | 0 | 100.0 | 6 | 1 | 85.7 |
Total | 185 | 75 | 71.2 | 199 | 61 | 76.5 | 213 | 47 | 81.9 |
Decision certainty | Very certain | Certain | Medium | Uncertain | Very uncertain | Overall grade |
|---|---|---|---|---|---|---|
Total | 167 | 69 | 20 | 2 | 1 | 1.46 |
Hypothesis (H3.1)—Data classification bias—without legend (6 classes)
“correct” = strictly correct (“don’t know”), “impression only” = neglecting classification, using lightness only (but correctly)
Group | Detection of central tendency | Detection of homogeneity | ||
|---|---|---|---|---|
Correct (%) | Impression only (%) | Correct (%) | Impression only (%) | |
Laymen | 0.0 | 92.9 | 0.0 | 42.9 |
School knowledge | 1.5 | 95.6 | 4.4 | 76.3 |
Expert | 7.2 | 90.1 | 9.0 | 55.9 |
Designer | 11.1 | 88.9 | 22.2 | 55.6 |
User | 1.7 | 96.1 | 4.4 | 72.8 |
Both | 8.1 | 85.5 | 6.5 | 48.4 |
Desktop | 4.0 | 92.1 | 7.9 | 59.5 |
Tablet | 6.3 | 87.5 | 6.3 | 68.8 |
Smartphone | 3.2 | 95.8 | 4.2 | 72.6 |
Etc. | 0.0 | 100.0 | 0.0 | 71.4 |
Total | 3.8 | 93.1 | 6.2 | 65.8 |
Decision certainty | Very certain | Certain | Medium | Uncertain | Very uncertain | Overall grade |
|---|---|---|---|---|---|---|
Total | 59 | 115 | 63 | 17 | 6 | 2.22 |
Hypothesis (H3.2)– Data classification bias—with legend (varying number of classes)
“correct” = strictly correct (“don’t know”), “impression only” = neglecting classification, using lightness only (but correctly)
Group | Detection of central tendency of 6 classes | Detection of central tendency of 4 classes | Detection of central tendency of 10 classes | Detection of homogeneity of 10 classes | ||||
|---|---|---|---|---|---|---|---|---|
Correct (%) | Impression only (%) | Correct (%) | Impression only (%) | Correct (%) | Impression only (%) | Correct (%) | Impression only (%) | |
Laymen | 14.3 | 64.3 | 14.3 | 57.1 | 14.3 | 64.3 | 7.1 | 57.1 |
School knowledge | 6.0 | 57.9 | 12.7 | 49.3 | 16.3 | 51.1 | 15.6 | 45.9 |
Expert | 11.8 | 40.0 | 18.3 | 34.9 | 17.1 | 40.5 | 21.6 | 45.0 |
Designer | 22.2 | 44.4 | 22.2 | 50.0 | 22.2 | 55.6 | 16.7 | 55.6 |
User | 7.3 | 54.7 | 13.9 | 48.3 | 16.7 | 51.7 | 17.2 | 47.2 |
Both | 10.0 | 40.0 | 16.9 | 27.1 | 15.3 | 33.9 | 20.3 | 42.4 |
Desktop | 12.2 | 44.7 | 15.4 | 41.5 | 18.7 | 42.3 | 21.1 | 43.9 |
Tablet | 3.1 | 59.4 | 12.5 | 31.3 | 9.4 | 46.9 | 9.4 | 43.8 |
Smartphone | 6.3 | 54.7 | 14.7 | 50.5 | 16.8 | 55.8 | 16.8 | 50.5 |
Etc. | 14.3 | 57.1 | 28.6 | 42.9 | 14.3 | 42.9 | 14.3 | 57.1 |
Total | 8.9 | 50.6 | 15.2 | 43.6 | 16.7 | 47.9 | 17.9 | 46.7 |
Decision certainty | Very certain | Certain | Medium | Uncertain | Very uncertain | Overall grade |
|---|---|---|---|---|---|---|
Total | 32 | 75 | 84 | 54 | 15 | 2.79 |
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Schiewe, J. Empirical Studies on the Visual Perception of Spatial Patterns in Choropleth Maps. KN J. Cartogr. Geogr. Inf. 69, 217–228 (2019). https://doi.org/10.1007/s42489-019-00026-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42489-019-00026-y