1 Introduction

The number of private cars continues to grow, and traffic accidents have become one of the most serious social problems in the world (Rongqiang et al. 2016). About 90% of traffic accidents are due to human causes (NHTSA 2002). In particular, drivers’ braking-related behaviors are considered to be an important cause of accidents (Ren et al. 2011). For example, some inexperienced drivers may use the gas pedal instead of the brake and cause an accident (Schmidt et al. 1997).

According to our previous studies (Wu et al. 2020b) and related research (Lyu et al. 2017, 2018; Hault-Dubrulle et al. 2011), drivers’ experience, gender, and physique as human factors may affect a driver's braking behavior and thus his driving safety. However, most studies have mounted sensors on the brake pad. Only a few studies (Stahl et al. 2014; Hou et al. 2019) focused on the analysis of driver's behavior pre-braking, but they used inconsistent definitions that differed from this paper (i.e., driver’s body actions before the brake pad are pressed).

Therefore, an in-depth analysis of driver pre-brake-related behaviors is necessary to determine the relationship between various human factors and possible traffic accidents.

With the advancement of sensors and Internet of Things (IoT) technology, human in-vehicle behavior can already be collected and analyzed with great accuracy. Among them, an accelerometer-based motion capture device to record the subject's whole-body movements can be applied to many different scenarios (Wu et al. 2020a). A dedicated kit with acceleration sensors and similar devices to capture motion can collect data on the subject’s body movements with high accuracy, even outside of a laboratory environment.

Moreover, based on the collected human body movements data, motion features with different action purposes can be decomposed in the frequency domain (Winter 2009). Thus, to facilitate the analysis of the similarities and differences between actions, action frequency analysis in previous studies has mainly used Fourier transform (Bruderlin and Williams 1995) and wavelet transform (Aminian and Najafi 2004), which are not suitable for decomposing human actions due to interpretation difficulties.

Therefore, based on a set of experiments performed at a vehicle test field, this study focused on analyzing drivers’ pre-braking actions and tried to propose an action decomposition-based local human body movement analysis method to discover similarities and differences in pre-braking actions among drivers with different driving experience, gender, and physique. The motion capture device called Xsens MVN Animate (Xsens 2022) was used for the data collection. Unlike traditional motion capture instruments, MVN can additionally collect human joint data, such as for spinal joints and toes, to calculate more joint angles to represent the subject's posture for motion analysis. Based on related joint angle calculations, an action decomposition method, such as Hilbert–Huang Transform (HHT), is applied to analyze the pre-braking actions in the instantaneous frequency domain. The HHT method is a kind of empirical decomposition, which can better decompose the realistic complex actions of human beings through nonlinear decomposition.

The results of this study will be useful in decomposing and discerning the specific actions that lead to accidents, providing insights into driver training for novice drivers, and guiding the construction of daily automated driver assistance or accident prevention systems (advanced driver assistance systems, ADASs).

The remainder of this paper is organized as follows: an overview of related studies on driver behaviors analysis, braking motion analysis, and Hilbert–Huang Transform will be provided in Sect. 2. In Sect. 3, the methodology, related measures definitions, and description of the dataset will be provided. Then, the experimental design, dataset, analysis results, and discussion will be provided in Sects. 4 and 5. Finally, we will summarize the research results and provide our perspective regarding promising future research in Sect. 6.

2 Related studies and hypotheses

2.1 Driver behaviors analysis

Most research has focused on driver behaviors to improve the safety of driving performance. For example, Cao et al. (2014) modeled the cognitive architecture underlying drivers’ skills and supported quantitative simulation of the driving behavior. Jia et al. (2020) analyzed different driving styles, including extreme acceleration and emergency braking behavior and other behaviors by using long short-term memory and convolutional neural network methods. Driving data metrics show that there is no specific time point after which driving behavior stabilizes for all drivers (Stavrakaki et al. 2020). However, Lodha et al. (2021) showed that the braking time in chronic stroke disease survivors was longer than in other groups. Nugroho et al. (2021) predicted the remaining age of brake lining by studying various driving behaviors and braking power. In summary, although there are many studies about driver behaviors, braking behaviors, and braking time, few are related to pre-braking behaviors.

2.2 Braking motion analysis and pre-braking behavior

Braking is a common manipulation during the driving process, and it is most related to traffic accidents. Proper braking behavior can keep driving safe and comfortable for the beings in the vehicle. Many researchers have analyzed the braking behaviors in some urgent scenarios related to potential accidents (Wu et al. 2018; Li et al. 2020; Pawar et al. 2020). Moreover, other researchers studied the braking actions in usual driving environments (Tu et al. 2015; Li et al. 2017; Xiao et al. 2019; Zhu et al. 2021). Most of the research investigated braking as a whole process but did not focus on pre-braking separately.

In summary, Table 1 shows that related studies have focused more on the accident itself, with the driver’s pre-braking action usually studied as one of the main maneuvers to avoid a collision. Not much research has been done on everyday driving behaviors, such as turning and stopping, with respect to pre-braking.

Table 1 Related studies about braking
Full size table

Furthermore, different studies used different definitions for pre-braking behaviors. For example, some studies defined the braking action as the action of slowing down when encountering an accident (Susumu et al. 2009).

Therefore, in this paper, we define “pre-braking behaviors” as the action behaviors exhibited by a driver's foot before it touches the brake pedal during a whole braking action.

As shown in Fig. 1, the entire braking behavior of the driver's right foot is divided into four stages: (a) starting to brake, (b) lifting the foot to the highest point, (c) descending to touch the brake pad, and (d) depressing the brake pad. Therefore, the “pre-braking behaviors” are defined as actions (a) to (c). Because action (d) has been extensively studied by previous research, this paper will not focus on it.

Fig. 1
figure 1

The pre-braking behaviors in this study

Full size image

2.3 The xsens MVN motion capture device

As shown in Fig. 2, the high precision accelerometer-based motion capture device named Xsens MVN (Troje 2002) was used in this study to collect the data on drivers’ body movements. Xsens MVN can record the 3D coordinates of a subject’s joints at a frequency of once every 4 ms. As a wearable motion capture system, unlike traditional camera-based motion capture devices, Xsens MVN can provide continuous data recording services including the outdoor situation by connecting a battery-operated dedicated recording device.

Fig. 2
figure 2

The Xsens MVN motion capture device

Full size image

The MVN has 17 wearable ultra-small trackers that are designed to withstand high impacts such as rolls and stunts. In contrast to traditional motion capture devices, the Xsens MVN device can collect data on 23 joints including spinal segments T12, T8, L5, L3, and toes as XML files with high precision. The details of the collectible joint data are shown in Table 2.

Table 2 Details of calculated measures for analysis
Full size table

2.4 Hilbert–Huang transform

Hilbert–Huang Transform is applied to analyze and generate motion data collected by motion capture systems due to its high performance in dealing with nonlinear data in the instantaneous frequency domain. Dong et al. (2020b) proposed a framework to analyze human captured motions using HHT based on multivariate empirical mode decomposition (MEMD). The previous research revealed that a common human action could be decomposed into multiple sub-actions with different purposes. For example, decomposed high-frequency sub-actions could be removed by HHT to achieve motion smoothing for robot motors (Dong et al. 2020a). Using these decomposed multiple sub-actions, Dong et al. (2021) also presented a method to generate realistic motion features for robot motion design, which demonstrated that HHT could provide motion training data for deep learning.

In summary, previous research showed that HHT could be adopted in human motion analysis and editing. However, different human actions contain distinct motion features and multiple sub-actions, according to the biomechanical mechanism of the human body structure (Winter 2009). Thus, it is necessary to perform an in-depth analysis of distinct human actions, such as pre-braking actions using statistical methods.

3 Methodology

3.1 Angle calculation of key joints

The MVN motion capture device used in this study can support the acquisition of coordinate data for a total of 23 joints in the whole body (Troje 2002). In order to better represent the driver's movements during the pre-braking action, as shown in Fig. 3, this study focused on three joint angles related to braking behaviors: the waist, right knee, and right ankle. Therefore, because an aimed angle needs to be calculated from the coordinates of three joints, the following data for seven joints were analyzed: pelvis, spinal joints L3 & L5, right upper leg, right lower leg, right foot, and right toe tip.

Fig. 3
figure 3

The angles for calculation

Full size image

Specifically, for the calculation of the knee angle, we can take the coordinates of the three joints, upper leg U (Xu, Yu, Zu), lower leg L (Xl, Yl, Zl), and foot F (Xf, Yf, Zf) and calculate the angle of knee \({{\varvec{\theta}}}_{{\varvec{k}}}\) by Eq. (1):

$${{\varvec{\theta}}}_{{\varvec{k}}}={\varvec{a}}{\varvec{r}}{\varvec{c}}{\varvec{c}}{\varvec{o}}{\varvec{s}}\frac{\overrightarrow{{\varvec{L}}{\varvec{U}}}\boldsymbol{ }\times \boldsymbol{ }\overrightarrow{{\varvec{L}}{\varvec{F}}}}{\left|\overrightarrow{{\varvec{L}}{\varvec{U}}}\right|\times \left|\overrightarrow{{\varvec{L}}{\varvec{F}}}\right|}$$
(1)

where the vectors \(\overrightarrow{{\varvec{L}}{\varvec{U}}}\) and \(\overrightarrow{{\varvec{L}}{\varvec{F}}}\) can be obtained by Eqs. (2) and (3):

$$\overrightarrow{{\varvec{L}}{\varvec{U}}}=\left(\boldsymbol{ }{{\varvec{X}}}_{{\varvec{u}}}-{{\varvec{X}}}_{{\varvec{l}}},\boldsymbol{ }{{\varvec{Y}}}_{{\varvec{u}}}-{{\varvec{Y}}}_{{\varvec{l}}},\boldsymbol{ }{{\varvec{Z}}}_{{\varvec{u}}}-{{\varvec{Z}}}_{{\varvec{l}}}\right)$$
(2)
$$\overrightarrow{{\varvec{L}}{\varvec{F}}}=\left(\boldsymbol{ }{{\varvec{X}}}_{{\varvec{f}}}-{{\varvec{X}}}_{{\varvec{l}}},\boldsymbol{ }{{\varvec{Y}}}_{{\varvec{f}}}-{{\varvec{Y}}}_{{\varvec{l}}},\boldsymbol{ }{{\varvec{Z}}}_{{\varvec{f}}}-{{\varvec{Z}}}_{{\varvec{l}}}\right)$$
(3)

Finally, the driver’s three joint angles include the angle of knee \({{\varvec{\theta}}}_{{\varvec{k}}}\), angle of ankle \({{\varvec{\theta}}}_{{\varvec{a}}}\), and angle of waist \({{\varvec{\theta}}}_{{\varvec{w}}}\) can be calculated. By analyzing the changes of these three joint angles, we can gain a description of the driver's relevant actions during pre-braking.

3.2 Hilbert–Huang transform

The Hilbert–Huang transform (HHT) is a process of empirical mode decomposition (EMD) of the original signal that applies the Hilbert Transform (HT) to each decomposed frequency component. Because HHT decomposes signals nonlinearly, it can achieve better results when analyzing nonlinear and nonstationary motion capture data than other methods such as short-time Fourier transform (STFT) (Huang and Shen 2014).

An analytic signal \({\varvec{z}}\left({\varvec{t}}\right)\) is defined as Eq. (4) in the complex plane, where \({z}_{r}\left(t\right)\) is the real part observed in the real world, and \({z}_{i}\left(t\right)\) is the imaginary part calculated by HT (Bracewell 1978).

$${\varvec{z}}\left({\varvec{t}}\right)={{\varvec{z}}}_{{\varvec{r}}}\left({\varvec{t}}\right)+{{\varvec{i}}{\varvec{z}}}_{{\varvec{i}}}\left({\varvec{t}}\right)$$
(4)

As shown in Eq. (5), HT transforms the real part \({z}_{r}\left(t\right)\) into its imaginary part \({z}_{i}\left(t\right)\) by considering the observed signal \({{\varvec{z}}}_{{\varvec{r}}}\left({\varvec{t}}\right)=A(t)\) cos \((\omega (t)t)\) (Bracewell 1978).

$${{\varvec{z}}}_{{\varvec{i}}}\left({\varvec{t}}\right)=\frac{1}{\pi }\mathrm{PV}{\int }_{-\infty }^{+\infty }\frac{{z}_{r}\left(\tau \right)}{t-\tau }{\varvec{d}}{\varvec{\tau}}=\frac{1}{\pi t}*{{\varvec{z}}}_{{\varvec{r}}}({\varvec{t}})$$
(5)

After the real part \({z}_{r}\left(t\right)\) and imaginary part \({z}_{i}\left(t\right)\) of \(z\left(t\right)\) are obtained, the instantaneous amplitude (AMP) \(A(t)\) and frequency \(\omega (t)\) are calculated according to Eq. (6).

$${\varvec{A}}\left({\varvec{t}}\right)=\sqrt{{{{\varvec{z}}}_{{\varvec{r}}}}^{2}\left({\varvec{t}}\right)+{{{\varvec{z}}}_{{\varvec{i}}}}^{2}\left({\varvec{t}}\right)},\boldsymbol{ }{\varvec{\omega}}({\varvec{t}})=\frac{d}{dt}{\mathbf{tan}}^{-1}\frac{{{\varvec{z}}}_{{\varvec{i}}}({\varvec{t}})}{{{\varvec{z}}}_{{\varvec{r}}}({\varvec{t}})}$$
(6)

However, as we can see from the definition of HT, only monochromatic wave signals, that is, only \(A(t)\) cos \((\omega (t)t)\), can be transformed by HT to calculate its imaginary part. Consequently, the instantaneous AMP and frequency of a composite wave made of distinct monochromatic waves cannot be obtained correctly. Meanwhile, because human motion data is not a monochromatic signal, HT is not satisfied by adopting nonlinear and nonstationary data such as motion capture data.

To deal with this issue, Huang and Shen (2014) provided a method called empirical mode decomposition (EMD), empirically decomposing a composite wave consisting of multiple monochromatic waves into a finite number of pseudo monochromatic waves, a so-called intrinsic mode function (IMF), and a residual without any frequency component, a so-called trend. Equation (7) demonstrates that an observed signal \(x\left(t\right)\) is decomposed into several IMFs \({c}_{i}\left(t\right)\) and a trend \(r(t)\).

$$x\left(t\right)=\sum_{i=1}^{n}{c}_{i}\left(t\right)+r(t)$$
(7)

The definition of IMF is as follows:

  1. (1)

    The number of extremes is equal to the number of zero crossings, or the difference between them is 1.

  2. (2)

    At any given time, the average of the envelopes connecting the maximum and minimum values is zero.

Based on the definition above, IMF is extracted from high frequency to lower frequency using an algorithm (Huang and Shen 2014). Then, the trend is the residual with no frequency component after extracting all IMFs. Because the IMF satisfies the HT assumption, after decomposing nonlinear and nonstationary data into IMFs, we can let \({z}_{r}\left(t\right)= {c}_{i}\left(t\right)\) to obtain \({z}_{i}\left(t\right)\) by Eq. (5). Then, the instantaneous AMP and frequency can be obtained correctly by Eq. (6) for each IMF.

To demonstrate how IMFs are shown in the instantaneous frequency domain, we used an artificial signal \(s\left(t\right)\) consisting of three monochromatic waves, Eq. (8), as an example of Hilbert spectral analysis (HSA). Please note that we used this example only to demonstrate HSA. Thus, for simplicity, the three monochromatic waves in artificial signal \(s\left(t\right)\) are stationary with constant frequency, while motion data are nonstationary with variable frequency.

$$s\left(t\right)=\mathrm{sin}\left(\frac{\pi t}{10}\right)+2\mathrm{sin}\left(\frac{\pi t}{20}\right)+cos\left(\frac{\pi t}{40}\right)$$
(8)

Figure 4 shows the instantaneous AMP and frequencies of all decomposed IMFs obtained by HT. The results are displayed in time on the horizontal axis, frequency on the vertical axis, and AMPs are presented by color.

Fig. 4
figure 4

An example Hilbert spectrum

Full size image

In this paper, we numbered the index of each IMF from low frequency to high frequency. Thus, IMF1 corresponds to \(\mathrm{cos}(\frac{\pi t}{40})\), IMF2 corresponds to \(2\mathrm{sin}\left(\frac{\pi t}{20}\right)\), and IMF3 corresponds to \(\mathrm{sin}\left(\frac{\pi t}{10}\right)\). Using the HSA, we can analyze pre-braking actions by decomposing angle of knee \({{\varvec{\theta}}}_{{\varvec{k}}}\), angle of ankle \({{\varvec{\theta}}}_{{\varvec{a}}}\), and angle of waist \({{\varvec{\theta}}}_{{\varvec{w}}}\) and calculate their instantaneous frequency and AMP for statistical analysis.

In addition, many studies have been conducted to extend the EMD from univariate to multivariate, expanding the range of applications of the HHT (Rehman and Mandic 2010). Therefore, in this study, we focused on the multi-channel of motion capture data in pre-braking actions and applied the MEMD to decompose the pre-braking actions into multivariate IMF signals.

As can be seen from the definition of EMD, HHT differs in principle from Fourier transform (FT). FT linearly decomposes a signal into monochromatic waves based on mathematical proof. In contrast, EMD empirically decomposes the signal into pseudo monochromatic waves, IMFs, with variable frequency and AMP. Therefore, HHT is more beneficial for analyzing pre-braking actions that are nonlinear and nonstationary motion capture data.

4 Experiments and dataset

4.1 Experiments

To obtain the target data, we conducted a set of driving experiments at Chang'an University, on the Connected and Automated Vehicle (CAV) Test Field, located in Xi’an, China in September 2019. A general civilian car (Volkswagen Sagitar, Automatic/1.6 L/3-box/5 seats) was used for the experiments. The steering wheel of the experimental vehicle was on the left side. As shown in Fig. 5, the CAV test field was oval-shaped, and all subjects were required to start at the green point (garage), drive clockwise for one lap, and then stop and reenter the garage. All subject drivers were asked to perform their usual driving in the test site while wearing the MVN motion capture device.

Fig. 5
figure 5

Map of the CAV test field

Full size image

This research focused on the driving movements before the driver turned right (right angle) and during parking (red points) where braking actions were certain to occur. Statistically, the average speed of the driver at the time of reaching the red point was 20 km/s. Some red balloons were set at the roadside to remind the driver to perform the relevant actions, but the specific operation was entirely up to the driver to perform according to daily habits (no verbal instruction). The starting time of the data used for analysis was determined based on the driver's foot movements.

Drivers’ physical data including knee height, ankle height and shoe length, etc. were collected before the main experiments to increase the accuracy of the collected data. On the other hand, being difficult to wear, this experiment did not use the sensor carrier suit of Xsens MVN Animate. Instead, a more convenient vest carrier suit from the Xsens Awinda is used.

As shown in Table 3, a total of 10 drivers with different driving experiences, genders, and physiques were invited to participate in the experiments, including five taxi drivers, four university students, and one university teacher. Because one’s knee height is correlated with one’s stature (RxKinetics 2020), knee height was used as a variable to differentiate physiques. The group with extensive driving experience had driven an average distance of more than 1000 km, and the novice drivers were basically students who just got their licenses, which means they almost did not have any practical driving experience. Statistically, the average age of experienced drivers was 42.4 years, and the average age of novice drivers was 24.6 years. All subjects were in good health and were asked to perform 10 experiments each. No additional instructions were given by the data recording staff during the experiment.

Table 3 Specific demographic information about the subjects
Full size table

4.2 Dataset selection and pre-processing

Based on the pre-processing, a total of 100 sets of driving data of pre-braking actions (including whole-body joint coordinates, speed, moving distance, etc.) were selected for the following movement decomposing via the HHT method. Finally, the aimed measures were calculated for each data set, including the action trend, the standard variance of all IMFs’ frequency and AMP for drivers' waist, knee, and ankle during the pre-braking actions.

The traditional HHT method mainly focuses on the decomposition of whole-body movements, which means a large amount of redundant data needs to be processed before the main analysis. In this paper, according to the characteristics of the target joints’ movement, we innovatively established a method for local movements decomposition and analysis. This meant that instead of disassembling the whole-body movements directly, in order to calculate the joint angle changes, we disassembled only the selected key joints’ changing movements into different sub-actions for the analysis.

Specifically, based on the key joints calculation and HHT method mentioned above, the drivers’ pre-braking actions for their “body–right leg” part (waist, knee, and ankle) were decomposed into different sub-actions by the motion data’s frequency.

As shown in Fig. 6, through a pre-analysis, a set of braking actions can be decomposed into many sets of IMFs according to the frequency, which can be numbered according to frequency as IMF 1–6. A larger IMF number (e.g., IMF 6) indicates a higher frequency of the action performed by the subject.

Fig. 6
figure 6

Different action modes from the pre-braking behaviors

Full size image

However, based on previous studies (Thorpe et al. 1996), when converting frequency to seconds, if the time of an IMF is less than 0.1 s, then the subject has no control over it, which means that it can be considered a noise action. Therefore, in this paper, only IMFs with a time greater than 0.1 s after conversion are discussed.

The AMP of each IMF can also be obtained and represented in different colors. The closer the color is closer to red, the greater the AMP. A stronger AMP represents a greater change of joint angle, which means a greater use of force.

In this research, in order to distinguish the actions represented by different IMFs and to analyze the differences between different groups of subjects, we converted the graph-based data to row data and pre-processed them. Because their frequency/AMP fluctuates with time, except the average value, we also converted the IMF data into computable values by taking the standard variance.

Therefore, because only IMF 1 and 2 were eligible (> 0.1 s) in our data set, the measures shown in Table 4 were used for the following inter-group comparative analysis.

Table 4 The measures using for analysis
Full size table

5 Analysis results and discussion

To compare the similarities and differences in pre-braking actions between drivers with different experience, gender, and physique, this section will discuss the results both statistically and graphically.

5.1 Statistics-based comparative analysis

As the first step, the values of the quantity, range, standard deviation, and standard error, etc. of the data were confirmed using basic statistics (Table 5).

Table 5 Basic statistics for HHT method results
Full size table

As shown in Table 5, the basic statistical results showed that all results had the first layer of IMF (IMF1), but only a portion of the data had the second layer of IMF (IMF2). Because the different levels of IMF layers represent different sub-actions, it was necessary to investigate the characteristics of the data that had IMF2. Therefore, the data related to IMF2 were counted separately according to different driving experience, gender, and physique before the analysis.

As shown in Table 6, the amount of data for IMF2 was relatively balanced when grouped by driving experience and gender. However, when grouped by physique (knee height), the amount of data for the Phys.50 group was higher than the other two groups by almost three times. This may represent a higher probability that subjects in the Phys.50 group will perform the sub-action represented by IMF2 relative to the other groups.

Table 6 Amount of data for the IMF2
Full size table

Therefore, to explain the findings, we compared the differences in detail for IMF1 and IMF2 values among the different groups, which were classified by driving experience, gender, and physique.

5.1.1 Differences between drivers with different driving experience

According to the preprocessing of row data by Kolmogorov–Smirnov Normality Test, we determined that the results did not conform to a normal distribution. Therefore, to compare the differences in pre-braking actions exhibited by subjects with different driving experience, the two types of data (average and standard variance data for IMF1 and IMF2 frequency and AMP) were analyzed using independent-samples Mann–Whitney U tests.

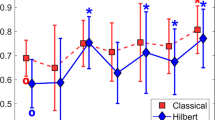
For the average data, as shown in Table 7, significant differences (p < 0.05) were identified only for the indicators Af1 of IMF1, which means that the experienced drivers had a lower speed of ankle joint movement change for sub-action IMF1.

Table 7 Results of Mann–Whitney U tests for driving experience (average data)
Full size table

For the standard variance data, as shown in Table 8, no significant differences (p < 0.05) were identified for all indicators of IMF1, which means that for drivers with different driving experience, there was no difference in their first sub-action (IMF1)’s frequency or AMP during the pre-braking action. However, unlike the results of IMF1, a significant difference was identified for measure Kfs2 and Kas2 from IMF2 (p < 0.05). This result indicates that in the group of subjects who performed the IMF2 sub-action, the experienced drivers did the IMF2 action with a greater knee vibration in both frequency and AMP than the novice drivers.

Table 8 Results of Mann–Whitney U tests for experiences (standard variance data)
Full size table

5.1.2 Differences between drivers of different genders

Next, to compare the differences in pre-braking actions exhibited by subjects of different gender, independent-samples Mann–Whitney U tests were used to analyze the data of IMF1 and IMF2’s frequency and AMP.

For the average data, as shown in Table 9, significant differences (p < 0.05) were identified for the indicators Ka1 of IMF1 and Ka2 of IMF2, and significant differences (p < 0.1) were identified for the indicator Af1, which means that the male drivers had a lower force on their knee joint for both sub-actions IMF1 and IMF2, and the male drivers may also have had a lower speed of their ankle joint movement change for sub-action IMF1. The results for Af1 and Ka2 were very similar to the results in Sect. 5.1.1 for the differences between drivers with different driving experience.

Table 9 Results of Mann–Whitney U tests for genders (average data)
Full size table

For the standard variance data, as shown in Table 10, although there was a significant difference at p < 0.1 for the Afs2 and Was2 measures of IMF2, there was no significant difference at p < 0.05 for all indicators. This means that for drivers with different gender, there was no difference in either sub-action (IMF1 and IMF2)’s frequency or AMP during the pre-braking action.

Table 10 Results of Mann–Whitney U tests for genders (standard variance data)
Full size table

5.1.3 Differences between drivers with different physiques

Finally, to compare the differences in pre-braking actions exhibited by subjects with different physiques, since some of the data does not fit the normal distribution, the Kruskal–Wallis test, one-way ANOVA test, and related post-hoc tests were used to analyze the data of IMF1 and IMF2’s frequency and AMP.

For the average data, as shown in Table 11, for IMF1, significant differences (p < 0.05) were identified for the indicators Wa1 and Ka1 of IMF1 and the indicators Wa2, Ka2, and Aa2 of IMF2. Moreover, when the significance level was relaxed to 0.1 (p < 0.1), a significant difference was confirmed for Aa1.

Table 11 Results of Kruskal–Wallis ANOVA test for physique (average data)
Full size table

As shown in Table 12, the results of post-hoc tests showed that for drivers with different physiques, a difference could only be confirmed between the Phys.50 and 55 levels. This means that drivers of Phys.50 may use a higher force than others on all joints (waist, knee, and ankle) for both sub-actions IMF1 and IMF2.

Table 12 Post-hoc test for Kas2 of IMF2 (average data)
Full size table

For the standard variance data, as shown in Table 13, significant differences (p < 0.05) were identified only for the indicator Kas2 of the IMF2. Moreover, when the significance level was relaxed to 0.1 (p < 0.1), a significant difference was also confirmed for Was2.

Table 13 Results of Kruskal–Wallis ANOVA test for physique (standard variance data)
Full size table

Similar to the results of the average data, based on the post-hoc tests for Kas2 (Table 14), the results indicate that the drivers at the Phys.55 level may have a significantly smaller knee vibration on AMP than the others for the sub-action of IMF2.

Table 14 Post-hoc test for Kas2 of IMF2 (standard variance data)
Full size table

5.1.4 Summary and discussion

In summary, for both types of data about sub-action IMF1, the results showed significant differences for measures Af1 (for different driving experience), Ka1 (for different genders), and Wa1 and Ka1 (for different physiques). Because the IMF1 sub-actions were similar for almost all subjects in terms of speed and power, IMF1 can be indicated as the common and necessary main action when pre-braking.

The results showed that during pre-braking, the experienced drivers’ ankle joint changing speed was slower than the novices, and female drivers may have had a higher force on their knee joint during the motion. Based on the results, one possible explanation is that the experienced drivers had enough anticipation of their future actions, so they moved their ankles more smoothly to maintain safety. Besides, the female drivers needed to use more force to move their lower legs via the knee joint to brake. Because braking is a common action in driving, this may cause female drivers to burn out faster while driving than males. Moreover, the related post-hoc tests for different physiques indicated similar results: the drivers that had Phys.50 needed to spend more force while pre-braking.

However, for sub-action IMF2, which existed only as part of drivers’ pre-braking behaviors, the results were more complicated. For example, the results indicated that the experienced drivers had a higher score on the measures of kfs2 and kas2, which means that for the sub-action IMF2, the experienced drivers’ knee joint’s changing movements were heavier than for the novices. These results are consistent with our previous studies (Wu et al. 2020b) that during pre-braking, experienced drivers’ foot movement distance was longer than the novice for safety (an experienced driver’s foot is kept away from the pedals to ensure the pedals are not depressed by accident), so experienced drivers needed to move their foot to the brake pad with a higher speed.

Based on our assumptions about experienced drivers (i.e., experienced drivers are safer and rationalize their driving behaviors), it can be deduced from the results that the IMF2 sub-action may be a relatively necessary safety assurance action during pre-braking.

Besides, the results also indicate that female drivers had a higher score on the measure of Ka2, similar to the sub-action IMF1. This result confirmed our hypothesis once again that female drivers tend to burn out faster while driving than males.

In addition, similar to the results of sub-action IMF1, the related post-hoc results of IMF2 indicate that the drivers with Phys.50 had a higher score on the measures Wa2, Ka2, Aa2, and Kas2, than the other two physiques, especially for Phys.55. Given the results for drivers with different driving experience, the results for different physiques can be explained because drivers with Phys.50 may have more consistent driving behaviors than the others. One possible explanation is that the driving environment of vehicles was designed primarily for divers of average size.

Therefore, in order to better explain these results, in particular to explain the results of IMF2, the motion data of subjects were compared and analyzed specifically using HHT spectra.

5.2 Graph-based Comparative Analysis

As described in Sect. 3.1, this paper focused only on the pre-braking part of the whole braking actions of the drivers. Unlike the statistical analysis, which did not take into account time, before analyzing the pre-braking actions’ HHT spectrum with time attributes, we first determined its time-relationship with the braking action of drivers.

First, we extracted the coordinates data of one driver's tiptoe during the pre-braking action and depicted in Fig. 7 its height change trajectory on the z-axis. This driver’s movements typically took about 6 s. In Fig. 7a, we can clearly see that the driver's tiptoe action during the pre-braking action went through a process of raising, reaching the peak, starting to land, and then touching the brake plate. The green dotted line shows the approximate area where the toe moves to its highest point, and the red dotted line shows the approximate point at which the pre-braking action ends.

Fig. 7
figure 7

Results of tiptoe motion and HHT spectra for waist, knee, and ankle

Full size image

Meanwhile, to facilitate comparison, we standardized the data for different lengths of time and resampled all motion samples to 0.65 s (average time) using linear interpolation. As the result, we calculated the average HHT spectrum for waist, knee, and ankle from all collected data (Fig. 7b–d). To compare these spectra by each group, the amplitudes of waist, knee, and ankle were set to 0 ~ 0.1 degrees, 0 ~ 0.5 degrees, and 0 ~ 2.0 degrees, respectively, because these ranges were appropriate enough to investigate the features among the three groups.

By calibrating the end time (red dashed line, meaning the foot touched the brake pad at about 0.6 s) of tiptoe action and HHT spectra, the results showed that the values of AMP were weaker (bluer) than others in the time period of 0.3 to 0.5 s (green dashed lines) in all HHT spectra, and the time period just coincided with the time period where the subject's tiptoe reached the peak (the curve flattened out).

These results may indicate that most drivers tend to diminish the forces used by their waist, ankle, and knee when the foot reaches the peak. Although each driver took slightly different amounts of time to do the pre-braking movements, the feature of time period from 0.3 to 0.5 s in the figure can be considered as a sign that a driver’s foot has reached the longitudinal peak point, which provided an important reference for the next analysis of the meaning of the various IMF sub-actions. In this study, we defined the time period from about 0.1 to 0.6 s as the main period, and the time period from 0.3 s to 0.5 s as the P period.

5.2.1 Sub-actions IMF1 and IMF2

Because the target IMF1 and IMF2 existed in the complex spectrum, we extracted them separately for the analysis at first. Figure 8 describes the average spectrum of IMF1 for the joints of waist, knee, and ankle.

Fig. 8
figure 8

Results of average IMF1 spectrum for waist, knee, and ankle during pre-braking

Full size image

As shown in Fig. 8, IMF1 had a relatively smooth frequency curve for all joints (waist, knee, and ankle), and during the main time period (about 0.1 ~ 06 s, including P period), its AMP showed a gentle decreasing trend. Because the frequency can represent the action speed and AMP can represent the force used, IMF1 fits our understanding of general pre-braking behaviors (uniform speed, AMP becomes smaller). These results may mean that the sub-action IMF1 may represent the basic action in whole pre-braking behaviors (raising the right foot to the brake plate; regular actions a, b, and c in Fig. 1).

However, compared to sub-action IMF1, sub-action IMF2 had a higher frequency, which may mean that the action represented by IMF2 was redundant or contained/involved assistant actions that were distinct from the basic action.

As shown in Fig. 9, IMF2 had a more oscillating curve than IMF1, which was characterized by a wave peak in P period (for knee and ankle), which means that the IMF2 sub-actions in P period would experience a process of surge and decrease in speed. Meanwhile, compared with IMF1, we also found that its AMP presented a drastically decreasing trend, and the stronger AMP occurred outside the P period (focus on the front), which could mean that the actions represented by IMF2 occurred mainly during the lift phase of the subject's foot. Combined with the results of statistical analysis and the conclusions of our previous research (Wu et al. 2020b), we speculate that IMF2 represents the transverse movement of the driver's foot. As a safety precaution, some drivers keep their feet as far away from the brake pad as possible. This results in significant lateral foot movement during braking.

Fig. 9
figure 9

Results of average IMF2 spectrum for waist, knee, and ankle during pre-braking

Full size image

However, according to the statistical analysis results of Sect. 5.1, some statistical differences were found between the different groups. Therefore, in order to validate our discussion of the results and to better analyze the differences found in Sect. 5.1, we compared the IMF1 and IMF2’s graphs of different groupings.

5.2.2 Graph comparative analysis of IMF1

As shown in Fig. 10, all drivers performed the IMF1 sub-action. Based on the results of statistical analysis for different driving experience of sub-action IMF1 (Novice > Exp. for Af1), we confirmed that the results in the graph were consistent with our previous conclusions. The results mainly showed that after P period, novice drivers tended to drop their foot more quickly, which is consistent with the results of our previous research (Wu et al. 2020b). In addition, by comparing the AMPs of each graph, we can determine that the novice drivers were more inclined to counterbalance the force used throughout the pre-braking process, rather than being as focused as the experienced driver.

Fig. 10
figure 10

Results of graph comparative analysis with different driving experience for IMF1

Full size image

Similar situations were found for different genders. As shown in Fig. 11, based on the results of statistical analysis of different genders for sub-action IMF1 (Female > Male for Ka1), the difference in the graph for the main time period was confirmed, especially before P period. In addition, by comparing the graphs, we found that the curve of the male was relatively smoother, which means that the speed change of the female knee joint was more drastic during the pre-braking process.

Fig. 11
figure 11

Results of graph comparative analysis with different gender for IMF1

Full size image

Moreover, As shown in Fig. 12, based on the results of statistical analysis of different genders for sub-action IMF1 (Phys.50 > Phys.55 for Wa1 and Ka1), the significant difference of AMP can easily be confirmed on the graphs. In addition, we also found among the graphs, that Phys.50 may have the highest performance for AMP during the main time period.

Fig. 12
figure 12

Results of graph comparative analysis of different physiques for IMF1

Full size image

In summary, for the sub-action IMF1 of pre-braking behaviors, in addition to identifying some differences in AMPs (shown in Sect. 5.1), there were no significant differences between groups in other measures. The results were in line with our expectation for IMF1 (a basic action of pre-braking). However, some differences for AMPs were big enough to be considered in future assisted driving designs.

5.2.3 Graph comparative analysis of IMF2

Only some of drivers may perform the IMF2 sub-action, based on the statistical analysis of different driving experiences for sub-action IMF2 (Exp. > Novice for Kfs2 and Kas2). As shown in Fig. 13, we confirmed that the results in the graph were consistent with our previous conclusion. Similar to the results of IMF1, the experienced drivers’ frequencies changed more smoothly, and their AMP values were stable and showed a decreasing trend.

Fig. 13
figure 13

Results of graph comparative analysis with different driving experience for IMF2

Full size image

Next, as shown in Fig. 14, based on the statistical analysis of different genders for sub-action IMF2 (Female > Male for Ka2), we found that significantly higher AMP values of females mainly occurred before P period, which was consistent with our previous discussion. In addition, we found that the frequency curve was smoother for men and experienced drivers.

Fig. 14
figure 14

Results of graph comparative analysis of different genders for IMF2

Full size image

Finally, as shown in Fig. 15, based on the statistical analysis of different physiques for sub-action IMF2 (Phys.50 > Phys.55 for Wa2, Ka2, Aa2, and Kas2), we confirmed the same difference in the graphs, which supported the discussion in the previous section. In addition, similar to the results for IMF1, we confirmed that Phys.50 may have the highest performance for AMP during the main time period. Moreover, by comparing all the plots, we found that Phys.50, as well as men and experienced drivers, had the smoothest frequency curve.

Fig. 15
figure 15

Results of graph comparative analysis of different physiques for IMF2

Full size image

In summary, for the sub-action IMF2 of pre-braking behaviors, we confirmed most of the differences at the AMP level, which confirmed our discussion results in Sect. 5.1. Moreover, we found a pattern that some groups (experienced drivers, males, Phys.50) had smoother frequency curves and their AMP decreased at a constant rate. Based on the assumption that experienced drivers behave more efficiently, we conclude that males and Phys.50 drivers may have performed relatively better under the current experimental conditions.

The related results demonstrate that a good driving environment needs to be fine-tuned according to the individual elements (driving experiments, gender and physique, etc.) of the specific driver. Which means that the findings of this study can provide data to support future assisted driving systems that automate the adjustment of the driving environment and apply the personalized training of novice drivers in the future.

6 Conclusion

To discover similarities and differences in pre-braking behaviors among drivers with different driving experience, genders, and physiques, this study analyzed drivers' pre-braking related local body joints movements by using a motion capture device and provided a Hilbert–Huang Transform (HHT)-based local human body movement analysis method to decompose the realistic complex pre-braking actions into many sub-actions by their frequencies.

Based on the results of angle analysis for 50 sets of experimental motion data collected from 10 drivers, the Hilbert–Huang Transform method found two important sub-actions during pre-braking: IMF1 and IMF2.

For these two sub-actions, based on related statistical analyses, the results showed that sub-action IMF1 may be the common and necessary action during pre-braking and sub-action IMF2 is a relatively necessary safety assurance action during pre-braking, because only some drivers performed the IMF2 sub-action. Based on this, we verified that IMF2 was the right foot transverse movement at the beginning part of the pre-braking process, which confirmed our previous work (Wu et al. 2020b).

Based on the graph-based comparative analysis and the assumption that experienced drivers behave more efficiently, we found that some groups (experienced, males, Phys.50) had consistent characteristics (smoother frequency curves and uniformly decreasing AMP values), which could mean that in this experimental environment, such drivers would have better performance and efficiency. For example, female drivers may tend to use more force to perform braking actions. Moreover, existing models of vehicles may be designed for people of medium size (Phys.50), so additional designs or devices may be necessary for drivers of other sizes. These results can be applied to the individualized training of new drivers and the development of related assistance systems in the future.

This study, which examined the differences in body movements during pre-braking between drivers with different characteristics, had some limitations: 1) for reasons of time and equipment, the sample size of 100 was small; 2) this study was merely explorative, and the statistical results may not to be taken as confirmatory.

In future work, we plan to conduct more relevant experiments and consider additional elements to enrich the driver behavior model. Moreover, we plan to collectively analyze eye-tracking data and motion capture data to determine the relationship between drivers' eye movements and body movements during braking.