Quantum circuits for discrete graphical models

Abstract

Graphical models are useful tools for describing structured high-dimensional probability distributions. The development of efficient algorithms for generating samples thereof remains an active research topic. In this work, we provide a quantum algorithm that enables the generation of unbiased and independent samples from general discrete graphical models. To this end, we identify a coherent embedding of the graphical model based on a repeat-until-success sampling scheme which clearly identifies whether a drawn sample represents the underlying distribution. Furthermore, we show that the success probability for finding a valid sample can be lower bounded with a quantity that depends on the number of maximal cliques and the model parameter norm. Moreover, we rigorously proof that the quantum embedding conserves the key property of graphical models, i.e., factorization over the cliques of the underlying conditional independence structure. The quantum sampling algorithm also allows for maximum likelihood learning as well as maximum a posteriori state approximation for the graphical model. Finally, the proposed quantum method shows potential to realize interesting problems on near-term quantum processors. In fact, illustrative experiments demonstrate that our method can carry out sampling and parameter learning not only with idealized simulations of quantum computers but also on actual quantum hardware solely supported by simple readout error mitigation.

1 Introduction

Modelling the structure of direct interaction between distinct random variables is a fundamental sub-task in various applications of artificial intelligence (Wang et al. 2013), including natural language processing (Lafferty et al. 2001), computational biology (Kamisetty et al. 2008), sensor networks (Piatkowski et al. 2013), and computer vision (Yin and Collins 2007). Probabilistic models, such as discrete graphical models (Wainwright and Jordan 2008), allow for an explicit representation of these structures and, hence, build the foundation for various classes of machine learning techniques. Existing literature on quantum algorithms for learning and inference of probabilistic models include quantum Bayesian networks (Low et al. 2014), quantum Boltzmann machines (Amin et al. 2018; Kieferova and Wiebe 2017; Wiebe and Wossnig 2019; Zoufal et al. 2021), and Markov random fields (Zhao et al. 2021; Bhattacharyya 2021; Nelson et al. 2021). These methods are either approximate or strongly rely on so-called fault-tolerant quantum computers—a concept that cannot yet be realized with the state-of-the-art quantum hardware. In this work, we derive a quantum circuit construction for probabilistic graphical model sampling that is exact and shows promise for scalability with near-term quantum computing hardware.

While discrete graphical models are powerful and may be employed for diverse use-cases, their applicability can face difficulties. More specifically, for structures with high-order interactions, probabilistic inference can become challenging. This stems from the fact that the calculation of the related normalizing constant is in general computationally intractable. A common way to circumvent the explicit evaluation of the normalizing constant is to compute the quantities of interest based on samples which are drawn from the graphical model. The problem of generating samples from graphical models has already been discussed in seminal works on the Metropolis-Hastings algorithm (Metropolis et al. 1953; Hastings 1970) and Gibbs sampling (Geman and Geman 1984). As of today, Markov chain Monte Carlo (MCMC) methods are still the most commonly used approach to generate samples from high-dimensional graphical models—a model’s dimension refers to the number of vertices of the underlying graph. MCMC methods are iterative, i.e., an initial guess is randomly modified repeatedly until the chain converges to the desired distribution. The actual time until convergence is model dependent (Bubley and Dyer 1997) and in general intractable to compute. A more recent promising line of research for sampling relies on random perturbations of the model parameters. These perturb-and-MAP (PAM) techniques (Hazan et al. 2013) compute the maximum a posterior (MAP) state of a graphical model whose potential function is perturbed by independent samples from a Gumbel distribution. The resulting perturbed MAP state can be shown to be an unbiased independent sample from the underlying graphical model. Assigning the correct Gumbel noise (see Appendix A.1 for details) and solving the MAP problem both result in algorithmic runtimes that are exponential in the number of variables. Efficient perturbations have been discovered (Niepert et al. 2021), sacrificing the unbiasedness of samples while delivering viable practical results. However, the exponential time complexity of MAP computation renders the method intractable.

In this work, we propose a method for generating unbiased and independent samples from discrete undirected graphical models on quantum processors—quantum circuits for graphical models (QCGM). The samples may be used accordingly for maximum likelihood learning, MAP state approximation, and other inference tasks. Instead of an iterative construction of samples as in MCMC or a perturbation as in PAM, our method coherently generates samples from measurements of a quantum state that reflects the probability distribution underlying the graphical model. The state preparation algorithm employs a repeat-until-success scheme where a subsystem measurement informs us whether a sample is drawn successfully or if it has to be discarded with a success probability that is independent of the number of variables. This is in contrast to MCMC or PAM samplers where individual samples are not guaranteed to reflect the properties of the desired probability distribution. Notably, the resources for QCGM scale in the worst-case exponentially in the number of cliques and the model parameter vector which can be a significant improvement compared to classical methods. To prove the practical viability of our approach, we provide proof-of-concept experimental results with quantum simulation as well as actual quantum hardware. Notably, the average fidelity of the quantum hardware results executed with simple readout error mitigation is 0.987. These results show that our method has the potential to enable unbiased and statistically sound sampling and parameter learning for practically interesting problems on near-term quantum computers.

2 Problem definition

In this section, we formalize the preliminaries and define the problem of drawing unbiased and independent samples from a graphical model using a coherent quantum embedding for Gibbs state preparation. Hence, this section sets the stage for the main results presented in Section 3. To simplify notation, we frequently use the short hand notation $A\oplus B:=|0\rangle \langle 0|\otimes A + |1\rangle \langle 1|\otimes B$ for scalars or matrices A and B.

2.1 Parametrized family of models

We consider positive joint probability distributions over n discrete variables $\varvec{X}_v$ with realizations $\varvec{x}_v\in \{0,1\}$ for $v\in V$. The set of variable indices $V=\{1,\dots ,n\}$ is referred to as vertex set and its elements $v\in V$ as vertices. Without loss of generality, the positive probability mass function (pmf) of the n-dimensional random vector $\varvec{X}$ can be expressed as

$$\begin{aligned} \mathbb {P}_{\varvec{\theta },\phi }(\varvec{X}=\varvec{x}) = \frac{1}{Z(\varvec{\theta })} \exp \left( \sum _{j=1}^d\varvec{\theta }_j \phi _j(\varvec{x}) \right) , \end{aligned}$$

(1)

where $\phi =(\phi _1,\dots ,\phi _d)$ is a set of basis functions or sufficient statistics that specify a family of distributions and $\varvec{\theta }\in \mathbb {R}^d$ are parameters that specify a model within this family. Each basis function $\phi _i$ depends on a specific sub-set $C\subseteq V$ of vertices—we call C a clique, and its vertices are called connected. Thus, $\phi$ implies a graphical structure $G=(V,E)$ among all vertices, called conditional independence structure. The number of parameters, d, is the sum over all clique states: $d=\sum _{C\in \mathcal {C}}2^{|C|}$, i.e., a clique C that contains |C| vertices has $2^{|C|}$ distinct clique states.

When $\phi$ is clear from the context, we simply write $\mathbb {P}_{\varvec{\theta }}$ and drop the explicit dependence on $\phi$. The quantity $Z(\varvec{\theta })=\sum _{\varvec{x}\in \{0,1\}^n} \exp \sum _{j=1}^d\varvec{\theta }_j \phi _j(\varvec{x})$ denotes the model’s partition function and is required for normalization such that $\mathbb {P}$ becomes a proper probability mass function. Equation 1 can be rewritten as

$$\begin{aligned} \mathbb {P}_{\varvec{\theta }}(\varvec{X}=\varvec{x})&= \frac{1}{Z(\varvec{\theta })} \prod _{C\in \mathcal {C}} \exp \left( \sum _{\varvec{y}\in \{0,1\}^{|C|}} \varvec{\theta }_{C,\varvec{y}} \phi _{C,\varvec{y}}(\varvec{x}) \right) \nonumber \\&\quad = \frac{1}{Z(\varvec{\theta })} \prod _{C\in \mathcal {C}} \psi _C(\varvec{x}_C), \end{aligned}$$

(2)

where $\mathcal {C}$ denotes the set of maximal cliques of the graph implied by $\phi$. A clique is maximal when no other clique contains it—e.g., the graph consists of two maximal cliques of size 3. The equality between (1) and (2) is known as the Hammersley-Clifford theorem (Hammersley and Clifford 1971). Setting

$$\begin{aligned} \phi _{C,\varvec{y}}(\varvec{x}) = \prod _{v\in C} \mathbbm {1}(\varvec{x}_v = \varvec{y}_v), \end{aligned}$$

(3)

is sufficient for representing any arbitrary pmf with conditional independence structure G (Pitman 1936; Besag 1975; Wainwright and Jordan 2008). In this case, the graphical model is called Markov random field. Moreover, $\phi (\varvec{x})=(\phi _{C,\varvec{y}}(\varvec{x}):C\in \mathcal {C}, \varvec{y}\in \{0,1\}^{|C|})$ represents an overcomplete family, since there exists an entire affine subset of parameter vectors $\varvec{\theta }$, each associated with the same distribution.

In machine learning, the maximum likelihood principle is applied to estimate the parameters of Eq. 1 based on a given data set $\mathcal {D}$.

2.2 Quantum embedding of probabilistic graphical models

Classically generating samples from Eq. 1 via naive inversion sampling is intractable as there are $\mathcal {O}(2^n)$ distinct probabilities involved. For special types of graphical models, e.g., decomposable models, the graphical structure can be exploited to yield inference methods whose time complexity is instead exponential in the size of the largest clique (Wainwright and Jordan 2008) and not in the number of variables. These methods are efficient whenever the size of the largest clique is bounded. However, in the general non-decomposable case, structure cannot be exploited. The aim of this work is hence to devise a coherent quantum embedding which enables an efficient sampling process for general graphical models. More explicitly, we prepare a quantum state whose sampling behavior reflects the sampling behavior of a graphical model. For this purpose, a Hamiltonian $H_{\varvec{\theta }}$ is defined which represents the conditional independence structure of the graphical model. Furthermore, the non-unitary mapping $\exp (-H_{\varvec{\theta }})$ is implemented by a gate-based quantum circuit $\varvec{C}$. Applying $\exp (-H_{\varvec{\theta }})$ to an initial state given as $|+\rangle ^{\otimes n}$, where n corresponds to the number of discrete variables in the graphical model, gives a Gibbs state of the form $2^{-n}{\exp (-H_{\varvec{\theta }})}$. Measuring this quantum state in the computational basis lets us directly extract unbiased samples that are generated by the graphical model at hand. Notably, a (unitary) quantum circuit $\varvec{C}$ mapping of the (non-unitary) transformation $\exp (-H_{\varvec{\theta }})$ requires the use of $n_{\varvec{a}}$ auxiliary qubits $\varvec{a}$, corresponding to a random variable $\varvec{A}$. The successful implementation of $\exp (-H_{\varvec{\theta }})$ is conditioned on measuring $\varvec{a}$ in the $|0\rangle ^{\otimes n_{\varvec{a}}}$ state. Hence, the probability for measuring a specific bit string $\varvec{x}$ from the graphical model as the output of the circuit may be written in terms of the Born rule as follows:

$$\begin{aligned} \mathbb {P}_{\varvec{C}}(\varvec{X}= \varvec{x},\varvec{A}=\varvec{0}) = \left| \left( \langle 0|^{\otimes n_{\varvec{a}}}\otimes \langle \varvec{x}|\right) \varvec{C}\left( |0\rangle ^{\otimes n_{\varvec{a}}}\otimes |+\rangle ^{\otimes n}\right) \right| ^2. \end{aligned}$$

(4)

Now, we can formally define the sampling problem.

Definition 1

(Graphical model quantum state preparation problem) Given any discrete graphical model over n binary variables, defined via $(\varvec{\theta },\phi )$, find a quantum circuit $\varvec{C}$ which maps an initial quantum state $|+\rangle ^{\otimes n}$ to a quantum state such that

$$\begin{aligned} \mathbb {P}_{\varvec{\theta }}(\varvec{X}= \varvec{x}) = \frac{ \mathbb {P}_{\varvec{C}}(\varvec{X}= \varvec{x},\varvec{A}=\varvec{0})}{\mathbb {P}_{\varvec{C}}(\varvec{A}= \varvec{0})}, \end{aligned}$$

(5)

as specified by Eqs. 1 and 4. Moreover, when $\varvec{A}\not =0$, the relation between $\mathbb {P}_{\varvec{\theta }}(\varvec{X}= \varvec{x})$ and $\mathbb {P}_{\varvec{C}}(\varvec{X}= \varvec{x},\varvec{A}\not =\varvec{0})$ is undefined. We denote the quantity $\mathbb {P}_{\varvec{C}}(\varvec{A}= \varvec{0})$ as “success probability.”

In what follows, we will eventually derive a circuit $\varvec{C}$ for which $\mathbb {P}_{\varvec{C}}(\varvec{A}=\varvec{0})$ is provably lower bounded by $\exp (-|\mathcal {C}|\Vert \varvec{\theta }\Vert _\infty )$, i.e., the success probability decays exponentially in the number of cliques and the norm of the parameter vector. In other words, the success probability is at least $\delta$ when $\Vert \varvec{\theta }\Vert _\infty \le -\log (\delta )/|\mathcal {C}|$.

Algorithm 1

Pauli-Markov sufficient statistics.

3 Main results

We devise the quantum algorithm QCGM in which each vertex of a graphical model over binary variables is mapped to one qubit of a quantum circuit. In addition, $|\mathcal {C}|+1$ auxiliary qubits are required to realize specific operations as explained below. Our result consists of two parts. First, we present a derivation of the Hamiltonian $H_{\varvec{\theta }}$ encoding the un-normalized, negative log-probabilities. Then, we employ $H_{\varvec{\theta }}$ to construct a quantum circuit that allows us to draw unbiased and independent samples from the respective graphical model.

3.1 The Hamiltonian

We start by transferring the sufficient statistics of the graphical model family into a matrix form which allows us to construct a $|C_{\max }|-$local Hamiltonian $H_{\varvec{\theta }}$ that encodes the parameters $\varvec{\theta }$ as well as the conditional independence structure G–with $C_{\max }$ corresponding to the largest clique in $\mathcal {C}$ and $|C_{\max }|$ to the number of nodes in $C_{\max }$. We now explain, step by step, how this Hamiltonian is constructed.

Definition 2

(Pauli-Markov sufficient statistics) Let $\phi _{C,\varvec{y}}:\{0,1\}^n\rightarrow \mathbb {R}$ for $C\in \mathcal {C}$ and $\varvec{y}\in \{0,1\}^{|C|}$ denote the sufficient statistics of some overcomplete family of graphical models. The diagonal matrix $\Phi _{C,\varvec{y}} \in \{0,1\}^{2^n \times 2^n}$, defined via

$$\begin{aligned} (\Phi _{C,\varvec{y}})_{i,j} = {\left\{ \begin{array}{ll} \phi _{C,\varvec{y}}(\varvec{x}^{(j)}),&{}\text {if }i=j\\ 0,&{}\text {otherwise}, \end{array}\right. } \end{aligned}$$

(6)

denotes the Pauli-Markov sufficient statistic, where $\varvec{x}^{(j)}$ denotes the j-th full n-bit joint configuration w.r.t. some arbitrary but fixed order.

A naive computation of the Pauli-Markov sufficient statistic for any fixed $(C,\varvec{y})$-pair is intractable due to the sheer dimension of $\Phi _{C,\varvec{y}}$. However, it turns out that $\Phi _{C,\varvec{y}}$ can be efficiently represented with a linear number of Kronecker products of single-qubit Pauli matrices as is described in Algorithm 1. In a nutshell, the algorithm marks all full joint states that coincide with $\varvec{y}\in \{0,1\}^{|C|}$ by setting the corresponding diagonal entry in the matrix $\Phi$ to 0 or 1, respectively.

Obviously, the Pauli representation of the tensor product computed by Algorithm 1 has length $\Theta (n)$. Hence, the algorithm runs in time linear in n. The correctness of Algorithm 1 is implied by the following theorem.

Theorem 1

(Statistics) Algorithm 1 computes $\Phi _{C,\varvec{y}}$ with $\mathcal {O}(n)$ Kronecker products.

The reader will find the proof of Theorem 1 in Appendix 3. Next, we may use the construction from Algorithm 1 to define $H_{\varvec{\theta }}$ which accumulates the conditional independence structure G of the underlying random variable via $\Phi _{C,\varvec{y}}$ as well as the model parameters $\varvec{\theta }$ as the first part of our main result—stated in the following theorem.

Theorem 2

(Hamiltonian) Assume an overcomplete binary graphical model specified by $(\varvec{\theta },\phi )$ encoded into a $|C_{\max }|-$ local Hamiltonian $H_{\varvec{\theta }} = -\sum _{C\in \mathcal {C}} \sum _{\varvec{y}\in \{0,1\}^{|C|}} \varvec{\theta }_{C,\varvec{y}} \Phi _{C,\varvec{y}}$ with $|C_{\max }|$ denoting the number of nodes in the largest clique $C_{\max }$ in $\mathcal {C}$, then $\mathbb {P}_{\varvec{\theta }}(\varvec{x}^{(j)})={\text {Tr}}\left[ {|j\rangle \langle j|\exp (-H_{\varvec{\theta }})}/{\text {Tr}}\left[ \exp \right. \right. \left. \left. (- H_{\varvec{\theta }})\right] \right]$ where ${\text {Tr}}$ is the trace and $|j\rangle \langle j|$ acts as projector on the $j^{\text {th}}$ diagonal entry of the matrix $\exp (-H_{\varvec{\theta }})/{\text {Tr}}\left[ \exp \right. \left. (-H_{\varvec{\theta }})\right]$.

The reader will find the proof of Theorem 2 in Appendix 4.

3.2 The circuit

Based on the Hamiltonian $H_{\varvec{\theta }}$ from the previous section, we now construct a circuit that implements the non-unitary operation $\exp {\left( - H_{\varvec{\theta }}\right) }$. The construction relies on the unitary embedding of $H_{\varvec{\theta }}$, which corresponds to a special pointwise polynomial approximation, and the factorization over the cliques. Application of this quantum circuit results in a quantum state whose sampling distribution is proportional to that of any desired graphical model over binary variables. Our findings are summarized in the following theorem.

Theorem 3

(Quantum circuit for discrete graphical models) Given any overcomplete discrete graphical model over n binary variables, defined via $(\varvec{\theta },\phi )$ with $\varvec{\theta }\in \mathbb {R}^d$. There exists a quantum circuit $\varvec{C}_{\varvec{\theta }}$ over $m=n+1+|\mathcal {C}|$ qubits that prepares a quantum state whose sampling distribution is equivalent to the graphical model. That is, it solves Problem 1, namely $\mathbb {P}_{\varvec{\theta }}(\varvec{x}) = \mathbb {P}_{\varvec{C}_{\varvec{\theta }}}(\varvec{X}=\varvec{x},\varvec{A}=\varvec{0})/\mathbb {P}_{\varvec{C}_{\varvec{\theta }}}(\varvec{A}=\varvec{0})$.

The reader will find the proof of Theorem 3 in Appendix 3. In practice, samples from the discrete graphical model are drawn by measuring the joint state of auxiliary and target qubits and discarding those samples where any of the auxiliary qubits is measured as $|1\rangle$. More explicitly, depending on the outcome of auxiliary qubit measurements, a sample is either valid and can be kept or has to be discarded if any auxiliary qubit is measured as $|1\rangle$.

Corollary 1

(Sampling success probability) The success probability for measuring a sample $\varvec{x}$ with a quantum circuit sufficing Theorem 3 is lower bounded via

$$\begin{aligned} \mathbb {P}(\text {\texttt {SUCCESS}})=\mathbb {P}_{\varvec{C}_{\varvec{\theta }}}(\varvec{A}=\varvec{0}) \ge \exp (-|\mathcal {C}|\Vert \varvec{\theta }\Vert _\infty )\;. \end{aligned}$$

Corollary 1 is proven in Appendix 6. It should be noted that while the lower bound on the success probability depends on the number of cliques, it is independent of the total number of variables. Interestingly, setting $\Vert \varvec{\theta }\Vert _\infty = k \log \left( \root |\mathcal {C}| \of {n} \right)$ expresses our lower bound on the success probability as a polynomial in n, i.e., $\mathbb {P}(\text {\texttt {SUCCESS}}) \ge n^{-k}$, for some constant k.

Fig. 1

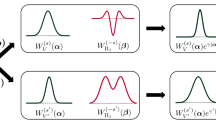
Exemplary quantum circuit $\varvec{C}_{\varvec{\theta }}$ as specified in Eq. 9. In this example, the underlying graph has vertex set $V=\{v_0,v_1,v_2\}$ and clique set $\mathcal {C}=\{A,B\}$. The circuit requires |V| target qubits denoted by the qubits $x_0,x_1,x_2$ and $|\mathcal {C}|+1=3$ auxiliary qubits, $a_0$ for the unitary embedding $U^j$ of the Hamiltonian characterizing the sufficient statistic and one for the real part extraction of each clique, i.e., $a_1$ and $a_2$

An exemplary circuit according to Theorem 3 is shown in Fig. 1. Each vertex in the graph is identified with a circuit qubit, i.e., the first n qubits of the circuit realize the target register $|\varvec{x}\rangle$ that represents the n binary variables of the graphical model. Furthermore, the latter $n_{\varvec{a}}=1+|\mathcal {C}|$ qubits represent an auxiliary register $|\varvec{a}\rangle$ which is required for the unitary embedding and the extraction of real parts as described in Appendix 3. The Hadamard gates at the beginning are required to bring the target register into the state $|+\rangle ^{\otimes n}$, as described in Section 2.2. The structural information corresponding to the cliques can be seen to be implemented via a unitary embedding. Finally, the sample readout is realized via a measurement of the target system and conditioned on the measurement outcome of the last $|\mathcal {C}|$ auxiliary qubits. Notably, these auxiliary qubits can already be measured before sampling the state of $|\varvec{x}\rangle$. This allows for an early restart whenever real part extraction fails.

The unitaries $U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}})$ are manipulating the quantum state to achieve proportionality to $\mathbb {P}_{\varvec{\theta }}$ with the target register $|\varvec{x}\rangle$. More specifically, these unitaries embed the statistics $\exp (\varvec{\theta }_{C,\varvec{y}} \Phi _{C,\varvec{y}})$ where $\Phi _{C,\varvec{y}}$ is computed via Algorithm 1. The embedding is

$$\begin{aligned} U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}})&= I^{\otimes n+1} + (\exp (i2\varvec{\gamma }_{C,\varvec{y}})\nonumber \\&\quad -1) (\Phi _{C,\varvec{y}} \oplus (I^{\otimes n} - \Phi _{C,\varvec{y}})) \end{aligned}$$

(7)

with $\varvec{\gamma }_{C,\varvec{y}} = (1/2) \arccos (\exp (\varvec{\theta }_{C,\varvec{y}}))$. The decomposition of $U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}})$ into basis gates is explained in Section 3.3. We see from Eq. 7 that the first auxiliary qubit arises from the construction of $U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}})$. Moreover, a real part extraction is required for each

$$\begin{aligned} U^C = \prod _{\varvec{y}\in \{0,1\}^{|C|}} U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}})\;. \end{aligned}$$

(8)

As described in Appendix 2, real part extraction is a repeat-until-success procedure—an auxiliary qubit indicates whether the extraction was successful. Since real parts of all $U^C$ are required, this contributes $|\mathcal {C}|$ additional auxiliary qubits, which gives us a total of $n_{\varvec{a}}=1+|\mathcal {C}|$. Making the real part extraction explicit reveals that our circuit construction shares a defining property of undirected graphical models.

Corollary 2

(Unitary Hammersley-Clifford) Take $U^C$ from Eq. 7 and set

$$ \tilde{U}_C = H_j ( I^{\otimes (|\mathcal {C}|-j-1)} \otimes ( ( I^{\otimes j} \otimes U^C) \oplus (I^{\otimes j} \otimes {(U^C)}^{\dagger } ))) H_j\;, $$

where $j:=j(C)$ is the 0-based index of the clique C in some arbitrary but fixed ordering of all cliques $\mathcal {C}$, and $H_j:= I^{\otimes (|\mathcal {C}|-j-1)} \otimes H \otimes I^{\otimes (n+1+j)}$. The circuit can then be rewritten as

$$\begin{aligned} \varvec{C}_{\varvec{\theta }} = \prod _{C\in \mathcal {C}} \tilde{U}^C\;, \end{aligned}$$

(9)

which reveals the clique factorization of probabilistic graphical models, as predicted by the Hammersley-Clifford theorem (Hammersley and Clifford 1971).

3.3 Decomposition of clique gates

At the core of our circuit construction lies a unitary embedding of the clique factors for each clique C and each corresponding clique-state $\varvec{y}\in \{0,1\}^{|C|}$ as given by Eq. 7. To arrive at a decomposition of $U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}})$ in terms of basis gates, one has to notice two facts: (i) $U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}})$ is diagonal, and (ii) the diagonal of $U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}})$ carries only two distinct values, namely $u_0=1$ and $u_1=\exp (i2\varvec{\gamma }_{C,\varvec{y}})$. Any unitary U with these properties can be decomposed whenever one can identify a unitary $U_f: |\varvec{x},a\rangle \rightarrow |\varvec{x},a~\texttt {XOR}~f(\varvec{x})\rangle$ with $f: \{0,1\}^n \rightarrow \{0,1\}$ such that the function value of f at $\varvec{x}$ indicates whether the corresponding diagonal entry is the first or the second value (Hogg et al. 1999, [Section 2.1]). We now apply this construction to find a decomposition of our clique gates.

Theorem 4

(Decomposition) Consider $U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}})$ from Eq. 7. It is $U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}}) = U^{C,\varvec{y}}_{\texttt {AND}} ( P(2\varvec{\gamma }_{C,\varvec{y}}) \otimes I^{\otimes n} ) U^{C,\varvec{y}}_{\texttt {AND}}$. Here, P is a phase gate, and $U^{C,\varvec{y}}_{\texttt {AND}}$ is a Boolean-AND gate over qubits in C, whose inputs are negated in accordance with $\varvec{y}$.

The reader will find the proof of Theorem 4 in Appendix 7. Finally, the above result implies an upper bound on the depth of $\varvec{C}_{\varvec{\theta }}$.

Corollary 3

(Depth of $\varvec{C}_{\varvec{\theta }}$) The depth of $\varvec{C}_{\varvec{\theta }}$ is in $\mathcal {O}(d\times {\text {depth}}(\texttt {AND}))$.

The corollary follows by observing that $\varvec{C}_{\varvec{\theta }}$ essentially consists of d $U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}})$ gates, which itself consist of two AND gates. Here, ${\text {depth}}(\texttt {AND})$ denotes the circuit depth of a unitary operator that implements a Boolean AND over $|C_{\max }|$ qubits (Nielsen and Chuang 2016).

4 Limitations

As shown in Corollary 1, drawing an unbiased and independent sample might fail with probability $1-\delta \le 1-\exp (-|\mathcal {C}|\Vert \varvec{\theta }\Vert _{\infty })$. The practical impact of this fact is studied in the experiments. However, measuring the extra qubits tells us whether the real part extraction succeeded. In expectation, we have to repeat the procedure at most $\exp (|\mathcal {C}|\Vert \varvec{\theta }\Vert _{\infty })$ times until we observe a success. As shown in Appendix 6, the exact success probability depends on $Z(\varvec{\theta })$.

In fact, computing this quantity requires a full and hence exponentially expensive simulation of the quantum system. In practice, we only have access to an empirical estimate $\hat{\delta }:=\hat{\mathbb {P}}(\text {\texttt {SUCCESS}})$ obtained from multiple QCGM runs. Amplification techniques (Brassard et al. 2000; Grover 2005; Yoder et al. 2014; Gilyen et al. 2019) can help us to increase the success probability at the cost of additional auxiliary qubits or a higher circuit depth. Specifically, applying a singular value transformation (Gilyen et al. 2019) can raise $\delta$ to $1 - \varepsilon$ for any desired $\varepsilon >0$ with additional depth $\Omega (\log (1/\varepsilon )\sqrt{\delta })$. Moreover, the real part extraction necessitates the use of additional auxiliary qubits—one per graph clique. The increase in qubit number can be prohibitive for the realization of large models with current quantum computers. In principle, the number of auxiliary qubits may be reduced with intermediate measurements. Since the real part extractions are applied in series, one may use a single auxiliary qubit which is measured and reset to $|0\rangle$ after every extraction. Due to limited coherence times and physical noise, increasing the qubit number or the circuit depth makes it harder to run the algorithm with near-term quantum hardware. Thus, we do neither apply intermediate measurements nor amplitude amplification in order to ensure the feasibility of our approach on actual quantum computing hardware. The hardware-related limitations of our method can be summarized as follows.

Theorem 5

(Resource limitations) The circuit construction from Theorem 3 requires $|\mathcal {C}|+1$ extra qubits. The expected runtime until a valid sample is generated is $\mathcal {O}(1/\delta )$ with $\delta =\exp (-|\mathcal {C}|\Vert \varvec{\theta }\Vert _{\infty })$, and hence, exponential in the number of cliques.

Finally, our method assumes a discrete graphical model family with binary variables and overcomplete sufficient statistics. Nevertheless, any discrete family with vertex alphabets of size k can be transformed into an equivalent family with $\mathcal {O}(n \log _2 k)$ binary variables. Clearly, increasing the number of variables increases the number of required qubits which complicates the execution of our method on actual quantum processors.

5 Inference

The four main inference tasks that can be done with graphical models are (i) sampling, (ii) MAP inference, (iii) parameter learning, and (iv) estimating the partition function. The ability to generate samples from the graphical model follows directly from Theorem 3. Here, we provide the foundations required to address inference tasks (ii)–(iv) based on our circuit construction.

5.1 MAP prediction

Computing the MAP state of a discrete graphical model is required when the model serves as the underlying engine of some supervised classification procedure. More precisely, the MAP problem is $\varvec{x}^* = {\text {arg\,max}}_{\varvec{x}\in \{0,1\}^n} \mathbb {P}_{\varvec{\theta }}(\varvec{x}) = {\text {arg\,max}}_{\varvec{x}\in \{0,1\}^n} \varvec{\theta }^\top \phi (\varvec{x})$. Theorem 2 asserts that our Hamiltonian $H_{\varvec{\theta }}$ carries $-\varvec{\theta }^\top \phi (\varvec{x})$ for all $\varvec{x}\in \{0,1\}^n$ on its diagonal. Since $H_{\varvec{\theta }}$ is itself diagonal, $-\varvec{\theta }^\top \phi (\varvec{x}^*)$ is the smallest eigenvalue of $H_{\varvec{\theta }}$. Computing the smallest eigenvalue and the corresponding eigenvector—which corresponds to $\varvec{x}^*$ in the $2^n$-dimensional state space—is a well-studied QMA-hard problem. Heuristic algorithms like the variational quantum eigensolver (Peruzzo et al. 2014) or variational quantum imaginary time evolution (McArdle et al. 2019; Yuan et al. 2019) can be applied to our Hamiltonian in order to approximate the MAP state.

Moreover, sampling from a model with inverse temperature $\beta$ can also be applied to compute the MAP state. However, this effectively samples from a model with parameter $\varvec{\theta }'=\beta \varvec{\theta }$. According to Corollary 1, driving the temperature to 0 drives $\Vert \varvec{\theta }'\Vert _{\infty }$ to $\infty$, which would result in an arbitrary small success probability.

5.2 Parameter learning

Parameters of the graphical model can be learned consistently via the maximum likelihood principle. Given a data set $\mathcal {D}$ that contains samples from the desired distribution $\mathbb {P}^*$, we have to minimize the convex objective $\ell (\varvec{\theta })=-(1/|\mathcal {D}|)\sum _{\varvec{x}\in \mathcal {D}} \log \mathbb {P}_{\varvec{\theta }}(\varvec{x})$ with respect to $\varvec{\theta }$. Differentiation reveals $\nabla \ell (\varvec{\theta })=\hat{\varvec{\mu }}-\tilde{\varvec{\mu }}$ where $\tilde{\varvec{\mu }}=(1/|\mathcal {D}|)\sum _{\varvec{x}\in \mathcal {D}}\phi (\varvec{x})$ and $\hat{\varvec{\mu }}=\sum _{\varvec{x}\in \{0,1\}^n}\mathbb {P}_{\varvec{\theta }}(\varvec{x}) \phi (\varvec{x})$. The latter quantity can be estimated by drawing samples from the graphical model while $\tilde{\varvec{\mu }}$ is a constant computed from $\mathcal {D}$. Notably, our circuit does not require a quantum-specific training procedure, since the circuit $\varvec{C}_{\varvec{\theta }}$ is itself parametrized by the canonical parameters $\varvec{\theta }$ of the corresponding family. This allows us to run any iterative numerical optimization procedure on a digital computer and employ our circuit as a sampling engine for estimating $\hat{\varvec{\mu }}$. That is,

$$\begin{aligned} \varvec{\theta }^{(t+1)} = \varvec{\theta }^{t} + \frac{1}{2|\mathcal {C}|} \nabla \ell (\varvec{\theta }) \end{aligned}$$

(10)

Therein, $\nicefrac {1}{2|\mathcal {C}|}$ is a stepsize that guarantees convergence to an $\epsilon$-optimal solution within $\mathcal {O}(|\mathcal {C}|)$ steps (Piatkowski 2018, [Theorem 2.4]).

We have to remark that our circuit allows for an alternative way to estimate the parameters. The circuit can be parametrized by a vector of rotation angles $\varvec{\gamma }$. Thus, we may learn $\varvec{\gamma }$ directly, utilizing a quantum gradient $\nabla _{\varvec{\gamma }}^{\varvec{x}}$ (Dallaire-Demers and Killoran 2018; Zoufal 2021), where

$$\begin{aligned} \left( \nabla _{\varvec{\gamma }}^{\varvec{x}}\right) _j = \textstyle {\frac{\partial }{\partial \varvec{\gamma }_j}} \sum \limits _{i\in \{0,1\}}|(\langle 0|^{\otimes |\mathcal {C}|}\otimes \langle i|\otimes \langle \varvec{x}|)\varvec{C}_{\varvec{\gamma }} |+\rangle ^{\otimes m}|^2. \end{aligned}$$

The corresponding canonical parameters can be recovered from $\varvec{\gamma }$ via $\varvec{\theta }_j = 2\log \cos (2\varvec{\gamma }_j)$.

5.3 Approximating the partition function

Estimating the partition function $Z(\varvec{\theta })$ of a graphical model allows us to compute the probability of any desired state directly via the exponential family form $\mathbb {P}_{\varvec{\theta }}(\varvec{x})=\exp (\varvec{\theta }^\top \phi (\varvec{x})-\ln Z(\varvec{\theta }))$. Computing $Z(\varvec{\theta })$ is a well-recognized problem because of its complexity—the problem is #P-hard. Nevertheless, given a set $\mathcal {S}$ that consists of samples from $\mathbb {P}_{\varvec{\theta }}$, the Ogata-Tanemura method (Ogata and Tanemura 1981; Potamianos and Goutsias 1997) can be applied to get an unbiased estimate of the inverse partition function via ${1}/{\hat{Z}}(\varvec{\theta }) = 2^{-n}/|\mathcal {S}| \sum _{\varvec{x}\in \mathcal {S}} 1/\exp (\varvec{\theta }^\top \phi (\varvec{x}))$. Moreover, following (Bravyi et al. 2021), there is a circuit that employs our $\varvec{C}_{\varvec{\theta }}$ to estimate $\tau (\theta )=2^{-n}2 Z(\varvec{\theta })$ with accuracy $\varepsilon$ and probability of at least 3/4. The procedure adds $\mathcal {O}(\log \nicefrac {1}{\varepsilon })$ extra auxiliary qubits and increases the depth to $\mathcal {O}( d {\text {depth}}(\texttt {AND}) ({\text {poly}}(n)+1/(\varepsilon \sqrt{\tau (\varvec{\theta })})))$. The basic idea is to apply quantum trace estimation as defined in (Bravyi et al. 2021, [Theorem 7]) to the matrix from Eq. E4 (provided in Appendix 5). Due to the high depth, the resource consumption of this procedure is prohibitive for current quantum computers. Nevertheless, it opens up avenues for probabilistic inference on upcoming fault-tolerant quantum hardware.

6 Experimental evaluation

Here, we want to evaluate the practical behavior of our method, named QCGM, by answering a set of questions which are discussed below. Theorem 3 provides the guarantee that the sampling distribution of our QCGM is proportional to that of some given discrete graphical model. However, actual quantum computers are not perfect and the computation is influenced by various sources of quantum noise, each having an unknown distribution (Nielsen and Chuang 2016). Hence, we investigate the following:

(Q1):

How close is the sampling distribution of QCGM on actual state-of-the-art quantum computing devices to a noise-free quantum simulation, classical Gibbs sampling, and classical perturb-and-MAP sampling?

Measuring the auxiliary qubits of $\varvec{C}_{\varvec{\theta }}$ tells us if the real part extraction has failed or not. While our theoretical insights provide a lower bound on the success probability, the exact success probability is unknown. The second question we address with our experiments is hence as follows:

(Q2):

What empirical success probability should we expect and how does $\hat{\delta }$ vary as a function of $\Vert \varvec{\theta }\Vert _{\infty }$?

Third, as explained in Section 5.2, the parameter learning of QCGM can be done analogously to the classical graphical model, based on a data set $\mathcal {D}$ and samples $\mathcal {S}$ from the circuit. As explained above, samples from the actual quantum processor will be noisy. It is known since long that error-prone gradient estimates can still lead to reasonable models as long as inference is carried out via the same error-prone method (Wainwright 2006). Our last question is thus as follows:

(Q3):

Can we estimate the parameters of a discrete graphical model in the presence of quantum noise?

Table 1 Average Hellinger fidelities (F) and their standard errors over ten runs, computed from $N=10,000$ samples

6.1 Experimental setup

For question ${\textbf {(Q1)}}$, we design the following experiment. First, we fix the conditional independence structures shown in the top row of Table 1. For each structure, we generate 10 graphical models with random parameter vectors drawn from a negative half-normal distribution with scales $\sigma \in \{\nicefrac {1}{10},\nicefrac {1}{4},\nicefrac {1}{2}\}$. QCGM is implemented using Qiskit (Abraham et al. 2019) and realized by applying the circuit $\varvec{C}_{\varvec{\theta }}$ to the state $|0\rangle ^{\otimes (|\mathcal {C}|+1)}\otimes |+\rangle ^{\otimes n}$. The probabilities for sampling $\varvec{x}$ are evaluated by taking $N=10,000$ samples (shots) from the prepared quantum state and computing the relative frequencies of the respective $\varvec{x}$. The quantum simulation is carried out by the Qiskit QASM simulator which is noise-free. Any error that occurs in the simulation runs is thus solely due to the fact that we draw a finite number of samples. The experiments on actual quantum computers are carried out on three superconducting quantum processors (IBM Quantum 2021): a 27-qubit IBM Quantum Falcon QPU (ibmq_ehningen), a 127-qubit IBM Quantum Eagle QPU (ibm_sherbrooke), and a 133-qubit IBM Quantum Heron QPU (ibm_torino). The results are post-processed with Matrix-free Measurement Mitigation (M3) (Nation et al. 2021).

For a comparison with classical sampling methods, we consider the benchmark methods described in Appendix A.1. First, Gibbs sampling is performed with a fixed burn-in of $b=10$ samples. Moreover, we discard b samples between each two accepted Gibbs samples to facilitate independence. These choices are heuristics and prone to error. Second, we apply perturb-and-MAP sampling (Papandreou and Yuille 2011; Hazan et al. 2013) with sum-of-gamma (SoG) perturbations (Niepert et al. 2021). The SoG approach is an efficient heuristic that results in a slightly biased sampling distribution (see Appendix A.1 for details).

The quality of each sampling procedure is assessed by the Hellinger fidelity, defined for two probability mass functions $\mathbb {P}$ and $\mathbb {Q}$ via $F(\mathbb {P},\mathbb {Q}) = (\sum _{\varvec{x}\in \{0,1\}^n} \sqrt{\mathbb {P}(\varvec{x})\mathbb {Q}(\varvec{x})})^2$. For question ${\textbf {(Q2)}}$, we consider the very same setup as above, but instead of F, we compute the empirical success rate of the QCGM as $\hat{\delta }=\text {number of succeeded samplings}/N$. This is computed for each of the 10 runs on each quantum computer and the quantum simulator.

Finally, for question ${\textbf {(Q3)}}$, we draw N samples from a graphical model with edge set $\{(0,1),(1,2)\}$ via Gibbs sampling. Based on these samples, learning $\varvec{\theta }$ is carried out as described in Section 5.2. We choose ADAM (Kingma and Ba 2015) for numerical optimization to compensate for the noisy gradient information. For each of the 30 training iterations, we report the estimated negative, average log-likelihood, and the empirical success rate. Since the loss function is convex, the optimization procedure is independent of the initial solution. For simplicity, we initialized the training at $\varvec{\theta }=\varvec{0}$.

Fig. 2

Left: Learning curve for QCGM over 30 ADAM iterations on a QASM simulation and an actual superconducting quantum processor (ibmq_ehningen). Right: The empirical success rate $\hat{\delta }$ of each training iteration

6.2 Experimental results

The results of our experimental evaluation are shown in Table 1 and Fig. 2. Numbers reported are average values and standard errors over 10 runs. Regarding question (Q1), we see that the fidelity of the simulation outperforms the classical benchmark methods. This can be explained by the fact that QCGM is guaranteed to return unbiased and independent samples from the underlying model. Gibbs sampling can only achieve this if the hyper-parameters are selected carefully, or, in case of PAM, when an exact perturbation and an exact MAP solver are considered. Moreover, the fidelity on actual quantum hardware degrades as the model becomes more complex. Yet, the average fidelity rarely drops below 0.98. Moreover, each of these cases occurs on the structures and (which are also the worst cases for Gibbs sampling). Since both models constitute the largest structures considered, they also correspond to the largest circuits which clearly suffer from the largest amount of hardware noise. On the larger QPUs (ibm_sherbrooke and ibm_torino) structure exhibits not only the worst fidelity but also the largest standard errors. We conjecture that QPUs with a large qubit count incur a larger uncertainty for multi-qubit operations that are required for implementing the two cliques of size three. When one considers the best result on each structure (and not the average), QCGM frequently attains fidelities of $>0.98$ also on quantum hardware. In summary, we conclude that QCGM produces valid samples in the presence of actual quantum noise and has the potential to outperform classical sampling methods.

Fig. 3

The empirical success rate $\hat{\delta }$ and its relation to the uniform norm of the parameter vector and the scale of the underlying parameter distribution, respectively. Each success rate is estimated from 10k shots for a model with structure $G=(\{0,1\},\{(0,1)\})$ and a random parameter vector $\varvec{\theta }$, sampled from a half-normal distribution with scales $\sigma \in \{\nicefrac {1}{10},\nicefrac {1}{4},\nicefrac {1}{2}\}$. Top: QASM simulation. Bottom: Superconducting quantum processor (ibm_torino)

For question (Q2), we see from Table 1 that the success probability degrades when the number of maximal cliques increases. For the simulation and the actual QPUs, the worst success probabilities are obtained on structures and which also incur the largest clique count ($|\mathcal {C}|$). The sheer number of variables (n) does not have the same impact, since structures and have the same number of variables but a consistently larger success probability. In Fig. 3, we consider the empirical success probability $\hat{\delta }$ as a function of the parameter’s uniform norm $\Vert \varvec{\theta }\Vert _{\infty }$ and the parameter prior’s scale $\sigma$, respectively. As predicted by Corollary 1, $\hat{\delta }$ degrades exponentially with increasing $\Vert \varvec{\theta }\Vert _{\infty }$, or, alternatively, with increasing $\sigma$. Interestingly, the second plot of Fig. 2 reveals that $\hat{\delta }$ also degrades as a function of the model’s entropy. Since we initialize the training with all elements of $\varvec{\theta }$ being 0, we start at maximum entropy. Parameters are refined during the learning and the entropy is reduced.

Finally, the first plot in Fig. 2 shows that the training progresses for both, simulated and hardware results. Although the hardware noise prevents the optimization to reach the same likelihood as the simulation, the likelihood improves with additional training iterations. We hence consider the answer to ${\textbf {(Q3)}}$ in the affirmative.

7 Conclusion

We introduce an exact representation of discrete graphical models with a quantum circuit construction that acts on $n+1+|\mathcal {C}|$ qubits that shows potential for compatibility with near-term quantum hardware. This method enables unbiased, hyper-parameter free sampling while keeping the theoretical properties of the undirected model intact, e.g., our quantum circuit factorizes over the set of maximal cliques as predicted by the Hammersley-Clifford theorem. Although our results are stated for binary models, equivalent results for arbitrary discrete state spaces can be derived, where multiple qubits encode one logical non-binary random variable. The full compatibility between the classical graphical model and our unitary embedding is significant, since it allows us to benefit from existing theory as well as quantum sampling. A distinctive property of QCGM is that the algorithm itself indicates whether a sample should be discarded. Here, we show a lower bound for the success probability depending only on the number of maximal cliques and the model parameter norm. The experiments conducted with numerical simulations and actual quantum hardware show that QCGMs perform well for certain conditional independence structures but suffer from small success probabilities for structures with large $|\mathcal {C}|$. When compared to state-of-the-art MCMC-based sampling methods, our proposed method has a subtle advantage in terms of parallelization. Given M quantum processors, we can produce $\delta M$ samples by running the proposed circuit once on each processor in parallel. In contrast, classical Markov chains have to perform an exponential number of iterations until each chain has reached the stationary distribution. However, this cannot be accelerated by running more chains in parallel, since each chain does not indicate whether it has attained stationarity. It remains open for future research to potentially remove the dependence of $\delta$ on the number of maximal cliques and to further explore the differences and potential relations in limiting factors between classical and quantum sampling methods. Finally, our results open up new avenues for probabilistic machine learning on quantum computers by showcasing that quantum models can be employed to generate unbiased and independent samples for a large and relevant class of generative models with sufficiently good fidelity.

Appendices

Appendix 1.  Probabilistic graphical models

Probabilistic graphical models are a framework that generalizes various important probability densities and probability mass functions. They are motivated by the fact that any n-dimensional random variable $\varvec{X}$ with state space $\mathcal {X}$ can obey a large number of conditional independences. These conditional independences can be exploited to devise efficient data structures and algorithms.

Definition 3

(Conditional independence structure) Any undirected graph $G=(V,E)$ can be interpreted as the conditional independence structure of some n-dimensional random variable $\varvec{X}$ via

$$ \varvec{X}_{v} \perp \hspace{-10.0pt}\perp \varvec{X}_{V{\setminus } (\mathcal {N}(v)\cup \{v\})} \mid \varvec{X}_{\mathcal {N}(v)} $$

where $A\perp \hspace{-10.0pt}\perp B\mid C$ indicates that A is independent of B given C and $\mathcal {N}(v)$ denotes the set of v’s neighbors in G.

In other words, every vertex of the conditional independence structure obeys the (local) Markov property.

Theorem 6

(Factorization (Hammersley and Clifford 1971)) Let $\varvec{X}$ be a random variable with strictly positive mass $\mathbb {P}$ and conditional independence structure G. Then, $\mathbb {P}$ factorizes over the cliques of G.

$$ \mathbb {P}(\varvec{x}) = \frac{1}{Z}\psi (\varvec{x}) = \frac{1}{Z} \prod _{C\in \mathcal {C}(G)} \psi _C(\varvec{x}_C), $$

Here, $Z=\sum _{\varvec{x}} \psi (\varvec{x})$ is a normalization constant, $\psi$ and $\psi _C$ are positive functions, and $\mathcal {C}(G)$ denotes the set of maximal cliques of the graph G.

While $\varvec{X}$ may have a continuous state space, here, we focus on random variables with discrete state spaces. In that case, it is straightforward to show that $\psi _C$ can always be written as follows:

$$ \psi _C(\varvec{x}) = \exp (\langle \varvec{\theta }_C,\phi _C(\varvec{x}_C)\rangle )\;, $$

where $\phi _C(\varvec{x}_C)=(\phi _{C,\varvec{y}}(\varvec{x}_C): \varvec{y}\in \mathcal {X}_C)$ with $\phi _{C,\varvec{y}}(\varvec{x}_C) = \prod _{v\in C} \mathbbm {1}(\varvec{x}_v = \varvec{y}_v)$ is a one-hot indicator vector that encodes the state $\varvec{x}_C$. Thus, by setting $\phi (\varvec{x})=(\phi _C(\varvec{x}_C): C\in \mathcal {C})$, every discrete undirected graphical model can be written in exponential family form:

$$\begin{aligned} \mathbb {P}(\varvec{x})&= \frac{1}{Z} \prod _{C\in \overline{\mathcal {C}}(G)} \psi _C(\varvec{x}_C) = \frac{1}{Z(\varvec{\theta })} \prod _{C\in \overline{\mathcal {C}}(G)} \exp (\langle \varvec{\theta }_C,\phi _C(\varvec{x}_C)\rangle )\\&= \frac{1}{Z(\varvec{\theta })} \exp \left( \sum _{C\in \overline{\mathcal {C}}(G)} \langle \varvec{\theta }_C,\phi _C(\varvec{x}_C)\rangle \right) = \exp (\left\langle \varvec{\theta }, \phi (\varvec{x}) \right\rangle - A(\varvec{\theta })) \end{aligned}$$

A plethora of applications of probabilistic graphical models arose in the last decades, including tasks from computer vision, natural language processing, and computational biology.

The corresponding algorithms typically involve the computation of one or more of the following quantities:

• 1. Marginal probabilities $\mathbb {P}_C(\varvec{X}_C=\varvec{y})=\mathbb {E}[\phi _{C,\varvec{y}}(\varvec{X})]$

• 2. Partition function $Z(\varvec{\theta })=\sum _{\varvec{x}} \prod _{C\in \mathcal {C}} \psi _C(\varvec{x})$

• 3. Maximum a posteriori (MAP) state, i.e., ${\text {MAP}}(\varvec{\theta })=\max _{\varvec{x}\in \mathcal {X}} \mathbb {P}(\varvec{x})$

• 4. Maximum likelihood parameter, i.e., $\varvec{\theta }^* = {\arg \max }_{\varvec{\theta }\in \mathbb {R}^d} \prod _{\varvec{x}\in \mathcal {D}} \mathbb {P}_{\varvec{\theta }}(\varvec{x})$

Solving or even approximating any of these inference tasks is computationally hard in general. A special case is constituted by the decomposable models. We say that the probability mass of a random variable is decomposable, whenever the underlying conditional independence structure G is chordal. That is, every induced cycle in the graph has exactly three vertices. The computational complexity of probabilistic inference, e.g., computing the partition function, in decomposable models scales exponentially in the size of the largest clique, and not with the total number of variables n as opposed to general (non-decomposable) models.

For inference tasks 1 and 2, the most general method, i.e., one that works with every conditional independence structure, is sampling. Assume that we have access to a set $\mathcal {D}$ of samples from $\mathbb {P}$. First, marginals for each clique can be obtained by estimating the expected sufficient statistic $\tilde{\mathbb {E}}[\phi _C(\varvec{X}_C)]$ from $\mathcal {D}$. Second, an unbiased estimate of the inverse partition function can be obtained, e.g., via the Ogata-Tanemura method (Ogata and Tanemura 1981; Potamianos and Goutsias 1997):

$$ \frac{1}{\hat{Z}(\varvec{\theta })} = \frac{1}{|\mathcal {X}||\mathcal {D}|} \sum _{\varvec{x}\in \mathcal {D}} \frac{1}{\psi (\varvec{x})}\;. $$

Moreover, for maximum likelihood estimation (task 4), the objective function can be written as follows:

$$ \ell (\varvec{\theta }) = \langle \varvec{\theta }, \tilde{\mathbb {E}}[\phi (\varvec{X})] \rangle - \ln Z(\varvec{\theta }) $$

whereas the gradient of $\ell$ can be shown to be

$$ \nabla \ell (\varvec{\theta }) = \tilde{\mathbb {E}}[\phi (\varvec{X})] - \hat{\mathbb {E}}[\phi (\varvec{X})] $$

where $\tilde{\mathbb {E}}$ denotes the expectation estimated from data set $\mathcal {D}$, and $\hat{\mathbb {E}}$ denotes the expectation computed w.r.t. a model with parameters $\varvec{\theta }$. Thus, sampling is sufficient to compute the gradient of the loss function and learn the model parameters $\varvec{\theta }$ from data.

As a consequence, in the manuscript at hand, we study how sampling from probabilistic graphical models can be addressed via quantum computation.

1.1 A.1  Classical baseline sampler

For comparison with our proposed method, we consider two classical sampling methods: a Monte Carlo method (PAM) and a Markov chain Monte Carlo method (Gibbs sampling).

With PAM, we can draw exact one-shot samples via MAP prediction (c.f., Section 5.1) in a perturbed model (Papandreou and Yuille 2011). That is, a new sample $\varvec{x}'$ is drawn by solving $\varvec{x}'={\text {arg\,max}}_{\varvec{x}\in \{0,1\}^n} \mathbb {P}'_{\varvec{\theta }}(\varvec{x}) = {\text {arg\,max}}_{\varvec{x}\in \{0,1\}^n} (\varvec{\theta })^\top \phi (\varvec{x})+\epsilon$. It can be shown that $\epsilon$ must come from a Gumbel distribution (arising in extreme value theory (Steutel and Harn van 2004)) in order to establish that $\varvec{x}'$ is sampled from $\mathbb {P}_{\varvec{\theta }}$. It is a continuous univariate distribution with density $g(z)=\exp (-(-z+\exp z))$. As explained in Papandreou and Yuille (2011), finding the Gumbel perturbation that facilitates unbiased sampling is intractable in general. A practical but approximate version of PAM can be realized via the sum-of-gammas approach. According to Niepert et al. (2021), we set $\varvec{\epsilon }_i=\sum _{s=1}^S \nicefrac {\varepsilon }{s} - \log (S)$ where $\varepsilon$ is gamma distributed with shape $\nicefrac {1}{|\mathcal {C}|}$ and scale 1. In our experiments, we fixed $S=10$. Finally, a PAM sample is drawn by solving ${\text {arg\,max}}_{\varvec{x}\in \{0,1\}^n} (\varvec{\theta }+\varvec{\epsilon })^\top \phi (\varvec{x})$. In our experiments, models were small enough to solve the maximization via an exhaustive enumeration of all states. In practice, approximate methods, e.g., max-product belief propagation (Wainwright and Jordan 2008), have to be used. Both the sum-of-gamma approach and an approximate MAP solver introduce a bias in the sampling procedure.

As opposed to plain Monte Carlo methods, Markov chain Monte Carlo (MCMC) methods generate a sequence of samples in which each sample depends on the previous one—the samples form a chain. After B steps, the elements of the chain are valid but dependent samples from our target distribution. To overcome the dependence, a fixed number of samples is discarded before the next sample is stored. Maybe the most popular MCMC method is the Metropolis-Hastings algorithm (Metropolis et al. 1953; Hastings 1970), which forms the basis of most practical MCMC algorithms. An overview can be found in Andrieu et al. (2003). Here, we will shortly present the Gibbs sampler (Geman and Geman 1984).

For Gibbs sampling, recall that undirected models obey the (local) Markov property, i.e., $\mathbb {P}_v(\varvec{x}_v \mid \varvec{x}_{V\setminus \{v\}}) = \mathbb {P}_v(\varvec{x}_v \mid \varvec{x}_{\mathcal {N}(v)})$. Moreover, let $\mathcal {C}(v)$ be the set of cliques which contain vertex v, the conditional marginal is simply

$$\begin{aligned} \mathbb {P}(\varvec{x}_v \mid \varvec{x}_{\mathcal {N}(v)}) = \frac{\prod _{C\in \mathcal {C}(v)} \psi _C(\varvec{x}_v,\varvec{x}_{\mathcal {N}(v)})}{\sum _{y\in \mathcal {X}_v} \prod _{C\in \mathcal {C}(v)} \psi _C(y,\varvec{x}_{\mathcal {N}(v)})}\;, \end{aligned}$$

(A1)

which can be computed in time $\mathcal {O}(|\mathcal {X}_v||\mathcal {C}(v)|)$. The Gibbs sampler starts with an arbitrary joint state $\varvec{x}^0$ and updates each variable by sampling from Eq. A1. If this process is repeated multiple times, the resulting joint state $\varvec{x}$ will be a valid sample from $\mathbb {P}$, independent of $\varvec{x}^0$.

Algorithm 2

Gibbs sampler.

The drawback of Gibbs sampling is the fact that many initial samples must be discarded in order to facilitate convergence to the stationary distribution of the Markov chain. In practice, one can apply statistical test, but none of them provides entirely reliable diagnostics whether the Markov Chain has stabilized. A body of theoretical work tries to lower bound the number of steps required for the distribution of the Markov chain to be close to the target (Jerrum and Sinclair 1997). Nevertheless, such results are highly problem-specific and do in general not lead to an actual number of iterations, but rather asymptotic statements. Thus, when running Gibbs sampling, one typically has no guarantee that the generated samples come from the desired distribution. Moreover, even when the chain has stabilized, consecutive samples are obviously not independent of each other. Thus, intermediate samples must be discarded. Again, the actual number of samples that must be discarded in order to guarantee independence is unknown in general.

In summary, the classical methods provide no guarantee that the generated samples are unbiased and independent of each other.

Appendix 2.  Extracting real parts

The real part of any complex $z\in \mathbb {C}$ can be written as $(z+\bar{z})/2$ where $\bar{z}$ denotes the complex conjugate of z. Similarly, for any $U\in \mathbb {C}^{N\times N}$, $(U+U^{\dagger })/2$ extracts $\Re U$, such that it may act on the n-qubit state $|\psi \rangle$. To see how this can be implemented on a gate-based quantum computer, as, e.g., in Somma et al. (2002), consider the unitary $R = U \oplus U^{\dagger }$.

To construct R, we introduce an additional, so-called, auxiliary qubit. When we initialize this extra qubit $|a\rangle$ with $|0\rangle$, the joint state of the system is $|0\rangle \otimes |\psi \rangle$. Now, bringing the extra qubit in the superposition state $|+\rangle$ and running the circuit, we get the state $R(H |0\rangle \otimes |\psi \rangle )$. Notably, the $|0\rangle$ ($|1\rangle$) component of $|a\rangle$ controls the application of U ($U^\dagger$) onto $|\psi \rangle$, weighted equally by $1/\sqrt{2}$. Finally, another H gate is applied to $|a\rangle$ and the auxiliary qubit is measured. The action of the real part extraction is derived as follows:

$$\begin{aligned} (H \otimes I^{\otimes n})R(H \otimes I^{\otimes n}) (|0\rangle \otimes |\psi \rangle )= \nicefrac {1}{2} \begin{pmatrix} U+U^\dagger &{}U-U^\dagger \\ U-U^\dagger &{}U+U^\dagger \end{pmatrix} (|0\rangle \otimes |\psi \rangle ). \end{aligned}$$

(B2)

Clearly, when we measure $|a\rangle =|0\rangle$, then the circuit successfully extracted the real part, i.e., $|\psi \rangle _{+} = \nicefrac {1}{2}(U+U^\dagger )|\psi \rangle =(\Re U)|\psi \rangle$. On the other hand, when we measure $|a\rangle =|1\rangle$, then the output of the circuit is $|\psi \rangle _{-} = \nicefrac {1}{2}(U-U^\dagger )|\psi \rangle =(\Im U)|\psi \rangle$, and thus, the imaginary part is extracted.

Appendix 3.  Proof of Theorem 1

The input to Algorithm 1 is a clique $C\subseteq V$ and a corresponding clique-state $\varvec{y}\in \{0,1\}^{|C|}$. For any $v\in C$, we denote its state by $\varvec{y}_v$. With $2\times 2$ diagonal matrices $M_v\in \{ I, |0\rangle \langle 0|, |1\rangle \langle 1|\}$, the output of Algorithm 1 can be written as $\Phi =\bigotimes _{v=1}^n M_v$. Let us expand the j-th diagonal entry of $\Phi$ as follows:

$$ (\Phi )_{j,j} = \left( \bigotimes _{v=1}^n M_v \right) _{j,j} = \prod _{v=1}^n \underbrace{\left( I^{\otimes (n-v)} \otimes M_v \otimes I^{\otimes (v-1)} \right) _{j,j}}_{a_{v,j}}\;, $$

whereas the second equality holds due to diagonality of $M_v$. Thus, for each $1\le j\le 2^n$, we have $(\Phi )_{j,j} = \prod _{v=1}^n a_{v,j}$ with $a_{v,j}\in \{0,1\}$. When $v\not \in C$, we have $a_{v,j}=1$ regardless of $\varvec{y}$, since $M_v=I$. Now, let us consider the case $v \in C$, i.e., $M_v = |\varvec{y}_v\rangle \langle \varvec{y}_v|$. We have $B_v:= M_v \otimes I^{\otimes (v-1)} = m_{v,0} I^{\otimes (v-1)} \oplus m_{v,1} I^{\otimes (v-1)}$ with $M_v=m_{v,0} \oplus m_{v,1}$. Thus, either the first half or the second half of $B_v$’s diagonal will be zero and $B_v$ is a $2^{v}\times 2^{v}$ matrix. Now, the $2^{n}\times 2^{n}$ matrix $I^{\otimes (n-v)} \otimes B_v$ carries $2^{n-v}$ consecutive copies of $B_v$ on its diagonal. Thus, we have $j=1 + p 2^{v} + q$ with $0 \le p \le 2^{n-v}-1$ and $0\le q \le 2^v-1$. Moreover, when $\varvec{x}^{(j)}={\text {bin}}(j)$ denotes the n-bit binary expansion of j, we have $j=\sum _{r=1}^n 2^{r-1} \varvec{x}^{(j)}_r$, which implies $q:= q(j) = \sum _{r=1}^{v} 2^{r-1} \varvec{x}^{(j)}_r$ and $p:= p(j) = \sum _{r=1}^{n-v} 2^{r-1} \varvec{x}^{(j)}_{r+v}$. Now, by definition of $B_v$, $q(j)<2^{v-1} \Rightarrow a_{v,j}=1-\varvec{y}_v$ and $q(j)\ge 2^{v-1} \Rightarrow a_{v,j}=\varvec{y}_v$. However, $q(j)<2^{v-1} \Leftrightarrow \varvec{x}^{(j)}_v=0$. Finally, the statements $\varvec{x}^{(j)}_v=0 \Rightarrow a_{v,j} = 1-\varvec{y}_v$ and $\varvec{x}^{(j)}_v=1 \Rightarrow a_{v,j} = \varvec{y}_v$ can be summarized into the statement $a_{v,j} = \mathbbm {1}(\varvec{x}^{(j)}_v = \varvec{y}_v)$, eventually yielding $(\Phi )_{j,j} = \prod _{v\in C} \mathbbm {1}(\varvec{x}^{(j)}_v = \varvec{y}_v)$ as desired. $\square$

Appendix 4.  Proof of Theorem 2

For the graphical model, we have $\mathbb {P}_{\varvec{\theta }}(\varvec{X}=\varvec{x}) = \exp (\varvec{\theta }^\top \phi (\varvec{x}) - A(\varvec{\theta }))$, where $\varvec{\theta }^\top \phi (\varvec{x}) = \sum _{C\in \mathcal {C}} \sum _{y\in \{0,1\}^{|C|}} \varvec{\theta }_{C,\varvec{y}} \phi _C(\varvec{x})$. According to Def. 2, the i-th diagonal entry of each $\Phi _{C,y}$ coincides with $\phi _{C,\varvec{y}}(\varvec{x}^{(j)})$ and hence $(H_{\varvec{\theta }})_{i,i}=-\varvec{\theta }^\top \phi (\varvec{x}^{(j)})$. Since $H_{\varvec{\theta }}$ is diagonal and real-valued, $(\exp _M(-H_{\varvec{\theta }}))_{i,i} = \exp (\varvec{\theta }^\top \phi (\varvec{x}^{(j)}))$. Observing that $\log {\text {Tr}}{\exp (-H_{\varvec{\theta }})}=A(\varvec{\theta })$ completes the proof. $\square$

Appendix 5.  Proof of Theorem 3

Graphical models with overcomplete statistics are shift-invariant. To see this, let $\varvec{1}$ be the d-dimensional vector of ones and $c\in \mathbb {R}$ an arbitrary constant. Now, notice that

$$\begin{aligned} \mathbb {P}_{\varvec{\theta }+\varvec{1}c}(\varvec{x})&=\frac{ \exp ((\varvec{\theta }+\varvec{1}c)^{\top } \phi (\varvec{x})) }{ \sum _{\varvec{x}^{'}} \exp ( {(\varvec{\theta }+\varvec{1}c)}^{ \top } \phi ({\varvec{x}^{'}}) ) }\\&\quad = \frac{\exp (\varvec{\theta }^\top \phi (\varvec{x}) + c|\mathcal {C}| )}{\sum _{\varvec{x}^{'}} \exp (\varvec{\theta }^{\top } \phi (\varvec{x}') + c|\mathcal {C}| )} = \mathbb {P}_{\varvec{\theta }}(\varvec{x})\;. \end{aligned}$$

Equality holds, since the vector $\phi (\varvec{x})$ is binary with exactly $|\mathcal {C}|$ ones (c.f., Eq. 3).

Due to shift invariance, we may subtract any fixed constant from all $\varvec{\theta }_j$ without altering the probability mass that corresponds to the graphical model. Hence, w.l.o.g. one can assume $\varvec{\theta }\in \mathbb {R}^d_{-}$ throughout this proof. For ease of notation, let us enumerate all $(C,\varvec{y})$-pairs from 1 to d. In this notation, we have $H_{\varvec{\theta }} = -\sum _{j=1}^d \varvec{\theta }_{j} \Phi _{j}$. Furthermore, let us define

$$\begin{aligned} {P^y}(x) = \exp (0) + (\exp (y)-\exp (0)) x^2 = c_0 + c_2 x^2. \end{aligned}$$

(E3)

${P^y}$ is a degree-2 polynomial with ${P^y}(0)=\exp (0)$ and $P^{y}(1) = \exp (y)$. In what follows, we construct a unitary implementation of this polynomial, applied to a specific diagonal matrix.

By construction, the clique-state factors defined in Eq. 7 are unitary, as $\left( U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}})\right) ^{-1} = \left( U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}})\right) ^{\dagger }$ can be verified easily. Extracting the real part of $U^j(\varvec{\gamma }_j)$ leads to

$$\begin{aligned} \begin{aligned} \Re U^j(\varvec{\gamma }_j) \!=\!&I^{\otimes n+1} \!+\! (\Re \exp (i2\varvec{\gamma }_j)-1) (\Phi _{C,\varvec{y}} \oplus ( I^{\otimes n} - \Phi _{C,\varvec{y}}))\\ =&I^{\otimes n+1} \!+\! \left( \cos (2\varvec{\gamma }_j)-1\right) (\Phi _{C,\varvec{y}} \oplus ( I^{\otimes n} - \Phi _{C,\varvec{y}}))\;. \end{aligned} \end{aligned}$$

Note that the involved matrices are diagonal, and hence, the result is diagonal too. For now, each diagonal entry of $\Re U^j(\gamma _j)$ has the form $G(x)=1+(\cos (2\varvec{\gamma }_j)-1)x^2$, where $x^2$ is a diagonal entry of $\Phi _j$ (or $I^{\otimes n}-\Phi _j$). Solving $G=P^y$ for $\varvec{\gamma }_j$ yields $\varvec{\gamma }_j = (1/2) \arccos (\exp (\varvec{\theta }_j))$ for $\varvec{\theta }_j\in \mathbb {R}_{-}$. We thus arrive at $\Re U^j(\varvec{\gamma }(y)) = P^y(U^j) = \exp (\varvec{\theta }_j \Phi _j) \oplus \exp (\varvec{\theta }_j (1-\Phi _j))$.

The second equality above holds because $\Phi _j$ is binary as well as idempotent, and $P^y(x)$ from Eq. E3 is constructed such that it coincides with $\exp$ on $\{0,y\}$ for $x\in \{0,1\}$. Note that the circuit parameters $\varvec{\gamma }$ are computed directly from $\varvec{\theta }$. One may think about $\varvec{\gamma }$ as a re-parametrization of the graphical model in the function space defined by $U^{d}(\varvec{\gamma }({\bar{\varvec{\theta }}_d})) U^{d-1}(\varvec{\gamma }({\bar{\varvec{\theta }}_{d-1}})) \dots U^1(\varvec{\gamma }({\bar{\varvec{\theta }}_{1}}))$. In what follows, we set $\bar{\varvec{\theta }}=\nicefrac {1}{2}\varvec{\theta }$ because the sampling probabilities of our quantum states are the square of the real amplitudes. All $\Phi _j$ are diagonal, which allows us to write the quantum circuit as

$$\begin{aligned} \begin{aligned} \varvec{C}_{\varvec{\theta }} \!=\! \prod _{j=1}^d \Re U^j(\varvec{\gamma }({\bar{\varvec{\theta }}_j})) \!=\!&\sqrt{\exp (- H_{\varvec{\theta }})} \oplus \sqrt{\exp ( H_{\varvec{\theta }}-\Vert \varvec{\theta }\Vert _1I^{\otimes n})} \;. \end{aligned} \end{aligned}$$

(E4)

Notice that the equality holds, since $\prod _j \Re U^j(\varvec{\gamma }({\bar{\varvec{\theta }}_j})) = \prod _j P^{\varvec{\theta }_j/2}(\Phi \oplus (I^{\otimes n}-\Phi ))= \exp ( \sum _j \varvec{\theta }_j/ (\Phi \oplus (I^{\otimes n}-\Phi ))) = \sqrt{\exp (- H_{\varvec{\theta }})} \oplus \sqrt{\exp ( H_{\varvec{\theta }}-\Vert \varvec{\theta }\Vert _1I^{\otimes n})}$. As explained in Appendix B, each real part extraction ($\Re$) involves one additional auxiliary qubit. Clearly, a naive implementation of Eq. E4 requires $d+1$ auxiliary qubits—one for the construction of all $U^j$ and one for each real part extraction. We can reduce this requirement by invoking the distributivity of real part extraction. Real part extraction is in general not distributive over complex matrix products. However, expanding $j\equiv (C,\varvec{y})$, investigating $\prod _{j=1}^d \Re U^j(\varvec{\gamma }({\bar{\varvec{\theta }}_j})) = \prod _{C\in \mathcal {C}} \prod _{\varvec{y}\in \{0,1\}^{|C|}} \Re U^{C,\varvec{y}}(\varvec{\gamma }({\bar{\varvec{\theta }}_{C,\varvec{y}}}))$, and recalling Definition 2 reveals that the indices of diagonal entries $\ne 1$ of $U^{C,\varvec{y}}(\varvec{\gamma }({\bar{\varvec{\theta }}_{C,\varvec{y}}}))$ are distinct for all $\varvec{y}\in \{0,1\}^{|C|}$. We may hence aggregate the real part extraction for the operators $U^{C,\varvec{y}}(\varvec{\gamma }({\bar{\varvec{\theta }}_{C,\varvec{y}}}))$ for all $\varvec{y}\in \{0,1\}^{|C|}$ without introducing any error, e.g.,

$$ \Re \begin{pmatrix} z_1&{}0\\ 0&{}1 \end{pmatrix} \Re \begin{pmatrix} 1&{}0\\ 0&{}z_2 \end{pmatrix} = \Re \begin{pmatrix} z_1&{}0\\ 0&{}z_2 \end{pmatrix}\;, $$

for $z_1,z_2\in \mathbb {C}$. This step is significant, since it reduces the number of additional auxiliary qubit from $d+1$ to $|\mathcal {C}|+1$. We arrive at the final expression for the circuit

$$\begin{aligned} \varvec{C}_{\varvec{\theta }} = \prod _{C\in \mathcal {C}} H_j ( I^{\otimes (|\mathcal {C}|-j-1)} \otimes ( (I^{\otimes j} \otimes U^C) \oplus ( I^{\otimes j} \otimes {(U^C)}^{\dagger } ) )) H_j\;, \end{aligned}$$

(E5)

where $U^C = \prod _{\varvec{y}\in \{0,1\}^{|C|}} U^{C,\varvec{y}}(\varvec{\gamma }({\nicefrac {1}{2}\varvec{\theta }_{C,\varvec{y}}}))$, $j:=j(C)$ is the 0-based index of the clique C in some arbitrary but fixed ordering of all cliques $\mathcal {C}$, and $H_j:= I^{\otimes (|\mathcal {C}|-j-1)} \otimes H \otimes I^{\otimes (n+1+j)}$. Finally, the probability of measuring $|0\rangle ^{\otimes (|\mathcal {C}|+1)} \otimes |\varvec{x}\rangle$ for some $\varvec{x}\in \{0,1\}^n$ is

$$\begin{aligned} \mathbb {P}_{\varvec{C}_{\varvec{\theta }}}(\varvec{X}\!=\! \varvec{x},\varvec{A}\!=\!\varvec{0}) =&\left| \left( \langle 0|^{\otimes (|\mathcal {C}|+1)}\otimes \langle \varvec{x}|\right) \varvec{C}_{\varvec{\theta }} \left( |0\rangle ^{\otimes (|\mathcal {C}|+1)}\otimes |+\rangle ^{\otimes n}\right) \right| ^2\\ \quad =&\left| \left( \langle 0| \otimes \langle \varvec{x}|\right) \prod _{C\in \mathcal {C}} \Re U^C \left( |0\rangle \otimes |+\rangle ^{\otimes n}\right) \right| ^2\\ =&\left| \langle \varvec{x}| \sqrt{\exp (-H)} |+\rangle ^{\otimes n} \right| ^2 \\ \quad =&\frac{1}{2^{n}} {\text {Tr}}\left[ |\varvec{x}\rangle \langle \varvec{x}| \exp \left( -H_{\varvec{\theta }}\right) \right] \propto \mathbb {P}_{\varvec{\theta }}(\varvec{x}) / 2^n \;, \end{aligned}$$

where we applied (B2) for each clique to establish the second equality. The proportionality with $\mathbb {P}_{\varvec{\theta }}$ is implied by Theorem 2. To achieve equality, as opposed to proportionality, we derive

$$\begin{aligned} \mathbb {P}_{\varvec{C}_{\varvec{\theta }}}(\varvec{A}\!=\!\varvec{0}) \!=\!&\sum _{\varvec{x}\in \{0,1\}^n} \left| \left( \langle 0|^{\otimes (|\mathcal {C}|+1)}\otimes \langle \varvec{x}|\right) \varvec{C}_{\varvec{\theta }} \left( |0\rangle ^{\otimes (|\mathcal {C}|+1)}\otimes |+\rangle ^{\otimes n}\right) \right| ^2\\ =&\sum _{\varvec{x}\in \{0,1\}^n} \left| \langle \varvec{x}| \sqrt{\exp (-H)} |+\rangle ^{\otimes n} \right| ^2 = \frac{1}{2^{n}}{\text {Tr}}\left[ \exp \left( -H_{\varvec{\theta }}\right) \right] \;. \end{aligned}$$

Now, clearly, $\mathbb {P}_{\varvec{C}_{\varvec{\theta }}}(\varvec{X}= \varvec{x},\varvec{A}=\varvec{0}) / \mathbb {P}_{\varvec{C}_{\varvec{\theta }}}(\varvec{A}=\varvec{0}) = \mathbb {P}_{\varvec{\theta }}(\varvec{x})$. $\square$

In the main part of the manuscript, we suppress the explicit dependence on $\varvec{\gamma }$ and $\bar{\varvec{\theta }}$ and write $U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}}):=U^{C,\varvec{y}}(\varvec{\gamma }({\nicefrac {1}{2}\varvec{\theta }_{C,\varvec{y}}}))$ to simplify the notation.

Appendix 6.  Proof of Corollary 1

We show that $\mathbb {P}_{\varvec{C}_{\varvec{\theta }}}(\varvec{A}=\varvec{0})$ can be lower bounded by a quantity that depends only on the number of cliques and the norm of the parameter vector. To this end, recall that

$$ Z(\varvec{\theta }) = \sum _{\varvec{x}\in \{0,1\}^n} \exp (\varvec{\theta }^\top \phi (\varvec{x}))\;. $$

Applying Hölder’s inequality to the exponent yields $|\varvec{\theta }^\top \phi (\varvec{x})| \le \Vert \phi (\varvec{x})\Vert _1 \Vert \varvec{\theta }\Vert _\infty$. According to Eq. 3, $\phi (\varvec{x})$ is a binary vector with exactly $|\mathcal {C}|$ non-zero entries, thus $\Vert \phi (\varvec{x})\Vert _1 = |\mathcal {C}|$ for all $\varvec{x}$. Moreover, as explained in Appendix E, we have $\varvec{\theta }\in \mathbb {R}^d_{-}$. Together with the positivity of $\phi (\varvec{x})$, this implies $-|\varvec{\theta }^\top \phi (\varvec{x})| = \varvec{\theta }^\top \phi (\varvec{x})$. Therefore,

$$\begin{aligned} \mathbb {P}_{\varvec{C}_{\varvec{\theta }}}(\varvec{A}=\varvec{0})&= \frac{1}{2^n} Z(\varvec{\theta }) = \frac{1}{2^n} \sum _{\varvec{x}\in \{0,1\}^n} \exp (\varvec{\theta }^\top \phi (\varvec{x}))\\ {}&\ge \frac{1}{2^n} \sum _{\varvec{x}\in \{0,1\}^n} \exp (-|\mathcal {C}| \Vert \varvec{\theta }\Vert _\infty ) = \exp (-|\mathcal {C}| \Vert \varvec{\theta }\Vert _\infty )\;. \end{aligned}$$

which shows that the success probability of our method does not depend on the number of variables n or the model’s treewidth. Instead, it depends on the number of cliques $|\mathcal {C}|$ and the norm of the model’s parameter vector $\Vert \varvec{\theta }\Vert _\infty$. Since $\Vert \varvec{\theta }\Vert _\infty \le \Vert \varvec{\theta }\Vert _p$ for all p, the lower bound holds for all p-norms, i.e., $\mathbb {P}_{\varvec{C}_{\varvec{\theta }}}(\varvec{A}=\varvec{0}) \ge \exp (-|\mathcal {C}| \Vert \varvec{\theta }\Vert _p)$. $\square$

Appendix 7.  Proof of Theorem 4

Suppose a function $f: \{0,1\}^n \rightarrow \{0,1\}$ and a unitary matrix U with diagonal entries $U_{j,j} = u_0$ for $f(\varvec{x}^{(j)}) = 0$ and $U_{j,j} = u_1$ for $f(\varvec{x}^{(j)}) = 1$, where $\varvec{x}^{(j)}$ is the j-th bit string in some arbitrary but fixed order, such that

$$\begin{aligned} U\sum _{j=1}^{2^M} |\varvec{x}^{(j)},a\rangle = \sum _{j=1}^{2^n} u_{f(\varvec{x}^{(j)})} |\varvec{x}^{(j)},a\rangle . \end{aligned}$$

Then, we know from Hogg et al. (1999), [Section 2.1] that U may be decomposed as $U=U_f(I^{\otimes M}\otimes W) U_f$ with $U_f: |\varvec{x},a\rangle \rightarrow |\varvec{x},a~{\text {XOR}}~f(\varvec{x})\rangle$ and $W = u_0 \oplus u_1$.

From Eqs. 3, 6, and 7, we can find that $(U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}}))_{j,j}=1$ whenever $\prod _{v\in C} \mathbbm {1}(\varvec{x}^{(j)}_v = \varvec{y}_v)=0$ and $(U^{C,\varvec{y}}({\varvec{\theta }_{C,\varvec{y}}}))_{j,j}=\exp (i2\varvec{\gamma }_{C,\varvec{y}})$ whenever $\prod _{v\in C} \mathbbm {1}(\varvec{x}^{(j)}_v = \varvec{y}_v)=1$. Now, we can set $f(\varvec{x}) = \prod _{v\in C} \mathbbm {1}(\varvec{x}_v = \varvec{y}_v) = \prod _{v\in C} (\varvec{x}_v\varvec{y}_v + (1-\varvec{x}_v)(1-\varvec{y}_v)) = \bigwedge _{v\in C} (\varvec{x}_v \wedge \varvec{y}_v) \vee (\lnot \varvec{x}_v \wedge \lnot \varvec{y}_v)$. It follows that in this case $U_f$ can be realized by a Boolean AND gate (also known as multi-controlled X gate) whose inputs are properly negated in accordance with $\varvec{y}$. Here, the corresponding unitary $U_{\texttt {AND}}^{C,\varvec{y}}$ acts on $n+1$ qubits, where the AND is applied to the qubits in clique C, negated w.r.t. $\varvec{y}$, and the output of the Boolean AND is assigned to the auxiliary qubit a. Thus, when a is initially $|0\rangle$, we have $U_{\texttt {AND}}: |\varvec{x},0\rangle \rightarrow |\varvec{x},0~\texttt {XOR}~\texttt {AND}(\varvec{x}_C \mid \varvec{y})\rangle$ as desired, where $\texttt {AND}(\varvec{x}_C \mid \varvec{y})$ denotes an AND gate whose j-th input is negated if the j-th entry of $\varvec{y}$ is 0. Decompositions for this type of gate are well known, and implementations are readily available in Qiskit (Abraham et al. 2019). Constructing W with a phase gate completes the proof. $\square$