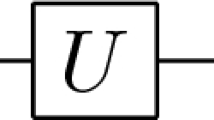1 Introduction

Quantum computing is expected to demonstrate advantages over classical computers in dealing with certain tasks, such as boson sampling (Spring et al. 2013; Wang et al. 2017; Bulmer et al. 2021) and integer factorization (Jiang et al. 2018; Peng et al. 2019). With the advent of noisy intermediate-scale quantum (NISQ) era (Preskill 2018; Bharti et al. 2022), Google has experimentally verified that when sampling the output of a pseudo-random quantum circuit, current NISQ devices can run faster than the state-of-the-art classical computers (Arute et al. 2019). Recently, the University of Science and Technology of China (USTC) has achieved more difficult sampling tasks on Zuchongzhi 2.1 to further push the frontier of quantum computational advantages (Zhu et al. 2022). However, the unavoidable system noise and the restricted coherence time prevent the execution of complicated quantum algorithms on NISQ devices. To accommodate the limitations of NISQ machines, variational quantum algorithms (VQAs) (McClean et al. 2016; Cerezo et al. 2021; Marco et al. 2020; Qian et al. 2022; Tian et al. 2023) which employ a classical optimizer to train a parametrized quantum circuit, have emerged. Concisely, VQAs alternately interact between quantum circuits and classical optimizers, while the former evolves the quantum state and outputs classical information by measurements, and the latter is responsible for seeking the best parameters of quantum circuit to minimize the discrepancy between the predictions and the targets. Pioneer studies have verified the power of VQAs in quantum finance (Roman et al. 2019; Pistoia et al. 2021), quantum chemistry (Grimsley et al. 2019; Arute et al. 2020; Kandala et al. 2017; Robert et al. 2021; Kais 2014; Wecker et al. 2015; Cai et al. 2020; Wang et al. 2019; Romero et al. 2018; Cervera-Lierta et al. 2021; Parrish et al. 2019), many-body physics (Huang et al. 2022; Lee et al. 2021; Endo et al. 2020), machine learning (Huang et al. 2021, 2022; Du and Tao 2021; Caro et al. 2022; Gili et al. 2022), and combinational optimization (Farhi et al. 2014; Zhou et al. 2020; Harrigan et al. 2021; Lacroix et al. 2020; Hadfield et al. 2019; Zhou et al. 2023) from both theoretical and experimental aspects.

Although VQAs promise the practical applications of NISQ machines, they are challenged by the scalability issue. The required number of measurements for VQAs scales with \(O(poly(n, 1/\epsilon ))\) with n being the problem size and \(\epsilon \) being the tolerable error, which implies an expensive runtime for large-scale problems. One canonical instance is the variational quantum eigensolver (VQE) (Peruzzo et al. 2014), which is developed to estimate the low-lying energies and corresponding eigenstates of molecular systems. VQE contains two key steps. First, the electronic Hamiltonian is reformulated to the qubit Hamiltonian \(H=\sum _{i=1}^M\alpha _iH_i\) through Jordan-Wigner, Bravyi-Kitaev, or parity transformations (Seeley et al. 2012; Bravyi and Kitaev 2002; Jordan and Wigner 1993), where \(H_i\in \{\sigma _X, \sigma _Y, \sigma _Z, \sigma _I\}^{\otimes n}\) and \(\alpha _i\in \mathbb {R}\) for \(\forall i \in [M]\), and M is the number of Pauli operators. The property of H is then estimated by a variational quantum circuit whose parameters are updated by a classical optimizer. Principally, it requires \(O(poly(M, 1/\epsilon ))\) queries to the quantum circuit in each iteration to collect the updating information (Gonthier et al. 2020). With this regard, VQEs towards large-scale molecules request an intractable time expense on the measurements. This scalability issue impedes the journey of VQEs to the quantum advantages.

Approaches for reducing the computational overhead of quantum measurements in VQE can be roughly classified into five categories, including operator grouping (Ralli et al. 2021; Verteletskyi et al. 2020; Zhao et al. 2020; Gokhale et al. 2019), ansatz adjustment (Tkachenko et al. 2021; Zhang et al. 2022), shot allocation (Arrasmith et al. 2020; van Straaten and Koczor 2021; Gu et al. 2021; Kübler et al. 2020; Menickelly et al. 2022), classical shadows (Huang et al. 2020; Hadfield et al. 2022), and distributed optimization (Pablo and Chris 2019; Barratt et al. 2021; Yuxuan 2022; Mineh and Montanaro 2022). Specifically, the operator grouping strategy focuses on finding the commutativity between local Hamiltonian terms \(\{H_i\}\) in H. The commutable Hamiltonians can be evaluated by the same measurements, which enable the measurement reduction (Kandala et al. 2017; Ralli et al. 2021; Verteletskyi et al. 2020; Zhao et al. 2020; Gokhale et al. 2019). Ansatz adjustment targets to tailor the layout of ansatz to reduce the circuit depth (Tkachenko et al. 2021; Tang et al. 2021; Grimsley et al. 2019) or the number of qubits (Zhang et al. 2022). For example, Ref. Tkachenko et al. (2021) attempts to assign two qubits with stronger mutual information to the adjacent locations with direct connectivity on the physical quantum chips, leading to shallower circuits over the original VQEs to reach a desired accuracy. Shot allocation aims to assign the number of shots among \(\{H_i\}\) in a more intelligent way. A typical solution is to allocate more shots to the terms with a larger coefficient \(|\alpha _i|\) and a larger variance of \(\langle {H_i}\rangle \) (Arrasmith et al. 2020). Another measurement reduction method, classical shadows, constructs an approximate classical representation of a quantum state based on few measurements of the state (Huang et al. 2020). With this representation, \(O(\log (M))\) measurements are enough to estimate the expectation value of whole observable with high precision.

On par with reducing computational complexity of the quantum part, we can reduce the computational time of the optimization of VQE by using multiple quantum processors (workers), inspired by the success of distributed optimization in deep learning and the growing number of available quantum chips. There are generally two types of distributed VQAs. The first paradigm is decomposing the primal quantum systems into multiple smaller circuits and running them in parallel (Barratt et al. 2021; DiAdamo et al. 2021). The second paradigm is utilizing the quantum cloud server in which the problem Hamiltonian can be pre-divided into several partitions and distributed into Q local quantum workers respectively. Each worker estimates the expectation value of partial local Hamiltonians with no more than O(poly(M/Q)) queries and delivers the result to the rest of the workers after a single iteration. Noticeably, such a methodology inevitably encounters the communication bottleneck, quantum circuit noise, and the risk of privacy leakage. As such, Ref. Yuxuan (2022) devises the QUantum DIstributed Optimization (QUDIO), a novel distributed-VQA scheme in a lazy communication manner, to address this issue. It is important to note that QUDIO utilizes local stochastic gradient descent (SGD) to optimize parameters based on a pre-divided subset of the entire samples, assuming that all samples are independent and identically distributed (i.i.d). However, the local Hamiltonians allocated to different quantum processors are not i.i.d. Therefore, the naive allocation method is not suitable for VQEs. Besides, the coefficients \(\{\alpha _i\}\) of the local Hamiltonian terms \(\{H_i\}\) are varied, leading to unbalanced contributions to the overall variance of Hamiltonian estimation. Such an estimation error can be exacerbated by the increased communication interval, which renders the trade-off between the acceleration ratio and the approximation error of VQEs.

To maximally suppress the negative effects of large communication interval on the convergence rate, here we propose a new quantum distributed optimization framework, called Shuffle-QUDIO. Different from QUDIO, for every local worker, the local Hamiltonian terms are randomly shuffled and sampled without replacement according to the worker’s rank before each iteration. From a statistical view, this operation alleviates the issue such that every local worker may only observe incomplete local Hamiltonians during the optimization. Moreover, the dynamic allocation of Hamiltonian terms alleviates the accumulated deviation with respect to the target Hamiltonian H after a large number of local updates. In this way, Shuffle-QUDIO achieves faster convergence while keeping low communication cost, leading to a high speedup with respect to time-to-accuracy. Consequently, it is particularly well-suited for addressing large-scale quantum chemistry problems. Another advantage of our proposal is its compatibility across various quantum hardware architectures, which makes it possible to unify existing quantum devices to accelerate the training of VQEs.

To theoretically exhibit the advance of our proposal, we prove that Shuffle-QUDIO allows a faster convergence rate than that of QUDIO. By leveraging the non-convex optimization theory, we exhibit that the dominant factors affecting the convergence rate are the number of distributed quantum machines K, the local updates (communication interval) W, and the global iterations T, i.e., O(poly(W, K, 1/T)). To benchmark the performance of Shuffle-QUDIO, we conduct systematic numerical experiments on VQEs under both fault-tolerant and noisy scenarios. The achieved results confirm that Shuffle-QUDIO achieves smaller approximation error over QUDIO, as well as lower communication overhead among clients and server, and sub-linear speedup ratio. In addition, we demonstrate that the performance of Shuffle-QUDIO under the noisy setting can be further boosted by combining the advanced operator grouping strategy. To further facilitate the development of a community of quantum acceleration algorithms, we provide an open-source code repository: https://github.com/QQQYang/Shuffle-QUDIO.

The remaining parts of this paper are organized as follows. Section 2 briefly introduces the preliminary knowledge about the optimization of variational quantum circuits. Section 3 presents the pipeline of the proposed algorithm and presents the convergence analysis. Section 4 exhibits numerical simulation results. Section 5 gives a summary and discusses the outlook.

2 Preliminary

The essence of VQE is tuning an n-qubit parameterized quantum state \(\rho ({\varvec{\theta }})=| \psi (\varvec{\theta }) \rangle \langle \psi (\varvec{\theta }) |\) with \(\varvec{\theta }\in \mathbb {R}^P\) to minimize the energy of a problem Hamiltonian

$$\begin{aligned} H=\sum _{i=1}^M\alpha _iH_i\in \mathbb {C}^{2^n\times 2^n}, \end{aligned}$$
(1)

where \(H_i\) refers to the i-th local Hamiltonian term with the weight \(\alpha _i\). The energy minimization is formulated by the loss function

$$\begin{aligned} L(\varvec{\theta },H):={{\,\textrm{Tr}\,}}\left( \rho ({\varvec{\theta }})H\right) =\sum _{i=1}^M\alpha _i{{\,\textrm{Tr}\,}}\left( \rho ({\varvec{\theta }})H_i\right) . \end{aligned}$$

With a slight abuse of notation, we denote \(H_i\) as \(\alpha _iH_i\) and simplify the above loss function as

$$\begin{aligned} L(\varvec{\theta },H)=\sum _{i=1}^M{{\,\textrm{Tr}\,}}\left( \rho ({\varvec{\theta }})H_i\right) . \end{aligned}$$

The parameterized quantum state is prepared by an ansatz with \(| \psi (\varvec{\theta }) \rangle =U(\varvec{\theta })| \phi \rangle \) and \(| \phi \rangle \) being an initial quantum state. A generic form of \(U(\varvec{\theta })\) is

$$\begin{aligned} U(\varvec{\theta }) = \prod _{l=1}^LU_{e}\prod _{i=1}^N\exp (-i\theta _{l,i}O_i), \end{aligned}$$
(2)

where \(O_i\) is a Hermitian matrix and \(U_{e}\) denotes a fixed unitary composed of multi-qubit gates. By iteratively updating the circuit parameters \(\varvec{\theta }\) to minimize the loss, the quantum state \(\rho ({\varvec{\theta }})\) is expected to approach the eigenstate of H with the minimum eigenvalue.

2.1 Optimization of VQE

Gradient descent (GD) based optimizers are widely used in previous literatures of VQE. The parameters \(\varvec{\theta }^{t+1}\) at the \((t+1)\)-th iteration is updated alongside the steepest descent direction with learning rate \(\eta \), i.e.,

$$\begin{aligned} \varvec{\theta }^{t+1}=\varvec{\theta }^t-\eta \nabla L(\varvec{\theta }^t,H). \end{aligned}$$
(3)

Unlike classical neural networks that utilize gradient back-propagation to update parameters (LeCun et al. 1988), VQE adopts the parameter-shift rule (Banchi and Crooks 2021; Wierichs et al. 2022) to obtain the unbiased estimation of the gradient. The gradient with respect to the i-th parameter is

$$\begin{aligned} \frac{\partial L(\varvec{\theta },H)}{\partial \theta _i}=\frac{L(\varvec{\theta }+\frac{\pi }{2}\varvec{e}_i,H)-L(\varvec{\theta }-\frac{\pi }{2}\varvec{e}_i,H)}{2}, \end{aligned}$$
(4)

where \(\varvec{e}_i\) denotes the indicator vector for the i-th element of parameter vector \(\varvec{\theta }\). When the number of trainable parameters is P, the required number of measurements to complete the gradient computation scales with O(poly(PM)) without applying any measurement reduction strategies.

Fig. 1
figure 1

The scheme of Shuffle-QUDIO. The Shuffle-QUDIO consists of three subroutines, including initialization, local updates and global synchronization. During the phase of initialization, multiple copies of the original ansatz and the corresponding problem Hamiltonian H are dispatched into each local processor. Note that each processor shares the same seed of the random number generator. For each iteration in the local updates, the set of observables \(\{H_i\}_{i=1}^M\) is randomly shuffled and the i-th local processor picks the subset of whole observables according to the assigned random number. In this way, the observables of each processor do not overlap with each other and the union of their observables exactly constitutes the problem Hamiltonian H. After W local updates, the parameters of each local ansatz are aggregated and then reassigned to all local processors, which is called global synchronization. When the maximal number T of iterations is reached, Shuffle-QUDIO executes the final synchronization and outputs the trained parameters

Full size image

2.2 Optimization of the distributed VQE

To accelerate the training of VQA, Ref. Yuxuan (2022) proposed the QUantum DIstributed Optimization (QUDIO) scheme. The key idea of QUDIO is to partition the problem Hamiltonian H in Eq. (1) into several groups and distribute them into multiple quantum processors to be manipulated in parallel. Mathematically, suppose that there are K available quantum processors \(\{\mathcal {Q}_i\}_{i=1}^K\), the Hamiltonian terms \(\{H_i\}_{i=1}^M\) are divided into K subgroups \(\{\mathcal {S}_i\}_{i=1}^K\), where \(\mathcal {S}_i=\cup _{j\in S_i} \{H_j\}\), so that \(\sum _{i=1}^K |S_i| =M\) and \(S_i\cap S_j=\emptyset \) when \(i\ne j\).

In the initialization process, the i-th subgroup \(\mathcal {S}_i\) is allocated to the i-th quantum processor \(\mathcal {Q}_i\) for \(\forall i \in [K]\). All local processors share the same initial parameters \(\varvec{\theta }^0\) with \(\varvec{\theta }_i^{(0,0)}=\varvec{\theta }^0\) for \(\forall i\in [K]\). The subsequent training process alternately switches between the local updates and the global synchronization. During the phase of local updates, each quantum processor follows the gradient descent rule to update the parameters to minimize the local loss function \(L(\varvec{\theta }_i,H_{S_i})=\sum _{j\in S_i}{{\,\textrm{Tr}\,}}(\rho ({\varvec{\theta }_i})H_j)\), i.e., the parameters of the i-th processor at the (t, w)-th step is updated as Eq. (3). After fulfilling W local updates, all parameters from distributed quantum processors are synchronized by averaging the collected parameters \(\varvec{\theta }^{t+1}=\frac{1}{K}\sum _{i=1}^K\varvec{\theta }_i^{(t,W)}\). Repeating the above two phases until the termination conditions (e.g., the maximum number of iterations) are met, the synchronized parameters are returned as the final parameters.

Ignoring the communication overhead among quantum processors, QUDIO with \(W=1\) is expected to linearly accelerate the optimization of VQE. However, the communication bottleneck could degrade the acceleration efficiency. An optional solution is to increase W to reduce the communication frequency. As indicated in Yuxuan (2022), the performance of VQA witnesses a rapid drop with the increased W.

3 Shuffle-QUDIO for VQE

The performance of QUDIO suffers from a high sensitivity of the communication interval. Intuitively, this issue originates from the fact that each quantum processor in QUDIO only perceives a static subset of the whole observable set during the entire training process. The i-th processor updates its local parameters based on the partial observations before communicating with other processors. Meantime, the coefficients \(\{\alpha _i\}\) and the variance of Pauli operators \(\{H_i\}\) differ from each other, leading to different contributions to the expectation estimation of H. As a result, the local processor fails to characterize the full property of the problem Hamiltonian H. With multiple local updates, the accumulation of bias further degrades the performance of QUDIO. To tackle this issue, here we devise a novel quantum distributed optimization scheme, called Shuffle-QUDIO, to avoid the performance drop when synchronizing in a low frequency.

Fig. 2
figure 2

The pseudocode of Shuffle-QUDIO

Full size image

3.1 Algorithm descriptions

The paradigm of Shuffle-QUDIO is depicted in Fig. 1, which consists of three steps.

  1. 1.

    Initialization. The variational quantum circuit \(U(\varvec{\theta })\) in Eq. (2) of each quantum processor is initialized with the same parameters \(\varvec{\theta }_i^{(0,0)}=\varvec{\theta }^0\) for \(i=\{1,...,K\}\) and all local Hamiltonian terms \(\{H_i\}\) are distributed to each processor.

  2. 2.

    Local updates. Each processor independently updates the parameters \(\varvec{\theta }^{(t,w)}_i\) following the gradient descent principle. First, Shuffle-QUDIO randomly shuffles the sequence of local Hamiltonian terms. Note that the random number of each processor is generated from the same random seed. Assuming the permutation vector is denoted by \(\pi ^{(t,w)}\), the visible Hamiltonians for the i-th processor at the t-th iteration are \(\mathcal {H}^{(t,w)}_i=\{H_{\pi ^{(t,w)}(j)}\}_{j=\frac{M}{K}(i-1)+1}^{\frac{M}{K}i}\) (suppose M is exactly divided by K). Then each processor estimates the gradient \(\varvec{g}_i^{(t,w)}\) by the parameter-shift rule. Note that \(\varvec{g}\) denotes the estimated gradient on the quantum device due to the finite number of measurements, while \(\nabla L\) refers to the corresponding accurate gradient. The parameters are updated as

    $$\begin{aligned} \varvec{\theta }^{(t,w+1)}_i=\varvec{\theta }^{(t,w)}_i-\eta \varvec{g}_i^{(t,w)}, \end{aligned}$$
    (5)

    where \(\eta \) is the learning rate. Repeat the above local updates for W local steps.

  3. 3.

    Global synchronization. Once the local updates are completed, the central server synchronizes parameters among all quantum processors in an averaged manner, i.e.,

    $$\begin{aligned} \varvec{\theta }^{t+1}=\frac{1}{K}\sum _{i=1}^K \varvec{\theta }^{(t,W)}_i. \end{aligned}$$
    (6)

    If the number of the global iterations reaches T, the parameters \(\varvec{\theta }^T\) are returned as the output; otherwise, return back to step 2.

The pseudocode of Shuffle-QUDIO is summarized in Fig. 2. Compared with conventional VQE which sequentially measures the expectation value of every single observable, the strategy of distributed parallel optimization accelerates the estimation of the complete observables by K times. Furthermore, the shuffling operation alleviates the deviation of the optimization direction during the local updates and thus warrants more stable performance after increasing communication interval. This is because in a statistical view, each processor can leverage the information of all local Hamiltonian terms to update local parameters in the training process.

Lemma 1

Let \(\{H_1,...,H_M\}\) be M Hermitian matrices in \(\mathbb {C}^{2^n\times 2^n}\), \(H=\sum _{i=1}^MH_i\). Let \(\rho (\varvec{\theta })\) be an n-qubit quantum state parameterized by \(\varvec{\theta }\). For any \(k\in \{1,...,M\}\), let \(H_{\pi (1)},...,H_{\pi (k)}\) be uniformly sampled without replacement from \(\{H_1,...,H_M\}\). Let \(L={{\,\textrm{Tr}\,}}(\rho (\varvec{\theta })H)\) and \(L_m={{\,\textrm{Tr}\,}}(\rho (\varvec{\theta })\sum _{i=1}^mH_{\pi (i)})\). Then we have

$$\begin{aligned} \mathbb {E}\left[ \frac{\partial L_m}{\partial \varvec{\theta }}\right] =\frac{m}{M}\frac{\partial L}{\partial \varvec{\theta }}. \end{aligned}$$
(7)

Refer to Appendix B for proof details. Lemma 1 implies that the direction of the expected gradient of each local quantum processor in Shuffle-QUDIO is unbiased. This guarantees that the local quantum circuits are individually optimized forward along the right direction when they do not communicate frequently with each other, which narrows the performance gap between a single processor and the synchronized model. By contrast, during the local updates of QUDIO, there always exists a bias between the locally estimated gradient and the global gradient. Specifically, Shuffle-QUDIO achieves smaller gradient deviation than vanilla QUDIO, as indicated by the following lemma, whose proof is provided in Appendix C.

Lemma 2

Assume the norm of local gradient \(\varvec{g}_k(\varvec{\theta }, H_k)\) is bounded by \(\left\| \varvec{g}_k\right\| ^2\le G^2\) where G is a positive constant, and \(K>1\). Compared with QUDIO, the discrepancy between the local gradient \(\varvec{g}_k(\varvec{\theta }, H_k)\) and the global gradient \(\left\| \nabla L(\varvec{\theta },H)\right\| \) in Shuffle-QUDIO is reduced from \(2(K^2+1)G^2\) to \((K-1)^2G^2\).

3.2 Convergence analysis

We next show the convergence guarantee of Shuffle-QUDIO. When running VQE on NISQ devices, the system imperfection introduces noise into the optimization. To this end, we consider the worst scenario in the convergence analysis, where the system noise is modeled by the depolarizing channel. It introduces an equal probability of bit-flip, phase-flip, and both bit- and phase-flip in a depolarizing channel and will finally drive the quantum system into maximally mixed state. Mathematically, the depolarizing channel \(\mathcal {N}_p\) transforms the quantum state \(\rho \in \mathbb {C}^{2^n\times 2^n}\) to \(\mathcal {N}_p(\rho )=(1-p)\rho +p\mathbb {I}/2^n\), and with increasing the noise strength p, the quantum state finally evolves to the maximally mixed state. As proved in Yuxuan et al. (2021), the depolarizing channel applied on each circuit depth can be merged at the end of the quantum circuit. Therefore, without loss of generality, the estimated gradient with respect to the i-th parameter is

$$\begin{aligned} \frac{\partial \overline{L}(\varvec{\theta },H)}{\partial \theta _i}=(1-p)\frac{\partial L(\varvec{\theta },H)}{\partial \theta _i}. \end{aligned}$$
(8)

The convergence rate of Shuffle-QUDIO is summarized by the following theorem whose proof is provided in Appendix D.

Theorem 1

Let the gradient of loss function L be F-Lipschitz continuous, G be the upper bound of the gradient norm, \(\eta \) be the learning rate of optimizer, p be the strength of depolarizing noise, T be the total number of global iterations, K and W be the number of distributed quantum processor and local iterations respectively, the convergence of Shuffle-QUDIO in the noisy scenario is summarized as

$$\begin{aligned}&\frac{1}{T}\sum _{t=1}^T\left\| \nabla L(\varvec{\theta }^t)\right\| ^2\le \frac{2(L\left( \varvec{\theta }^1)-L(\varvec{\theta }^{T+1})\right) }{\eta T}\nonumber \\&+\frac{4F^2\eta ^2W^2G^2(K-1)}{KT}\nonumber \\&+\frac{\left( 2K(K-2+2p)+(\eta F+1)(1-p)^2\right) G^2}{T} \end{aligned}$$
(9)

Theorem 1 reveals that an increased quantum noise rate p leads to poor convergence of Shuffle-QUDIO, which emphasizes the significance of error mitigation (Endo et al. 2018, 2021; Strikis et al. 2021; Yuxuan et al. 2022) in quantum optimization. Meantime, the shorter communication interval W among distributed quantum processors guarantees a better performance of Shuffle-QUDIO. Note that although a large W still hinders the distributed optimization, Shuffle-QUDIO achieves faster convergence than QUDIO for equivalent W values. Refer to Appendix D for a detailed discussion.

This divergence in performance between QUDIO and Shuffle-QUDIO stems from their distinct constraints on Hamiltonians. Shuffle-QUDIO is specifically designed for quantum chemistry and quantum many-body physics problems, while QUDIO is more suitable for machine learning tasks, such as data classification and regression. The different targets of the two algorithms result in different achievements. Therefore, we consider QUDIO and Shuffle-QUDIO as complementary to each other. Regarding the performance, we would like to emphasize that QUDIO is inferior to Shuffle-QUDIO in learning quantum chemistry problems due to the difference in the distribution of local Hamiltonians. QUDIO is designed for i.i.d examples, whereas the local Hamiltonians allocated to different quantum processors are not i.i.d. As such, QUDIO suffers from an obvious performance drop when increasing the communication interval among quantum chips. By contrast, the proposed Shuffle-QUDIO allows smaller approximation error as well as lower communication overhead among clients and server, and lower runtime cost, which provides bigger potential to achieve higher speedup with more quantum resource available and faster communication.

From the technical view, although the proof of Theorem 1 is derived from the classical results on local SGD (Haddadpour et al. 2019), there are some key differences between them. First, in classical local SGD, each worker independently samples a mini-batch from the whole dataset without other limitations. By contrast, the distributed quantum processors randomly sample the local Hamiltonian terms without replacement in each local iteration, which means that the Hamiltonian terms of each processor do not overlap and the union exactly constitutes the complete molecule Hamiltonians. This special sampling method guarantees the integrity of the problem Hamiltonian, but poses a challenge for theoretical analysis. Second, our analysis does not rely on the strong assumptions, such as convexity or Polyak-Lojasiewicz (PL) condition (Sweke et al. 2020). Furthermore, the quantum noise in NISQ devices inevitably shifts the quantum state and biases the estimated gradients, which differentiates VQE from classical machine learning.

4 Numerical results

To verify the effectiveness of Shuffle-QUDIO, we apply it to estimate the ground state of several molecules with the lowest energy. Jordan-Wigner transformation (Jordan and Wigner 1993) is employed to transform these electronic Hamiltonians into the qubit Hamiltonians represented by Pauli operators. For example, the LiH system is totally described by 12 qubits and 631 local Pauli terms \(\{\sigma _I,\sigma _X,\sigma _Y,\sigma _Z\}^{\otimes 12}\). The ansatz is designed in a hardware-efficient style inspired by Kandala et al. (2017), whose layout is shown in Fig. 3. We conduct numerical experiments on classical device with Intel(R) Xeon(R) Gold 6267C CPU @ 2.60GHz and 128 GB memory. For each setting, the experiment is repeated for 5 times with different random seeds to mitigate the effect of randomness. Stochastic gradient descent is used to update trainable parameters, where the learning rate is set as \(\eta = 0.4\).

Fig. 3
figure 3

Layout of hardware-efficient ansatz. The gate “Rot” represents the concatenation of rotation gate \(R_z\), \(R_y\), \(R_z\), and \(\theta \) represents the rotation angle

Full size image
Fig. 4
figure 4

Comparison of speedup of QUDIO and Shuffle-QUDIO for VQE to solve the ground state of LiH. The label “\(W=a\)” refers that the number of local iterations is a. The label “linear speedup” represents the reference line of the linear speedup

Full size image

4.1 Acceleration ratio

We consider the speedup w.r.t time-to-accuracy as the performance indicator of Shuffle-QUDIO and compare it with QUDIO. Specifically, denote \(T_{acc}(K,W)\) as the time spent on training the model to reach a specific accuracy under the setting of K quantum processors and W local iterations. Mathematically, \(T_{acc}(K,W)\) can be modeled as

$$\begin{aligned} T_{acc}(K,W)&\!=\!C_{acc}*T_{iter}\left( \frac{M}{K}\right) +C_{acc}*\frac{T_{comm}(K)}{W} \nonumber \\&\!=\!C_{acc}*\left[ T_{iter}\left( \frac{M}{K}\right) +\tilde{T}_{comm}(K,W)\right] , \end{aligned}$$
(10)

where \(C_{acc}\) is the number of iterations required for training a model to reach a specific accuracy, \(T_{iter}(*)\) is the wall-clock time of every optimization iteration, \(T_{comm}(*)\) denotes the wall-clock time spent in one communication, and \(\tilde{T}_{comm}(K,W)=\frac{T_{comm}(K)}{W}\) can be regarded as the average communication time allocated evenly into every iteration. The speedup with respect to time-to-accuracy, denoted as \(s^{K,W}\), is defined as \(s^{K,W}=T_{acc}(K,W)/T_{acc}(1,1)\). Intuitively, the positive effects on communication time reduction (small \(\tilde{T}_{comm}(K,W)\)) and negative effects on convergence drop (large \(C_{acc}\) or \(T_{acc}(K,W)\)) caused by increasing W lead to a trade-off between achieving shorter running time and faster convergence when adjusting W.

Figure 4 shows the results of solving the ground state of LiH. The right panel illustrates that increasing K from 1 to 4 nearly achieves a linear speedup for \(W=1,2,4,8,16\), and there is no significant difference of performance between different W. However, the speedup of \(W=1\) decreases when the number of local nodes (K) reaches 8 due to the communication bottleneck for larger K and small W. To alleviate this, we can increase W to reduce communication frequency. When \(W=8\), the highest speedup among all settings is achieved. It is worth noting that larger \(W=16\) achieves lower speedup than \(W=8\) at point \(K=8\) due to the poor convergence brought by the large W. When K continues to grow, such as \(K=16\), the performance of all settings begins to decline because the increase in communication cost resulting from a large number of communication nodes outweighs the decrease in computational cost for estimating the expectation of the Hamiltonian. Therefore, a larger W does not guarantee higher speedup w.r.t time-to-accuracy than smaller W. Please refer to Appendix F for more detailed explanations.

Furthermore, comparing the left panel with the right panel of Fig. 4, we observe that Shuffle-QUDIO allows for larger K (\(K=8\)) and W (\(W=8\)) than QUDIO (\(K=4\) and \(W=4\)) and achieves a higher speedup ratio.

Fig. 5
figure 5

Training process of VQE optimized by QUDIO and Shuffle-QUDIO respectively. Each data point is collected after the synchronization. The dashed black line denotes the exact ground state energy (GSE) at the same setting. The first row: the loss curve with respect to iterations in QUDIO. With exponentially increasing W, the convergence of training is severely degraded, as depicted in subplot at first row, sixth column. The second row: the loss curve with respect to the iterations in Shuffle-QUDIO. The speed of loss decrease sees a relatively slow decay with W growing. When \(W=32\) (second row, sixth column), the loss still converges to the same level of \(W=1\) within 200 iterations

Full size image
Fig. 6
figure 6

Energy potential surface of molecule LiH. The black line with label “ExactEigensolver” represents the exact energy potential surface of the molecule LiH

Full size image
Fig. 7
figure 7

Mean value \(\overline{Err}\) and standard deviation \(\delta (Err)\) of the approximation error. Each data point is collected over various bond distances and random seeds. Shuffle-QUDIO outperforms QUDIO in achieving smaller approximation error and lower sensitivity to communication frequency W

Full size image

4.2 Sensitivity to communication frequency

We compare QUDIO with Shuffle-QUDIO to show how the increased number of local iterations W effects their performance under the ideal scenario. The molecules LiH with varied inter-atomic length, i.e., 0.3Å to 1.9Å with step size 0.2Å, are explored. For QUDIO, the entire set of Pauli terms constituting the problem Hamiltonian is uniformly partitioned into 32 subsets and distributed into 32 local quantum processors. The accessible Hamiltonian terms for each local processor remain fixed during the whole training process. The number of local iterations W varies in \(\{1,2,4,8,16,32\}\).

The simulation results of VQE for the molecule LiH with 0.5Å are illustrated in Fig. 5. Because the number of local iterations W varies among different settings, we uniformly collect data point after every 32 iterations (i.e., the least common multiple of all W) to guarantee the loss is obtained exactly after synchronization. The first row of Fig. 5 records the loss curves of QUDIO with respect to the training steps under different local iterations W. QUDIO experiences a severe drop of performance, and an evident gap between the estimated and the exact results appears when \(W\ge 8\). By contrast, as shown in the bottom row of Fig. 5, Shuffle-QUDIO well estimates the exact ground energy even when \(W=32\). Comparing the subplots of the same column, Shuffle-QUDIO shows a distinct advantage in improving the convergence of the distributed VQE when requiring a lower communication overhead. For example, Shuffle-QUDIO achieves \(-6.8Ha\) at the 96-th iteration with \(W=8\), while QUDIO only reaches \(-4.1Ha\).

The potential energy surface of LiH solved by the conventional VQE is shown in Fig. 6, where the left panel describes the results of QUDIO with the varied number of local iterations W and the right panel records the results of Shuffle-QUDIO. There exists a distinct boundary among the potential energy surfaces estimated by the different level of W in QUDIO. More precisely, the estimated potential energy surface is gradually away from the exact potential energy surface (black line) with the increased W, which reveals the vulnerability of QUDIO when reducing the communication frequency among distributed workers. By contrast, Shuffle-QUDIO exhibits a fairly stable performance even when increasing W from 1 to 32, drawn from the nearly coincident curves of potential energy surface at each setting of W. Note that the slight gap between the exact potential energy surface and the optimal estimated results originates from the restricted expressive power of the employed ansatz, which does not guarantee the prepared state definitely covers the ground state of LiH.

To further quantify the stability of Shuffle-QUDIO, we statistically compute the mean and standard deviation of the approximation error \(Err=\left| E^{VQE}-E^{ideal}\right| \) over various bond distances and random seeds. As illustrated in Fig. 7(a), the average approximation error \(\overline{Err}\) of QUDIO exponentially scales with increased W. When \(W\ge 8\), the approximation error estimated by QUDIO exceeds 2Ha, which fails to capture the ground state of LiH. Instead, Shuffle-QUDIO achieves an imperceptible increment (0.093) of the approximation error when W grows from 1 to 32, making it possible to largely reduce the communication overhead with a little performance drop. Figure 7(b) depicts the standard deviation of the approximation error derived by both methods, showing that Shuffle-QUDIO enjoys a smaller variance and a stronger stability than those of QUDIO. These observations provide the convincing empirical evidence that Shuffle-QUDIO efficiently reduces the susceptibility to W in the quantum distributed optimization.

Fig. 8
figure 8

Speedup of operator grouping to VQE for \(\mathrm{H_2}\). The label “base” refers to the case that no operator grouping is applied. The label “linear speedup” represents the reference line of linear speedup

Full size image

4.3 Sensitivity to quantum noise

To better characterize the ability of Shuffle-QUDIO run on NISQ devices, we benchmark its performance under the depolarizing noise and the realistic quantum noise modeled by PennyLane (Bergholm et al. 2018). The noise strength of the global depolarizing channel p ranges from 0 to 0.3 with step size 0.1. The realistic noise model is extracted from the 5-qubit IBM ibmq_quito device. Note that the measurement error introduced by a finite number of shots is also considered.

We first benchmark the performance of Shuffle-QUDIO with the operator grouping when the shot noise is considered. In practice, the process begins by distributing the entire Hamiltonians across local quantum processors. Subsequently, we implement operator grouping on these local Hamiltonians. For each processor, the operators within its local Hamiltonian are organized into several groups. Operators within the same group are selected for their ability to commute qubit-wise, a feature that facilitates the simultaneous measurement of multiple operators by measuring their common eigenbases. Rotation gates may be applied as needed to align the quantum state with the appropriate basis for measurement.

The results are shown in Fig. 8. After applying operator grouping to the molecule Hamiltonian, the trainable quantum state fast converges to the ground state of the molecule than that of the original measurement strategy. In the light of the speedup provided by the operator grouping, we can integrate this technique into the framework of Shuffle-QUDIO to gain better performance. On the other hand, with growing number of quantum processors, the acceleration rate with the operator grouping strategy gradually decays. This phenomenon partially results from the fact that a small number of Hamiltonian terms leads to a small proportion of operators that can be grouped together.

Fig. 9
figure 9

Performance comparison in NISQ era. ideal represents the fault-tolerant case without noise, \(p=a\) represents the case where there exists a depolarizing channel with strength a in the circuit, NISQ represents the case of running on a real NISQ device

Full size image

We next apply QUDIO, QUDIO with the operator grouping, Shuffle-QUDIO, and Shuffle-QUDIO with the operator grouping to estimate the ground energy of the \(\mathrm{H_2}\) molecule under both the system and shot noise. For each method, the hyper-parameters are set as \(K=4\), \(W=32\), and the number of measurements is 100. Each setting is conducted for 5 times to capture the effect of stochastic noise on the performance. The simulation results are shown in Fig. 9. When the depolarizing noise is not big enough (\(p<=0.2\)), Shuffle-QUDIO achieves much smaller approximation error than QUDIO. When \(p=0.3\), it appears that the overwhelming noise disables both Shuffle-QUDIO and QUDIO. Under the realistic noise setting, Shuffle-QUDIO still works well with a tolerable approximation error 0.063. By contrast, QUDIO is incapable of estimating the accurate ground state energy. Note that although parameter random initialization leads to nonnegligible fluctuations in the final approximation error, the advantage of Shuffle-QUDIO over QUDIO remains significant and cannot be ignored. Moreover, the operator grouping can further widen the performance gap between QUDIO and Shuffle-QUDIO, by inhibiting the negative effect of quantum noise on Shuffle-QUDIO.

Fig. 10
figure 10

Performance comparison of various model aggregation algorithms. The closer the curve is to the upper left, the more accurate the estimated ground state energy is

Full size image

4.4 Aggregation strategy

Shuffle-QUDIO narrows the discrepancy among distributed processors by randomly changing the observables of each processor in every local iteration, which partially guarantee the rationality of taking average of all models for synchronization. To further explore the effect of various aggregation strategy on the performance of Shuffle-QUDIO, we devise three additional model aggregation algorithms, named as random aggregation, median aggregation and weighted aggregation.

  • Random aggregation: randomly select a local processor and distribute its parameters of quantum circuit to other processors.

  • Median aggregation: rank all local processors by their loss value and select the median as the synchronized quantum circuit.

  • Weighted aggregation: combine all quantum circuits of local processors by loss-induced weighted summation. The smaller the value of the loss function for a local processor, the bigger contributions the processor makes to the synchronized quantum model.

Fig. 11
figure 11

Training process of VQE for hydrogen molecule optimized by shot-based distributed VQE and Hamiltonian-based distributed VQE (Shuffle-QUDIO) respectively. The label “\(K=a\)” refers that the number of nodes is a. Each setting is run with \(W=1\). The dashed black line denotes the exact ground state energy (GSE) at the same setting

Full size image

Refer to Appendix G for more details.

We implement four quantum model aggregation methods in the framework of Shuffle-QUDIO to solve the ground state energy of molecule \(\mathrm{H_2}\) and \(\textrm{LiH}\). The hyper-parameters are set as \(W\in \{1,2,4,8,16,32\}\), \(K\in \{1,2,4,8,16\}\). Figure 10 demonstrates the cumulative distribution function (CDF) of the approximation error to ground state energy. It appears no large cleavage of the approximation error among four aggregation strategies, indicating the strong robustness of Shuffle-QUDIO to quantum model aggregation. This stability may give credit to the introduction of the shuffle operation during distributed quantum computation, which diminishes the bias among different local quantum models. On the other hand, it is worth noting that average aggregation always achieves smaller approximation error with higher probability than random aggregation in the statistical sense. This difference of CDF implies that a superior aggregation algorithm for the quantum distributed optimization could further enhance the efficiency of Shuffle-QUDIO. We leave the design of an optimal aggregation method as the future work.

4.5 Comparison with shot-based method

In addition to Shuffle-QUDIO/QUDIO, which partitions the whole Hamiltonian terms into multiple small sets and distributes them to multiple quantum processors, another intuitive method to accelerate VQE is to allocate the total budget of shot number into multiple quantum nodes. We refer to these two strategies as the Hamiltonian-based method and the shot-based method, respectively, in our work. Let \(S^{total}\) denote the total shot budget in shot-based distributed VQE. Let K be the number of quantum processors. let M denote the number of Hamiltonian terms of a molecule. Let \(S^{single}\) denote the number of shot for each quantum processor in QUDIO/Shuffle-QUDIO. If \(S^{total}=S^{single}*K\), the running time of shot-based distributed VQE is equal to that of QUDIO/Shuffle-QUDIO with \(W=1\). However, the shot noise of shot-based distributed VQE differs from that of QUDIO/Shuffle-QUDIO. With the budget of shot number \(S^{total}\), the allocated number of shot for each Hamiltonian term in shot-based distributed VQE and QUDIO/Shuffle-QUDIO is \(\frac{S^{total}}{KM}\) and \(\frac{S^{total}}{M}\) respectively. Therefore, QUDIO/Shuffle-QUDIO introduces smaller shot noise than shot-based distributed VQE.

To investigate the difference between proposed Shuffle-QUDIO and the shot-based method, we conduct numerical experiments to demonstrate the performance of these two methods to solve the ground state of hydrogen molecule. In this study, we set \(M=15\) and \(S^{total}=15,000\). As shown in the top row of Fig. 11, the training process of Hamiltonian-based distributed VQE (Shuffle-QUDIO) with \(K=15\) is equivalent to that of other 4 settings (\(K=\{1,2,4,8\}\)). The bottom row of Fig. 11 depicts the training process of shot-based distributed VQE with varying values of K. When K increases from 1 to 15, the number of shot allocated to each Hamiltonian term gradually decreases, leading to greater disturbance and poorer convergence in the estimation of the energy.

5 Discussion

In this paper, we propose Shuffle-QUDIO, as a novel distributed optimization scheme for VQE with faster convergence and strong noise robustness. By introducing the shuffle operation into each iteration, the Hamiltonian terms received by each local processor are not fixed during the optimization. From the statistical view, the shuffle operation warrants that the gradients manipulated by all local processors are unbiased. In this way, Shuffle-QUDIO allows an improved convergence and a lower sensitivity to communication frequency as well as quantum noise. Meanwhile, the operator group strategy can be seamlessly embedded into Shuffle-QUDIO to reduce the number of measurements in each iteration. Theoretical analysis and extensive numerical experiments on VQE further verify the effectiveness and advantages in accelerating VQE and guaranteeing small approximation errors in both ideal and noisy scenarios.

Although the random shuffle operation performs well on the \(\mathrm H_2\) and LiH molecules, the performance can be further improved by developing more advanced shuffling strategies. First, instead of random shuffle, we can design a problem-specific and hardware-oriented Hamiltonian allocation tactic, which can eliminate the deviation of the optimization path of local models and better adapt to the limited quantum resources of various local processors. Second, due to the existence of barren plateau (McClean et al. 2018; Marrero et al. 2021; Wang et al. 2021; Cerezo et al. 2021; Arrasmith et al. 2021) in the optimization of ansatz, the training of local quantum models may get stuck. Inspired by the study that local observables enjoy a polynomially vanishing gradient (Cerezo et al. 2021), a promising direction is to group Hamiltonian terms with similar locality in QUDIO to avoid the barren plateau of some processors. Finally, a more fine-grained partition of the quantum circuit structure besides observables can be employed to reduce the number of parameters to be optimized for each local processor, as implemented in Zhang et al. (2022).

Another feasible attempt to enhance the performance of distributed VQE in practice is to unify Shuffle-QUDIO with other measurement reduction techniques. One successful example is operator grouping, as discussed in Section 4.3. Specifically, when optimizing the circuit run on each distributed quantum processor, we can utilize the operator grouping strategy to reduce the required number of measurements of the allocated Hamiltonian. In this way, the measurement noise in the framework of Shuffle-QUDIO is eliminated under finite budget of shot number. Other two methods, like shot allocation and classical shadows, can be also integrated into Shuffle-QUDIO in the similar manner.

Besides the potential improvements in convergence and speedup for Shuffle-QUDIO, the data privacy leakage during transmitting gradient information among local nodes should be avoided. One the one hand, the shuffle operation in Shuffle-QUDIO naturally adds randomness to the system, hindering the recovery of intact data. On the other hand, previous studies proposed differential privacy (Du et al. 2022, 2021) and blind quantum computing (Li et al. 2021) to protect data security. When combining these techniques and Shuffle-QUDIO, it remains open to explore the consequent influence on the convergence of optimization.

Apart from utilizing the quantum-specific properties to enhance Shuffle-QUDIO, we can also leverage the experience from classical distributed optimization, such as Elastic Averaging SGD (Zhang et al. 2015), decentralized SGD (Koloskova et al. 2020). It is worth noting that the flexibility of Shuffle-QUDIO makes it easy to replace some components with advanced classical techniques, as discussed in Section 4.4. Taken together, it is expected to utilize Shuffle-QUDIO and its variants to speed up the computation of variational quantum circuits and tackle real-world problems with NISQ devices.

In summary, we believe that the significant speedup w.r.t time-to-accuracy, and the scalability of our proposed algorithm make a valuable contribution to the field of quantum chemistry and quantum computing in general. With increasing number of quantum chips in the future, Shuffle-QUDIO provides a more practical way in applying VQE on large-scale molecules, and it has the potential to significantly impact the field of quantum chemistry and beyond.

The appendix is organized as follows. Appendix A introduces basic notations and properties of the loss function. Appendices B, C, and D present the proofs of Lemma 1, Lemma 2, and Theorem 1, respectively. Appendix G explains the aggregation methods discussed in Section 4.4. Appendix H demonstrates the additional experiment results and analysis about Shuffle-QUDIO.