Abstract
The vehicle routing problem (VRP) is an example of a combinatorial optimization problem that has attracted academic attention due to its potential use in various contexts. VRP aims to arrange vehicle deliveries to several sites in the most efficient and economical manner possible. Quantum machine learning offers a new way to obtain solutions by harnessing the natural speedups of quantum effects, although many solutions and methodologies are modified using classical tools to provide excellent approximations of the VRP. In this paper, we employ 6 and 12 qubit circuits, respectively, to build and evaluate a hybrid quantum machine learning approach for solving VRP of 3- and 4-city scenarios. The approach employs quantum support vector machines (QSVMs) trained using a variational quantum eigensolver on a static or dynamic ansatz. Different encoding strategies are used in the experiment to transform the VRP formulation into a QSVM and solve it. Multiple optimizers from the IBM Qiskit framework are also evaluated and compared
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Quantum computing
Quantum computing has provided novel approaches for solving computationally complex problems over the last decade by leveraging the inherent speedup(s) of quantum calculations compared to classical computing. Quantum superposition and entanglement are two key factors that give a massive speed up to calculations in the quantum domain compared to classical counterparts (Montanaro 2016; Jordan 2024; Horodecki et al. 2009). Because of this, addressing optimization problems by quantum computing is an appealing prospect. Multiple approaches, such as Grover’s algorithm (Grover 1996), adiabatic computation (AC) (Farhi et al. 2000), and quantum approximate optimization algorithm (QAOA) (Farhi et al. 2014), have been proposed to use quantum effects and, as such, have served as the basis for solving mathematically complex problems using quantum computing. The performance of classical algorithms has generally been found to be subpar when applied to larger dimensional problem spaces (National Academies of Sciences (2019)). On a multidimensional problem, classical machine learning optimization techniques frequently require a significant amount of CPU and GPU resources and long computation time. The reason for this is that ML techniques are needed to resolve NP-hard optimization problems (Dasari et al. 2020).
1.2 Vehicle routing problem
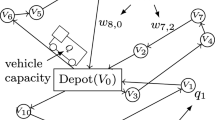
The vehicle routing problem is an intriguing optimization problem because of its many uses in routing and fleet management (Harwood et al. 2021), but its computational complexity is NP-hard (Kumar and Panneerselvam 2012; Mohanty et al. 2023). Moving automobiles as quickly and cheaply as feasible is always the objective. VRP has inspired a plethora of precise and heuristic approaches (Harwood et al. 2021; Srinivasan et al. 2018), all of which struggle to provide fast and trustworthy solutions. The VRP’s bare bones implementation comprises sending a single vehicle to deliver items to many client locations before returning to the depot to restock (Feld et al. 2019). By optimizing a collection of routes that are available and all initiate and conclude at a single node called the depot, the maximum reward sought by VRP is often expressed as the inverse of total distance traveled or mean service time. Even with just a few hundred delivery locations, finding the best solution to this problem is computationally challenging.
To be precise, in every VRP with parameters (n, k), there are (\(n-1\)) locations, k motor vehicles, and a depot D (Azad et al. 2023; Harwood et al. 2021). The solution is a collection of paths whereby each vehicle takes exactly one journey, and all k vehicles start and conclude at the same location, D. The best route is one that requires k vehicles to drive the fewest total miles. This problem may be thought of as a generalization of the well-known “traveling salesman” problem, whereby a set of k salesmen must service an aggregate of (\(n-1\)) sites with a single visit to each of those places being guaranteed (Harwood et al. 2021). In most practical settings, the VRP issue is complicated by other constraints, such as limited vehicle capacity or limited time for coverage. As a consequence, several other approaches, both classical and quantum, have been proposed as potential ways forwards. Currently, available quantum approaches for optimizing a system include the quantum approximate optimization algorithm (QAOA) (Azad et al. 2023), the quadratic unconstrained binary optimization (QUBO) (Glover et al. 2020), and quantum annealing (Irie et al. 2019; Crispin and Syrichas 2013; Office 2019).
1.3 Quantum support vector machine (QSVM)
The goal of the support vector machine (SVM) technique is to find the best line (or decision boundary) between two classes in n-dimensional space so that new data may be classified quickly. This optimum decision boundary is referred to as a hyperplane. The most extreme vectors and points that help construct the hyperplane are selected using SVM. The SVM method is based on support vectors, which are used to represent these extreme instances. Typically, a hyperplane cannot divide a data point in its original space. In order to find this hyperplane, a nonlinear transformation is applied to the data as a function. A feature map is a function that transforms the features of provided data into the inner product of data points, also known as the kernel (Havlicek et al. 2019; Rebentrost et al. 2014; Kariya and Behera 2024).
Quantum computing produces implicit calculations in high-dimensional Hilbert spaces using kernel techniques by physically manipulating quantum systems. Feature vectors for SVM in the quantum realm are represented by density operators, which are themselves encodings of quantum states. The kernel of a quantum support vector machine (QSVM) is made up of the fidelities between different feature vectors, as opposed to a classical SVM; the kernel conducts an encoding of classical input into quantum states (Havlicek et al. 2019; Leporini and Pastorello 2021).
1.4 Novelty and contribution
-
In this work, we propose a new method to solve the VRP using a machine learning approach through the use of QSVM.
-
In this context, we came across recent and older works in QSVM (Kariya and Behera 2024; Gentinetta et al. 2024; Rebentrost et al. 2014) and VQE algorithms (Cerezo et al. 2021), which are used to solve optimization problems such as VRP. However, none of them use a hybrid approach to arrive at a solution.
-
Our work implements this new approach of solving VRP using gate-model simulation of a 3-city or 4-city problem on a 6-qubit or 12-qubit system, respectively, using a parameterized circuit that is proposed as a solution to VRP.
-
We apply quantum encoding techniques such as amplitude encoding, angle encoding, higher-order encoding, IQP Encoding, and quantum algorithms such as QSVM, VQE, and QAOA to construct circuits for VRP and assess the results and summarize our findings.
-
We evaluate our solution using a variety of classical optimizers, as well as fixed and variable Hamiltonians to draw statistical conclusions.
1.5 Organization
The paper is organized as follows. Section 2 discusses the fundamental mathematical concepts such as QAOA, the Ising model, quantum support vector machine, amplitude encoding, angle encoding, higher-order encoding, IQP encoding, and VQE. Section 3 discusses the formulation and solution of VRP utilizing the concepts covered in the preceding section. Section 3.2 includes the fundamental components of circuits required to solve VRP using QSVM. Section 4 covers the outcomes of the QSVM simulation consisting of two sub-sections. Section 4.1 covers the outcome of simulation results of all the encoding schemes used, Finally, in Sect. 4.2, we conclude by comparing the results of QSVM solutions using various optimizers in the Qiskit platform on the VRP circuit and discuss the feasibility of higher qubit solutions as the future directions of research.
2 Background
Dealing with methods and processes for resolving combinatorial optimization problems is the foundation of solving routing challenges. The objective function is then derived by converting the mathematical models into their quantum counterparts. We arrive at the objective function’s solution by iteratively maximizing or minimizing the mathematical model. In this section, we provide an outline of our solution strategy’s key concepts.
2.1 QAOA
The quantum approximate optimization algorithm (QAOA) was proposed by Farhi et al. (2000, 2014) using an adiabatic quantum computation framework as the algorithm’s foundation. It is a hybrid algorithm because both classical and quantum approaches are utilized. Quantum adiabatic computation entails transitioning between the eigenstates of the driver Hamiltonian and the problem Hamiltonian. The Hamiltonian problem can be expressed as
It is well known that the combinatorial optimization problem may be effectively addressed by determining the eigenstate of C with the maximum energy. Likewise, we use driver Hamiltonian as
Here, \({\sigma }^x_j\) denotes the \({\sigma }^x\) Pauli operator on bit \(z_j\), and B is the mixing operator. Let us additionally define two operators
This enables the system to develop under C for \(\gamma \) time and B for \(\beta \) time. Essentially, QAOA creates the following state,
Here, \(|s\rangle \) represents the superposition state of all inputs. The expectation value of the cost function \(\sum ^m_{\alpha {=1}}{\langle }\beta {,}\gamma ~{|C_\alpha }\)\({|}\beta {,}\gamma ~{\rangle }\) provides the solution, or an approximate solution to the problem (Zhou et al. 2020).
2.2 Ising model
The Ising model is a well-known mathematical representation of ferromagnetism in statistical mechanics (Singh 2020; Brush 1967). In the model, discrete variables (\(+1\) or \(-1\)) represent magnetic dipole moments of “spins” in one of two possible states. Each spin can interact with its neighbors because they are organized in a network, commonly a lattice (when there is periodic repetition in all directions of the local structure). The spins interact in pairs, with one value of energy when the two spins are identical and another value when they are dissimilar. However, heat reverses this tendency, permitting the formation of alternative structural phases. The model is a condensed representation of reality that allows phase transitions to be identified. The subsequent Hamiltonian describes the entire spin energy:
where \(J_{ij}\) is the interaction between adjacent spins i and j, and h is an external magnetic field. At \(h=0\), the ground state is ferromagnetic if J is positive. At \(h=0\), the ground state is antiferromagnetic if J is negative in a bipartite lattice. Thus, for the purpose of clarity and within the scope of this paper, the Hamiltonian can be expressed as
Here, \({\sigma }_z\) and \({\sigma }_x\) represent the z and x Pauli operators, respectively. For the sake of simplification, we can presume the following conditions to be ferromagnetic (\(J_{ij}>0\)) if there is no external impact on the spin: \(h=0\). The Hamiltonian may therefore be reformulated as follows:
2.3 Quantum support vector machine
SVM (Rebentrost et al. 2014; Kariya and Behera 2024) is a supervised algorithm that constructs hyperplane with \(\textbf{w} \cdot \textbf{x} + b = 0\) such that \(\textbf{w}\cdot \textbf{x} + b \ge 1\) for a training point \(\textbf{x}_i\) in the positive class, and \(\textbf{w}\cdot \textbf{x} + b \le -1 \) for a training point \(\textbf{x}_i\) in the negative class. During the training process, the algorithm aims to maximize the gap between the two classes, which is intuitive as we want to separate two classes as far as possible, in order to get a sharper estimate for the classification result of new data samples like \(\mathbf {x_0}\). Mathematically, we can see the objective of SVM is to find a hyperplane that maximizes the distance \(2/ |\textbf{w}|\) constraint to \(\mathbf {y_i}(\textbf{w}\cdot \mathbf {x_i} + b) \ge 1\). The normal vector \(\textbf{w}\) can be written as \(\textbf{w} = \sum _{i=1}^{M} \alpha _i \textbf{x}_i\) where \(\alpha _i\) is the weight of the \(i^{th}\) training vector \(\textbf{x}_i\). Thus, obtaining optimal parameters b and \(\alpha _i\) is the same as finding the optimal hyperplane. To classify the new vector is analogous to knowing which side of the hyperplane it lies, i.e., \( y_i(\textbf{x}_0) = sign(\textbf{w}.\textbf{x} + b) \). After having the optimal parameters, classification now becomes a linear operation. From the least-squares approximation of SVM, the optimal parameters can be obtained by solving a linear equation
In a general form of F, we adopt the linear kernels \(K_{i,j} = \kappa (\textbf{x}_i,\textbf{x}_j) = \textbf{x}_i. \textbf{x}_j \). Thus, to find the hyperplane parameters, we use matrix inversion of F: \((b,{\mathbf {\alpha }_i}^T)^T = {\tilde{F}^{ - 1}} (0,{\textbf{y}_i}^T)^T\).
2.3.1 Quantum kernels
The main inspiration of a quantum support vector machine is to consider quantum feature maps that lead to quantum kernel functions, which are hard to simulate in classical computers. In this case, the quantum computer is only used to estimate a quantum kernel function, which can be later used in kernel-based algorithms. For simplicity, assuming the data points \(x,z \in \mathcal {X}\), the nonlinear feature map of any data point is
The kernel function \(\kappa (x, z)\) can be computed as
The state \(|\phi (x)\rangle \) can be prepared by using a unitary gate U(x), and thus \(|\phi (x)\rangle =U(x)|0\rangle \). Thus, the kernel fuction becomes
From the above, we can say that the kernel \(\kappa (x, z)\) is simply the probability of getting an all-zero string when the circuit \(U^{\dagger }(x) U(z)|0\rangle \) is measured or this kernel is an \(\left| 0^n\right\rangle \) to \(\left| 0^n\right\rangle \) transition probability of a particular unitary quantum circuit on n qubits (Havlicek et al. 2019; Glick et al. 2024). This can be implemented using the following kernel estimation circuit (Fig. 1).
2.4 Amplitude encoding (AE)
In the process of amplitude embedding (Araujo et al. 2021), data is encoded into the amplitudes of a quantum state. A N-dimensional classical data point x is represented by the amplitudes of an n-qubit quantum state \(| \psi _x \rangle \) as
where \(N=2^n\), \(x_i\) is the i-th element of x, and \(|i\rangle \) is the i-th computational basis state.
In order to encode any data point x into an amplitude-encoded state, we must normalize the same by following
where \(x_{norm}\)= \(\sqrt{\sum _{i=1 }^N|x_i|^2}\).
2.5 Angle encoding (AgE)
While the above-described amplitude encoding expands into a complicated quantum circuit with huge depths, the angle encoding employs N qubits and a quantum circuit with fixed depth, making it favorable to NISQ computers (LaRose and Coyle 2020; Qiskit 2024). We define angle encoding as a method of classical information encoding that employs rotation gates (the rotation could be chosen along x, y, or z axis). In our scenario, the classical information consists of the node and edge weights assigned to the vehicle’s nodes and pathways which are further assigned as parameters to ansatz.
where \({x}_i\) represents the classical information stored on the angle parameter of rotation operator R.
2.6 Higher-order encoding (HO)
Higher-order encoding is a variation of angle encoding where we have an entangled layer and an additional sequential operation of rotation angles of two entangled qubits (Qiskit 2024). This can be loosely defined as follows:
Similar to angle encoding, we are free to choose the rotation.
2.7 IQP encoding (IqpE)
IQP-style encoding is a relatively complicated encoding strategy. We encode classical information (Paddle Quantum 2024)
where r is the depth of the circuit, indicating the repeating times of \(\textrm{U}_{\textrm{Z}}({x}) \textrm{H}^{\otimes n}\). \(\textrm{H}^{\otimes n}\) is a layer of Hadamard gates acting on all qubits. \(\textrm{U}_{\textrm{Z}}(\textbf{x})\) is the key step in IQP encoding scheme:
where S is the set containing all pairs of qubits to be entangled using \(R_{Z Z}\) gates. First, we consider a simple two-qubit gate: \(R_{Z_1 Z_2}(\theta )\). Its mathematical form \(e^{-i \frac{i}{2} Z_1 \otimes Z_2}\) can be seen as a two-qubit rotation gate around ZZ, which makes these two qubits entangled.
2.8 VQE
Variational quantum eigensolver (VQE) is another hybrid quantum-classical algorithm used for the estimation of the eigenvalue of a matrix or Hamiltonian H (Peruzzo et al. 2014) of significant size. The primary objective of this approach is to ascertain a trial qubit state from a wave function \(| \psi (\mathbf {\theta }) \rangle \) that relies on a collection of parameters \(\mathbf {\theta }= \theta _1,\theta _2,\cdots \), which are often referred to as the variational parameters. The expectation of an observable or Hamiltonian H in a state \(| \psi (\mathbf {\theta }) \rangle \) can be expressed as follows:
By spectral decomposition
where \(\lambda _i\) and \({| \psi \rangle }_i\) are the matrix H’s eigenvalues and eigenstates, respectively. Additionally, because H’s eigenstates are orthogonal, \(\left\langle \psi _{i} \mid \psi _{j}\right\rangle =0\) If \(i \ne j\). The wave function \(| \psi (\mathbf {\theta }) \rangle \) can be expressed as a superposition of eigenstates.
Hence, the expectation is given by
Hence, \( E(\mathbf {\theta }) \ge \lambda _{\min }\). The VQE method involves the iterative adjustment of the parameters \(\mathbf {\theta }=\theta _{1}, \theta _{2}, \ldots \) in order to minimize the value of \(E(\mathbf {\theta })\). This property of VQE is advantageous when attempting to solve combinatorial optimization problems; specifically, the approach involves using a parameterized circuit to establish the trial state of the algorithm, with the cost function denoted as \(E(\mathbf {\theta })\), which is also the expected value of the Hamiltonian in this state. It is possible to derive the ground state of the desired Hamiltonian by iteratively minimizing the cost function. A classical optimizer uses a quantum computer to calculate its gradient and assess the cost function at each step of the optimization process.
3 Methodology
3.1 Modelling VRP in QSVM
By mapping the cost function to an Ising Hamiltonian \(H_c\), the vehicle routing problem can be solved (Lucas 2014). The solution to the problem is determined by minimizing the Ising Hamiltonian \(H_c\). Consider a graph with n vertices and \(n-1\) edges and an arbitrary connectivity. Assuming we must route a vehicle between two non-adjacent vertices in the graph, consider a binary decision variable \(x_{ij}\) whose value is 1 if there is an edge between i and j with an edge weight \(w_{ij}>0\) and 0 otherwise. Now, the VRP problem necessitates \(n \times (n-1)\) selection variables. We define two sets of nodes for each edge from \(i\rightarrow j\): source \(s\left[ i\right] \) and target t[j]. \(s\left[ i\right] \) contains the nodes j to which i sends an edge \(j\ \epsilon \ s[i]\). The collection \(t\left[ j\right] \) comprises the nodes i to which the node i delivers the edge \(i\ \epsilon \ t[j]\). The VRP is defined as follows (Azad et al. 2023, Qiskit: Vehicle Routing 2024):
where k and n represent the number of vehicles and locations respectively; there are \(n-1\) locations for vehicles to traverse if the starting point is considered to be the 0th location or Depot D. Notably, the following restrictions apply to this (Mohanty et al. 2023):
The first two restrictions establish that each node may only be visited once by the delivering vehicle. The middle two limitations enforce the requirement that after product delivery, the vehicle must return to the depot. The last two restrictions enforce the requirements for eliminating sub-tours and are constrained on \(u_i\), with \(Q>q_j>0\), and \(u_i,Q, q_i \in \mathbb {R}\). For the VRP equation and constraints, the VRP Hamiltonian can be expressed as follows (Azad et al. 2023).
\(A > 0\) is indicative of a constant. The vector representation of the collection of all binary decision variables \(x_{ij}\) is
Using the antecedent vector, we can construct two new vectors for each node: \(\overrightarrow{z}_{S[i]}\) and \(\overrightarrow{z}_{T[i]}\) (at the start of the section, we defined two sets for source and target nodes, so two vectors will represent them).
These vectors will contribute to the development of the QUBO model of VRP (Date et al. 2019; Glover et al. 2020; Kochenberger et al. 2014; Guerreschi 2021). The QUBO model of a connected graph \(G=(N,V)\) is specified as follows:
where Q is a quadratic edge weight coefficient, g is a linear node weight coefficient, and c is a constant. To determine the coefficients in the QUBO formulations of \(H_{VRP}\) as shown in Eq. 24, the equations in Eq. 27 are first substituted in terms of \(H_{b}\) and \(H_{c}\), respectively. Subsequently, the expression of \(H_{VRP}\) is expanded and rearranged in accordance with Eq. 28.
Hence, in the QUBO formulation of the Eq. 24, the coefficients \(\textrm{Q}(n(n-1) \times n(n-1))\), \(\textrm{g}(n(n-1) \times 1)\), and \(\textrm{c}\) are derived. The coefficients associated with the QUBO formulation of Eq. 24 are shown below.
\(\mathbb {J}\) is the matrix containing all ones, \(\mathbb {I}\) and \(e_0={\left[ 1,0,\cdots ..,0\right] }^T\) are the identity matrices. The binary decision variable \(x_{ij}\) is converted to the spin variable \(s_{ij} \in \left\{ -1,1\right\} \) using the formula \(x_{ij}=(s_{ij}+1)/2\).
From the aforementioned equations, we may expand Eq. 28 to form the Ising Hamiltonian of VRP (Glover et al. 2020).
The following are definitions for the terms \(J_{ij}, h_i\), and d:
3.2 Analysis and circuit building
3.2.1 VRP
In the current section, we proceed to create a circuit based on gates using the IBM gate model. The implementation of this model is carried out using the Qiskit framework (et al. 2024), enabling us to effectively execute the aforementioned formulation. In the context of a given vehicle routing problem (VRP) that incorporates qubits, the initial state is established as \(| + \rangle ^{\otimes n(n-1)}\). This state represents the ground state of \(H_{mxr}\), which is achieved by applying the Hadamard gate to each qubit that has been initialized to the zero state. Subsequently, we proceed to build the subsequent state.
The energy E of the state \(| \beta ,\gamma \rangle \) is computed using the expectation of \(H_{c}\) from Eq. 18. Again, based on the Ising model, the term \(H_{c}\) can be expressed in terms of Pauli operators as follows:
Thus, the expression for a single term of state in \(| \beta ,\gamma \rangle \) as \(\beta _0,\gamma _0\) reads as follows:
\(e^{-i{H}_{mxr}\beta _0}e^{-i{H}_{c}\gamma _0}.\) The first term \({H}_{\mathrm {c\ }}\) can be expanded as follows:
It can be noted that, by the application of CNOT(CX) gate before and after “M,” the diagonal elements of the above matrix can be swapped.
Expanding the matrix and observing the upper and lower blocks, we can rewrite
\(\left[ \begin{matrix}1&{}0\\ 0&{}{e}^{-2i{J}_{ij}{\gamma }_{0}}\end{matrix}\right] \) is a phase gate. Looking at the 2nd term of \({H}_{\textrm{c}}\), we get
Figure 2a picturizes the fundamental circuit with two qubits and gate selections for \({H}_{\textrm{c}}\). Similarly, \(H_{mxr}\) is merely a rotation along the X axis, as depicted by the U gate in Fig. 2b.
The above sample circuits can be used for the solution of VRP combined with the VQE and QAOA approach. However, in this paper, we are focusing on a machine learning solution of VRP by use of QSVM; thus, we need to construct a QSVM circuit using various encoding schemes. Simple interpretation and implementation of encoding schemes are described in upcoming sub-sections.
3.2.2 Amplitude encoding
As we look into AE, a single qubit state is represented by
for two qubits
Now, applying Ctrl U and Anti-CTRL U on the above state, we achieve
Here, \(\theta _1 = \tan ^{-1} \frac{\sqrt{\gamma ^2+ \delta ^2}}{\sqrt{\alpha ^2 + \beta ^2}}\), \(\theta _2= \tan ^{-1}\frac{\delta }{\gamma }\), \(\theta _3= \tan ^{-1}\frac{\beta }{\alpha }\) Combining VRP and amplitude encoding circuit eliminates the need of Hadamard gates and \(H_{mxr}\) components, and we end up with the following skeleton circuits (Fig. 3a).
3.2.3 Angle encoding
For a two-qubit scenario, angle encoding translates to the following example. We define the \(R_y\) gate as follows:
3.2.4 Higher-order encoding
For a two-qubit scenario, HO encoding translates to the following: We define the \(R_y\) gate as follows:
3.2.5 IQP encoding
For a two-qubit scenario, IqpE translates to the following:
4 Results
4.1 VQE simulation of QSVM and VRP
We build the Hamiltonian with a uniform distribution of weights between 0 and 1, and then run it along with the ansatz via IBM’s three available VQE optimizers (COBYLA, L_BFGS_B, and SLSQP). We run the circuit up to two layers and gather data using all of the available optimizers. We run the experiment again with a fixed Hamiltonian and, subsequently, a set of variable Hamiltonians to see whether the QSVM and encoding approach can effectively reach the classical minimum. Our results indicate that COBYLA is the most efficient optimizer, followed by SLSQP and L BFGS B. In the sections that follow, we will have a look at the results obtained using various QSVM encoding schemes. We define two terms—accuracy and error—in the context of outcomes’ interpretability. An error occurs when the solution deviates from the classical minimum more often than it reaches it, whereas accuracy is defined as the number of times the solution reaches the classical minimum. Percentages based on the distribution of the outcomes are used to evaluate both terms.
\(T =\) Total number of Simulation runs
\(N =\) Total number of times solution reaches classical minimum
4.1.1 Amplitude encoding
With a large number of gates, the AE circuit has proven to be the most complex of all encoding circuits. We can simulate no more than six qubit computations due to this complexity. Despite its complexity, AE has a high, nearly perfect accuracy rate (\(100\%\)) and a very low error rate (\(0\%\)) for 50-iteration fixed Hamiltonian simulations. The trend is present in both the first and second layers. The first layer accuracy for a variable Hamiltonian simulation is \(96\%\), and the second layer accuracy is \(94\%\) across all optimizers. Figure 4 depicts the results of 50 iterations of simulating SVM with amplitude encoding on a VRP circuit with fixed and variable Hamiltonian. The decline in accuracy, however, can be attributed to simulation or computational errors, as all the errors are greater than 100% and are therefore considered aberrations. Most likely, the simulation hardware cannot accommodate the VQE procedure.
4.1.2 Angle encoding
Angle encoding is the second encoding (Fig. 5), following amplitude encoding; we have experimented with SVM VRP simulation, which yields high accuracy and low error rates. Observing Tables 1 and 2, angle encoding is the second most precise encoding employed in our investigations. For fixed Hamiltonian simulations over 50 iterations with 6 qubits angle encoding, the first layer, including all optimizers, achieves \(100\%\) accuracy and \(0\%\) error. In the second layer simulation (over 50 iterations), the accuracy decreases to \(98\%\) for COBYLA, \(96\%\) for SLSQP, and \(86\%\) for L_BGFS_B, which is a greater decrease than the other two. These declines are attributable to optimizer-dependent statistical errors. Similarly, for 12-qubit simulations of SVM VRP, the accuracy rates are higher in the first layer, which consists of COBYLA at \(100\%\), SLSQP at \(92\%\), and L_BGFS_B at \(88\%\), reiterating that the accuracy is highly dependent on the optimizer. As we move to the second layer of 12-qubit simulations on fixed Hamiltonian, we observe a decline in precision as the level of optimization rises. In this case, COBYLA winds up with \(80\%\), L_BGFS_B with \(70\%\), and SLSQP with \(84\%\). Here, SLSQP’s accuracy loss is less than that of the other two optimizers. The variable Hamiltonian with 12 qubits demonstrates a comparable trend. On the initial layer, we observe high accuracy with COBYLA at \(96\%\), L_BGFS_B at \(86\%\), and SLSQP at \(90\%\). Moving to the second stratum, the accuracy figures drop significantly, with COBYLA at \(76\%\) and L_BGFS_B at \(62\%\), while SLSQP maintains excellent accuracy at \(86\%\). In every scenario of our investigation, it is evident that over optimization reduces accuracy rates.
4.1.3 Higher-order encoding
After amplitude and angle encoding, higher-order encoding is the third most prevalent encoding in our SVM VRP simulation experiment. This is also the third most accurate encoding in our experiment. For both 6 qubit and 12 qubit simulations, HO encoding yields moderately accurate results; however, as the number of circuit layers is increased, the accuracy of the HO encoding scheme deteriorates, rendering it inappropriate. Figure 6 depicts the statistics of the HO encoding scheme for fixed and variable Hamiltonian simulations of SVM VRP circuits over 50 iterations for both 6 qubit and 12 qubit simulations. COBYLA achieves \(78\%\) accuracy for a 6-qubit HO encoding circuit on a fixed Hamiltonian, while L_BGFS_B achieves \(66\%\) accuracy and SLSQP achieves \(70\%\) accuracy. As we proceed to the second layer, the accuracy considerably decreases, with COBYLA at \(34\%\) and SLSQP, L_BGFS_B at \(16\%\), respectively. Similar trends can be observed in variable Hamiltonian simulations of HO encoding with 6 qubits, with COBYLA at \(76\%\), SLSQP at \(62\%\), and L_BGFS_B at \(58\%\) for the first layer; for the second layer, the accuracy drops to \(36\%\), \(34\%\), and \(36\%\) for COBYLA, L_BGFS_B, and SLSQP, respectively. The 12-qubit simulation yields superior results than the 6-qubit simulation and improves COBYLA’s accuracy. For fixed Hamiltonian simulations, COBYLA achieves an accuracy of \(92\%\), compared to \(78\%\) for 6 qubit. For variable Hamiltonian simulations, COBYLA stores \(76\%\) for 6 qubit in the first layer, and \(92\%\) for 12 qubit in the first layer. The tendencies for L_BGFS_B and SLSQP are ambiguous for both cases (fixed and variable Hamiltonian simulations); it is reassuring to conclude that an increase in layer decreases accuracy and that COBYLA outperforms the other two optimizers and ensures stable performance.
4.1.4 IQP encoding
IQP encoding (Fig. 7) is the last and least accurate encoding in our experiment to simulate an SVM VRP circuit. The results are plotted in Fig. 7 and in Tables 1 and 2. As we can see from the figures and tables, accuracy is consistently poor for fixed and variable Hamiltonian simulations in both 6-qubit and 12-qubit circuits. The accuracy further declines as layers increase. Hence, this encoding is unsuitable in our experiment of SVM VRP circuits.
4.2 Inferences from simulation
As we scan through the results of SVM VRP simulations across the encoding schemes, we observe some clear and distinct trends regarding the experiment. Tables 1 and 2 summarize the results obtained from the plots of all the encoding schemes used in this experiment. We list these trends as our outcomes of this experiment in the below points:
-
The approach to solving VRP using machine learning is successful and is capable of accomplishing the same or a superior result than the conventional approach using VQE and QAOA.
-
The use of encoding/decoding schemes can serve the purpose of creating superposition and entanglement and eliminate the additional effort required to construct the mixer Hamiltonian when solving the VRP using the standard approach of QAOA and VQE.
-
While the standard approach to solving VRP or any combinatorial optimization problem requires a few layers of circuit depth (2 in most cases), we are able to achieve the same on the first layer itself with this approach, proving that it is more efficient than the standard approach.
-
We also observe a distinct trend that as the number of layers increases, the accuracy decreases, which can be used to determine where to limit the optimization depth.
-
Encoding/decoding schemes reduce the number of optimization layers but increase the circuit’s complexity by introducing more gates. Therefore, when selecting an encoding scheme, we must take into account the complexity of the generated circuit and the number of required gates, as well as the number of classical resources (memory, CPU) it will require. There must be a trade-off between circuit complexity and the desired problem accuracy.
-
Despite the fact that amplitude encoding provided the greatest accuracy, it could not be used to simulate a 12-qubit VRP scenario due to the large number of gates required. Angel encoding, on the other hand, was found to be much simpler due to a significantly smaller number of gates, as well as providing excellent accuracy (\(96\%\) for COBYLA, and \(92\%\) for SLSQP and L_BGFS_B in variable hamiltonian simulation) across all the available optimizers. This again demonstrates that the complexity of circuits and the number of gates used are the most important considerations when choosing an encoding/decoding scheme.
Table 3 Table consisting of quantum depth and quantum cost of various encoding schemes compared with standard VQE implementation of VRP -
It can be noticed that AgE performs the best in terms of circuit complexity and accuracy rates due to the formation of a single layer of superposition. In other encodings (HO, IqpE), we observe multi-layered complex superposition structures, which is the reason for fluctuations or error rates. Also in the fact that increasing layers also increases the superposition structures and therefore decreases the accuracy.
-
Using COBYLA as an optimizer, HO encoding yielded intriguing results with reduced accuracy in circuits with fewer qubits (6 qubits) and higher accuracy in circuits with more qubits (12 qubits) for both fixed and variable Hamiltonian simulations. The trend is disregarded by SLSQP and L_BGFS_B. This demonstrates that the algorithm’s performance is extremely dependent on the optimizer; therefore, when evaluating the algorithm’s performance, the most efficient optimizer should be selected by comparing the available optimizers.
-
The IQP encoding scheme performed the worst in this experiment, with the lowest accuracy and highest error rates among all other encodings used for one-layer, two-layer, fixed, and variable Hamiltonians simulations. Therefore, the IqpE method cannot be used to solve VRP using QSVM.
-
All of the optimizers used in the experiments performed well across AE, AgE, and HO encodings; however, COBYLA outperformed the other two due to its consistently high level of accuracy, but SLSQP is more resistant to accuracy fluctuations caused by an increase in optimization depth or in the presence of multi-layered circuits.
4.3 Complexity and cost considerations
Along with the inferences and observation, we want to touch upon the complexity of the quantum circuits particularly the number of qubits, quantum cost, and circuit depth in this section. Here, we compare the SVM VRP solution with the standard VQE solution that is described in our previous work (Mohanty et al. 2023).
In order to compare, we have listed the quantum cost and circuit depth of standard VQE implementation with that of SVM VRP implementation each consisting of 6 and 12 qubits with one and two layers (Table 3). We can broadly derive the following observations from Table 3.
-
Transitioning from the conventional VQE method for VRP to using a quantum support vector machine results in a rise in the number of gates, elevating quantum depth and cost.
-
The rise in quantum cost and depth is not linear and varies depending upon the encoding scheme employed when comparing different encoding schemes with the conventional VQE implementation of VRP.
-
Increasing the number of layers and qubits in various techniques consistently leads to a rise in quantum depth and quantum cost. The extent of this increase varies based on the encoding method used.
-
For the VQE standard, amplitude encoding, and angle encoding, there is a proportionate rise in depth and cost, roughly doubling as we go through layers and qubits.
-
Higher-order encoding (HO) and IQP encoding exhibit a much smaller rise in cost and depth over layers and qubits compared to amplitude and angle encoding.
-
As the number of qubits increases from 6 to 12, the depth and cost rise by almost four times compared to the 6-qubit scenario; however, the increase is somewhat less than four times for HO and IQP encodings.
-
Based on the depth and cost analysis, it is evident that HO and IQP provide lower costs and circuit depths compared to amplitude and angle encoding, but their findings are less precise. Amplitude and angle encoding provide the highest level of precision. This helps in determining the balance between cost and accuracy when choosing encoding techniques for QSVM.
4.4 Experimental setup, data gathering, and statistics
This experiment is conducted within the ambit of the QISKIT framework. While performing the experiment, we used a quantum instance object, and the ansatz runs inside the quantum instance object. A random seed is added to quantum instance to stabilize VQE results. All the experiments have been run \(50+50\) times, one with a fixed Hamiltonian matrix and the other by varying the Hamiltonian matrix. The objective of the experiments is to ensure that the results of experiments are just not dependent on a single Hamiltonian. This is also to ensure that the used circuits achieve classical minimum or near classical minimum regardless of the Hamiltonian used. Thus, apart from the plots, Tables 1 and 2 become the figure of merit. In addition to the many hours of testing and debugging, it is to be noted that the results reported here amounted to 150 h of CPU time on a 24-core AMD workstation using Qiskit’s built-in simulators (et al. 2024).
5 Conclusion
In this paper, we presented a novel technique for solving VRP through the use of a 6- and 12-qubit circuit-based quantum support vector machine (QSVM) with a variational quantum eigensolver for both fixed and variable Hamiltonians. In the experiment, multiple encoding strategies were used to convert the VRP formulation into a QSVM and solve it. In addition, we utilized multiple classical optimizers available within the QISKIT framework to measure the output variation and accuracy rates. Consequently, our machine learning-based approach to resolving VRP has proven fruitful thus far. Using a QSVM to implement a gate-based simulation of a 3-city or 4-city VRP on a 6-qubit or 12-qubit system accomplishes the goal. The method not only resolves VRP, but also outperforms the conventional method of resolving VRP via multiple optimization phases involving only VQE and QAOA. In addition, selecting appropriate encoding methods establishes the optimal balance between circuit complexity and optimization depth, thereby enabling multiple approaches to solve CO problems using machine learning techniques.
Data Availability
All the data provided in this manuscript is generated during the simulation and can be provided upon reasonable request.
References
Araujo IF, Park DK, Petruccione F, da Silva AJ (2021) A divide-and-conquer algorithm for quantum state preparation. Sci Rep 11(1):6329. https://doi.org/10.1038/s41598-021-85474-1
Azad U, Behera BK, Ahmed EA, Panigrahi PK, Farouk A (2023) Solving vehicle routing problem using quantum approximate optimization algorithm vol 24. Available from: https://ieeexplore.ieee.org/document/9774961
Brush SG (1967) History of the Lenz-Ising model. Rev Mod Phys 39:883–893. https://doi.org/10.1103/RevModPhys.39.883
Cerezo M, Arrasmith A, Babbush R, Benjamin SC, Endo S, Fujii K et al (2021) Variational quantum algorithms. Nat Rev Phys 3(9):625–644. https://doi.org/10.1038/s42254-021-00348-9arXiv:2012.09265
Crispin A, Syrichas A (2013) Quantum annealing algorithm for vehicle scheduling. In: 2013 IEEE International Conference on Systems, Man, and Cybernetics, pp 3523–3528. ISSN: 1062-922X. Available from: https://ieeexplore.ieee.org/document/6722354
Dasari V, Im MS, Beshaj L (2020) Solving machine learning optimization problems using quantum computers. In: Blowers M, Hall RD, Dasari VR (eds). Online Only, United States: SPIE. Available from: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/11419/2565038/Solving-machine-learning-optimization-problems-using-quantum-computers/10.1117/12.2565038.full
Date P, Patton R, Schuman C, Potok T (2019) Efficiently embedding QUBO problems on adiabatic quantum computers. Quantum Inf Process 18(4):117. https://doi.org/10.1007/s11128-019-2236-3
et al (2024) MSA.: Qiskit: an open-source framework for quantum computing. Available from: https://github.com/Qiskit/qiskit/tree/0.25.0
Farhi E, Goldstone J, Gutmann S (2014) A quantum approximate optimization algorithm. Available from: arXiv:1411.4028v1
Farhi E, Goldstone J, Gutmann S, Sipser M (2000) Quantum computation by adiabatic evolution. Available from: https://arxiv.org/abs/quant-ph/0001106v1
Feld S, Roch C, Gabor T, Seidel C, Neukart F, Galter I et al (2019) A hybrid solution method for the capacitated vehicle routing problem using a quantum annealer vol 6. Available from: https://www.frontiersin.org/article/10.3389/fict.2019.00013
Gentinetta G, Thomsen A, Sutter D, Woerner S (2024) The complexity of quantum support vector machines
Glick JR, Gujarati TP, Corcoles AD, Kim Y, Kandala A, Gambetta JM et al (2024) Covariant quantum kernels for data with group structure
Glover F, Kochenberger G, Ma M, Du Y (2020) Quantum Bridge Analytics II: QUBO-Plus, network optimization and combinatorial chaining for asset exchange. 4OR. 18(4):387–417. Publisher Springer
Grover LK (1996) A fast quantum mechanical algorithm for database search. Available from: https://arxiv.org/abs/quant-ph/9605043v3
Guerreschi GG (2021) Solving quadratic unconstrained binary optimization with divide-and-conquer and quantum algorithms. arXiv:2101.07813
Harwood S, Gambella C, Trenev D, Simonetto A, Bernal D, Greenberg D (2021) Formulating and solving routing problems on quantum computers. IEEE Trans Quantum Eng 2:1–17. https://doi.org/10.1109/TQE.2021.3049230
Havlicek V, Corcoles AD, Temme K, Harrow AW, Kandala A, Chow JM et al (2019) Supervised learning with quantum enhanced feature spaces. Nature 567:209–212
Horodecki R, Horodecki P, Horodecki M, Horodecki K (2009) Quantum entanglement. Rev Mod Phys 81:865–942. https://doi.org/10.1103/RevModPhys.81.865
Irie H, Wongpaisarnsin G, Terabe M, Miki A, Taguchi S (2019) Quantum annealing of vehicle routing problem with time, state and capacity. In: Feld S, Linnhoff-Popien C (eds) Quantum Technology and Optimization Problems. Lecture Notes in Computer Science. Cham Springer International Publishing pp 145–156. Available from: https://link.springer.com/chapter/10.1007/978-3-030-14082-3_13
Jordan S (2024) Available from: https://quantumalgorithmzoo.org/#ONML. https://quantumalgorithmzoo.org/
Kariya A, Behera BK (2024) Investigation of quantum support vector machine for classification in NISQ era
Kochenberger G, Hao JK, Glover F, Lewis M, Lü Z, Wang H et al (2014) The unconstrained binary quadratic programming problem: a survey. J Combin Optim 28. https://doi.org/10.1007/s10878-014-9734-0
Kumar SN, Panneerselvam R (2012) A survey on the vehicle routing problem and its variants. Intell Inf Manage 4(3):9
LaRose R, Coyle B (2020) Robust data encodings for quantum classifiers. Phys Rev A 102:032420. https://doi.org/10.1103/PhysRevA.102.032420
Leporini R, Pastorello D (2021) Support vector machines with quantum state discrimination. Quantum Rep 3(3):482–499
Lucas A (2014) Ising formulations of many NP problems. Front Phys 2. https://doi.org/10.3389/fphy.2014.00005
Mohanty N, Behera BK, Ferrie C (2023) Analysis of the vehicle routing problem solved via hybrid quantum algorithms in the presence of noisy channels. IEEE Trans Quantum Eng 4:1–14. https://doi.org/10.1109/tqe.2023.3303989
Montanaro A (2016) Quantum algorithms: an overview. npj Quantum Inf 2(1):15023. https://doi.org/10.1038/npjqi.2015.23
National Academies of Sciences E (2019) Chapter: 3 Quantum Algorithms and Applications. In: Quantum Computing: Progress and Prospects. Available from: https://www.nap.edu/catalog/25196/quantum-computing-progress-and-prospects
Office FE (2019) Application of digital annealer for faster combinatorial optimization. FUJITSU Sci Tech J 55(2):7
Paddle Quantum (2024) Available from: https://qml.baidu.com/tutorials/machine-learning/encoding-classical-data-into-quantum-states.html
Peruzzo A, McClean J, Shadbolt P, Yung MH, Zhou XQ, Love PJ et al (2014) A variational eigenvalue solver on a photonic quantum processor. Nat Commun 5(1):4213. https://doi.org/10.1038/ncomms5213
Qiskit (2024) Lecture 5.1 - building a quantum classifier. Available from: https://www.youtube.com/watch?v=-sxlXNz7ZxU
Qiskit: vehicle routing (2024). Available from: https://qiskit.org/ecosystem/optimization/tutorials/07_examples_vehicle_routing.html
Rebentrost P, Mohseni M, Lloyd S (2014) Quantum support vector machine for big data classification. Phys Rev Lett 113(13). https://doi.org/10.1103/physrevlett.113.130503
Singh SP (2020) The Ising model: brief introduction and its application. IntechOpen. Publication Title: Solid State Physics - Metastable, Spintronics Materials and Mechanics of Deformable Bodies - Recent Progress. Available from: https://www.intechopen.com/chapters/71210
Srinivasan K, Satyajit S, Behera BK, Panigrahi PK (2018) Efficient quantum algorithm for solving travelling salesman problem: an IBM quantum experience. arXiv preprint arXiv:1805.10928v1
Zhou L, Wang ST, Choi S, Pichler H, Lukin MD (2020) Quantum approximate optimization algorithm: performance, mechanism, and implementation on near-term devices. Phys Rev X 10(2):021067. Publisher American Physical Society. https://doi.org/10.1103/PhysRevX.10.021067
Acknowledgements
The authors recognize the support of the Department ’Centre for Quantum Software and Information, UTS’ and Sydney Quantum Academy. The authors are also grateful to the IBM Quantum Experience platform and their team for developing the Qiskit platform and providing open access to their simulators for running quantum circuits and performing the experiments reported here (et al. 2024).
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Contributions
The authors confirm their contribution to the paper as follows: Study conception and design: N.M., B.K.B., C.F. Data collection: N.M. Analysis and interpretation of results: N.M., B.K.B., C.F. Draft manuscript preparation: N.M., B.K.B., C.F. All authors reviewed the results and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mohanty, N., Behera, B.K. & Ferrie, C. Solving the vehicle routing problem via quantum support vector machines. Quantum Mach. Intell. 6, 34 (2024). https://doi.org/10.1007/s42484-024-00161-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42484-024-00161-4