Classical splitting of parametrized quantum circuits

Abstract

Barren plateaus appear to be a major obstacle for using variational quantum algorithms to simulate large-scale quantum systems or to replace traditional machine learning algorithms. They can be caused by multiple factors such as the expressivity of the ansatz, excessive entanglement, the locality of observables under consideration, or even hardware noise. We propose classical splitting of parametric ansatz circuits to avoid barren plateaus. Classical splitting is realized by subdividing an N qubit ansatz into multiple ansätze that consist of $\mathcal {O}(\log N)$ qubits. We show that such an approach allows for avoiding barren plateaus and carry out numerical experiments, and perform binary classification on classical and quantum datasets. Moreover, we propose an extension of the ansatz that is compatible with variational quantum simulations. Finally, we discuss a speed-up for gradient-based optimization and hardware implementation, robustness against noise and parallelization, making classical splitting an ideal tool for noisy intermediate scale quantum (NISQ) applications.

1 Introduction

Variational quantum algorithms (VQAs) Cerezo et al. (2021) are a promising approach to solve a wide range of problems, such as finding the ground state of a given hamiltonian via the variational quantum eigensolver (VQE) Peruzzo et al. (2014), solving combinatorial optimization problems with the quantum approximate optimization algorithm (QAOA) Farhi et al. (2014) or solving classification problems using quantum neural networks Farhi and Neven (2018).

Variational quantum algorithms are suitable for noisy intermediate scale quantum (NISQ) Preskill (2018) hardware as they can be implemented with a small number of layers and gates for simple tasks. However, a scalability problem arises with the increasing number of qubits, hindering a possible advantage. Variational quantum algorithms rely on a feedback loop between a classical computer and a quantum device. The former is used to update the parameters of the ansatz conditioned on the measurement outcome obtained from the quantum hardware. This procedure is iterated until convergence. Classical optimizers use the information on the cost landscape of the parametric ansatz to find the minimum. The updates on the parameters move the ansatz to a lower point on the cost surface. In 2018, McClean et al. showed that for a wide range of ansätze the cost landscape flattens with the increasing number of qubits, making it exponentially harder to find the solution for the optimizer McClean et al. (2018). The flattening was first observed by looking at the distribution of gradients across the parameter space, and the problem was named barren plateaus (BPs). A variational quantum algorithm is said to have a BP if its gradients decay exponentially with respect to one of its hyper-parameters, such as the number of qubits or layers.

Since the discovery of the BP problem, there has been significant progress that improved our understanding of what causes barren plateaus, and several methods to avoid them have been proposed. It has been shown that noise Wang et al. (2021), entanglement Ortiz Marrero et al. (2021), and the locality of the observable Cerezo et al. (2021) play an essential role for determining whether an ansatz will exhibit barren plateaus. It has also been shown that the choice of ansatz (e.g. its expressivity) for the circuit is one of the decisive factors that impact barren plateaus Holmes et al. (2022). For instance, the absence of barren plateaus has been shown for quantum convolutional neural networks (QCNN) Cong et al. (2019); Pesah et al. (2021) and tree tensor networks (TTN) Grant et al. (2018); Zhao and Gao (2021). In contrast, the hardware efficient ansatz (HEA) McClean et al. (2018); Zhao and Gao (2021); Kandala et al. (2017) and matrix product states (MPS) Zhao and Gao (2021) have been shown to have barren plateaus.

One of the essential discoveries showed that barren plateaus are equivalent to cost concentration and narrow gorges Arrasmith et al. (2022). This implies that barren plateaus are not only a result of the exponentially decaying gradient but also of the cost function itself, and they can be identified by analyzing random points on the cost surface. As a result, gradient-free optimizers are also susceptible to barren plateaus, and do not offer a way to circumvent this problem Arrasmith (2021).

Many methods have been suggested to mitigate barren plateaus in the literature. Some of these methods suggest to use different ansätze or cost functions Wu et al. (2021); Zhang et al. (2021), determining a better initial point to start the optimization Grant et al. (2019); Liu et al. (2023); Rad et al. (2022); Zhang et al. (2022), determining the step size during the optimization based on the ansatz Sack et al. (2022), correlating parameters of the ansatz (e.g., restricting the directions of rotation) Volkoff and Coles (2021); Holmes et al. (2022), or combining multiple methods Patti et al. (2021); Broers and Mathey (2021).

In this work, we propose a novel idea in which we claim that if any ansatz of N qubits is classically separated to a set of ansätze with $\mathcal {O}(\log N)$ qubits, the new ansatz will not exhibit Barren Plateaus. This work is not the first proposal in the literature that considers partitioning an ansatz. However, our proposal is significantly different. Most work in the literature first considers an ansatz and then emulates the result of that ansatz through many ansätze (exponentially many in general) with less number of qubits (which increases the effective size of quantum simulations) using gate decompositions, entanglement forging, divide and conquer or other methods Bravyi et al. (2016); Peng et al. (2020); Tang et al. (2021); Perlin et al. (2021); Eddins et al. (2022); Saleem et al. (2021); Fujii et al. (2022); Marshall et al. (2022); Tang et al. (2021). On the other hand, this work proposes using ansätze that are classically split, meaning that there are no two-qubit gate operations between the subcircuits before splitting. This way, there is no need for gate decompositions or other computational steps. We also investigate an extension of this ansatz design by combining classically split layers with standard layers. Our results show that this approach provides many benefits such as better trainability, robustness against noise and faster implementation on NISQ devices.

In the remainder of the paper, we start by giving an analytical illustration of the method in Sect. 2. Then, we provide numerical evidence for our claim in Sect. 3 and extend our results to practical use cases by comparing binary classification performance of classical splitting (CS) for classical and quantum data. Next, we propose an extension of the classical splitting ansatz and perform experiments to simulate the ground state of the transversal-field Ising hamiltonian. Finally, we discuss the advantages of employing CS, make comments on future directions in Sect. 4 and give an outlook in Sect. 5.

2 Avoiding Barren Plateaus

Barren plateaus (BPs) can be identified by investigating how the gradients of an ansatz scale with respect to a parameter. Here, we will start with the notation of McClean et al. and extend it to CS McClean et al. (2018). The ansatz is composed of consecutive parametrized (V) and non-parametrized entangling (W) layers. We define $U_l(\theta _l) = \text{ exp }(-i\theta _l V_l)$, where $V_l$ is a Hermitian operator and $W_l$ is a generic unitary operator. Then the ansatz can be expressed with a multiplication of layers,

$$\begin{aligned} U(\varvec{\theta }) = \prod _{l=1}^{L} U_l(\theta _l)W_l. \end{aligned}$$

(1)

Then, for an observable O and input state of $\rho$, the cost is given as

$$\begin{aligned} C(\varvec{\theta }) = \text{ Tr }[OU(\varvec{\theta })\rho U^\dagger (\varvec{\theta })]. \end{aligned}$$

(2)

The ansatz can be separated into two parts to investigate a certain layer, such that $U_- \equiv \prod _{l=1}^{j-1} U_l(\theta _l)W_l$ and $U_+ \equiv \prod _{l=j}^{L} U_l(\theta _l)W_l$. Then, the gradient of the $j^\textrm{th}$ parameter can be expressed as

$$\begin{aligned} \partial _{j} C(\varvec{\theta }) = \frac{\partial C(\varvec{\theta })}{\partial {\theta _j}} = i\,{\text {Tr}}[[V_j,U_+^\dagger OU_+]U_- \rho U_-^\dagger ]. \end{aligned}$$

(3)

The expected value of the gradients can be computed using the Haar measure. Please see Appendix A for more details on the Haar measure, unitary t-designs and details of the proofs in this section. If we assume the ansatz $U(\theta )$ forms a unitary 2-design, then this implies that $\langle \partial _{k}C(\varvec{\theta }) \rangle =0$ McClean et al. (2018). Since the average value of the gradients are centered around zero, the variance of the distribution, which is defined as,

$$\begin{aligned} \text{ Var }[\partial _{k}C(\varvec{\theta })] = \langle (\partial _{k}C(\varvec{\theta }))^2 \rangle - \langle \partial _{k}C(\varvec{\theta }) \rangle ^2, \end{aligned}$$

(4)

can inform us about the size of the gradients. The variance of the gradients of the $j^\textrm{th}$ parameter of the ansatz, where $U_-$ and $U_+$ are both assumed to be unitary 2-designs, and the number of qubits is N, is given as McClean et al. (2018); Holmes et al. (2022),

$$\begin{aligned} \textrm{Var}[\partial _{j} C(\varvec{\theta })] \approx \mathcal {O}\left( \frac{1}{2^{6N}} \right) . \end{aligned}$$

(5)

Fig. 1

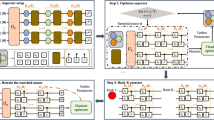
All types of ansätze used in this work. (a) An N-qubit generic ansatz consisting of L layers of the parametrized unitary U are separated in to $k=N/m$ many m-qubit ansätze. This ansatz will be referred to as the classically split (CS) ansatz. The standard ansatz can be recovered by setting $m=N$. (b) Extended classically split (ECS) ansatz. This is an extension to the CS ansatz. First L layers of the ansatz consists of $k=N/m$ many m qubit U blocks. Then, T layers of N qubit V layers are applied. (c) A simple ansatz that consists of $R_Y$ rotation gates and CX gates connected in a “ladder" layout. (d) Hardware Efficient Ansatz (HEA) that is used to produce the quantum dataset. Parameters of the first column of U3 gates are sampled from a uniform distribution $\in [-1,1]$, while the rest of the parameters are provided by the dataset Schatzki et al. (2021). (e) EfficientSU2 ansatz with “full" entangler layers Treinish et al (2022)

This means that for a unitary 2-design the gradients of the ansatz vanish exponentially with respect to the number of qubits N. Details of this proof is provided in Appendix  A. Now, let us consider the CS case. We split the ansatz $U(\varvec{\theta })$ to k many m-qubit ansätze, where we assume without loss of generality that $N=k \times m$. Then, we introduce a new notation for each classically split layer,

$$\begin{aligned} U_l^i(\theta _l^i) = e^{-i\theta _l^i V_l^i} W_l^i, \end{aligned}$$

(6)

where index l determines the layer and index i determines which sub-circuit it belongs to. This notation combines the parametrized and entangling gates under $U_l^i$. Then, the overall CS ansatz can be be expressed as,

$$\begin{aligned} U(\varvec{\theta }) = \prod _{l=1}^{L} \bigotimes _{i = 1}^{k} U_l^i(\theta _l^i) = \bigotimes _{i = 1}^{k} \prod _{l=1}^{L} U_l^i(\theta _l^i) = \bigotimes _{i = 1}^{k} U^i(\varvec{\theta ^i}). \end{aligned}$$

(7)

The CS ansatz can be seen in Fig. 1a. Next, we will assume the observable and the input state to be classically split, such that they both can be expressed as a tensor product of m-qubit observables or states. This assumption restricts our proof to be valid only for m-local quantum states and m-local observables. It is important to note here that we use a definition that is different from the literature throughout the paper. For this proof, an m-local observable is an observable such that there are no operators that act on overlapping groups of m qubits. A generic m-local observable can be expressed as,

$$\begin{aligned} O_{m\text{-local }} = \sum _{i=1}^{k} O_i \otimes \mathbbm {1}_{\bar{i}} = \sum _{i=1}^{k} \bigotimes _{j=1}^{k} \left( O_i - \mathbbm {1} \right) \delta _{i,j}+\mathbbm {1}, \end{aligned}$$

(8)

where $O_i$ is an observable over the qubits $\{(i-1)m+1,(i-1)m+2,...,im\}$, and $\bar{i}$ represents the remaining $N-m$ qubits. Then, the cost function becomes;

$$\begin{aligned} \begin{aligned} C(\varvec{\theta })&= \sum _{i=1}^{k} \text{ Tr }[\bigotimes _{j = 1}^{k} \left( \left( O_i \!-\! \mathbbm {1} \right) \delta _{i,j}\!+\!\mathbbm {1} \right) U^j(\varvec{\theta }^j) \rho _j U^{j\dagger }(\varvec{\theta }^j)]\\&= \sum _{i=1}^{k} \prod _{j=1}^{k} \text{ Tr }[\left( \left( O_i \!-\! \mathbbm {1} \right) \delta _{i,j}+\mathbbm {1}\right) U^j(\varvec{\theta }^j) \rho _j U^{j\dagger }(\varvec{\theta }^j)]\\&= \sum _{i=1}^{k} \text{ Tr }[O_i U^i(\varvec{\theta }^i) \rho _i U^{i\dagger }(\varvec{\theta }^i)]. \end{aligned} \end{aligned}$$

(9)

This can be written as a simple sum,

$$\begin{aligned} C(\varvec{\theta }) = \sum _{i=1}^{k} C^i(\varvec{\theta ^i}), \end{aligned}$$

(10)

where,

$$\begin{aligned} C^i(\varvec{\theta ^i}) = {\text {Tr}}[O_i U^i(\varvec{\theta ^i}) \rho _i U^{i\dagger }(\varvec{\theta ^i})]. \end{aligned}$$

(11)

Then, the costs of each classically separated circuit are independent of each other. The gradient of $j^{th}$ parameter of the $i^{th}$ ansatz can be written as,

$$\begin{aligned} \begin{aligned} \partial _{i,j} C(\varvec{\theta })&= \partial _{i,j} C^i(\varvec{\theta ^i})\\&= \partial _{i,j}( {\text {Tr}}[O_i U^i(\varvec{\theta }^i) \rho _i U^{i\dagger } (\varvec{\theta ^i})]). \end{aligned} \end{aligned}$$

(12)

Now, let us consider each ansatz $U^i(\varvec{\theta }^i)$ to be a unitary 2-design. We want to choose the integer m such that it scales logarithmically in N. Hence, we choose $\beta$ and $\gamma$ appropriately, such that $m = \beta \log _\gamma N$ holds. Then, if we combine Eq. (5) with Eq. (12), the variance of the gradient of $j^\textrm{th}$ parameter can be expressed as

$$\begin{aligned} \textrm{Var}[\partial _{j} C(\varvec{\theta })] \approx \mathcal {O}\left( \frac{1}{2^{(6m)}} \right) = \mathcal {O}\left( \frac{1}{N^{6\beta \log _\gamma 2}}\right) . \end{aligned}$$

(13)

Here, the dependence on i or j becomes irrelevant (a simpler choice for ansatz design would be to choose every new ansatz to be the same), so it can be dropped for a simpler notation. Similar to Eq. (5) the variance scales with the dimension of the Hilbert space (e.g. $\mathcal {O}(2^m)$). Then, the overall expression scales with, $\mathcal {O}(N^{-6\beta \log _\gamma 2})$, where $\beta$ and $\gamma$ are constant (e.g. $\beta =1$ and $\gamma =2$ results in $m=\log _2N$). As a result, the variance of the CS ansatz scales with $\mathcal {O}(\text{ poly }(N)^{-1})$ instead of $\mathcal {O}(\exp (N)^{-1})$. Therefore, a CS ansatz, irrespective of its choice of gates or layout, can be used without leading to barren plateaus.

3 Numerical experiments

In this section, we report results of four numerical experiments. We investigate the scaling of gradients under CS by computing variances over many samples in Sect. 3.1. Then, we perform three experiments to observe how CS affects the performance of an ansatz. This task by itself leads to many questions as there are multitudes of metrics that one needs to compare and as many different problems one can consider. For this purpose, we consider problems well known in the literature, where trainability of ansätze plays a significant role.

First, we perform binary classification on a synthetic classical dataset in Sect. 3.2. The dataset contains two distributions that are called as classes. The goal is to predict the class of each sample. We perform the same task for distribution of quantum states in Sect. 3.3. Then, we give practical remarks in Sect. 3.4. Finally, we propose an extension to the CS ansatz and employ it for quantum simulating the ground state of the transverse field Ising Hamiltonian in Sect. 3.5.

For the first three experiments (Sects. 3.1 to 3.3), we consider the CS ansatz with layers that consist of $R_Y$ rotation gates and CX entangling gates applied in a ladder formation for each layer. This layer can be seen in Fig. 1c. As the observable, we construct the 1-local observable defined in Eq. (14), where $Z_i$ represents the Pauli-Z operator applied on the $i^\text {th}$ qubit and $\mathbb {1}_{\bar{i}}$ represents the identity operator applied on the rest of the qubits.

$$\begin{aligned} O = \frac{1}{N} \sum _{i=1}^{N} Z_i \otimes \mathbbm {1}_{\bar{i}} \end{aligned}$$

(14)

3.1 Barren Plateaus

Barren Plateaus are typically identified by looking at the variance of the first parameter over a set of random samples McClean et al. (2018). Recently, it has been shown that this is equivalent to looking at the variance of samples from the difference of two cost values evaluated at different random points of the parameter space Arrasmith et al. (2022). In particular, in the presence of barren plateaus this difference is exponentially suppressed, and, thus, barren plateaus also affect gradient-free optimizers Arrasmith (2021). For this reason, we will focus on the variance of the cost function as a more inclusive indicator for barren plateaus, rather than the gradients to provide a broader picture.

The experiments were performed using analytical gradients and expectation values, assuming a perfect quantum computer and infinite number of measurements, using Bergholm et al. (2020) and Paszke et al. 2019. Variances are computed over 2000 samples, where the values of the parameters are randomly drawn from a uniform distribution over $[0,2\pi ]$.

We start by presenting the variances over different values of m and N in Fig. 2. We fix the number of layers (L) to N, so that the ansatz exhibits barren plateaus in the setting without CS ($m=N$). The results indicate that a constant value of m resolves the exponential behaviour, as expected from Eq. (13). Furthermore, it is evident that larger values of m can allow the ansatz to escape barren plateaus, given that m grows slow enough (e.g. $\mathcal {O}(\log N)$). Note that we study the variances with respect to randomly chosen parameter sets, and not the variance during the optimization procedure to find the optimal set of parameters minimizing the cost function. Thus, our results essentially show the expected variance at beginning of the optimization procedure with a randomly chosen initial point. Having a large variance at this state is key to find the path towards the global minima. Throughout the optimization procedure, the variance of the cost function will eventually decrease as the algorithm converges.

Fig. 2

The variance of the change in cost vs. the number of qubits for varying values of m. Each color/marker represents a certain value of m and data points of the standard ansatz ($m=N$) is plotted with a dashed black line

Fig. 3

The variance of the change in cost vs. the number of layers for $m=4$ (solid lines) and $m=N$ (dashed lines) with varying number of qubits

Our theoretical findings illustrate that the CS can be used to avoid barren plateaus irrespective of the number of layers. In our first experiment, we numerically showed that this holds when we set $L=N$. Recent findings showed that, a transition to barren plateaus happens at a depth of $\mathcal {O}(\log N)$ for an ansatz with a local cost function Cerezo et al. (2021). Therefore, there is great importance in investigating the behaviour for larger values of L. For considerably low values of N (e.g. $N<32$), we can assume a constant value for m (e.g. $m=4$), such that m is approximately $\mathcal {O}(\log N)$. We present variances of two ansätze ($m=4$, $m=N$) for up to 200 layers and 16 qubits in Fig. 3. For the standard ansatz, we see a clear transition to barren plateaus with increasing number of layers, as expected Cerezo et al. (2021). On the other hand, the CS ansatz ($m=4$) shows a robust behavior from small to large number of layers.

These two experiments show the potential of the CS in avoiding barren plateaus. However, the question of whether this potential can be transferred in-to practice (e.g. binary classification performance or quantum simulation) still lacks an answer. Next, we will be addressing this question.

3.2 Binary classification using a classical dataset

In this experiment, we will continue using the same ansatz with same assumptions to perform binary classification using a classical dataset. Our goal here is to compare performance of the CS ansatz to the standard case for increasing number of qubits. We need a dataset that can be scaled for this purpose. However, datasets are typically constant in dimension and do not offer an easy way to test the scalability in this sense. Therefore, we employ an ad-hoc dataset that can be produced with different number of features.

Three datasets ($N=4$, 8 and 16) were produced using the make_classification function of scikit-learn¹ Pedregosa et al. (2011). This tool allows us to draw samples from an N-dimensional hypercube, where samples of each class are clustered around the vertices. Each dataset contains 420 training and 180 testing samples. Each of the data samples were encoded using one $R_Y$ gate per qubit, such that each ansatz uses the same number of features of the given dataset. Please see Appendix C for more details on the production of the dataset and distributions of samples.

The binary classification was performed using the expectation value over the observable defined in Eq. (14) and the binary cross entropy function was used as the loss function during training, such that,

$$\begin{aligned} L(y, \hat{y}) = - y \log \hat{y} - (1-y) \log (1-\hat{y}), \end{aligned}$$

(15)

where y (i.e. $y \in \{0,1\}$) is the class label of the given data sample and $\hat{y}$ is the prediction (i.e. $\hat{y} \!=\! \text{ Tr }[OU\!(\varvec{\theta })\!\rho (x) U^\dagger (\varvec{\theta })]$, where x is the data sample).² The ADAM optimizer Kingma and Ba (2017) with a learning rate of 0.1 was used and all models are trained for 100 epochs using full batch size (bs=420).³ We report our results based on 50 runs for each setting.

Classification performance of ansätze for changing values of m using the three datasets are presented in Fig. 4. Here, the results show the distribution of accuracies over the test set. For the $N=4$ case, we see that the standard ($m=N$) ansatz performs the best. However, this is not the case as we go to more qubits. For the 8 and 16 qubit cases, it is evident that $m<N$ ansätze can match the performance of the standard ansatz. We can also see that the constant choice of $m=4$ can provide a robust performance with increasing number of qubits (at least up-to $N=16$), matching our expectations. Training curves of all settings are presented in Appendix D.

Fig. 4

Box plot of the best test accuracy obtained over 50 runs plotted with respect to the relevant local number of qubits (m). Each column represents a problem with a different sample size (4, 8, 16). Each marker is placed on the median, boxes cover the range from the first to third quartiles and the error bars extend the quartiles by 3 times range. Each m value is plotted with a different marker and color

3.3 Binary classification using a quantum dataset

The binary classification performance of the CS over the classical datasets provides the first numerical evidence for their advantage against the standard ansätze. It is also important to investigate if they can be extended to problems where the data consists of quantum states. Our proof in Sect. 2 assumed the input states to be tensor product states. Now, we remove this constraint and use a quantum dataset.

For this experiment, we use the NTangled dataset Schatzki et al. (2021). NTangled dataset provides parameters to produce distributions of quantum states that are centered around different concentrable entanglement (CE) Beckey et al. (2021) values. CE is a measure of entanglement, which is defined as follows,

$$\begin{aligned} \text{ CE }(|{\Psi }) = 1 - \frac{1}{2^N} \sum _{\alpha \in Q} \text{ Tr }[\rho _\alpha ^2], \end{aligned}$$

(16)

Table 1 Classification performance of ansätze with different values of m over different distributions of quantum states from the NTangled dataset Schatzki et al. (2021). Average of 50 runs are presented with errors showing the difference to maximum and minimum observed values. Best average value of each metric for the given task is printed in bold

where Q is the power set of the set $\{1,2,...,\text{ N }\}$, and $\rho _\alpha$ is the reduced state of subsystems labeled by the elements of $\alpha$ associated to $|{\Psi }$. The NTangled dataset provides three ansätze trained for different concentrable entanglement (CE) values for $N=3, 4$ and 8. We choose the Hardware Efficient Ansatz (Fig. 1d) with depth=5, such that the parameters of the first layer of U3 gates are sampled from a unitary distribution $\in [-1,1]$ and the others are provided by the dataset. Then, we apply the same CS ansatz used in Sect. 3.2 and perform binary classification such that the CE values are the labels of classes. The CE distributions of the produced quantum states are presented in Appendix E.

For the binary classification task, the same training settings are used as in Sect. 3.2, except this time models are trained until 50 epochs, as most models were able to reach $100\%$ test accuracy. We report our results using different pairs of distributions in Table 1. In the case of $N=4$, we observed that CS can perform at similar accuracy, even if the ansatz do not have any entangling gates ($m=1$). We see that entangling gates are needed for better performance if the problem gets harder (e.g. 0.25 vs. 0.35 case). If we go to a problem with more qubits, we can safely say that the CS ansatz can match the performance of the standard ansatz and converge faster.

3.4 Practical remarks on classical splitting

The efficacy of CS relies on the parts of the circuit before and after the set of gates that undergo CS. This can be seen most clearly if we set $m=1$ and apply CS to the entire circuit after a possible initialization. In this case, we only perform single qubit operations after initialization. Hence, if the initialization produces a tensor product state, then the circuit subject to CS with $m=1$ can no longer generate any entanglement. Similarly, if we initialize with the HEA (Fig. 1d) and apply CS with $m=1$ to the remaining circuit, then no tensor product state can be found.

More generally, $m=1$ produces a circuit that cannot change the amount of entanglement. For other choices of m, the picture becomes more complicated but, generally, the set of states that can be generated by the quantum circuit before CS will be reduced to a subset based on the characteristics of the remaining initialization.

A naïve implementation of CS therefore requires knowledge of the correct initialization such that the final solution can still be reached with the classically split circuit. In generic applications, this knowledge is likely not available. Hence, an adaptive approach to CS should be considered.

One adaptive approach would be to increase m to check for improvements. After we observe no further training improvement with $m=1$, we could move to $m=2$. This enlarges the set of states the quantum circuit can reach, and thus may lead to further training improvements, at the cost of possibly stronger BP effects. However, if $m=1$ has already converged fairly well, then the state is already fairly close to the $m=2$ solution and it is unlikely to find a BP. With $m=2$ converged, we can then move to $m=4$ and continue the process by doubling m one step at a time.

If, for example, we consider the $N=4$ “0.25 vs. 0.3” case of Table 1, we may start training with $m=1$. This training converges to about $90\%$ accuracy. Increasing m to $m=2$ will lead to further improvements that converge to about $98\%$ accuracy. Finally, we can further improve the $98\%$ to $100\%$ accuracy by going to $m=4$.

In this way, we utilize the efficiency of CS to obtain an approximate solution which we then refine by trading efficiency for circuit expressivity through increasing m. At this point, the efficiency reduction should no longer lead to insurmountable complications as we already are close to the optimal solution for the current m value.

Another adaptive approach would be to use CS to check and bypass plateaus. For example, if a VQE appears to be converged, it may also just be stuck in a plateau. Applying CS at this point would reduce the effect of the plateau. Thus, if the VQE continues optimizing after classically splitting a seemingly converged circuit, we can conclude that this was in fact a plateau. After a suitable number of updates using the classically split circuit, we can then return to the full circuit in the hopes of having passed the plateau.

Unfortunately, this approach cannot be used to positively distinguish between true local optima and plateaus since the CS reduces expressivity and thus introduces artificial constraints. Hence, if the set of states expressible by the classically split circuit is orthogonal to the gradient in the cost function landscape, then a plateau will be replaced with a local optimum and, thus, no improvements will be obtained. In this case, we therefore cannot conclude that the VQE has converged simply because CS shows no improvements. However, experimenting with different implementations of CS may result in cases that do not replace the plateau with an artificial local optimum.

3.5 Extending classical splitting to VQE

Until now, we have investigated using CS for binary classification problems. It succeeded by showing an overall better training performance in Sect. 3.2 and a competitive performance and faster convergence in Sect. 3.3. In this section, we consider simulating the ground state of the transverse-field Ising hamiltonian (TFIH) on a 1D chain. The TFIH with open boundary conditions can be defined as

$$\begin{aligned} H = -J \sum _{i=1}^{N-1} Z_i Z_{i+1} -h \sum _{i=1}^{N} X_i, \end{aligned}$$

(17)

for N lattice sites, where J determines the strength of interactions and h determines the strength of the external field. Simulating the TFIH on a 1D link requires at least nearest neighbour interactions between qubits on the 1D lattice as the ground state. This contradicts with the assumption we made, when we proved absence of barren plateaus for classically split ansätze in Sect. 2, since the TFIH does not fit the definition we had for an m-local observable in Eq. (8). Therefore, we need to rely on the numerical experiments to talk about barren plateaus under the new constraints.

The CS ansätze can only produce local entangled states, for this reason we need an extension of the ansatz in Fig. 1a. We propose to extend the CS ansatz by adding standard layers at the end. The reason for adding them at the end is to keep the base of light cones⁴ produced by the classically split layers constant. Then, when we add the standard layers, the light cones will grow at a pace that is determined by the newly-added part.⁵ This way, the overall ansatz can still escape barren plateaus as long as the newly-added part does not exhibit barren plateaus.

We define the extended classically split (ECS) ansatz with two types of layers. First L layers consist of classically split m qubit gate blocks. Then, there are T layers of any no-BP ansatz (see Fig. 1b). Since the first L layers can only produce m-local product states (i.e. $m < \mathcal {O}(\log N)$), the existence of barren plateaus depends only on the remaining T layers. This way we can choose very large L, but need to keep T small as standard ansätze reach BPs rather rapidly (e.g. depth $> \mathcal {O}(\log N)$ leads to barren plateaus for such an ansatz Cerezo et al. (2021)). In Fig. 5, we provide numerical evidence to show that addition of L layers do not decrease the size of the gradients. The variance saturates faster to higher values and the Renyi-2 entropy to lower values respectively with increasing total depth for constant T layers.

Fig. 5

The variance of the change in cost vs. the total number of layers for $m=3, N=12$ and the observable $\hat{O}=Z_0Z_1$ with varying number of the L and T layers ($L+T=D$) are shown in the upper panel. The lower panel shows the Renyi-2 entropies of the same system for a subsystem size of two. $T=D$ line is shown with a black dashed line to emphasize that it is the standard case. Other colors represents different values the ECS ansatz can take. Both figures shows that the variances and entanglement entropy saturate faster and to higher and lower values respectively for constant values of T

Fig. 6

Fidelity values after optimization with 100 different initial points using different values of normal and split layers

These results suggest that it might be possible to leverage this feature of the ECS ansatz to add more layers which can contribute to finding the ground state with a better success rate without sacrificing trainability Anschuetz and Kiani (2022). This is also important from an overparameterization perspective as it improves generalization capacity of QML models Larocca et al. (2021). We perform experiments with the TFIH to test this idea.

We consider the Hamiltonian defined in Eq. (17) with $J=1, h=1$. Then, we implement the ECS ansatz with $m=3, N=D=12$ and $m=4, N=D=16$. Each side of the ansatz consists of EfficientSU2 layers with ladder connectivity (similar to Fig. 1e). Then, we consider different values for L and T layers, where the percentage of split layers correspond to $p=L/D$ and $L+T=D$. Total depth (D) corresponds to $L+T$, where $p=100\%$ is equivalent to the CS ansatz, $p=0\%$ is equivalent to the standard EfficientSU2 ansatz and other values explore hybrid use cases of the ECS ansatz.

We report the final fidelities of 100 runs in Fig. 6. Each run starts with a set of parameters drawn from a uniform distribution $[ -0.1,0.1]$. The ADAM Kingma and Ba (2017) optimizer with 0.1 learning rate is used and optimization was performed for 1000 iterations and reached a convergence in all cases. Circuits are simulated with no shot noise. This choice was made to investigate if the ECS ansatz can achieve the same level of success compared to its standard equivalent under infinite resources assumptions. Otherwise, results in Fig. 5 shows us that the ECS ansatz needs orders of magnitudes less number of shots.

The upper panel shows results for the $N=D=12$ setting. Here, we see that the standard ansatz ($p=0\%$) manages to find the ground state with a success probability (amount of runs reaching close to 1.0 fidelity) of approximately 0.5. Increasing the percentage of split layers improve the success rate. As expected, increasing it too much and eventually making it $100\%$ results in loss of performance, as the ansatz becomes inadequate to represent the TFIH ground state.

The lower panels shows results for the $N=D=16$. The effect of moving to a regime with more qubits is seen as a drop in success probability for the $p=0\%$ ansatz. This time increasing the percentage of split layers improve success probability at larger values. This suggests that the relationship between number of qubits and the amount of the split layer might be more intricate than it seems.

4 Discussion

In this work, we showed that the CS of the ansätze can be used to escape barren plateaus both analytically and numerically. Then, we investigated if the CS hinders the learning capacity of the ansatz. Our experiments showed that this is not the case, and the classically split ansatz can match the performance at low number of qubits and is potentially superior at larger number of qubits.

In general the benefits of CS comes from the reducing the effective Hilbert Space that the CS ansatz can explore. CS only allows the ansatz to produce m-qubit tensor product states, if the input state is also a tensor product state following our assumptions in Sect. 2. This, as a result, reduces the expressivity of the ansatz. Nevertheless, this also allows the ansatz to avoid barren plateaus Holmes et al. (2022) by limiting the scaling behavior to the more favorable case of m-qubit systems. In the case of the CS, the exponential increase of the Hilbert space dimension is prevented and instead a polynomial scaling is enforced. For the m-local CS ansatz, each local Hilbert space have $\dim (H_k)=2^m=N^{\beta \log _2\gamma }$. Although the advantage of using classical splitting may look trivial, there are many benefits of employing such an ansatz besides the numerical experiments we performed in Sect. 3.

In our binary classification experiments using a classical dataset, we relied on single qubit and single rotation gate data encoding. This meant that any classically split ansatz had less information in each group. This could in fact be improved with embedding methods such as data re-uploading, where one can encode all the data points to each single qubit independently, such that there are alternating layers of rotation gates that encode the data and parametrized gates that are to be optimized Pérez-Salinas et al. (2020). Data re-uploading ansätze shows great classification performance even for low number of qubits. Since the classical splitting doesn’t have a limit on the amount of layers, data re-uploading would potentially be great way to get a performance increase.

CS can provide faster training when used with gradient based optimizers. In general, the exact gradients of ansätze are computed with the well-known parameter shift rule Mitarai et al. (2018); Schuld et al. (2019). However, this requires two instances of the same circuit to be executed per parameter. This quickly results in a bottleneck for the optimization procedure. An ansatz with $L=N$ layers, where each layer has N parameters, requires $\mathcal {O}(N^2)$ circuit executions to compute gradients for a single data sample. On the other hand, CS provides cost functions that are independent of each other, as it was shown in Eq. (11). This allows gradients to be computed simultaneously across different instances of the classically split ansatz. As a result, the classically split ansatz optimization requires $\mathcal {O}(N\log N)$ circuit executions for $m=\mathcal {O}(\log N)$.

Table 2 Two qubit gate counts of different ansätze transpiled for hypothetical devices that has a 2D grid topology (square lattice with no diagonal connections)

The bottleneck in optimization is only one of the challenges of implementing scalable Variational quantum algorithms. Another problem that is worth mentioning here is the amount of two-qubit gates. NISQ hardware provides limited connectivity of qubits. The topology of the devices plays an essential role in the efficient implementation of quantum circuits Weidenfeller et al. (2022). Typically, a quantum circuit compilation (or transpilation) procedure is required to adapt a given circuit to be able to be compatible with the capabilities of the devices (e.g. converting gates to native gates, applying SWAP gates to connect qubits which are not physically connected) Botea et al. (2018).

Classical splitting provides a significant reduction in number of two qubit gates as it divides a large qubit to many circuits with less qubits. To show the scale of the reduction, we can construct a set of hypothetical devices that has a 2D grid topology (square lattice with no diagonal connections). We start by considering the CS ansatz that consists the ansätze in Fig. 1c and extend it to a fully entangled architecture. A linear entangled ansatz has $\mathcal {O}(N)$ two qubit gates, while a fully entangled one has $\mathcal {O}(N^2)$ per layer. Then, we use Qiskit’s transpiler⁶ Treinish et al (2022) to fit these ansätze to the hypothetical devices and report the two qubit gate counts in Table 2.

The amount of gates are not only important to have a better implementation but also to have a more precise results, since NISQ devices come with noisy gates. We consider the CX gate errors reported by IBM for their devices, which can be taken as $\mathcal {O}(10^{-2})$ on average⁷. Then, as a figure of merit, we can assume 50% to be the limit, in which we can still get meaningful results. This would allow us to use 50 CX gates at most. Now, the results from Table 2 implies that it is possible to construct a 36 qubit, 2 layer ansatz with linear entanglement, if we employ CS. This would not be possible for the standard case as it comes with more than twice two qubit gates. The reduction only gets better if we consider a full entanglement case. Following the same logic, to implement a 36 qubit, 36 layer, fully entangled ansatz, a CX gate error of $\mathcal {O}(10^{-6})$ is needed, while the classically split ansatz only requires a CX gate error of $\mathcal {O}(10^{-4})$. A similar reduction in noise is also possible for other types of circuit partitioning methods Basu et al. (2022).

Classically splitting an ansatz further allows faster implementation on hardware. A generic ansatz consists of two-qubit gates that follow one and another, matching a certain layout. We mentioned some of these as ladder/linear or full. However, this means that the hardware implementation of such an ansatz requires execution of these gates sequentially, taking a significant amount of time. To overcome such obstacles, ansätze such as the HEA (see Fig. 1d) are widely used in the literature Kandala et al. (2017). CS an ansatz can reduce the implementation time significantly since it allows simultaneous two-qubit gates across different local circuits. This can mean a speed-up of from $\mathcal {O}(N/ \log N)$ to $\mathcal {O}((N/ \log N)^2)$ depending on the connectivity of the original ansatz.

The formulation we used in Sect. 3.2 allows the CS ansatz to be implemented on smaller quantum computers instead of a single large quantum computer. This means that for similar problems, there are many implementation options available. These include using one large device, using many small devices (e.g., $\mathcal {O}(N/\log N)$ many $\mathcal {O}(\log N)$ qubit devices) and parallelizing the task or using one small device and performing all computation sequentially. All of these features makes the classical splitting an ideal approach for Quantum Machine Learning (QML) applications using NISQ devices.

Simulating larger size systems requires a deep ansatz (linear or larger in system size) in general Cerezo et al. (2021). Although a problem-agnostic ansatz can perform well at small sizes, BPs preclude the scalability. Our results show that the ECS can help circumvent this issue and allow deeper ansätze. On the other hand, the ECS ansatz also brings the quantum circuit closer to the classically simulatable limit. It appears that there might be a transition point where the ECS ansatz is deep enough to represent the ground state of interest without leading to BPs. We were not able to formulate how or if this point can be identified for an arbitrary system size of a given problem.

5 Conclusion

In this work, we presented some foundational ideas of applying CS to generic ansätze. Our results indicate many benefits of using CS, such as better trainability, faster hardware implementation, faster convergence, robustness against noise and parallelization under certain conditions. These suggest that CS or variations of this idea might play an essential role in how we are designing ansätze for QML problems. We also presented an extension to the initial CS idea so that these types of ansätze can be used in VQE. The initial results that we presented in this work suggest that CS can help improve the trainability and reach better error values. However, it is still an open question to what extent VQE can benefit from classical splitting. Our results encourage employing approaches that are based upon classically splitting or partitioning parametrized quantum circuits Bravyi et al. (2016); Peng et al. (2020); Tang et al. (2021); Perlin et al. (2021); Eddins et al. (2022); Saleem et al. (2021); Fujii et al. (2022); Marshall et al. (2022), as they are in general more robust against hardware noise. We consider in-depth analysis and applications with VQE and QAOA as future directions for this work.

Appendices

Appendix A

When analyzing the size of the gradients of an ansatz we need tools that allows integration over all states allowed by the ansatz over the d-dimensional Hilbert Space. This can be achieved by using the Haar measure. Haar measure is an invariant measure over the SU(d) group. An ensemble of unitary operators U is called as a unitary t-design if they are equal to the Haar measure $\mu (U)$ up-to polynomial order t. Then, the expectation of ensemble U, where unitary $V_i$ can be sampled with probability $p_i$ is given as,

$$\begin{aligned} \mathbb {E}_{H}^t(\rho ) = \int U^{\otimes t} \rho (U^{\otimes t})^{\dagger } \,dU = \sum _i p_iV_i^{\otimes t}\rho (V_i^{\otimes t})^\dagger . \end{aligned}$$

(18)

Then, to perform symbolic integration over the Haar measure we will need to use some properties of the measure Puchala and Miszczak (2017). For the first moment we have,

$$\begin{aligned} \int d\mu (U)U_{ij}U_{km}^* = \frac{\delta _{ik}\delta _{jm}}{d}, \end{aligned}$$

(19)

where d is the dimension of the Unitary, such that $d=2^N$ and N is number of qubits. Then, for the second moment we have,

$$\begin{aligned} \begin{aligned}&\int d\mu (U)U_{i_1j_1}U_{i_2j_2}U_{k_1m_1}^*U_{k_2m_2}^* = \\ {}&= \frac{ \delta _{i_1k_1}\delta _{j_1m_1}\delta _{i_2k_2}\delta _{j_2m_2} + \delta _{i_1k_2}\delta _{i_2k_1}\delta _{j_1m_2}\delta _{j_2m_1} }{d^2+1} \\ {}&- \frac{ \delta _{i_1k_1}\delta _{j_2m_2}\delta _{j_1m_2}\delta _{j_2m_1} + \delta _{i_1k_2}\delta _{i_2k_1}\delta _{j_1m_1}\delta _{j_2m_2} }{d(d^2+1)} \end{aligned} \end{aligned}$$

(20)

Then one can derive the following identities for integrals over the Haar measure McClean et al. (2018); Cerezo et al. (2021); Holmes et al. (2022),

$$\begin{aligned} \int d\mu (U)\text{ Tr }[UAU^\dagger B] = \frac{\text{ Tr }[A]\text{ Tr }[B]}{d}. \end{aligned}$$

(21)

We can extend this to the second moment to obtain the following identity,

$$\begin{aligned} \begin{aligned}&\int d\mu (U)\text{ Tr }[UAU^\dagger BUCU^\dagger D] = \\ {}&= \frac{\text{ Tr }[A]\text{ Tr }[C]\text{ Tr }[BD]+\text{ Tr }[AC]\text{ Tr }[B]\text{ Tr }[D]}{d^2-1}\\ {}&- \frac{\text{ Tr }[AC]\text{ Tr }[BD]+\text{ Tr }[A]\text{ Tr }[B]\text{ Tr }[C]\text{ Tr }[D]}{d(d^2-1)}. \end{aligned} \end{aligned}$$

(22)

We also have,

$$\begin{aligned} \begin{aligned}&\int d\mu (U)\text{ Tr }[UAU^\dagger B]\text{ Tr }[UCU^\dagger D] = \\ {}&= \frac{\text{ Tr }[AC]\text{ Tr }[B]\text{ Tr }[D]+\text{ Tr }[AC]\text{ Tr }[BD]}{d^2-1}\\&- \frac{\text{ Tr }[AC]\text{ Tr }[B]\text{ Tr }[D]+\text{ Tr }[A]\text{ Tr }[C]\text{ Tr }[BD]}{d(d^2-1)}. \end{aligned} \end{aligned}$$

(23)

Now, we can use these identities to compute the average value of the gradients. Let’s start by reminding ourselves the definitions we used before. The ansatz is composed of consecutive parametrized (V) and non-parametrized entangling (W) layers. We define $U_l(\theta _l) = \text{ exp }(-i\theta _l V_l)$, where $V_l$ is a Hermitian operator and $W_l$ is a generic unitary operator. Then, the curcuit ansatz can be expressed with a multiplication of layers,

$$\begin{aligned} U(\varvec{\theta }) = \prod _{l=1}^{L} U_l(\theta _l)W_l \end{aligned}$$

(24)

For an observable O and an input state $\rho$, the cost function is given as

$$\begin{aligned} C(\varvec{\theta }) = \text{ Tr }[OU(\varvec{\theta })\rho U^\dagger (\varvec{\theta })] \end{aligned}$$

(25)

The ansatz can be separated into two parts to investigate a certain layer, such that $U_- \equiv \prod _{l=1}^{j-1} U_l(\theta _l)W_l$ and $U_+ \equiv \prod _{l=j}^{L} U_l(\theta _l)W_l$. Then, the gradient of the $j^{th}$ parameter can be expressed as McClean et al. (2018)

$$\begin{aligned} \partial _{j} C(\varvec{\theta }) = \frac{\partial C(\varvec{\theta })}{\partial {\theta _j}}&= i\,\text{ Tr }[[V_j,U_+^\dagger OU_+]U_- \rho U_-^\dagger ] \end{aligned}$$

(26)

Fig. 7

The variance of the gradients of the first parameter of the ansatz as a function of the number of qubits for varying values of m. Each color/marker represents a certain value of m and data points of the standard ansatz ($m=N$) is plotted with a dashed black line

Then the expected value of the gradient with respect to the unitary group can be computed by using the Haar integral such that,

$$\begin{aligned} \langle \partial _{j}C(\varvec{\theta }) \rangle = i \int d\mu (U_-)d\mu (U_+) \text{ Tr }[[V_j,U_+^\dagger OU_+]U_- \rho U_-^\dagger ] \end{aligned}$$

(27)

$$\begin{aligned} = \frac{i\text{ Tr }[\rho ]}{d} \int d\mu (U_+) \text{ Tr }[[V_j,U_+^\dagger OU_+] = 0, \end{aligned}$$

(28)

where we use Eq. (21) to obtain (27) and use the fact that trace of the commutator is zero in (28). This proves that the gradients are centered around zero. Then, the variance of the gradient can inform us about the size of the gradients. The variance is defined as,

$$\begin{aligned} \begin{aligned}&\text{ Var }[\partial _{j}C(\varvec{\theta })] = \langle (\partial _{j}C(\varvec{\theta }))^2 \rangle - \langle \partial _{j}C(\varvec{\theta }) \rangle ^2 \\ {}&= \langle (\partial _{j}C(\varvec{\theta }))^2 \rangle \end{aligned} \end{aligned}$$

(29)

We can compute the expected value of the variance using the same logic. Then we have,

$$\begin{aligned} \begin{aligned}&\text{ Var }[\partial _{j}C(\varvec{\theta })] = \\ {}&=- \int d\mu (U_-)d\mu (U_+) \text{ Tr }[[V_j,U_+^\dagger OU_+]U_- \rho U_-^\dagger ]^2 \\ {}&= -\frac{1}{d^2-1} \int d\mu (U_+) \left( \text{ Tr }[\rho ]^2\text{ Tr }[[V_j,U_+^\dagger OU_+]]^2 \right. \\ {}&\left. + \text{ Tr }[\rho ^2]\text{ Tr }[[V_j,U_+^\dagger OU_+]^2] \right) \\ {}&+ \frac{1}{d(d^2-1)} \int d\mu (U_+) \left( \text{ Tr }[\rho ^2]\text{ Tr }[[V_j,U_+^\dagger OU_+]^2] \right. \\ {}&\left. +\text{ Tr }[\rho ]^2\text{ Tr }[[V_j,U_+^\dagger OU_+]]^2 \right) \end{aligned} \end{aligned}$$

(30)

$$\begin{aligned} = - \left( \text{ Tr }[\rho ^2] - \frac{1}{d} \right) \frac{1}{d^2-1} \int d\mu (U_+) \text{ Tr }[[V_j,U_+^\dagger OU_+]^2] \end{aligned}$$

(31)

We use Eq. (23) to obtain Eq. (30). Then, use the fact that commutator being traceless to obtain Eq. (31). To compute the integral of Eq. (31) we need another identity such that Holmes et al. (2022),

$$\begin{aligned} \begin{aligned}&\text{ Tr }[[V_j,U_+^\dagger OU_+]^2] = \\ {}&2\text{ Tr }[U_+ V_j U_+^\dagger O U_+ V_j U_+^\dagger O] - 2\text{ Tr }[U_+ V_j^2 U_+^\dagger O^2]. \end{aligned} \end{aligned}$$

(32)

Then, the variance becomes,

$$\begin{aligned}{} & {} \text{ Var }[\partial _{j}C(\varvec{\theta })] = \nonumber \\{} & {} - \left( \text{ Tr }[\rho ^2] - \frac{1}{d} \right) \frac{2}{d^2-1} \int d\mu (U_+) \left( \text{ Tr }[U_+ V_j^2 U_+^\dagger O^2] \right. \nonumber \\{} & {} \left. +\text{ Tr }[U_+ V_j U_+^\dagger O U_+ V_j U_+^\dagger O] \right) . \end{aligned}$$

(33)

The first integral can be computed using Eq. (21) and the second can be computed using Eq. (22). Then we obtain,

$$\begin{aligned} \begin{aligned}&\text{ Var }[\partial _{j}C(\varvec{\theta })] = \\ {}&- \left( \text{ Tr }[\rho ^2] - \frac{1}{d} \right) \frac{2}{d^2-1} \left( \right. \frac{1}{d^2-1}(\text{ Tr }[V]^2 \text{ Tr }[O]^2 \\ {}&+ \text{ Tr }[V^2] \text{ Tr }[O^2]) - \frac{1}{d(d^2-1)}(\text{ Tr }[V]^2 \text{ Tr }[O]^2 \\ {}&+ \text{ Tr }[V^2] \text{ Tr }[O^2]) - \frac{1}{d}\text{ Tr }[V^2] \text{ Tr }[O^2] \left. \right) \\ {}&= - \left( \text{ Tr }[\rho ^2] - \frac{1}{d} \right) \frac{2\text{ Tr }[V^2] \text{ Tr }[O^2]}{d^2-1} \left( \frac{d-1}{d(d^2-1)}(1 \right. \\ {}&\left. +\text{ Tr }[V]^2 \text{ Tr }[O]^2) - \frac{1}{d} \right) . \end{aligned} \end{aligned}$$

(34)

Finally, the asymptotic behavior of the variance can be expressed as

$$\begin{aligned} \text{ Var }[\partial _{j}C(\varvec{\theta })] \approx \mathcal {O} \left( \frac{1}{d^6} \right) \approx \mathcal {O} \left( \frac{1}{2^{6N}} \right) , \end{aligned}$$

(35)

where $d=2^N$. Thus, the variance vanishes exponentially with respect to N.

Fig. 8

The log plot of variance of the gradients of the first parameter of the ansatz vs. number of layers for $m=4$ (solid lines) and $m=N$ (dashed lines) with varying number of qubits

Appendix B

Fig. 9

Cost landscapes of ansätze with different settings. Parameters of the ansatz are reduced down to two using PCA and the x and y axis of the plots represents the PCA variables in same scale but with arbitrary units. The cost values (shown with the color map) are obtained using the definitions in Sect. 3.2. First column shows cost values of an $L=2$ standard ansatz for increasing number of qubits. Second column shows the results for the same ansatz but with $L=N$ layers. As, expected the landscape flattens with more qubits and we see a single color for $N>12$. Third column shows results for splitting (for $m=4$) of the ansatz in the case of $L=N$ layers. We see that the landscape does not become flatter with more qubits

Fig. 10

Distributions of the ad-hoc dataset used in Sect. 3.2. Each panel shows distribution of a single feature from one of three datasets. N denotes the size of the dataset (number of features), while f denotes the feature number. There exists 600 samples of N features for a size N dataset. Colors represent two classes. During training, data samples are divided with a 420/180 train/test ratio. The dataset is produced using make_classification function of scikit-learn Pedregosa et al. (2011) with a class separation value of 1.0, 2% class assignment error and no redundant or repeated features

Fig. 11

Training curves showing four different metrics for the problem described in Sect. 3.2. Panels of each row show a different metric. First three columns show training results from $L=2$ ansätze, the last three columns show training results from $L=N$ ansätze for $N\in${4,8,16}. Each value of m is plotted with a different color. Lines are obtained by averaging 50 runs and their standard deviation is shown with shades

Fig. 12

Batch size comparison for the training of $N=16$, $m=16$ and $m=4$. Training the $N=L=16$ model requires vast computational resources, especially memory. This restricted us from using a full batch size during the training of $N=m=L=16$ setting. Therefore, we presented results from a training that used a batch size of 60 instead of 420 (full). Here, we show training curves for $m=4$ on addition to $m=16$ for two different batch size (bs). Behaviour of the curves show that the gain in performance has nothing to do with the batch size difference

Appendix C

Appendix D

 

Fig. 13

Distributions of the NTangled Schatzki et al. (2021) dataset with respect to the CE values described in Sect. 3.3. The HEA ansatz (Fig. 1d) is used to produce the distributions. Each training set has 420 and each test set has 180 data samples. We see a mismatch for $\text {CE}\in${0.40,0.45} in the 8 qubit case. We are not sure what causes this, but it is not an issue for our problem as we are not interested in the CE values themselves but the quantum states as a whole. So, they are valid quantum state distributions as long as they can be separated with a given metric for our problem. Our results show that this is in fact true

Fig. 14

Training curves showing four different metrics for the problem described in Sect. 3.3. Panels of each row show a different metric. Each column presents a different task, where N determines the problem size and the CE values are the labels of the classes. Each value of m is plotted with a different color. Lines are obtained by averaging 50 runs and their standard deviation is shown with shades

Appendix E