An invitation to distributed quantum neural networks

Abstract

Deep neural networks have established themselves as one of the most promising machine learning techniques. Training such models at large scales is often parallelized, giving rise to the concept of distributed deep learning. Distributed techniques are often employed in training large models or large datasets either out of necessity or simply for speed. Quantum machine learning, on the other hand, is the interplay between machine learning and quantum computing. It seeks to understand the advantages of employing quantum devices in developing new learning algorithms as well as improving the existing ones. A set of architectures that are heavily explored in quantum machine learning are quantum neural networks. In this review, we consider ideas from distributed deep learning as they apply to quantum neural networks. We find that the distribution of quantum datasets shares more similarities with its classical counterpart than does the distribution of quantum models, though the unique aspects of quantum data introduce new vulnerabilities to both approaches. We review the current state of the art in distributed quantum neural networks, including recent numerical experiments and the concept of circuit-cutting.

1 Introduction

By now we have sufficient evidence that classical computers can learn. Decades of research in artificial intelligence (AI) (Russell and Norvig 2010; Mitchell 1997; Bishop 2006) and specifically deep learning (DL) (LeCun et al. 2015; Goodfellow et al. 2016; Schmidhuber 2015), have yielded powerful learning algorithms that are now employed in everyday tasks across several industries. With the rise of quantum computers, the natural question that arises is whether quantum computers, too, can learn. Quantum computing is the paradigm of computation that employs concepts from quantum mechanics (Nielsen and Chuang 2011). Attempting to answer this question requires a thorough exploration of quantum computing (QC) and machine learning (ML). With several directions in its agenda, the emerging field of quantum machine learning (QML) (Biamonte et al. 2016; Schuld and Petruccione 2018; Wittek 2014; Ciliberto et al. 2018; Cerezo et al. 2022), explores the intersection of quantum computing and machine learning. This interaction can have various objectives depending on whether the data or the environment is either classical or quantum (Aïmeur et al. 2006; Dunjko and Briegel 2018; Schuld and Petruccione 2018). The direction we consider here is to consider whether quantum computers can be used to provide benefits in training neural networks specifically. This question, too, has been asked and explored with various objectives in mind (Benedetti et al. 2019a). Present-day quantum computers are known as noisy intermediate-scale quantum devices (NISQ) (Preskill 2018). They are overshadowed by high error rates and a small number of qubits, which hinders their capabilities. However, there is a growing debate over what algorithms these devices can be used for. In this paper, we overview the concept of distributed quantum neural networks and suggest that this might underpin the first real application of quantum computers in the NISQ era. Drawing inspiration from artificial neural networks (ANNs), quantum neural networks (QNNs) have emerged as a new class of promising quantum algorithms. While there are many approaches to training quantum neural networks, until recently they have all been inherently sequential, aimed at training a quantum neural network on a single quantum computer. Yet, training a classical neural network on a single core is not always feasible in large-scale classical machine learning. When working with large datasets or sophisticated models, training is often distributed (Verbraeken et al. 2020). Dubbed distributed deep learning (DDL), these techniques are employed either because of the size of the dataset or because the model itself is too large to be processed on a single core. Employing multiple cores or even multiple machines overcomes this problem and typically leads to faster training time. Distributed deep learning brings together high-performance computing communication protocols and the thriving field of deep neural networks (Ben-Nun and Hoefler 2019; Chahal et al. 2020; Mayer and Jacobsen 2020; Langer et al. 2020). One work that is often cited as a large-scale success story is Goyal et al. (2017), which trains the ImageNet dataset (Deng et al. 2009) across 256 graphical processing units (GPUs) in 1 h. In a single-node fashion, training the ImageNet would normally take several days.

The limitations motivating DDL are even more pronounced in the quantum setting and an emerging set of techniques is being developed to mirror the classical paradigm. In this paper, we extend the ideas of distributed deep learning to quantum neural networks by reviewing and consolidating the existing literature. Our aim is to make more concrete the current set of vaguely similar ideas directing the research toward a more unified and directed goal of distributed QNNs. We define a distributed QNN as a learning algorithm employing multiple quantum computers (quantum processing units (QPUs), by analogy), which we refer to as nodes. We identify some common themes in the distribution of QNNs and discuss the implications.

The rest of this paper is organized as follows. The next three Sections 2, 3, and 4 give a primer on the ingredients required to understand distributed QNNs. Notably, Section 2 introduces deep learning concepts and expands on some of the well-known classical distributed deep learning frameworks. Section 3 introduces quantum computing along with distributed quantum computing concepts. Section 4 overviews quantum machine learning with a focus on quantum neural networks. Section 5 gives a more detailed overview of data parallelism considered through the quantum lens while emphasizing two data encoding types and their distributed forms: basis encoding in Section 5.1 and amplitude encoding in Section 5.2. Section 6 achieves the same for model parallelism while briefly commenting on vertical splitting of quantum circuits, and expanding more on some of the recent works in the so-called “circuit-cutting” schemes. In Section 7 we discuss the relevance of these works in the NISQ era and provide an overview of software that facilitates distributed deep learning as well as the quantum approaches.

2 Distributed deep learning

2.1 A brief history of deep neural networks

Neural networks are the machinery behind the current most prevalent machine learning method — deep learning (LeCun et al. 2015). Fueled by the availability of big data and the increase in processing power, this technology provides an ecosystem for creating self-learning agents able to find abstractions that are oftentimes not visible to other types of ML algorithms.

Fig. 1

Computational architecture scaling. (a) is an illustration of the scaling up method of computation. In this approach, the processing power is increased as more core processing units are added to a single device. Whereas in (b), the computational capacity is scaling out, which represents connecting distinct smaller devices each with an individual number of processing units to achieve higher processing capabilities. The latter is the distributed approach we assume for scalability here

2.1.1 Structure of neural networks

The building block of a neural network is the neuron. The artificial neuron — very much inspired by the human biological neuron — has a classical input–output structure. The first architectural model was proposed in McCulloch and Pitts (1943) in 1943, known as the McCulloch-Pitts (MP) neuron. Each of the input values of a neuron x has a corresponding weight coefficient w — which is the parameter that determines how important the input is to the output. The role of a neuron is to connect with other neurons. A neural network has an input layer, so-called hidden layers, and an output layer. The depth of the network is determined by the number of hidden layers. The reason deep learning architectures are preferred to shallow ones, lies in the ability of hidden layers to reach higher levels of abstraction, thus discovering more intricate patterns in datasets. The ability to extract information typically increases with the number of hidden layers, and as long as new and useful information is extracted from the data source, the number of layers is tuned accordingly.

Training begins by calculating the input sum of the weighted parameters (and the bias b), thus:

$$\begin{aligned} z = \sum _{i=1}^{n}w_ix_i + b. \end{aligned}$$

(1)

The output can be noted as $y = f(z)$. The function f is known as the activation function, and it is highly non-linear. The process of training the weights goes through two main processes: the first one is computing gradients using the backpropagation algorithm (Rumelhart et al. 1986; Hinton et al. 2006), and the second one is an optimization procedure generally using gradient descent methods (Kingma and Ba 2015; Ruder 2016). From Eq. (1), the cost function (i.e., mean squared error) can be defined as:

$$\begin{aligned} C(w) = \frac{1}{n} \sum _{i=1}^{n} (y'^{(i)}- y^i)^2 \end{aligned}$$

(2)

where n is the number of samples, $y'$ is the predicted value and y the actual value.

In its simplest form, given the one-directional transmission of information in a neural network, such a network is called a feedforward neural network. In the stacked layers of feedforward neural network architectures, the output of a layer defines the input of the following. When a feedforward neural network has no hidden layers, it is called a perceptron (Rosenblatt 1957). Besides feedforward neural networks, there exists another class of neural networks called Hopfield neural networks (Hopfield 1982), that represent a class of recurrent and fully interconnected networks.

Several stacked layers of a neural network introduce deep neural networks (DNNs) making such an architecture a deep architecture. Even though deep learning is a much older paradigm, the last decades have brought the invention of many widely applied deep learning architectures (Goodfellow et al. 2016) based on feedforward and recurrent networks, notably convolutional neural networks (CNNs), several architectures of recurrent neural networks (RNNs) — such as long-short term memory (LSTM) — generative adversarial networks (GAN), deep Boltzmann machines (DBMs), variational autoencoders (VAEs) and others. Each of the available architectures might be a better fit for different problems. CNNs for instance, work particularly well with images and are applied to problems in computer vision (Szeliski 2010; Krizhevsky et al. 2012). Computer vision problems are machine learning applications that train the computer program to identify images. Along with CNNs, RNNs are usually the go-to candidates for natural language processing (NLP) problems (Yin et al. 2017). NLP represents a set of problems that usually require the identification of natural human language.

Fig. 2

Architecture overview of data parallelism and model parallelism approaches in distributed neural network training. a) The dataset D is split into three equal parts ${(D_1, D_2, D_3)}$ across n available devices (here three nodes), where each device holds an identical copy of the entire model M. b) The model M is split across n devices (here three nodes), while each device holds a copy of the entire dataset D. In both scenarios, parameters are subsequently synchronized among the devices either asynchronously or synchronously. Gradients are exchanged using one of the parameter exchange protocols such as the MPI

2.1.2 Scaling DNNs

It is evident that there are many problems for which neural networks are good candidates as a solution, including classifying objects, image recognition, forecasting, medical diagnosis, and more. Inspired by the idea that classical approaches of neural networks and deep learning are a machine learning success story, these techniques have begun their journey in the quantum world as well. The quantum approaches and their achievements are further explored here in Section 4.

Oftentimes it suffices to have a single machine to perform tasks. But, processing a task requires computational power. More complex tasks require more computational power in which case the processing system needs to be scaled in terms of resources. For smaller scales of processing it remains convenient to add resources to the same processing machine. This approach is known as scaling up, or vertical scaling (Fig. 1a). In reality, any processing machine can be scaled up, however, the cost of advancing such an architecture becomes exponential the higher the need to scale. A more pragmatic solution is often given by scaling out, also known as horizontal scaling (Fig. 1b). In simple terms, this means having the required number of resources in different machines, rather than in a single machine. At large scales, this solution is more cost-efficient. This outlines the need for distributed systems.

It is often implied that a distributed system is running a single process (task) at a time. In other words, all the participating devices are working toward one single output. Albeit, the reliable distribution of resources and processes has its own challenges. Having resources distributed to form a cluster requires communication and synchronization protocols. Relevant in this context, one issue that is prevalent directly in the training of neural networks is the communication overhead.

Another reason that motivates distributed training of deep learning architectures, is the fact that either the dataset or the model could get prohibitively large. It is because of these two elements that can be paralleled, that there exist two techniques of distribution: data parallelism and model parallelism (Fig. 2). In these scenarios, either the dataset or the model is split across nodes, respectively. Parallel or distributed processing often has different connotations. Parallel processing can be used in terms of multi-core processing in a single device; while distributed processing refers to the processing taking place in different nodes. The goal in either processing remains the same: to output the result coming from all the devices as if it were coming from one. This is why oftentimes the two terms are used interchangeably. The data and model-parallel distribution architectures can be used in either context. In our theoretical assumptions, we assume that distribution takes place in different devices, which we will refer to as nodes, while we refer to the collection of nodes in a distributed architecture as cluster.

2.2 Distributed deep learning

When training a deep learning architecture, there are two elements that could become prohibitively large: the dataset or the model (Ben-Nun and Hoefler 2019). Either the working dataset or the model may be too large to fit into a single available device. Inspired by techniques from parallel computing, the solution to overcoming this limitation is in distributing the largest elements. The first to consider is data parallelism. In this scenario, the dataset is split across the available nodes, while each node holds an entire copy of the model. The second approach, model parallelism, assumes the model is split across the nodes, while each node holds an entire copy of the dataset. The distribution of resources across several nodes takes several forms (Fig. 2). The data and the model approach are inherently linked to other parameters to consider when building a distributed architecture.

Fig. 3

Centralized and decentralized exchange of gradients in two distributed setting architectures. In a) we see the main node and three secondary nodes sending gradients to the main node as well as receiving gradients broadcasted from the central node. This architecture is known as the parameter server scheme. In b), four nodes each send and receive gradients in an all-reduce scheme without the need for a central node to orchestrate the communication. In both scenarios the dataset D has been cut into n equal splits, while the model M remains intact in every node

2.2.1 Data and model parallelism

Data parallelism techniques used to train neural networks are very often focused on training CNNs (Zinkevich et al. 2010; Recht et al. 2011; Dean et al. 2012). For a categorization based on the proposed architectures in the data-parallel approach see Table 1 in Mayer and Jacobsen (2020). Model parallelism on the other hand has been explored in several works such as Refs. Coates et al. (2013) and Dean et al. (2012). DistBelief (Dean et al. 2012) is a framework that allows the training of a model in a parameter-server architecture. In this type of setting, one parameter node orchestrates the communication of the rest of the nodes in the cluster. In the DDL scheme, data parallelism is used and explored more than model parallelism, in part because it allows better cluster utilization (Langer et al. 2020). Furthermore, beyond data and model-parallel approaches, there are other approaches to the classification of distributed protocols. One such notable architecture is pipeline parallelism (Huang et al. 2019; Narayanan et al. 2019) which involves pipelining the network layers in different nodes. In some works, there exists a so-called domain parallelism approach which can be sub-categorized as a data-parallel approach (Gholami et al. 2018). In domain parallelism, the data points themselves are split across different processors. It can also be inferred that there exist hybrid approaches to distribution, which make use of distributing both the model as well as the dataset (Gholami et al. 2018; Xing et al. 2015; Jia et al. 2019). The DistBelief architecture mentioned earlier is one such hybrid architecture. A study in Krizhevsky et al. (2012) on parallelizing the training of CNNs, proposes to split the two different types of layers constituting the architecture of modern CNNs, in two different ways: (i) one can apply data parallelism to convolutional layers which contain the majority of computation, and (ii) for fully connected layers which contain a small amount of computation, model parallelism may be more suited. In this work, however, we focus primarily on the distinctions between data and model distribution in the quantum setting.

2.2.2 Centralized and decentralized architecture

When designing concrete architectures based on either distribution, there are a number of choices one can make. First and foremost, the distributed architecture can be centralized or decentralized, as in Fig. 3. In centralized architectures, there is one appointed node that collects and broadcasts the information. In the jargon of DDL, this analogy is known as the parameter server architecture (Li et al. 2014; Gupta et al. 2017). In contrast, a decentralized architecture does not employ a parameter node that orchestrates communication (Sergeev and Balso 2018; Daily et al. 2018). It instead, employs communication techniques such as the all-reduce algorithm. In this scenario, each of the nodes has the same role of calculating, sending, and receiving gradients. It remains an open question as to whether the centralized or the decentralized approach is more suited to which scenarios. Evidently, that depends on several factors, and there may not be an architecture to fit all use cases. The obvious drawback of the parameter server method is that the main nodes can quickly become communication bottlenecks, potentially leading to failure. On the other hand, in a decentralized architecture, the communication cost increases with the number of nodes. This can lead to increased network maintenance complexity. There are works that evaluate the two approaches under certain conditions. For instance, Lian et al. (2017) concludes that there exists a regime in which decentralized algorithms outperform centralized ones in the distributed setting, in the scenario when the communication in the network remains low. As quantum technology evolves, it is likely that higher-level functions will continue to be performed by centralized classical devices, while low-level computations are distributed among several QPU nodes.

2.2.3 Synchronous and asynchronous scheduling

Another distinctive feature of the topology of choice is the way in which parameters are exchanged — a problem known as scheduling. In the scenario of the deep learning distribution, the parameters that need to be exchanged are the calculated gradients. The scheduling can take the form of synchronous or asynchronous scheduling. In the former, the nodes wait on each other for the exchange of the gradients, and gradients are exchanged only when all the working nodes have finished the respective calculations. Given that some nodes may be faster than others, this technique facilitates a uniform exchange. The result is broadcasted at the same time to all the nodes, once all the nodes have finished calculation (Iandola et al. 2016; Coates et al. 2013). Asynchronous communication, on the other hand, implies that the gradients are exchanged as soon as respective nodes have finished their designated calculations. When speaking of good cluster utilization, it is asynchronous communication that comes into the picture. In asynchronous communication, neither of the nodes waits for the progress of the other nodes. The faster nodes are not hindered by the slower ones. The result is broadcasted to the nodes that have finished the communication without the barrier of waiting on the slower workers (Recht et al. 2011; Dean et al. 2012; Keuper and Pfreundt 2015). There are evident advantages and disadvantages with either of the techniques further discussed in Chahal et al. (2020). Beyond the canonical approaches, there exist more relaxed scheduling strategies such as the stale synchronous (Gupta et al. 2017; Ho et al. 2013) and the non-deterministic communication methods (Ben-Nun and Hoefler 2019). In the context of quantum computation, new limitations arise in communicating quantum information. However, classical co-processors will likely be employed in any use of QPUs and will be relied heavily upon in such hybrid scenarios to optimize QNNs.

2.2.4 Communication protocols

When it comes to the exchange protocols used to facilitate communication, this is where techniques from high-performance computing (HPC) come in. One of the most used methods is the all-reduce algorithm that takes on various forms depending on the architecture (Thakur et al. 2005). Several out-of-the-box software packages provide access to distributed training. As such, gradients are exchanged using certain communication protocols. For instance, in Horovod (Sergeev and Balso 2018), the training is supported in the ring-allreduce architecture to facilitate data-parallel training approach (Patarasuk and Yuan 2009). Horovod uses message passing interface protocol (MPI) for sending and receiving the gradients (Walker et al. 1996) among the nodes. As we will see shortly, quantum information cannot be copied, so the naive application of many communication protocols does not apply to the communication of quantum information. Generalizations exist but require many advances in quantum technology infrastructure.

3 Essential quantum computing

3.1 Fundamental concepts

Quantum computing is based on the principles of quantum mechanics. The idea of using the postulates of quantum mechanics to build a new kind of computer was first introduced in the 1980s in two seminal studies by Benioff (1980) and Feynman (1982). Feynman’s proposal of quantum computation is backed by the idea that our quantum universe can only be simulated by quantum computers — in contrast to classical computers. Another negative argument that we must move to quantum from classical is the end of Moore’s law (Prati et al. 2017; Markov 2014), which famously extrapolated the trends of computing and predicted that computing power will double every 2 years. To achieve this, transistors have been shrinking in size at a comparable rate. However, things can only shrink so much before they are the size of an individual atom — at which point, control over them would effectively render them as components of a quantum computer.

There are, of course, positive arguments for quantum computers as well, which often begin with the promise of exponential speed-ups for some quantum algorithms (Nielsen and Chuang 2011). By now, there are dozens of quantum algorithms that can provide speed-ups over their classical counterparts (Montanaro 2016). Training of neural networks is one. But, before jumping straight into QNNs, we first overview the basic quantum information concepts required.

3.1.1 Quantum bits

In quantum computers, the information is processed via the means of its building blocks called qubits. Unlike bits, qubits have the ability to be in superposition and entanglement. The parallel of a qubit in the classical world of computing is a bit. A bit has two states 0 and 1, whereas a qubit has two states $\vert {0}\rangle$ and $\vert {1}\rangle$, and many other states as well. The two states $\vert {0}\rangle$ and $\vert {1}\rangle$ technically form a basis in a two-dimensional complex vector space (the $\vert {\cdot }\rangle$ symbol denotes its vector nature). This ability of a qubit to be in a continuum of its two basis states is called superposition. Superposition simply represents a linear combination of classical states:

$$\begin{aligned} \vert {\psi }\rangle = \alpha \vert {0}\rangle + \beta \vert {1}\rangle . \end{aligned}$$

(3)

Coefficients $\alpha$ and $\beta$ are complex numbers $(\alpha , \beta \in \mathbb {C})$ and are often called amplitudes.

Multiple qubits are represented as superpositions in a higher-dimensional vector space. For n qubits, the basis states consist of all binary strings of length n: $\vert {b}\rangle = |b_1 b_1\cdots b_n\rangle$. Since there are $2^n$ such basis vectors, the entire space has dimension $2^n$ and an arbitrary state of quantum information can be written as

$$\begin{aligned} \vert {\psi }\rangle = \sum _{b=1}^{2^n} \alpha _b |b\rangle , \end{aligned}$$

(4)

where the amplitudes must satisfy a normalization condition,

$$\begin{aligned} \Vert \vert {\psi }\rangle \Vert ^2 = \sum _{b=1}^{2^n} |\alpha _b|^2 =1. \end{aligned}$$

(5)

3.1.2 Superposition and entanglement

A state $\vert {\psi }\rangle$ from Eq. (4) may be simply one of the basis states. In this case, there is no superposition and the information could be represented by the bits labeling it. Often, quantum computation is assumed to start in the so-called zero states $\vert {00\cdots 0}\rangle$.

Two or more interacting qubits exhibiting properties of correlation can be entangled, which is easiest to introduce by example. The prototypical entangled state is the so-called Bell state: $\vert {\Psi ^+}\rangle =\frac{1}{\sqrt{2}} (\vert {00}\rangle + \vert {11}\rangle )$. The state is entangled because it cannot be written as two individual single-qubit states. For a system of many qubits, most states are entangled. The easiest way to interpret entangled states is as a superposition of correlated classical states.

Understanding the entire nature of superposition and entanglement is an open research question. But, suffice it to say, at least some of each is necessary to achieve novelty in a computation — otherwise, a classical computer could straightforwardly replicate it. Since most quantum computations are assumed to begin in the unentangled state $\vert {00\cdots 0}\rangle$, entanglement must be built up as the computation proceeds.

3.1.3 Quantum gates and circuits

The high-level ideas of computation remain the same in the quantum setting as in the classical setting. Similar to classical computers that use gates, quantum computers manipulate qubits via quantum gates. Gates map quantum states into other quantum states. In digital logic, the NAND gate is universal — any other logical function can be implemented using only this gate. Similarly, any quantum gate can be decomposed into a sequence of one- and two-qubit gates drawn from a small finite set of universal gates. As such, it is both sufficient and convenient to distinguish between gates that act on a single qubit and gates that act on two qubits.

We will not need to know here which particular gates can or are often used, so we will imagine them as abstract and arbitrary. Quantum gates compose operations in a structured pattern forming quantum circuits. In Fig. 4 the colored boxes represent one-qubit gates and two-qubit gates. The boxes which go through two lines are two-qubit gates, while the ones which go through only one line are one-qubit gates.

In general, two-qubit gates create entanglement, which requires either a physical connection between pairs of qubits or some other communication that mediates the interaction.

Fig. 4

A sample quantum circuit in four qubits initialized in the ground state $\vert {0}\rangle$. The gates are applied chronologically from left to right, representing the arrow of time, followed by the measurement. Two-qubit gates create entanglement, one-qubit gates create superposition

3.1.4 Measurement

In Fig. 4, the final symbol on the quantum circuit is the measurement. This is how quantum data is read. Measurement transforms qubits into bits. It is both probabilistic and irreversible, destroying any entanglement or superpositions in the process. For a general state as in Eq. (4), the outcome of the measurements is a single binary string b or its corresponding basis state $|b\rangle$. The probability of observing that outcome is $|\alpha _b|^2$. A consequence of this is that quantum superpositions cannot be read in the conventional sense. However, repeatedly measuring many equally prepared copies of quantum data can give sufficient statistical information to reconstruct it — a process referred to as tomography.

One of the most fundamental facts about qubits is that no procedure exists which can create copies of them. This fact is often referred to as the no cloning theorem. Since many communication protocols are predicated on creating and distributing copies of classical data, no-cloning presents an immediate challenge to naive generalizations.

3.2 Distributed quantum computing

The core concept of distributed computation naturally extends from classical to quantum computing. The underlying idea is that of using multiple quantum processors to process quantum information (input), toward producing one single output. By connecting multiple quantum devices over a network, one can achieve architectural scalability by scaling out. The same principles of scaling as in Fig. 1 can apply to quantum devices as well. Here we overview the main techniques that facilitate and promote distributed quantum computation. The idea of a scalable quantum architecture peak with the ambitious project of the quantum internet (Kimble 2008; Wehner et al. 2018; Cacciapuoti et al. 2020; Cuomo et al. 2020; Rohde 2021) as one of the main goals for distributed quantum computing.

The quantum internet implies quantum devices connected in a quantum network style with classical and quantum communication links. This network will thus allow communication between qubits on different devices apart from each other. A crucial element in the functionality of the quantum internet is quantum repeaters. Like classical repeaters, their role is to propagate the signal into the further nodes. For the same reason, they are placed between the nodes. However, unlike classical repeaters, quantum repeaters operate very differently in how they perforate the signal. Quantum repeaters perform the so-called entanglement swapping protocol which allows for entanglement distribution. There exist quantum protocols that facilitate the exchange of classical information such as quantum key distribution and superdense coding (Cacciapuoti et al. 2020). Whereas quantum communication can occur over classical channels via quantum teleportation (Nielsen and Chuang 2011). Informally, teleportation requires two classical bits and an entangled pair of qubits to be transmitted between the sender and the receiver. Other than the hardware challenges which currently hinder most of the quantum research, the state of the development of the quantum internet remains with many interesting open challenges (Cacciapuoti et al. 2020).

At present day, there exist small quantum devices that can be accessed via the cloud (IBM Quantum Experience 2022). These cloud-based devices offer access to quantum computation via the Internet. Classically, cloud-based approaches are certainly convenient due to their complete computation infrastructure accessible via the Internet. However, a lot of the discussion around cloud computation revolves around the security of the network (Almorsy et al. 2016). On the quantum front, there exists the idea of blind quantum computation (Arrighi and Salvail 2006; Broadbent et al. 2009) which provides a barrier of encryption to either of the nodes accessing the information transmitted. In this protocol which is applicable in a cloud-based environment, the server receives an encrypted algorithm from the client. In this way, the protocol provides security under the assumption of hidden calculations. However, there are certain aspects the server will know about the calculation such as the bandwidth of the calculation size and allocated resources for execution. Much of the current research in this area is focused on the verifiable aspects of the blind computation (Fitzsimons 2016).

The long-term vision of a quantum network, where superposition and entanglement are preserved, results in what can simply be interpreted as a single (albeit very large) quantum processor. Ensuring that the processor works well will surely require concepts properly termed distributed quantum computation in analogy with the classical techniques they will borrow from. But, here we are interested in the bottom-up problem, wherein we assume at some point in the nearer future we will have access to multiple small QPUs, not necessarily connected to a quantum internet, and ask: can we use these in parallel to train a QNN?

4 Quantum machine learning

4.1 A brief overview of QML

Quantum machine learning encompasses a variety of algorithms that are, broadly speaking, of variational nature, as opposed to the more popular quantum algorithms, such as Shor’s algorithm (Shor 1997) that are deterministic in nature. Other kinds of algorithms which can be called deterministic include Refs. Deutsch (1985), Deutsch and Jozsa (1992), Grover (1997), Cleve et al. (1997), Brassard et al. (1998), and Montanaro (2016). Here we are concerned with the variational ones. Quantum machine learning is the emerging relationship between quantum computing and machine learning. Collectively, the term QML is used interchangeably in several distinct scenarios regarding the direction of the field and the components used. The directions can take the form of quantum phenomena improving machine learning algorithms, or machine learning algorithms further improving quantum algorithms and designs. The two components needed for this scenario to work — data and algorithms — in either case, can be quantum or classical. Below we take a look at the four main paradigms.

4.1.1 Four paradigms

The first big chunk and usually the entry point in QML is called quantum-enhanced machine learning. In this scenario, machine learning analysis of classical data is processed on a quantum computer. Dunjko et al. (2016) proposes an agent-environment paradigm in four scenarios in which either is Classical or Quantum (CC, CQ, QC, QQ) (Fig. 5) as an attempt to give this new field more organization and perhaps a direction. The context of quantum-enhanced machine learning is desirable due to the power of quantum computers to work with complex linear and matrix computations, as well as the idea of quantum parallelism. The inspiration stems from the fact that the large amount of data needed for machine learning algorithms to yield better results will harness this power, consequentially leading to improvements in runtime and convergence time (Lloyd et al. 2013). That is also the main goal of this type of setup — speed-ups. However, in this case, data needs to be encoded into a quantum state, then queried and retrieved from a quantum RAM — that introduces issues of its own such as whether the time cost of this action is too high to pay for, in turn, quantum speed-ups.

Fig. 5

The four quantum machine learning development paradigms compared against data and algorithms type, either of which is considered to be classical or quantum. Classical ML on the upper-left corner for context

The second direction, quantum-applied machine learning is concerned with finding optimal ways to apply machine learning in quantum experiments with the goal of enhancing their performance or finding solutions. These various applications encompass accomplishments beyond quantum computing applications such as particle physics, quantum many-body physics, chemical and material physics, and more (Carleo et al. 2019; Dawid et al. 2022). To zoom in, some important implementations in quantum computing that have shown promising results take place in quantum control (Bukov et al. 2018; Niu et al. 2019), quantum error-correction (Nautrup et al. 2019; Torlai and Melko 2017), quantum state tomography (Torlai et al. 2018; Xu and Xu 2018).

The third paradigm, quantum-inspired machine learning, comes up with new ways to design and evaluate classical machine learning algorithms, that are primarily inspired by quantum theory. As reviewed in Arrazola et al. (2020), the complexity gap between classical and quantum algorithms keeps changing with the new algorithms coming into the picture and the complexity bounds are still somewhere between polynomial and exponential. Due to their relevance in machine learning algorithms, the study in question reviews the “flagship” algorithms of quantum computing - quantum algorithms for linear algebra (Harrow et al. 2009; Kerenidis and Prakash 2016). Arrazola et al. (2020) questions whether these asymptotic bounds achieved via quantum processing in several quantum-inspired algorithms may be useful in practical real-life applications. The study in Tang (2019) explores the realm of linear-algebraic operations applied in recommendation systems which build on the work of in Kerenidis and Prakash (2016) that proves exponential improvements over classical algorithms for recommendation systems. However, Tang (2019) narrows that gap by proving that another class of classical algorithms reaches the same exponential improvements.

The fourth category, quantum-generalized machine learning or fully quantum machine learning is the case where the data, as well as the infrastructure, are bona fide quantum. Given the still lagging state of the art of the two components, this approach remains rather futuristic, to be answered at its full scale at this point in time. Nevertheless, among the first attempts to generalize classical machine learning models have been proposed in line with unsupervised classification protocols for quantum data (Sentís et al. 2019) and quantum anomaly detection (Liu and Rebentrost 2018), among others.

4.1.2 Translational QML

Several of the classical machine learning algorithms have been appropriated in the quantum realm: quantum support vector machines (Anguita et al. 2003), quantum principal component analysis (Lloyd et al. 2014), quantum reinforcement learning (Dong et al. 2008), quantum algorithms for clustering (Aïmeur et al. 2006), quantum recommendation systems (Kerenidis and Prakash 2016) and many others. A notable subroutine on which many such QML works are based on is the so-called HHL algorithm (Harrow et al. 2009), which proposes a solution to the linear systems of equations using quantum operations. In turn, HHL achieves exponential improvement in time complexity over the best-known classical algorithm for the same task. However, there are certain strict conditions that must be met that could otherwise hinder the time advantage. For an analysis of its caveats, see Aaronson (2015), while for an overview of the HHL in some QML methods, see Duan et al. (2020).

More recently, QML research has slightly shifted focus beyond computational complexity comparisons with the classical counterparts, to the flavor of building better quantum models (Schuld and Killoran 2022). In this context, several works (Holmes et al. 2022; Sim et al. 2019; Abbas et al. 2021; Wright and McMahon 2019; Du et al. 2020; Banchi et al. 2021; Hubregtsen et al. 2021) explore expressibility, generalization power and trainability of a model — all crucial elements when building robust learning algorithms. Attention is also given to the complexity bounds that shift between classical and quantum data for quantum models (Liu and Rebentrost 2018; Huang et al. 2021a, b).

Fig. 6

A basic structure of the parameterized quantum circuits with qubits and gates analogy, involving the data encoding stage, the ansatz to be optimized, measurement, and an optimization scheme

4.2 Quantum neural networks

Quantum neural networks represent a class of hybrid quantum-classical models that are executed in both quantum processors as well as classical processors to perform one single task. QNNs are currently one of the most trending topics in quantum machine learning (Beer et al. 2020). They are often interchangeably referred to as variational or parameterized quantum circuits (VQCs or PQCs) (McClean et al. 2016; Bharti et al. 2022; Cerezo et al. 2021a). Several studies review more in-depth the increasing body of proposed methods for implementing a QNN or similar model classes (Schuld et al. 2014; Benedetti et al. 2019a; Mangini et al. 2021; Li and Deng 2021).

Some of the first works that address the question of quantum neural networks do so from a biological perspective extending on the idea of cognitive perspectives (Kak 1995; Chrisley 1995; Lewenstein 1994). Others similarly early ones do so from a hardware perspective (Behrman 2000; Ventura and Martinez 2000). However, with more contemporary approaches concerning QNNs, its definition has evolved with now to refer to tangents in classical artificial neural network research due to their parameters which require optimization via a training procedure.

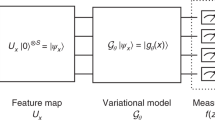
The QNN architecture has a structure that loosely resembles that of classical neural networks, depicted in Fig. 6, hence the analogous name. Evidently, when working with classical data, a preliminary step is to encode the classical data into quantum states. Otherwise, the first step of the QNN training procedure is to define a cost function C, which as in the classical case, maps the actual parameter values to the predicted ones. This step is then followed by the circuit with parameters $U(\theta )$ which need to be optimized using an optimization strategy — often referred to as ansatz for the parameterized quantum circuit (e.g., Kandala et al. 2017). This step of the procedure resembles the multi-layered architecture of neural networks, as the ansatz can be composed of multiple layers with the same architecture. The estimation of the gradients $C(\theta )$ occurs in a quantum machine. The optimization task is thus to minimize the value of the cost function. This is followed by the measurement step which is used to introduce non-linearity. The output of the measurement is then compared with the cost function dependent on the task via the training procedure and then the parameters are updated accordingly. Different types of classical optimizers are used for training $\theta$ often based on the gradient descent methods (Cerezo et al. 2021a; Sweke et al. 2020).

Evidently, it is natural that there remain several open issues in quantum neural network research. One of the main challenges for QNNs remains the linear-non-linear compatibility between neural network computation and quantum mechanics. Neural network computation is done in a non-linear fashion, that is, the activation function that triggers each neuron is non-linear, otherwise, the idea of layers in neural networks would serve no purpose. On the other hand, quantum systems behave in a linear way, which gives rise to the first incompatibility. Among other works and proposals in response to this caveat, Cao et al. (2017) designs a quantum neuron as a building block to quantum neural networks based on the so-called repeat-until-success technique to get past the linearities of quantum circuits. Several other fundamental issues are discussed and summarized in Allcock et al. (2020) including, the sequential nature of training neural networks, which clashes with the parallel processing power of quantum algorithms. In essence, taking advantage of quantum superposition and managing to parallelize the training of neural networks is a step in the right direction, however, in training neural networks data is calculated and stored at many intermediate steps — an inherent property of the backpropagation algorithm. A recent approach suggests using the rule called parameter-shift, which mimics the way backpropagation works (Mitarai et al. 2018; Schuld et al. 2019, 2020). Finally, the parameters needed for training need to be encoded in quantum states, a process that is time-consuming, and the topic of further discussion in Section 5.

To add to the discussion, QNNs are prone to the so-called barren plateaus phenomenon (McClean et al. 2018; Cerezo et al. 2021b) which entail flat region in the optimization landscape for even modest numbers of qubits and gates. Although there has been progress toward escaping this phenomenon be it by initialization methods (Grant et al. 2019) or newer QNN architecture that are not prone to barren plateaus (Pesah et al. 2021). Despite the inherent drawbacks, there are continuous attempts to resolve these issues and unite the two paradigms of AI and QC due to the seemingly promising rewards. To support this, there have been a number of notable works which go along the lines of optimizing versions of parameterized quantum circuits for quantum data (Cong et al. 2019; Beer et al. 2020). Furthermore, to align with the deep learning architectures, there are several proposals that extend the main deep architectures into quantum structures such as RNNs (Bausch 2020), CNNs (Cong et al. 2019; Henderson et al. 2019; Kerenidis et al. 2020), GANs (Lloyd and Weedbrook 2018; Dallaire-Demers and Killoran 2018; Zoufal et al. 2019) and more (Mangini et al. 2021). Further enhancing the capabilities of these structures is one potential avenue where the research will go. In the context of QNNs as well, there is an emphasis on the expressibility, trainability, and generalization power of these model classes.

However, whatever direction QNN research and applications take, the need to scale out will soon become apparent, which brings us to distributed QNNs.

5 Data parallelism: splitting the dataset

The concept of data in quantum processing is very different from that in the classical world. Straightforwardly, quantum data is the data that is output from any quantum computer or quantum processor. To explain it, one can contrast it with how classical data works (Resch and Karpuzcu 2019). Classical data can be saved in permanent storage, moved, and copied as needed. On the other hand, quantum data is rather short-lived. Its lifetime ends with the end of the execution of a program. A very different property is that quantum data cannot be copied as per the no-cloning theorem. The no-cloning theorem does not allow the creation of an identical copy of an arbitrary quantum state (Wootters and Zurek 1982). The discussion on quantum data is tightly linked to its processing mechanism, such as a quantum random access memory (QRAM) (Giovannetti et al. 2008b, b; Arunachalam et al. 2015). Being able to retain quantum states longer or query them requires storage capacities to be put in place. This becomes particularly relevant in the discussion of quantum machine learning. In what we call quantum-enhanced machine learning, classical data needs to a priori be encoded into quantum states, which inherently is a time–costly process (Aaronson 2015). Additionally, for many of the proposed approaches, the presence of a QRAM is a mandatory feature. On the other hand, fully quantum machine learning that operates with quantum data is starting to sprout, and there are reasons to believe that it will be a more of an effective direction, as it removes the need for quantum pre-processing.

As is the case with the enhanced QML algorithms workflow, the dataset first needs to be encoded into quantum states (Schuld and Petruccione 2018). In this context, this is the case when working with classical data and quantum algorithms (CQ). As such, data encoding is a crucial part of designing quantum machine learning algorithms. There exist several methods of encoding classical data applied across several works in QML that make use of data encodings frameworks (Farhi and Neven 2018; Rebentrost et al. 2014; Havlíček et al. 2019; Harrow et al. 2009; Schuld et al. 2020; Wiebe et al. 2012; Lloyd et al. 2020; Schuld and Killoran 2019; Skolik et al. 2021) and further push the ongoing research in this domain. Some of the most explored encodings in the context of QML include basis encoding, amplitude encoding, angle encoding (tensor product encoding), and Hamiltonian encoding. We refer the reader to other encodings as well as more in-depth analysis in Refs. Schuld and Petruccione (2018), Weigold et al. (2020), and Weigold et al. (2021). Depending on the purpose of the computation, there are certain techniques better suited than the others. Weigold et al. (2020) concludes that amplitude encoding allows for compact storage and as such can be useful for storing a large amount of data in a small number of qubits. Whereas basis encoding is preferred should arithmetic computations take place. LaRose and Coyle (2020) explores several encoding types in a noiseless environment as well as under the influence of noise for binary quantum classifiers. In general, encoding data into quantum states is far from being a straightforward process. This part of the workflow is often a bottleneck (Aaronson 2015) in achieving practical advantage. The research is still ongoing and crucial to the success of quantum machine learning algorithms. Moreover, the question of data encoding is relevant beyond QML, such as in quantum simulations, another promising area of research.

Below we discuss two main data encoding techniques and how they would perform in data-distributed equivalents.

First and foremost, let D be a classical dataset of size M, where each data point x is an N-feature vector.

$$\begin{aligned} D = \{x^{(1)}, ... x^{(m)}, ..., x^{(M)}\} \end{aligned}$$

(6)

The process of data distribution begins with splitting D into L available nodes:

$$\begin{aligned} D_1&= \{x^{(1)},\dots , x^{(K)}\} , \end{aligned}$$

(7a)

$$\begin{aligned} D_2&= \{x^{(K+1)},\dots , x^{(2K)}\} , \end{aligned}$$

(7b)

$$\begin{aligned}&\vdots \nonumber \\ D_j&= \{x^{((j-1)K+1)},\dots , x^{(jK)}\} , \end{aligned}$$

(7c)

$$\begin{aligned}&\vdots \nonumber \\ D_L&= \{x^{(L-1)},\dots , x^{(M)}\}. \end{aligned}$$

(7d)

where $D = D_1 + D_2 + \dots + D_L$. Each of the L splits of data is processed in a different node. They each hold an equal amount K of different data points from the same dataset. Here we consider classical data to be quantum data after it is encoded into quantum states. When D is encoded into quantum states using either of the available encoding techniques, what is produced is quantum data. We can denote the obtained quantum dataset with $\vert {D}\rangle$ (Fig. 7).

Fig. 7

The split of the quantum dataset across three quantum nodes (QPUs). The quantum model is kept unchanged and loaded into all three nodes

5.1 Basis encoding with data distribution

The first encoding technique we consider is the basis encoding. This procedure has two substantial steps. Prior to encoding, each data point needs to be approximated to some finite precision in bits. Typically, single-bit precision is assumed for brevity. Otherwise, a constant number of extra qubits is required. We will follow convention here and assumed each feature is specified by a single bit such that each data point is an N-bit string.

Each of the data points is encoded in a computational basis state uniquely defined by its bit string. The entire dataset is encoded as a uniform superposition of these computational states. The dataset defined in Eq. (6) in the basis encoding will result in the following quantum data:

$$\begin{aligned} \vert {D}\rangle = \frac{1}{\sqrt{M}} \sum _{m=1}^M \vert {x^{(m)}}\rangle , \end{aligned}$$

(8)

where $x^{(m)}$ represents a single random data point in the dataset. To encode the classical dataset D into a quantum dataset, N qubits are required (and a constant factor more if the features are represented with more bits). Preparing $\vert {D}\rangle$ requires O(NM) gates (Ventura and Martinez 2000).

Examples of basis encoding (Wiebe 2020) of QML techniques employed for different tasks include neural networks for classification (Farhi and Neven 2018; Schuld et al. 2017), quantum data compression (Romero et al. 2017), quantum Boltzmann machines (Amin et al. 2018), to name a few.

In the distributed context, assuming the split according to Eq. (), to encode each of the portions of the dataset (i.e., Eq. (7c)) it also requires N qubits for each of the dataset chunks. We consider $\vert {D}\rangle$ to be one quantum state on LN qubits. This will result in:

$$\begin{aligned} \vert {D}\rangle = \vert {D_1}\rangle \otimes \vert {D_2}\rangle \otimes \dots \otimes \vert {D_j}\rangle \otimes \dots \vert {D_L}\rangle \end{aligned}$$

(9)

where each $\vert {D_j}\rangle$ is,

$$\begin{aligned} \vert {D_j}\rangle = \frac{1}{\sqrt{K}} \sum _{m=(j-1)K+1}^{jK} \vert {x^{(m)}}\rangle . \end{aligned}$$

(10)

The preparation of each $\{D_j\}$ requires O(NK) gates since each partition contains K data points. In total, across all partitions, O(NKL) gates are needed. Replacing the parameters from $K L = M$ yields O(NM) gates, the same as in the undistributed scenario. This is not surprising, of course, but one still wonders what has been gained.

There are a few observations we can make. Firstly, using this approach of data encoding to perform data distribution, in the end, requires more qubits than the single-node approach. While a single-node dataset requires N qubits, L splits of the dataset require LN qubits. This way, the number of qubits required grows with the number of splits. However, the total number of the gates NM remains the same. In the end, what has been achieved with this splitting technique is the reduction of gates per node, precisely by a factor of L.

Therefore, the positive aspect yielded in this procedure is the lower depth of state preparation per each individual split in comparison to the preparation of the larger circuit. Lower-depth circuits obviously require less time to implement, but also incur fewer errors, which again translates to time in the error-corrected regime, but is far more relevant in the NISQ era. Errors grow at least linearly in the depth of the circuit, hence so-called shallow circuits are of great interest, a fact we will discuss later.

More subtle is the notion of quantumness in the distributed approach. While it is clear in splitting we may have lost the naive parallelism afforded by quantum data, it is also likely that a significant amount of entanglement will also be lacking. This can be naively inferred to as less quantum as a solution, but not necessarily less powerful. As these considerations will be relevant to all splitting procedures we consider, further discussion of parallelism and entanglement will be deferred to Section 7.2.

5.2 Amplitude encoding with data distribution

Amplitude encoding is another widespread encoding technique that is widely used in the context of quantum machine learning. This technique uses amplitudes of the quantum state to encode the dataset (Schuld and Petruccione 2018).

All the data samples with their attributes are concatenated and can be constructed as,

$$\begin{aligned} \alpha= & {} \left( x_1^{(1)}, \ldots , x_N^{(1)}, x_1^{(2)}, \ldots , x_N^{(2)}, \ldots x_1^{(j)}, \ldots , x_N^{(j)},\ldots ,\right. \nonumber \\{} & {} \left. x_1^{(M)}, \ldots , x_N^{(M)} \right) , \end{aligned}$$

(11)

which is a single vector of length MN. The dataset D encoded in amplitudes can be characterized as:

$$\begin{aligned} \vert {D}\rangle = \frac{1}{|\alpha |}\sum _{i=1}^{MN} \alpha _i \vert {i}\rangle , \end{aligned}$$

(12)

where $|\alpha |$ is the normalization, or length of the vector $\alpha$:

$$\begin{aligned} |\alpha |^2 = \sum _{i=1}^{MN}\alpha _i^2, \end{aligned}$$

(13)

which is necessary recalling that all quantum states require normalization.

Amplitude encoding is certainly a more compact way of encoding data in comparison to the basis encoding given that it requires $\log (MN)$ qubits to encode the dataset defined in Eq. (6). Regarding the splitting of the dataset, here, as well, we assume Eq. (9). The full dataset will be a tensor product of quantum splits which encodes each of the subsets of data.

Assuming L splits, and applying Eq. () and Eq. (9) invokes the following in amplitude encoding, a $\vert {D_j}\rangle$ split will be characterized as:

$$\begin{aligned} D_j = \{x^{((j-1)K+1)}, \dots , x^{(jK)}\}. \end{aligned}$$

(14)

then $\alpha _j$:

$$\begin{aligned} \alpha _j \!=\! (x_1^{((j-1)K+1)}, \dots , x_N^{((j-1)K+1)}, \dots , x_1^{(jK)}, \dots , x_N^{(jK)}) \end{aligned}$$

(15)

where $\alpha \in \mathbb {R}^{KN}$. A split $D_j$ can then be written:

$$\begin{aligned} \vert {D_j}\rangle = \frac{1}{\vert {\alpha _j}\vert } \sum _{i}^{KN} \alpha _{j,i} \vert {i}\rangle . \end{aligned}$$

(16)

Consequently, encoding each of the splits L requires $\log (KN)$ qubits. Each split has K data points with N features. Assuming an equal split of the dataset where $K = \frac{M}{L}$, all the splits L together subsequently yield $L \log (\frac{M}{L} N)$. Assuming $M\gg L$, the total number of qubits is $L \log (MN)$, and again we see that data splitting has increased the number of qubits need by a factor of L.

One thing to be noted about the splitting of the data vector in amplitude encoding is the role of the normalization constant. Distribution of the dataset will result in L different normalization constants per data split, which may in turn disproportionately change the structure of data in L different ways. Of course, it could also be the case that the variance in the magnitude of the normalization constant is insignificant, which we might expect for very large data sets.

An obvious splitting technique in amplitude encoding is between data samples, such that each node receives a state $|D_j\rangle$ consisting of the feature vector $x^{(j)}$ of a single data point from D. Interestingly, arriving at this splitting is natural when starting from the hybrid quantum-classical approach to QNNs. There, the dataset is paired with labels $y^{(j)}$, for each $x^{(j)}$, which is compared to the output of the QML model in a sequential fashion. One notable exception is a recent set of simulated experiments (Huang et al. 2021a) which make natural uses of TensorFlow’s built-in distributed computing ecosystem to distribute the dataset over 30 nodes.

Fig. 8

Model parallelism example architectures. a) Horizontal and vertical split of a neural network model. b) A visual representation of the DistBelief (Dean et al. 2012) architecture that features both data and model parallelism as an example architecture of hybrid parallelism. Here the dataset as well as the model are split across the available nodes. c) Quantum-inspired horizontal and vertical split of a quantum circuit. The horizontally cut sub-circuits $N_n$ would require classical communication among the nodes. The vertical cuts $V_n$ would require quantum tomography. d) A visualization of the quantum-inspired hybrid approach following the architecture of DistBelief in b. The quantum circuit is split across 4 devices using both data and model parallelism

5.3 Data parallelism discussion

Basis and amplitude encoding are the prototypical techniques for constructing quantum data. Due to the current limitations of quantum hardware, other more “natural” encodings have been considered dubbed hardware-efficient. Angle encoding (Schuld and Killoran 2019; Skolik et al. 2021; Haug et al. 2023), which is done at the single-qubit level and hence does not entangle states within feature vectors, is more akin to basis encoding. Whereas, encoding at the Hamiltonian level (Havlíček et al. 2019; Wecker et al. 2015; Cade et al. 2020; Wiersema et al. 2020) typically involves two-qubit entangling gates and, in the context of parallelization, more akin to amplitude encoding.

The angle encoding technique was recently used in data parallelization experiments to distinguish letters from the MNIST database (Du et al. 2021). There, the authors devised a protocol to execute multiple rounds of local gradient training before communicating with a central node which averaged the current parameter values before redistributing them. The experiments investigated accuracy versus a number of local gradient evaluations, finding fewer local gradient evaluations to perform better independent of the number of local nodes. The overall speed-up to a given accuracy threshold, however, scaled linearly with the number of local nodes.

A generic approach to encoding classical data is to consider,

$$\begin{aligned} |D_j\rangle = U_{\text {enc}}(x^{(j)})|0\rangle , \end{aligned}$$

(17)

where $U_{\text {enc}}$ is some encoding circuit. In this context we are somewhat constrained in types of data splitting we ought to consider. By the very nature of the setup, we already have an implicit splitting between feature vectors. As noted, this is typically processed in series, but in the hybrid quantum-classical setting can be naively distributed using existing classical protocols. In this style of splitting, no entanglement is generated across features, while intradata entanglement would presumably persist. However, we do note that even within this paradigm, quantum training (with access to QRAM, for example) may recover interdata entanglement (Liao et al. 2021; Pascanu et al. 2013; Shang and Wah 1996). On the other hand, further splitting within each feature vector could be considered. However, detailed knowledge of $U_{\text {enc}}$ would be required, and this may consist of removing entanglement between features, which is likely the only advantage the QML model is empowered by — be it computational or expressive. We mention the possibility, though, as such a split might properly be considered a model splitting rather than a data splitting, which is an excellent segue.

6 Model parallelism: splitting the model

Model parallelism makes use of the idea of distributing the neural network and its parameters. In quantum machine learning, a model can be understood as a parameterized quantum circuit — i.e., a quantum circuit with variably specified gates. How these circuits are “split” is superficially the same as how models are split classically but differs greatly in the details.

Classically, we can point out two types of model splits: horizontal and vertical splitting as in Fig. 8a. In horizontal splitting, it is the layers of the network that are split. While vertical splitting is applied between the layers, leaving individual layers unaffected. The latter feature makes vertical splitting a more versatile technique. This is why classical vertical splitting is generally preferred over horizontal splitting (Langer et al. 2020). This, however, cannot be used as a naive heuristic for quantum scenarios, as we will see below.

The existing quantum literature in distributed QNNs explores horizontal splits rather than vertical splits. Interestingly, there are certain limitations in the classical analog which make the horizontal splitting approach the last resort to turn to for distribution (Langer et al. 2020). In addition, it is often left implicit that model parallelism does not always yield concurrent working nodes due to the inherent property of data dependency in neural networks.

The straightforward model architectures we have considered in Fig. 8c involve splitting the quantum circuit horizontally or vertically, although several other different split methods can be approximated. Intuitively, splitting the quantum circuit vertically may not necessarily yield an advantage. As will be discussed below, each gate or wire cut incurs a cost that grows exponentially.

In the case where a splitting strategy is restricted to communicating classical information between nodes, merging the different parts of the circuit requires the exponentially difficult task of quantum tomography. A strictly vertical split then is maximally inefficient. As in the literature, then, we will mostly focus on horizontal splitting.

At present, there exist several architectures which can be considered horizontal splits on the model. Generally speaking, these works correspond to a few major classes of horizontal splitting, as we will describe below. The taxonomy can be of different flavors, however below we choose to differentiate between incoherent and coherent splitting, the presence of communication throughout the calculation, and sampling.

We summarize the general techniques in Fig 9. Consider the gate G as a two-qubit gate whose action is to be split across two separate quantum computing nodes. For any G there are a number of recipes that allow exact or approximate emulation using only pairs of gates $L_k$ that act separately on each node. The labels carry some “physical” meaning here in that gates which act across subsystems are referred to as “global” while gates that act individually on subsystems are termed “local”. Properly, the action of the global gate G can be computed as a sum of locally acting gates $L_k$:

$$\begin{aligned} G = \sum _{k} c_k L_k, \end{aligned}$$

(18)

where $c_k$ are known real-valued coefficients. Each term in the sum requires a unique computation, the results of which need to be combined in post-processing. The key differentiating factor for how this is accomplished is whether it is achieved using quantum measurements or not.

Fig. 9

The two of the main paradigms of horizontal splitting introduced in the quantum circuit-cutting literature. In a) is depicted the paradigm of splitting gates (or wires) incoherently (classically) as in Peng et al. (2020). Whereas the architecture in b) splits the gates coherently (quantumly) as in Marshall et al. (2022)

6.1 Incoherent versus coherent splitting

In horizontal model splitting, as depicted in Fig 9, either there is a measurement or there is no measurement. Not depicted, however, is the idea of simply cutting a wire (Peng et al. 2020), which is analogous to the measurement-based gate-splitting scenario, which we discuss first. Note that, in the jargon of quantum physics, things which preserve quantum information are termed coherent while things that do not are incoherent.

6.1.1 Incoherent splitting

Incoherent splitting refers to methods as depicted in Fig 9a. In these schemes, the overall global circuit is simulated by a sequence of local circuits that include a quantum measurement of the qubits affected by the cut. Since the measurement is an operation that destroys quantum information — transforming it into classical information — this approach is called incoherent splitting. We note that it has elsewhere been referred to as “time-like” splitting (Mitarai and Fujii 2021a), but we will avoid this terminology as it references a concept in relativistic physics.

Ideas similar to classical horizontal parallelism have been proposed in the quantum circuits literature, oftentimes unrelated to the quantum machine learning literature. An equivalent to the idea of a horizontal circuit split has been proposed in Peng et al. (2020). This solution is offered precisely to get across the limited number of qubits available on individual devices. Overall, the scheme involves some classical computation to cut and distribute circuit descriptions among the nodes and also to post-process the results of measurements. The bulk of the overhead occurs in the number of quantum circuits that need to be run, which grows exponentially with the number of cuts. However, as they point out, actual overhead could be much less depending on the structure of the circuit. In the extreme case where two clusters of qubits have no entanglement across them, the splitting can be achieved with no overhead at all. Some applications (e.g., Hamiltonian simulation) which fall between these extremes are discussed.

These splitting methods were used in Chen et al. (2018) to simulate random 56 qubit quantum circuits of depth 22 on a single personal computer. In Eddins et al. (2022), the technique was referred to as entanglement forging and used to enact 10 qubit quantum circuits with a single 5 qubit nuclear magnetic resonance (NMR) quantum processor.

Since measurements are made in an incoherent splitting procedure, the problem of data analysis can be considered a statistical one. In response to this, Perlin et al. (2020) introduced a maximum likelihood tomography to approximate the result of the measurements which need to be performed across all circuit splits. They found a slightly enhanced performance in some numerical experiments over the naive recombination of the measurement data.

As noted in the canonical work of Peng et al. (2020), the success of splitting techniques will depend highly on the existent structure of the circuit to be split, assuming an optimal (or at least sensibly obvious) choice of split location. The examples considered possessed a clustering structure where the cut location would obviously correspond to cluster links. If such a structure needs to be first found, classical pre-processing may become difficult. In Tang et al. (2021), the authors introduce an automated tool, called CutQC, which uses the framework of integer programming to optimize the location of circuit cuts (effectively minimizing the number required). They demonstrate the tool with various simulations of quantum algorithms by obtaining not only orders of magnitude speed-ups in simulation time, but also the ability to go well beyond was is simulatable classically. In particular, they demonstrate the simulation of 100-qubit algorithms, whereas full circuit simulations on typical classical hardware are limited to roughly 30 qubits. Similarly, Saleem et al. (2021) uses a graph-based approach to optimize the cut locations in the wire-cutting scenario.

The most recent example of incoherent wire-splitting is Lowe et al. (2022), which utilizes randomized measurements and one-way classical communication to create a conceptually simple splitting procedure which again has an exponential overhead in the number of wire cuts. The authors were able to classically simulate a 129-qubit QAOA circuit using this technique.

6.1.2 Coherent splitting

In contrast to incoherent splitting, Fig 9b depicts the same cut location, but a simulation strategy that preserves quantum information by using quantum gates rather than measurements. Since quantum information is preserved in each circuit, this is dubbed coherent. It was first introduced in Mitarai and Fujii (2021a) where it was called “space-like” cutting.

While conceptually similar to Peng et al. (2020), the coherent splitting technique (Mitarai and Fujii 2021a) can achieve some quantifiable advantages depending on which gates are cut. In essence, efficiency comes down to how many terms are in the sum of Eq. (18), and that depends on which G is being split and how many times. Moreover, in a real device, it may be more applicable to enact single-qubit gates than perform measurements. The same authors improved upon the gate decomposition technique, substantially reducing the number of local terms $L_k$ in Eq. (18). They also introduced a novel sampling technique we discuss further below.

More recently, Piveteau and Sutter (2022) proposed a method called “circuit knitting” which again is motivated by the promise of using present-day quantum processors through the partitioning of large quantum circuits into smaller sub-circuits. The resulting output of each sub-circuit is then “knitted” using classical communication. This work is conceptually different from all those previously discussed in that those works considered only classical communication in the final post-processing of the data. Piveteau and Sutter (2022) found that classical communication is advantageous when multiple instances of the same gate will be split. However, prior entanglement between the nodes is necessary to realize this advantage.

These ideas have further motivated explorations in specifically splitting QNNs in the context of quantum machine learning (Marshall et al. 2022). Rather than minimizing the number of cuts as in previous work, Marshall et al. (2022) focuses on minimizing the size of the sub-circuits needed to approximate the result. They further test this hybrid circuit-cutting architecture in the MNIST dataset, but training a quantum classifier with 64 qubits using eight nodes (each, of course having 8 qubits). Such a simulation directly on 64 qubits would be infeasible both in classical simulation and in today’s quantum hardware. This work points out an important additional feature of the idea of distribution in QNNs. Notably, the problem of barren plateaus is eased because sub-circuits have a smaller number of qubits leading to larger gradients. This has been corroborated in Tüysüz et al. (2022), which explores parallel execution and combination of small sub-circuits in QNNs, finding an avoidance of barren plateaus.

6.2 Model parallelism discussion

Here we have made a distinction between incoherent and coherent splitting techniques. There are two points to make in this regard. First, it is not likely that one technique is strictly better than the other and the use of either technique will depend heavily on the context of the circuits being executed. Indeed, Mitarai and Fujii (2021b) considers the case of a hybrid technique in which multiple splits in a single circuit may use a combination of both incoherent and coherent splitting. The second point is that this dichotomy is not the only current differentiator in the horizontal splitting techniques existing in the literature.

We have alluded to two other distinctions already. The first is whether or not communication is used in the protocol. The existence of communication is not strictly optional but borne out of the necessity of cutting procedures. Communication takes place in Refs. Piveteau and Sutter (2022) and Lowe et al. (2022) in order to merge the different sub-circuits on the fly rather than in post-processing. Again, since the cutting protocol will depend on the context, the existence of communication will as well. Indeed the context may even preclude communication due to technical limitations.

The second distinction requires more thought. Since the coefficients $c_k$ are generically negative numbers, the total sum may require high precision to accurately calculate exactly or estimate. To get around this, let us rewrite Eq. (18) as follows,

$$\begin{aligned} G = N \sum _{k} \frac{|c_k|}{N}\frac{c_k}{|c_k|} L_k, \end{aligned}$$

(19)

where $N = \sum _k |c_k|$. From here we can see that the quantities $p_k = |c_k|/N$ form a discrete probability distribution. By treating the application of $L_k$ as a random variable, the expectation of G can be Monte Carlo sampled, which may result in fewer circuits to run. This was first considered by Mitarai and Fujii (2021b), where it was pointed out that the quantity $N^2$ corresponds to the overhead incurred due to splitting. Since there is no loss in generality in making this move and standard probabilistic bounds can be straightforwardly applied, it is likely that this sampling-based splitting approach will be more favored.

Recall that in data parallelism, the same classical protocols are applied to quantum data parallelism. However, we see that for model splitting, the resultant quantum protocol is fundamentally different as it requires potentially many different models to be run serially and then post-processed. Whereas, in classical horizontal splitting, the models do not actually change — communication protocols are introduced to retain the capacity of the full model. It is thus not likely that powerful classical hybrid protocols utilizing both vertical and horizontal model parallelism, such as DistBelief (Dean et al. 2012) depicted in Fig. 8b, will be generalized to the quantum setting. However, we can naively infer a quantum hybrid architecture in which both quantum data and quantum model are split as in Fig. 8d. Such a model might be realized when distribution can be achieved with efficient entanglement distribution or a fully coherent quantum communication network is available.

Finally, we mentioned the implied classical-quantum hybrid horizontal splitting technique of Bravyi et al. (2016), which makes use of both quantum and classical resources to simulate large quantum systems with “virtual qubits” running in parallel to a quantum computer.

7 Discussion

This overview paper was an introduction to the distributed techniques present in classical deep learning as applied to the novel field of quantum neural networks. In this final discussion we mention some related ideas and comment on the nascent topics of NISQ and quantum software before concluding.

7.1 Related techniques

Beyond data parallelism, there exist other strategies that go along the lines of optimizing the amount of data for learning algorithms. Data reduction techniques, often known as coreset techniques in classical machine learning (Bachem et al. 2017), are a prime example. The main idea behind coresets is that for a dataset D, there exists a subset S which approximates D for a particular task. Importance sampling is typically the first step in the process of finding such S. Coreset techniques are typically algorithm-type specific, however, can also be generalized. Making the same parallels to quantum computation, the size of the datasets remains an obvious problem when qubits are at a premium. The question of whether one can use coreset techniques in hybrid quantum-classical architectures has been explored in Harrow (2020); Tomesh et al. (2021). Harrow (2020) work presents several examples of hybrid algorithms making use of data reduction techniques, notably in clustering, regression, and boosting. Tomesh et al. (2021) builds on this work by extending it to the realm of variational algorithms. The works in question can certainly be part of the greater solution to handling large quantum datasets. Data reduction techniques are not typically discussed in the context of distributed learning. The underlying principles that guide data reduction techniques are not necessarily similar.

QNNs require classical optimization, which has been studied in a parallelized context in Self et al. (2021), where the procedure is called information sharing. The novelty of their proposal is in its application to a particular style of optimizing, but the general idea could be considered a form of a distributed QNN where the parameters are distributed across nodes. Although most optimizers are adaptive — meaning the QNN parameters at one point in time depending on measurement results at a previous point in time — many optimizers require evaluation of costs at several simultaneous parameter values. This suggests an obvious form of distribution, as in Self et al. (2021).

Fig. 10

Architecture stack of an example software infrastructure running numerical experiments as in Xing and Broughton (2021). The process is initiated by Kubernetes pulling the two docker images from the container registry: the Tensorflow QCNN image and the Tensorboard image (Tensorboard is Tensorflows’ graphical user interface of results overview). The images were built locally and uploaded to the container registry. After pulling the images Kubernetes creates pods (which can be thought of as actual processors or in software as jobs), the number of which is determined by the number of the replica parameter. Parallelism is managed by the number of pods. Pods are then deployed in Kubernetes nodes. Pod distribution over nodes is transparently managed by Kubernetes. At the end of the job, the master pod writes to the Google Cloud Storage bucket. At the same time, results get uploaded to Comet.ml via REST APIs. Note that Tensorboard can be used as a visual tool for reading the results without the need for external software. TFJob operator, part of the Kubeflow project, is Kubernetes’ custom resource that facilitates the deployment of Tensorflow instances in a Kubernetes cluster. The entire process can be categorized into two parts: the deployment phase responsible for the setup, and the runtime or in our scenarios of ML optimization, the training phase

7.2 NISQ and beyond

The primary motivation for many of the existing QML techniques is to serve the needs, or limitations, of the NISQ era. Recall, NISQ devices are both small (in qubit number) and noisy (limiting circuit depth) (Preskill 2018; Chen et al. 2022), which is why shallow circuits are of great interest Bravyi et al. (2018); Dunjko and Briegel (2018); Arute et al. (2019). Many of the techniques we have discussed above are suitable in the NISQ regime, not requiring a fixed (large) number of densely interacting qubits and not restricted to noiseless computation.

Combining the training of QNNs across many of the nodes may yield advantages be it in terms of time complexity, or in terms of generalization power, scalability, and explainability. Of the two main architectures, in classical deep learning, data parallelism is the more explored one. That is for several reasons. Firstly, it is practically easier to split the dataset rather than the model. When it comes to splitting the model there exist different strategies which can be more suited to the task at hand. Secondly, it is widely accepted that data parallelism allows better cluster utilization (Langer et al. 2020).

Naive data splitting is straightforwardly applied when using mature AI software packages (Huang et al. 2021a). We expect such techniques to find use in the first NISQ implementations of QNNs. However, the restricted size of NISQ devices will also see the use of horizontal splitting techniques. Incoherent splitting is likely more suited to early NISQ devices since no new capabilities are required. In addition to reducing the demand on the number of qubits, splitting techniques can reduce the depth of the circuit as well — depending of course on the structure.

One may wonder why such techniques have not been widely adopted and applied to existing devices. Typically, the larger the dataset is, the more relevant it becomes to distribute the dataset. Distributing smaller datasets may not yield obvious advantages. In the initial works that here we consider equivalent to model distribution, there are assumptions that can be made on the complexity of the datasets. For instance, Marshall et al. (2022) observe that synthetic quantum data performs better in their technique than classical high-dimensional data. As it currently stands, the number of qubits available may be sufficient, but the level of noise needs to be reduced to allow for sufficiently deep circuits. Determining what types of data and what structural features of circuits are most suited to splitting is an open area of research. What is clear, however, is that a principled approach to the development of software for this purpose is needed.

7.3 Software tools

There exist a number of software packages and libraries that implement distributed deep learning strategies. The Tensorflow software (Abadi et al. 2016), for instance, implements distributed training techniques as an out-of-the-box feature. In Tensorflow, there are several strategies for distributing resources (Distributed training with TensorFlow 2022). For instance, the MirroredStrategy as a distributed technique makes use of all the available central processing units (CPU) or GPU resources in a single device. MultiWorkerMirroredStrategy is a synchronous distributed strategy that makes use of multiple devices, each potentially containing multiple GPUs or CPUs. All of the aforementioned strategies support synchronous training. A few all-reduce implementations of choice are also available. Other than the methods above, there exists the ParameterServerStrategy which implements asynchronous communication. In addition to Tensorflow, there exist a number of other libraries one of which is the Horovod library (Sergeev and Balso 2018), that implements the ring-allreduce algorithm across a distributed cluster using NCCL (NVIDIA Collective Communication Library (NCCL) 2022) as the communication library. Other software that facilitates the same principles are MXNet (Chen et al. 2015), PyTorch (Paszke et al. 2017), CNTK (Seide and Agarwal 2016) etc. A more complete list of software available that support distributed deep learning can be found in Table 3 in Mayer and Jacobsen (2020).

Tensorflow Quantum (Broughton et al. 2020) is the quantum machine learning extension that allows simulating hybrid quantum circuit models. As an example in terms of how the distributed implementation would look in quantum neural networks, TensorFlow Quantum provides a blog post setting up the architecture (Xing and Broughton 2021) for distributed training of QNNs. This example implements the MultiWorkerMirroredStrategy. The backbone architecture of these experiments is the quantum convolutional neural network (QCNN) architecture developed in Cong et al. (2019). Figure 10 gives an overview of the architecture stack enabling such experiments. Furthermore, on the quantum front, quantum software such as Qiskit (Aleksandrowicz et al. 2019) or Pennylane (Bergholm et al. 2018) can be used either for simulations or experiments on actual quantum devices (Fingerhuth et al. 2018). Table 2 in Benedetti et al. (2019a) summarizes some of the works which implement QNNs across different quantum hardware platforms for different tasks (Otterbach et al. 2017; Ristè et al. 2017; Grant et al. 2018; Tacchino et al. 2019; Benedetti et al. 2019b; Coyle et al. 2020; Rocchetto et al. 2019; Ding et al. 2019; Ren et al. 2022).

In relation to the techniques useful for the distributed approaches, Tang et al. (2021) mentioned above, develops CutQC which is a software package that automates the location of wire cuts when splitting a quantum circuit. In similar lines, Parekh et al. (2021) builds Interlin-q on top of the real-time quantum networks simulator QuNetSim (Diadamo et al. 2021). Interlin-q is a software package that helps in designing distributed algorithms. It follows a general centralized architecture where a client node is responsible for propagating information to the computing nodes, via a middle point controller node.

7.4 Closing remarks

A lot of work in circuit-cutting schemes gives special attention to the role of entanglement when distributing qubits. The question of entanglement is heavily addressed in distributed quantum computing and quantum internet research (Cirac et al. 1999; Gyongyosi and Imre 2019). The first step in distributed quantum networks is to establish entanglement via entanglement distribution techniques. There exist several strategies for entanglement distribution which can be cost-effective (Streltsov et al. 2012). However, entanglement can be fragile and lost over time and as such it needs robust techniques for its preservation over long distances. This is a crucial element to consider in distributed quantum machine learning schemes as well. In the avenue of quantum neural networks, Sharma et al. (2022) demonstrates the crucial role of entanglement in training QNNs. The work in question expands on the data as a resource in classical machine learning, by demonstrating entanglement as an asset in the quantum setting. More concretely, the presence of entanglement reduces the demand for quantum data, something that was once thought to be of necessity in exponential order. Following this, it is pivotal to account for entanglement as a resource in distributed training. Such accounting directly relates to the overhead in distributed quantum learning.

One possible avenue of development in the distributed scenario is to see how the splitting of the circuit plays out in different proposed quantum deep learning architectures, beyond the feedforward QNNs. Some of the possible questions we are interested in exploring include a comparison of classical versus quantum training time and training accuracy. Tangentially, we note that all of the proposals for QNNs assume the circuit model of quantum computation. Following classical DDL literature, there remain several scenarios to consider on the quantum front regarding parameter scheduling, architectural centralization, and further into communication protocols. It may also be more natural to consider distributed quantum computing in alternative models such as measurement-based quantum computing (Raussendorf et al. 2003).

A natural descendant of the distributed architectures is the concept of federated learning (McMahan et al. 2017) which makes use of end-user data locally rather than assuming one single central storage. This paradigm is proposed to mitigate privacy and security issues that concern centralized training architectures. Federated learning from a quantum perspective has been initiated in Refs. Chehimi and Saad (2021), Chen and Yoo (2021), and Li et al. (2021). These techniques may eventually overlap with the distributed QNN approach we considered here.

In a recent issue of Quantum Science and Technology, leaders in the field of quantum computing were asked, “What would you do with 1000 qubits?” (Morello 2018). As in one response (Perdomo-Ortiz et al. 2018), many have suggested QML as one of the first applications that may provide an advantage over classical techniques. However, this question — and much of the reaction — was posed before distributed techniques became popular in the quantum information community. Anything you can do with 1000 qubits, you can do with ten 100-qubit devices and a bit of time. So perhaps this threshold is much closer than many suspects.