Abstract
Generative modelling has become a promising use case for near-term quantum computers. Due to the fundamentally probabilistic nature of quantum mechanics, quantum computers naturally model and learn probability distributions, perhaps more efficiently than can be achieved classically. The quantum circuit Born machine is an example of such a model, easily implemented on near-term quantum computers. However, the Born machine was originally defined to naturally represent discrete distributions. Since probability distributions of a continuous nature are commonplace in the world, it is essential to have a model which can efficiently represent them. Some proposals have been made in the literature to supplement the discrete Born machine with extra features to more easily learn continuous distributions; however, all invariably increase the resources required. In this work, we discuss the continuous variable Born machine, built on the alternative architecture of continuous variable quantum computing, which is much more suitable for modelling such distributions in a resource-minimal way. We provide numerical results indicating the model’s ability to learn both quantum and classical continuous distributions, including in the presence of noise.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
With the dawn of the noisy intermediate-scale quantum (NISQ) (Preskill 2018) device era comes a possibility of performing useful and large-scale computations that implement quantum information processing. While NISQ technologies do not entail fault-tolerance or large numbers of qubits (generally in the range of about 50–200) which we expect to be necessary for obtaining useful processing power, they do provide avenues for brand new methods of exploiting quantum information. One type of framework which can utilise the restricted architectures of NISQ devices is that of hybrid quantum-classical (HQC) methods, which have found many applications recently in fields like quantum chemistry (Peruzzo et al. 2014) and quantum machine learning (QML) (Benedetti et al. 2019). These depend on dividing an algorithm into several parts which can be delegated to either quantum and classical servers, reducing the amount of quantum resources required to generate a solution.
In the field of quantum machine learning (QML) (Biamonte et al. 2017; Dunjko and Briegel 2018; Ciliberto et al. 2018; Benedetti et al. 2019; Lamata 2020), the benefits of HQC are key in approaches that employ parameterized quantum circuits (PQC) (also referred to as a quantum neural networks), which act as an ansatz solution to some particular problem that can be optimised classically. QML has employed PQCs for several problems, including classification (Farhi and Neven 2018; Schuld and Killoran 2019; Havlíček et al. 2019; Schuld et al. 2018; LaRose and Coyle 2020), generative modelling (Benedetti et al. 2019; Liu and Wang 2018; Verdon et al. 2017; Romero and Aspuru-Guzik 2019; Zoufal et al. 2019), and problems in quantum information and computation themselves (Morales et al. 2018; Cincio et al. 2018; Khatri et al. 2019; Cerezo et al. 2020; LaRose et al. 2019; Romero et al. 2017). The ‘learnability’ and expressive power of these models have been also been studied (Schuld et al. 2020; Gil Vidal and Theis 2020; LaRose and Coyle 2020; Coyle et al. 2020; Du et al. 2020). One can, for example, use quantum states as sources of probability distributions, with measurement playing the role of random sampling. These quantum states are obtained via PQCs which are composed of a number of tunable quantum gates with parameters that can be optimised using a classical subroutine. The process is typically iterative, requiring smaller quantum circuits with less depth to be run several times, thus decreasing information loss and quantum resource requirements. Alternatively, one could use coherent quantum training procedures (Verdon et al. 2018) which may in fact be necessary to see quantum advantages in certain cases (Wright et al. 2020).
QML is not restricted to a specific quantum computing paradigm and several models have shown potential in recent years, often divided into two broad categories: discrete- and continuous-variable (Lloyd and Braunstein 1999) (DV and CV) systems. DV systems allow for individually addressable states that are finite, often preferred for their analogous nature to classical computers. CV systems, on the other hand, deal with quantum states which behave as bosonic quantum modes (and are therefore referred to commonly as qumodes) which effectively have infinite eigenstates with an added difficulty in addressing each individual state. This challenge notwithstanding, CV quantum computers allow for a far more effective manner of dealing with problems which require continuous values, making them a perfect candidate for modelling continuous distributions. Furthermore, much progress has been made in the field of QML using continuous variables, with software packages specifically created to deal with such scenarios (Killoran et al. 2018).
In this work, we use the CV model to study the Born machine (BM) (Cheng et al. 2018; Benedetti et al. 2019; Liu and Wang 2018), a mathematical model which generates statistics from a probability distribution p(x) according to the fundamental randomness of quantum mechanics, i.e. Born’s measurement rule (see Section 3). We can generate samples of a distribution defined according to Born’s rule via the measurement of some quantum state, making this a generative QML method. Most commonly, a quantum circuit Born machine (QCBM) is implemented, meaning the quantum state is prepared as by a PQC, although other definitions are possible, for example the parameterisation of density matrices via a combination of classical and quantum resources (Verdon et al. 2019; Liu et al. 2020; Martyn 2019). The output distribution is then altered via a classical optimisation of the PQC’s parameters in order to match the distribution of some target data. The target distribution may be the output of a quantum system—such as a quantum computer or an experimental measurement—making the quantum generative model naturally suited for learning it. Furthermore, Born machines are promising candidates for models which could demonstrate a quantum advantage in machine learning in the near term (Du et al. 2020; Coyle et al. 2020; Alcazar et al. 2020; Sweke et al. 2020; Liu et al. 2020).
2 Continuous variable quantum computing
Here, we give a brief overview of the nature of CV quantum computing as is pertinent to the rest of the work. For a full treatment of the topic, please refer to Weedbrook et al. (2012) and Braunstein and van Loock (2005). CV states can be represented in both phase space and Fock space (Moyal 1949; Goldstein et al. 2002; Curtright and Zachos 2011), owing to the wave-particle duality of quantum mechanics. Importantly, both formulations give equivalent predictions about the behaviour of quantum systems. Owing to the discrete nature of the Fock space formulation, in this work, we focus on the phase space approach in order to extract the benefits of continuous variables from CV systems.
In the phase space formulation, any state of a single qumode can be represented as a real-valued function F(x,p), \((x,p) \in \mathbb {R}^{2}\) in phase space called the Wigner quasi-probability function (Wigner 1932; Killoran et al. 2019; Curtright and Zachos 2011). The two axes of phase space are then the quadrature variables governed by quadrature operators \(\hat {x}\) and \(\hat {p}\) which have a continuous and infinite basis with eigenstates |x〉 and |p〉 and eigenvalues ψ(x) and ϕ(p). The marginals of the Wigner function are the probability distributions of each of the quadrature variables, |ψ(x)|2 and |ϕ(p)|2.
The Hamiltonian H governing the evolution of such systems can be seen as a polynomial function of the quadrature operators \(H = H(\hat {x}, \hat {p})\) with arbitrary but fixed degree. This Hamiltonian can be decomposed into a series of CV quantum gates (see Table 1) in order to be implemented in a quantum circuit setting.These are known as either Gaussian, which are generally easy to implement on quantum devices and to simulate, or non-Gaussian, which present problems in both areas. For a more in-depth discussion of these properties, please see Appendix 1.
3 Continuous variable Born machine
Having defined the CV model, we can now construct a continuous variable Born machine (CVBM). As discussed in the “Introduction”, the Born machine can generate statistics sampled from a probability distribution according to Born’s measurement rule:
The state |ψ(𝜃)〉 is generated by evolving the vacuum state |0〉 according to a Hamiltonian H that is constructed from CV gates given in Table 1. These gates form a PQC which is parameterised by the variables governing each gate (indicated in Eq. 1 by 𝜃). These parameters should be easily tunable and allow for an evolution to any state that can serve as the solution to the given problem.
Taking the distribution associated to the state, |ψ(𝜃)〉 we can utilise it as a generative model, which when measured in some pre-determined basis will generate samples of a distribution of interest. This model is parameterised by 𝜃, which defines an n-qumode quantum circuit U(𝜃) made up of a set of quantum gates such that:
The final ingredient is the measurement of this parameterised state to extract samples. This is key to the resource efficiency of the model. Here, a sample from a single qumode (either its position, x, or momentum, p) is extracted by measuring the corresponding quadrature using the infinite basis of operators in a homodyne measurement (see Appendix 2).
The parameters of these gates then need to be trained to solve the problem at hand. This generally involves a so-called cost function whose value depends on the output of the model as well as some training data samples which needs to be minimised by varying the parameters of the circuit U(𝜃). In practice, we usually cannot compute this cost function exactly, and optimising an estimator of it from samples is referred to as empirical risk minimisation (Vapnik 1992). Suitable cost functions are problem-dependent, and there is rarely a unique choice for a suitable cost, with different options varying in efficiency and accuracy. The choice of ansatz circuit, in the naive case, may be problem-agnostic or if we have further prior information about the problem, the ansatz may problem-dependent. Both of these choices have advantages and disadvantages. Once the value of the cost function converges to a minimum, if it is suitably faithful, the CVBM has the capacity to generate samples that emulate those of a target distribution. Importantly, the purpose of the CVBM is not to simply memorise and exactly reproduce the samples that were fed into it during the training, but rather to generalise to the entire distribution. This target distribution may originate from a classical source, in which case the CVBM can act as an alternative to a classical generative model. As a simple and obvious example of how the CVBM may represent classical distributions, we can examine the canonical Gaussian distribution. Indeed, a Gaussian distribution Eq. 11 is parameterised in a way that has direct correspondence with the Squeezing S(ζ) and Displacement D(α) gates (see Table 1) via its standard deviation and mean respectively. Thus, a CVBM circuit composed of only those two gates is expressive enough to capture any Gaussian distribution (for multidimensional Gaussians, we simply need to add a qumode for each new dimension). Other classical distributions are not necessarily as straightforward, but we expect that a well-tailored and sufficiently deep CVBM could be suitably adapted. On the other hand, if the distribution has a quantum origin, we may use the CVBM as a means of studying the underlying quantum system. For example in performing weak compilation (Coyle et al. 2020), where the target distribution is generated from another CVBM with fixed parameters. Alternatively, we may use it as a controllable proxy to study the characteristics of an unknown quantum system. In the latter case, we may consider the CVBM to be a synthetic quantum data generator where the target system is difficult to reproduce or access.
Now comes the question of quantum advantage in such a model. Similarly to arguments about the natural use of quantum computers for the simulation of quantum systems, we may expect that using the CVBM to learn (continuous) probability distributions which are quantum mechanical in nature exhibits a natural advantage. On the other hand, for certain classical distributions, we may also hope for an advantage in using a quantum model over a classical competitor, but this is still an open question. Evidence to this nature was shown in Sweke et al. (2020) and Coyle et al. (2020) where a distribution was constructed which could be learned efficiently by a quantum model, but by no efficient classical model. The problem was contrived, but opened the door to a provable advantage for quantum generative modelling. Matching such arguments to the limitations of NISQ devices is a major question of open research. More relevant to the CVBM model is the work of Douce et al. (2017), which showed that an extension of instantaneous quantum computation (e.g. Bremner et al. 2016) into the continuous variable regime admitted probability distributions which cannot be classically emulated. We leave the incorporation of such complexity theoretic arguments to future work. However, we stress that the previous discussion only applies to the representational ability of the CVBM. The ability to represent a distribution does not imply the ability to efficiently learn it, when only given a collection of samples. Indeed, by making the Gaussian-learning problem only apparently slightly more complex (by moving to a Gaussian mixture distribution), it is not even known if there exists a polynomial time algorithm to (agnostically) learn mixtures of Gaussians in d dimensions (Diakonikolas) and even parameter estimation of the mean and variance requires assumptions (Ashtiani et al. 2018).
3.1 Previous work
The CVBM is introduced as a resource-efficient method of generating continuous probability distributions. In order to do so, it is instructive to revisit other attempts to generate continuous distributions using quantum generators (here we compare only the sample generation mechanism, and not specifics of the model or training, which we discuss for the CVBM in the following sections). As discussed above, the CVBM allows sample generation via single homodyne measurements of a particular quadrature, for example the position x, so an element of a real sample vector is generated without any post-processing.
Firstly, the work of Liu and Wang (2018) numerically tested the performance of a QCBM when trained differentiably to learn a continuous distribution composed of a mixture of Gaussian distributions. This work used 10 qubits which results in approximating the real distribution using 210 = 1024 basis states without any measurement post-processing. Similarly, Zoufal et al. (2019) used an adversarially trained Born machine to represent discretised versions of continuous distributions (specifically log-normal, triangular, and Gaussian). Secondly, the work of Romero and Aspuru-Guzik (2019) and Anand et al. (2020) explicitly addresses this question of generating real valued distributions using a (discrete) Born machine as a generator in an adversarially trained scenario. Specifically, previous works utilised a Born machine to generate n-bit binary strings, x ∈{0,1}n by simply taking the measurement result from measuring (for example) every qubit in the computational basis, which generates one bit, xi ∈{0,1} per qubit. In contrast, the innovation of Romero and Aspuru-Guzik (2019) was to instead evaluate the expectation value (for example) of the Pauli-Z observableFootnote 1 from the measurement results to generate a real value, xi ∈ [− 1,1] for each qubit. More concretely, the final sample is an n bit string, \(\boldsymbol {x} \in \mathbb {R}^{n}\) generated by the following process:
The intermediate quantity, \(\tilde {\boldsymbol {x}}\), is the vector of expectation values for each qubit, \(\tilde {\boldsymbol {x}} \in [-1, 1]^{n}\), which is fed into a classical function, \(f:\mathbb {R}^{n} \rightarrow \mathbb {R}^{n}\). The function could be, for example, one layer of a classical feedforward neural network, where ϕ := (W,b) are the weights and biases of the network. This method addresses the continuous distribution problem, but at the expense of adding \(\mathcal {O}(n/\epsilon ^{2}\log \delta )\) extra measurements which must be evaluated (and hence circuits which must be run) in order to compute the expectation values, \(\tilde {\boldsymbol {x}}\), with sufficiently high probability (1 − δ) by Hoeffding’s inequality (Hoeffding 1963). Hence, this adds a large overhead to the efficiency of the model in order to generate a single sample, \(\boldsymbol {x} \in \mathbb {R}^{n}\). An alternate approach, intermediate to Liu and Wang (2018) (using a completely discrete output) and Romero and Aspuru-Guzik (2019) (which increases the number of circuit evaluations), is to use a QCBM, with n qubits, and convert the resulting n bit binary outputs into real valued numbers with a corresponding precision. Again, this method is resource intensive as n qubits are required to generate each vector element in \(\mathbb {R}\), and so is less ideal than our main approach. We illustrate this latter method numerically in Section 5 to contrast with the efficiency of the CVBM to learn a Gaussian distribution. Finally, we mention that one may consider our work as a specification and implementation of the idea proposed in Killoran et al. (2019) to use CV quantum circuits to non-linearly transform probability distributions for generative modelling.
4 Training
In this work, we are specifically interested in training a CVBM to generate data samples which behave as if they were sampled from some unknown target continuous probability distribution. We need to be able to do this while having access only to some limited number of training samples from the distribution we wish to learn as well as samples from the CVBM at any point in the training process. The metric we choose to implement in training our model based on these requirements is the Maximum Mean Discrepancy (MMD).
4.1 Maximum mean discrepancy
The MMD is a suitable metric for our purposes in several respects, having been used to train discrete Born machines previously (Liu and Wang 2018; Hamilton et al. 2019; Coyle et al. 2020; Hamilton and Pooser 2020) and requiring a relatively low number of samples from each distribution (Sriperumbudur et al. 2009). This minimal sample complexity enables efficient training at scale via differentiable methods, in contrast to methods relying on metrics equipped with exponential sample complexity, such as the Kullback-Leibler (KL) divergence (Zhu et al. 2019) or Wasserstein distance (Benedetti et al. 2019).
A key component of the MMD is the kernel function (defined below) and ML methods which use them are unsurprisingly known collectively as ‘kernel methods’ (Gretton et al. 2007; Hofmann et al. 2008; Schuld and Killoran 2019). The so-called kernel-trick is useful for comparing data, even when the underlying feature map may be difficult to compute. They use a similarity measure κ(x,x′) between two data points x and \(\boldsymbol {x}^{\prime }\) in order to construct models that capture the properties and patterns of a data distribution. This measure of distance is related to the inner products of a feature space, the idea of which is key to kernel methods.
Kernels are symmetric functions of the form \(\kappa : {\mathscr{H}} \times {\mathscr{H}} \rightarrow \mathbb {C}\) where \({\mathscr{H}}\) is a Hilbert space, often called a feature space. One can embed data samples from their original sample space \(\mathcal {X}\) into a space \({\mathscr{H}}\) via a mapping \(\phi : \mathcal {X} \rightarrow {\mathscr{H}}\). This is called a feature map and plays the the role of a ‘filter’ for the samples, with the aim to, say, achieve a reduction in dimensionality or some form of useful restructuring of the data that might aid in the training procedure. A (positive definite, real-valued) kernel inner product should also have the property \(\kappa (\boldsymbol {x} ,\boldsymbol {x}^{\prime }) \geq 0\) as well as being symmetric: κ(x,x′) = κ(x′,x).
A typical example is the so-called Gaussian kernel:
where x and y are two data points (generally called feature vectors), ||⋅||2 is the Euclidean distance between them and σ is a constant which represents the variance or the ‘bandwidth’ which determines the scale at which the points are compared. The kernel value decreases with distance between the two data points and as such is an effective similarity measure (Gretton et al. 2012).
Quantum kernels
One nice consequence of implementing kernels is that any positive definite kernel can be replaced by another and this opens up the doors to a brand new approach of improving ML algorithms. Before moving on to the MMD itself, we note the fact that quantum states are like feature vectors themselves in that they also reside in Hilbert spaces and allow for a very natural definition of a quantum kernel. If we find an effective way of encoding input data points \(\boldsymbol {x} \in \mathcal {X}\) into quantum states |ϕ(x)〉, then we realise a feature map. Furthermore, the overlap of two quantum states can then be implemented as a kernel distance, with increasing orthogonality of two states leading to a decrease in kernel value.
In order to compute this overlap, one could use CV SWAP-test like primitives, Chabaud et al. (2018) and Kumar et al. (2020), but due to the special form of the kernel, it can be evaluated more simply on NISQ devices (Havlíček et al. 2019) by running a unitary and then its inverse, each of which parameterised in some manner by the two data points to be compared. Quantum kernels have already been explored within the CVQC framework and we refer to Schuld and Killoran (2019) for further reading. For the purposes of this work, we employ several different encodings of classical data samples into CV quantum kernels to explore their efficiency and effectiveness in training the CVBM. While determining a good kernel mapping is a complex and generally problem-dependent issue, there are grounds for the use of quantum kernels as they may promise a far more complex mapping than anything that can be achieved classically and could prove to be useful in settings involving large datasets and particularly in terms of high dimensionality or correlation within the data. Quantum kernels were first investigated in the context of generative modelling in Coyle et al. (2020) and Kübler et al. (2019).
MMD estimator
The kernel acts as a feature map which embeds data samples in a Reproducing Kernel Hilbert Space (RKHS) (Schuld and Killoran 2019) and it can be shown that the MMD is a metric describing exactly the difference in mean embeddings between two distributions from which the samples are collected (Gretton et al. 2007; 2012). With this, we can define a cost function associated with the metric for distributions P and Q:
where \(\mathbf {x} \sim Q\) indicates a sample x drawn from distribution Q and κ is the MMD kernel. Given i.i.d. samples drawn from each distribution, the MMD can be estimated by replacing the expectation values in Eq. 6 by their empirical values to produce the (unbiased) MMD estimator:
with M samples \(\tilde {\mathbf {x}} := (\mathbf {x}_{1}, ... ,\mathbf {x}_{M})\) drawn from distribution P and N samples \(\tilde {\mathbf {y}} := (\mathbf {y}_{1}, ..., \mathbf {y}_{N})\) drawn from Q. Given a large enough number of samples, Eq. 7 should converge to the true expectations given in Eq. 6. The MMD is useful as an estimator due to the relatively low number of samples it requires to satisfy the above requirement (Sriperumbudur et al. 2009) (\(\mathcal {O}(\epsilon ^{-2})\) to reach a precision 𝜖). The estimator allows for a practical, numerical implementation to train a model in order to reproduce samples from a target distribution. In this work, we want to apply it to the CVBM.
4.2 Training the CVBM
The CVBM is parameterised by the operations given in Table 1 and in order to be able to train it efficiently, we need to determine a way to quickly navigate the parameter space of the MMD estimator for any quantum circuit composed of any of the given operations. A common method used in many machine learning algorithms is gradient descent, often implemented in a stochastic fashion, with many varieties to facilitate a tradeoff between accuracy and speed (Ruder 2017).
A key component of gradient descent is the calculation of loss function gradients with respect to each of the parameters. For each parameter 𝜃k, we need to determine \(\partial _{\theta _{k}} {\mathscr{L}}_{\text {MMD}}[P(\theta ),Q]\) wherein the distribution P(𝜃) is a CVBM circuit composed of gates parameterised by 𝜃 := 𝜃1,...,𝜃l.
The work of Liu and Wang (2018) shows that in the case of the discrete Born machine, by measuring an observable \(\hat {O} = |{\boldsymbol {x}}\rangle \langle {\boldsymbol {x}}|\), the gradient of the probability distribution generated by a QCBM, p𝜃, with respect to parameter 𝜃k is:
Where the parameters \(\theta _{k}^{\pm }\) imply that the gate parameter 𝜃k has been shifted by an amount \(\pm \frac {\pi }{2}\). In the CVQC case, this needs to be adapted for CV operators by adding specific scaling factors and choosing different shift amounts for \(\theta _{k}^{\pm }\) depending on the circuit gate (see Table 2). We chose to implement the analytic gradients derived in Schuld et al. (2019) (also see Mitarai et al. (2018), Crooks (2019), and Banchi and Crooks (2020)) for the Gaussian gates of Table 1 as well as additional approximations of gradients for the cubic phase gate V (γ) and Kerr gate K(κ) (see Appendices 3, 4 for details of the approximation and a derivation of the gradients).
The gradient of the MMD estimator with respect to the CVBM parameters can be described by:
where p,q samples \(\tilde {\boldsymbol {a}} := \{\boldsymbol {a}_{1},...,\boldsymbol {a}_{R}\}\), \(\tilde {\boldsymbol {b}} := \{\boldsymbol {b}_{1},...,\boldsymbol {b}_{S}\}\) are drawn from shifted circuits \(p_{\theta _{k}^{+}}(\boldsymbol {a})\) and \(p_{\theta _{k}^{-}}(\boldsymbol {b})\) respectively while \(\tilde {\mathbf {x}} = \{\boldsymbol {x}_{1}, ... , \boldsymbol {x}_{M}\}\) and \(\tilde {\mathbf {y}} = \{\boldsymbol {y}_{1}, ... ,\boldsymbol {y}_{N}\}\) are drawn from the CVBM and the target distribution. Using the above equation and the scaling factors and shift amounts given in Table 2, we can determine the gradient of the MMD estimator with respect to any gate from the set given in Table 1. Note that the error on the gradient for non-Gaussian gates scales approximately as the small-angle approximation error \(\sinh (t) \approx t\).
We train the CVBM iteratively by implementing batch gradient descent for each parameter 𝜃k:
with t representing the iteration number and μ being the learning rate (Ruder 2017). This is done sequentially for each 𝜃k per iteration of the training in order to update their values in a way that minimises the MMD estimator Eq. 7. The training terminates once a set number of iterations has been performed or else when the cost function observed to converge.
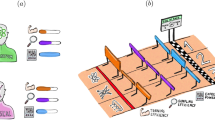
In Fig. 1, we emphasise the key ingredients of the model; a compact data encoding method for continuous distributions via the CVBM itself, an efficient training method via the MMD and a potentially classically hard-to-compute ingredient in the quantum kernel. In the next section, we validate its efficacy through numerical results on example classical and quantum distributions.
Components of the hybrid quantum-classical CVBM. The quantum hardware is used to produce measurement samples of the parameterised circuit U(𝜃k) as well as samples from circuits with shifted parameter values \(\theta _{k}^{\pm }\). These samples are then employed to classically compute the value of the cost function as well as its gradient in order to update the circuit parameters. If the cost function implements a kernel, this can be a classical function (such as the Gaussian kernel displayed in the figure) or quantum in nature, for example by running the corresponding encoding circuit Eϕ(x), with ϕ(x) being a quantum feature encoding for a data point x. In the latter case, the data and model samples would be fed into the quantum computer in the ‘quantum kernel circuit’ part of the diagram
5 Numerical experiments
Here, we present numerical results demonstrating the performance of the model on both classical and quantum data sets, as well as the impact of a noise channel and several different kernels. The simulations are implemented using Xanadu’s Strawberry Fields API (Killoran et al. 2018), which uses the symplectic matrix approach in simulating Gaussian states (see Eq. A.17) and a truncation of dimensions in Fock space when dealing with non-Gaussianity. Throughout all experiments, a cutoff dimension of 7 was used unless explicitly stated otherwise, owing to the fact that states with higher Fock numbers are likely to have little impact on the statistics of the single and two-qumode states that were used.
5.1 A classical distribution
An obvious choice of classical distribution to train the model on is the canonical Gaussian distribution. The classical Gaussian probability density function (PDF) is parameterised by mean μ and standard deviation σ (which can correspond to the displacement α and squeezing ζ operators as discussed above). To generate data representing the (single mode) classical Gaussian PDF, we take M samples from π, as given by:
To illustrate the (perhaps obvious) advantage of using our method (learning a continuous distribution with a continuously parameterised model), we compare to a discrete variable Born machine, which outputs binary strings of length n. From a theoretical perspective, we note that it is possible to efficiently load a discretised version of a continuous (but efficiently integrable) distribution on a quantum computer (Grover and Rudolph 2002), but this may also not be practical for the near term. As mentioned in Section 3.1, methods were proposed to do this approximately using Born machines in Liu and Wang (2018) and Zoufal et al. (2019). We use a slightly different method than Liu and Wang (2018) and Zoufal et al. (2019) here to approximate a continuous distribution with a Born machine by scaling the precision to which each real-valued number is represented to. In Fig. 2, we use a discrete Born machine (QCBM) with 2,4, and 6 qubits to learn a Gaussian distribution, \(\mathcal {N}(0, 1)\), with increasingly higher precision, and also we use the CVBM with a single qumode to learn the same distribution. For the QCBM, we simulate the results using Pyquil (Smith et al. 2016) and for an ansatz we choose a hardware efficient layered ansatz. Each layer consists of CZ matching the topology of a sublattice of the Rigetti Aspen-7 chip, with parameterised Ry(𝜃) gates. For the 2, 4, and 6 qubit QCBMs, we use 8,4, and 6 layers respectively resulting in 64,16, and 36 trainable parameters. To convert between the binary outputs of the QCBM, and the continuous valued data, we use a simple conversion algorithm described in Kondratyev and Schwarz (2019). We also mention that the comparisons we make here are preliminary, and open the door to rigorous comparison and benchmarking between the CVBM and other models.
Comparing a QCBM to our CVBM for learning a simple Gaussian distribution (a) with mean, μ = 0, and standard deviation σ = 1. In (c), we show the QCBM with increasing numbers of qubits (2,4, and 6 qubits respectively, which results in increased precision for each sample). The QCBM is trained with the Adam optimiser (Kingma and Ba 2015) using the Sinkhorn divergence (Coyle et al. 2020; Feydy et al. 2018; Genevay et al. 2017; Genevay et al. 2018). In (b), we show a single qumode with one parameterised squeezing and displacement gate for the CVBM, which can produce a much better fit to the data distribution with significantly fewer resources
5.2 Quantum distributions
Next, we focus on learning quantum distributions, i.e. one which arises as a result of measurements on a quantum state. This in some sense is equivalent to learning parameters which affect a quantum state, and in turn, gives some information about the parameters of the unitary which prepared the state, as a form of weak compilation, as noted by Coyle et al. (2020). We first generate data by preparing and sampling from a state (a ‘data’ state) with fixed parameters in the unitaries. We then use a CVBM with the same unitary gates as those that prepared the data state, and train the parameters of this independent CVBM. In this way, the CVBM learn to reproduce the statistics of the data state. Figure 4 shows the learning process for a Gaussian and a non-Gaussian state using a classical kernel (4). Figure 3 shows how the quality of the learning is impacted by the number of samples from the CVBM and its gradient calculations for both Gaussian and non-Gaussian circuits. Since we have access to both the target distribution and that of the CVBM, we can compare them using Kullback-Leibler divergence (KL) (van Erven and Harremoës 2012). Increasing both the number of samples of the CVBM for each training run and the number of samples for the shifted circuits may lead to better learning outcomes in the best possible case.
Effect of sample number on the performance of the CVBM as measured by comparing the target distribution and CVBM using KL-divergence (van Erven and Harremoës 2012). We keep the number of samples from the target distribution fixed at 500 samples and vary the number of samples that the CVBM produces at each training iteration (main plot) while keeping the shifted circuit 2 samples at 50. In the inlaid plot, the shifted circuit sample number is varied while keeping the target and CVBM samples constant at 500. The Gaussian circuit (and its target) consists of a squeezing gate and a displacement gate. In the non-Gaussian case, we investigate a cubic phase gate and a squeezing gate. The plot is of the best (smallest) KL out of 50 runs
The slightly larger discrepancy in Fig. 4b is due to a combination of factors that make learning non-Gaussian distributions difficult. The cost function landscape has multiple local minima and the number of samples to accurately capture the distribution is higher. However, having more samples is simultaneously not a tactic to get out of such local minima. This issue calls for a future investigation into finding better kernel functions for non-Gaussianity—ones which could capture this behaviour more effectively and efficiently. In the Gaussian case, however (Fig. 4a), the model converges to a very good approximation of the original distribution within less than 25 iterations of training while requiring only 50 samples (measurements) of the quantum state. This bodes well for the application of the method in—for example—characterising experimental data in the CV setting with very few data samples.
5.3 Quantum kernels
Here, we explore the behaviour of the MMD estimator with two separate kernel mappings: the cubic phase kernelϕV Eq. 12 and the squeezed kernel Eq. 13ϕS. For data point x = x1,x2,...,xn, we can implement n modes, applying the given unitary with strength xi to the qumode indexed by i.
The full feature map is given by the tensor product of each of these states, for example, with Eq. 12, \(\phi _{V}: \mathbf {x} \rightarrow |{V_{\mathbf {x}_{i}}}\rangle := \bigotimes _{i=1}^{n}|{V_{x_{i}}}\rangle \). We can then compute the overlap of two mapped states \(|{V_{\mathbf {x}_{i}}}\rangle \) and \(|{V_{\mathbf {x}_{i}^{\prime }}}\rangle \) to extract the kernel as in Eq. 5. Note that the overlap is computed by expressing the state in Fock space with a selected dimensional cut-off dependent on the number of qumodes required to estimate the kernel. Figure 5 demonstrates the behaviour of the MMD estimator during training for both of the quantum kernels as well as the classical Gaussian kernel given in Eq. 4.
A 3-qumode Gaussian CVBM composed of squeezing, displacement and beamsplitter gates is trained to learn a distribution generated by another CV circuit made up of the same components in a different order. The plot illustrates the behaviour of the loss when using a classical Gaussian kernel Eq. 4, a cubic phase kernel Eq. 12, and a squeezed kernel Eq. 13. We use 100 data samples each for the CVBM and the target distribution with 50 samples from shifted circuits to calculate MMD gradients. The shading around the plots indicates the standard deviation for each kernel after 5 runs of the training algorithm
While both quantum kernels exhibit a convergence to some minimum of the MMD loss, they do not show any improvement over the classical kernel with regard to the resulting distributions. The squeezed kernel, while more erratic, gives a better final result while the cubic kernel is very poor for this task (note the cut-off dimension used in simulating Fock space for both kernels was 15). This is by no means a reason to discount the use of quantum kernels in such algorithms, but does indicate that more analysis needs to be done for which types of data might benefit more from particular mappings.
5.4 Noise
Finally, we investigate the effect of a simple noise model on the training of the CVBM. In general, noise in quantum systems can be modelled using a completely positive trace preserving (CPTP) map, \(\mathcal {N}\), which can equivalently be expressed in an operator-sum (Nielsen and Chuang 2011) formalism, decomposed into Kraus operators. For the CVBM, we choose a simple noise model available in Strawberry Fields (Killoran et al. 2018), in order to study the effect of loss, whose Kraus representation, acting on a state, ρ, is modelled by:
where
This has the effect of coupling a mode \(\hat {a}\) to another mode in the vacuum state \(\hat {b}\) via the transformation:
which is then traced out. The noise parameter T represents energy transmissivity and T = 1 represents the identity map. For T = 0, the state is mapped to a vacuum state. Figure 6 shows the effect of noise on the CVBM learning process for both Gaussian and non-Gaussian quantum states.
Plots of MMD loss for single-mode CVBM learning a Gaussian (a) and non-Gaussian (b) single-qumode state. The CVBM is coupled to a loss channel with different values of parameter T (as given in Eq. 14). We use 100 data samples each for the CVBM and the target distribution with 50 samples from shifted circuits to calculate MMD gradients as well as the classical Gaussian kernel Eq. 4. The shading around the plots indicates the standard deviation for 5 runs of the training algorithm
As might be expected, the Gaussian state is significantly more robust to noise since the noise channel given by Eq. 14 couples the mode of interest to a vacuum state which is itself a Gaussian distribution. However, we can see that in the non-Gaussian case the algorithm adapts to some level of noise also, lending credence to using a CVBM in less-than-perfect experimental set-ups. Note that the target distribution data is assumed to have no noise channel affecting it as the assumption is that its source is unknown. However, the CVBM can also be used to determine the strength of noise on quantum data if its own coupling to a relevant noise channel can be manipulated.
6 Conclusion
In conclusion, we have presented the continuous variable Born machine, a generative model suitable for learning continuous-valued distributions, based on the continuous variable model of quantum computation. While there is still much to be explored (in particular, in the areas of selecting more apt kernels for the MMD estimator—be they classical or quantum in nature—as well as optimizing its implementation both on the classical and quantum hardware), it promises to be an interesting tool in exploring the relationship between the statistics of quantum experiments on CV states and the unitaries that ‘compile’ them. It should be noted that the larger the number of samples from the target distribution, the more accurate the CVBM result is in producing relevant samples or in determining how close its circuit is to reproducing a particular state, particularly in the case of non-Gaussian states. It can also be implemented in learning classical distributions, particularly with high dimensionality, in cases where their parameterisation is perhaps difficult to capture with a classical model. Finally, we mention it is an interesting future direction to study the effects and mitigation of ‘barren plateaus’ (McClean et al. 2018; Cerezo et al. 2021) in these models, which present a unique challenge due to the inherently ‘global’ nature of the generative modelling problem.
Notes
Note that Romero and Aspuru-Guzik (2019) allow measurements of any single qubit observable, P, which does not have to be the Pauli Z operator. However, for illustration purposes, we assume the measurement is done in the computational basis.
References
Preskill J (2018) . Quantum 2:79. https://doi.org/10.22331/q-2018-08-06-79. https://quantum-journal.org/papers/q-2018-08-06-79/. Publisher: Verein zur Förderung des Open Access Publizierens in den Quantenwissenschaften
Peruzzo A, McClean J, Shadbolt P, Yung MH, Zhou XQ, Love PJ, Aspuru-Guzik A, O’Brien J.L. (2014) . Nature Communications 5:4213. https://doi.org/10.1038/ncomms5213. https://www.nature.com/articles/ncomms5213
Benedetti M, Lloyd E, Sack S, Fiorentini M (2019) . Quantum Science and Technology 4(4):043001. https://doi.org/10.1088/2058-9565/ab4eb5. Publisher: IOP Publishing
Biamonte J, Wittek P, Pancotti N, Rebentrost P, Wiebe N, Lloyd S (2017) . Nature 549(7671):195. https://doi.org/10.1038/nature23474. Publisher: Nature Publishing Group
Dunjko V, Briegel HJ (2018) . Reports on Progress in Physics 81 (7):074001. https://doi.org/10.1088/1361-6633/aab406. Publisher: IOP Publishing
Ciliberto C, Herbster M, Ialongo AD, Pontil M, Rocchetto A, Severini S, Wossnig L (2018) . Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 474 (2209):20170551. https://doi.org/10.1098/rspa.2017.0551. Publisher: Royal Society
Lamata L (2020) . Machine Learning: Science and Technology 1(3):033002. https://doi.org/10.1088/2632-2153/ab9803. Publisher: IOP Publishing
Farhi E, Neven H. (2018) arXiv:1802.06002
Schuld M, Killoran N (2019) . Phys Rev Lett 122(4):040504. https://doi.org/10.1103/PhysRevLett.122.040504
Havlíček V, Córcoles AD, Temme K, Harrow AW, Kandala A, Chow JM, Gambetta JM (2019) . Nature 567(7747):209. https://doi.org/10.1038/s41586-019-0980-2
Schuld M, Bocharov A, Svore K, Wiebe N (2018) arXiv:1804.00633. [quant-ph]
LaRose R, Coyle B (2020) . Phys Rev A 102(3):032420. https://doi.org/10.1103/PhysRevA.102.032420. Publisher: American Physical Society
Benedetti M, Garcia-Pintos D, Perdomo O, Leyton-Ortega V, Nam Y, Perdomo-Ortiz A (2019) . npj Quantum Information 5(1):1. https://doi.org/10.1038/s41534-019-0157-8
Liu JG, Wang L (2018) arXiv:1804.04168
Verdon G, Broughton M, Biamonte J (2017) arXiv:1712.05304. [cond-mat, physics:quant-ph]
Romero J, Aspuru-Guzik A (2019) arXiv:1901.00848. [quant-ph]
Zoufal C, Lucchi A, Woerner S (2019) . npj Quantum Information 5(1):1. https://doi.org/10.1038/s41534-019-0223-2. Number: 1 Publisher: Nature Publishing Group
Morales MES, Tlyachev T, Biamonte J (2018) . Phys Rev A 98(6):062333. https://doi.org/10.1103/PhysRevA.98.062333
Cincio L, Subaşı Y, Sornborger AT, Coles PJ (2018) . New Journal of Physics 20 (11):113022. https://doi.org/10.1088/1367-2630/aae94a. arXiv:1803.04114
Khatri S, LaRose R, Poremba A, Cincio L, Sornborger AT, Coles PJ (2019) . Quantum 3:140. https://doi.org/10.22331/q-2019-05-13-140. Publisher: Verein zur Förderung des Open Access Publizierens in den Quantenwissenschaften
Cerezo M, Poremba A, Cincio L, Coles PJ (2020) . Quantum 4:248. https://doi.org/10.22331/q-2020-03-26-248. Publisher: Verein zur Förderung des Open Access Publizierens in den Quantenwissenschaften
LaRose R, Tikku A, O’Neel-Judy É, Cincio L, Coles PJ (2019) . npj Quantum Information 5(1):1. https://doi.org/10.1038/s41534-019-0167-6
Romero J, Olson JP, Aspuru-Guzik A (2017) . Quantum Science and Technology 2 (4):045001. https://doi.org/10.1088/2058-9565/aa8072. arXiv:1612.02806
Schuld M, Sweke R, Meyer JJ (2020) arXiv:2008.08605. [quant-ph, stat]
Gil Vidal FJ, Theis DO (2020) Frontiers in Physics, 8. https://doi.org/10.3389/fphy.2020.00297. Publisher: Frontiers
Coyle B, Mills D, Danos V, Kashefi E (2020) . npj Quantum Information 6(1):1. https://doi.org/10.1038/s41534-020-00288-9. Number: 1 Publisher: Nature Publishing Group
Du Y, Hsieh MH, Liu T, You S, Tao D (2020) arXiv:2007.12369. [quant-ph]
Verdon G, Pye J, Broughton M (2018) arXiv:1806.09729. [quant-ph]
Wright LG, McMahon PL, McMahon PL (2020) In: Conference on Lasers and Electro-Optics, paper JM4G.5 (Optical Society of America, 2020), p. JM4G.5. https://doi.org/10.1364/CLEO_AT.2020.JM4G.5
Lloyd S, Braunstein SL (1999) . Phys Rev Lett 82(8):1784. https://doi.org/10.1103/PhysRevLett.82.1784
Killoran N, Izaac J, Quesada N, Bergholm V, Amy M, Weedbrook C (2018) arXiv:1804.03159. [physics, physics:quant-ph]
Cheng S, Chen J, Wang L (2018) . Entropy 20(8):583. https://doi.org/10.3390/e20080583. Number: 8 Publisher: Multidisciplinary Digital Publishing Institute
Verdon G, Marks J, Nanda S, Leichenauer S, Hidary J (2019) arXiv:1910.02071. [quant-ph]
Liu J, Mao L, Zhang P, Wang L (2020) . Machine learning: Science and technology. https://doi.org/10.1088/2632-2153/aba19d
Martyn J (2019) Physical Review A 100(3). https://doi.org/10.1103/PhysRevA.100.032107
Du Y, Hsieh MH, Liu T, Tao D (2020) . Phys Rev Res 2(3):033125. https://doi.org/10.1103/PhysRevResearch.2.033125. Publisher: American Physical Society
Alcazar J, Leyton-Ortega V, Perdomo-Ortiz A (2020) . Machine Learning: Science and Technology 1(3):035003. https://doi.org/10.1088/2632-2153/ab9009
Sweke R, Seifert JP, Hangleiter D, Eisert J (2020) arXiv:2007.14451. [quant-ph]
Weedbrook C, Pirandola S, García-Patrón R, Cerf NJ, Ralph TC, Shapiro JH, Lloyd S (2012) . Rev Mod Phys 84(2):621. https://doi.org/10.1103/RevModPhys.84.621
Braunstein SL, van Loock P (2005) . Rev Mod Phys 77(2):513. https://doi.org/10.1103/RevModPhys.77.513
Moyal JE (1949) . Math Proc Camb Philos Soc 45(1):99
Goldstein H, Poole C, Safko J (2002) . American Journal of Physics 70(7):782. https://doi.org/10.1119/1.1484149. Publisher: American Association of Physics Teachers
Curtright TL, Zachos CK (2011) arXiv:1104.5269
Wigner E (1932) . Phys Rev 40(5):749. https://doi.org/10.1103/PhysRev.40.749
Killoran N, Bromley TR, Arrazola JM, Schuld M, Quesada N, Lloyd S (2019) . Phys Rev Res 1(3):033063. https://doi.org/10.1103/PhysRevResearch.1.033063. Publisher: American Physical Society
Vapnik V (1992). In: Moody JE, Hanson SJ, Lippmann RP (eds) . Morgan-Kaufmann, Burlington, pp 831–838. http://papers.nips.cc/paper/506-principles-of-risk-minimization-for-learning-theory.pdf
Douce T, Markham D, Kashefi E, Diamanti E, Coudreau T, Milman P, van Loock P, Ferrini G (2017) . Phys Rev Lett 118:070503. https://doi.org/10.1103/PhysRevLett.118.070503
Bremner MJ, Montanaro A, Shepherd DJ (2016) . Phys Rev Lett 117:080501. https://doi.org/10.1103/PhysRevLett.117.080501
Diakonikolas I In: Handbook of Big Data (Chapman and Hall/CRC, 2016). Num Pages: 18
Ashtiani H, Ben-David S, Harvey N, Liaw C, Mehrabian A, Plan Y, Bengio S, Wallach H, Larochelle H, Grauman K, Cesa-Bianchi N, Garnett R (2018) In: Advances in Neural Information Processing Systems. https://proceedings.neurips.cc/paper/2018/file/70ece1e1e0931919438fcfc6bd5f199c-Paper.pdf, vol 31. Curran Associates, Inc
Anand A, Romero J, Degroote M, Aspuru-Guzik A (2020) arXiv:2006.01976. [quant-ph]
Hoeffding W (1963) . J Am Stat Assoc 58(301):13. https://doi.org/10.1080/01621459.1963.10500830
Hamilton KE, Dumitrescu EF, Pooser RC (2019) . Phys Rev A 99(6):062323. https://doi.org/10.1103/PhysRevA.99.062323. Publisher: American Physical Society
Hamilton KE, Pooser RC (2020) . Quantum Machine Intelligence 2(1):10. https://doi.org/10.1007/s42484-020-00021-x
Sriperumbudur BK, Fukumizu K, Gretton A, Schölkopf B, Lanckriet GRG (2009) arXiv:0901.2698. [cs, math]
Zhu D, Linke NM, Benedetti M, Landsman KA, Nguyen NH, Alderete CH, Perdomo-Ortiz A, Korda N, Garfoot A, Brecque C, Egan L, Perdomo O, Monroe C (2019) . Science Advances 5(10):eaaw9918. https://doi.org/10.1126/sciadv.aaw9918. https://advances.sciencemag.org/content/5/10/eaaw9918. Publisher: American Association for the Advancement of Science Section: Research Article
Gretton A, Borgwardt KM, Rasch M, Schölkopf B, Smola A (2007) In: Schölkopf B, Platt JC, Hoffman T (eds) Advances in Neural Information Processing Systems 19. http://papers.nips.cc/paper/3110-a-kernel-method-for-the-two-sample-problem.pdf. MIT Press, pp 513–520
Hofmann T, Schölkopf B, Smola A (2008) . Annals of Statistics 36(3):1171. https://doi.org/10.1214/009053607000000677. Publisher: The Institute of Mathematical Statistics
Gretton A, Borgwardt KM, Rasch MJ, Schölkopf B, Smola A (2012) . Journal of Machine Learning Research 13:723. http://jmlr.csail.mit.edu/papers/v13/gretton12a.html
Chabaud U, Diamanti E, Markham D, Kashefi E, Joux A (2018) . Phys Rev A 98 (6):062318. https://doi.org/10.1103/PhysRevA.98.062318. Publisher: American Physical Society
Kumar N, Chabaud U, Kashefi E, Markham D, Diamanti E (2020) arXiv:2009.13201. [quant-ph]
Kübler JM, Muandet K, Schölkopf B (2019) . Phys Rev Res 1(3):033159. https://doi.org/10.1103/PhysRevResearch.1.033159. Publisher: American Physical Society
Ruder S (2017) arXiv:1609.04747. [cs]
Schuld M, Bergholm V, Gogolin C, Izaac J, Killoran N (2019) . Phys Rev A 99 (3):032331. https://doi.org/10.1103/PhysRevA.99.032331. Publisher: American Physical Society
Mitarai K, Negoro M, Kitagawa M, Fujii K (2018) . Phys Rev A 98(3):032309. https://doi.org/10.1103/PhysRevA.98.032309. Publisher: American Physical Society
Crooks G.E. (2019) arXiv:1905.13311. [quant-ph]
Banchi L, Crooks GE (2020) arXiv:2005.10299. [quant-ph]
Kingma DP, Ba J (2015) In: Bengio Y, LeCun Y (eds) 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings. arXiv:1412.6980
Feydy J, Séjourné T, Vialard FX, Amari SI, Trouvé A, Peyré G (2018) arXiv:1810.08278
Genevay A, Peyré G, Cuturi M (2017) arXiv:1706.00292. [stat]
Genevay A, Chizat L, Bach F, Cuturi M, Peyré G (2018) arXiv:1810.02733. [math, stat]
Grover L, Rudolph T (2002) arXiv:0208112
Smith RS, Curtis MJ, Zeng WJ (2016) arXiv:1608.03355. [quant-ph]
Kondratyev A, Schwarz C (2019) available at SSRN 3384948. https://doi.org/10.2139/ssrn.3384948
van Erven T, Harremoës P (2012) arXiv:1206.2459
Nielsen MA, Chuang IL (2011) Quantum Computation and Quantum information: 10th Anniversary, 10th edn. Cambridge University Press, New York
McClean JR, Boixo S, Smelyanskiy VN, Babbush R, Neven H (2018) arXiv:1803.11173. [physics, physics:quant-ph]
Cerezo M, Sone A, Volkoff T, Cincio L, Coles PJ (2021) . Nature Communications 12(1):1791. https://doi.org/10.1038/s41467-021-21728-w. https://www.nature.com/articles/s41467-021-21728-w. Nature Communications, 12(1):1791
Acknowledgements
The authors would like to thank Maria Schuld for helpful input on continuous variable states.
Funding
This work was supported by Entrapping Machines, 16 (grant FA9550-17-1-0055) and the EPSRC Programme Grant DesOEQ (EP/P009565/1).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Gaussian and non-Gaussian gates
States for which the Hamiltonian is at most quadratic in \(\hat {x}\) and \(\hat {p}\) are called Gaussian (Weedbrook et al. 2012). For the single qumode, the most common Gaussian quantum gates are rotation: R(ϕ), displacement: D(α), and squeezing: S(r,ϕ) (see Table 1). The simplest two-mode gate is the beamsplitter, BS(𝜃), which is a rotation between two qumodes. These gates are parameterised accordingly: ϕ,𝜃 ∈ [0, 2π], \(\alpha \in \mathbb {C} \cong \mathbb {R}^{2}\), and \(r \in \mathbb {R}\).
Importantly, Gaussian gates are linear when acting on quantum states in phase space. On n qumodes, a general Gaussian operator has the effect (Killoran et al. 2019):
with symplectic matrix M (Weedbrook et al. 2012) and complex vector \(\boldsymbol {\upbeta } \in \mathbb {C}^{2n}\). The variables x and p contain the position and momentum information of each qumode, and are vectors in \(\mathbb {C}^{n}\). Because of this linearity, Gaussian states and their operators are so-called easy operations of a CV quantum computer. They can be efficiently simulated using classical methods and are generally easy to implement experimentally (Weedbrook et al. 2012; Killoran et al. 2019).
In order to achieve a notion of universality (Lloyd and Braunstein 1999) in the CV architecture, we need the ability to construct a Hamiltonian that can translate to every possible state in the Hilbert space. This is done by introducing something called a non-Gaussian transformation into the toolbox, which is essentially a non-linear transformation on (x,p). Non-Gaussian gates involve quadrature operators that have a degree of 3 or higher. Some examples we consider in this work are the cubic phase gateV (γ) and the Kerr interactionK(κ) with \(\gamma , \kappa \in \mathbb {C} \cong \mathbb {R}^{2}\). Non-Gaussian gates are generally difficult to implement and difficult to accurately simulate using a classical processor, as they cannot be decomposed in the same fashion as Gaussian gates Eq. A.17. This lack of decomposition implies that a completely accurate classical simulation of non-Gaussianity requires access to infinite matrices, thus requiring a choice of cut-off dimension which introduces some errors. On a quantum processor, this notion of infinity is inherent in the native physics of the hardware.
A list of the CV gates used throughout this work as well as their exponential operator form is presented in Table 1. Note that the squeezing gate is parameterised by ζ and encompasses the parameters r (squeezing strength) and ϕ (squeezing direction) via the relationship ζ = reiϕ.
Appendix 2: Measurement
Classical information can be extracted from CV systems via three types of measurement: homodyne, heterodyne, and photon counting. For the purposes of the CVBM, we are interested largely in homodyne detection, which returns real, continuous values of the two quadratures of a CV state. In contrast, a heterodyne measurement allows one to extract both position and momentum simultaneously from the state (with a failure probability given by the uncertainty principle) via the operators |x + ip〉〈x + ip| in a ‘coherent’ basis. Braunstein and van Loock (2005):
By tuning the angle to ϕ = 0, we can extract the position, x, and for ϕ = π/2, we can get the momentum p. For this work, we set ϕ = 0 for all examples, and leave incorporation of alternative measurement strategies to future work. A full output sample, x, can then be determined by measuring all n qumodes.
Appendix 3: Unbiased gradient estimator of the probability of a CV quantum circuit
Here, we give a derivation for the gradient of the MMD cost function \(\partial {\mathscr{L}}_{\textrm {MMD}}\) with respect to each of the parameters of the CV gates as given in Table 2. The derivation is largely based on work done in Liu and Wang (2018) and gradients for Gaussian gates that were derived in Schuld et al. (2019). For the cubic phase gate V (γ) and Kerr gate K(κ), the partial derivative approximations originated as a part of this thesis and the derivation are given in Appendix 4.
The form of the maximum mean discrepancy given in Liu and Wang (2018) is:
where p𝜃(x) and π(x) are two probability distributions, while ϕ is a feature mapping, which can be a kernel function. When written in terms of expectation values of the samples, the above equation takes the exact same form as Eq. 6 in the text.
If we then take a partial derivative of Eq. C.19 with respect to one of the parameters (say 𝜃k) that the distribution p𝜃(x) depends on, we get:
If we now treat p𝜃(x) as a Born machine with observable x, i.e. the distribution we are interested in training, then we need to determine its derivative with respect to a particular parameter, ∂p𝜃/∂𝜃k. Luckily, we can refer to Schuld et al. (2019) for the derivatives of each of the Gaussian gates with respect to their parameters as well as to Appendix 4 for the non-Gaussian ones. For the sake of demonstrating the method, we choose the displacement gate D(α). In Schuld et al. (2019), its partial derivative is given as:
According to the same paper, this gradient corresponds to the gradient of an observable, which in our case would be the homodyne measurement (B.18). Since the gradient of the Born machine is parameterised the same way, we arrive at the partial derivative:
Where \(\alpha ^{\pm } = \alpha \pm s, s \in \mathbb {R}\). Substituting Eq. C.22 into Eq. C.20 we get:
Then, we can use the symmetric condition of the kernel, κ(x,y) = κ(y,x) to arrive at the form of the gradient given in Table 2. The same method can be applied to each of the parameters of each of the CV gates in order to derive the rest of the gradients given in Table 2.
Appendix 4: Partial derivatives for non-Gaussian transformations
While in Schuld et al. (2019) the gradients that are derived for Gaussian gates are analytic and based on their decomposition into covariance matrices in phase space, no such simplification was possible for the non-Gaussian gates:
Luckily, these unitaries exhibit certain properties which can be exploited in order to derive an approximate gradient. We take the cubic phase gate V (γ) as an example.
First, we notice that regardless of what dimension we choose to truncate the unitary matrix that describes the gate at, the form of it will always look like:
where the terms (x11...xNN) come from the N −dimensional matrix of the operator \(\hat {x}^{3} = \Big (\sqrt {\frac {\hbar }{2}}(\hat {a} + \hat {a}^{\dagger })\Big )^{3}\) and whose values will vary slightly depending on the dimension at which we truncate the operators \(\hat {a}\) and \(\hat {a}^{\dagger }\). The derivative of the cubic phase gate with respect to its parameter γ is then of the form:
Now we can use the hyperbolic function identity:
And the fact that for x ≪ 1, \(\sinh (x) \approx x\) to write out the partial derivative as a linear combination of the cubic phase gate with shifted parameters:
This is in a form that is well-suited to be implemented by the gradient of the MMD cost function as shown in Appendix 3. The error \(\sinh (x) \approx x\) scales as O(x3) and so for sufficiently small values of x the gradient approaches the exact analytical solution.
When we turn to the Kerr gate K(κ), we find that we can write it out in a similar form to the one in Eq. D.26 and thus we are left with a partial derivative given by:
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Čepaitė, I., Coyle, B. & Kashefi, E. A continuous variable Born machine. Quantum Mach. Intell. 4, 6 (2022). https://doi.org/10.1007/s42484-022-00063-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42484-022-00063-3