Optimizing quantum heuristics with meta-learning

Abstract

Variational quantum algorithms, a class of quantum heuristics, are promising candidates for the demonstration of useful quantum computation. Finding the best way to amplify the performance of these methods on hardware is an important task. Here, we evaluate the optimization of quantum heuristics with an existing class of techniques called “meta-learners.” We compare the performance of a meta-learner to evolutionary strategies, L-BFGS-B and Nelder-Mead approaches, for two quantum heuristics (quantum alternating operator ansatz and variational quantum eigensolver), on three problems, in three simulation environments. We show that the meta-learner comes near to the global optima more frequently than all other optimizers we tested in a noisy parameter setting environment. We also find that the meta-learner is generally more resistant to noise, for example, seeing a smaller reduction in performance in Noisy and Sampling environments, and performs better on average by a “gain” metric than its closest comparable competitor L-BFGS-B. Finally, we present evidence that indicates the meta-learner trained on small problems will generalize to larger problems. These results are an important indication that meta-learning and associated machine learning methods will be integral to the useful application of noisy near-term quantum computers.

1 Introduction

Machine learning is a powerful tool for tackling challenging computational problems (Vandal et al. 2017; Libbrecht and Noble 2015; Berral et al. 2010). A recent explosion in the number of machine learning applications is driven by the availability of data, improved computational resources and deep learning innovations (Jordan and Mitchell 2015; Mehta et al. 2019; LeCun et al. 2015). Interestingly, machine learning has also been applied to the problem of improving machine learning models, in a field known as meta-learning (Vilalta and Drissi 2002; Lemke et al. 2015).

In general, meta-learning is the study of models which “learn to learn.” A prominent example of a meta-learner model is one that learns how to optimize parameters of a function (Andrychowicz et al. 2016; Li and Malik 2016; Ravi and Larochelle 2016; Chen et al. 2017). Traditionally, this function might be a neural network (Andrychowicz et al. 2016) or a black-box (Chen et al. 2017). Meta-learning and other new methods, including Auto-ML (Feurer et al. 2015), are changing the way we train, use and deploy machine learning models (Munkhdalai and Yu 2017; Santoro et al. 2016; Nichol et al. 2018). Here, we use a meta-learner to find good parameters for quantum heuristics, and compare that approach to other parameter optimization strategies.

Figure 1 shows an example of what the implementation of a meta-learner might look like, in the context of optimizing the parameters of a parametrized quantum circuit, illustrated as a quantum processing unit (QPU). In this work, we refer to a QPU and a quantum circuit interchangeably.

Fig. 1

Meta-learner training on a Quantum Processing Unit (QPU—green). This diagram illustrates how the meta-learner used in this work can optimize the parameters of a quantum circuit (see Section 3 for a full description). Here, we outline a high-level description for each time-step, such as T − 2 (shown). A model, in our case a long short-term memory (LSTM) recurrent neural network (blue) (Section 2), takes in the gradients of the cost function. The LSTM outputs parameters ϕ for the QPU to try at the next step. This procedure takes place over several time-steps in a process known as unrolling. The costs from each time-step are summed to compute the loss, ${\mathscr{L}}$ (purple), at time T

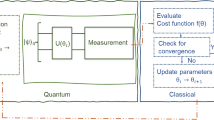
Recent progress in quantum computing hardware has encouraged the development of quantum heuristic algorithms that can be simulated on near-term devices (Mohseni et al. 2017; Preskill 2018). One important heuristic approach involves a class of algorithms known as variational quantum algorithms. Variational quantum algorithms are “hybrid” quantum-classical algorithms in which a quantum circuit is run multiple times with variable parameters, and a classical outer loop is used to optimize those parameters (see Fig. 2). The Variational Quantum Eigensolver (VQE) (Peruzzo et al. 2014), quantum approximate optimization algorithm and its generalization Quantum Alternating Operator Ansatz (QAOA) (Farhi 2014; Hadfield et al. 2019) are examples of algorithms that can be implemented in this variational setting. These algorithms are effective in optimization (Guerreschi and Matsuura 2019; Rieffel et al. 2019; Niu et al. 2019) and simulation of quantum systems (Hempel et al. 2018; O’Malley et al. 2016; Rubin 2016). The classical subroutine is an optimization of parameters and is an important part of the algorithm both in terms of the quality of solution found and the speed at which it is found.

Fig. 2

A single time-step of a general variational quantum algorithm, where the classical processing unit (CPU—blue) outputs parameters ϕ dependent on some evaluation, in this case the expectation value 〈H〉 by the quantum processing unit (QPU—green). The quantum subroutine is encoded by a quantum circuit U(ϕ) (Fig. 3) parameterized by ϕ, and it is responsible for generating a state |ψ(ϕ)〉. This state is measured in order to extract relevant information (e.g., expectation value of a Hamiltonian). The classical subroutine suggests parameters ϕ based on the values provided by a quantum computer, and sends new parameters back to the quantum device. This process is repeated until the given goal is met, i.e., convergence to a problem solution (e.g., the ground state of a Hamiltonian)

Techniques for the classical outer loop optimization are well-studied (Peruzzo et al. 2014; Wecker et al. 2016; 2015; Guerreschi and Smelyanskiy 2017; Guerreschi and Matsuura 2019; Nannicini 2019) and several standard optimization schemes can be used. However, optimization in this context is difficult, due to technological restrictions (e.g., hardware noise), and to theoretical limitations such as the stochastic nature of quantum measurements (Knill et al. 2007) or the barren plateaus problem (McClean et al. 2018). Therefore, it is imperative to improve not only the quantum part of the hybrid algorithms, but also to provide a better and more robust framework for classical optimization. Here, we focus on the classical optimization subroutine and suggest meta-learning as a viable tool for parameter setting in quantum circuits. Moreover, we demonstrate that these methods, in general, are resistant to noisy data, concluding that these methods may be especially useful for algorithms implemented with noisy quantum hardware.

We compare the performance of optimizers for parameter setting in quantum heuristics, specifically variational quantum algorithms. The optimization methods we compare are L-BFGS-B (Byrd et al. 1995), Nelder-Mead (Nelder and Mead 1965), evolutionary strategies (Salimans et al. 2017) and a Long Short Term Memory (LSTM) recurrent neural network model (Hochreiter and Schmidhuber 1997)—the meta-learner. While in the production of this work, we noticed similar research (Verdon et al. 2019) exploring the potential of gradient-free meta-learning techniques as initializers. Here, we use a gradient-based version of the meta-learner as a standalone optimizer (not an initializer), and a larger set of other optimizers. Though we include a diverse range of techniques, clearly, there are other optimizers that might be used, for example SPSA (James et al. 1992; Spall et al. 2006; Moll et al. 2018; Kandala et al. 2017); however, our analysis focuses on those described above.

This comparison is performed in three different simulation environments: Wave Function, Sampling, and Noisy. The Noisy environment is an exact wave function simulation with parameter setting noise. The simulation environments are defined in detail in Section 3.

The first heuristic we explore for this comparison is QAOA (Farhi 2014; Hadfield et al. 2019) for the MAX-2-SAT and Graph Bisection constraint satisfaction problems (Papadimitriou 1994). Second, VQE (Peruzzo et al. 2014) is used for estimating the ground state of Free Fermions models a special subclass of Fermi-Hubbard models (1963). We show that, broadly speaking, the meta-learner performs as well or better than the other optimizers, measured by a “gain” metric defined in Section 4. Most notably, the meta-learner is observed to be more robust to noise. This is highlighted through showing the number of near-optimal solutions found in each problem by the different optimizers over all simulation environments. The takeaway of this paper is that these methods show promise, specifically the features of robustness and adaptability to hardware, and how meta-learning might be applied to noisy near-term devices.

In Section 2, we describe the background of the heuristics and optimizers. Then, in Section 3, we outline the general setup including problems, the optimizers, and the simulation environments. Section 4 details the methods, including the metrics, optimizer configuration, and meta-learner training. In Section 5, we discuss our results. Finally, in Section 6, the work is summarized and we suggest paths forward.

2 Background

2.1 Quantum alternating operator ansatz

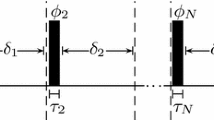
The quantum approximate optimization algorithm (Farhi 2014) and its generalization the quantum alternating operator ansatz (Hadfield et al. 2019) (QAOA) form families of parameterized quantum circuits for generating solutions to combinatorial optimization problems. After initializing a suitable quantum state, a QAOA circuit consists of a fixed number p blocks (see Fig. 3), where each block is composed of a phase unitary generated from the cost function we seek to optimize, followed by a mixing unitary. The phase unitary typically yields a sequence of multiqubit Pauli-Z rotations each with phase angle γ. In the original proposal of Farhi et al. (Farhi 2014), the mixing unitary is a Pauli-X rotation of angle β on each qubit. However, extending the protocol to more general encodings and problem constraints naturally leads to a variety of more sophisticated families of mixing operators (Hadfield et al. 2017; Hadfield et al. 2019). At the end of the circuit a measurement is performed in the computational (Pauli-Z) basis to return a candidate problem solution.

Fig. 3

General parameterized quantum circuit, with arbitrary unitaries U_j(ϕ_j), input state |0〉, and classical register c, where ϕ = [ϕ₁,ϕ₂,...,ϕ_n] are the parameters of the circuit. Though the unitaries do not necessarily act on all qubits, we have arranged them here in “blocks,” similar to the general architectures of QAOA and VQE, where a block of operations may be repeated many times in a circuit, with different parameters. In the case of VQE, a block might be a series of single-qubit rotations or a set of entangling gates (such as CNOT), and for QAOA, a block might be a phase unitary encoding the cost function or a mixing unitary for searching the solution space

An important open research area is to develop strategies for determining good sets of algorithm parameters (i.e., the γ and β values for each block) which yield good (approximate or exact) solutions with nonnegligible probability. These parameters may be determined a priori through analysis, or searched for as part of a classical-quantum hybrid algorithm using a variational or other approach. Prior work on parameter setting in QAOA includes analytic solutions for special cases (Wang et al. 2018), comparison of analytical and finite difference methods (Guerreschi and Smelyanskiy 2017), a method for learning a model for a good schedule (Wecker et al. 2016), and comparison of standard approaches over problem classes (Nannicini 2019).

We evaluate parameter setting strategies for QAOA for MAX-2-SAT and Graph Bisection, both NP-hard combinatorial optimization problems (Papadimitriou 1994; Ausiello et al. 2012). We use standard (Farhi 2014) and generalized (Hadfield et al. 2019) QAOA methods, respectively. The latter problem mapping is of particular interest as it utilizes an advanced family of QAOA mixing operators from Hadfield et al. (2019) that has recently been demonstrated to give advantages over the standard mixer (Wang et al. 2019).

2.2 Variational quantum eigensolver

The VQE (Peruzzo et al. 2014) is a hybrid optimization scheme built on the variational principle. It aims to estimate the ground-state energy of a problem Hamiltonian through iterative improvements of a trial wave function. The trial wave function is prepared as a quantum state using a parameterized quantum circuit, and the expectation value of the Hamiltonian with respect to this state is measured. This energy value is then passed to a classical device, which uses optimization techniques (SPSA, BFGS, etc.) to update the parameters. The process is repeated for a fixed number of iterations, or until a given accuracy achieved.

The initial demonstration of VQE used Nelder-Mead, a standard derivative-free approach, for parameter setting after observing that gradient descent methods did not converge (Peruzzo et al. 2014). Since then, examples in the literature include the use of Simultaneous Perturbation Stochastic Approximation (SPSA) in Moll et al. (2018), where the authors argue simultaneous perturbation methods might be particularly useful for fermionic problems, but classical problems (such as MaxCut) may favor more standard techniques (i.e., gradient descent). Other routines used include COBLYA, L-BFGS-B, Nelder-Mead, and Powell in Romero et al. (2018). Finally, in Moseley et al. (2018), the authors explore the use of Bayesian optimization for parameter setting in VQE.

2.3 Meta-learning

Meta-learning is the study of how to design machine learning models to learn fast, well, and with few training examples (Bengio et al. 1990). One specific case is a model, referred to here as a meta-learner (Ravi and Larochelle 2016), which learns how to optimize other models. A model is a parameterized function. Meta-learners are not limited to training machine learning models; they can be trained to optimize general functions (Chen et al. 2017). In the specific area of using models to optimize other models, early research explored Guided Policy Search (Li and Malik 2016), which has been superceded by LSTMs (Andrychowicz et al. 2016; Chen et al. 2017; Bello et al. 2017; Wichrowska et al. 2017). An LSTM is a recurrent neural network, developed to mitigate vanishing or exploding gradients prominent in other recurrent neural network architectures (Bengio et al. 1994; Hochreiter 1998). It consists of a cell state, a hidden state, and gates, and all three together are called an LSTM cell. At each time-step, changes are made to the cell state dependent on the hidden state, the gates (which are models), and the data input to the LSTM cell. The hidden state is changed dependent on the gates and the input. The cell state and hidden state are then passed to the LSTM cell at the next time-step. A full treatment of an LSTM is given in reference Hochreiter and Schmidhuber (1997). An LSTM is good for learning long-term (over many time-steps) dependencies, like those in optimization.

Meta-learners have been used for fast general optimization of models with few training examples (Ravi and Larochelle 2016): Given random initial parameters we seek to achieve a fast convergence to “good” (defined by some metric) general parameters. This same problem feature appears for QAOA, where good parameters may follow some common distribution across problems (Wecker et al. 2016). A meta-learner could be used to find general good parameters, and fine-tuning left to some other optimizer (Verdon et al. 2017), though this approach was not explored here (Fig. 4).

Fig. 4

Effective single-qubit rotation gate fidelity plotted as a function of the noise on input parameters. Parameters are sampled from a normal distribution with standard deviation σ and centered on the target input value

3 Setup

3.1 Simulation environments

We compare optimization methods in “Wave Function,” “Sampling,” and “Noisy” simulation environments. The Wave Function case is an exact wave function simulation. For Sampling, the simulation emulates sampling from a hardware-implemented quantum circuit, where the variance of the expectation value evaluations is dependent on the number of samples taken from the device. In these experiments, we set the number of shots (samples from the device) to 1024.

Lastly, in the Noisy case, we have modelled only parameter setting noise in an exact wave function simulation, which is a coherent imperfection resulting in a pure state.¹ We assume exact, up to numerical precision, computation of the expectation value (via some theoretical quantum computer which can compute the expectation value of a Hamiltonian given a state up to arbitrary precision). Then, for each single-qubit rotation gate, we added normally distributed, standard deviation σ = 0.1, noise to the parameters at each optimization step. In order to determine σ, we evaluate the relationship between the fidelity of an arbitrary rotation (composed of three single-qubit Pauli rotation gates R_Z(α)R_Y(β)R_Z(γ)), around the Bloch sphere and the noise σ (see Fig. 4). Assuming industry standard single-qubit gate rotations of 99% (Krantz et al. 2019) a value of σ = 0.1 is approximated resulting in the noise in rotations illustrated in Fig. 5 . All simulations were performed with Rigetti Forest (2019) simulators and circuit simulations performed on an Intel(R) Core(TM) i7-8750H CPU with 6 cores.

Fig. 5

Rotation of initial state |0〉 (green) by rotation operator R_Z(π/4)R_Y(π/3)R_Z(0) to new state (orange arrow, red point). When noise of σ = 0.1 is applied to the parameter setting we see a distribution of final states (blue) over 100 trials

3.2 Optimizers

3.2.1 Local optimizers

Nelder-Mead and L-BFGS-B are gradient-free and gradient-based approaches, respectively, which are standard local optimizers (Guerreschi and Smelyanskiy 2017; Wecker et al. 2016; 2015; Nannicini 2019). Local optimizers have a notion of location in the solution space. They search for candidate solutions from this location. They are usually fast and are susceptible to finding local minima. L-BFGS-B is a local optimizer and has access to the gradients. Out of all optimizers chosen it is the closest to the meta-learner in terms of information available to the optimizer and computational burden (i.e., the cost of computing the gradients). Nelder-Mead was chosen as it appears throughout the literature (Peruzzo et al. 2014; Guerreschi and Smelyanskiy 2017; Verdon et al. 2017; Romero et al. 2018) and provides a widely recognized benchmark.

3.2.2 Evolutionary strategies

Evolutionary strategies are a class of global black-box optimization techniques: A population of candidate solutions (individuals) are maintained, which are evaluated based on some cost function. Genetic algorithms and evolutionary strategies have been used for decades. More recent work has shown these techniques to be competitive in problems of reinforcement learning (Vidnerová and Neruda 2017; Salimans et al. 2017).

All implementations of evolutionary strategies are population-based optimizers. In the initial iteration, the process amounts to a random search. In each iteration, solutions with lower costs are more likely to be selected as parents (though all solutions have a nonzero probability of selection). Different methods for selecting parents exist, but we used binary tournament selection, in which two pairs of individuals are selected, and the individual with the lowest cost from each pair is chosen to be a parent.

In more precise terms, parents are the candidate solutions selected to participate in crossover. Crossover takes two parent solutions and produces two children solutions by randomly exchanging the bitstring defining the first parent with the second. Each child replaces its parent in the population of candidate solutions. The process is repeated, so costs for each child are evaluated, and these children are used as parents for the next iteration (Beasley et al. 1993). In our case, the bitstring is divided into n subsections, where n is the number of parameters passed to the quantum heuristic. Each subsection is converted to an integer using Gray encoding and then interpolated into a real value in the range [−π/2,π/2]. Gray codes are used as they avoid the Hamming walls found in more standard binary encodings (Charbonneau 2002).

It is the bitstrings that are operated on by the genetic algorithm. When two individuals are selected to reproduce, a random crossover point, b_c is selected with probability P_c. Two children are generated, one with bits left of b_c from the first parent and bits to the right of b_c originating from the second parent. The other child is given the opposite arrangement. Intuitively, if b_c is in the region of the bitstring allocated to parameter ϕ_k, the first child will have angles identical to the first parent before ϕ_k and angles identical to the second parent after ϕ_k. Again, the second child has the opposite arrangement. The effect on parameter ϕ_k is more difficult to describe. Finally, after crossover is complete, each bit in each child’s bitstring (chromosome) is then flipped (mutated) with probability P_m. Mutation is useful for letting the algorithm explore candidate solutions that may not be accessible through crossover alone.

Evolutionary strategies are highly parallelizable, robust, and relatively inexpensive (Salimans et al. 2017) making them a good candidate for the optimization of quantum heuristics.

3.2.3 Meta-learning on quantum circuits

The meta-learner used in this work is an LSTM, shown unrolled in time in Fig. 1. Unrolling is the process of iteratively updating the inputs, x, cell state, and hidden state, referred to together as s, of the LSTM. Inputs to the model were the gradients of the cost function w.r.t. the parameters, preprocessed by methods outlined in the original work (Andrychowicz et al. 2016). At each time-step, they are

$$ x^{t} = \begin{cases} \left( \frac{\log({\left|\nabla \langle H \rangle^{t}\right|})}{r},\text{sign}(\nabla \langle H \rangle^{t})\right) & \text{if}\ \left|{\nabla \langle H \rangle^{t}}\right|\geq e^{-r} \\ (-1,\exp(r)\nabla \langle H \rangle^{t}), & \text{otherwise} \end{cases} $$

(1)

where r is a scaling parameter, here set to 10, following standard practice (Andrychowicz et al. 2016; Ravi and Larochelle 2016). The terms ∇〈H〉^t are the gradients of the expectation value of the Hamiltonian at time-step t, with respect to the parameters ϕ^t. This preprocessing handles potentially exponentially large gradient values while maintaining sign information. Explicitly, the meta-learner used here is a local optimizer. At some point ϕ^t in the parameter space, where t is the time-step of the optimization, the gradients x^t are computed and passed to the LSTM as input. The LSTM outputs an update Δϕ^t, and the new point in the parameter space is given by ϕ^t+ 1 = ϕ^t + Δϕ^t. It is possible to use these models for derivative-free optimization (Chen et al. 2017), however, given that the gradient evaluations can be efficiently performed on a quantum computer, scaling linearly with the number of gates, and that the optimizers usually perform better with access to gradients, we use architectures here that exploit this information. In reference McClean et al. (2018), the authors show that the gradients of the cost function of parameterized quantum circuits may be exponentially small as a function of the number of qubits, the result of a phenomena called the concentration of quantum observables. In cases where this concentration is an issue, there may be strategies to mitigate this effect (Grant et al. 2019), though it is not an issue in the small problem sizes used here.

Though only one model (a set of weights and biases) defines the meta-learner, it was applied in a “coordinatewise” way: For each parameter a different cell state and hidden state of the LSTM are maintained throughout the optimization. Notably, this means that the size of the meta-learning model is only indirectly dependent on the number of parameters in the problem. We used a gradient-based approach, exploiting the parameter-shift rule (Schuld et al. 2019) for computing the gradients of the loss function with respect to the parameters. These were used at both training and test time.

All model training requires some loss function. We chose the summed losses,

$$ \mathcal{L}(\omega) = \mathbb{E}_{f} \left[ \sum\limits_{t=0}^{T} \omega_{t} f(\phi_{t}) \right], $$

(2)

where $\mathbb {E}_{f}$ is the expectation over all training instances f and T is a time-horizon (the number of steps the LSTM is unrolled before losses from the time-steps t < T are accumulated and backpropagated, and the model parameters updated). The hyperparameters ω_t are included, though are set to ω_t = 1 for all t in these training runs. This can be adjusted to weigh finding optimal solutions later in the optimization more favorably, a practice for balancing exploitation and exploration. In situations where exploration is more important, other loss functions can be used, such as the expected improvement or observed improvement (Chen et al. 2017). However, in this instance, we chose a loss function to rapidly converge, meaning fewer calls to the QPU. This has the effect of converging to local minima in some cases, though we found that this loss function performed better than the other gradient-based optimizer (L-BFGS-B) for these problems.

3.3 Problems

3.3.1 Free Fermions model

Hubbard Hamiltonians have a simple form, as follows:

$$ \begin{array}{@{}rcl@{}} H = &- t {\sum}_{\langle i,j \rangle}{\sum}_{\sigma=\{\uparrow,\downarrow\}}(a^{\dagger}_{i, \sigma} a_{j, \sigma} + a^{\dagger}_{j, \sigma} a_{i, \sigma}) \\ &+ U {\sum}_{i} a^{\dagger}_{i, \uparrow} a_{i, \uparrow} a^{\dagger}_{i, \downarrow} a_{i, \downarrow}- \mu {\sum}_{i} {\sum}_{\sigma=\{\uparrow,\downarrow\}} a^{\dagger}_{i, \sigma} a_{i, \sigma}, \end{array} $$

(3)

where $a_{i,\sigma }^{\dag }, a_{i,\sigma }$ are creation and annihilation operators, respectively, of a particle at site i with spin σ. In this model there is a hopping term t, a many body interaction term U and an onsite chemical potential term μ. This model gained importance as being a possible candidate Hamiltonian to describe superconductivity in cuprate materials. However, recent numerical studies have shown that there are some significant differences between the model and what is seen in experiments, such as the periodicity of charged stripes that the model supports (LeBlanc et al. 2015; Schulz 1993; Huang et al. 2017). However, the model is quite interesting itself, with many different phases of interest. The model is also quite difficult to solve, especially when going to large lattice sizes and large values of U/t. This has led to many studies and much method development on classical computers, and is still widely researched today.

For VQE, we look for the ground state of the simplified spinless three-site Free Fermions model with unequal coupling strengths t_ij ∈ [− 2,2] and U = μ = 0, Fig. 6. The Hamiltonian of this model can be mapped through the Jordan-Wigner transformation (Jordan and Wigner 1928) to the qubit Hamiltonian

$$ \begin{array}{@{}rcl@{}} H_{FH} &=& \frac{1}{2}\left( t_{12}\hat{X}_{1}\hat{X}_{2} + t_{12}\hat{Y}_{1}\hat{Y}_{2} +t_{23} \hat{X}_{2}\hat{X}_{3}\right. \\&&\left.+ t_{23}\hat{Y}_{2} \hat{Y}_{3} + t_{13}\hat{X}_{1}\hat{Z}_{2}\hat{X}_{3} + t_{13}\hat{Y}_{1}\hat{Z}_{2} \hat{Y}_{3}\right) \end{array} $$

(4)

where $\hat {X}$, $\hat {Y}$, and $\hat {Z}$ are the Pauli-X, Pauli-Y, and Pauli-Z matrices, respectively. Based on the results of Woitzik (2018, 2020), we use a circuit composed of 3 blocks. Each block consists of three single-qubit rotations R_Z(α)R_Y(β)R_Z(γ) applied to all qubits, followed by entangling CNOT gates acting on qubits (1,2) and (2,3), where the first entry is the control qubit and the second is the target.

Fig. 6

Sketch of a spinless three-qubit Free Fermions model that is used for the VQE optimization. Coupling strengths are not necessarily equal and take values from [− 2,2]

3.3.2 MAX-2-SAT

Given a Boolean formula on n variables in conjunctive normal form (i.e., the AND of a number of disjunctive two-variable OR clauses), MAX-SAT is the NP-hard problem of determining the maximum number of clauses which may be simultaneously satisfied. The best classical efficient algorithm known achieves only a constant factor approximation in the worst case, as deciding whether a solution exists that obtains better than a particular constant factor is NP-complete (Papadimitriou 1994). For MAX-2-SAT, where each clause consists of two literals, the number of satisfied clauses can be expressed as

$$ C = \sum\limits_{(i,j)\in E} \Tilde{x}_{i} \lor \Tilde{x}_{j} $$

(5)

where x~_i in each clause represents the binary variable x_i or its negation, and E is the set of clauses. We use an n-qubit problem encoding where the j th qubit logical states |0〉_j,|1〉_j encode the possible values of each x_j. Transforming to Ising spin variables (Hadfield 2018) and substituting with Pauli-Z matrices lead to the cost Hamiltonian

$$ \widehat{C} = {\sum}_{(i,j)\in E} \frac{1}{4} (1 \pm \hat{Z}^{(i)})(1\pm\hat{Z}^{(j)}) $$

(6)

which is minimized when the number of satisfied clauses is maximized. The sign factors + 1 or − 1 in $\widehat {C}$ correspond to whether each clause contains x_i or its negation, respectively. Note that C and $\widehat {C}$ are not equivalent; C gives a maximization problem, while $\widehat {C}$ gives a minimization problem, with the same set of solutions.

For our QAOA implementation of MAX-2-SAT we use the original (Farhi 2014) initial state $|{s}\rangle =\tfrac 1{\sqrt {2^{n}}}{\sum }_{x} |x\rangle$, phase operator $U_{P}(\widehat {C},\gamma )=\exp (-i\gamma \widehat {C})$, and mixing operator $U_{M}(\beta )=\exp (-i\beta {\sum }_{j=1}^{n} \hat {X}^{(j)})$. The instances we consider below have n = 8 qubits, 8 clauses, and QAOA circuit depth p = 3. We further explore instances with n = 12 and p = 5 (Fig. 9).

3.3.3 Graph Bisection

Given a graph with an even number of nodes, the Graph Bisection problem is to partition the nodes into two sets of equal size such that the number of edges across the two sets is minimized. The best classical efficient algorithm known for this problem provably yields only a $\log$-factor worst-case approximation ratio (Krauthgamer and Feige 2006). Both this problem and its maximization variant are NP-hard (Papadimitriou 1994).

For an n-node graph with edge set E we encode the possible node partitions with n binary variables, where x_j encodes the placement of the j th vertex. In this encoding, from the problem constraints the set of feasible solutions is encoded by strings x of Hamming weight n/2. The cost function to minimize can be expressed as

$$ C = \sum\limits_{(i,j) \in E} \mathrm{XOR(x_{i}, x_{j})} $$

(7)

under the condition ${\sum }^{n}_{j=1} x_{j} = n/2$. Transforming again to Ising variables gives the cost Hamiltonian

$$ \widehat{C} = \frac{1}{2} \sum\limits_{(i,j) \in E} (1 - \hat{Z}^{(i)}\hat{Z}^{(j)}). $$

(8)

A mapping to QAOA for this problem was given in (Hadfield et al. 2019, App. A.3.2) from which we derive our construction. We again encode possible partitions x with the n-qubit computational basis states |x〉. For each problem instance we uniformly at random select a string y of Hamming weight n/2 and use the feasible initial state |y〉. The phase operator $U_{P}(\widehat {C},\gamma )=\exp (-i\gamma \widehat {C})$ is constructed in the usual way from the cost Hamiltonian. For the mixing operator we employ a special case of the XY -mixer proposed in Hadfield et al. (2019). This class of mixers affects state transitions only between states of the same Hamming weight, which will importantly restrict the quantum state evolution to the feasible subspace. For each node $j=1,\dots ,n$, we define the XY partial mixer

$$U_{j}(\beta)=\exp\left( -i\beta \left( \hat{X}^{(j)} \hat{X}^{(j+1)}+ \hat{Y}^{(j)} \hat{Y}^{(j+1)} \right) \right)$$

with σ^(n+ 1) := σ⁽¹⁾. We define the overall mixer to be the ordered product $U_{M}(\beta )= U_{n}(\beta ) \dots U_{2}(\beta )U_{1}(\beta )$. Observe that as each partial mixer preserves feasibility, so does U_M(β), and so QAOA will only output feasible solution samples. We consider problem instances with n = 8 qubits, 8 edges, and QAOA circuit depth p = 3.

4 Methods

4.1 Metrics

Here, we outline two metrics used to evaluate and compare the optimizers. The first metric used is the gain, $\mathcal {G}$, to the minimum,

$$ \mathcal{G} = \mathbb{E}_{f} \left[ \frac{f_{F}-f_{I}}{f_{\min}-f_{I}}\right] $$

(9)

where $\mathbb {E}_{f}$ is the expectation value over all instances f, f_F is the converged cost of the optimizer, f_I is the initial cost (determined by the initial parameters) and $f_{\min \limits }$ is the ground-state energy. $f_{\min \limits }$ was determined by evaluating all possible solutions in the cases of MAX-2-SAT and Graph Bisection, and by exact diagonalization of the Hamiltonian for finding the ground state of the Free Fermions model. This number is the expectation over instances f of the “gain” to the global minimum from the initialized parameters. In the case of local optimizers (meta-learner, L-BFGS-B, Nelder-Mead) we initialized to the same parameters. The metric outlines the average progress to the global minimum from an initialization. Secondly, the quality of the final solution was also evaluated by a distance to global minima metric, $\mathcal {D}$,

$$ \mathcal{D} = \frac{|{f_{\min} - f_{F}}|}{|{f_{\min}-f_{\max}}|} * 100 $$

(10)

where $f_{\max \limits }$ is the maximum possible energy. This metric gives a sense of the closeness to the global minima, as a percentage of the extent.

4.2 Configuring optimizers

We evaluated the optimizers on 20 problems from 5 random initializations each, to increase the probability of reaching the ground state by all optimizers. The initializations were kept the same between the local optimizers (L-BFGF-B, Nelder-Mead, and meta-learner).

Evolutionary strategies used 5 different random initializations for each problem. L-BFGS-B and Nelder-Mead were implemented using Scipy (Jones et al. 2001), where the gradients for L-BFGS-B were computed by analytic means and quantum circuit simulation. We implemented and configured the evolutionary strategies methods in-house. For all tests, a small population size of 20 was used to limit the number of calls to the simulator (sizes on the order of 100 are typical and may improve performance). Both MAX-2-SAT and Graph Bisection problems with QAOA used m = 60 bits to represent parameters. VQE simulations had more parameters to optimize, so m = 297 bits were used for these problems. All tests used a probability of crossover of P_c = 0.9, and a probability of mutation of P_m = 0.01. These parameters were selected by a sparse grid search.

On these small problems, the SciPy default hyperparameters of standard optimizers L-BFGS-B and Nelder-Mead were found to give generally good performance. Any tuning did not contribute meaningfully to the performance, though we expect at larger problem sizes more tuning will be required as the optimization landscape increases in ruggedness. We found these hyperparameters generalized well.

4.3 Training the meta-learner

For the MAX-2-SAT and Graph Bisection problems the model was trained on just 200 problems, whereas in the case of optimizing Free Fermions models the meta-learning model quickly converged and training was truncated at 100 problems. The loss function is given in Eq. (2), where values ω_t = 1∀t are used. For the preprocessing of the gradients, the hyperparameter r in Eq. (1) is set to 10. For all training an Adam optimizer (Kingma and Ba 2014) was used with a learning rate of 0.003, β₀ = 0.9, β₁ = 0.999, 𝜖 = 1.0^− 8 and zero weight decay. These training schedules were consistent across simulation type (Wave Function, Sampling, and Noisy). We included a “curriculum” method, implemented in Chen et al. (2017), whereby the time-horizon of the meta-learner is extended slowly throughout the training cycle. This was started at 3 iterations and capped at 10, at the end of the training cycle. Optimization was terminated if it converged, under standard convergence criteria. Overall, 9 models were trained (3 simulation environments × 3 problem classes).

5 Discussion and results

Figure 7 shows the performance of the optimizers measured by the gain metric in the three simulation environments. The gain metric converges in the same sense as an optimizer converging on one problem instance, this is as expected given it is an average over many problem instances. A value close to 1 is desirable, indicating the ability of an optimizer to progress to the global minima from a starting point. Figure 8 shows the total number of near-optimal solutions found by each optimizer. We define near-optimal as finding a solution within 2% of the global optima computed by Eq. (10). The closest comparable competitor to the meta-learner in these plots is L-BFGS-B, given both optimizers had access to the gradients. This is reflected in their performance, particularly in Fig. 7.

Fig. 7

Left to right columns: Free Fermions models, Graph Bisection and MAX-2-SAT problems. Top to bottom rows: Wave Function, Sampling, and Noisy simulations, defined in Section 3. Optimizers: Evolutionary strategies (blue), Nelder-Mead (green), L-BFGS-B (red), meta-learner (purple). x-axis: Shared within a column, QPU iteration is number of calls to the QPU. y-axis: Shared within a row, $\mathcal {G}$, the gain, is the value computed by Eq. (9) and represents the average progress toward the minimum from the initial evaluation of 〈H〉. L-BFGS-B and the meta-learner have access to the gradient and make numerous calls to auxiliary quantum circuits (simulated in the same environment as the expectation value evaluation circuits) to compute the gradients. The number of calls to evaluate gradients of parameters is N_g = 2M, where M is the number of parameterized gates in the circuit. The QPU iteration variable captures this, i.e., is the total number of calls to a QPU for an optimizer. Error bars are the standard error on the mean, $\sigma _{f} /\sqrt {n}$ where n is the number of examples and σ_f the standard deviation of the performance of the optimizers. Note that negative values of $\mathcal {G}$ are observed, corresponding to on average performing worse than the initial evaluation

Fig. 8

Bubble and bar plots of the frequency of near-optimal solutions. The size of each bubble is dependent on the total number of times an optimizer came within 2% of the global optima across all problem instances (computed by Eq. (10)); the largest bubble is L-BFGS-B in the Wave Function environment (115). Repetitions are included, i.e., if an optimization ended in a near-optimal solution it was counted, regardless of whether it was found in a previous optimization. We found that if one optimizer performed well in one task, it performed well, relative to the other optimizers, in another (by this metric), so each bubble is not divided into each problem class. The right bar plot represents the summation across optimizers within a simulation type. The bottom bar plot represents the summation within an optimizer across simulation types. (N, Noisy; S, Sampling; W, Wave Function)

It is important to recognize that the comparison in Fig. 7 has limited scope. Optimization is a hard problem: There are many ways to improve application specific performance of different algorithms and metrics to evaluate that performance. For example, the gradient-based optimizers (meta-learner and L-BFGS-B) evaluate auxiliary quantum circuits many times in order to compute the gradients. Recognizing there are always limitations to comparing optimization methods, we draw conservative conclusions.

5.1 General performance

Additionally to meta-learning functioning as an optimizer in variational quantum algorithms, we find competitive performance of this meta-learning algorithm, at small instance size, over a range of problem classes, using the gain metric $\mathcal {G}$ defined in Eq. (9) (see Fig. 7).

The metric $\mathcal {G}$ was used to evaluate and compare the optimizers, though this value can hide significant features. For example, an optimizer that finds good (but not optimal) solutions frequently will perform better than an optimizer that finds bad solutions frequently and optimal solutions infrequently. There are other cases that the reader may have in mind. This particular example is addressed in Fig. 8. The number of times the optimizer comes within 2% of the ground state (across all problems), as calculated by Eq. (10), is counted. We observe an expected reduction in performance as noise is increased; this is discussed further in the subsection below.

5.2 Noise

As expected, there is a reduction in performance for all optimizers as “noise” increases: Performance is worse in Sampling than in Wave Function and is worse in Noisy than in Sampling. What is notable is that the meta-learner is more resilient to this increase in noise than other methods. For example, in Free Fermions model problems, L-BFGS-B performance reduces by 0.35 whereas the meta-learner only reduces by 0.2, from around the same starting point (Free Fermions models column, Fig. 7). This pattern is repeated across problem classes, to varying degrees. We believe this is a promising sign that meta-learning will be especially useful in noisy near-term quantum heuristics implemented on hardware. In the case of simulation, we believe this resistance can be explained by the optimizer knowing how to find generally good parameters, having learned from noisy systems already. This needs to be distinguished from another potential benefit of these algorithms, where the models learn how to optimize in the presence of hardware-specific traits. In the latter case, the meta-learner may learn a model that accounts for hardware-specific noise. Further, in Fig. 8, we see a reduction in performance, measured by the total number of near-optimal solutions, for all optimizers. However, this effect is least apparent in the global optimizer (evolutionary strategies) and the meta-learner. Additionally, the meta-learner finds significantly more near-optimal solutions (80) for Noisy simulation than the next best optimizer (evolutionary strategies—17). These are promising results on the potential use cases of these optimizers in hybrid algorithms implemented on noisy quantum hardware.

5.3 Evolutionary strategies

Evolutionary strategies exhibit an oscillatory behavior when gain to global optima versus function call is plotted, the first generation corresponds to a random search, then the fittest individual (i.e., best solution) found in the previous generation is evaluated first in the next generation. Hence, we observe a spike in performance every 21 evaluations (the size of the population plus the fittest individual). As such we only plot every 21 iterations, giving a smooth curve. We reiterate here that given other performance/time metrics, including for example if optimizers are parallelized, other analysis including different comparison metrics will be needed to determine the respective use cases of meta-learners vs evolutionary strategies. Indeed, while Fig. 7 suggests that evolutionary strategies perform well for particularly hard problems (Graph Bisection, Noisy), preliminary results in Fig. 8 indicate that the meta-learner tends to outperform evolutionary strategies when searching for a near-optimal solution.

5.4 Problems and algorithms

The Free Fermions models were the simplest to solve (they are small problems confined to parameter values [− 2,2]). This is reflected in the performance of the gradient-based optimizers. Evolutionary strategies underperform. This is most likely a result of the size of the parameter space: Though the problem size (in terms of the number of variables) is smaller, there are significantly more parameters in this implementations we have considered of VQE (24) than QAOA (6).

Of the two classical optimization problems we consider, the Graph Bisection problem is harder than MAX-2-SAT, in the sense of worse classical approximability. While MAX-2-SAT can be approximated up to a constant factor, the best classical efficient algorithms known for Graph Bisection perform worse with increasing problem size (Papadimitriou 1994; Ausiello et al. 2012). This contrast appears in the performance of all optimizers: In general, every optimizer performs worse in Graph Bisection than in MAX-2-SAT by the gain metric.

5.5 Scaling

Figure 9 provides evidence that the meta-learner model may be generalized. A model trained on smaller QAOA problem instances (n = 8, p = 3) is extended to larger problems (n = 12, p = 5). We chose L-BFGS-B for this comparison as it is the closest comparable competitor in terms of information available and performance. The meta-learner is competitive with or even better than L-BFGS-B, as evaluated by the Gain metric, in the initial optimization though appears to have worse asymptotic behavior. This may be because the meta-learner encourages large steps in the initial optimization, where the margin for error on the step is larger than when further in the minima. At a high level, the initial and final steps can be thought of as regions with distinct properties, it is unsurprising the meta-learner performs differently in each region.

Fig. 9

Gain to minimum of L-BFGS-B and meta-learner optimizers in a Wave Function environment applied to QAOA problems Graph Bisection and MAX-2-SAT. These problems are 12 variable problems with QAOA hyperparameter p = 5. This is contrasted with the problems explored in Fig. 7, which are 8 qubit problems with p = 3. The meta-learner is the model trained on this previous problem set. QPU iteration is the number of calls made to a quantum circuit. In this case, each optimization step is N_g = 2M = 20, where M = 10

This small demonstration is not extensive enough to make any serious conclusions regarding the generalization of the meta-learner for optimizing quantum circuits, though it indicates similar findings in the field that these models can extend to larger system sizes (Andrychowicz et al. 2016).

6 Conclusion

In this work we compared the performance of a range of optimizers (L-BFGS-B, Nelder-Mead, evolutionary strategies, and a meta-learner) across problem classes (MAX-2-SAT, Graph Bisection, and Free Fermions Models) of quantum heuristics (QAOA and VQE) in three simulation environments (Wave Function, Sampling, and Noisy). We highlight three observations. The first is that the meta-learner outperforms L-BFGS-B (the closest comparable competitor) in most cases, when measured by an average percent gain metric $\mathcal {G}$. Secondly, the meta-learner performs better than all optimizers in the Noisy environment, measured by a total number of near-optimal solutions metric $\mathcal {D}$. Finally, the meta-learner generalizes to slightly larger systems for QAOA problems, which reflects other findings in the field. We conclude that these are promising results for the future applications of these tools to optimizing quantum heuristics, because these tools need to be robust to noise and we are often looking for near-optimal solutions.

During the production of this work, a related preprint (Verdon et al. 2019) was posted online. In that preprint, the authors consider only gradient-free implementations of meta-learners. Their training set is orders of magnitude larger, as the meta-learner is learning to optimize from more limited information. However, taking into account the QPU calls required to compute the gradients, N_g = 2M where M is the number of parameterized gates, their gradient-free implementation required significantly fewer queries to a QPU during optimization. As both architectures have different advantages and trade-offs between resource overhead, training time, and performance should be considered for a given use case. Their conclusions are similar to ours regarding the potential of meta-learning methods, and suggest using them as an initialization strategy.

The meta-learning methods evaluated here are relatively new and are expected to continue to improve in design and performance (Wichrowska et al. 2017). There are several paths forward, we highlight some here. Though there is no investigation into the scaling of meta-learner performance to larger problem sizes, this in part is limited by the inability to simulate large quantum systems quickly, and exacerbated by the further burden of computing the gradients. It is an open question as to how meta-learners will perform with quantum heuristics applied to larger problem sizes. In a closely related vein, these methods will be explored on hardware implementations, for two reasons. The first is that quantum computing will soon be beyond the realm of reasonable simulation times, and testing these algorithms on systems with higher number of variables will have to be done on hardware. The second is that these meta-learners may be able to learn hardware-specific features. For example, in this work the meta-learner is a single model applied to different parameters. This approach is called “coordinatewise.” If instead applied in a “qubitwise” fashion, where different models are trained for parameters corresponding to each qubit in a given hardware graph, there may be local variability in the physics of each qubit that the meta-learner accounts for in its model and optimization.

In terms of further investigations into the specifics of the problems and quantum heuristics considered, we emphasize that our QAOA implementation of Graph Bisection used a different type of mixer and initial state than MAX-2-SAT. An important question to answer is to what degree the differences in performance we observed between MAX-2-SAT and Graph Bisection are due to the change of mixer and initial state, as opposed to the change of problem structure. Additional possible mixer variants and initial states for Graph Bisection are suggested in Hadfield et al. (2019), which we expect to further affect QAOA performance, and hence also affect the performance of our parameter optimization approaches. An important open area of research is to better characterize the relative power of different QAOA mixers and the inherent trade-offs in terms of performance, resource requirements, and the difficulty of finding good algorithm parameters. In this direction, recent work (Wang et al. 2019) has demonstrated that superposition states may perform better than computational basis states as QAOA initial states.

Finally, heuristics play a prominent role in solving real-world problems: They provide practical solutions—not necessarily optimal—for complex problems (where an optimal solution is prohibitively expensive), with reasonable amount of resources (time, memory etc.). Therefore, we see significant potential for applications of quantum heuristics, implemented not only on near-term quantum devices—especially for variational quantum algorithms—but also for hybrid computing in fault-tolerant architectures. Thus, it is imperative to characterize the classical components, such as the meta-learner, that learn properties of quantum devices toward the deployment of effective quantum heuristics for important practical applications.