Abstract
The anisotropy of the swelling of rubber is examined both theoretically and experimentally. The Flory theory is extended to account for anisotropic swelling, allowing the determination of the average molecular weight between cross-links for rubber with swelling anisotropy for the first time. In addition, specimens from five commercial rubbers manufactured using either compression-moulding or sheet-rolling processes are swollen in appropriate organic solvents. Their linear dimensions and mass are carefully recorded before swelling, in the swollen state, and after drying, to obtain three linear swelling ratios which can differ by up to 10% within each specimen. Compression-moulded rubbers are shown to be transversely isotropic after moulding, whereas rolled rubbers exhibit full anisotropy, with different swelling ratios in all three directions. None of the rubbers examined were found to be truly isotropic. The new anisotropic swelling theory is applied to the experimental data to determine the average molecular weight between cross-links, which is determined as up to 0.5% larger than the value obtained using the Flory isotropic swelling theory.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The swelling of cross-linked elastomers in the presence of organic liquids is a well-known phenomenon and is frequently used to provide basic information about the cross-link density of an elastomeric network. Flory [1, 2] and Gee [3] first employed thermodynamics to relate conformational entropy to the deformation of an isotropic cross-linked network in the 1940s. During the interaction between elastomer and solvent, the diffusion of the solvent drives an expansion of the polymer chains and a swelling equilibrium is reached when the swelling due to the solvent and the retractive forces from the stretched chains are balanced [4]. Assuming tetrafunctional cross-links, the widely used Flory-Rehner theory [5] states that
where \(\upsilon_{{{\text{2m}}}}\) is the volume fraction of elastomer in the swollen equilibrium state, \(\chi_{1}\) is the Flory- Huggins polymer–solvent interaction parameter, \(\rho\) is the density of the elastomer, \(\upsilon_{1}\) is the molar volume of the solvent and \(\overline{M}_{{\text{c}}}\) is the molecular weight of chains between cross-links. The volume fraction \(\upsilon_{{{\text{2m}}}}\) is typically obtained by carrying out swelling experiments and measuring the mass m of the material in the swollen (ms) and unswollen (mu) states, as
where \(\rho_{{\text{s}}}\) is the density of the solvent. This approach is regularly used to determine quantitatively the molecular weight of elastomers between cross-links and can be related to a rubbery modulus through the use of network models such as the Gaussian or Phantom Chain approaches [4].
There are a number of simplifying assumptions [6] in this approach, particularly when considering filled rubbers [7]: the presence of the filler is generally ignored and the network of cross-links is assumed uniform and isotropic. Bruck extended Flory’s approach to produce a solution applicable to transversely isotropic rubber [8]. Despite these limitations and Bruck’s extension, Flory’s approach is still widely used for the determination of cross-link density and the molecular weight between cross-links \(\overline{M}_{c}\) with the assumption of isotropic swelling [9, 10].
When rubber is cross-linked and manufactured in any industrial context, the flow processes that shape the component and align chains take place simultaneously with the cross-linking reactions and the polymer chains typically have insufficient time to relax. This leads to rubber products where there is a residual alignment of the chains in one or more preferential directions, depending on the manufacturing process. During sheet rolling processes and injection moulding, the rubber is subjected to a complex set of deformation in the three directions simultaneously, imparting generic anisotropy to the network structure [11, 12]. Compression-moulded rubber sheets are somewhat simpler, manifesting in-plane isotropy [13, 14]
Thus, anisotropy appears to be an intrinsic part of rubber processing despite the lack of a suitable theory to determine cross-link density for anisotropic systems. In this study, we first extend the Flory theory to account for generic anisotropy of swelling and then apply the theory to a series of directional swelling measurements on five different filled elastomers, including compression-moulded and rolled rubber sheets, to examine the nature of the anisotropy, and its influence on the determination of the molecular weight between cross-links.
Theory
Anisotropic swelling
Following Flory’s [5] notation, the total change in Gibbs free energy due to the swelling of a polymer in a solvent is given by \(\Delta F = \Delta F_{{\text{M}}} + \Delta F_{{{\text{el}}}}\) where subscripts \({\text{M}}\) and \({\text{el}}\) refer to the free energy of mixing and the elastic free energy, respectively. The free energy of mixing is unaffected by any initial anisotropy and is given by [5]
where \(k_{{\text{B}}}\) is Boltzmann’s constant; \(T\) is the absolute temperature; \(\upsilon_{1}\) is the volume fraction of solvent; \(\upsilon_{2}\) is the volume fraction of polymer; and \(n_{1}\) is the number of solvent molecules.
The elastic free energy is instead given by
where \(\Delta H_{{{\text{el}}}}\) is the change in enthalpy of the network due to swelling, here assumed to be negligible since the deformation process occurs without a change in the internal free energy of the network; and \(\Delta S_{{{\text{el}}}}\) is the change in entropy associated with the configurational change of the network due to swelling. Using statistical theory, the latter can be expressed as [5]
where \(v_{{\text{e}}}\) is the effective number of chains in the network, and \(\alpha_{x} {, }\alpha_{y} {\text{ and }}\alpha_{z}\) are the linear swelling ratios.
The thermodynamic definition of chemical potential at constant temperature and pressure is
where \(N_{{\text{A}}}\) is Avogadro’s number. The change in chemical potential of the solvent in the swollen network is therefore
where \(\mu_{1}\) is the chemical potential of the solvent in the solution; and \(\mu_{1}^{0}\) is the chemical potential of the pure solvent. For a polymer of infinite molecular weight (i.e. in the absence of chain ends) [5]
Using the chain rule,
and evaluating the first set of partial derivatives gives
Expressing the increment in swollen volume in terms of the addition of \(n_{1}\) solvent molecules of molar volume \(v_{1}\), one can write
and hence, the second set of partial derivatives from equation (9) can be expressed as
Therefore, Eq. 7 can be written as
which, using \(N_{{\text{A}}} k_{{\text{B}}} = R\) and expressing \(v_{{\text{e}}} = N_{{\text{A}}} \tilde{v}_{{\text{e}}}\) as a molar quantity, simplifies to
Noting that \(\upsilon_{1} + \upsilon_{2} = 1\) and setting Eq. 14 to zero (i.e. at the swelling equilibrium, where \(\upsilon_{2} = \upsilon_{{{\text{2m}}}}\)), gives
Expressing \(\tilde{v}_{{\text{e}}} /V_{0}\) in terms of the average molecular weight between cross-links \(\overline{M}_{{\text{c}}}\) in the classical way gives
where \(\rho\) is the density of the unswollen polymer. If required, a correction for unentangled ends from pre-cross-linked chains of finite molecular weight \(M\) can be included, in which case an extra term \(\left( {1 - \frac{{2\overline{M}_{c} }}{M}} \right)\) appears on the right-hand side of Eq. 16.
Therefore, for a generic rubber with anisotropic swelling with principal swelling ratios \(\alpha_{{\text{x}}}^{{}} {, }\alpha_{{\text{y}}}^{{}} {\text{ and }}\alpha_{{\text{z}}}^{{}}\), the average molecular weight between cross-links is given for the first time as
Relationship to existing swelling theories
Equation 17 reduces to the classical Flory-Rehner expression for an isotropic rubber [2] by letting \(\alpha_{x} = \alpha_{y} = \alpha_{z} = \alpha = \upsilon_{2m}^{ - 1/3}\) , giving
Also, by letting \(\alpha_{x} = \alpha_{y} = \alpha \ne \alpha_{z}\) one recovers the expression derived by Bruck for 2-dimensional isotropy [8]
Consequences of the anisotropic swelling theory on \(\overline{M}_{{\text{c}}}\)
As an illustration of the significance of swelling anisotropy on the computation of \(\overline{M}_{{\text{c}}}\), the ratio between the molecular weight between cross-links obtained using a set of anisotropic linear swelling ratios \(\alpha_{x} , \, \alpha_{y} , \, \alpha_{z}\) and the molecular weight between cross-links obtained using the geometric mean swelling ratio\(\alpha = \sqrt[3]{{\alpha _{x} \alpha _{y} \alpha _{z} }}\) is computed for a representative swelling state of \(\alpha = 1.5\), by plotting contours of \(\frac{{\overline{M}_{{\text{c}}}^{{{\text{aniso}}}} }}{{\overline{M}_{{\text{c}}}^{{{\text{Flory}}}} }}\) for a range of \(\alpha_{x}\) and \(\alpha_{y}\) values in Fig. 1 Bruck’s expression corresponds to the solution along the diagonals \(\alpha_{x} = \alpha_{y}\) on Fig. 1.
a Contour plot of the ratio \(\frac{{\overline{M}_{{\text{c}}}^{{{\text{aniso}}}} }}{{\overline{M}_{{\text{c}}}^{{{\text{Flory}}}} }}\) between the molecular weight between cross-links obtained using a set of anisotropic linear swelling ratios \(\alpha_{x} , \, \alpha_{y} , \, \alpha_{z}\) (Eq. (17)) and the molecular weight between cross-links obtained using the geometric mean swelling ratio \(\alpha = \sqrt[3]{{\alpha _{x} \alpha _{y} \alpha _{z} }}\) (i.e., Flory’s isotropic swelling solution, Eq. (18)) as a function of the in-plane linear swelling ratios, for\(\alpha = \sqrt[3]{{\alpha _{x} \alpha _{y} \alpha _{z} }} = 1.5\) for 1 ≤ α ≤ 3.5; b close-up of the region 1.4 ≤ α ≤ 1.6
Materials and methods
Raw materials
Five cross-linked carbon black-filled elastomers were studied. Two of these were obtained as unvulcanised compounds and subsequently compression-moulded into thin sheets: a carbon-black filled and sulphur cross-linked oil extended ethylene-propylene-diene rubber (EPDM1), kindly provided by Dr T. Alshuth from the DIK, Germany, and a commercial grade of carbon-black filled natural rubber (NR) kindly provided by Trelleborg Industrial AVS. Uncured samples were stored in sealed bags in a freezer prior to use.
Three further carbon-black filled elastomers were kindly provided pre-cured by J-Flex Rubber Products, in large 0.5 mm thick sheets produced by commercial rolling processes: a nitrile butadiene rubber compound, NBR, a chloroprene rubber compound, CR, and a further ethylene-propylene-diene rubber compound, EPDM2.
Manufacturing processes
Compression-moulding
EPDM1 and NR were cross-linked into rectangular sheets ~ 0.5 mm in thickness using 150 × 150 mm flash moulds using a Daniels heated press [15]. Figure 2a schematically illustrates the compression-moulding process using a heated press. An appropriate quantity of uncured compound was cut using a knife and placed near the centre of a pre-heated mould. The press platens were then rapidly closed. The moulding time and temperature employed for each material were provided by the suppliers; a mould temperature of 160 °C was used for both elastomers and the materials were held at temperature for 7.5 min for EPDM1 and 10 min for NR. The moulding procedure consisted of an initial 1-min stage where the pressure was cycled on and off between 0 and 100 bar to remove any air trapped in the cavity and ensure a better flow of the rubber. After this, the pressure was raised to 150 bar for the rest of the vulcanisation time as specified. It should be noted that this is not the true pressure acting on the material since the metal frame of the mould acts as a stop and takes the majority of the pressing force. At the end of the process, the mould was removed from the heated press and the vulcanised rubber was carefully removed from the mould and allowed to cool to room temperature. No mould release was used.
Sheet rolling
EPDM2, NBR and CR were provided pre-vulcanised in large 0.5 mm thick sheets by J-Flex Rubber Products. Although the specific processing conditions are confidential, the manufacturing procedure essentially consists of a rolling, or calendaring process, in which the rubber is gradually thinned through heated rollers until the required thickness and curing state is achieved. Figure 2b illustrates schematically the manufacturing process for sheet-rolling, indicating the two major forces applied during manufacturing.
Physical characterisation
An approximate measure of the filler content in cured specimens was obtained from thermogravimetric analysis (TGA) with a TA Instruments SDT Q600. The methodology consisted of first heating to 550 °C at a rate of 10 °C min−1 under a N2 atmosphere. After cooling to 330 °C at the same rate, the atmosphere was changed from inert to oxidative (air) and the samples reheated to 800 °C at a rate of 10 °C min−1. The final relative weight loss during the oxidative atmosphere is associated with carbon black oxidation and is used as an indicator of filler content, \(\phi_{{\text{c}}}^{{{\text{TGA}}}}\), and is reported in the traditional way as parts per hundred rubber (phr) in Table 1, based on three repeats (± 1SD) [16]. With CR and NBR, the carbon residue from the elastomer also oxidises and can give an erroneous estimation of carbon black. In general, the oxidative decomposition of the carbons in the main chain of the polymer occurs at a slightly lower temperature than the filler. In these cases, the derivative of the weight change with respect to temperature was used to identify the overlap of the two oxidative stages [17]. The peak at the highest temperature is associated with the carbon-black content, and this point is used to separate the weight loss associated with filler from that of rubber. In the case of CR, it was particularly challenging to identify this clearly and the value reported in Table 1 should be considered with care.
The glass transition temperatures Tg were determined using a TA Instruments DSC Q10 differential scanning calorimeter (DSC). Cured specimens of ~ 8 mg mass were first heated up to 140 °C at a rate of 20 °C min−1 to erase any thermal history, then cooled to – 75 °C and reheated up to 300 °C at the same rate, all in an N2 atmosphere. A high heating rate was used to limit material degradation during the measurement. The TA Universal Analysis software was used to calculate Tg as the mid-point of the temperature inflection using three tangent lines and Tg values are reported in Table 1 based on three repeats (± 1SD).
The vulcanised density ρ2 was measured using a Mettler Toledo XS105 analytical balance fitted with a density kit based on Archimedes’ principle. De-ionised water at room temperature was used as the medium to measure the density of rectangular specimens of ~ 0.25 g mass. The averages of nine repeats (± 1SD) are reported in Table 1.
Mechanical characterisation
An Instron 5969 tensile testing machine equipped with a 100 N load cell and an Instron counterbalanced travelling extensometer was used to determine the mechanical properties of the five elastomers analysed. Dumb-bell specimens were cut using a hand-operated Wallace specimen cutting press fitted with a cutter type 1BA according to BS ISO 527–2 [18]. For the rolled rubbers, one set of specimens was cut parallel (∥) to the rolling direction and another perpendicular (⊥) to the rolling direction. For the compression-moulded rubbers, specimens were cut in two orthogonal directions, aligned with the mould axes. All materials were tested under standard laboratory conditions at room temperature, (19 ± 1) °C, at a nominal strain rate of 0.03 s−1. The small strain modulus (obtained from linear regression on the first 1% strain of the stress–strain data), E1%, the secant modulus at 100% strain, E100%, and the strain to break, εB, are reported in Table1 as averages (± 1SD) based on three repeats.
A Shore A durometer was employed according to BS ISO 7619-1 [19] to measure the hardness, H, of each material in the direction of the sheet normal. The average of three repeats (± 1SD) is reported in Table 1.
Swelling experiments
Rectangular specimens of approximately 20 × 20 × 0.5 mm (~ 0.15 g) were cut from the vulcanised sheets using a straight edge and a sharp knife. Four separate swelling specimens were used for each material. The mass before swelling, m0, was recorded using a Mettler Toledo XS105 analytical balance. The specimens were then immersed individually in ~ 50 ml of solvent in sealed glass vials. The solvents were selected to have a Hildebrand solubility parameter δs similar to that of the specific elastomer δp [20]. The solvent used for each elastomer and the relevant parameters is reported in Table 2. The Flory–Huggins parameter,\(\chi\), represents the energetic change due to the interaction between the solvent and the polymer. Generally, a good solvent interaction is found when \(\chi\) is below 0.5 [21].
To determine an appropriate swelling equilibrium time, Ts, each specimen was held in the sealed solvent-filled vial for up to 192 h at room temperature, (19 ± 1) °C. During the swelling stage, the specimens were kept in the dark to avoid photo-oxidation [3]. The mass in the swollen state, ms, was recorded using a Mettler Toledo XS105 analytical balance at several time intervals. To reduce evaporation of the solvent during measurements in the swollen state, after the specimens were removed from the solvent and the excess was cleaned from the surface with a paper towel, they were covered with pre-weighed aluminium foil.
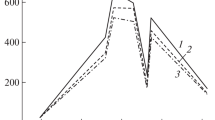
The mean mass swelling ratio, defined as the mean (± 1SD) ratio of the mass at time t, ms(t), to the pre-swelling mass m0, is shown in Fig. 3 for each elastomer. Four specimens were analysed for each material. The data indicate that the interaction between elastomers and solvents reaches equilibrium very quickly and that no major variation in mass is recorded after 1 h. To be certain of full swelling, a swelling time of Ts = 48 h was selected for all experiments. This time represents a good balance between a well-established equilibrium and avoiding network degradation [7].
Post-swelling, a suitable drying time to remove the solvent was determined for each elastomer on specimens swollen for 48 h. Swollen specimens were wiped with a tissue, weighed and placed in an open box below a fume extractor to allow the evaporation of the solvent. The mass of specimens was monitored for a further 168 h at room temperature, (19 ± 1) °C. The drying mass ratio, defined as the mean (± 1SD) ratio of the drying mass at time t, md(t), to the pre-swelling mass m0, is presented in Fig. 4 for each elastomer. After ~ 10 h, no further change in weight could be observed. A drying time of Td = 48 h was selected to obtain the final dried weight, md, for all further experiments, to ensure that complete evaporation of the solvents had taken place. In all cases, the final ratio is less than unity. This is because oils, other additives and residual uncross-linked oligomers are washed out of the elastomers during swelling.
Linear dimensions metrology
The different stages of the swelling and drying processes and the resulting linear dimensions are schematically represented in Fig. 5. The linear dimensions of length l, width w, and thickness t, of each rectangular specimen were measured before swelling (subscript 0), in the swollen state after Ts = 48 h (subscript s) and after drying for Td = 48 h (subscript d). The length and width were measured using a calibrated HP Scanjet G4010 scanner system operating at 1200 dpi (corresponding to 47.24 pixels per mm) was used to measure the planar dimensions, providing a resolution of ± 0.02 mm, and a corresponding measurement uncertainty on the linear swelling ratio of ± 0.1%. Specimens were carefully placed between glass plates on the bed of the scanner during measurements. Care was taken to mark two corners of each rectangle in such a way as to make consistent measurements of the length and width of each rectangular specimen, and three measurements were made along each in-plane direction of every specimen. Typical in-plane linear swelling ratios recorded were between 1.2 and 1.6.
The thickness was recorded by placing the rubber on a rigid glass substrate and measuring using a Hildebrand rubber thickness gauge with a resolution of ± 1μm according to ISO 23529 [23]. The gauge applies a small force P = ~ 0.276 N on a circular flat probe of radius ri = 2 mm during the measurement, providing a thickness reading of tmeas. Since the probe force leads to a small deformation of the rubber during the measurement, to obtain more precise measurements of the actual thickness t (t0 or td) in unswollen specimens, the deformation of the rubber sheet caused by the probe, tprobe, is quantified and accounted for using Lebedev et al.’s [24] elastic solution to the contact problem of a circular flat probe on an elastic layer of finite thickness on a rigid substrate
where ν is Poisson’s ratio, G is the shear modulus and κ is a coefficient here approximated by a second-order function of \(p = r_{{\text{i}}} /t\) as \(\kappa = 0.17p^{2} + 1.047p + 0.98\), based on the numerical data provided in ref [24]. In applying this correction, the shear modulus is obtained from the average value of the in-plane measurements of the small strain tensile modulus E1% and assuming isochoric deformation (Poisson’s ratio \(\nu = 0.5\)) to give \(G = E_{1\% } /3\). For unswollen rubbers, this leads to values of tprobe of up to 3 μm.
For swollen rubbers, the shear modulus is reduced by the swelling, and for this purpose, is estimated using the volume fraction of rubber in the swollen systems, here obtained from measurements of swollen and dry mass using the respective densities, as \(G^{\prime} = G\left( {\upsilon_{2} } \right)^{1/3}\) [4]. To avoid evaporation of the solvent during the thickness measurements of ts, these were measured in a flat-bottomed glass dish containing a small quantity of solvent. For swollen rubbers, the correction to the measured thickness tprobe ranges between 1 and 6 μm.
In each case, the recorded thickness is thus obtained from the sum \(t_{{{\text{meas}}}} + t_{{{\text{probe}}}}\), where tprobe is in each case evaluated employing relevant properties. Typical linear swelling ratios in the thickness direction were recorded between 1.3 and 1.7.
Results
Swelling ratios
Dimensional swelling ratios \(\alpha_{i}\) and \(\alpha^{\prime}_{i}\) can be computed from the linear dimensions in two ways: relative to the initial (pre-swelling) state (dashed), or relative to the dried (post-swelling and drying) state (undashed). These are given by
Figure 6 shows the two swelling ratios for each dimension for all five materials, separated into compression-moulded and rolled rubbers.
Similarly, swelling mass ratios \(\overline{m}\) and \(\overline{m}^{\prime}\) can be computed from the mass measurements in two ways: relative to the initial (pre-swelling) state (dashed), or relative to the dried (post-swelling and drying) state (undashed) (Fig. 7). These are computed from
As shown in Fig. 4, the dried weight can be considerably lower than the pre-swelling weight. This suggests that oils and other small molecules are able to leave the rubber before the dry weight is remeasured and it is reasonable to assume that this takes place during swelling as opposed to during drying. Therefore, it is more appropriate to consider the ratios of swollen to dried measurements for the purpose of analysis and this ratio is used in the following section. In other elastomers where oil and small molecule fractions are insignificant, it is more efficient to use the ratio relative to the pre-swelling state.
Average molecular weight between cross-links
The average molecular weight between cross-links, \(\overline{M}_{{\text{c}}}\), can now be computed using the general result obtained earlier for anisotropic swelling, Eq. (17), making use of the measured linear swelling ratios, and the values obtained are shown in Table 3. For comparison, \(\overline{M}_{{\text{c}}}\) is also calculated using a volume ratio computed from the product of the linear ratios (i.e., assuming isotropic swelling with \(\alpha = \sqrt[3]{{\alpha _{x} \alpha _{y} \alpha _{z} }} = 1.5\)), and again separately from the mass ratio obtained from weight measurements alone (assuming isotropy).
Although differences of almost 10% are present between some of the largest and smallest linear swelling measurements in different directions within the same specimen, the effect of this anisotropy of swelling on the computation of \(\overline{M}_{{\text{c}}}\) is limited. This can be seen by comparing \(\overline{M}_{{\text{c}}}^{{{\text{aniso}}}}\), obtained from the linear swelling ratios, with \(\overline{M}_{{\text{c}}}^{{{\text{Flory}}}}\), obtained from the volume swelling ratio (i.e., equivalent to using \(\alpha = \sqrt[3]{{\alpha _{x} \alpha _{y} \alpha _{z} }} = 1.5\)). The elastomer where this effect is largest is NBR, where \(\overline{M}_{{\text{c}}}\) obtained from the linear swelling ratios is ~ 0.4% larger than \(\overline{M}_{{\text{c}}}\) obtained by assuming isotropy from the volume ratio.
The differences between the volume and mass measures are generally more substantial and are instead most likely to be associated with irregularities in the specimen dimensions, errors in the density measurements and/or possible variations in the swelling state due to the different procedures and timescales involved for mass and dimensional measurements.
Mechanical anisotropy
The mechanical properties of dumb-bell specimens whose axis is either parallel to the rolling direction or perpendicular to the rolling direction are shown in Fig. 8. For compression-moulded specimens two mutually perpendicular directions were selected, aligned with the mould axes.
Nominal stress–strain response under uniaxial deformation for specimens aligned perpendicular to or parallel to the rolling direction (NBR, CR and EPDM2), or for compression-moulded specimens (EPDM1, NR), two orthogonal directions aligned with the mould axes. Offsets for clarity: EPDM1 = 0; NR = 4; NBR = 11; CR = 14; EPDM2 = 16
The data shows convincingly that specimens manufactured by compression-moulding are mechanically transversely isotropic with respect to the thickness axis. Specimens manufactured by rolling processes instead manifest visible differences in their mechanical response when tested parallel or perpendicular to the rolling direction. This is consistent with the observations made using linear swelling measurements, which showed similar in-plane swelling ratios for compression-moulded materials but different in-plane swelling ratios for rolled materials.
Discussion
Soluble fraction during swelling
It was noted in Fig. 4 during monitoring of the drying process that all the materials dry to a smaller weight than their weight prior to swelling. This indicates a loss of material relative to the initial state, which is expected to include oils, small unaggregated filler particles and uncross-linked oligomers. This is referred to as the soluble mass fraction φs, and can be computed as the difference between the mass before swelling m0 and after drying md. The mean soluble mass fraction of each elastomer is reported in Table 4, with two standard errors of the mean. Also shown in Table 4 are estimates of the fraction of oils and plasticisers obtained from TGA experiments obtained from the mass fraction at the first inflection point.
EPDM1 and EPDM2 contain the largest soluble mass fraction based on the swelling experiments. In both EPDM grades, this mass fraction is considerably larger than the oil content estimated by thermogravimetry. This confirms the hypothesis that in the EPDM, the soluble fraction consists not only of oils but also of other additives, including carbon-black and unbound oligomers. This presents an additional factor to be considered in the determination of crosslink density.
Averages of the soluble fractions of the mass φs obtained from weight measurements before and after swelling experiments and from TGA experiments, for the five filled elastomers. It was not possible to obtain reliable TGA estimates for CR and NR.
Anisotropy induced by manufacturing
The manufacturing process is imparting a degree of anisotropy to the rubber network, which manifests itself clearly in linear swelling measurements as well as in mechanical tests. The swelling data suggests that the elastomers are swelling more in the thickness direction (see Fig. 2), independently of the material or manufacturing method. This means that chains are more able to extend in the presence of a solvent in the thickness direction than in the other directions. Since the specimens are in mechanical equilibrium prior to swelling, the most likely explanation is that the lengths of rubbery chains between cross-links are greater along the thickness direction than in the other directions. It is plausible that, as the uncross-linked compounds are compressed, chains align in the plane and have insufficient time to relax before cross-linking takes place. Since the rubbers are highly filled, the filler may be preventing the system from equilibrating once the specimens are removed from the press or from the rolls.
Compression moulding consists of an approximately symmetric, or equibiaxial, extension of the elastomer as it is driven to fill the cavity when the press is closed. The linear swelling data is consistent with this symmetry, showing no detectable variation in swelling ratio between the two in-plane directions. The mechanical tests are also consistent with this, showing no detectable change in mechanical properties in the plane.
The rolled elastomers show linear swelling ratios increasing in the following order, from smallest to largest: length (rolling direction); width (roller axis); thickness. Typical two-roll mills impose conditions of plane strain on a compound during cross-linking. Thus, to a first approximation chains will be more stretched in the rolling direction, relatively undeformed in the transverse direction, and more compressed in the thickness direction, when they are cross-linking. Again, the presence of the filler may prevent a full relaxation from taking place outside of the rolls. Swelling ratios are consistent with this since the rolling direction exhibits the smallest linear swelling and the thickness direction the largest, with the transverse direction somewhere in between. The mechanical data, which probes only the two in-plane directions, is consistent with this, showing a stiffer response along the rolling direction than transverse to it. This is the sign of a rubber whose chains have some preferential alignment in the rolling direction.
It is evident from the anisotropy of swelling that none of the materials (with the possible exception of EPDM1) are completely isotropic in their post-production state. Analysis of specimens produced from these two simple manufacturing techniques commonly used in industry and academia showed that post-production, there can already be a significant anisotropy in the material, even if the in-plane mechanical data is not able to show it (such as if the case with the compression-moulded rubbers). More complex processing techniques such as injection moulding likely bring about even more complex anisotropies that influence the mechanical response during service in specific directions.
The anisotropy taking place during rubber manufacturing is an important consideration that should be accounted for when modelling the response of rubbers, and, to our knowledge, no constitutive model presently includes process-induced anisotropy. This is of particular relevance since the effect is added to any deformation-induced anisotropy. This topic is the subject of ongoing research in our laboratory.
Differences between swelling measurement techniques
Table 3 has shown that there is generally good agreement between the calculations of the molecular weight between cross-links using linear swelling measurements \(\overline{M}_{{\text{c}}}^{{{\text{aniso}}}}\) and the same calculations using volumetric swelling measurements \(\overline{M}_{{\text{c}}}^{{{\text{Flory}}}}\). This is perhaps not that unexpected given that the levels of anisotropy observed here are relatively moderate. However, there can be greater disagreement between the molecular weight between cross-links calculated from dimensional measurements and from mass measurements \(\overline{M}_{{\text{c}}}\). EPDM1, NR and CR produce almost identical values using volume or mass but for EPDM2, mass measurements lead to a 25% larger molecular weight than using volume and NBR mass measurements to a 16% smaller molecular weight. There are a number of possible reasons for this, including irregularities in specimen dimensions and errors in the density measurements, but both of these are expected to be small. We attribute the discrepancy to variations in the swelling state at the point of measurement due to the different procedures and timescales involved for mass and dimensional measurements. It is worth noting from Fig. 4 that NBR appears to dry considerably more quickly than the other elastomers, whereas EPDM2 is among the slower elastomers to dry. Greater measurement accuracy might be possible by taking into consideration these timescales.
Conclusions
This study has developed a new swelling theory allowing the determination of the average molecular weight between cross-links that accounts for the general anisotropy of swelling. In addition, swelling experiments and measurements of linear dimensions have been carried out to quantify the degree of anisotropy in five commercial-filled elastomers, and are supported by physical and mechanical characterisation protocols.
Compression-moulded rubbers were shown to be transversely isotropic after moulding, whereas rolled rubbers exhibited anisotropy in all three directions. In all cases, the swelling was largest in the thickness direction and in rolled rubbers, it was smallest in the rolling direction. All of the five rubbers examined exhibited some degree of anisotropy, and it is expected that due to traditional manufacturing methods, most if not all, rubbers produced will be anisotropic to some degree.
The new anisotropic swelling theory was applied to the experimental data to determine the average molecular weight between cross-links and compared to the existing Flory theory that assumes isotropic swelling. In all cases, the average molecular weight between cross-links was larger when considering anisotropy, although the difference was not substantial for the cases examined here.
References
Flory PJ (1942) Thermodynamics of high polymer solutions. J Chem Phys 10(1):51–61
Flory PJ, Rehner J (1943) Statistical mechanics of cross-linked polymer networks II. Swelling. J Chem Phys 11:512–550
Gee G (1946) The interaction between rubber and liquids. IX. The elastic behaviour of dry and swollen rubbers. Trans Faraday Soc 42:585–598
Treloar LRG (1975) The physics of rubber elasticity, 3rd edn. Clarendon, Oxford, pp 59–79
Flory PJ (1953) Principles of polymer chemistry. Cornell University Press, Ithaca, USA
Flory PJ, Erman B (1982) Theory of elasticity of polymer networks. 3. Macromolecules 15(3):800–806
Valentín JL, Carretero-González J, Mora-Barrantes I, Chassé W, Saalwächter K (2008) Uncertainties in the determination of cross-link density by equilibrium swelling experiments in natural rubber. Macromolecules 41(13):4717–4729
Bruck SD (1961) Extension of Flory-Rehner theory of swelling to an anisotropic polymer system. J Res Nat Bur Stand 65(6):485–487
James HM, Guth E (1947) Theory of the increase in rigidity of rubber during cure. J Chem Phys 15(9):669–683
Schlögl S, Trutschel M-L, Chassé W, Riess G, Saalwächter K (2014) Entanglement effects in elastomers: macroscopic vs microscopic properties. Macromolecules 47(9):2759–2773
Wheelans MA (1978) Injection moulding on rubber. Rubber Chem Technol 57(5):1023–1043
Lavebratt H, Stenberg B (1993) Anisotropy in injection-moulded styrene-butadiene rubbers. Part 2: discs delaminated by water-jet cutting techniques. Plast, Rubber Compos Process Appl 20(1):15–24
Azaar K, Rosca ID, Vergnaud JM (2002) Anisotropic swelling of thin EPDM rubber discs by absorption of toluene. Polymer 43(15):4261–4267
Blow CM, Demirli HB, Southwart DW (1975) Anisotropy in molded nitrile rubber. Rubber Chem Technol 48(2):236–245
De Focatiis DSA (2012) Tooling for near net-shape compression moulding of polymer specimens. Polym Testing 31(4):550–556
Loadman MJ (1998) Analysis of rubber and rubber-like polymers, 4th edn. T, The Netherlands
Schawe J (2002) Analysis of carbon black in elastomers based on chloroprene. In: Mettler Toledo AG (ed) Elastomer Handbook, vol 2. Analytical, Switzerland
ISO 527-2:2012. Plastics — Determination of tensile properties — Part 2: Test conditions for molding and extrusion plastics. BSI: United Kingdom, 2012
ISO 7619-1:2010. Rubber, vulcanized or thermoplastic — Determination of indentation hardness — Part 1: Durometer method (Shore hardness). BSI: United Kingdom, 2010
Rabek JF (1980) Experimental methods in polymer chemistry: physical principles and applications. Wiley-Blackwell, Chichester, England
Sperling LH (2005) Introduction to physical polymer science. Wiley, Hoboken, New Jersey, p 84
Brandrup J, Immergut EH, Grulke EA (1990) Polymer handbook, 4th edn. Wiley, New York, USA
ISO 23529:2010. Rubber: General procedures for preparing and conditioning test pieces for physical test methods. BSI: United Kingdom, 2010; p 26
Lebedev NN, Ufliand IS (1958) Axisymmetric contact problem for an elastic layer. J Appl Math Mech 22(3):442–450
Acknowledgements
The authors gratefully acknowledge the contributions of Dr. T. Alshuth of the German Institute of Rubber Technology (DIK) in supplying the EPDM1 compound, of J-Flex Rubber Products in providing the EPDM2, NBR and CR sheets, and of Trelleborg Industrial AVS in supplying the NR compound. VAF acknowledges Dean of Engineering funding from the University of Nottingham.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fernandes, V.A., De Focatiis, D.S.A. Anisotropic swelling of rubber: extension of the Flory theory. J Rubber Res 25, 401–412 (2022). https://doi.org/10.1007/s42464-022-00183-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42464-022-00183-2