Introduction

The damping capabilities of elastomers and their ability to withstand large deformations without being plastically deformed have led to their adoption in many applications such as car bearings, transmission belts and vibration dampers. In operation and due to dynamic loading, fatigue failure is expected to occur. To predict such failure and for the lifetime estimation of components in operation, a thorough knowledge about the material properties and its behaviour under different loading conditions is required.

Besides the non-linear deformation behaviour of elastomers, their viscoelastic properties lead to heat dissipation when subjected to continuous dynamic loading. This may alter the applied loading conditions. As a consequence, the implementation of a finite viscoelastic model to analyse the damage evolution is important. In the following section, an overview of the existing finite viscoelastic models are presented.

Finite viscoelastic material models

The effect of the viscoelastic behaviour on loading conditions was examined experimentally by Gent [9]. In this study, with the aid of the introduced rotary machine, it was shown that a rotary shear produces higher energy dissipation per cycle than a simple shear oscillation with the same shear angle. This is due to the circumferential force caused by the viscoelastic behaviour. The presented testing machine in [9] was used to investigate the fatigue behaviour of elastomers in [14].

The influence of inelasticity on the lifetime of elastomers was discussed by Juhre et al. [13]. In their contribution, the MORPH material model, proposed by Ihlemann and Besdo [3] was compared to the Yeoh hyperelastic model. It was shown that, due to the fact that a standard hyperelastic model cannot display the inelastic effects, the resulting circumferential force due to viscoelasticity is neglected, which in turn leads to misleading lifetime predictions.

In the essay introduced by Haupt and Lion [10], a finite linear viscoelastic theory was presented. The model is based on the generalisation of the one dimensional differential equation of the Maxwell model to finite deformation and does not require a decomposition of the deformation gradient. The theory was shown to be thermodynamically consistent and suitable to describe the dynamic material behaviour. In the contribution of Yagimli [20] the model suggested by Haupt and Lion was extended to incorporate the kinetics of the epoxy curing process. The heat generation and the resulting temperature development as well as the shrinkage of the epoxy resin as a result of the curing process were successfully modelled.

In the work presented by Chadwick [4], the temperature dependence of the mechanical material parameters are discussed and a finite strain entropic thermoelastic model was introduced. Dippel et al. [7] used the approach introduced by Chadwick to formulate a material model that incorporates the temperature dependency of mechanical properties. Using different configurations, five states of deformation were modelled. In the thermo-mechanical configuration, the deformation gradient is split into a thermal and a mechanical part. The mechanical part is further decomposed into isocohoric and volumetric deformations. In the last step, the isochoric deformation gradient can be decomposed into an elastic and an inelastic part. This model was then simplified by Johlitz [12] where no thermo-mechanical configuration was used. Instead, a thermal part was added to the free energy. In both contributions [7, 12], using the material parameters determined experimentally, the developed material model was validated with respect to mechanical experiments. The effect of varying the deformation amplitude and the loading frequency was addressed. It was shown, that heat dissipation increases with increasing the deformation amplitude and loading frequency.

A modified material model for finite viscoelasticity was presented by Schröder et al. [15]. This model is based on the multiplicative decomposition of the deformation gradient in order to present different types of deformations. The simulation results were compared with experimental tests that were carried out on an engine bearing. Good agreement was found to occur between experiments and simulations of the force displacement hysteresis. Furthermore, in a recently published paper by Schröder et al. [16], numerical studies were conducted to investigate the influence of the loading amplitude, loading frequency and the material parameters on the self-heating phenomena in elastomers.

Based on the concept of internal state variables, a non linear finite viscoelasticity model was presented by Holzapfel and Simo [11]. The thermodynamic potential is additively decomposed into purely thermoelastic and non-equilibrium parts. The implemented rate equation is in a convoluted form and can be integrated using a second order midpoint rule. The implementation of this integration algorithm for the nonlinear viscoelasticity as well as a summary of an overall implementation of a thermomechanical model was discussed in the text book by Simo and Hughes [18].

Scope of the present work

The aim of this paper is to investigate through numerical studies, the thermo-mechanical coupling effects experienced by an elastomer sample in the rotary dynamic testing machine, introduced by Gent [9]. For this purpose, a finite viscoelastic model is needed to describe the viscoelastic behaviour and the self- heating phenomena of elastomers.

The presented article is structured as follows: Firstly, the model mentioned in references [17, 18] is presented. The loading case is then presented and discussed. This is followed by a parametric study using finite element analysis is performed. This work investigates the effect of the loading boundary conditions,as well as, the material parameters on the dissipation behaviour of the material and the resulting changes in the applied loading conditions.

Material model

In the contribution of Simo et al. [18] the stored energy function \({W}^o(\mathbf {C})\) is decomposed additively into volumetric \(U^o(J)\) and isochoric parts \(\overline{W^o}\) as follows:

$$\begin{aligned} {W}^o(\mathbf {C})= \overline{W^o}(\overline{\mathbf {C}})+ U^o(J), \end{aligned}$$
(1)

where J is the determinant of the deformation gradient tensor \(\mathbf {F}\). In the reference configuration, the deformation can be presented through the right Cauchy–Green tensor as expressed in Eq. (2). The isochoric part of the right Cauchy–Green tensor is calculated using Eq. (3).

$$\begin{aligned} \mathbf {C}=&\mathbf {F}^T\mathbf {F} \end{aligned}$$
(2)
$$\begin{aligned} \overline{\mathbf {C}}=&J^{\left( \frac{-2}{3}\right) }\mathbf {C} \end{aligned}$$
(3)

Stresses are obtained through the partial differentiation of the strain energy function by the deformation: In the present discussion, the partial differentiation with respect to \(\mathbf {C}\) is referred to as \(\partial _{\mathbf {C}} W^o(\mathbf {C})\) as shown in Eq. (4). The deviatoric part of the instantaneous stress tensor is expressed by Eq. (5). The deviatoric part in the reference configuration is calculated by applying the \(\mathrm {DEV} [\cdot ]\) operator as shown in Eq. (6).

$$\begin{aligned} \mathbf {S}^o=&2 \partial _{\mathbf {C}} W^o(\mathbf {C})=\overline{\mathbf {S}^o}+ J \frac{\partial {U^0}}{\partial {J}} \mathbf {C}^{-1} \end{aligned}$$
(4)
$$\begin{aligned} \mathbf {\overline{S^o}}=&J^{\left( \frac{-2}{3}\right) } \mathrm {DEV}[ 2 \partial _{\mathbf {C}} \overline{W^o}(\overline{\mathbf {C}})]. \end{aligned}$$
(5)
$$\begin{aligned} \mathrm {DEV}[\mathbf {\cdot }]=&(\mathbf {\cdot })- \frac{1}{3} [(\cdot ):\mathbf {C}] \mathbf {C}^{-1} \end{aligned}$$
(6)

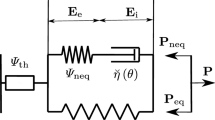
In this study, modelling the viscoelastic properties is done by using a single Maxwell element in parallel with a spring element (3-parameter model). For the non linear viscoelasticity, the free energy function is postulated as follows [17, 18]:

$$\begin{aligned} \psi (\mathbf {C},\mathbf {Q})= \overline{W^o}(\overline{\mathbf {C}})+ U^o(J)- \frac{1}{2}\overline{\mathbf {C}}:\mathbf {Q}+ \psi _{I}(\mathbf {Q}), \end{aligned}$$
(7)

where \(\mathbf {Q}\) is an internal variable used to describe the non equilibrium forces on the dash pot. The energy term (\(\psi _{I}\)) is a function of the internal variable \(\mathbf {Q}\) and is defined at the thermodynamic equilibrium state as the Legendre transformation of the function \(\overline{W^o}(\overline{\mathbf {C}})\) as follows [17, 18]:

$$\begin{aligned} \psi _{I}(\mathbf {Q})= - \gamma _{i} \overline{W^o}(\overline{\mathbf {C}}) + \frac{1}{2}\overline{\mathbf {C}}:\mathbf {Q} \end{aligned}$$
(8)

\(\gamma _{i}\) is a non-dimensional relative moduli that relates the inelastic shear modulus of the maxwell arm \(\mu _{i}\) to the instantaneous shear modulus \(\mu ^o\). On the other hand, \(\gamma _{\infty }\) is the moduli that relates the shear modulus at equilibrium state \(\mu _{\infty } \) to the instantaneous shear modulus as follows.

$$\begin{aligned} \gamma _{i}= \frac{\mu _{i}}{\mu ^o} \quad \gamma _{\infty }= \frac{\mu _{\infty }}{\mu ^o} \quad \gamma _{i}+ \gamma _{\infty } = 1. \end{aligned}$$
(9)

In analogy to Maxwell model, the evolution of the internal stress variable is defined by the rate Eq. (10) and leads to the convolution representation in Eq. (11).

$$\begin{aligned} \dot{\mathbf {Q}}(t)+ \frac{1}{\tau } \mathbf {Q}(t) = \frac{\gamma _{i}}{\tau } \mathrm {DEV}[ 2 \partial _{\mathbf {C}} \overline{W^o}(\overline{\mathbf {C}}(t))]. \end{aligned}$$
(10)
$$\begin{aligned} \mathbf {Q}(t)=\frac{\gamma _{i}}{\tau } \int \limits _{-\infty }^{t} \exp \left[ -\frac{t-s}{\tau }\right] \mathrm {DEV}[ 2 \partial _{\mathbf {C}} \overline{W^o}(\overline{\mathbf {C}}(t))]\text {d}s , \end{aligned}$$
(11)

where \(\tau \) is the relaxation time. For the finite viscoelastic model, the Second Piola Kirshoff stress tensor is decomposed into initial and non equilibrium parts as shown in Eq. (12) [18].

$$\begin{aligned} \mathbf {S}(t)=\mathbf {S}^o(t)-J^{\left( \frac{-2}{3}\right) } \mathrm {DEV}[\mathbf {Q}(t)]. \end{aligned}$$
(12)

In Eq. (12), initially the value of the internal variable \(\mathbf {Q}\) is zero and increases with time due to viscous dissipation. An equilibrium state is reached when \(\mathbf {Q}\) reaches the value \(\mathbf {Q}=\gamma _{i}\mathbf {\overline{S^o}}(t)\) and the stress is only calculated with the equilibrium part (\(\mathbf {S}(t)=\gamma _{\infty }\mathbf {\overline{S^o}}(t)\)) [16]. With partial integration of Eq. (11) and its substitution into Eq. (12) the following definition of the Second Piola Kirchhoff stress is obtained:

$$\begin{aligned} \mathbf {S}(t)= & {} J \frac{\partial {U^0}}{\partial {J}} \mathbf {C}^{-1}(t)+ \gamma _{\infty }J^{\left( \frac{-2}{3}\right) } \mathrm {DEV}[ 2 \partial _{\mathbf {C}} \overline{W^o}(\overline{\mathbf {C}}(t))]\nonumber \\&+J^{\left( \frac{-2}{3}\right) } \gamma _{i}\mathbf {H}(t) \end{aligned}$$
(13)
$$\begin{aligned} \mathbf {H}(t)= & {} \int \limits _{-\infty }^{t} \mathrm {exp}\left[ -\frac{t-s}{\tau }\right] \frac{\mathrm {d}}{\mathrm {d}s}\mathrm {DEV}[ 2 \partial _{\mathbf {C}} \overline{W^o}(\overline{\mathbf {C}}(s))]{\mathrm {d}}s , \end{aligned}$$
(14)

with the definition of the algorithmic internal variable \(\mathbf {H}(t)\) in Eq. (14), the non equilibrium part of the stress \(\mathbf {S_i}\) is computed using Eq. (15).

$$\begin{aligned} \mathbf {S}_{i}=J^{\left( \frac{-2}{3}\right) } \gamma _{i}\mathbf {H}(t) \end{aligned}$$
(15)

Viscous dissipation is caused by the non equilibrium part of the stress. The inequalities shown in 16 and 17 present the viscous dissipation. The calculation of the viscous dissipation is based on references [1, 11].

$$\begin{aligned} D_\mathrm{int}=\mathbf {S}_{i}:\dot{\mathbf {G}} \ge 0. \end{aligned}$$
(16)

The tensor \(\mathbf {G}\) is an internal variable that is regarded as a strain tensor [viscous strain] similar to the right Cauchy–Green tensor \(\mathbf {C}\). In the work of Behnke et al. [1], the dissipation was calculated using a fourth order viscosity tensor as shown in Eq. (17):

$$\begin{aligned} D_{int}= \mathbf {S}_{i}:\mathbf {\underline{\underline{\eta }}}^{-1} :\mathbf {S}_{i}\ge 0 \end{aligned}$$
(17)

To reduce the numerical effort, the inverse of the fourth order tensor \(\mathbf {\underline{\underline{\eta }}}\) is approximated to (\(\mathbf {\underline{\underline{\eta }}}^{-1}\approx \frac{1}{\eta }\mathbf {1}^4\)), where \(\eta =\mu _i\tau \) and \(\mathbf {1}^4\) is the fourth order identity tensor. In this paper, the presented material model is implemented for the Neo Hooke strain energy function as follows:

$$\begin{aligned} W^o(\mathbf {C})=\frac{\mu ^o}{2}(\overline{\mathbf {C}}:\mathbf {1}-3)+\frac{k}{2}(J-1)^2, \end{aligned}$$
(18)

where k is the bulk modulus. According to Eq. (13) the second piola kirchhoff stress is calculated as shown in Eq. (19):

$$\begin{aligned} \mathbf {S}(t)= & {} kJ(J-1) \mathbf {C}^{-1}(t)+ \mu ^o(\gamma _{\infty })J^{\left( \frac{-2}{3}\right) } \mathrm {DEV}[\mathbf {1}]\nonumber \\&+ J^{\left( \frac{-2}{3}\right) } (\gamma _{i})\mathbf {H}(t) \end{aligned}$$
(19)

With the push forward operation, the Kirchhoff and Cauchy stresses are calculated in the current configuration (Kirchhoff Stress \(\mathbf {T}=\mathbf {F}\mathbf {S}\mathbf {F}^T\), Cauchy stress \(\mathbf {\tilde{T}}= \frac{1}{J}\mathbf {T}\)).The consistent tangent modulus is then derived for both the elastic and the inelastic part. The constitutive equations were then implemented in an user subroutine (UMAT) to be used in the presented numerical studies using the finite element software Abaqus standard.

For further details about the model and its implementation the reader may refer to the references [1, 2, 17, 18]. The thermodynamical consideration and the thermodynamic consistency of the model are discussed in [2, 6, 11, 17, 18].

Case study and boundary conditions

In the study mentioned above by Juhre et al. [13], the idea of the test rig designed by Gent [9] was implemented to conduct fatigue tests under non proportional loading conditions. In the dissertation provided by Klauke [14], the test rig was modified and the working principle of the test rig was discussed in details. In the following case study, the same loading condition used in [14] will be simulated.

After implementing the material model stated in the previous section in an user subroutine, a CAD drawing was prepared for the sample. The sample geometry is then discretised by C3D8HT elements (coupled Temperature–displacement hybrid elements with 8 nodes) and a thermo-mechanical simulation is done using the FEM software Abaqus standard. Figure 1 shows the dimensions of the sample used in the study and Fig. 2 shows the boundary conditions. As shown in Fig. 2, the displacement vector (U1) is applied to reference point (RP1), while the displacement at the reference point (RP2) is held fixed. The definition of the displacement vectors is shown in Eq. (20). The order of the column vector is of (x, y, z). The specimen design leads to the highest stresses being concentrated in the middle part of the sample and not in positions where the sample is clamped [8, 14].

Fig. 1
figure 1

Dimensions of the used specimen in the study

Full size image
$$\begin{aligned} U1&= {\left\{ \begin{array}{ll} \begin{bmatrix} u\,t \\ 0 \\ 0 \end{bmatrix} , &{} 0 \le t \le 1\, s \\ {\begin{bmatrix} u\,\mathrm {cos}(\omega t)\\ 0 \\ u\,sin(\omega t) \end{bmatrix}},&t >1 \, s \end{array}\right. } \end{aligned}$$
(20)
Fig. 2
figure 2

Specimen geometry used in the study

Full size image

Analysis

To calculate the reaction force, the displacment boundary conditions shown in Eq. (20) are applied. In the first step of the simulation the upper face of the sample is deformed in the X-direction, resulting in a shearing angle of \(45^{{\circ }}\) (\(u_x=3\) mm). In the second step, the upper surface of the sample was rotated for one cycle around the Y-axis with a frequency of 0.1 Hz. The assigned mechanical properties are for carbon black filled natural rubber. The mechanical properties are listed in Table 1 and are taken from [16] except for the value of the relaxation time. The relaxation time is assigned a value of 0.8 s. The chosen relaxation time is calculated using the standard Williams–Landel–Ferry (WLF) equation with the temperature set to 298 K. Other parameters of WLF equation are taken from [16] and are listed in Table 2.

Table 1 Assigned material parameters for the simulation
Full size table
Fig. 3
figure 3

Reaction forces as result of rotating a constant shear load

Full size image

Figure 3 shows that beside the reaction force \(F_{r}\) , another force \(F_{u}\) in the tangential direction is induced as a result of the viscoelastic behaviour during changing the loading direction. During the rotation of the upper sample face around the Y-axis, the material point experiences a cyclic loading leading to energy dissipation. Due to viscoelastic behaviour, the displacement vector will not have the same direction as the reaction force vector (a phase difference between both vectors would occur). The resulting dissipation is proportional to the tangential force \(F_{u}\). This behaviour was also reported by Gent et al. [9], Juhre et al. [13] and Klauke [14].

The force \(F_{r}\) is the force required to keep the deformation amplitude constant and is defined as the projection of the reaction force in the deformation direction. The force \(F_{u}\) is the force orthogonal to it. For an ideal elastic material, the force \(F_{u}\) is zero as the reaction force vector will have the same direction as the displacement vector.

In the next section, the influence of different parameters on the dissipation induced force (\(F_{u}\)) and the self-heating phenomena are investigated. The studied parameters are the relaxation time, loading amplitude, loading frequency as well as the initial temperature of the sample. The studies are presented along with the discussion of the obtained results.

Effect of changing the relaxation time

As shown in the previous section, a tangential force is induced as a result of the dissipation occurring in the material. The work done by the tangential force is converted into a heat energy which results in an increase of the specimen temperature per cycle. Changing the temperature due to self-heating will change the values of temperature-dependent parameters such as the relaxation time.

The relaxation time (\(\tau \)) is a temperature-dependent parameter that describes the decay of stress under constant loading strain. For a Maxwell arm, it is defined as \((\tau =\frac{\eta (\theta )}{\mu _i }\)) where \(\eta \) is the viscosity of the dash pot and \(\mu _i\) is the shear modulus of the spring. The change of the viscosity in dependence of the temperature can be described using the standard Williams–Landel–Ferry equation [19].

$$\begin{aligned} \eta (\theta )=\eta _{0}\exp \left( -\frac{C_{1}(\theta -\theta _{t})}{C_{2}+\theta -\theta _{t}}\right) , \end{aligned}$$
(21)

where \(C_{1} , C_{2}\) are standard parameters and \(\theta _{t}\) is the glass transition temperature. The values of these parameters are taken from [16] and are listed in Table 2.

Changing the relaxation time as a result of the temperature increase (due to self- heating) will alter the value of the dissipation induced tangential force \(F_{u}\). Multiple simulations were carried out to estimate the tangential force \(F_{u}\) at various relaxation time values and loading frequencies.

Fig. 4
figure 4

Effect of varying the relaxation time on the tangential force \(F_{u}\) at different frequencies

Full size image

Figure 4 indicated, that at a given frequency, the value of the force \(F_{u}\) is significantly affected by the change in relaxation time. For example, at a frequency of 0.1 Hz, the maximum dissipation occurs at \(\tau =1.5\) s and decreasing the value of the relaxation time decreases the dissipation and the resulting force \(F_{u}\). At all values of the set relaxation times, the maximum obtained force \(F_{u}\) is nearly equal to 425 N. This maximum value of \(F_{u}\) depends on the relaxation time, the shear modulus of the inelastic arm, specimen geometry and the amount of the displacement vector (U1). It is observed that the maximum value of the force \(F_{u}\) shifts to higher frequencies as the relaxation time decreases. To facilitate the discussion, the relaxation time at a certain frequency corresponding to the maximum dissipation will be referred as the critical relaxation time \(\tau _{c}\).

In order to monitor the continuous change in the value of the force \(F_{u}\) versus the temperature, another simulation with the same material parameters in Table 1 is conducted. The relaxation time is set this time as a function of temperature through the Williams–Landel–Ferry (WLF) equation. The parameters of the WLF equation are listed in Table 2.

Table 2 Parameters used in WLF-equation [16]
Full size table

The loading frequency is set to 1 Hz and at the upper and lower surface of the sample a heat transfer coefficient from the rubber to the steel is assigned equal to \(\alpha = 0.022\) mW/mm\(^2\) K [15]. Initial temperature for the simulation is 298 K (corresponds to a relaxation time of \(\tau =0.8\) s). In Fig 5, a 2D drawing of the sample fixed between the two steel holders is shown.

Fig. 5
figure 5

Rubber sample fixed between two steel holders

Full size image

As shown in Fig. 6, the force \(F_{u}\) increases with the temperature increase (decrease of the relaxation time) until a certain limit of the relaxation time is reached, after which the dissipation is less and the temperature increases at a slower rate. It should be noted, that starting from approx. 25 s (\(\varDelta \theta =30\) K), the slope of the force curve increases rapidly as the critical relaxation time \(\tau _c\) at loading frequency of 1 Hz is reached indicating an increase in the dissipation.

Fig. 6
figure 6

Effect of changing the relaxation time on the temperature development and the force \(F_{u}\)

Full size image

Figure 7 shows the relation between the temperature of the sample, the relaxation time and the resulting dissipation force \(F_u\) at a loading frequency of 1 Hz. As the temperature increases, the relaxation time decreases and the resulting dissipation force increases. This behaviour continues until \(\tau _c\) is reached (in this case \(\tau _c=0.15\) s) and afterwards the dissipation decreases again as the temperature increases.

Fig. 7
figure 7

Effect of increasing the temperature on the dissipation process

Full size image

Effect of changing the initial temperature

To study the effect of changing the initial temperature on the resulting dissipation, three simulations with three different starting temperatures were conducted. The shear angle is \(45^{{\circ }}\) and the loading frequency is equal to 1 Hz. The following figure shows the simulation results.

Fig. 8
figure 8

Effect of changing the initial temperature on the dissipation process

Full size image

As shown in Fig. 8, heat dissipation is highly affected by changing of the initial temperature. In the case of 1 Hz loading, the maximum dissipation is expected to occur at a temperature of 320 K (\(\tau _{c}=0.15\) s as shown in Fig. 4). That explains why the curve with a starting temperature of 298 K initially heats up at a lower rate than the other curves. As heat dissipation continues, the temperature is increased until the corresponding temperature of the maximum dissipation is reached. After this point, higher dissipation occurs resulting in an increase in the temperature change \(\varDelta \theta \) increases.

Effect of changing the loading frequency

In Fig. 9, the effect of changing the frequency is shown. In this analysis, for a better monitoring of the self-heating phenomena, the sample height is changed to 4 mm and the temperature of the upper and the lower surface of the sample is set constant to 315 K. The initial temperature of the whole sample is 315 K. It can be seen that, the higher the frequency, the higher the temperature increase (\(\varDelta \theta \)) as well as the steady state temperature.

Fig. 9
figure 9

Effect of changing the loading frequency on the dissipation process

Full size image

During the dynamic loading, the sample temperature increases and the relaxation time decreases accordingly. Increasing the initial temperature of the sample would result in the same behaviour as shown in Fig. 9 but with lower values of temperature change (\(\varDelta \theta \)).

The temperature increase per cycle is dependent on both, the relaxation time and the loading frequency. It is important to note that, if the relaxation time is not temperature dependent, the dissipation energy per cycle would be constant. A temperature dependent relaxation time would change the dissipation energy per cycle and the resulting steady state temperature would be different. The results shown in Fig. 9 are for a temperature-dependent relaxation time.

Effect of changing the loading amplitude

Simulations with constant relaxation time (\(\tau \) = 0.15 s) and different shear angles at 1 Hz loading frequency are performed to examine the effect of changing the loading amplitude on the dissipation behaviour of the material and the resulting temperature increase. As seen in Fig. 10, an increase in the shearing angle increases the dissipation and results in an increase of the steady state temperature.

Fig. 10
figure 10

Effect of changing the loading amplitude on the dissipation process

Full size image

Heat dissipation as a result of the amplitude modulation of the load

The heat dissipation due to changing the loading direction has been studied in the previous sections. It is seen that a large amount of heat dissipation is estimated. In this section the sample will not be rotated, instead, it will be sheared only in the x-direction. The loading amplitude is varied sinusoidally (amplitude modulation) and the loading direction is kept in the x-direction.

To monitor the heat dissipation and the temperature increase as a result of the amplitude modulation of the load, the boundary conditions in Eq. (20) are adjusted so that a sinusoidal displacement signal is applied. The new boundary conditions are as follows:

$$\begin{aligned} U1&= {\begin{bmatrix} u\,\sin (\omega t)\\ 0 \\ 0 \end{bmatrix}} \nonumber \\ U2&= \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \end{aligned}$$
(22)

The frequency of the loading is kept equal to 1 Hz. The initial temperature of the sample is set to 315 K and the upper and lower surfaces of the sample are kept at a constant temperature of 315 K. The sample used has a height of 4 mm (the shear amplitude is \(45^{{\circ }}\) when the displacement reaches \(u= 4\) mm) and the relaxation time is set as a function of temperature \(\tau (\theta )\). The following Fig. 11 shows the temperature distribution in the sample. The results for the temperature values are in (K).

Fig. 11
figure 11

Effect of the amplitude modulation on the temperature distribution throughout the sample

Full size image

The temperature increase, due to self-heating, after reaching the steady state temperature is \(\varDelta \theta = 6\) K. This value is much less when compared with temperature increase associated with rotating the loading direction at constant amplitude. With this kind of loading (Amplitude modulation with constant loading direction), the rate of heat generation is less and a steady state is reached faster. The same behaviour was observed in the experimental results discussed by Gent et al. [9]. In the case of the direction modulation with fixed amplitude, the energy dissipation is constant throughout the cycle, while in the case of amplitude modulation with fixed direction, the energy dissipation varies during the cycle. The results show a significant difference in the steady state temperature between the two cases of loading. These results still need to be verified experimentally.

The temperature increase and the steady state temperature is highly affected by the height of the sample and the thermal conductivity of the material. Increasing the sample thickness leads to an increase in the steady state temperature.

Conclusion

In this work, a model for finite viscoelasticity was implemented and used in a parametric study conducted on specimen experiencing a non proportional loading condition. The goal of the study was to use this material model to investigate the effect of the material parameters and loading conditions on the dissipation process and its resulting forces and heat development.

The induced forces due to dissipation depend on the relaxation time of the material. Decreasing the relaxation time would significantly change the dissipation forces (in dependence of the loading frequency). The effect of the starting temperature was studied. It was shown that at 1 Hz loading frequency, the heat dissipation decreases when the starting temperature increases.

The influence of changing the loading frequency and loading amplitude was investigated. It was concluded that, increasing the frequency as well as the amplitude of the loading would increase the heat development and the resulting steady state temperature. Material parameters, such as relaxation time should be experimentally determined at various temperatures and loading frequencies.

The implemented material model sufficiently describes the inelastic behaviour and the associated self-heating phenomena. Prior to fatigue testing experiments, testing conditions such as loading frequency, amplitudes and thermal boundary conditions can be simulated using the presented model. The heat dissipation and the resulting induced forces and temperature rise can be estimated. The experimental set up can be then adjusted to limit the thermal effects due to self-heating and therefore avoid any change in the loading conditions during testing.

The model can be further modified to simulate larger deformations using higher order energy functions and model more than one Maxwell arm to improve the description of the viscoelastic behaviour of the material. In the near future, the implemented model will be extended to describe the damage evolution in the material for the life time prediction of elastomeric components.