Introduction

Due to their mechanical properties, especially their high deformability, elastomers have a wide range of applications. The design of components requires an understanding of failure and wear, which in turn requires an understanding of crack initiation and propagation. Nowadays there are several well-established concepts to characterize cracks in the context of brittle fracture like the J-integral [5, 23]. However, when applied to elastomers, the question of the influence of dissipative material behavior on this concept arises. In the context of the present work, material forces are used to describe the influence of the dissipative material behavior on the crack. The material behavior of elastomers is presented by through constitutive models, which includes a suitable visco-elastic characterization. This material description is finally used to describe crack propagation experiments by material forces and to verify the applicability of the extended approach.

The foundation of material or configurational forces is the work of Eshelby [10], in which the elastic energy-momentum tensor is introduced to describe the force on defects and inhomogeneities in an elastic continuum. In a later work [9], he recognizes that the material forces on a crack in a purely elastic body under quasi-static load correspond to the well-known J-integral. The concept of material forces offers a more general interpretation of the J-integral and thus a unified approach to the description of cracks in complex materials such as hyperelastic [29], viscoelastic/elastoplastic [19, 20] ,or magnetoelasticity [12].

From a phenomenological point of view, polymers exhibit both non-linear finite elastic and inelastic behavior including deformation induced damage effects. Describing this behavior with a constitutive model has been an active research area for many years. Though, most of the approaches can only account for some of these effects. Experimental observations, in which elastomers have been loaded by a step in strain, have shown that the stress relaxes towards a state of equilibrium (e.g. [11]). Based on such tests, the mechanical behavior of elastomers under infinitely slow loading is described using hyperelastic material models. There are numerous different approaches for the formulation of such models, which are compared for example in [17].

Polymers under cyclic loading show that the non-equilibrium behavior is dependent on both rate and temperature [16, 22]. A widely used way to model the time dependence of relaxation is to use dimensionless relaxation modules, which are usually represented by a Prony series (e.g. [13]). This approach shows good results, especially for small strains. Another approach is to decompose the deformation gradient multiplicatively into an elastic and a viscous part, which is used for example by the Bergström–Boyce model (BB model) [4]. Compared to the Prony series, this model is not based on a single hereditary integral with stress-like internal variables, but the inelastic part of the deformation represents strain-like tensorial state variables. This approach uses a non-linear evolution equation for the strain-like variable to better model the relaxation in the finite strain regime.

This paper is organized as follows: In the second section, the mechanical behavior of carbon black-filled rubber is investigated. For this purpose, the BB model and the Prony are introduced and the experimental methodology is presented. Subsequently, the equilibrium and viscous behavior are analyzed separately. Then, in the third section, the cracking behavior of rubber is investigated, first introducing the methodology for determining the material forces and then presenting a numerical example for crack characterization. Finally, to sum up, a conclusion is drawn in section “Conclusions”.

The material behavior of carbon black filled elastomers

Continuum mechanical description of the BB model

Each body \({\mathcal {B}}\) consists of a set of material particles and is described through its configurations \(\varOmega _i\). Then let \(\vec {X}\) be a one-to-one correspondence between a Particle and the Point that \({\mathcal {B}}\) occupies within \(\varOmega _0\) at reference time \(t_0\). The function \(\phi \) maps all Points \(\vec {X}\) of this reference configuration onto points \(\vec {x}=\psi (\vec {X},t)\) of the current configuration. To describe the transition between the reference and the instantaneous configuration, the deformation gradient \(\mathsf {F}\) is introduced by \(\mathsf {F}=\partial \vec {x}/\partial \vec {X}\) and the volume change J, which is defined by \(J=\det (\mathsf {F})\). Furthermore, the eigenvalues of the deformation gradient \(\lambda _i\) in the main strain space describe the elongation of the body \({\mathcal {B}}\). The BB model is based on a multiplicative decomposition of the deformation gradient, which is based on experimental observations. As a consequence, the simplified material behavior of a polymer can be modeled as two networks, as shown in Fig. 1. The elastic equilibrium behavior is modeled by a single spring in A, whereas the spring and damper in B represent the time-dependent viscous component. Thus, an applied deformation \(\mathsf {F}\) affects both networks in equal measure, while the deformation in B can be decomposed by the relationship

$$\begin{aligned} \mathsf {F}_\mathrm {B}=\mathsf {F}_\mathrm {e}\mathsf {F}_\mathrm {v}, \end{aligned}$$
(1)

into the deformation of the damper \(\mathsf {F}_\mathrm {v}\) and the spring \(\mathsf {F}_\mathrm {e}\). With the viscous part \(\mathsf {F}_\mathrm {v}\), an intermediate configuration is introduced, in which virtual unloading of the elastic part in B takes place and thus a stress-free relaxed state prevails. If one compares the BB model with one-term Prony series, the difference becomes apparent in the description of the damper. In the Prony series, the strain rate in the damper is described as a linear function of the Stress in B. Whereas in the BB model the rate is based on a non-linear relationship, which is derived from a Reptition-type tube theory.

Fig. 1
figure 1

One dimensional rheological representation of the BB model

Full size image

An important finding from this micromechanically inspired idea is that the viscous flow is energetically activated, as the tube-like conformation areas of the polymer chains act as an energy barrier. Consequently, the relaxation process is described through

$$\begin{aligned} \dot{\gamma _\mathrm {B}} = {\dot{\lambda }}_{0} \left[ {\overline{\lambda }}_\mathrm {chain}-1 \right] ^{c} \cdot \left[ \frac{\Vert {{\,\mathrm{dev}\,}}({\sigma }^{B})\Vert _F}{{\hat{\tau }}} \right] ^{m} \cdot \mathsf {N}\left( {\sigma }_\mathrm {B}\right) , \end{aligned}$$
(2)

which defines the effective flow rate in network B. The first part of the Eq. (2) describes the dependence on the actual chain elongation via the material parameters c and \({\dot{\lambda }}_{0}\) as well as the principle macroscopic stretch state \({\overline{\lambda }}_\mathrm {chain}\). The principal macroscopic stretch state is based on the 8-chain assumption [1] and defined by \({\overline{\lambda }}_\mathrm {chain}= \sqrt{I_1/3}\). The second part of the Eq. (2) describes the connection of \(\dot{\gamma _\mathrm {B}}\) to the applied stress, which is assumed to be energetically activated. This relation is modeled through a generically expressed power-law, depending on the material parameters \({\hat{\tau }}\) and m and an effective stress measure \(\Vert {{\,\mathrm{dev}\,}}({\sigma }^{B})\Vert _F\), where \(\Vert \Vert _F\) is the Frobenius norm and \({{\,\mathrm{dev}\,}}({\sigma })\) is deviatoric part of the Cauchy stress tensor. N() is a function to provide the direction of the viscoelastic flow depending on the viscous stress in B. For a more detailed explanation of the BB model, especially with regard to the numerical implementation, the reader is referred to [6].

For a constitutive description of the mechanical behavior, a function of the Helmholtz free-energy density is introduced

$$\begin{aligned} \varPsi (\mathsf {F})=\varPsi _\mathrm {v}(J) +\varPsi _\mathrm {i}(\tilde{\mathsf {F}}), \end{aligned}$$
(3)

which can be split into a volumetric and isochoric part. The isochoric part of the deformation is characterized by \(\tilde{\mathsf {F}}=J^{-1/3}\mathsf {F}\). To account for the idealization of incompressible materials \(\varPsi _\mathrm {v}\) is introduced in [3] as

$$\begin{aligned} \varPsi _\mathrm {v}(J)=\kappa (J-1)^2, \end{aligned}$$
(4)

where the scalar \(\kappa \) can be interpreted as hydrostatic pressure. For the isochoric response of the material, \(\varPsi _\mathrm {i}\) can be defined by a phenomenological approach like the Ogden model [21]

$$\begin{aligned} \varPsi _\mathrm {i}({\tilde{\lambda }}_i)=\sum _{p=1}^n\frac{\mu _p}{\alpha _p}\left( {\tilde{\lambda }}_1^{\alpha _p}+{\tilde{\lambda }}_2^{\alpha _p}+{\tilde{\lambda }}_3^{\alpha _p}-3\right) , \end{aligned}$$
(5)

where \(\alpha _p\) and \(\mu _p\) are material parameters and n the number of terms. A micromechanically inspired approach is the Extended Tube Model [14]

$$\begin{aligned} \begin{aligned} \varPsi _\mathrm {i}({\tilde{\lambda }}_i)&=\frac{G_\mathrm {c}}{2} \left[ \frac{1-\delta ^2({\tilde{I}}_1-3)}{1-\delta ^2({\tilde{I}}_1-3)}+\ln \left( 1-\delta ^1({\tilde{I}}_1-3)\right) \right] \\&\quad +\frac{2G_\mathrm {e}}{\beta ^2}\sum ^3_{p=1}\left( {\tilde{\lambda }}_p^{-\beta }-1 \right) , \end{aligned} \end{aligned}$$
(6)

where \(\delta \) and \(\beta \) are material parameters, describing the finite extension of the polymer and global rearrangements of cross-links upon deformation, \({\tilde{I}}_1={\tilde{\lambda }}_1^2+{\tilde{\lambda }}_2^2+{\tilde{\lambda }}_3^2\) is the first invariant of the isochoric part of the Cauchy–Green tensor, \(G_\mathrm {c}\) the shear modulus characterized by the cross-linking of the network, and \(G_\mathrm {e}\) the shear modulus defined by the confining tube constrains.

To reproduce the viscous material behavior it is useful to split the isochoric free energy further by

$$\begin{aligned} \varPsi (\mathsf {F},\mathsf {F}_\text {e})=\varPsi _\text {v}(J) +\varPsi _\text{i,}\infty(\tilde{\mathsf {F}}) +\varPsi _\text {i,v}(\tilde{\mathsf {F}}_\text {e}) \end{aligned}$$
(7)

into an elastic \(\varPsi _{\mathrm{i},\infty }\) and a viscous \(\varPsi _\mathrm {i,\mathrm {v}}\) part. The elastic part characterizes the equilibrium state. Where the viscous part defines a dissipative potential, describing a non-equilibrium state. By deriving Eq. (7) with respect to the deformation gradient

$$\begin{aligned} \frac{\partial \varPsi (\tilde{\mathsf {F}},\tilde{\mathsf {F}}_\text{e})}{\partial \mathsf {F}}=\mathsf {P}_\text {v} +\mathsf {P}_{\mathrm{i},\infty } +\mathsf {P}_\mathrm {i,v}, \end{aligned}$$
(8)

a relationship can be found for the spherical \(\mathsf {P}_\mathrm {v}\) and deviatoric \(\mathsf {P}_{\mathrm {i},\infty }\) part of the 1-Piola–Kirchhoff stress. Furthermore, the quantity \(\mathsf {P}_\mathrm {i,v}\) can be introduced, which can be interpreted as non-equilibrium stress.

Experimental procedure

To model complex material behavior correctly tensile tests under uniaxial (UA, \(\lambda _1;\,\lambda _2=\lambda _3=1/\sqrt{\lambda _1}\)), plane strain (PS, \(\lambda _1;\,\lambda _2=1;\,\lambda _3=1/\lambda _1\)) and equibiaxial (EB, \(\lambda _1=\lambda _2;\,\lambda _3=1/\lambda _1^2\)) loads were carried out to parametrize the material models. The PS and EB tests were carried out on the biaxial test machine, built by Coesfeld GmbH & Co, Dortmund, Germany, which is described in more detail by [25]. Besides, uniaxial tensile tests were carried out on an universal tension-testing machine Z010 of ZwickRoell, Ulm, Germany. A NR20 (natural rubber, \(20\,\mathrm {phr}\) carbon black) material mixture from Weber & Schaer GmbH & Co. KG. was used. The compounding recipe is shown in Table 1. The samples were vulcanized with sulfur as a crosslinker for 10 minutes at \(150\,^{\circ }\mathrm {C}\). For the PS and EB test, a square specimen of \(77\,\mathrm {x}\,77\,\mathrm {x}\,1.8\,\mathrm {mm}^3\) with a bulge (diameter \(5.5\,\mathrm {mm}\)) was used. For the UA tests, a dumbbell specimen with a length of \(75\,\mathrm {mm}\) was stamped out of the square specimen after preconditioning.

Table 1 Composition of ingredients in parts per hundred rubber (phr)
Full size table

In preliminary tests, the strain fields of the test specimens were determined through an optical method of grey-value correlation, using the ARAMIS software from GOM GmbH, Braunschweig. Thus, a second-order polynomial, describing the mean strain as a function of displacement, was used to evaluate the experimental strains. The material parameters are determined in two stages: For the purely elastic characterization, the test specimen is loaded step by step with relaxation times in between to a maximum strain and then also unloaded again, as shown in Fig. 2. In a second test, the rate-dependent characterization is done by series of tests, each with one load cycle of different maximum strains and strain rates, which are listed in Table 2.

Table 2 List of the applied stretch rates and maximum stretches
Full size table

The determination of the material parameters represents a non-linear optimization problem. To solve this problem, a suitable measure for the quality of the fit and a non-linear optimizer is required. All experiments were strain-controlled, thus the difference between simulated and experimental stresses was used to determine the error. A common measure of error is the normalized mean absolute deviation (“NMAD”), which is estimated according to [15] by

$$\begin{aligned} \varepsilon _\mathrm {NMAD}=\frac{\langle |\mathsf {P}_\mathrm {sim}-\mathsf {P}_\mathrm {exp}|\rangle }{\langle |\mathsf {P}_\mathrm {exp}|\rangle }. \end{aligned}$$
(9)

This error measure is considered robust and can be used for the comparison of several tests with different strain and stress amplitudes due to its standardization. Within this work, the “Differential-Evolution” and “Basin-Hopping” algorithms from the Python-based software SciPy are used as optimizers. The stress for the simulated material behavior for the purely elastic behavior is determined in an own Python routine. The cyclic experiments were simulated in a FE analysis with a single second-order hexahedral element and corresponding boundary conditions.

Equilibrium behavior

The results of the step test in Fig. 2 show that the stress on the loading path relaxes faster than on the unloading path. In [16] this phenomenon is interpreted as a proof that the equilibrium behavior can only be represented by a hysteresis. Another explanation is given in [2]. The relaxing parts of the polymer on the load path are subjected to tensile forces, whereas those on the unloading path are under compressive load. This causes a fundamentally different behavior. Another aspect is the different distance to the equilibrium state. Although the total elongation at each stage is the same due to the same external displacement, this does not imply the same loading of the viscous parts, since the material cannot completely relax at any stage. Experimental confirmation of one explanation seems possible only by infinitely long relaxations test, which is not possible.

Fig. 2
figure 2

Stretch \(\lambda \) and stress \(\mathsf {P}\) curve over time t in a step test. Loading times \(\varDelta t_\mathrm {D}\) and relaxation times \(\varDelta t_\mathrm {r}\) at each step \(\varDelta P\)

Full size image

However, the following investigation aims to determine the most suitable test parameters to determine the equilibrium curve. The equilibrium stress is in the range between the stresses after the steps with the same strain. Determining the value from the arithmetic mean leads to an overestimation of the equilibrium, because the stress on the loading path relaxes faster. Suitable test parameters lead to a small difference in stress \(\varDelta P\) and therefore to the smaller error in determining the equilibrium points. The studied parameters are \(\varDelta t_\mathrm {D}\) and \(\varDelta t_\mathrm {r}\), which accordingly describe the finite time to apply the deformation and the relaxation time on each load step. The Fig. 3 shows the influence of the loading time on the different stresses from loading and unloading with the same strain magnitude of a PS tensile test.

Fig. 3
figure 3

Influence of loading time \(\varDelta t_\mathrm {D}\) on the difference of stresses between loading and unloading path of step tests after a relaxation time of \(\varDelta t_\mathrm {r}=60\,\mathrm {s}\)

Full size image

The Fig. 3 also shows, that the difference decreases with increasing strain. This is due to the fact that the relaxation process is energetically activated. Because at higher strains there are also significantly higher stresses, the material relaxes much faster towards equilibrium. Furthermore, the figure also shows that a decreasing loading time leads to a strong decrease in the difference. This becomes particularly clear comparing test with \(\varDelta t_\mathrm {D}=1\,\mathrm {s}\) and \(\varDelta t_\mathrm {D}=10\,\mathrm {s}\). An analogous comparison of relaxation times of \(1\,\mathrm {min}\) and \(10\,\mathrm {min}\) was done. The difference in stresses decreases with increasing relaxation time. However, the minimization of the difference and thus of the error does not seem to be justified by the significantly higher experimental effort. For the determination of the equilibrium stress, it is, therefore, appropriate to carry out step tests with \(\varDelta t_\mathrm {r}>60\,\mathrm {s}\) and \(\varDelta t_\mathrm {D}>10\,\mathrm {s}\), which is equivalent to stretch rates of \({\dot{\lambda }}<0.01\,\mathrm {s}^{-1}\).

Parameter identification of the material model

The step tests were carried out and the corresponding points on the equilibrium curve were determined. These points were used to parameterize both an extended Tube model and a second-order Ogden model, which lead to the material parameters in Table 3. The points are shown together with the result of the extended Tube model in Fig. 4. The extended tube model has the smallest normalized error of \(\varepsilon _\mathrm {NMAD}=0.054\). Especially the behavior during uniaxial and equibiaxial tension can be well reproduced by the model. On average, the predicted stresses deviate less than \(0.02\,\mathrm {MPa}\) from those in the experiments. On the other hand, the behavior in plane tension can be described much worse, resulting in a mean error of \(0.131\,\mathrm {MPa}\). The results of the Ogden model with two parameters show a similar quality with \(\varepsilon _\mathrm {NMAD}=0.057\).

Table 3 Parameters of two hyperelastic material models for NR20
Full size table
Fig. 4
figure 4

The markers show the stretch-strain behavior of NR20, which was derived experimentally from the step tests. Besides, the lines show the course of the parameterized extended tube model

Full size image

The cyclic tests were carried out and the results were used to parameterize a BB model using the Ogden model as hyperelastic part in the FE software ABAQUS. In comparison to this, a Prony series with 10 links based on the extended tube model was characterized in ANSYS. The error for both models is \(\varepsilon _\mathrm {NMAD}=0.096\). A comparison of some experiments with the corresponding simulated results is shown in the Fig. 5. The corresponding material parameters are listed in Table 4. The illustration shows that viscous behavior can be represented quite well in some load cases like Fig. 5a, b whereas the other two cases are not described sufficiently.

One reason for the deviations between the calculated and the experimental stress curves is the path dependent relaxation. As described in the last section, the relaxation is faster on the loading path than during unloading. The models cannot represent this behavior properly. A further problem is the dependence of the relaxation on the current stretch. Again the Prony series cannot model this. The BB model describes this via the principal macroscopic stretch \({\overline{\lambda }}_\mathrm {chain}\), which is only determined by the first invariant of the elongation. Therefore, load cases, which include a change in the second invariant of the Cauchy–Green tensor, cannot be capture by the BB model correctly.

Fig. 5
figure 5

Comparison of simulated and measured stress stretch curves for different load cycles. a UA tension at \(0.3\,\mathrm {s}^{-1}\). b BA tension at \(0.01\,\mathrm {s}^{-1}\). c PS tension at \(2.4\,\mathrm {s}^{-1}\). d BA tension at \(1.4\,\mathrm {s}^{-1}\). The BB model was calculated with ABAQUS and the Prony series with Ansys

Full size image
Table 4 Parameters of two viscoelastic material models for NR20
Full size table

Crack behavior

Material forces

The starting point for this approach is the Eshelby stress tensor or energy momentum tensor of elastostatics, which is defined as

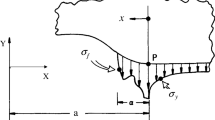
$$\begin{aligned} \mathsf {Q}=\varPsi {\delta }-\mathsf {P}^\mathrm{T} \cdot \nabla \vec {u}, \end{aligned}$$
(10)

where \({\delta }\) is the Kronecker delta and \(\nabla \vec {u}\) is the gradient of the displacement. The sink in the field of \(\mathsf {Q}\) at a crack tip can be interpreted as a driving force for the crack growth and is called material force. Material forces differ from the “normal” forces in that they are described by changes in material and not in the actual physical reference system, see [18] for an extensive explanation. In a two-dimensional elastic body with a crack, a shrinking path S around the tip is defined, like in Fig. 6. Applying the divergence theorem the material forces \(\vec {R}\) can be calculated by

$$\begin{aligned} \vec {R} = \lim _{r\rightarrow 0} \int _S \left( \mathsf {Q} \vec {n} \right) \mathrm{d}s, \end{aligned}$$
(11)

where r describes the radius of the shrinking path S and \(\vec {n}\) the normal vector to the path. For a general calculation of \(\vec {R}\), a closed integration path via an arbitrary path \(\varGamma \), including the crack edges \(\varGamma ^+\) and \(\varGamma ^-\), will be defined. This contour characterizes the defect-free material area \(A^{\varGamma }\), which does not contain the crack tip. For this path, the Eq. (11) is extended by

$$\begin{aligned} \vec {R} = \int _\varGamma \left( \mathsf {Q} \vec {n} \right) \mathrm{d}s+ \int _{\varGamma ^++\varGamma ^-} \left( \mathsf {Q} \vec {n}\right) \mathrm{d}s - \int _{A^\varGamma } \left( \nabla \cdot \mathsf {Q}^\mathrm{T}\right) \mathrm{d}A. \end{aligned}$$
(12)

The surface integral in Eq. (12) is called dissipation force and defines the inelastic body force. With purely elastic material behavior and straight crack growth, the contour integral over the edges and the surface integral vanish, and the Eq. (12) is simplified to a path independent vectorial J-integral. A prerequisite for the use of this concept is that the constitutive material laws are derived from the Helmholtz free energy and that a change in non-elastic strains is accompanied by a dissipative potential [19].

Fig. 6
figure 6

a Section of a cracked body with different ways of integration. Schematic representation of the energy momentum tensor as a vector field with b only a sink at the crack tip for purely elastic materials and c sink at the crack tip and away from it for dissipative materials

Full size image

Numerical example

For the numerical investigation of cracks, the tests on the biaxial testing machine were simulated. The discretization for the FE model is shown in Fig. 7, which uses plane quadrilateral elements with a second order shape functions. The crack tip was modeled by collapsed quadrilateral elements.

Fig. 7
figure 7

FE-mesh of the symmetrical biaxial sample with used boundary conditions including model dimensions

Full size image

The material forces were calculation in an own user-subroutine. For this, the line integral in Eq. (11) was converted into a surface integral via a virtual crack extension as described in [26]. All required parameters were determined or interpolated at the integration points. The integration was done numerically via the Gaussian quadrature.

In the first step, the relation between material forces in the direction of crack growth and the radius of the line integrals is analyzed. A displacement was applied to the upper side of the model to stretch the sample outside the crack region up to \(\lambda _{y} = 1.25\). The strain rate is initially set to \({\dot{\lambda }}_{y} = 0.5\,\mathrm {s}^{-1}\). The material is described by the extended-tube model extended by a prony series, which was defined in section“ Parameter identification of the material model”. Figure 8 shows the results of this investigation.

Fig. 8
figure 8

Proportion of material force in the direction of crack growth \(R_x\) as a function of the distance to the tip r

Full size image

The graph shows a local maximum point with \(8.3\,\mathrm {N}/\mathrm {mm}\) at the first element row around the crack tip and decreases to a value of \(7.5\,\mathrm {N}/\mathrm {mm}\) at \(r=0.3\,\mathrm {mm}\). This phenomenon has been described in the literature with elasto-plastic material, see [20, 27]. The area with the same strain magnitude around the crack tip is kidney-shaped. However, the evaluation of the material forces are carried out by circular line integrals, which is going through areas with different strain rates and thus also different material stiffness. From a distance of \(r=0.3\,\mathrm {mm}\), \(R_{x}\) begins to rise to a value of \(9.2\,\mathrm {N}/\mathrm {mm}\) at the very edge of the specimen. This increase is due to the viscous behavior of the material, converting energy independent of crack propagation. In addition, the rate of change decreases with distance to the crack tip, since the strain rates and thus also the dissipation becomes smaller. This area acts as a material shield, since parts of the energy introduced from the outside do not flow further to the crack, but dissipate on the surface. The phenomenon of material shielding or reverse anti-shielding is described in [28].

In a second step, three quantities and their dependencies on stretch rate are compared: \(R_{x,\mathrm {T}}\) is calculated by a path of the first element row around the crack, \(R_{x,\mathrm {F}}\) is determined by a path along the edge of the sample and the vectorial J-integral \(J_{x}\). \(R_{x,\mathrm {T}}\) characterizes the driving force of the crack growth. \(R_{x,\mathrm {F}}\) consists of both the driving and the global dissipation forces. Therefore, this quantity includes all dissipative processes even those far away from the crack tip, analogous to the tearing energy [24]. These values are compared to the \(J_{x}\), which was calculated with a purely elastic material without Prony extension. \(J_{x}\) characterizes the crack behavior under infinitely slow loading rates. Again the model was loaded by a displacement with the same magnitude of \(\lambda _{y} = 1.25\), but at different rates.

Fig. 9
figure 9

Material forces at the crack tip \(R_{x,\mathrm {T}}\), at the edge of the specimen \(R_{x,\mathrm {F}}\) and \(J_{x}\) for a hyperelastic material depending on the rate of the load

Full size image

Figure 9 shows that \(J_x\) underestimates the driving force \(R_{x,\mathrm {T}}\). At very low strain rates such as \({\dot{\lambda }}_{y} =0.005\,\mathrm {s}^{-1}\), this error is only \(17\%\). However, at higher strain rates like \({\dot{\lambda }}_{y} =2.5\,\mathrm {s}^{-1}\), the error increases up to \(40\%\). Furthermore, this approach fails to examine the influence of the load rates. On the other hand, \(R_{x,\mathrm {F}}\) overestimates the value of \(R_{x,\mathrm {T}}\). At \({\dot{\lambda }}_{y} =2.5\,\mathrm {s}^{-1}\) this error is \(7\%\) but increases to \(30\%\) at \({\dot{\lambda }}_{y} =0.005\,\mathrm {s}^{-1}\).

The Fig. 9 also shows that the material forces acting directly on the crack tip are of the same order of magnitude as those acting in the region far from the crack tip. This is again an indication that under the investigated boundary conditions the dissipative effects for the crack propagation are of the same order of magnitude as the viscous effects far from the crack tip. Additionally, \(R_{x,\mathrm {F}}\) depends on the sample size. Therefore, for an exact description of the crack behavior of elastomers, these energetic parts must be considered separately.

Both \(R_{x,\mathrm {T}}\) and \(R_{x,\mathrm {F}}\) increase with the loading rates. For the investigated range the relation between the two quantities and the logarithm of the stretch rate is approximately linear. The increase of \(R_{x,\mathrm {F}}\) is due to the fact that the stiffness of the material increases with increasing rate. If the test specimen is loaded with the same strain amplitude but at different strain rates, the external forces do more work, which in turn leads to an increase in material forces. Compared to \(R_{x,\mathrm {F}}\), the value of \(R_{x,\mathrm {T}}\) increases much faster. This finding suggests that at higher load rates a higher proportion of the work is done independently of crack growth compared to lower rates.

Conclusions

In this contribution, a BB model as well as a Prony series were parameterized based on experiments to describe the rate-dependent viscous behavior of natural rubber. To model even complex loading conditions not only UA and PS, but also EB tests were carried out. The models show some difficulties in correctly characterizing the dissipative behavior, for which reasons were discussed.

Common methods for crack characterization such as the J-integral or the tearing energy fail to include the influence of dissipative effects in inelastic materials or to isolate them from effects far away from the crack tip. Therefore, here the concept of material forces and dissipation rate was used to separate these energetic quantities within a framework of finite element analysis. In the next step, this separation has to be performed experimentally and compared with the numerical results through thermographic measurements like [7, 8].