Stochastic Continuous Modeling for Pillar Stress Estimation and Comparison with 2D Numerical, and Analytical Solutions in an Underground Stone Mine

Abstract

Pillar collapses are events that due to their severe consequences can be classified as high risk. The design of pillars in underground room-and-pillar operations should migrate to risk-based design approaches. The authors of this work proposed a risk-based pillar design methodology that integrates stochastic discrete element modeling for pillar strength estimation, and stochastic finite volume modeling (FVM) for stress estimation. This paper focuses on the stochastic FVM component for stress estimation. The mining and geomechanical aspects of a case study mine (CSM) are described and pillar stresses are estimated by using three approaches: (1) analytical solutions, (2) 2D finite element modeling, and (3) 3D finite volume modeling. This operation extracts a 30° dipping deposit, which makes current underground stone mine design guidelines inapplicable for this CSM. This work compares results from each stress estimation approach and discusses uses the point estimate method as a simplified stochastic approach to evaluate the effect of rock mass elastic properties variability on pillar stress distribution. Results from this work show that the three estimation approaches lead to different estimations, possibly, due to the wide range of assumptions each estimation approach considers. It was also determined that the horizontal to vertical stress ratio has a significant impact on pillar stress magnitude. Therefore, it is recommended to perform in situ stress measurements, or assume worst-case-scenario values to account and reduce uncertainty due to this parameter. The stochastic stress estimation approach used in this paper provides results that can integrate a risk-based pillar design framework.

1 Introduction

Pillar design is one of the most critical tasks in underground room and pillar mine design. Not only should the dimensions of these support elements maximize the volume of material extracted, but also ensure the global stability of the operation. Even though the collapse of pillars in hard rock mines are events that occur with less frequency in comparison to other ground instability issues, it has been reported that their consequences are much more severe [1, 2, 3, 4]. Air blasts, cascade pillar collapses, surface subsidence, and reserves sterilization are some of the causes the collapse of a pillar can produce. Pillar collapses should be treated as high-risk events; therefore, their design, excavation, and monitoring should implement risk management approaches. In a previous work, the authors proposed a risk-based pillar design methodology that integrates stochastic discrete element modeling for pillar strength estimation, and stochastic continuous numerical modeling for pillar stress determination [5]. This paper focuses on the pillar stress determination section of the proposed methodology by evaluating the stresses on a case study mine (CSM). Results from the 3D stochastic finite volume pillar stress estimation model are compared with a 2D finite element model and analytical solutions.

When an excavation takes place in a rock mass, the equilibrium state of the system is modified. This causes the stress state to change until a new equilibrium is reached. In the room and pillar mining method, the rock pillars should be designed so these elements can withstand the increment in stress magnitude caused due to the removal of rock material. There are a series of factors that influence the magnitude and orientation of the loads applied to the pillars [6]. Among some of these factors are included the in situ stress conditions; the mining-induced stress changes; the span of the openings between pillars; the arrangement, shape, and orientation of the pillars; ground water; and the effect of geological features such as joints, karsts, and faults.

There are two main approaches used to estimate the stress applied to a pillar structure: analytical and numerical. Analytical pillar stress determination methods are mathematical expressions derived from physical principles. Analytical techniques have been used successfully to estimate stresses in underground operations; however, their applicability is limited to a series of assumptions that often overestimate pillar stress values. On the other hand, numerical methods are computational simulation techniques used to solve complex stress-deformation analyses based on the governing equations for solid and deformable bodies. Numerical modeling has been proven useful to estimate the stresses acting around underground mine excavations. Multiple authors have used continuous modeling methods such as finite element method (FEM), finite volume method (FVM), or boundary element method to estimate stresses around underground mine pillars and evaluate multiple design scenarios [2, 7, 8]. Numerical approaches may yield different values depending on whether the solution implemented allows to account for a 3D solution or not [9]. In this work, 2D and 3D continuous solutions will be compared to determine differences between both approaches.

Uncertainty is a term that reflects the degree of knowledge an observer has with regard to certain parameter or process. Some authors have discussed that even though variability and uncertainty are two different concepts, in the context of rock engineering, both terms define intertwined processes [10]. This means that characterizing the variability of a measurable parameter (e.g., intact rock strengths, discontinuities orientation, rock density) helps to reduce uncertainty (or increase our degree of knowledge). Dunn discussed the impact of geotechnical uncertainty on underground mine design, and the importance of adequately characterizing it to improve safety through an adequate risk assessment process [11]. In this work, a simplified stochastic approach is used to evaluate the effect of rock mass elastic properties’ variability on pillar stress distribution and variability. This analysis seeks to reduce the uncertainty in the pillar stress estimation process.

This work is divided in three sections. The initial section describes the CSM operational conditions, mining methods, and geomechanical setting. The second section presents the methodology used to evaluate pillar stresses in the mine by using three different estimation approaches. It also discusses the usage of the point estimate method as a simplified stochastic approach for characterizing the effect of rock mass properties variability on pillar stresses. Finally, results from all stress estimation approaches are compared and discussed in the context of current pillar design standards, and risk-based design approaches.

2 Case Study Mine and Geomechanical Conditions

The CSM consists of an underground operation that extracts an approximately 30-m (≈ 100 ft)-thick limestone seam. The ore body is located in the limb of a regional syncline structure oriented approximately N36°E and dipping 30° towards the SE. As the deposit gets deeper and closer to the limb of the fold structure, the ore body gets thinner and flattens out. Figure 1 shows an isometric view of the surface and the mine excavations. It is possible to observe how the tunnels follow the trend of the ore body. The tunnels are colored according to their depth with respect to the mine entrance, where blue indicates those tunnels that are at the same level of the mine’s portal, and those marked in red indicate the deepest levels with respect to the mine’s entry. This section describes the mining methods and introduces the geomechanical conditions of the operation.

Fig. 1

Isometric view of the CSM tunnels from the surface

3 Mining Methods

This operation’s mining method consists of a room and pillar with eventual stoping. In the areas of the mine where the limestone seam is consistent and thick enough, 12.8-m (42 ft)-wide and 30-m (100 ft)-high stopes are conformed. The excavation process starts with an initial 12.8 m (42 ft) by 7.6 m (25 ft) top drift (hanging wall tunnel), followed by a bottom drift (foot wall tunnel) with the same dimensions. The top and bottom drift are separated by a 15.2-m (50 ft) sill, which is extracted by vertical long hole drilling. Figure 2 illustrates the configuration of the stopes.

Fig. 2

Stopes configuration indicating dimensions of the sill and top and bottom drifts. Modified after [12]

The open stopes are supported by squared 24-m (80 ft)-wide and 30-m (100 ft)-tall pillars, with a 0.8 width-to-height ratio (W/H). Figures 2 and 3 describe the mining sequence used in the mine. The process begins with the opening of a top drift close to the hanging wall of the deposit as indicated in Fig. 3a. This initial tunnel will become the roof of the first stope when fully excavated. A bottom drift close to the ore body’s footwall is then excavated underneath the initial top drift as indicated in Fig. 3b. At the same time, the top hanging wall drift for the second stope is also advanced parallel to the initial stope bottom drift. The bottom drift of the second stope is excavated underneath the second stope top drift as shown in Fig. 3c. At this point, the top and bottom drifts for both stopes have been excavated. The portion of rock in between top and bottom drifts is referred to as the sill bench. A crosscut connecting the first stope bottom drift and the second stope top drift is then excavated. At the same time, the sill bench is drilled using vertical long hole drilling from the first stope top drift to the first stope bottom drift as indicated in Fig. 3d. Later, the sill bench is blasted and the blasted material is mucked through the second stope top drift, as shown in Fig. 3e. Finally, the sill bench on stope 2 and the ore between pillars are drilled for subsequent blasting. Figure 3g, h indicates the final layout of the stopes after excavation, where (g) represents a cross-section in between the pillars, and (h) represents a cross-section through one of the pillars.

Fig. 3

Excavation sequence. (a) Excavation of the hanging wall top drift for stope 1, (b) excavation of the bottom foot wall drift for stope 1 and top hanging wall drift for stope 2, (c) excavation of the bottom drift for stope 2, (d) stope 1 bottom drift and the stope 2 top drift are communicated through the excavation of a connection crosscut. Long hole drilling from top to bottom drifts in stope 1 is also prepared; (e) long hole blasting takes place leading to the conformation of the open stope. Blasted material in stope 1 is removed from the stope 2 top drift; (f) blasting pattern is drilled for stop 2 full excavation, and removal of material between pillars connecting stopes 1 and 2, (g) final configuration of the sopping on a section that does not intersect a pillar, and (h) final configuration of the sopping on a section intersecting a pillar

Main ground instability hazards encountered in the CSM are related to the presence of discontinuities, and karst features. Discontinuities such as the bedding plane, sub-vertical, and oblique joint sets intercept forming rock blocks that fall or slide from the back and the ribs of the excavation. This failure mechanism was previously discussed and analyzed by the authors as evidenced in Fig. 4a and b [13]. On the other hand, the presence of karst features intersecting pillars poses an additional pillar stability hazard as discussed by Baggett et al. [14] and Soni et al. [15, 16]. The following section describes relevant geomechanical aspects necessary to design and evaluate pillar conditions in the CSM. These aspects are components of the mine’s geotechnical model, and will be used throughout this work to base engineering design recommendations.

Fig. 4

Geotechnical conditions observed in the CSM. a Rock bocks fallen from the back of a top drift, b intersection of bedding plane and vertical discontinuities forming rock wedges supported by rock bolts, and c karst features intersecting rock pillars in a non-stoped area [17]

4 Geomechanical Conditions

Geomechanical parameters from the operations were obtained from previous field exploration and laboratory testing campaigns undergone in the mine. Already-existing geotechnical information was complemented with field observations, and laser scans of the study area. The geomechanical parameters discussed in this section are the most relevant parameters for pillar design. Among the geomechanical parameters mentioned in this section are included the intact rock properties, discontinuity setting, stress setting, and rock mass mechanical properties.

4.1 Intact Rock Properties

A summary of geomechanical properties of the intact rock was provided by the mine operator. The database consisted of results from a series of density tests, uniaxial compressive tests, and Brazilian tensile tests. For each rock unit (Hanging wall, Ore Body, and Footwall), a total of six samples were tested for density, uniaxial compressive strength, and tensile strength. The database did not contain information about the specific location where the samples were taken from in the CSM. Table 1 summarizes measured properties from the laboratory tests, including, density, uniaxial compressive strength, Brazilian tensile strength, Young’s modulus, and Poisson’s ratio. The mean and standard deviation are reported for each lithology.

Table 1 Intact rock property test results from CSM [18]

Intact rock properties are used as inputs in analytical and numerical analysis. The lack of knowledge of where exactly these rock samples were taken and the limited amount of laboratory tests provide uncertainty to any following analysis. In this work, it will be assumed that these parameters are normally distributed following the mean and standard deviations reported on Table 1. The nature and continuity of this deposit makes this an acceptable assumption for preliminary evaluations.

4.2 Discontinuities

In previous work, the authors performed the discontinuity mapping of section A [19]. Figure 5 summarizes the orientation, trace length, and fracture density distributions for the mapped discontinuities on that section. Four main discontinuity sets were identified during the mapping process. The bedding plane set, marked as SET 4, reported an approximate strike of N34°E, and a dip of 29° towards SE. The second discontinuity set, referred as SET 1, corresponded to a sub-vertical joint set perpendicular to the bedding plane orientation. SET 2 and SET 3 were identified as steeply dipping oblique joints.

Fig. 5

Stereo net analysis and trace length and fracture density summary statistics for a section in the CSM [19]

4.3 Rock Mass Properties

Due to the scale of the mine openings, rock mass response not only depends on the intact rock properties, but also on the discontinuities that compose it such as bedding planes, joints, and karsts. A commonly accepted criterion to estimate rock mass properties is the Generalized Hoek–Brown failure criterion [20]. This failure criterion allows to account for the effect of discontinuities in rock strength by considering a geological strength index (GSI). The GSI is a classification system that considers the structure or blockiness of the rock mass and the surface condition of the discontinuities. In the generalized Hoek–Brown criterion, the rock mass strength and deformation properties are estimated by reducing the intact rock properties according to the GSI value observed in the field. Equation 1 presents the generalized Hoek–Brown criterion equation for rock mass strength. In this equation, ${\sigma }_{1}$ is the maximum principal stress, ${\sigma }_{3}$ is minimum principal stresses, and ${\sigma }_{ci}$ is the uniaxial compressive strength of the intact rock. ${m}_{b}$, s, and a are constants that depend on the intact rock material constant ${m}_{i}$, the GSI for the specific rock mass, and a disturbance factor D that depends on how much is the rock mass affected due to blasting or stress relaxation. The intact rock material constant ${m}_{i}$ should be ideally obtained from triaxial laboratory tests.

$${{\varvec{\sigma}}}_{1}={{\varvec{\sigma}}}_{3}+{{\varvec{\sigma}}}_{{{\varvec{c}}}_{{\varvec{i}}}}{\left\{{{\varvec{m}}}_{{\varvec{b}}}\left(\frac{{{\varvec{\sigma}}}_{3}}{{{\varvec{\sigma}}}_{{{\varvec{c}}}_{{\varvec{i}}}}}\right)+{\varvec{s}}\right\}}^{{\varvec{a}}}$$

(1)

Equations 2, 3, and 4 can be used to calculate the parameters ${m}_{b}$, s, and a.

$${m}_{b}={m}_{i}{e}^{\left[\frac{\left(GSI-100\right)}{\left(28-14D\right)}\right]}$$

(2)

$$s={e}^{\left[\frac{(GSI-100)}{(9-3D)}\right]}$$

(3)

$$a=\frac{1}{2}+\frac{1}{6}\left[{e}^{\left(-\frac{GSI}{15}\right)}-{e}^{\left(-\frac{20}{3}\right)}\right]$$

(4)

Deformational properties of the rock mass can also be estimated using the following expression derived by Hoek and Diederichs [21]. This equation estimates the rock mass deformation modulus (${E}_{rm})$ based on the intact rock deformation modulus (${E}_{i})$, the GSI, and the disturbance factor (D) as shown in Eq. 5.

$${E}_{rm}={E}_{i}\left\{0.02+\frac{1-{~}^{D}\!\left/ \!{~}_{2}\right.}{1+{e}^{\left[\left(60+15D-GSI\right)/11\right]}}\right\}$$

(5)

The generalized Hoek–Brown criterion is used to estimate rock mass properties (Fig. 6). Table 2 presents the generalized Hoek–Brown parameters for the ore body, the footwall, and hanging wall. The uniaxial compressive strength and Young’s modulus obtained from uniaxial compressive tests, and GSI values observed in the field, were used to estimate rock mass properties. An average GSI value of 75 was used in this analysis. GSI values had been reported around the study area. Even though the operation is an underground mine with little blasting control, a disturbance factor of 0 was assumed since the simulations performed were intended to determine elastically stresses in a mine-wide model.

Fig. 6

Generalized Hoek–Brown failure criterion by lithology

Table 2 Generalized Hoek–Brown properties for hanging wall, ore body, and foot wall according to laboratory data and field observations

4.4 In Situ Stress

The worlds stress map (WSM) and the Virginia Geology were used to understand principal stress orientation close to the CSM location. Figure 7 presents a google earth view including Virginia Geology and WSM information [22].

Fig. 7

Virginia geology overlapped with world stress map information

Figure 8 shows two WSM data points located over the same geological province (Valley and Ridge) where the mine is located. Point A is a data point obtained using earthquake focal mechanisms measured in Giles county, 11 miles away east from Blacksburg. Point B is located further north in Botetourt county 38 miles away NW from Blacksburg. Point B was measured by borehole breakout; in this test, there were measured 5 breakouts along 427 m at a depth of 2.21 km. According to the data, these two measurements are from July 6, 1993.

Fig. 8

World stress map information measured close to Blacksburg area. (A) Stress measured by using earthquake focal mechanisms in Giles county, VA. (B) Stress measured during well bore breakout in Botetourt county, VA

Table 3 presents a summary of the orientations of the two selected points from the stress map. Both values indicate a maximum horizontal stress (${\sigma }_{H}$) oriented towards north west ranging in its azimuth from 35° to 55°, with a mean between 40° and 45°. This ${\sigma }_{H}$ orientation is approximately parallel to the strike of the ore body and the mine drifts and stopes, indicating favorable conditions for the mine stability. No stress magnitude is reported on any of the observed data points. Therefore, there is uncertainty on the possible horizontal to vertical stress ratio. It is recommended to evaluate different horizontal-to-vertical stress ratio through numerical simulations to evaluate the less favorable conditions when estimating pillar loading conditions.

Table 3 Stress orientation summary

5 Methodology

The following section describes three pillar stress estimation approaches used to evaluate stresses in the CSM. Results from each numerical and analytical approach are compared and evaluated in the context of current pillar design standards. In addition, the point estimate method (PEM) is suggested as a method to evaluate the effect of rock mass elastic properties’ variability on pillar stress distribution.

6 Analytical Methods for Pillar Stress Estimation

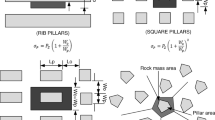
Analytical methods consist of mathematical expressions derived from the physical principle of static equilibrium. The most common analytical method for pillar stress estimation is the tributary area theory. This method states that the load shed to the pillars is proportional to the open area that corresponds to each of the pillars in the excavation layout. It is assumed that the ground topography above the excavations is completely flat, and the ore body is continuous, consistent, and flat-lying. In addition, the method only accounts for the stress component acting parallel to the pillar’s axis [23]. The tributary area method has a series of variants that have been developed for multiple applications and particular cases. Lunder [6] described very well many of these variants. Considering the CSM conditions, the tributary area approach and the variant for inclined seams proposed by Pariseau [24] will be used to analytically estimate pillar stresses on the mine at different depth levels from an analytical stand point.

Pariseau’s inclined pillar stress formulas are expressed in terms of the extraction ratio. It is also function of the in situ stress on top of the pillar, the horizontal-to-vertical stress ratio, and the dip of the deposit. Equation 6 and Eq. 7 represent the average normal stress and average shear stress applied to the pillar, respectively.

$${\sigma }_{p}=\frac{\gamma h*\frac{\left(1+{K}_{o}\right)+\left(1-{K}_{o}\right)\mathrm{cos}2\alpha }{2}}{(1-ER)}$$

(6)

$${\tau }_{p}=\frac{\gamma h*\frac{\left(1-{K}_{o}\right)\mathrm{sin}2\alpha }{2}}{(1-ER)}$$

(7)

where ${\sigma }_{p}$ is the average normal pillar of stress (MPa), ${\tau }_{p}$ is the average shear pillar stress (MPa), $\gamma$ is the average specific weight of overburden $\left(MN/{m}^{3}\right)$, $h$ is the depth below the surface (m), ${K}_{o}$ is the ratio of in situ horizontal to vertical stress, $\mathrm{ER}$ is the extraction ratio, and $\alpha$ is the dip of the seam (°).

Notice that when the horizontal to vertical stress ratio (${K}_{o})$ is 1.0, or when the dipping of the deposit is 0°, the results from the inclined pillar stress formula are the same of those obtained using the conventional tributary area formula, and there is no shear stress component.

7 2D Finite Element Modeling for Pillar Stress Estimation

A preliminary finite element analysis using the software RS2 from Rocscience was carried out to compare pillar stress estimation empirical approaches in the CSM [25]. Figure 9 indicates the numerical model setup, where nine stopes are excavated leaving eight pillars as support elements. Stope and pillar dimensions are the same as the ones described in previous sections. Three geotechnical units were defined, the hanging wall, the ore body, and the foot wall. The stopes are excavated on the ore body and the supporting pillars are constituted of the ore body material. The analysis was performed in the elastic range. The generalized Hoek–Brown failure criterion was used, and the material properties were selected from Table 2. The stress condition was defined using a gravity field stress considering the surface topography from Fig. 9. The displacements on the sides and the bottom of the model were restrained in both vertical and horizontal directions. Due to the limited information on stress magnitude, four stress scenarios were assumed in the analysis by assigning the horizontal-to-vertical stress ratio (${K}_{o}$) values of 0.5, 1.0, and 1.5.

Fig. 9

RS2 pillar stress estimation model setup

A stress measurement line crossing all pillars through the center was defined. This horizontal line was used to measure normal stress, shear stress, maximum principal stress, and minimum principal stress at multiple elements along each pillar. These measurements were used to calculate average values and standard deviations for each stress component. Figure 10 indicates on red the measurement line that crosses each pillar in the model.

Fig. 10

Stress measurement line along the conformed pillars in the 2D finite element model

The depth from the surface to the center of each pillar was measured. Table 4 summarizes these measurements. Due to the irregular surface topography shown in Fig. 9, the increase in depth between the pillars is not linear. Therefore, stresses applied to each pillar increase in a non-linear way. It is important to consider these depths to compare stress estimation results obtained from the tributary area approach and the inclined pillar stress formula.

Table 4 Pillar depth from the ground surface

8 3D Finite Volume Modeling for Pillar Stress Estimation

Surface topography and mine design information were used to generate a 3D mine geometry in Rhinoceros [26]. Figure 11 shows a plane view of the mine’s tunnels and the surface topography. A simulation area of 1000 ha was defined to perform the numerical simulation. The selected area corresponds to the sections of the mine where most of the geotechnical data was collected. The dip and strike of the ore body were constant, and the area was actively in operation.

Fig. 11

Plane view of the CSM with elevation contours

Due to that the underground excavation information was outdated and the stope geometry was not fully represented by the triangulated surfaces, a simplified mine geometry aligned with current pillar design and excavations was generated. Figure 12a presents the surface topography overlaid with the underground excavation surface triangulations limited by the defined modeling area marked on red. Figure 12b shows the simplified mine excavations represented by approximately 415-m-long, 12.8-m-wide, and 30-m-high stopes, marked in yellow. The crosscuts between stopes are marked in orange, leaving 24-m-wide squared pillars between stopes. Griddle was used to create a mesh model to import the geometry into the software 3DEC Version 7.0 from ITASCA [27]. A finer mesh was used close to the excavations and the ore body.

Fig. 12

Isometric view of the simulation area. a Simulation area overlaid with current underground excavation tunnels. b Simulation area overlaid with simplified mine model

The ore body was divided into three lithologies, hanging wall, ore body, and footwall. Material properties were defined as elastic for each rock unit since the purpose of the simulation was to map ultimate pillar stress distribution in the mine. Table 5 summarizes the elastic properties for each lithology considered in the model. The simulation used the rock mass Young’s modulus estimated using the generalized Hoek–Brown criterion as presented in Table 2. The rock mass Young’s modulus was the only parameter considered as variable.

Table 5 Input material properties for 3D numerical model

In situ stress conditions were defined using the “insitu topography” command. This approach enabled to account for the effect of changing topography on pillars’ stress distribution. Velocity vectors normal to the sides and the bottom of the model were fixed to 0 m/s. Figure 13 shows the vertical stress magnitude of the in situ condition of the model. Boundary conditions are also marked with blue squares indicating a velocity boundary on the faces.

Fig. 13

In situ vertical stress model and boundary conditions

In situ stress data presented in the previous section indicated that maximum principal orientation is parallel to the strike of the ore body. The model was set so the ore body’s strike was parallel to the X-axis. Due to the lack of direct stress measurements, three different horizontal-to-vertical stress ratios were evaluated to define a less favorable condition (the stress condition yielding the highest pillar stress estimates). Table 6 summarizes the horizontal to vertical stress ratios for each scenario. ${\sigma }_{H}$ represents the maximum horizontal stress which will be parallel to the X-axis in all three scenarios, ${\sigma }_{h}$ represents the horizontal stress parallel to the Y-axis, and ${\sigma }_{v}$ represents the vertical stress which is parallel to the Z-axis. In stress scenario 1, all three stress magnitudes were the same. In scenario 2, ${\sigma }_{H}$ and ${\sigma }_{v}$ had the same magnitude and ${\sigma }_{h}$ was 0.5 times lower than ${\sigma }_{v}$. Scenario 3 assumed that both ${\sigma }_{H}$ and ${\sigma }_{h}$ were 1.5 times higher than ${\sigma }_{v}$. The selection of these three stress conditions was made based on that it would enable to capture all possible stress scenarios in the case study mine. However, it is important to acknowledge that real stress orientation magnitudes will not be known until a detailed field stress measurement study takes place on the site.

Table 6 Horizontal to vertical stress ratios for the different stress scenarios

The model was run initially until reaching equilibrium to obtain in situ stress conditions after 8000 cycles. Figure 13 shows the vertical stress of the in situ stress model prior to excavation. The excavation process took place in one step where all the stopes and crosscuts were removed all at once. The simulation was run for additional 10,500 steps using rock mass elastic properties until reaching equilibrium. Figure 14 shows the vertical stress around the excavations.

Fig. 14

Case study simplified 3D pillar stress model colored by vertical stress distribution in pillars

3DEC’s built-in scripting language FISH was used to write a function to map each pillar and estimate average vertical stress. Pillars were labeled from 1 to 72 starting from the pillar 1 on level 8 until pillar 9 on level 1, following the labeling indicted in Fig. 15. All zones inside each pillar were assigned a group number corresponding to each pillar label. For instance, all zones inside pillar 1 in level 8 were assigned a zone group equals to 1. In Fig. 15, each pillar is colored according to each pillar number. In addition, the function looped through all zones of each pillar and calculated the average vertical stress. A text file was generated and the values were reported on this file for further analysis. Average vertical stress was also mapped as an additional zone attribute. Figure 16 shows each pillar colored by its average vertical stress.

Fig. 15

Pillar model arrangement with zones colored by pillar

Fig. 16

Case study simplified 3D pillar model mapped by average vertical stress on the pillars

Results from the stress estimation model for each stress scenario were compared with analytical and 2D numerical solutions. A detailed discussion on these models’ results will be provided in the results and discussion section. The following section describes simplified stochastic approach to account for the effect of rock mass material properties variability in pillar stress distribution.

9 Stochastic Finite Volume Modeling Using the Point Estimate Method

Once pillar stress model was evaluated and compared with analytical and 2D numerical approaches, a simplified stochastic modeling approach was used to characterize the effect of material properties on pillar stress distribution. The point estimate method (PEM) was used to account for the effect of material properties variability on pillar stress distribution. The PEM is a stochastic analysis method that allows to estimate the mean and standard deviation of a resulting parameter by only accounting for a limited amount of realizations. The tested realizations are selected based on point estimates of the input parameters. The point estimates are defined based on the mean and standard deviations of each input parameter. There are two-point estimates for each input parameter. The first one is one standard deviation above the mean value of the parameter ($\mu +\sigma )$, and the second one is one standard deviation below the mean value of the parameter ($\mu -\sigma )$. The mean and standard deviation of the output distribution is calculated based on output results obtained from the point estimate permutation. Figure 17 presents a visual description of this approach, where a numerical model is run considering the input parameters point estimates, and results are used to estimate the first and second moments of the resulting distribution. This method has been widely used and implemented in geotechnical engineering. In recent years, it has been applied in mining engineering problems to estimate rock mass properties’ variability and the effect of materials variability in stope design [28, 29]. The benefit of this method is that with fewer simulations (less computing time), one can obtain an idea of output variability of certain parameter of interest (characterize uncertainty).

Fig. 17

Point estimate method visual explanation, modified after [29]

An exploratory data analysis was performed in R Studio to evaluate potential correlation between input parameters. In addition, the correlation between deformation moduli among lithologies was explored, as shown in Fig. 18. In situ stress changes occur when two contiguous lithological units have the different stiffnesses [30]. The variables selected for the stochastic analyses were each lithology’s deformation modulus. Due to the weak to non-correlation between deformation moduli among lithologies observed on the exploratory data analysis, and the limited available data, the simulations were run assuming that the parameters were not correlated.

Fig. 18

Correlation matrix between lithologies’ elastic moduli

A 2ⁿ factorial scheme was defined to determine the point estimate method trials, resulting in eight (2³) point estimate trials. Table 7 shows the point estimates for each lithology’s deformation modulus at each simulation. Each trial was run for each stress scenario obtaining a total of 24 pillar stress estimation models, with an average processing time of 5 h and 42 min. The output variable of interest was the average vertical pillar stress calculated using the previously mentioned FISH function. The pillar vertical stress averaged through all zones within the pillar was calculated for each of the 72 pillars in the model’s pillar arrangement. Therefore, a 72 × 1 size vector containing the average vertical pillar stresses was the result for each simulation.

Table 7 Point estimate method trials using a 2n factorial scheme for the deformation modulus of each lithology

Since no correlation was assumed between input parameters, the expected value (average) for each pillar stress considering elastic properties’ variability was calculated using Eq. 8, where ${R}_{i}$ is the vertical pillar stress vector for the ith simulation, and n is the total number of simulations.

$${{\varvec{\mu}}}_{\mathbf{R}\mathbf{e}\mathbf{s}\mathbf{u}\mathbf{l}\mathbf{t}\mathbf{s}}=\frac{1}{{2}^{{\varvec{n}}}}\sum\nolimits_{{\varvec{i}}=1}^{{{2}{\varvec{n}}}}{{\varvec{R}}}_{{\varvec{i}}}$$

(8)

Pillar stress variance was calculated using Eq. 9, where ${\mu }_{\mathrm{Results}}$ is the average vertical pillar stress vector considering elastic properties’ variability, ${w}_{i}$ is a weighting factor for each trail (since there was no correlation between input variables, this weighting is $\frac{1}{{2}^{n}}$ for all simulations), and ${R}_{i}$ is the vertical pillar stress vector for the ith simulation.

$${{{\varvec{\sigma}}}_{\mathbf{R}\mathbf{e}\mathbf{s}\mathbf{u}\mathbf{l}\mathbf{t}\mathbf{s}}}^{2}=\left(\sum\nolimits_{{\varvec{i}}=1}^{{{2}{\varvec{n}}}}{{\varvec{w}}}_{{\varvec{i}}}\times {{{\varvec{R}}}_{{\varvec{i}}}}^{2}\right)-{{{\varvec{\mu}}}_{\mathbf{R}\mathbf{e}\mathbf{s}\mathbf{u}\mathbf{l}\mathbf{t}\mathbf{s}}}^{2}$$

(9)

Results obtained from each simulation were exported into a.csv file. R studio was used to compute the average and standard deviation for each pillar using Eq. 8 and 9, respectively. Once average and standard deviations were calculated for each pillar in the model, a FISH function was written to map back the pillars in the model with the calculated properties.

10 Results and Discussion

Results from the 3D stress estimation models were compared with analytical and 2D finite element numerical modeling results. Figure 19 shows the comparison of analytical and 2D numerical modeling approaches with those obtained using 3DEC in this section for each stress scenario. For this comparison, the average pillar stress of all pillars at the same depth (or in the same level) was calculated and plotted against their depth. Three-dimensional pillar stress estimation results fall between analytical and 2D numerical stress estimation results. The 3D numerical solution allows to account for most of the assumptions the analytical and 2D numerical solution consider. This possibly indicates that both the analytical and the 2D numerical solution fail to capture actual pillar stress concentration. The analytical solution overestimates normal stresses, whereas the 2D FEM approach underestimates pillar stress magnitude.

Fig. 19

Analytical vs. 2D and 3D numerical normal stress estimation on the CSM pillars

Figure 20 summarizes the average vertical pillar stress for each pillar within the analyzed pillar arrangement for each stress scenario obtained from the 3DEC models using the PEM. In addition, 95% confidente intervals were marked with discontinuous lines taking into account the standard deviation estimated using the PEM. All pillars at the same level are highlighted indicating that they are at the same depth. It is possible to observe that there is variability in average pillar stress even in those pillars that are at the same depth. Changes in the surface topography could be one of the reasons for such variability. Another factor that should be considered is that pillars on the abbutments are subjected to a lower load. This could be due to that the free faces of those pillars are not fully exposed; therefore, some of the load could be shed to the abutments of the excavated area.

Fig. 20

Average and 95% confidence interval for pillar stresses at the CSM for each stress scenario based on 3DEC PEM models

Figure 21 indicates standard deviation values obtained for each pillar using the point estimate method. In general, most of the pillars for the three stress scenarios have a standard deviation ranging from 0.002 to 0.5 MPa. There are two pillars in particular that present higher stresses and standard deviations in comparison to the others, pillar 16, and pillar 29. Figure 22 shows an isometric view of the pillar arrangement. The top figures represent average vertical stress on the pillars for each of the stress scenarios. Pillar stresses are plotted using the same scale for each stress scenario. Pillar stress magnitude increases as the horizontal to vertical stress ratio (${K}_{o}$) moves from 0.5 (stress scenario 2) to 1.0 (stress scenario 1), and from 1.0 to 1.5 (stress scenario 3). Table 8 summarizes minimum and maximum average vertical pillar stress for each stress scenario. Another important observation is that pillars that present higher average stresses were also those that presented higher standard deviations.

Fig. 21

Pillar stress standard deviation at the CSM for each stress scenario

Fig. 22

Isometric view of pillar vertical stress average and standard deviation for each stress scenario

Table 8 Minimum and maximum pillar average vertical stress for each stress scenario

A top view of the pillar arrangement was overlaid with surface topography elevation contours to evaluate why particularly pillars 16 and 29 presented higher average and standard deviation vertical stress values. Figure 23 shows that stress distribution on the pillar arrangement does follow the trend of surface topography, where the central area of the pillar arrangement coincides with the valleys on the surface.

Fig. 23

Plan view of the pillar arrangement colored by average vertical pillar stress for the most unfavorable stress scenario (stress scenario 3), overlaid with surface elevation contours

Results from this analysis yield a series of observations that are worth to note with in this work. These observations are divided in three sections: (1) stress estimation approaches, (2) uncertainty characterization and data availability, and (3) results in the context of current pillar design standards.

A 3D finite volume model was used to estimate pillar stresses in a simplified CSM model. Results from this assessment were compared with those obtained from a 2D finite element numerical model, and an analytical solution. Results indicated that both the 2D numerical solution and the analytical approach fail to reproduce results from the 3D model. Both 2D numerical solutions and analytical approaches are tied to a series of assumptions that fail to represent actual stress conditions in the field. For instance, the inclined pillar stress formula assumes that the surface topography is flat, neglects the self-supporting capacity of the ground (pressure arch), and does not consider the effect of the out-of-plane stress. These assumptions lead to an overestimation of pillar stress. Although 2D numerical approaches allow to consider for the effect of topography at a particular cross-section, they assume that the pillar and the surface topography are infinite in length, neglecting the squared cross-section of the actual pillar. These assumptions cause 2D numerical solutions to underestimate stress concentration on pillars. Similar observations have been done by Elmo et al. [10] when assessing the role of 2D and 3D numerical simulation in pillar stress estimation. Not only, are these results valid in underground pillar design, but also, they are applicable to the analysis of rock slope stability in surface operations. Obregon compared 2D and 3D numerical solutions in slope stability problems, obtaining that 2D solutions tend to be conservative. He also observed that 3D slope stability solutions produce similar results to 2D when the slope length-to-height ratio is greater than 10 [9].

One of the objectives of this paper was to characterize pillar stress variability. The point estimate method was used as a practical stochastic approach to estimate the effect of rock mass elastic properties’ variability on pillar stress distribution. This method successfully enabled to estimate standard deviation values for each pillar in reasonable processing times (a total of 137 h). It is worth mentioning that the only parameter considered variable was the rock mass elastic modulus, and that no correlation was assumed between these parameters. These assumptions were reasonable given the pre-existing data, and the geologic nature of the deposit. It is encouraged to explore the effect of other parameters in pillar stress variability such as the potential variability of rock density and deformation modulus with depth, and the water table.

This work indicates that results obtained from the tributary area formula overestimate actual pillar stresses for the mine. The tributary area method results in stress estimations that are 50% higher than the values obtained for the stress scenario 1, and 20% higher than the values obtained from stress scenario 3 (the less favorable stress condition). From a safe-design standpoint, the tributary area method is valid for dimensioning pillars in underground dipping stone mines. However, not considering the significant difference between both estimations may compromise valuable reserves. In addition, it is worth mentioning that stress measurements are not common in underground stone mine operations. Simulations from this work also showed that the horizontal-to-vertical stress ratio is a parameter that has significant influence on pillar stress magnitude; therefore, a better characterization of this parameter may provide valuable information in the pillar design process.

11 Conclusions

In this paper, a three-dimensional finite volume modeling approach was used to evaluate pillar stress distribution in the CSM considering a simplified mine design, actual surface topography, and rock mass properties for each lithology. Three different stress scenarios were evaluated to account for the uncertainty related to current stress conditions in the mine. In addition, a stochastic approach using the point estimate method was implemented to evaluate the effect of elastic properties in pillar stress variability. Some of the conclusions derived from this section are as follows:

• The 3D FVM approach presented a reliable method to estimate pillar stress in the CSM. This approach addresses some of the assumptions and limitations from other stress estimation methods, allowing for a more precise estimation.

• Results from 2D FEM, 3D FVM, and analytical solutions yield different pillar stress estimation values. It is important that the practitioner understands the limitations and applicability of each estimation technique. Ideally, it is recommended to compare different solutions so the designs are based on informed decisions. In addition, further site investigation and monitoring is recommended to further refine any engineering design derived from this study.

• The horizontal-to-vertical stress ratio has a significant influence on pillar stresses at the case study mine because of the dipping formation being mined. Therefore, it is recommended to perform in situ stress measurements to reduce the uncertainty associated to this parameter. In case, it is impossible or uneconomical to perform such measurements; it is recommended to evaluate numerical models assuming different scenarios and design based on the worst-case scenarios.

• A simplified stochastic modeling approach demonstrated that variability in rock mass elastic properties does have an impact in pillar stress magnitude. The implementation of these stochastic analysis techniques is beneficial in the uncertainty characterization during the design process.

Results obtained in this paper will be used to implement the risk-based pillar design approach proposed by the authors in the CSM [5].