1 Introduction

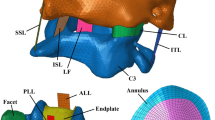
The intervertebral disc (IVD) is a complex biological structure due to its biphasic nature, composed of the annulus fibrosus (AF), the nucleus pulposus (NP) and two cartilaginous endplates (CEP) [1]. By acting as a shock absorber, the intervertebral disc ensures, together with the other spinal structures, to support high loads and maintain the stability, mobility, and flexibility of the spine [2, 3]. The IVD is the cushion among the Functional Spinal Unit (FSU), and it is responsible for the axial compression transmitted along the spine to the lower limbs [4].

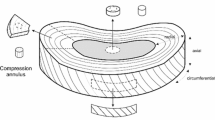
The AF involves 15–25 concentric layers of fibrocartilage that distribute the pressure around the disc, preventing damage to the endplate or vertebral body [5, 6]. The NP involves a mixture of water, collagen, and proteoglycans, which provides an extraordinary biomechanical characteristic to the disc, ensuring its stiffness, compressive strength, and swelling characteristics [7]. The NP’s internal shape and pressure change over time depending directly on the water content and the physiological stresses on the spine [8,9,10]. These changes differ according to the daily or overnight activities, resulting in 16 h of daily loading (reduction in disc height) and 8 h of nightly recovery (recovery in disc height) [9]. The CEPs are the junction between the vertebrae and the IVD enabling the loading transmission, but its main function is to act as a mechanical barrier and to allow nutrient transport from and within the IVD [11, 12].

The viscoelastic nature and properties of the healthy and intact IVD come from its complex structure, showing an intermediate behaviour between solid and fluid. These properties have been demonstrated from simple stress–strain curves in which the J-shape curves (stress versus strain curve) can be observed, and energy dissipation occurs upon removal of the load [2, 7, 13,14,15,16,17,18,19]. Although this topic is often discussed in the literature, there is still a lack of understanding of the viscoelastic mechanical response of the disc, so new strategies and methods are currently being developed [20]. The IVD’s main characteristics is the ability to act as cushion for the spine, due to the bulging and swelling pressures of NP. These characteristics change with age and in pathological conditions. Indeed, 577 million cases of low back pain were recorded in 2017 [21]. Disc herniation is a common pathology which consists of a local displacement of NP or AF material beyond the disc space boundary [22,23,24]. This pathology can cause several discomforts starting from a compression of the spinal cord that can lead to pain or numbness. In biomechanical terms, a disc herniation induces an instability of the FSU by increasing the Range of Motion (ROM), as well as the Neutral Zone (NZ) and the stresses on the facet joints. This can also lead to excessive swelling of the AF and the IVD will act as a deflated tire, thus accelerating the degeneration process [25,26,27,28]. So, a full mathematical simplified comprehension of how this biological structure works might be very useful in clinical practice to develop new treatments.

Indeed, the IVD’s mechanical properties have been mathematically analysed in the literature. Modelling disc time-dependent behaviour (creep behaviour) is a common path used to gain insight into the complicated relationship between external loads and IVD mechanobiology and its homeostasis [29]. A valid approach might involve simplifying these complex mechanobiological behaviours by modelling creep to understand the mechanism behind the daily and overnight activities that influence the NP pressure, with a daily decreasing and nightly increasing in the disc height due to nutrient and water transport, hydration, cell viability, matrix synthesis and mechanosensitive activity of the disc [9, 30,31,32,33,34,35]. Many attempts have been made in the literature to model the time-dependent behaviour of the IVD. Indeed, several mathematical models have been used such are: Single or Double Kelvin Voigt [35,36,37,38] standard linear solid model [39,40,41,42,43] Kohlrausch Williams Watts (KWW) [34, 44] and a combination of other rheological models [36, 37, 45], fluid transport model [46, 47] or biphasic model [48]. These models differ in their governing laws, depending on the physical–mathematical modelling adopted.

Hence, this work involved an in-vitro study performed on human cadaveric lumbar spines. The aim was to investigate which mathematical models could simply describe the viscoelastic characteristics in the IVD that exhibits during long-term loading without considering the biological aspects. The paper is divided into distinct sections. The next section deals with the materials and methods employed, then it deals with Specimens' preparation and experimental procedure, as well as how the data were evaluated, and the mathematical models adopted. The results section first provides the findings obtained by modelling the creep curves with the mathematical models, followed by the correlation analysis of the model parameters found. Finally, all results will then be analysed in the discussion section. Briefly in this paper, we have decided to focus on the use of classical rheological models and the Nutting’s Power law for describing the long-term behaviour of the intervertebral disc. The rheological models adopted are a combination of springs and dissipators, as they are among the most widely used tools in the literature for describing the intermediate behaviour between solid and fluid; meanwhile, the Nutting’s Power law is an exponential law that consider the biphasic behaviour of the material. A careful description of the models adopted in the analysis of the results will be given next. Therefore, the models adopted were evaluated on the creep data to determine whether they can provide a good modelling and fitting of the IVD creep behaviour, followed by correlation and linear regression analysis. This study represents a first starting point for the authors to assess the literature status of IVD's mechanics mathematical modelling and to fully comprehend it, so it will be possible to investigate how IVD is deformed during daily and nightly activities, resulting in the final focus of future work.

2 Materials and methods

2.1 Specimens’ preparation and experimental procedure

The experimental procedure (see Fig. 1) involved seven lumbar segments (L4-5) which were harvested from frozen human spines with an average age of 48 years (range: 38–58) (Table 1). Prior to preparation, the specimens were screened for signs of severe deformity, degeneration, or bone defects. Specimens classified with a degree of disc degeneration greater than 1 were excluded in the FSU considered, according to [49] (Table 1). The specimens were stored at − 20 °C in triple plastic bags and they were thawed at 4 °C for 16 h before the experiment. All soft tissues, as well as muscles and fat were removed, while the IVDs were kept intact (Fig. 1A). The cranial and caudal ends were horizontally aligned and embedded in polymethyl methacrylate, (Technovit 3040, Heraeus-Kulzer, Wertheim/Ts, Germany) to maintain fixation during the test, which was also ensured by screws inserted before the potting, followed by x-ray (Fig. 1B). The specimens were fixed between the flanges and gimbal system of the Universal spine tester [50] (Fig. 1C). In addition, the specimens were driven to the neutral position by locking the freedom degrees in the gimbal system, so that only the axial translation was enabled and measured by an inductive linear displacement sensor (BTL2-P1-0225, Balluff, Neuhausen, Germany) attached to the spine tester. A creep test, non-disruptive, was performed by applying an axial compression load of 500N perpendicular to the superior endplate (to simulate upper body loading according to experimental procedure already assessed [25, 26]) for 15 min. The disc height reduction (DHR) has been used as a benchmark for the analysis of the results. As the specimens were driven to the neutral position, the initial overall length of the FSU, including the PMMA embedding, was experimentally measured by the machine, thanks to the displacement sensor. To identifying the DHR, it was considered that the specimen's lowering, following the application of load, was dependent only on the IVD. Therefore, the total length of the specimen (FSU + PMMA) was measured immediately after load application and at the end of the 15 min test. The difference of these measurements with the initial ones were interpreted as the reduction in disc height. The maximum values of disc height reduction (DHR) for each specimen were identified (Table 1).

Fig. 1
figure 1

A Specimen prepared after removal of all soft tissues; B X-Ray of the specimen after embedding; C Specimen fixed in the Universal Spine tester machine

Full size image
Table 1 Specimens information about age, sex, grade of degeneration and Max value of Disc height reduction
Full size table

2.2 Data evaluation

The Disc Height Reduction (DHR) was evaluated using the classical rheological models and Nutting's power law (Wolfram Mathematica v13.0, Wolfram Research of Champaign, Illinois, USA). The NMnimize function of the software was used for the optimization of the cost function adopted to fit the data. Wolfram Mathematica software automatically choose the optimization method. In this case the optimization was constrained, so the optimization methods adopted by the software were either Differential Evolution or Nelder-Mead, since they have a high ability to handle constraints and the nonlinear nature of the objective functions. This was followed by a correlation analysis between the identified model parameters and the maximum value reached by the DHR. Correlation matrices were calculated by using RStudio software v2023.12.0 (Posit, PBC, Vienna, Austria) and significant correlations (Pearson correlations, r) were found by setting a significance value (p-value) of less than 0.05.

2.3 Mathematical models

The classical rheological models [51,52,53,54,55] represent the viscoelastic behaviour as a mathematical combination of springs and dashpots, which describe the solid behaviour following the Hooke’s law and fluid behaviour following the Newton’s law, respectively. The classical rheological models used are the Maxwell’s model, i.e., a spring in series with a dashpot; Kelvin–Voigt’s model, i.e., a spring in parallel with a dashpot; First Standard Linear Solid model (SLS1), i.e., Kelvin–Voigt model in series with a spring and Second Standard Linear Solid model (SLS2), i.e., Maxwell’s model in parallel with a spring. However, it is necessary to specify that the SLS1 and SLS2 models are roughly the same, where the difference between them lies not in the behavior described but in the combination of model parameters. Table 2 shows the governing equations of the rheological models and creep functions. The graphic representation of these models are, also, inside the Table 2, where the parameters constants are in terms of η and the Young modulus (E), as they are commonly used in the literature representation, even if the governing equation will refer to the simple stiffness k for the springs because the creep functions have been obtained in terms of displacements (\(u\left(t\right)\)) and force \((F\left(t\right))\). Several model parameters are presented in the governing equations (Table 2). Among them, there are the stiffnesses of the springs (\(k, {k}_{1}\) and k), the viscosity of the dashpots (\(\upeta \)), the time constants, which are the time required to reach the regime (\({\tau }_{0},{\tau }_{1}\) and \({\tau }_{2}\)), where \({\tau }_{i}=\frac{\eta }{{k}_{i}}\). Lastly, the Nutting's power law [50,51,52,53,54] is a power relationship between displacement, force and time as following: \(u=C{F}^{\alpha }{t}^{\beta }\). The terms C, \(\alpha \) and \(\beta \) are characteristic of the material. It is a general law experimentally obtained, that describe the viscoelastic behaviour of materials. More specifically, it represents the behaviour of a solid following Hooke's law when \(\beta =0\) and \(\alpha =1\), and of a viscous fluid following Newton-Petroff's law when \(\beta =\alpha =1\).

Table 2 Schematic representation of the four classical rheological models with the governing equation and the corresponding creep function
Full size table

3 Results

3.1 Findings

During the creep tests, the load application resulted in an immediate reduction of the IVD height from the initial values (mean values 0.94 mm ± 0.19 mm). Subsequent measurements of the change in disc height showed a characteristic time-dependent creep behaviour. After 15 min, the disc height decreased by an average of 1.14 mm ± 0.24 mm (min: 0.91 mm and max: 1.44 mm) (Table 1). This means that the IVDs lost 0.20 mm due to creep during the 15-min compression. Then, each curve was evaluated with the different rheological models and Nutting’s law to identify which constitutive model better fit the original data. Each original creep curve, with the DHR versus time, was plotted for each specimen with the four rheological models and the power law as a function of time, with an enlargement focusing on the regime part of the curve. Figure 2 shows an example of the fitting procedure for one specimen. Table 3 shows the average parameters of the Maxwell, Kelvin–Voigt, SLS1 and SLS2 models obtained from all specimens. For the Power law, the average values were: \(C=\text{0,64}\pm 0.11\), \(\beta = \text{0,06}\pm 0.01\) and \(\alpha =\text{0,03}\pm 0.03\). The parameters of all models are reported for each specimen in Table A1, A2, A3, A4 and A5 (Appendix). All the raw data creep curves were plotted by fitting with the Nutting’s power Law and SLS1 models (see Fig. 3 and 4 respectively).

Fig. 2
figure 2

Creep curves for one specimen with the raw data (grey curve) fitted with the Maxwell model (cyan curve), Kelvin–Voigt model (orange curve), SLS1 model (green curve), SLS2 curve (blue curve) and Power law (red curve) and enlargement in the black box to better visualize the fitting curves

Full size image
Table 3 The average model parameters of Maxwell, Kelvin, SLS1 and SLS2 models (Standard deviation in bracket)
Full size table
Fig. 3
figure 3

Enlargement of the creep curves for each specimen overlapped with the raw data (curves with symbols) fitted with the Nutting’s Power law: Red for Specimen 1; Cyan for Specimen 2; Orange for Specimen 3; Green for Specimen 4; Yellow for Specimen 5; Magenta for Specimen 6 and Blue for Specimen 7

Full size image
Fig. 4
figure 4

Enlargement of the creep curves for each specimen overlapped with the raw data (curves with symbols) fitted with the SLS1 model: Red for Specimen 1; Cyan for Specimen 2; Orange for Specimen 3; Green for Specimen 4; Yellow for Specimen 5; Magenta for Specimen 6 and Blue for Specimen 7

Full size image

3.2 Correlation analysis

The correlation matrices (see Fig. 5) were found between the parameters of the rheological models and the maximum value of DHR from each specimen, followed by a linear regression analysis (see Fig. 6). For the Maxwell model, a negative correlation was found between the stiffness and the maximum value of the DHR (\(r=-0.97\), with \({R}^{2}=0.94\)). For the Kelvin–Voigt model, a negative correlation was found between the stiffness and the maximum value of the DHR (\(r=-0.98\), with \({R}^{2}=0.96\)) and with the time constant (\(r=-0.75\), with \({R}^{2}=0.5\)). For the SLS1 model, a negative correlation was found between the stiffness \({k}_{1}\) and the maximum value of the DHR (\(r=-0.91\), with \({R}^{2}=0.79\)) and with stiffness \({k}_{2}\) (\(r=-0.83\), with \({R}^{2}=0.63\)). For the SLS2 model, a negative correlation was found between the stiffness \({k}_{1}\) and the maximum value of the DHR (\(r=-0.99\), with \({R}^{2}=0.98\)).

Fig. 5
figure 5

Correlation matrixes with the model parameters obtained from each specimen and the maximum value of DHR: A Maxwell model; B Kelvin–Voigt model; C SLS1 model; D SLS2 model

Full size image
Fig. 6
figure 6

Linear Regression curves with \({R}^{2}\) values obtained for the rheological models: A Maxwell: negative correlation between the stiffness and the maximum value of DHR; B Kelvin–Voigt: negative correlation between the stiffness and the maximum value of DHR; C SLS1: negative correlation between the stiffness \({k}_{1}\) and the maximum value of DHR; D SLS1: negative correlation between the stiffness \({k}_{1}\) and the maximum value of DHR

Full size image

4 Discussion

Over the decades, the viscoelastic behaviour of the IVD has been investigated to understand how the disc can act as a shock absorber, thus ensuring not only its extreme load-bearing ability but also its mobility and flexibility [13, 14, 55, 56]. Hence, a full understanding of the creep behaviour is crucial, which refers to the tendency of a material to deform in a prolonged manner when stressed over a long period, and the energy stored will be used to return to the initial state. This is the viscoelasticity that characterizes the biological tissues [51, 57].

During the daily time, the disc supports prolonged compressive forces responding with height reduction, disc bulging, and increasing NP pressure. This follows a recovery time that occurs during sleep to recover the undeformed state, in which height is restored, and at the same time, disc bulging is reduced, and NP pressure decreased [9, 10]. The correct balance between daily activity and overnight recovery should be 16 h versus 8 h [58,59,60,61]. However, recovery frequently never corresponds to the same time as daily activity, and as a result, the right balance is often not reached. Hence, the incorrect balancing causes several effects: the disc not recovers its height, and it is unable to reduce the disc bulging and consequently the NP pressure is not decreased properly. All these effects will progressively not only cause greater deformation and loss of height but will induce greater disc bulging, that it is an indirect parameter of internal disc pressure [62,63,64]. In the long run with advancing age, this will cause a chronic non-physiological alteration of the deformed and strained state of the IVD: this might be one of the determined factors affecting the evolution and progression of herniated discs and so low back pain.

According to all these considerations, in this work, an in-vitro study was conducted, in which creep tests were performed on human specimens under an axial load of 500 N for 15 min. Only 15 min was chosen for the test since following in vivo intradiscal pressure studies done by Wilke et al. [9], it was observed that after 15 min there was a nearly constant trend in disc pressure. This allowed us to hypothesize that 15 min was a good estimate for obtaining a reasonably likely creep curve for the disc. In addition, the testing protocol was not intended to be destructive. Indeed, the aim was to model the resulting creep curves by mathematically simplifying them through viscoelastic models considering the biphasic disc behaviour. The creep test conducted resulted in this immediate decrease in disc height that is comparable to the range summarised by [4]. The creep curves were modelled through the classical rheological models and Nutting's power law by referring to the DHR. In this mathematical modelling, not only was the final disc height reduction studied, but also the behaviour through which the disc reaches that final value was investigated. These models were chosen because they can capture time-dependent deformation under persistent loads. The creep curves shown that there is no linear relation between the reduction in disc height and the time (Fig. 2). A correlation analysis has been also made to find any Pearson correlations between the model parameters and the maximum value of DHR (Fig. 5). Therefore, starting with the significant correlation values, a linear regression was made between the stiffness and time constant parameters of the models and the maximum value of DHR (Fig. 6).

The creep curves obtained showed a non-linear trend, typical characteristic of the creep curves exhibited by viscoelastic materials. As illustrated in Fig. 1, Maxwell's model fails to capture creep curves because it is based on a linear governing law and cannot model non-linear trends. Similarly, the Kelvin–Voigt model is not representative of the non-linear creep curve. Although the Kelvin–Voigt model has an exponential governing law, it is a very simple linear one and thus cannot accurately describe the observed non-linear trend. Instead, the SLS1 and SLS2 can capture the trend of data, as they are very similar models, although missing the upward ramp of the curve, as shown in the enlargement of the creep fitting curves from SL1 model in Fig. 4. This is an important limitation of these models because the first part of the creep curve is representative of the immediate reduction of the disc height, after which which the disc will continue to deform over the time with its non-linear trend characteristic of its viscoelastic behaviour. Finally, Nutting's law seems to be the best fitting between the other laws (Fig. 3), despite to the fact that this formulation considers the intermediate viscoelastic behaviour of IVD between solid and fluid. Anyway, the fitting is not always successful and sometimes cannot take some regions of data. This might reflect that the Nutting’s law models the mechanical response at the macroscopic level, without considering what is happening at the microscopic level with the exchange of nutrients, just as the disc bulge and disc height changes. All mechanical parameters depend on biological ones, and each is a consequence of the other. Consequently, any mathematical model must consider this deep connection.

This in-vitro study has several limitations. First, owing to the self-evident problems in using live human tissues, the specimens tested were frozen and thawed. Considering the high-water content in the biological tissues, especially for the intervertebral disc, freezing and thawing certainly affected the results obtained, biasing the true viscoelastic nature of the tissues. Secondly, the age of the specimens considered is another relevant factor to consider. The average age is 48 years, with patients older than 50 years. This is a limitation given the physiological degeneration conditions that the intervertebral disc experiences with advancing age, leading to changes in the water content and proteoglycan conditions of the nucleus pulposus. The age combined with the effects of freezing and thawing have altered the creep response of the specimens, hence they have also changed the fitting of the data. A fresh and younger tissue would possess higher and more responsive viscoelastic creep capacities, with higher bulging and recovery capacity. Since they are human specimens, though, it must be acknowledged that it is extremely difficult to find younger and fresh specimens.

Further in-vitro studies should focus on longer creep including recovery time to simulate the daily and overnight activities, which are the intention of the authors to carry out successively. An attempt should be made to understand how the disc deforms and recovers, and why sometimes these mechanics fail causing disc damage thought a different experimental protocol that should involve repeated test. This might be related to the evolution and progression of diseases, such as herniated discs, not only in the lumbar spine but also in the cervical one.

5 Conclusion

This in-vitro study provided insight into how the mathematical models currently used in the literature are unable to fully describe the creep behaviour of the IVD, and consequently, on how it is necessary to find new mathematical models. The classical rheological models used are not able to well fit the creep curves, while the Nutting’s power law seems to be the better one because it considers the biphasic behaviour of the disc. Nevertheless, simplified mathematical modelling, like the one employed in this study, could certainly be valuable in the engineering field, facilitating new clinical solutions development by supporting the design of disc prostheses or other innovations for the treatment of intervertebral disc disease. In the engineering field, practicality is the key, and the complexity of the mechanobiological behaviours of the intervertebral disc makes it difficult to accurately simulate such dynamics with traditional prostheses. Similar mathematical approaches could provide a more realistic basis for prosthesis design, allowing simple mechanical responses to be more faithfully replicated at the macroscopic level while neglecting the microscopic explanations for that behaviour. Indeed, this could improve the effectiveness of the new prostheses by allowing them to simulate the bearing action of the disc and respond mechanically in a similar way, as indicated by the curves resulting from the modelling of the in-vitro results./