1 Introduction

In recent decades, how to effectively address uncertainty in decision-making problems has emerged as a crucial challenge, attracting significant attention from various domains [1, 2]. The challenge of dealing with uncertainty has prompted the creation of multiple methods, each designed to tackle this complexity in its own way. These methods include fuzzy sets [3, 4], evidence theory [5, 6] and neutrosophic sets [7]. Together, they offer a broad range of tools for effectively managing and interpreting uncertain data, demonstrating the diversity and depth of strategies available for navigating through uncertainty. They have been applied across a wide spectrum of activities, including but not limited to medical diagnosis [8] and decision-making processes [9]. Among the multitude of methods developed to tackle uncertainty, Multisource information fusion techniques stand out due to their capability to integrate complementary information.

Evidence theory (ET) [10, 11], which builds upon Bayes probability theory, has been widely recognized for its flexibility and effectiveness in representing uncertainty without the need for prior information. In particular, ET simplifies uncertainty into measurable components by allocating basic probability assignments to subsets of outcomes instead of just singletons [12]. Furthermore, ET follows the associative and commutative laws, making it strong in theory and practical for real applications [13]. Moreover, ET utilizes Dempster’s combination rule to blend evidence. Expanding on these advantages, ET has spurred research in areas such as transforming belief function assignments into probabilities [14], clustering [15], evaluating evidence reliability [16] and others [17].

Despite the significant benefits highlighted in ET, one notable challenge arises with Dempster’s combination rule: it can lead to counterintuitive results when dealing with highly conflicting evidence [18]. Effectively reconciling highly conflicting evidence remains an open issue. To navigate this challenge, previous studies have proposed two main strategies [19]: modifying Dempster’s combination rule and preprocessing the evidence itself. Researchers interested in the first category have developed various fusion rules tailored to address specific issues in certain scenarios, including the cautious combination rule which aims to minimize the impact of conflicting evidence [20, 21]. However, this modification process often compromises key properties, like commutativity and associativity.

In this paper, our attention is centered on the second category, where typical methods feature Murphy’s simple average method for combining bodies of evidence [22]. This serves as a foundation for subsequent innovations in the field. Deng et al. [23] introduced an important concept in evidence support, using the Jousselme distance to calculate a weighted average across various pieces of evidence. However, Jiang emphasized the Jousselme distance’s limitations and subsequently proposed a novel correlation coefficient tailored for mass functions [24]. Building on these foundations, Xiao [25] introduced the belief Jensen–Shannon divergence, a method that modifies evidence before combining them using Murphy’s simple average method. Whereas, Xiao’s approach simplifies the process by treating multi-element subsets as single-element subsets when quantifying discrepancies between pieces of evidence. This method overlooks the complex relationship between single-element and multi-element subsets, which also arises in [26, 27]. To overcome these limitations, Xiao [5] proposed the reinforced belief divergence, an advanced measure aimed at fixing the shortcomings of the belief Jensen-Shannon divergence. However, while the reinforced belief divergence demonstrates significant improvement in evidence fusion accuracy, it, along with the method introduced by Wang et al. [28] and another recent approach by Huang et al. [29], faces challenges in terms of increased computational demands in multisource information fusion scenarios. This implies that while these methods offer significant improvements in fusion effectiveness, they also introduce complexities that may limit their applicability in resource-constrained environments. Additionally, some researchers some researchers prefer to discount each piece of evidence to adjust the reliability of evidence from different sources [30]. Contextual discounting methods are employed to account for varying degrees of reliability based on the context in which the evidence is collected [31, 32]. Although a lot of work has been done, there is still room for improvement.

In this paper, a new belief divergence measure via cosine function, named \({\mathbb{B}}{\mathbb{C}}\), is introduced, designed to quantify the difference between evidences. The proposed \({\mathbb{B}}{\mathbb{C}}\) divergence can effectively captures the interaction between subsets of single elements and those composed of multiple elements, and it satisfies the properties of boundedness, non-degeneracy, and symmetry. Based on the \({\mathbb{B}}{\mathbb{C}}\) divergence along with belief entropy, a new multisource information fusion method is developed. The proposed method utilizes \({\mathbb{B}}{\mathbb{C}}\) divergence to assess the differences between evidences in order to calculate credibility weight, and employs belief entropy to evaluate the uncertainty within each evidence for determining information volume weight. Subsequently, we integrate credibility and information volume into a weighted evidence average before applying Dempster’s combination rule. To highlight the applicability of the proposed method, we provide two application cases to demonstrate its effectiveness.

The remainder of this paper is structured as follows. Essential theoretical concepts are introduced in Sec. 2. In Sec. 3, the \({\mathbb{B}}{\mathbb{C}}\) divergence within evidence theory is detailed, a comparative analysis is conducted, and the multisource information fusion method based on the \({\mathbb{B}}{\mathbb{C}}\) divergence and belief entropy is presented, providing a comprehensive approach to effectively integrate evidence from various sensors. In Sec. 4, two case studies to showcase the real-world practicality of our proposed fusion approach and its results are analyzed. The paper concludes with the Sec. 5, summarizing the findings.

2 Preliminaries

Definition 1

(Framework of discernment) Let us consider that \(\Theta\) is a set comprising elements \({\mathcal {F}}_p\) that are both mutually exclusive and collectively exhaustive, for p ranging from 1 to N. It is expressed as

$$\begin{aligned} \Theta = \big \{{\mathcal {F}}_1, {\mathcal {F}}_2, {\mathcal {F}}_3, {\mathcal {F}}_4, \ldots , {\mathcal {F}}_N\big \} \end{aligned}$$
(1)

In this context, \(\Theta\) is identified as the frame of discernment (FOD), with every \({\mathcal {F}}_p\) representing an individual proposition or a singular subset element. The power set \(2^\Theta\), which consists of \(2^N\) elements, includes:

$$\begin{aligned} 2^\Theta = \{\emptyset , \{{\mathcal {F}}_1\},\dots , \{{\mathcal {F}}_N\}, \{{\mathcal {F}}_1, {\mathcal {F}}_2\}, \{{\mathcal {F}}_1, {\mathcal {F}}_3\}, \dots , \Theta \} \end{aligned}$$
(2)

Here, \(\emptyset\) indicates no elements, showing a scenario where none of the propositions occur within the closed-world assumption of ET, ensuring all possible outcomes are considered.

Definition 2

(Basic probability assignment) Within the framework \(\Theta\), a basic probability assignment (BPA) \(m\), as referenced in [10, 11], assigns a value between 0 and 1 to each subset of \(\Theta\), as demonstrated:

$$\begin{aligned} m: 2^\Theta \rightarrow [0, 1], \end{aligned}$$
(3)

It abides the rule of

$$\begin{aligned} \sum _{{\mathcal {F}}_p \in 2^\Theta } m({\mathcal {F}}_p) = 1, \end{aligned}$$
(4)
$$\begin{aligned} m(\emptyset ) = 0. \end{aligned}$$
(5)

The BPA \(m\), often referred to as a mass function, measures the level of support provided to a hypothesis \({\mathcal {F}}_p\). A subset \({\mathcal {F}}_p\) with \(m({\mathcal {F}}_p) > 0\) is referred to as a focal element.

Definition 3

(Dempster’s rule of combination) Given two BPAs, \(m_1\) and \(m_2\), on the \(\Theta\), we can merge them into a single combined BPA, \(m\), as referenced in [10, 11]. This process is outlined as follows:

$$\begin{aligned} m({\mathcal {F}}_p) = {\left\{ \begin{array}{ll} \frac{\sum \limits _{\begin{array}{c} {\mathcal {F}}_s \cap {\mathcal {F}}_l = {\mathcal {F}}_p \end{array}} m_1({\mathcal {F}}_s)m_2({\mathcal {F}}_l)}{1-K}, &{} {\mathcal {F}}_p \ne \emptyset \\ 0, &{} {\mathcal {F}}_p = \emptyset \end{array}\right. } \end{aligned}$$
(6)

and \(K\) is given by:

$$\begin{aligned} K = \sum _{{\mathcal {F}}_s \cap {\mathcal {F}}_l = \emptyset } m_1({\mathcal {F}}_s)m_2({\mathcal {F}}_l), \end{aligned}$$
(7)

where \({\mathcal {F}}_p, {\mathcal {F}}_s, {\mathcal {F}}_l\) \(\in\) \(2^\Theta\); \(K\) represents the amount of conflict between \(m_1\) and \(m_2\).

Definition 4

(Pignistic probability transform). Suppose \(m\) is a BPA, which is converted into a probability distribution using the pignistic probability transform, as described by Smets in 1994 [33]. This transformation is accomplished through the following formula:

$$\begin{aligned} {BetP}_m({\mathcal {F}}_p) = \sum _{{\mathcal {F}}_s \subseteq \Theta } \frac{|{\mathcal {F}}_p \cap {\mathcal {F}}_s|}{|{\mathcal {F}}_s|} \frac{m({\mathcal {F}}_s)}{1 - m(\emptyset )} \end{aligned}$$
(8)

where \(|{\mathcal {F}}_p \cap {\mathcal {F}}_s|\) represents the number of elements that are common to both sets \({\mathcal {F}}_p\) and \({\mathcal {F}}_s\). In a traditional ET framework, the BPA \(m(\emptyset )\) stands for the belief ascribed to the empty set in a closed world. Therefore, with this assumption, the equation is defined as:

$$\begin{aligned} {BetP}_m({\mathcal {F}}_p) = \sum _{{\mathcal {F}}_s \subseteq \Theta } \frac{|{\mathcal {F}}_p \cap {\mathcal {F}}_s|}{|{\mathcal {F}}_s|} m({\mathcal {F}}_s) \end{aligned}$$
(9)

The pignistic probability transform effectively transforms a BPA function into a conventional probability distribution by distributing the belief uniformly across all possible outcomes. When considering a specific event \({\mathcal {F}}_p\) as a single element, the formula can be further simplified to:

$$\begin{aligned} {BetP}_m({\mathcal {F}}_p) = \sum _{{\mathcal {F}}_s \subseteq \Theta , {\mathcal {F}}_p \subseteq {\mathcal {F}}_s} \frac{m({\mathcal {F}}_s)}{|{\mathcal {F}}_s|} \end{aligned}$$
(10)

3 The proposed method

In this section, an innovative form of belief divergence is defined, which is derived from the application of the cosine function and we explore several notable attributes of this divergence and provide proof of these properties. Additionally, numerical examples are presented to demonstrate the effectiveness of our proposed divergence measure. Furthermore, we introduce a novel method for multisource information fusion.

3.1 New belief divergence measure

Definition 5

Let \(m_1\) and \(m_2\) be two BPAs in \(\Theta\). The belief cosine divergence measure, called \({\mathbb{B}}{\mathbb{C}}(m_1, m_2)\), is defined by:

$$\begin{aligned} {\mathbb{B}}{\mathbb{C}}(m_1, m_2) = 1 - \cos \left( \frac{\pi }{4} \sum _{{\mathcal {F}}_p \in \Theta }|BetP_{m_1}({\mathcal {F}}_p) - BetP_{m_2}({\mathcal {F}}_p)|\right) \end{aligned}$$
(11)

where

$$\begin{aligned} {BetP}_m({\mathcal {F}}_p) = \sum _{{\mathcal {F}}_s \subseteq \Theta {\mathcal {F}}_p \subseteq {\mathcal {F}}_s } \frac{m({\mathcal {F}}_s )}{|{\mathcal {F}}_s |}, \text { and note that } {\mathcal {F}}_p \text { is a single-element subset. } \end{aligned}$$

The pignistic probability transform keeps the confidence in single items the same and divides the confidence in groups with more than one item evenly among the individual items. This method changes belief functions into a regular probability distribution. Our \({\mathbb{B}}{\mathbb{C}}\) divergence method accurately shows the relationship between singleton and multiple elements, avoiding the mistake of treating multiple elements as singleton elements when measuring the difference between evidences.

3.2 Properties

In this subsection, several key properties of the \({\mathbb{B}}{\mathbb{C}}\) divergence are presented and outlined in detail. Let \(m_1\), \(m_2\) and \(m_3\) be three BPAs on \(\Theta\). The properties of the \({\mathbb{B}}{\mathbb{C}}\) divergence are outlined as follows:

Property 1

Boundedness: \(0 \le {\mathbb{B}}{\mathbb{C}}(m_1, m_2) \le 1\);

Proof

Given \({\mathbb{B}}{\mathbb{C}}(m_1, m_2) = 1 - \cos \left( \frac{\pi }{4} \sum _{{\mathcal {F}}_p \in \Theta }|BetP_{m_1}({\mathcal {F}}_p) - BetP_{m_2}({\mathcal {F}}_p)|\right)\), we have:

$$\begin{aligned} 0 \le \sum \limits _{{\mathcal {F}}_p \in \Theta }| {BetP}_{m_1}({\mathcal {F}}_p) - {BetP}_{m_2}({\mathcal {F}}_p)| \le 2. \end{aligned}$$

and

$$\begin{aligned} 0 \le \frac{\pi }{4}\sum \limits _{{\mathcal {F}}_p \in \Theta }| {BetP}_{m_1}({\mathcal {F}}_p) - {BetP}_{m_2}({\mathcal {F}}_p)| \le \frac{\pi }{2}. \end{aligned}$$

For \(\cos (x)\), its range is always in [0, 1] if \(x \in [0, \frac{\pi }{2}]\). Thus, we can prove \(0 \le {\mathbb{B}}{\mathbb{C}}(m_1, m_2) \le 1\). \(\square\)

Property 2

Non-degeneracy: \({\mathbb{B}}{\mathbb{C}}(m_1, m_2) = 0\) if and only if \(m_1 = m_2\);

Proof

Suppose \(m_1 = m_2\), then for all \({\mathcal {F}}_p \in \Theta\), \({BetP}_{m_1}({\mathcal {F}}_p) = {BetP}_{m_2}({\mathcal {F}}_p)\), and thus:

$$\begin{aligned} \sum _{{\mathcal {F}}_p \in \Theta } | {BetP}_{m_1}({\mathcal {F}}_p) - {BetP}_{m_2}({\mathcal {F}}_p)| = 0. \end{aligned}$$

This results in:

$$\begin{aligned} {\mathbb{B}}{\mathbb{C}}(m_1, m_2) = 1 - \cos (0) = 0. \end{aligned}$$

Conversely, suppose \({\mathbb{B}}{\mathbb{C}}(m_1, m_2) = 0\), it must be the case that the argument of the cosine is 0, which implies that:

$$\begin{aligned} \sum _{{\mathcal {F}}_p \in \Theta } | {BetP}_{m_1}({\mathcal {F}}_p) - {BetP}_{m_2}({\mathcal {F}}_p)| = 0, \end{aligned}$$

leading to \({BetP}_{m_1}({\mathcal {F}}_p) = {BetP}_{m_2}({\mathcal {F}}_p)\) for all \({\mathcal {F}}_p\), and hence \(m_1 = m_2\). \(\square\)

Property 3

Symmetry: \({\mathbb{B}}{\mathbb{C}}(m_1, m_2) = {\mathbb{B}}{\mathbb{C}}(m_2, m_1)\).

Proof

The absolute value function and the summation operation are both commutative, meaning that the order of the elements does not affect the final result. Therefore, the sum of absolute differences between the belief functions of \(m_1\) and \(m_2\) remains unchanged regardless of the order in which we consider the subsets \({\mathcal {F}}_p\) of \(\Theta\).

$$\begin{aligned}{} & {} \sum _{{\mathcal {F}}_p \in \Theta } | {BetP}_{m_1}({\mathcal {F}}_p) - {BetP}_{m_2}({\mathcal {F}}_p)| \\{} & {} \quad = \sum _{{\mathcal {F}}_p \in \Theta } | {BetP}_{m_2}({\mathcal {F}}_p) - {BetP}_{m_1}({\mathcal {F}}_p)|. \end{aligned}$$

This implies that:

$$\begin{aligned} {\mathbb{B}}{\mathbb{C}}(m_1, m_2) = {\mathbb{B}}{\mathbb{C}}(m_2, m_1). \end{aligned}$$

\(\square\)

Thus, the belief cosine divergence metric \({\mathbb{B}}{\mathbb{C}}\) fulfills the crucial properties of boundedness, non-degeneracy, and symmetry for any given BPAs \(m_1\) and \(m_2\) defined on the frame of discernment \(\Theta\). These properties ensure that \({\mathbb{B}}{\mathbb{C}}\) is a reliable and consistent measure of divergence between belief mass assignments.

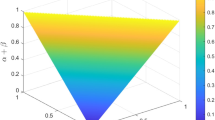
Example 1

Suppose that \({m}_1\) and \({m}_2\) represent two BPAs within the frame of discernment \(\Theta = \{{\mathcal {F}}_1, {\mathcal {F}}_2\}\). The assignments are specified as:

$$\begin{aligned}{} & {} m_1: m_1(\{{\mathcal {F}}_1\}) = \alpha , \quad m_1(\{{\mathcal {F}}_2\}) = \beta , \quad m_1(\Theta )= 1 -\alpha -\beta ; \end{aligned}$$
(12)
$$\begin{aligned}{} & {} m_2: m_2(\{{\mathcal {F}}_1\}) = \beta , \quad m_2(\{{\mathcal {F}}_2\}) = \alpha , \quad m_2(\Theta )= 1 - \alpha -\beta . \end{aligned}$$
(13)

In this example, \(\alpha\) and \(\beta\) are values that fall within the range of \([0, 1]\), ensuring that their combined sum also adheres to this boundary, consistent with the principles of ET.

From Fig. 1, we can see that variations in \(\alpha\) and \(\beta\) induce symmetric modifications in the belief values assigned by \(m_1\) and \(m_2\). Meanwhile, the (\({\mathbb{B}}{\mathbb{C}}\)) varying with \(\alpha\) and \(\beta\) remains consistent, emphasizing the inherent symmetry of \({\mathbb{B}}{\mathbb{C}}\). This reflects the expected symmetric characteristics of \({\mathbb{B}}{\mathbb{C}}\) within the framework of ET..

Fig. 1
figure 1

The results of \({\mathbb{B}}{\mathbb{C}}\) varying with \(\alpha\) and \(\beta\) in Example 1

Full size image

Example 2

Suppose that \(m_1\) and \(m_2\) are identified as two BPAs within the frame of discernment \(\Theta = \{{\mathcal {F}}_1, {\mathcal {F}}_2, {\mathcal {F}}_3\}\). The configuration of these BPAs is as follows:

$$\begin{aligned}&m_1 : m_1(\{{\mathcal {F}}_1\}) = \alpha , \quad m_1(\{{\mathcal {F}}_2\}) = \beta , \quad m_1(\{{\mathcal {F}}_3\}) = 1 - \alpha - \beta ; \end{aligned}$$
(14)
$$\begin{aligned}&m_2 : m_2(\{{\mathcal {F}}_1\}) = 0.4, \quad m_2(\{{\mathcal {F}}_2\}) = 0.6. \end{aligned}$$
(15)

where \(\alpha\) and \(\beta\) are values ranging from 0 to 1, inclusive of their combined sum, this limitation adheres to the principles of ET.

In Fig. 2, consider the scenario where \(\alpha\) is 0.4 and \(\beta\) is 0.6. In this case, \(m_1\) assigns a belief of 0.4 to \({\mathcal {F}}_1\) and 0.6 to \({\mathcal {F}}_2\), exactly mirroring the beliefs assigned by \(m_2\). This perfect alignment indicates a complete conflict between \(m_1\) and \(m_2\), resulting in our confidence in these beliefs dropping to its lowest point, namely 0. Conversely, if both \(\alpha\) and \(\beta\) are 0, \(m_1\) places all belief in \({\mathcal {F}}_3\), leading to the highest possible confidence level of 1. Remarkably, regardless of how \(\alpha\) and \(\beta\) vary, our confidence level remains within the bounds of 0 and 1. This example highlights how belief confidence is maintained within reasonable limits in the ET framework.

Fig. 2
figure 2

The results of \({\mathbb{B}}{\mathbb{C}}\) varying with \(\alpha\) and \(\beta\) in Example 2

Full size image

Example 3

Assuming the existence of two BPAs, \(m_1\) and \(m_2\), within the frame of discernment \(\Theta\), where \(m_1\) and \(m_2\) represent belief distributions. Here, \(\gamma\) is a variable confined to the range of 0 to 1. Additionally, \(T\) denotes a variable subset with a cardinality \(t\), belonging to the set \({V_T}\) and ranging from 1 to 20, as detailed in Table 1. The mass assignments are defined as follows:

$$\begin{aligned}&m_1 : m_1(\{{\mathcal {F}}_2\}) = \gamma , \quad m_1({V_T}) = 1 - \gamma ; \end{aligned}$$
(16)
$$\begin{aligned}&m_2 : m_2(\{{\mathcal {F}}_2\}) = 0.8, \quad m_2({V_T}) = 0.2. \end{aligned}$$
(17)

Figure 3 demonstrate the operational dynamics of the \({\mathbb{B}}{\mathbb{C}}\) divergence measure. In Fig. 3b, as \(\gamma\) gradually increases from 0 to 0.8, with \(t\) remaining constant, \(m_2\) increasingly aligns with \(m_1\),resulting in a decrease in the \({\mathbb{B}}{\mathbb{C}}\) divergence between them, which is in line with our expectations. When \(\alpha\) reaches 0.8, \(m_1\) and \(m_2\) converge to become identical, leading to a stabilization of the \({\mathbb{B}}{\mathbb{C}}\) divergence measure at 0. This stabilization persists regardless of any changes in \(t\), thereby confirming the non-degeneracy of the \({\mathbb{B}}{\mathbb{C}}\) divergence. In Fig. 3c, the divergence value observed for \(t = 1\) is significantly higher than for other \(t\) values. This is due to the fact that when \(t = 1\), there is only a single element in \(T\), resulting in no intersection between subsets. As the number of elements in \(T\) increases from 2 to 20, the divergence value gradually rises as well, reflecting the absence of subset intersection and the increasing uncertainty associated with the expansion of \(T\).

Fig. 3
figure 3

The results of \(\mathcal{B}\mathcal{C}\) varying with \(\gamma\) and t in Example 3

Full size image
Table 1 Variable set \(T\)
Full size table

3.3 A novel \({\mathbb{B}}{\mathbb{C}}\) divergence-based multisource information fusion method

In this section, a novel method for multisource information fusion is introduced, based on the principles of \({\mathbb{B}}{\mathbb{C}}\) divergence and belief entropy. This method utilizes the \({\mathbb{B}}{\mathbb{C}}\) divergence to precisely quantify the differences among various evidences, assigning credibility weights inversely to these measured discrepancies. The improved belief entropy is used to calculate the uncertainty of each piece of evidence, generating the information volume. By combining the weights from \({\mathbb{B}}{\mathbb{C}}\) divergence and belief entropy, we obtain a comprehensive weight. With this comprehensive weight, the average evidence is computed. Finally, Dempster’s rule is applied to fuse the weighted average evidence.

This approach enables a detailed analysis of evidence, capturing both minor and major differences. One key benefit is its ability to avoid the common mistake of treating multi-element subsets as single-element ones. This distinction ensures more accurate and fair weighting of evidence, improving the overall fusion process. For clarity, the complete fusion process is illustrated in the flowchart in Fig. 4.

Fig. 4
figure 4

Flowchart of the proposed method

Full size image

Step 1: Obtain the credibility weight of evidence

Step 1-1: Consider \(k\) independent BPAs defined over a frame of discernment \(\Theta\) that comprises \(N\) elements, namely \(\{{\mathcal {F}}_1, {\mathcal {F}}_2, \ldots , {\mathcal {F}}_N\}\). The divergence between any two BPAs \(m_i\) and \(m_j\) ( \(i, j = 1, 2, \ldots , k\)) is calculated using Eq. (11). Then, a divergence matrix \(D_{k \times k}\) can be constructed as follows:

$$\begin{aligned} D_{k \times k} = \begin{bmatrix} 0 &{} {\mathbb{B}}{\mathbb{C}}(m_1, m_2) &{} \dots &{} {\mathbb{B}}{\mathbb{C}}(m_1, m_k) \\ {\mathbb{B}}{\mathbb{C}}(m_2, m_1) &{} 0 &{} \dots &{} {\mathbb{B}}{\mathbb{C}}(m_2, m_k)\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {\mathbb{B}}{\mathbb{C}}(m_k, m_1) &{} {\mathbb{B}}{\mathbb{C}}(m_k, m_2) &{} \dots &{} 0 \end{bmatrix}. \end{aligned}$$
(18)

Step 1-2: Calculate the average divergence based on the matrix \(D_{k \times k}\), denoted by \(\tilde{{\mathbb{B}}{\mathbb{C}}}(m_i)\). This calculation is formulated as follows:

$$\begin{aligned} \tilde{{\mathbb{B}}{\mathbb{C}}}(m_i) = \frac{\sum _{\begin{array}{c} j=1 \\ j \ne i \end{array}}^k {\mathbb{B}}{\mathbb{C}}(m_i, m_j)}{k - 1} \quad \end{aligned}$$
(19)

Step 1-3: The support degree of evidence \(m_i\) is computed as the reciprocal of the average divergence measure, defined as follows:

$$\begin{aligned} S(m_i) = \frac{1}{\tilde{{\mathbb{B}}{\mathbb{C}}}(m_i)} \end{aligned}$$
(20)

Step 1-4: The credibility weight \(Crd(m_i)\) for evidence \(m_i\) is defined as follows:

$$\begin{aligned} Crd(m_i) = \frac{S(m_i)}{\sum _{j=1}^k S(m_j)}. \end{aligned}$$
(21)

Step 2: Obtain the information volume of evidence

Belief entropy, which extends Shannon entropy, is often used to measure the information volume of evidence [34]. However, it has limitations, such as not considering the intersections between elements in the discernment framework. In this paper, we use an improved belief entropy based on both belief and plausibility functions [12], offering more comprehensive information.

Step 2-1: Calculate the belief entropy \(BE(m_i)\) for the evidence \(m_i\) as follows:

$$\begin{aligned} BE(m_i)= & {} \sum _{{\mathcal {F}}_l \in \Theta } BetP_{m_i}({\mathcal {F}}_l) \log _2 \left( \frac{1}{BetP_{m_i}({\mathcal {F}}_l)} \right) \nonumber \\{} & {} + \sum _{{\mathcal {F}}_l \in 2^\Theta } m_i({\mathcal {F}}_l) \log _2 (2^{|{\mathcal {F}}_l|} - 1). \end{aligned}$$
(22)

Step 2-2: To prevent assigning weights to non-informative evidence, the information volume \(IV(m_i)\) is defined in the following manner:

$$\begin{aligned} IV(m_i) = \exp (-{BE}_{m_i}), \quad \forall i = 1, \ldots , k. \quad \end{aligned}$$
(23)

Step 2-3: The information volume weight, represented as \(\tilde{IV}(m_i)\), is obtained by standardizing the information volume as follows:

$$\begin{aligned} \tilde{IV}(m_i) = \frac{IV(m_i)}{\sum _{j=1}^k IV(m_j)}. \quad \end{aligned}$$
(24)

Step 3: Generate and combine the weighted average evidence

Step 3-1: The final weight of evidence \(m_i\), represented by \(\tilde{ACrd}(m_i)\), is calculated by adjusting it according to the information volume \(\tilde{IV}(m_i)\) and credibility \(Crd(m_i)\) as follows:

$$\begin{aligned} \tilde{ACrd}(m_i) = \frac{Crd(m_i) \times \tilde{IV}(m_i)}{\sum _{j=1}^k Crd(m_j) \times \tilde{IV}(m_j)} \quad \end{aligned}$$
(25)

Step 3-2: The weighted average evidence, denoted by \(\tilde{m}\), is calculated as detailed below:

$$\begin{aligned} \tilde{m}({\mathcal {F}}) = \sum _{i=1}^k \tilde{ACrd}(m_i) \times m_i({\mathcal {F}}). \quad \end{aligned}$$
(26)

Step 3-3: The process of aggregating the weighted average evidence employs Dempster’s combination rule \(k - 1\) times, as specified in Eq. (6). Consequently, the ultimate combined outcome is formulated as:

$$\begin{aligned} m({\mathcal {F}}) = \underbrace{\tilde{m} \oplus \tilde{m} \oplus \ldots \oplus \tilde{m}}_{k-1\, \text {times}} \end{aligned}$$
(27)

4 Application

In this section, to better demonstrate the proposed method, three applications are introduced to illustrate the effectiveness of the proposed \({\mathbb{B}}{\mathbb{C}}\) divergence-based multisource information fusion approach.

4.1 Application in target detection

The target detection framework is outlined as \(\Theta = \{{\mathcal {F}}_1, {\mathcal {F}}_2, {\mathcal {F}}_3\}\), encompassing a set of sensors \({S_1, S_2, S_3, S_4, S_5}\) deployed for target monitoring. These sensors detect targets and compile reports in the form of BPAs, specifically \(m_1(\cdot )\), \(m_2(\cdot )\), \(m_3(\cdot )\), \(m_4(\cdot )\) and \(m_5(\cdot )\). These BPAs refer to the mass functions generated in [6] and are listed in Table 2. According to the table, \(m_1\), \(m_3\), and \(m_4\) support \({{\mathcal {F}}_1}\) as the real target, whereas \(m_2\) exhibits ambiguity in identifying the target, and \(m_5\) proposes \({{\mathcal {F}}_3}\) as the actual target. Thus, \(m_2\) and \(m_5\) are identified as sources of noise and consequently should receive reduced weighting in the final fusion result.

Table 2 The BPAs gathered from five sensors for target detection
Full size table

4.1.1 Target detection based on the multisource information fusion

This section provides a detailed explanation of the calculation steps.

Step 1-1: Calculate the divergence measure matrix \(D_{5 \times 5}\) is constructed as follows:

$$\begin{aligned} D_{5 \times 5} = \begin{bmatrix} 0 &{} 0.1150 &{} 0.0031 &{} 0.0412 &{} 0.3707 \\ 0.1150 &{} 0 &{} 0.0974 &{} 0.2396 &{} 0.3506 \\ 0.0031 &{} 0.0974 &{} 0 &{} 0.0664 &{} 0.3116 \\ 0.0412 &{} 0.2396 &{} 0.0664 &{} 0 &{} 0.6173 \\ 0.3707 &{} 0.3506 &{} 0.3116 &{} 0.6173 &{} 0 \\ \end{bmatrix}. \end{aligned}$$
$$\begin{aligned} {\textbf {Step 1-2:}}~&\text {Calculate the average divergence}\, \tilde{{\mathbb{B}}{\mathbb{C}}}(m_i)&\\&\tilde{{\mathbb{B}}{\mathbb{C}}}(m_1)=0.1325,&\\&\tilde{{\mathbb{B}}{\mathbb{C}}}(m_2)=0.2006,&\\&\tilde{{\mathbb{B}}{\mathbb{C}}}(m_3)=0.1196,&\\&\tilde{{\mathbb{B}}{\mathbb{C}}}(m_4)=0.2411,&\\&\tilde{{\mathbb{B}}{\mathbb{C}}}(m_5)=0.4125.&\\ {\textbf {Step 1-3:}}~&\text {Calculate the support degree}\, S(m_i)\, \text {of}\, m_i.&\\&S(m_1) = 7.5478,&\\&S(m_2) = 4.9840,&\\&S(m_3) = 8.3584,&\\&S(m_4) = 4.1472,&\\&S(m_5) = 2.4240.&\\ {\textbf {Step 1-4:}}~&\text {Compute the credibility degree}\, Crd(m_i)\, \text {of}\, m_i&\\&Crd(m_1) = 0.2749,&\\&Crd(m_2) = 0.1815,&\\&Crd(m_3) = 0.3044,&\\&Crd(m_4) = 0.1510,&\\&Crd(m_5) = 0.0883.\\ {\textbf {Step 2-1:}}~&\text {Generate the improved belief entropy}\, BE(m_i)\, \text {of}\, m_i&\\&BE(m_1) = 2.0253,&\\&BE(m_2) = 2.0848,&\\&BE(m_3) = 2.4395,&\\&BE(m_4) = 1.6641,&\\&BE(m_5) = 1.5867.\\ {\textbf {Step 2-2:}}~&\text {Measure the information volume}\, IV(m_i)\, \text {of}\, m_i&\\&{IV}(m_1) = 7.5782,&\\&{IV}(m_2) = 8.0426,&\\&{IV}(m_3) = 11.4669,&\\&{IV}(m_4) = 5.2811,&\\&{IV}(m_5) = 4.8875. \\ {\textbf {Step 2-3:}}~&\text {Obtain the normalized information volume}\, \tilde{IV}(m_i)\, \text {of}\, m_i&\\&\tilde{IV}(m_1) = 0.2034,&\\&\tilde{IV}(m_2) = 0.2159,&\\&\tilde{IV}(m_3) = 0.3078,&\\&\tilde{IV}(m_4) = 0.1418,&\\&\tilde{IV}(m_5) = 0.1312. \\ {\textbf {Step 3-1:}}~&\text {Normalized adjusted credibility}\, \tilde{ACrd}(m_i)&\\&\tilde{ACrd}(m_1) = 0.2521,&\\&\tilde{ACrd}(m_2) = 0.1767,&\\&\tilde{ACrd}(m_3) = 0.4225,&\\&\tilde{ACrd}(m_4) = 0.0965,&\\&\tilde{ACrd}(m_5) = 0.0522. \\ {\textbf {Step 3-2:}}~&\text {Obtain the weighted average evidence}\, \tilde{m}&\\&\tilde{m}(\{{\mathcal {F}}_1\})= 0.3979,&\\&\tilde{m}(\{{\mathcal {F}}_2\}) = 0.1361,&\\&\tilde{m}(\{{\mathcal {F}}_3\}) = 0.0984,&\\&\tilde{m}(\{{\mathcal {F}}_1,{\mathcal {F}}_2\}) = 0.1381,&\\&\tilde{m}(\{{\mathcal {F}}_2,{\mathcal {F}}_3\}) = 0.0178,&\\&\tilde{m}(\{{\mathcal {F}}_1,{\mathcal {F}}_2,{\mathcal {F}}_3\}) =0.2116. \end{aligned}$$

Step 3-3:  Employing Dempster’s rule of combination within the context of ET, the process involves the integration of the weighted average evidence through four successive fusions, as illustrated in Fig. 5.

Table 3 Combination results with different types of methods
Full size table
Fig. 5
figure 5

Comparison of belief values obtained with different methods for different numbers of sensors

Full size image

4.1.2 Discussion

Table 3 and Fig. 5 present the results of combining conflicting evidence using various methods. Dempster’s rule shows a \({\mathcal {F}}_1\) score of 0.6350, which is relatively low. Murphy’s method and Deng et al.’s method achieve 0.7837 and 0.8394, respectively. In contrast, our proposed method achieves a peak belief score of 0.8653 for the correct target \({\mathcal {F}}_1\), outperforming the other methods. For other targets, our method maintains low scores of 0.1022 for \({\mathcal {F}}_2\) and 0.0119 for \({\mathcal {F}}_3\), demonstrating its accuracy in identifying the correct target. Other methods, like Huang et al.’s, show slightly higher scores on these targets (0.1520 on \({\mathcal {F}}_2\) and 0.0142 on \({\mathcal {F}}_3\)). In summary, our method achieves the highest belief score for the correct target and minimizes errors on other targets, demonstrating superior performance in merging conflicting evidence. This significant improvement primarily due to from our innovative approach, which adeptly manages the interactions between individual and combined evidence sets. We introduce a new measure, referred to as the \({\mathbb{B}}{\mathbb{C}}\) measure, which cleverly assesses the degree of disagreement among evidence pieces. This is crucial for understanding how different pieces of evidence relate to each other. Furthermore, we assign weights to each evidence based on its reliability and the amount of information it offers, ensuring that more credible and informative evidence carries greater weight in the final decision. Our method excels in navigating through and reconciling conflicting evidence, thereby enhancing the accuracy and reliability of target detection systems.

4.1.3 Sensitivity analysis

In the context of the previously mentioned experiments, we conduct a sensitivity analysis to evaluate the stability of our representative \({\mathbb{B}}{\mathbb{C}}\) measure compared to other methods, such as Dempster’s rule, Murphy’s method, and methods from Deng et al., Lin et al., Jiang, Xiao, Kaur and Srivastava, and Huang et al. For this analysis, we created different initial data by randomly varying the focal elements of \(m_1\) within the range \([-0.1, 0.1]\) a hundred times, while keeping other focal elements unchanged. Each time, we used these variations to combine the generated BPAs. The results, shown in Fig. 6, illustrate the overall trend in the combined target BPAs across the compared methods.

All the methods correctly identify \({\mathcal {F}}_1\) as the target. However, the belief values derived from Dempster’s rule are significantly lower than those obtained from the other methods. Notably, the proposed method in this study demonstrates higher belief values for target \({\mathcal {F}}_1\) compared to the methods of Deng, Xiao, Lin, and Jiang et al. Consequently, the proposed method shows superior performance for target \({\mathcal {F}}_1\) and greater robustness than Dempster’s rule.

Fig. 6
figure 6

Sensitivity analysis of different methods

Full size image

4.2 Application in pattern recognition

The Iris dataset is popular for machine learning studies and is available in the UCI repository. It categorizes Iris flowers into three species: Setosa, Versicolor, and Virginica, which we denote as \(\Theta = \{Se, Vc, Vi\}\). We describe each flower using four measurements: the lengths and widths of both its sepals and petals. In this work, we use the data referenced as [6] and apply BPAs to analyze the data, as detailed in Table 4. Notably, we assume that the sepal width measurement (the second feature) is subject to interference from noise.

Table 4 The obtained BPA of an Iris instance with noisy data
Full size table

4.2.1 Iris classification based on the multisource information fusion

This section provides a detailed explanation of the calculation steps.

Step 1-1: Construct the divergence measure matrix \(D_{4 \times 4}\) as follows:

$$\begin{aligned} D_{4 \times 4} = \begin{bmatrix} 0 &{} 0.4680 &{} 0.1211 &{} 0.1443 \\ 0.4680 &{} 0 &{} 0.6180 &{} 0.6417 \\ 0.1211 &{} 0.6180 &{} 0 &{} 0.0011 \\ 0.1443 &{} 0.6417 &{} 0.0011 &{} 0 \\ \end{bmatrix}. \end{aligned}$$
$$\begin{aligned} {\textbf {Step 1-2:}}~&\text {Compute the average divergence}\, \tilde{{\mathbb{B}}{\mathbb{C}}}(m_i)&\\&\tilde{{\mathbb{B}}{\mathbb{C}}}(m_1)=0.2444,&\\&\tilde{{\mathbb{B}}{\mathbb{C}}}(m_2)=0.5759,&\\&\tilde{{\mathbb{B}}{\mathbb{C}}}(m_3)=0.2467,&\\&\tilde{{\mathbb{B}}{\mathbb{C}}}(m_4)=0.2623,&\\ {\textbf {Step 1-3:}}~&\text {Calculate the support degree}\, S(m_i)\, \text {of}\, m_i.&\\&S(m_1) = 4.0910,&\\&S(m_2) = 1.7365,&\\&S(m_3) = 4.0534,&\\&S(m_4) = 3.8118,&\\ {\textbf {Step 1-4:}}~&\text {Calculate the credibility degree}\, Crd(m_i)\, \text {of}\, m_i&\\&Crd(m_1) = 0.2988,&\\&Crd(m_2) = 0.1268,&\\&Crd(m_3) = 0.2960,&\\&Crd(m_4) = 0.2784,&\\ {\textbf {Step 2-1:}}~&\text {Generate the improved belief entropy}\, BE(m_i)\, \text {of}\, m_i&\\&BE(m_1) = 1.6956,&\\&BE(m_2) = 0.0808,&\\&BE(m_3) = 1.2016,&\\&BE(m_4) = 1.1644,&\\ {\textbf {Step 2-2:}}~&\text {Measure the information volume}\, IV(m_i)\, \text {of}\, m_i&\\&{IV}(m_1) = 5.4499,&\\&{IV}(m_2) = 1.0841,&\\&{IV}(m_3) = 3.3255,&\\&{IV}(m_4) = 3.2041,&\\ {\textbf {Step 2-3:}}~&\text {Obtain the normalized information volume}\, \tilde{IV}(m_i)\,\text {of}\,m_i&\\&\tilde{IV}(m_1) = 0.4172,&\\&\tilde{IV}(m_2) = 0.0830,&\\&\tilde{IV}(m_3) = 0.2546,&\\&\tilde{IV}(m_4) = 0.2453,&\\ {\textbf {Step 3-1:}}~&\text {Normalized adjusted credibility}\, \tilde{ACrd}(m_i)&\\&\tilde{ACrd}(m_1) = 0.4471,&\\&\tilde{ACrd}(m_2) = 0.0377,&\\&\tilde{ACrd}(m_3) = 0.2703,&\\&\tilde{ACrd}(m_4) = 0.2449,&\\ {\textbf {Step 3-2:}}~&\text {Obtain the weighted average evidence}\, \tilde{m}&\\&\tilde{m}(\{Se\})= 0.5016,&\\&\tilde{m}(\{Vc\}) = 0.2950,&\\&\tilde{m}(\{Vi\}) = 0.1663,&\\&\tilde{m}(\{Se,Vc\}) = 0.0137,&\\&\tilde{m}(\{Se,Vi\}) = 0.0023,&\\&\tilde{m}(\{Vc,Vi\}) =0.0188.&\\&\tilde{m}(\{Se,Vc,Vi\}) =0.0023. \end{aligned}$$

Step 3-3: Apply Dempster’s rule of combination, we proceed to merge the weighted average evidence, denoted by \(\tilde{m}\), through a series of three iterations. The fusing results are presented in Table 5.

4.2.2 Discussion

As shown in Table 5, Dempster’s method fails under all conditions because the belief value of Se remains 0. When there are only two sets of BPAs, only the methods of Xiao, Huang, and our proposed method can successfully identify the class, with recognition rates above the 0.6 threshold. Notably, our method achieves the highest belief value of 0.6517. With three sets of BPAs, the previous methods continue to identify the class, and the methods of Deng and Jiang also become effective. However, our method still holds the highest belief value at 0.7670. When the number of BPAs increases to four, Murphy’s method and the methods of Kaur and Srivastava still do not work. Other methods, along with our proposed method, successfully identify the class, with our method achieving the highest belief value of 0.8477. Therefore, our proposed method not only achieves the highest belief value but also requires fewer sets of evidence to do so.

Figure 7 illustrates the belief values for the class Se obtained through various methods. This comparison clearly shows that both Dempster’s rule and Murphy’s method inaccurately assign Vc as the true class, with belief values of 0.9988 and 0.5546, respectively. Conversely, the true class Se is assigned belief values of 0 and 0.4422, respectively, leading to counter-intuitive identification outcomes. Other methods successfully recognize the real class, albeit with varying belief values for Se. Specifically, Kaur and Srivastava’s method and Deng’s method assign relatively lower belief values to Se at 0.5310 and 0.7301, respectively. In contrast, Xiao’s method and Huang et al.’s method both attribute a belief value of approximately 0.82 to Se. However, our proposed method assigns Se class the highest belief value of 0.8477, surpassing the other methods. It is apparent that Dempster’s rule and Murphy’s method are limited in their application scope, particularly when faced with highly conflicting evidence where their performance tends to falter. While other compared methods, including our proposed approach, can accurately identify the true class, our method notably achieves a superior identification effect. Therefore, our proposed method not only accurately identifies the true class but also exhibits superior accuracy and robustness.

Table 5 Experiment of different methods in the Iris data set
Full size table
Fig. 7
figure 7

Comparison of the belief values obtained with different methods

Full size image

4.3 Application in Monte Carlo simulations

In order to thoroughly evaluate our approach, we conduct experiments using 100 Monte Carlo simulations. These simulations addressed scenarios where sources either fully agreed or completely conflicted. In the scenario of complete agreement, all sensor evidence in each simulation supported the same object. We averaged the simulated BPAs over 100 iterations to obtain the final BPA. Conversely, in the complete inconsistency scenario, the sensor evidence supported different single-class objects, with some evidence correctly identifying the object. The BPA was generated in a similar manner. Separate experiments were conducted for these two cases. This methodology provides a rigorous assessment of the robustness and reliability of the proposed multi-source fusion method under varying conditions. By analyzing the results of these simulations, we can better understand the performance of our approach in different scenarios of evidence conflict.

4.3.1 Scenario of complete agreement

We conduct 100 Monte Carlo simulations and average the results to obtain the BPAs, as shown in Table 6. From this table, it is evident that \(m_1\), \(m_2\), \(m_3\), \(m_4\), and \(m_5\) consistently support \(\{F1\}\) as the true target, with no evidence acting as noise data. This consistent support clearly indicates a scenario of complete agreement.

In this scenario, the evidence consistently identifies the true target, leading to nearly equal weight factors assigned to each BPA in the final fusion result. This equal weighting ensures an accurate and fair representation of the true target in the final fused outcome. As illustrated in Table 7, all methods successfully identify the true target and assign it similar confidence values. This is expected, as both the comparison methods and our proposed multi-source information fusion method are designed to handle highly conflicting evidence while accurately identifying the correct target. When dealing with non-conflicting evidence sources, the confidence values for the true target are nearly identical across all methods. Moreover, our method demonstrates a slight advantage, achieving a confidence value of 0.9950, which is marginally higher than the other comparison methods.

Table 6 The BPAs averaged results from multiple Monte Carlo simulations
Full size table
Table 7 Combination results with different types of methods
Full size table

4.3.2 Scenario of complete conflicting

Similarly, we perform 100 Monte Carlo simulations and averaged the results to obtain the BPAs. The results are shown in Table 8, which simulates a scenario where a sensor indicates 0 for a specific category. In each Monte Carlo simulation, we imposed a constraint that sets the support of the third sensor for the first object and the composite object of the three as 0. In this scenario, evidence \(m_2\) supports object \({\mathcal {F}}_2\), evidence \(m_3\) supports object \({\mathcal {F}}_3\), while the other three sets of evidence clearly support object \({\mathcal {F}}_1\), creating a conflict situation. The fusion results using the proposed method and various existing methods are presented in Table 9.

As shown in Fig. 8, the fusion results are more clearly demonstrated. It can be observed that all methods, except for Dempster’s, correctly identify the target. Dempster’s method struggles with highly conflicting evidence, leading to incorrect identification. Murphy’s average method, which averages the evidence, fails to differentiate between BPAs effectively in highly conflicting scenarios. Deng et al. and Jiang’s methods correctly identifies the target but only considers the distance between evidence without accounting for the information volume within the evidence. Xiao’s method uses belief divergence to measure differences between evidences but overlooks the influence of multiple subsets. Lin et al.’s method and Kaur and Srivastava’s method treat multiple subsets as single subsets, failing to adequately reflect the distinct impacts of different subsets. The proposed method demonstrates greater practicality for decision-making applications by achieving the highest belief value of 0.9560 in handling highly conflicting evidence. This showcasing the robustness and effectiveness of our method in managing and fusing conflicting evidence.

Table 8 The BPAs Averaged Results from Multiple Monte Carlo Simulations
Full size table
Table 9 Combination results with different methods
Full size table
Fig. 8
figure 8

Comparison of the belief values obtained with different methods

Full size image

5 Conclusion

In this paper, a new divergence measure called belief cosine \({\mathbb{B}}{\mathbb{C}}\) divergence specifically designed for multisource information fusion is introduced. This method refines traditional divergence measures by integrating the cosine function, thus providing an advanced approach for managing multisource information fusion. It adeptly identifies subtle similarities and differences across evidence sources, addressing the limitations of existing metrics effectively. Furthermore, the \({\mathbb{B}}{\mathbb{C}}\) divergence adheres to critical properties like boundedness, non-degeneracy, and symmetry. Compared to other single-parameter metrics, the proposed belief cosine divergence demonstrates enhanced applicability. Based on the \({\mathbb{B}}{\mathbb{C}}\) divergence, a novel multisource information fusion method is presented. The proposed method effectively manages uncertainty and imprecision throughout the entire information fusion process. A target detection case is conducted to showcase the effectiveness and applicability of our proposed method. Crucially, the experiment definitively confirms the reliability and robustness of our approach to fusing information from multiple sources. Furthermore, an experiment using the Iris dataset is conducted to investigate the \({\mathbb{B}}{\mathbb{C}}\) divergence’s influence on the final fusion outcome. This exploration confirms the superior identification capabilities and practicality of our method, effectively managing uncertainty and integrating multiple information sources to enhance decision accuracy. Compared to the methods proposed by Xiao, Jiang, Lin et al. and ohters, our method demonstrates a higher belief degree for the accurate target, especially when integrating significantly conflicting evidence. In the future, we plan to investigate the properties of \({\mathbb{B}}{\mathbb{C}}\) further and explore the applicability of our method in more complex environments.