Developing a multi-objective model for a multi-level supply chain of blood products under uncertainty and the global pandemic: a hybrid robust optimization approach

Abstract

The global COVID-19 pandemic has caused a substantial decrease in the blood supply and its products as a vital commodity. It has had adversely affected on the activities of blood organizations and facilities as well as public health. In this critical situation, the particular supply and blood demand products have affected certain sensitive managerial decisions. The purpose of the present study is to develop a multi-objective formulation for a multi-level supply chain of blood products under uncertainty and global pandemic conditions. The modeling is based on three objectives: minimizing the costs of the entire blood supply chain network, minimizing the pandemic virus transmission by donors in each of the blood donation centers, and maximizing the attractiveness of the blood donation centers in order to optimize the blood supply chain conditions and meet the needs of patients in the best possible way. Besides, since uncertainty is an integral part of supply chains, an efficient combination of scenarios, intervals and fuzzy robust optimization approaches is applied. As the results show, using robust approaches to deal with uncertain parameters can provide excellent conditions for efficient responses to those who demand blood products as well as pandemic patients who need the plasma of survivors.

Article Highlights

• A multi-objective model for a multi-level supply chain of blood products under uncertainty and the COVID-19 pandemic.

• Taking into account the amount of blood donation and the demand for blood uncertainty and the COVID-19 conditions at a complete supply chain.

• Two “Scenario-based robust” and “Hybrid heuristic robust” optimization approaches that could face different types of uncertainty.

1 Introduction

Generally, a crisis refers to any event that occurs suddenly while it may aggravate the conditions, stop society from its normal functioning and cause human, economic and environmental damages. Managing this situation involves taking some practical measures before and after the occurrence of the crisis in order to reduce its destructive effects [1].

The coronavirus disease 2019 (COVID-19) is one of the recent crises that occurred worldwide at the end of 2019. So far, it has afflicted almost every country and more than 696,491,670 people, with a death toll of 6,925,484 until October 2023 [2].

Pandemic-induced crises are differ from other occurrences due to their particular conditions, including long-term disruption in all systems and the ever-increasing contamination rate. If not controlled, these conditions cause irreparable losses in many supply chains worldwide, such as blood supply chains (BSCs) as vital networks in the health system.

Blood and its products are one of the vital strategic items for all nations and governments in the world. Blood transfusion is required due to various accidents and incidents such as car accidents, burns and surgeries. Women in childbirth and premature babies need blood, too. There is still no substitute for blood; only the blood donated by human beings can save the lives of other human beings. Lack of suitable substitutes for blood and its products, limited storage time and the constant need for blood and its products have made blood donation particularly important.

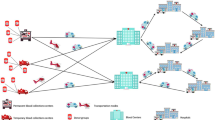
Accordingly, blood product supply chain management is a very challenging area in humanitarian logistics. It includes the flow of blood products from donors to patients at five levels as (I) blood centers, (II) fixed blood collection facilities, (III) mobile blood collection facilities, (IV) demand points such as hospitals, clinics, relief centers, and field hospitals, and finally (V) patients. Moreover, the six processes of collection, testing, product production, distribution, storage and blood transfusion are performed during this flow. In this regard, reducing organizational costs is critical in increasing the level of service and the satisfaction of the affected people [3].

Uncertainty can considerably affect the efficiency of the supply chains, especially in BSC networks (SCNs) where the only suppliers are those who donate blood voluntarily. This has caused uncertainty in the supply of the required blood. The demand for blood products is another parameter that is unpredictable most of the time, and the constant possibility of natural and human disasters, like the global pandemic spread discussed in the current study, has caused uncertainty in demand for blood products. The literature on the BSC hierarchy indicates that some studies have dealt with several levels simultaneously, while others have focused on only one specific level.

Although the virus has spread recently, the number of recoveries has increased significantly. Those who recover from the pandemic develop natural immune systems in their blood against the disease. Therefore, their blood plasma contains pandemic antibodies that can be used to prepare improved plasma products to treat other patients with the disease. As statistics emphasize, only 1.88% of those who recovered donated blood plasma. Accordingly, it is essential to adopt policies to encourage recovered people to donate plasma. An apheresis method seems to be a good option to meet the purpose. After a blood component (plasma in this case) is separated through special equipment, the rest are returned to the donor’s bloodstream. Also, the quantity of the product obtained in this method is higher than that in the usual method of donating and producing the product (i.e., the apheresis method). In addition, through apheresis, it is possible to improve the donation of all blood products; since blood is not an ordinary material, its unique characteristics and the supply chain that it requires complicate the issue and may ultimately lead to a shortage of blood and a growth in the death rate. In additions, expired blood is often not accepted; blood donors are a infrequent asset, and donations have to occur at specific intervals. Even after eligible volunteers apply, only a few (5%) refer to donation sites. These conditions emphasize the need to examine the psychological factors involved in the issue and the ways to motivate donors. Of the most important features of a BSC, one may refer to the relatively irregular supply of donated blood, uncertain demand for blood products, mismatched supply and demand, and, above all, perishability of blood products.

So far, as the literature suggests, many studies have dealt with BSCs and the various processes involved in them, including inventory management, location, distribution, blood transfusion, planning for critical situations, and selection of solution approaches [11]. However, to the best of the authors’ knowledge, as a significant research gap, little research has been done on improving the overall efficiency of BSCs and their levels, including donors and various blood facilities, in the face of epidemics. The main purpose of the current study is to present a multi-objective supply chain formulation for blood products to improve the attractiveness of blood centers during the epidemic. Accordingly, by optimizing the overall cost and the attractiveness of blood donation centers, an attractive efficient environment is provided. It can help to remove barriers to blood donation and improve blood health.

In general, the study is conducted to analyze the following question:

• (a) To what extent does the adaptation of BSCs to the critical conditions resulting from the spread of the pandemic play a role in controlling the disease and reducing the disorders in those chains?

• (b) How minimize the spread of the pandemic virus in the presence of blood donors in mobile, regional, and local blood centers?

• (c) How do the attractiveness of blood centers, public awareness, adherence to health protocols, and better employee performance affect the demand response?

• (d) Can separate mobile facilities operating through apheresis increase the blood donation for plasma production?

Some of the special features and innovations of the proposed formulation are as follows: (a) Comprehensive minimization of all types of costs of the entire network is considered the first objective. (b) For the first time, the objective of minimizing the spread of the coronavirus has been developed. This goal is pursued by increasing the plasma supply from recovered people to reduce the shortage of this product at various demand points. (c) maximize the attractiveness of the blood collection centers (BCCs) (d) Arranging the means of transportation for the effective transfer of blood products to the provincial centers of the candidate country and sets various incentive policies for blood donation.

The main remaining sections of the paper is organized as follow. The related literature is reviewed in Sect. 2. The mathematical modelling is explained in Sect. 3. In Sect. 4, the solution approaches, including robust scenario-based approach and hybrid heuristic robust optimization approach, are described. Designing and analyzing the numerical test examples, as well as, a practical case study, and comprehensive sensitivity analyses are represented in Sect. 5. Concluding remarks and managerial insights are clarified in Sect. 6.

2 Literature review

Here, the most recent relevant studies of BSCs under uncertain conditions and global pandemic are reviewed. Jabbarzadeh et al. [4] presented a dynamic formulation for a robust BSC at the blood collection level in several periods after a crisis. They aimed to minimize the costs by determining the location and allocation of facilities. The results of the robust optimization method showed that the proposed solution could increase the satisfaction of blood demanders within the budget limits.

Doan et al. [5] presented a red blood cell supply chain at a hospital level with 11 departments, adjusted the inventory and optimally allocated blood to each department. The purpose was to optimize the costs, wastage, and blood shortage by designing a hybrid integer programming formulation. The problem was solved by the CPLEX software, and the results showed a reduction of 72%, 90% and 108,540 units in blood shortage, blood wastage and costs, respectively. Ganpinar and Centero [6] designed a stochastic integer programming formulation for a single-level BSC, intending to minimize the cost of blood wastage and shortage in a hospital. The model was solved by the branch-and-bound algorithm. The results represented a reduction in blood wastage, shortage and total costs by 17.4%, 91.43% and 20.7%, respectively. Rajendran and Ravindran [7] investigated platelet ordering strategies at the hospital level by applying a stochastic integer programming formulation and innovative methods to increase productivity. Dillon et al. [8] presented a stochastic planning model to manage a red blood cell inventory in a single-level supply chain to reduce the maintenance costs, shortage and wastage of red blood cells. Ghandforoosh and San [9] designed a SCN for the optimal transfer of platelets from regional centers to hospitals as two separate levels. For this purpose, they used a non-convex planning model. Arvan et al. [10] designed a SCN of blood products, including red blood cells, platelets, plasma, and whole blood. The network operated at blood collection, processing and distribution levels in a location-allocation problem. They also included the communication of hospitals to reduce the shortages at the demand points in a hybrid integer programming formulation. Samani et al. [11] presented a hybrid integer programming formulation of designing a supply chain of blood products at the levels of blood donation, collection and distribution under crisis conditions. Shirazi et al. [12] designed a four-echelon supply chain to locate the blood collection centers, allocate to find the collection centers to the temporary or permanent plasma-processing facilities. They focused on blood substitutability throughout the supply chain. Fallahi et al. [13] designed an integrated green SCN of regular and convalescent plasma in the pandemic outbreak. Kochakkashani et al. [14] developed a SCN for vaccine and pharmaceutical clusters under pandemic conditions. Ash et al. [15] proposed a multi-period multi-objective distributionally robust formulation for the Canadian healthcare SCN to increase resilience during the Coronavirus. Abdolazimi et al. [16] designed a multi-level BSC network regarding uncertain conditions, and disruption in COVID-19. Their proposed formulation tackled humanitarian factors such as selecting the most suitable locations in the chain to cover all patients and minimizing the amount of spoiled blood under COVID-19. The results emphasized that adding mobile blood facilities would mitigate the delivery time. Tirkolaee et al. [17] designed a multi-level BSCN under uncertainty of capacity, demand, and blood disposal rates. Their bi-objective Mixed-Integer Linear Programming (MILP) formulation has two objective functions which aim to minimize network costs and maximize job opportunities while considering the adverse effects of the pandemic. For an efficient and reliable integrated BSCN for COVID-19 patients, Abdolazimi et al. [18] proposed a mathematical model to optimize blood use, minimize wastage, prevent shortages, and reduce unnecessary transfusions in all hospitalized patients. Their study has addressed the consideration of multiple factors, including perishability and scarceness of blood, simultaneously. According to the most relevant leading works, the state-of-the-art and an updated literature review can be represented as Table 1.

Table 1 The literature of the proposed blood supply chain network under the COVID-19 epidemy

Considering the research literature and the results of the studies on the types of modeling in BSCs, the present study aims at a complete supply chain of blood products under uncertainty and the pandemic crisis. Since parameters such as the amount of blood donation and the demand for blood have inherent uncertainty, robust, stochastic, convex, and potential optimization approaches are developed to deal with uncertainty. Therefore, the problem investigated in this research is whether the use of optimization approaches to face uncertain parameters can be of benefit and to what extent.

The main goal of the current study is to design a multi-level supply chain network for blood products, focusing on the conditions of the spread of the coronavirus and donation attractiveness; In such a way that taking into account the critical conditions, i.e., the outbreak of the widespread disease of pandemic, not only the amount of blood supply products in two dimensions related to normal patients and patients with corona will increase and as a result, the rate of its contagion will decrease, but also, by managing the entire supply chain network, cost wastage and more importantly, wastage or lack of blood products can be prevented.

Some of the special features and innovations of the proposed formulation are as follows: (I) Comprehensive minimization of all types of costs of the entire network is considered the first objective. (II) For the first time, the objective of minimizing the spread of the coronavirus has been developed; This goal is pursued by increasing the plasma supply from recovered people to reduce the shortage of this product in various demand points. Also, the minimization of the spread of the disease through the maximization of the satisfaction of the applicants of this type of plasma is followed in the second objective function. (III) maximizing the attractiveness of blood centers. It is calculated through the corresponding constraints and values such as advertising budget, staff experience, the time required for donating blood, and donors’ sensitivity to them.

The rest of this paper is organized as follows. Section 3 discusses the problem and the mathematical formulation. Section 4 describes the solution approach and the proposed algorithm. In Sect. 5, the proposed formulation is implemented and evaluated with references to deterministic and non-deterministic models, and the calculation results are analyzed through a developed realization model. Finally, the study’s conclusion and the suggestions for future research are represented in Sect. 6.

3 Mathematical modeling

The model developed in this study addresses the uncertainties involved in the blood supply and its products. The corresponding parameters include demand, maximum coverage radius, blood donation rate, and the amount of the supplied blood products. In this regard, sometimes, deterministic assumptions for the parameters in optimization problems may lead to impossible supply chain designs or sub-optimal solutions. Therefore, the goals set for the model are to minimize the costs of the whole blood SCN, minimize the spread of the disease by donors in each of the blood centers, and maximize the attractiveness of the blood centers.

This makes it possible to meet the demands better, especially in the case of pandemic patients who need the plasma of survivors. As an elegant point, for blood demand, the blood type compatibility topic is considered, analyzed, and solved by professional doctors and hematologists. Table 2 explains the features of the model.

Table 2 Characteristics of the proposed model

The sets, indices, decision variables and parameters defined for the model are presented below.

Sets and indices:

$S$	A set of scenarios for the states of the five parameters (As mentioned later) $(s\in S)$
$I={I}^{\mathrm{^{\prime}}}\cup {I}^{^{\prime\prime} }$	Set of regular doners and those having recovered from coronary heart disease $({i}^{\mathrm{^{\prime}}},{i}^{^{\prime\prime} }\in I)$
$M$	Set of candidate locations for mobile facilities $(m\in M)$
$L$	Set of candidate locations for local blood centers $(l\in L)$
$R$	Set of candidate locations for regional blood centers $(r\in R)$
M $\cup$ L $\cup$ R = W	The whole set of centers responsive to donors $(w\in W)$
${P}_{1}\cup {P}_{2}\cup {P}_{3}\cup {P}_{4}\cup {P}_{5}=P$	Whole blood (P1), red blood cells (P2), platelets (P3), plasma type (I) (belonging to normal people) (P4), and type (II) plasma (belonging to people having recovered from coronary heart disease)(P5)$({P}_{i}\in P)$
${k}_{1}\cup {k}_{2}\cup {k}_{3}=k$	Set of lifetimes of whole blood products, red blood cells, and platelets $(k\in K)$ (By day)
$H$	Set of demand points $\left(h\in H\right)$
A = ${A}^{\mathrm{^{\prime}}}\cup {A}^{^{\prime\prime} }$	Set of simple blood collection and apheresis $\mathrm{methods }\left({a}^{\mathrm{^{\prime}}},{a}^{^{\prime\prime} }\in A\right)$
$T$	Set of periods $\left(t\in T\right)$
J	A set of objective functions (j $\in$ J)

Parameters:

${Dm}_{hpat}^{s}$	Hospital demand h for blood products p obtained by collection method a during t under scenario s
${Fa}_{l}$	The cost of setting up a local blood center $l$
${Fb}_{r}$	The cost of setting up a regional blood center $r$
${Fc}_{{m}^{\mathrm{^{\prime}}}{m}^{^{\prime\prime} }t}$	The cost of moving each mobile device from place ${m}^{\mathrm{^{\prime}}}$ to place ${m}^{^{\prime\prime} }$ during t
${Ta}_{pt}$	The cost of transporting each unit of blood product $p$ per kilometer per t
${Oa}_{ipt}$	The cost of collecting each unit of blood product $p$ from donor group $i$ during t
${Pa}_{pt}$	The cost of production per unit of blood product p in regional blood centers in t
${Hc}_{pt}$	The cost of maintaining each unit of blood product p during period t
${Sa}_{l{p}_{1}t}$	Local blood center capacity l to collect whole blood ${(p}_{1})$ during period t
${Sb}_{pt}$	The capacity of mobile facilities to collect blood products p during t
${Sc}_{rpat}$	The capacity of regional center r to collect and produce blood products p obtained by collection method a during period t
${Se}_{rpat}$	The capacity of regional center r to store blood products p obtained by collection method a during period t
${Sk}_{hpat}$	Demand point capacity h to store blood products p obtained by collection method a during period t
${Da}_{im}$	The amount of route between the donor group i and facility m
${Db}_{{i}^{\mathrm{^{\prime}}}l}$	The amount of route between the donor group ${i}^{\mathrm{^{\prime}}}$ and the local center l
${Dc}_{ir}$	The amount of route between the donor group i and the regional center r
${Dd}_{mr}$	The amount of route between facility m and the regional center r
${De}_{lr}$	The amount of route between the local center l and the regional center r
${Dh}_{rh}$	The amount of route between the regional center r and demand point h
${Ra}_{m}$	Maximum coverage radius of mobile facility m to serve donors
${Rb}_{l}$	Maximum coverage radius of the local center l to serve donors
${Rc}_{r}$	Maximum coverage radius of the regional center r to serve donors
${Po}_{p}$	Percentage of blood product production p
${Ea}_{hpat}$	Expiry cost per unit of extra blood product p obtained by collection method a at the demand point h during t
${\tau }_{w}$	Time spent on the blood donation process at the blood center w
${\sigma }_{w}$	The advertising budget in the blood center w
${\vartheta }_{w}$	Experience factor in the blood center w
$S{\tau }_{w}$	Donor sensitivity to time ${\tau }_{w}$
$S{\sigma }_{w}$	Donor sensitivity to advertising ${\sigma }_{w}$
$S{\vartheta }_{w}$	Donor sensitivity to experience factor ${\vartheta }_{w}$
${Dr}^{s}$	Average donation rate under scenario s
${Pop}_{w}$	The population of the area allocated to the blood center w
${Ub}_{w}$	The best productivity available in the blood center w
${\pi }^{s}$	Probability of scenario s
$\varphi$	A very large number
$\varepsilon$	A number from zero to one
α	The probability of being infected with the coronavirus by another person in period t

Decision variables:

${YL}_{l}$	If local blood center l is launched, 1; otherwise, 0
${YR}_{r}$	If the center of region r is set up, 1; otherwise, 0
${ZA}_{imt}^{s}$	If donor group i is allocated by mobile facility m in period t under scenario s, 1; otherwise, 0
${ZB}_{{i}^{\mathrm{^{\prime}}}lt}^{s}$	If donor group ${i}^{\mathrm{^{\prime}}}$ is allocated to local center l in period t under scenario s, 1; otherwise, 0
${ZC}_{irt}^{s}$	If donor group i is allocated to regional center r during period t under scenario s, 1; otherwise, 0
${MV}_{{m}^{\mathrm{^{\prime}}}{m}^{^{\prime\prime} }t}^{s}$	If the mobile facility passes from place ${m}^{\mathrm{^{\prime}}}$ to ${m}^{^{\prime\prime} }$ in interval t under scenario s, 1; otherwise, 0
${XA}_{impt}^{s}$	The amount of blood product p donated by donor group i on mobile device m during t under scenario s
${XB}_{{i}^{\mathrm{^{\prime}}}l{p}_{1}t}^{s}$	The amount of whole blood p1 donated by donor group ${i}^{\mathrm{^{\prime}}}$ at local center l during t under scenario s
${XC}_{irpt}^{s}$	The amount of whole blood p donated by donor group i in regional center r during t under scenario s
${XD}_{mrpt}^{s}$	The amount of whole blood p transferred by mobile facility m to regional blood center r during period t under scenario s
${XE}_{lr{p}_{1}t}^{s}$	The amount of whole blood p1 transferred from local center l to regional center r during t under scenario s
${XG}_{rhpakt}^{s}$	The amount of blood product $p$ obtained from collection method a with age $k$ days posted by regional center $r$ to the point of demand $h$ during $t$ under scenario ${\text{s}}$
${XH}_{rhpakt}^{s}$	The amount of blood product $p$ obtained from collection method a with age $k$ day consumed at the point of demand h during $t$ under scenario $s$
${PR}_{rpat}^{s}$	The amount of blood product p produced by collection method a in regional center r during ${\text{t}}$ under scenario $s$
${SH}_{hpat}^{s}$	Deficiency of blood product p obtained from collection method a at the point of demand h during $t$ under scenario ${\text{s}}$
${EX}_{hpat}^{s}$	The amount of extra blood product p obtained from collection method a expired at the point of demand h during period $t$ under scenario $s$
${IR}_{rpat}^{s}$	Blood product inventory level p obtained from collection method a in regional center r during $t$ under scenario $s$
${IH}_{hpakt}^{s}$	Blood product inventory level p obtained from collection method a with age $k$ days at the point of demand h during $t$ under scenario $s$
${AT}_{wt}^{s}$	The attractiveness of blood center w under scenario s during t

Accordingly, the five uncertain parameters are ${Ra}_{m}^{..}$, ${Rb}_{l}^{..}$, ${Rc}_{r}^{..}$, ${Po}_{p}^{..}$, and ${Dm}_{hpat}^{..}$.

3.1 Mathematical model

The objective functions are organized as follows:

$$\begin{aligned} Min Z_{1} & = \mathop \sum \nolimits_{l} Fa_{l} \cdot YL_{l} + \mathop \sum \nolimits_{r} Fb_{r} \cdot YR_{r} \\ & \quad + \mathop \sum \nolimits_{{m^{\prime}}} \mathop \sum \nolimits_{{m^{\prime\prime} = m{\prime} }} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} \pi^{s} \cdot Fc_{{m^{\prime\prime}m^{\prime}t}} \cdot MV_{{m^{\prime\prime}m^{\prime}t}}^{s} \\ & \quad + \mathop \sum \nolimits_{{m^{\prime}}} \mathop \sum \nolimits_{{m^{\prime\prime} = m{\prime} }} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} \pi^{s} \cdot Oa_{ipt} \cdot \left( {XA_{ibpt}^{s} + XB_{{i^{\prime}lp1t}}^{s} + XC_{irpt}^{s} } \right) \\ & \quad + \mathop \sum \nolimits_{m} \mathop \sum \nolimits_{l} \mathop \sum \nolimits_{r} \mathop \sum \nolimits_{h} \mathop \sum \nolimits_{p} \mathop \sum \nolimits_{a} \mathop \sum \nolimits_{k} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} \pi^{{s}{}} \cdot Ta_{pt} \cdot \left( {Dd_{mr} \cdot XD_{mrpt}^{s} + De_{lr} \cdot XE_{lrp1t}^{s} + Dh_{rh} \cdot XG_{rhpakt}^{S} } \right) \\ & \quad \mathop { + \sum }\nolimits_{r} \mathop \sum \nolimits_{p \ne p1} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} \pi^{s} \cdot Pa_{pt} \cdot PR_{rpa^{\prime}t}^{s} \\ & \quad + \mathop \sum \nolimits_{r} \mathop \sum \nolimits_{h} \mathop \sum \nolimits_{p} \mathop \sum \nolimits_{a} \mathop \sum \nolimits_{k} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} \pi^{s} \cdot HC_{pt} \cdot \left( {IR_{rpat}^{s} \cdot IH_{hpakt}^{s} } \right) \\ & \quad + \mathop \sum \nolimits_{h} \mathop \sum \nolimits_{p} \mathop \sum \nolimits_{a} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} \pi^{s} \cdot Ea_{hpat} .EX_{hpat}^{s} \\ \end{aligned}$$

(1)

$$MinZ_{2} = \mathop \sum \nolimits_{i} \mathop \sum \nolimits_{m} \mathop \sum \nolimits_{l} \mathop \sum \nolimits_{r} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} a_{t}^{s} \left( {ZA_{imt}^{s} + ZB_{{i^{\prime}lt}}^{s} + ZC_{irt}^{s} } \right)$$

(2)

$$MaxZ_{3} = \mathop \sum \nolimits_{w} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} \pi^{s} \cdot AT_{wt}^{s}$$

(3)

Subject to:

$$\mathop \sum \nolimits_{p \ne p1} XA_{impt}^{S} \le \varphi ZA_{imt}^{S} \quad \forall \;i,m,t,S$$

(4)

$$XB_{{i^{\prime}lp1t}}^{S} \le \varphi ZB_{i^{\prime}lt}^{S} \quad \forall \;i^{\prime } ,l,t,S$$

(5)

$$\mathop \sum \nolimits_{p} XC_{irpt}^{S} \le \varphi ZC_{irt}^{S} \quad \forall \;i,r,t,S$$

(6)

$$\mathop \sum \nolimits_{r} \mathop \sum \nolimits_{p \ne p1} XD_{mrpt}^{S} \le \varphi \mathop \sum \nolimits_{m^{\prime}} MV_{m^{\prime}mt}^{S} \quad \forall \;m,t,S$$

(7)

$$\mathop \sum \nolimits_{m} \mathop \sum \nolimits_{p \ne p1} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} XD_{mrpt}^{S} \le \varphi YR_{r} \quad \forall \;r$$

(8)

$$\mathop \sum \nolimits_{r} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} XE_{lrp1t}^{S} \le \varphi YL_{l} \quad \forall \;l,p_{1}$$

(9)

$$\mathop \sum \nolimits_{l} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} XE_{{lrp_{1} t}}^{s} \le \varphi YR_{r} \quad \forall \;r,p_{1}$$

(10)

$$\mathop \sum \nolimits_{h} \mathop \sum \nolimits_{p} \mathop \sum \nolimits_{a} \mathop \sum \nolimits_{k} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} XG_{rhpakt}^{S} \le \varphi YR_{r} \quad \forall \;r$$

(11)

$$ZA_{imt}^{s} \cdot Da_{im} \le Ra_{m} \mathop \sum \nolimits_{m^{\prime}} MV_{m^{\prime}mt}^{S} \quad \forall \;i,m,t,S$$

(12)

$$ZB_{{i^{\prime}lt}}^{S} \cdot Db_{{i^{\prime}l}} \le Rb_{l}^{s} \cdot YL_{l} \quad \forall \;i^{\prime},l,t,S$$

(13)

$$ZC_{irt}^{S} \cdot DC_{ir} \le RC_{r} \cdot YR_{r} \quad \forall \;i,r,t,S$$

(14)

$$\mathop \sum \nolimits_{{m^{\prime}}} MV_{{m^{\prime}m^{\prime\prime}t}}^{S} \le 1\quad \forall \;m^{\prime\prime},t,S$$

(15)

$$\mathop \sum \nolimits_{{m^{\prime\prime}}} MV_{{m^{\prime}m^{\prime\prime}t}}^{S} \le 1\quad \forall \;m^{\prime},t,S$$

(16)

$$\mathop \sum \nolimits_{{m^{\prime\prime}}} MV_{{m^{\prime}m^{\prime\prime},t}}^{S} \le \mathop \sum \nolimits_{m} MV_{{mm^{\prime},t - 1}}^{S} \quad \forall \;m^{\prime},t \ge 2,S$$

(17)

$$\mathop \sum \nolimits_{m} ZA_{i^\prime mt}^{S} + \mathop \sum \nolimits_{l} ZB_{i^\prime lt}^{S} + \mathop \sum \nolimits_{r} ZC_{i^\prime rt}^{S} \le 1\quad \forall \;i^\prime ,t,S$$

(18)

$$\mathop \sum \nolimits_{m} ZA_{{i^{\prime \prime } mt}}^{S} + \mathop \sum \nolimits_{r} ZC_{{i^{\prime \prime } rt}}^{S} \le 1\quad \forall \;i^{\prime \prime } ,t,S$$

(19)

$$Po_{p} \cdot \left( {\mathop \sum \nolimits_{l} XE_{{lrp_{1} t}}^{S} + \mathop \sum \nolimits_{{i^{\prime}}} XC_{{i^{\prime}rp_{1} t}}^{S} } \right) = PR_{{rpa^{\prime}t}}^{S} \quad \forall \;r,p \ne p_{1} ,p_{5} ,a^\prime ,t,S$$

(20)

$$\mathop \sum \nolimits_{m} XD_{mrpt}^{S} + \mathop \sum \nolimits_{i} XC_{irpt}^{S} = PR_{{rpa^{\prime\prime}t}}^{S} \quad \forall \;r,p \ne p_{1} ,a^{\prime\prime},t,S$$

(21)

$$\mathop \sum \nolimits_{i} XA_{impt}^{S} \le S\;b_{pt} \quad \forall \;m,p,t,S$$

(22)

$$\mathop \sum \nolimits_{{i^{\prime}}} XB_{{i^{\prime}lp_{1} t}}^{S} \le S\;a_{{lp_{1} t}} \quad \forall \;l,t,S$$

(23)

$$PR_{rpat}^{S} \le S\;C_{rpat} \cdot YR_{r} \quad \forall \; r,p,a,t,S$$

(24)

$$IR_{rpat}^{S} \le S\;e_{rpat} \cdot YR_{r} \quad \forall \;r,p,a,t,S$$

(25)

$$\mathop \sum \nolimits_{k} IH_{hpakt}^{S} \le S\;k_{hpat} \quad \forall \;h,p,a,t,S$$

(26)

$$\mathop \sum \nolimits_{i} XA_{impt}^{S} = \mathop \sum \nolimits_{r} XD_{mrpt}^{S} \quad \forall \;m,t,S$$

(27)

$$\mathop \sum \nolimits_{{i^{\prime}}} XB_{{i^{\prime}lp_{1} t}}^{S} = \mathop \sum \nolimits_{r} XE_{{lrp_{1} t}}^{S} \quad \forall \;l,t,S$$

(28)

$$IR_{rpat}^{S} = IR_{rpa,t - 1}^{S} + PR_{rpat}^{S} - \mathop \sum \nolimits_{h} \mathop \sum \nolimits_{k \ge 2} XG_{rhpakt}^{S} \quad \forall \;r,p,a,t,S$$

(29)

$$IH_{hpakt}^{S} = IH_{hpa,k - 1,t - 1}^{S} + \mathop \sum \nolimits_{r} XG_{rhpakt}^{S} - \mathop \sum \nolimits_{r} XH_{rhpakt}^{S} \quad \forall \;h,p,a,k \ge 2,t,S$$

(30)

$$\mathop \sum \nolimits_{r} \mathop \sum \nolimits_{k} XH_{rhpakt}^{S} + EX_{hpat}^{S} + SH_{hpat}^{S} = Dm_{hpat}^{S} \quad \forall \;h,p,a,t,S$$

(31)

$$\mathop \sum \nolimits_{r} \mathop \sum \nolimits_{k} { }XH_{rhpakt}^{S} \ge S\;t{ } \cdot Dm_{hpat}^{S} \quad \forall \;h,p,a,t,S$$

(32)

$$\mathop \sum \nolimits_{i} {\text{XA}}_{{{\text{impt}}}}^{S} \le {\text{Dr}}^{S} \cdot Pop_{m} \cdot \left({\text{AT}}_{{{\text{mt}}}}^{S} \right)/Ub_{m} \quad \forall \;m,p,t,S$$

(33)

$$AT_{{mt}}^{S} = \tau _{m}^{{ - S\tau _{m} }} \cdot \sigma _{m}^{{S\sigma _{m} }} \cdot \vartheta _{m}^{{S\theta _{m} }} \cdot \mathop \sum \nolimits_{{m^{\prime}}} MV_{{m^{\prime}mt}}^{S} \quad \forall {\text{~}}m,t,{\text{~}}S$$

(34)

$$\mathop \sum \nolimits_{{i^{\prime}}} {\text{XB}}_{{i^{\prime}{\text{lp}}_{1} {\text{t}}}}^{S} \le {\text{Dr}}^{S} \cdot Pop_{l} \cdot \left({\text{AT}}_{{{\text{lt}}}}^{S} \right)/Ub_{l} \quad \forall \;l,t,S$$

(35)

$$AT_{lt}^{S} = \tau_{l}^{{ - S^{{}} \tau_{l} }} \cdot \sigma_{l}^{{S\sigma_{l} }} \cdot \vartheta_{l}^{{S\theta_{l} }} \cdot YL_{l} \quad \forall \;l,t,S$$

(36)

$$\mathop \sum \nolimits_{i} {\text{XC}}_{{{\text{irpt}}}}^{S} \le {\text{Dr}}^{S} \cdot Pop_{r} \cdot \left({\text{AT}}_{{{\text{rt}}}}^{S} \right)/Ub_{r} \quad \forall \;r,p,t,S$$

(37)

$$AT_{rt}^{S} = \tau_{r}^{{ - S^{{}} \tau_{r} }} \cdot \sigma_{r}^{{S^{{}} \sigma_{r} }} \cdot \vartheta_{r}^{{S\theta_{r} }} YR_{r} \quad \forall \;r,t,S$$

(38)

$$YL_{l} { },YR_{r} { },ZA_{imt}^{S} { },ZB_{{i^{\prime}lt}}^{S} { },ZC_{irt}^{S} ,MV_{{m^{\prime}m^{\prime\prime}t}}^{S} { } \in \left\{ {0,{1}} \right\}$$

(39)

$$\begin{aligned} & XA_{impt}^{S} ,XB_{{i^{\prime}lp_{1} t}}^{S} ,XC_{irpt}^{S} ,XD_{mrpt}^{S} ,XE_{{lrp_{1} t}}^{S} ,XG_{rhpakt}^{S} , \\ & XH_{rhpakt}^{S} ,PR_{rpat}^{S} ,SH_{hpat}^{S} ,EX_{hpat}^{S} ,IR_{rpat}^{S} ,IH_{hpakt}^{S} ,{\text{AT}}_{{w{\text{t}}}}^{S} \ge 0{ },\;int \\ \end{aligned}$$

(40)

The objective function (1) deals with minimizing the costs of the entire SCN. The costs include those of setting up regional and local blood centers, moving mobile blood collection equipment to each location, collecting blood in each of the mobile, regional and local blood collection centers, transferring blood from each center to another, preparing products in regional blood centers, storing blood in regional blood centers and demand points, and setting penalties for blood expiration at demand points. Objective function (2) deals with minimizing the possibility of pandemic transmission by the donors assigned to each of blood centers. In the second objective, by using parameter α, which represents the percentage of disease transmission from a person with COVID-19 disease to healthy people, the percentage of disease transmission in the presence of blood donors in mobile, regional, and local blood centers is calculated (The determining method of parameter α is explained in Sect. 4).

Objective function (3) discusses maximizing the attractiveness of blood centers. It is calculated through the corresponding constraints and values such as advertising budget, staff experience, the time required for donating blood, and donors’ sensitivity to them.

Constraint (4) states that blood donation is possible in any mobile blood collection center if the donors are assigned to that center. Constraint (5) states that donating whole blood in local blood centers is possible if normal donors are assigned to that center. Constraint (6) states that it is possible to donate whole blood or blood products in regional blood centers if the donors are assigned to that center. Constraints (7) and (8) state that the allocation of mobile blood collection centers to regional blood centers is possible if both of these facilities are established. Constraints (9) and (10) state that allocating regional blood centers to local blood centers is possible if both regional and local blood centers are set up. Constraint (11) indicates that hospitals are allocated only to the regional blood centers set up. Constraints (12) to (14) indicate that donors are served based on the maximum coverage radius. According to constraints (15) and (16), only one mobile blood collection center should be sent to each location, and each mobile facility can only be sent to one location. Constraint (17) emphasizes that the movement of a mobile facility from the first place to the second is possible if that facility was located in the first place in the previous period. Constraints (18) and (19) state that each donor group can be assigned to only one of the related blood centers. The amount of each blood product produced by a stochastic approach or through apheresis and collected in each regional blood center is calculated under constraints (20) and (21). Constraints (22) and (23) respectively determine the capacity of local and mobile blood collection centers to collect each of the blood products in each period. Constraint (24) specifies the capacity of regional blood centers to collect and produce blood products by an apheresis method in each period. Constraints (25) and (26) express the capacity of each warehouse in regional blood centers and demand points to store each blood product, respectively. Constraint (27) balances the input and output flow of the mobile blood collection center. Constraint (28) balances the inflow and the outflow of local blood centers. Constraints (29) and (30) establish the inventory balance for regional blood centers and demand points, respectively. Constraint (31) calculates the shortage of each blood product in the demand points at the end of each period. Constraint (32) represents the minimum demand that must be satisfied. Constraints (33) to (38) calculate the amount of blood donation in each blood center based on the attractiveness of these centers separately. Finally, Eqs. (39) and (40) show the status of the decision variables.

4 Proposed solution approaches

In the following, two different solution approaches are proposed. The first is based on the uncertainty in the scenario type, but the second approach is based on a combination of uncertainty types.

4.1 A robust scenario-based approach

This approach, also known as the Mulvey robust approach, applies the concept of ideal planning in line with the scenario-based description of the problem data and is less sensitive to dataset changes. Despite its constraints, the approach is advantageous over non-deterministic linear programming and is generally more practical [12]. It can be used with the two goals of being justified and optimal for all scenarios. According to the scenarios and the input data in this study, the yielded response is a robust one. Mulvey’s model consists of two basic components. One is a structural component that is the fixed component of the model and only deals with deterministic data, and the other is a control component that includes stochastic data [19,20,21].

As mentioned, robust optimization with Muley’s approach is used to solve the presented scenario model. It should be noted that, according to the sensitivity analysis, the parameters related to the maximum coverage radius of different facilities, demand, average donation rate, and the percentage of blood product production are considered non-deterministic parameters. In the following, the parameters added compared to the scenario model are introduced along with the control variables.

Control variables:

${\delta }_{hpat}^{s}$: Unmet blood demand product p from hospital h under scenario s in period t.

${\theta }_{j}^{s}$: Linear coefficient of the jth objective function under scenario s.

The first, second and third objectives are as follows due to the presence of non-deterministic parameters in them:

$$\begin{aligned} Z_{1s}^{\prime} & = \mathop \sum \nolimits_{l} Fa_{l} \cdot YL_{l} + \mathop \sum \nolimits_{r} Fb_{r} \cdot YR_{r} + \mathop \sum \nolimits_{{m^{\prime}}} \mathop \sum \nolimits_{{m^{\prime\prime} = m^{\prime} }} \mathop \sum \nolimits_{t} Fc_{{m^{\prime\prime}m^{\prime}t}} \cdot MV_{{m^{\prime\prime}m^{\prime}t}}^{S} \\ & \quad + \mathop \sum \nolimits_{{m^{\prime}}} \mathop \sum \nolimits_{{m^{\prime\prime} = m^{\prime} }} \mathop \sum \nolimits_{t} Oa_{ipt} \cdot \left( {XA_{ibpt}^{S} + XB_{{i^{\prime}lp1t}}^{S} + XC_{irpt}^{S} } \right) \\ & \quad + \mathop \sum \nolimits_{{m^{{}} }} \mathop \sum \nolimits_{l} \mathop \sum \nolimits_{r} \mathop \sum \nolimits_{h} \mathop \sum \nolimits_{p} \mathop \sum \nolimits_{a} \mathop \sum \nolimits_{k} \mathop \sum \nolimits_{t} Ta_{pt} \cdot \left( {Dd_{mr} \cdot XD_{mrpt}^{S} + De_{lr} \cdot XE_{lrp1t}^{S} } \right. \\ & \quad \left. { + Dh_{rh} \cdot XG_{rhpakt}^{S} } \right) + \mathop \sum \nolimits_{r} \mathop \sum \nolimits_{p \ne p1} \mathop \sum \nolimits_{t} Pa_{pt} \cdot PR_{rpa^{\prime}t}^{S} \\ & \quad + \mathop \sum \nolimits_{{r^{{}} }} \mathop \sum \nolimits_{h} \mathop \sum \nolimits_{p} \mathop \sum \nolimits_{a} \mathop \sum \nolimits_{k} \mathop \sum \nolimits_{t} HC_{pt} \cdot \left( {IR_{rpat}^{S} .IH_{hpakt}^{S} } \right) \\ & \quad + \mathop \sum \nolimits_{{h^{{}} }} \mathop \sum \nolimits_{p} \mathop \sum \nolimits_{a} \mathop \sum \nolimits_{t} Ea_{hpat} \cdot EX_{hpat}^{S} \\ \end{aligned}$$

$$\begin{aligned} Z_{1s} & = Min\;Z_{1s}^{\prime} \\ {\text{Min}}\;Z_{1} & = \mathop \sum \nolimits_{s} \pi^{s} Z_{1s} + \lambda_{1} \mathop \sum \nolimits_{s} \pi^{s} \left( {\left( {Z_{1s} - \mathop \sum \nolimits_{s} \pi^{s} Z_{1s} } \right) + 2\theta_{1}^{s} } \right) + \omega_{1} \mathop \sum \nolimits_{h} \mathop \sum \nolimits_{p} \mathop \sum \nolimits_{a} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} \pi^{s} \delta_{hpat}^{s} \\ \end{aligned}$$

(41)

$$\begin{aligned} Z_{2s}^{\prime} & = \mathop \sum \nolimits_{i} \mathop \sum \nolimits_{m} \mathop \sum \nolimits_{l} \mathop \sum \nolimits_{r} \mathop \sum \nolimits_{t} a_{t}^{s} \left( {ZA_{imt}^{s} + ZB_{{i^{\prime}lt}}^{s} + ZC_{irt}^{s} } \right) \\ Z_{2s} & = Min Z_{2s}^{\prime} \\ {\text{Min}}\;Z_{2} & = \mathop \sum \nolimits_{s} \pi^{s} Z_{2s} + \lambda_{2} \mathop \sum \nolimits_{s} \pi^{s} \left( {\left( {Z_{2s} - \mathop \sum \nolimits_{s} \pi^{s} Z_{2s} } \right) + 2\theta_{2}^{s} } \right) + \omega_{2} \mathop \sum \nolimits_{h} \mathop \sum \nolimits_{p} \mathop \sum \nolimits_{a} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} \pi^{s} \delta_{hpat}^{s} \\ \end{aligned}$$

(42)

$$\begin{aligned} Z_{3s}^{\prime} & = \mathop \sum \nolimits_{w} \mathop \sum \nolimits_{t} {\text{AT}}_{{{\text{wt}}}}^{{\text{s}}} \\ Z_{3s} & = Max\;Z_{3s}^{\prime} \\ {\text{Max}}\;Z_{3} & = \mathop \sum \nolimits_{s} \pi^{s} Z_{3s} - \lambda_{3} \mathop \sum \nolimits_{s} \pi^{s} \left( {\left( {Z_{3s} - \mathop \sum \nolimits_{s} \pi^{s} Z_{3s} } \right) + 2\theta_{3}^{s} } \right) - \omega_{3} \mathop \sum \nolimits_{h} \mathop \sum \nolimits_{p} \mathop \sum \nolimits_{a} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} \pi^{s} \delta_{hpat}^{s} \\ \end{aligned}$$

(43)

The first expression of objective (41), which is related to the robust part of the model solution, addresses the minimization of the average cost function if any one of the scenarios is used. The second expression is about minimizing the variance of Eq. (42), and the remaining expressions of the objective discuss penalties in the robust part of the formulation. Accordingly, the mentioned cases are also true for the second and third objective functions.

Constraints

The constraints of the proposed scenario-based robust formulation are presented as follows.

$$\mathop \sum \nolimits_{r} \mathop \sum \nolimits_{k} XH_{rhpakt}^{s} + EX_{hpat}^{s} + \delta_{hpat}^{s} = Dm_{hpat}^{s} \quad \forall \;h,p,a,t,s$$

(44)

$$Z_{js} - \pi^{s} Z_{js} + \theta_{1}^{s} \ge 0\quad \forall \;s,j$$

(45)

$$\delta_{hpat}^{s} , \theta_{1}^{s} , \theta_{2}^{s} , \theta_{3}^{s} \ge 0 , int\quad \forall \;h,p,a,t,s$$

(46)

Constraint (44) is a demand constraint. The new constraints (45) relate to the linearization of the objectives added to the model. Constraint (46) also shows the status of the control variables.

4.2 A hybrid heuristic robust optimization approach

A hybrid heuristic robust optimization approach has been applied to deal with the uncertainty of the problem in this study. The approach is adopted from the study by Pishvaee et al. [20]. It will be explained according to the detailed structure of the problem presented here.

A comprehensive taxonomy comprising sources of uncertainty, corresponding parameters, and other factors that may cause uncertainty is provided, along with a systematic and up-to-date literature review of optimal BSCs that work with uncertain input data. A hybrid robust optimization formulation is also used to handle several types of uncertainty comprising stochastic, deep and epistemic uncertainties. Uncertainty in the maximum coverage radius is provided by various non-deterministic facilities, which are expressed as deterministic scenarios. Therefore, the percentage of producing blood products is considered fuzzy as the demand changes in a specific period.

In order to demonstrate robust optimization approaches to deal with any type of uncertainty in the proposed blood SCN model, first, the uncertain parameters of the model are introduced. Then, the methods of dealing with each are discussed. The non-deterministic parameters of the presented mathematical model include ${Ra}_{m}, {Rb}_{l}$ and ${Rc}_{r}$ as separate deterministic scenarios, ${Po}_{p}$ as a fuzzy scenario, and the demand parameter (${Dm}_{hpat}),$ considered as an interval scenario.

In order to provide a robust optimization formulation to deal with several types of uncertainty, firstly, the robust optimization approaches adopted to deal with each type of uncertainty are explained, and then an innovative hybrid robust formulation is presented.

Uncertainty in the maximum coverage radius via different facilities is represented as uncertain conversion rates, which are clarified as scenarios due to the available evidence. In order to describe this type of uncertainty, scenario-based robust stochastic planning is explained in this section. As mentioned, Muley et al. [19,20,21] developed a robust optimization formulation through a scenario-based stochastic programming formulation, where deterministic discrete scenarios are considered for non-deterministic parameters. In the following, the parameters that have been added to the deterministic model, compared to the scenario model, as well as the control variables, are discussed:

Control variables:

${\delta }_{imt}^{s}$: The violation rate is a non-deterministic parameter.

${\delta }_{i\mathrm{^{\prime}}lt}^{s}$: The violation rate is a constraint that includes a non-deterministic parameter.

${\delta }_{irt}^{s}$: The violation rate is a constraint that includes a non-deterministic parameter.

${\theta }_{j}^{s}$: Linear coefficient of the jth objective function under scenario s.

The other decision variables are similar to the previous ones, so they are not mentioned. According to what preceded, the first, second, and third objective functions are Eqs. (41–43).

Also, the constraints of the proposed scenario-based mathematical formulation are presented as follows:

$$ZA_{imt}^{s} \times Da_{im}^{{}} + \delta_{imt}^{s} = Ra_{m}^{s} \mathop \sum \nolimits_{r} MV_{{m^{\prime}mt}}^{s} \quad \forall \;i,m,t,s$$

(47)

$$ZB_{{i^{\prime}lt}}^{s} \times Db_{{i^{\prime}l}}^{{}} + \delta_{{i^{\prime}lt}}^{s} = Rb_{l}^{s} \times YL_{l}^{{}} \quad \forall \;i^{\prime},l,t,s$$

(48)

$$ZC_{irt}^{s} \times Dc_{ir}^{{}} + \delta_{irt}^{s} = Rc_{r}^{s} \times YR_{r}^{{}} \quad \forall \;i,r,t,s$$

(49)

$$Z_{js} - \pi^{s} Z_{js} + \theta_{1}^{s} \ge 0\quad \forall \;s,j$$

(50)

$$\theta _{1}^{s} ,\theta _{2}^{s} ,\theta _{3}^{s} ,\delta _{{imt}}^{s} ,\delta _{{i^{\prime}lt~}}^{s} ,\delta _{{irt}}^{s} \ge 0{\text{~}},\;int\quad \forall \;i,m,{\text{l}},{\text{r}},t,s$$

(51)

Constraints (47) to (49) include the positive variables of ${\delta }_{imt}^{s}$, ${\delta }_{{i}{\prime}lt}^{s}$ and${\delta }_{irt}^{s}.$ Also, constraints (50) are the linearization robust constraints of the objective functions added to the model. Finally, Constraint (51) shows the state of the control variables.

Due to the lack of reliable data to obtain the probability or probability distribution of the blood demand amounts as well as various fluctuating factors affecting the demand, this parameter is explained as a known interval but without an assumption for a certain possibility or probability of deterministic values. In this section, firstly, a brief introduction of robust convex planning approaches is presented so as to deal with deep uncertainty. Then, the Bertsimas-Sim approach is adopted to consider demand uncertainty.

Soyster [22] developed a linear optimization formulation for data uncertainty management to produce feasible solutions for all the deterministic amounts of non-deterministic data belonging to a convex set. Accordingly, this approach is too conservative in practice, and the objective value of the obtained robust solution is much worse than that of the nominal problem solution. To address the mentioned conservatism issue, El Ghaoui et al. [23], Ben-Tal et al. [24], and Selvi et al. [25] developed less conservative robust counterparts dealing with ellipsoidal uncertainty sets. However, the most crucial impediment of such an approach is that it converts a linear mathematical formulation into a robust nonlinear albeit convex equivalent mathematical formulation. Bertsimas et al. [26, 27] used a new approach for robust linear optimization with multivariate non-deterministic sets where the developed robust counterpart remained linear. This approach is due to the unrealistic assumption that all non-deterministic parameters take their worst value simultaneously. The well-defined formulation in this approach provides complete control over the degree of conservation for each constraint i such that only a predetermined number of non-deterministic parameters are changed and the optimal solution is deterministic for any maximum change of parameters in row i. The Bertsimas-Sim approach is adopted here to establish a robust counterpart for the demand-satisfying constraint whose compact form is as follows:

$$X = Dm_{hpat} \quad \forall \;h,p,a,t$$

(52)

where $D{m}_{hpat}$ is a nondeterministic parameter that takes values in the symmetric interval of $\left[{\overline{Dm} }_{hpat}-{\widehat{Dm}}_{hpat},{\overline{Dm} }_{hpat}+{\widehat{Dm}}_{hpat}\right]$. In this interval, ${\overline{Dm} }_{hpat}$ is a nominal value (e.g., Medium or median). Also, ${\widehat{Dm}}_{hpat}$, as the constant value of the deviation of the demand parameter, is around its nominal value. For constraint (27), ${\Gamma }_{hpat}$ is defined as an input parameter, which is called the uncertainty budget. This parameter changes in $\left[0,\left|{J}_{hpat}\right|\right]$ over time. It should be mentioned that ${J}_{hpat}$ is the number of non-deterministic parameters in constraint (19). Consider the following formula for constraint (20):

$$- X + Dm_{hpat} + \mathop {Max}\limits_{{\left\{ {S_{hpat} \cup \left\{ {t_{hpat} } \right\}S_{hpat} \subseteq J_{hpat} ,\left| {S_{hpat} } \right| = \left| {\Gamma_{hpat} } \right|,t_{hpat} \in J_{hpat} \backslash S_{hpat} } \right\}}} \left\{ {\widehat{Dm}_{hpat} + \left( {\Gamma_{hpat} - \left| {\Gamma_{hpat} } \right|} \right)\widehat{Dm}_{hpat} } \right\} = 0\quad \forall \;h,p,a,t$$

(53)

$$\beta_{hpat} = \max \left\{ {\widehat{Dm}_{hpat} + \left( {\Gamma_{hpat} - \left| {\Gamma_{hpat} } \right|} \right)\widehat{Dm}_{hpat} } \right\}$$

The essential level of protection is the constraint on the uncertainty in the parameters. In this regard, the maximum deviation for the uncertain parameters is taken into consideration for $\left|{\Gamma }_{hpat}\right|$; that is, these parameters take their worst values. In addition, the ${\Gamma }_{hpat}-\left|{\Gamma }_{hpat}\right|$ is the allowed deviation of the parameter for one of them. According to Pishvaee et al. [20], the constraints on the demand parameter are summarized in the following equations.

$$- X + Dm_{hpat} + q_{hpat} \cdot \Gamma_{hpat} + r_{hpat} = 0\quad \forall \;h,p,a,t$$

(54)

$$q_{hpat} + r_{hpat} \ge \widehat{Dm}_{hpat} \quad \forall \;h,p,a,t$$

(55)

$$q_{hpat} , r_{hpat} \ge 0\quad \forall \;h,p,a,t$$

(56)

According to the above equations, constraint (4) in the mathematical model is converted into constraints (57) to (59) and inserted into the non-deterministic model:

$$Dm_{hpat} + q_{hpat}^{s} \cdot \Gamma_{hpat}^{s} + r_{hpat}^{s} - \mathop \sum \nolimits_{r} \mathop \sum \nolimits_{k} XH_{rhpakt}^{s} - Sh_{hpat}^{s} - EX_{hpat}^{s} = 0\quad \forall \;h,p,a,{\text{t}},s$$

(57)

$$q_{hpat}^{s} + r_{hpat}^{s} \ge \widehat{Dm}_{hpat} \quad \forall \;h,p,a,t,s$$

(58)

$$q_{hpat}^{s} , r_{hpat}^{s} \ge 0\quad \forall \;h,p,a,t,s$$

(59)

Due to the variety of the factors that can have significant effects on the amount of blood product production, it is impossible to predict the amount of this production based on the past data. Accordingly, it is presented in the form of fuzzy numbers, where the corresponding probability distribution is extracted due to the knowledge of experts. Rahmanzadeh et al. [21] developed fuzzy robust programming approaches (i.e., non-deterministic robust programming and flexible robust programming) to extend the goal of the robust optimization theory to fuzzy mathematical programming. In this study, the non-deterministic robust approach is adopted to consider the uncertainty in the percentage of blood product production, which is considered fuzzy numbers.

Thus, $P{o}_{p}$ is a non-deterministic parameter presented in the form of trapezoidal fuzzy numbers (i.e., $Po=P{o}_{(1)},P{o}_{(2)}, P{o}_{(3)}, P{o}_{(4)}$). According to Pishvaee et al. [20], the constraint regarding the allocation of donors to blood centers can be presented as follows:

$$\left( {\gamma_{p}^{s} \cdot Po_{p}^{{\left( {s1} \right)}} + \left( {1 - \gamma_{p}^{s} } \right) \cdot Po_{p}^{{\left( {s2} \right)}} } \right) \cdot \left( {\mathop \sum \nolimits_{l} XE_{lrp1t}^{s} + \mathop \sum \nolimits_{i^{\prime}} XC_{i^{\prime}rp1t}^{s} } \right) = PR_{rpa^{\prime}t}^{s} \quad \forall \;r,p \ne p1,a,t,s$$

(60)

It should be noted that, in this formula, $\gamma$, as a confidence level, is the chance constraint defined by the decision maker, and it is reasonable to be $\gamma \succ 0.5$. Also, the expression $\eta \cdot ({\gamma }_{p}^{s}\cdot P{o}_{p}^{(s1)}+(1-{\gamma }_{p}^{s})\cdot P{o}_{p}^{(s2)}-P{o}_{p}^{(s1)})$ is added to each of the objectives of the mathematical formulation in the present research. In this expression, $\eta$ refers to the penalty un for any possible constraint violation, containing the non-deterministic parameter. Moreover, ${\gamma }_{p}^{s}\cdot P{o}_{p}^{(s1)}+(1-{\gamma }_{p}^{s})\cdot P{o}_{p}^{(s2)}-P{o}_{p}^{(s1)}$ is the difference between the worst value of the non-deterministic parameter and the value applied in the chance constraint. Accordingly, $\eta \cdot ({\gamma }_{p}^{s}\cdot P{o}_{p}^{(s1)}+(1-{\gamma }_{p}^{s})\cdot P{o}_{p}^{(s2)}-P{o}_{p}^{(s1)})$ controls the feasibility of the robust solution.

$$\left( {\gamma _{p}^{s} \cdot Po_{p}^{{\left( {s1} \right)}} + \left( {1 - \gamma _{p}^{s} } \right) \cdot Po_{p}^{{\left( {s2} \right)}} } \right) \cdot \left( {\mathop \sum \limits_{l} XE_{{lrp1t}}^{s} + \mathop \sum \limits_{{i^{\prime } }} XC_{{i^{\prime } rp1t}}^{s} } \right) = PR_{{rpa^{\prime } t}}^{s} \quad \forall \;r,p \ne p1,a,t,s$$

(61)

It should also be mentioned that the minimum confidence level (i.e., $\gamma$) is variable and is optimized due to the objectives and the constraints.

According to the preceding points, the general form of the mathematical model of this research after dealing with innovative hybrid uncertainty is as follows:

• The uncertain parameters for the percentage of blood product production ($P{o}_{p}$) are as fuzzy numbers.

• The demand ( $D{m}_{hpat}$) is in the form of intervals.

• The maximum coverage radii of different facilities ($R{a}_{m},R{b}_{l},R{c}_{r}$) as considered as scenarios.

Based on the applied hybrid robust optimization approach, the objectives of the required mathematical formulation are as follows:

$$\begin{aligned} {\text{Min }}Z_{1} & = \mathop \sum \nolimits_{s} \pi^{s} Z_{1s} + \lambda_{1} \mathop \sum \nolimits_{s} \pi^{s} \left( {\left( {Z_{1s} - \mathop \sum \nolimits_{s} \pi^{s} Z_{1s} } \right) + 2\theta_{1}^{s} } \right) \\ & \quad + \omega_{1} \mathop \sum \nolimits_{i} \mathop \sum \nolimits_{m} \mathop \sum \nolimits_{l} \mathop \sum \nolimits_{r} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} \pi^{s} \left(\delta_{imt}^{s} + \delta_{i^{\prime}lt}^{s} + \delta_{irt}^{s} \right) \\ & \quad + \eta_{1} \cdot \mathop \sum \nolimits_{p} \mathop \sum \nolimits_{s} \gamma_{p}^{s} \cdot Po_{p}^{{\left( {s1} \right)}} + \left( {1 - \gamma_{p}^{s} } \right) \cdot Po_{p}^{{\left( {s2} \right)}} - Po_{p}^{{\left( {s1} \right)}} \\ \end{aligned}$$

(62)

$$\begin{aligned} {\text{Min }}Z_{2} & = \mathop \sum \nolimits_{s} \pi^{s} Z_{2s} + \lambda_{2} \mathop \sum \nolimits_{s} \pi^{s} \left( {\left( {Z_{2s} - \mathop \sum \nolimits_{s} \pi^{s} Z_{2s} } \right) + 2\theta_{2}^{s} } \right) \\ & \quad + \omega_{2} \mathop \sum \nolimits_{i} \mathop \sum \nolimits_{m} \mathop \sum \nolimits_{l} \mathop \sum \nolimits_{r} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} \pi^{s} \left(\delta_{imt}^{s} + \delta_{i^{\prime}lt}^{s} + \delta_{irt}^{s} \right) \\ & \quad + \eta_{2} \cdot \mathop \sum \nolimits_{p} \mathop \sum \nolimits_{s} \gamma_{p}^{s} \cdot Po_{p}^{{\left( {s1} \right)}} + \left( {1 - \gamma_{p}^{s} } \right) \cdot Po_{p}^{{\left( {s2} \right)}} - Po_{p}^{{\left( {s1} \right)}} \\ \end{aligned}$$

(63)

$$\begin{aligned} {\text{Min }}Z_{3} & = \mathop \sum \nolimits_{s} \pi^{s} Z_{3s} + \lambda_{3} \mathop \sum \nolimits_{s} \pi^{s} \left( {\left( {Z_{3s} - \mathop \sum \nolimits_{s} \pi^{s} Z_{3s} } \right) + 2\theta_{3}^{s} } \right) \\ & \quad + \omega_{3} \mathop \sum \nolimits_{i} \mathop \sum \nolimits_{m} \mathop \sum \nolimits_{l} \mathop \sum \nolimits_{r} \mathop \sum \nolimits_{t} \mathop \sum \nolimits_{s} \pi^{s} \left(\delta_{imt}^{s} + \delta_{i^{\prime}lt}^{s} + \delta_{irt}^{s} \right) \\ & \quad + \eta_{3} \cdot \mathop \sum \nolimits_{p} \mathop \sum \nolimits_{s} \gamma_{p}^{s} \cdot Po_{p}^{{\left( {s1} \right)}} + \left( {1 - \gamma_{p}^{s} } \right) \cdot Po_{p}^{{\left( {s2} \right)}} - Po_{p}^{{\left( {s1} \right)}} \\ \end{aligned}$$

(64)

The constraints (1–11), (13–14), (15–19), (21–23), (28–29) of the mathematical formulation are similar. Nevertheless, the remaining constraints change as follows:

$$ZA_{imt}^{s} \cdot Da_{im} + \delta_{imt}^{s} = Ra_{m} \mathop \sum \nolimits_{m^{\prime}} MV_{m\prime mt}^{S} \quad \forall \;i,m,t,s$$

(65)

$$ZB_{i^\prime lt}^{S} \cdot Db_{i^\prime l} + \delta_{i^\prime lt}^{s} = Rb_{l}^{s} YL_{l} \quad \forall \;i^{\prime},l,t,s$$

(66)

$$ZC_{i^{\prime}rt}^{S} \cdot Dc_{ir} + \delta_{irt}^{s} = Rc_{r}^{s} \cdot YL_{r} \quad \forall \;i,r,t,s$$

(67)

$$\mathop \sum \nolimits_{{m^{\prime}}} MV_{{m^{\prime}m^{\prime\prime}t}}^{s} \le 1\quad \forall \;m^{\prime\prime},{\text{t,s}}$$

(68)

$$\left( {\gamma _{p}^{s} Po_{p}^{{\left( {s1} \right)}} + \left( {1 - \gamma _{p}^{{\left( s \right)}} } \right) \cdot Po_{p}^{{\left( {s2} \right)}} } \right) \cdot \left( {\sum\limits_{l} {XE_{{lrp_{1} t}}^{s} } + \sum\limits_{{i^{\prime } }} {XC_{{i^{\prime } rp_{1} t}}^{s} } } \right) = PR_{{rpa^{\prime } t}}^{s} \quad \forall \;r,{\text{p}} \ne p_{1} ,p_{5} ,a^{\prime } ,{\text{t,s}}$$

(69)

$$\sum\limits_{a} {PR_{rpat}^{s} \le Sc_{rpat} \cdot YR_{r} \quad } \forall \;r,p,t,s$$

(70)

$$\mathop \sum \nolimits_{a} IR_{rpat}^{s} \le Se_{rpat} { } \cdot YR_{r} \quad \forall \;r,p,t,s$$

(71)

$$\mathop \sum \nolimits_{a} \mathop \sum \nolimits_{k} IH_{hpakt}^{s} \le Sk_{hpat} \quad \forall \;h,p,t,s$$

(72)

$$\mathop \sum \nolimits_{i} XA_{impt}^{s} = \mathop \sum \nolimits_{r} XD_{mrpt}^{s} \quad \forall \;m,t,s$$

(73)

$$\mathop \sum \nolimits_{{i^{\prime}}} XB_{{i^{\prime}lp_{1} t}}^{s} = \mathop \sum \nolimits_{r} XE_{{lrp_{1} t}}^{s} \quad \forall \;l,t,s$$

(74)

$$Dm_{hpat} + q_{hpat}^{s} \cdot \Gamma_{hpat}^{s} + r_{hpat}^{s} - \sum\limits_{r} {\sum\limits_{k} {XH_{rhpakt}^{s} - EX_{hpat}^{s} \quad } } \forall \;h,p,a,t,s$$

(75)

$$q_{hpat}^{s} + r_{hpat}^{s} \ge \widehat{Dm}_{hpat} \quad \forall \;h,p,a,t,s$$

(76)

$$\mathop \sum \nolimits_{r} \mathop \sum \nolimits_{k} { }XH_{rhpakt}^{s} \ge St{ } \cdot Dm_{hpat}^{s} \quad \forall \;h,p,a,t,s$$

(77)

$$\mathop \sum \nolimits_{i} {\text{XA}}_{{{\text{impt}}}}^{{\text{s}}} \le {\text{Dr}}^{{\text{s}}} \cdot Pop_{m} \cdot { }\left({\text{AT}}_{{{\text{mt}}}}^{{\text{s}}} \right)/Ub_{m} \quad \forall \;m,p,t,s$$

(78)

$${\text{AT}}_{{{\text{mt}}}}^{{\text{s}}} = \tau_{m}^{{ - S\tau_{m} }} \cdot \sigma_{m}^{{S\sigma_{m} }} \cdot \vartheta_{m}^{{S\vartheta_{m} }} \cdot \Sigma_{{m^{\prime } }} MV_{{m^{\prime } mt}}^{S} \quad \forall \;m,t,s$$

(79)

$$\mathop \sum \nolimits_{{i^{\prime}}} {\text{XB}}_{{i^{\prime}{\text{lp}}_{1} {\text{t}}}}^{{\text{s}}} \le {\text{Dr}}^{{\text{s}}} \cdot Pop_{l} \cdot { }\left({\text{AT}}_{{{\text{lt}}}}^{{\text{s}}} \right)/Ub_{l} \quad \forall \;l,t,s$$

(80)

$${\text{AT}}_{{{\text{lt}}}}^{{\text{S}}} = \tau_{l}^{{ - S\tau_{l} }} \cdot \sigma_{l}^{{S\sigma_{l} }} \cdot \vartheta_{l}^{{S\vartheta_{l} }} \cdot YL_{l} \quad \forall \;l,t,s$$

(81)

$$\mathop \sum \limits_{i} {\text{XC}}_{{{\text{irpt}}}}^{{\text{s}}} \le {\text{Dr}}^{{\text{s}}} \cdot Pop_{r} \cdot {\text{~}}({\text{AT}}_{{{\text{rt}}}}^{{\text{s}}} )/Ub_{r} \quad \forall \;r,p,t,s$$

(82)

$${\text{AT}}_{{{\text{lt}}}}^{{\text{S}}} = \tau_{r}^{{ - S\tau_{r} }} \cdot \sigma_{r}^{{S\sigma_{r} }} \cdot \vartheta_{r}^{{S\vartheta_{r} }} \cdot YR_{r} \quad \forall \;r,t,s$$

(83)

$$Z_{js} - \pi^{s} Z_{js} + \theta_{1}^{s} \ge 0\quad \forall \;s,j$$

(84)

And constraints (1–11), (13–14), (15–19), (21–23), (28–29)

$$YL_{l} ,YR_{r} ,ZA_{imt}^{s} ,ZB_{{i^{\prime}lt}}^{s} ,ZC_{irt}^{s} ,MV_{{m^{\prime}m^{\prime\prime}t}}^{s} \in \left\{ {0,{1}} \right\}$$

(85)

$$\begin{aligned} & XA_{impt}^{s} { },{ }XB_{{i^{\prime}lp_{1} t}}^{s} { },XC_{irpt}^{s} { },{ }XD_{mrpt}^{s} { },XE_{{lrp_{1} t}}^{s} { },XG_{rhpakt}^{s} , \\ & XH_{rhpakt}^{S} ,PR_{rpat}^{S} ,Sh_{hpat}^{S} ,EX_{hpat}^{S} ,IR_{rpat}^{S} ,\theta_{1}^{S} ,\theta_{2}^{S} ,\theta_{3}^{S} , \\ & IH_{hpakt}^{S} ,{\text{AT}}_{wt}^{S} ,\delta_{imt}^{S} ,\delta_{i,lt}^{S} ,\delta_{irt}^{S} ,q_{hpat}^{S} ,r_{hpat}^{S} \ge 0 \\ \end{aligned}$$

(86)

5 Computational results

5.1 Designing example problems and analyzing numerical results

Here, the hybrid robust optimization approach, the scenario-based robust approach, and the deterministic approach are compared in terms of efficiency. For this purpose, due to the structure and characteristics of the studied problem, a series of different numerical examples are designed and the calculation results are discussed. It should be noted that all the numerical example problems are solved by the improved weighted Chebyshev approximation method, which was selected as the best solution. It is categorized among the methods for solving multi-objective problems. It uses a precise approach to find Pareto optimal solutions [28, 29, 30] and [33,34,35]. The main structure of the applied approach is as described in Eq. (93):

$$\begin{aligned} & {\text{Min}}\left\{ {\eta + \omega \mathop \sum \nolimits_{i = 1}^{r} \left( {\frac{{z_{i} - z_{i}^{*} }}{{z_{i}^{*} }}} \right)} \right\} \\ & {\text{Subject}}\;{\text{to}}: \\ & y_{i} \left( {\frac{{z_{i} - z_{i}^{*} }}{{z_{i}^{*} }}} \right) \le \eta \quad \forall \;i = 1, \ldots ,r \\ \end{aligned}$$

(87)

Here, ω is a parameter that takes small and positive values, and η is a free variable. Also, the preference of the objective r is specified by using the weighting factor y_i; in such a way that ${\sum }_{i=1}^{r}{y}_{i}=1$.

To exact solve the proposed mathematical model, three solution methods have been examined, and the best and most efficient one (improved weighted Chebyshev approximation) is selected. The LP-metric, AUGMECON2, and improved weighted Chebyshev are three famous, most popular, and widely used methods for solving multi-objective problems. Since the three mentioned methods are used to solve different problems, these were chosen for comparison to choose the best and most efficient accurate solution approach for the presented mathematical model. It should be noted that several exact solution approaches have been introduced and presented to solve multi-objective problems. However, the three mentioned methods are the most compatible for solving the proposed multi-objective mathematical model.

Various numerical example problems are shown in Table 3.

Table 3 Numerical examples generated for the problem in the present study

The other parameter values used in the numerical examples are presented in Table 4, all based on uniform distribution. Besides, the weights required for the improved weighted Chebyshev method are considered the same for all the objective functions (i.e., 0.33). The values of all the coefficients are also $\lambda =5$,$\omega =3$ and $\eta =0.5$ when dealing with uncertainty.

Table 4 Values of the parameters used in the numerical examples

To solve the mathematical formulation by the improved weighted Chebyshev approximation approach, the GAMS software version 24.1.3 and the CPLEX solver have been applied in a system with a CPU of Cori7 6700 HQ and a RAM of 16 GIG DDR4. The analysis is carried out according to Table 5 and Fig. 1.

Table 5 The results of the numerical examples for the three proposed formulations and their comparison

Fig. 1

The results of implementing the numerical examples on the proposed mathematical formulation

In order to deal with the uncertainty, robust programming approaches are applied owing to their ability to provide a robust solution. According to Table 5 and Fig. 1, in the “Hybrid heuristic robust optimization” approach, the value of the first objective or costs (Z₁) is closer to reality and more than the other two approaches. Although according to the proposed mathematical formulation, the first objective is minimization and the “Deterministic optimization” approach has performed better and provided better results, but without considering the uncertainty, the value of costs is far from the reality and it is not possible to rely on the results. Therefore, the “Hybrid heuristic robust optimization” approach has provided more logical and realistic results.

In the case of the second objective, i.e., minimization of the contagion rate (Z₂), both the “Scenario-based robust optimization” and “Hybrid heuristic robust optimization” approaches have performed worse than the “Deterministic optimization” approach and have provided higher values, But the approach of “Hybrid heuristic robust optimization” compared to the “Scenario-based robust optimization” approach has provided better results (has lower values).

Finally, regarding the third objective (Z₃), which is the maximization of attractiveness, the “Deterministic optimization” approach has been better than the other approaches. Therefore, the computational results emphasize that the “Scenario-based robust optimization” and “Hybrid heuristic robust optimization” approaches (especially the hybrid) perform better than “Deterministic optimization” approach in terms of the predetermined performance criteria (except for the second objective function rate).

In general, the main managerial-practical insights can be concluded as follows:

• The performance and attractiveness of a BSC can be enhanced significantly if the number of the collection centers and the amount of blood sent from the receiving centers to the demand nodes are increased.

• On the other hand, as the dimensions of the problem grow, especially the number of blood products, the solution time of the proposed mathematical formulation increases.

5.2 A case study

As a real-world healthcare system, the following practical example can be described. Iran, with an area of 1,648,000 km², is the 17th largest country in the world. It consists of 1245 cities and 31 provinces with about 85 million people. According to the experts in the Blood Transfusion Organization (BTO) of Iran, the current BSC network in Iran needs to be improved as much as possible. In 2018, 3,600,000 units of blood and blood products were transferred to 800 hospitals; however, in March 2020, with the decrease in donor visits due to the spread of COVID-19, the number of blood donations in the whole country decreased by 35%. After the situation was managed through vaccine injection, the total amount of donated blood in Iran increased by 7% in the first half of 2021 compared to the previous year. The blood reserves of the country are now about 20 percent lower than that last year. In addition, Iran is among the countries that started the plasma therapy for COVID-19 patients from the earliest days, but reports indicate that the amount of plasma received from coronary arteries in Iran is about half the required amount. New protocols concerning 14 days after vaccination and 28 days after coronary artery diseases have effectively reduced the disease.

Considering the challenges that the Blood Transfusion Organization of Iran is faced with, providing an efficient approach in the form of a comprehensive mathematical formulation can greatly help to improve the efficiency of the blood chain network and its management. In the mathematical model proposed here, it is desired to determine the best locations to set up blood centers with specific capacities. The aim is to have a network with low costs and high attractiveness with some influential factors taken into account such as advertisement and blood donation time.

The proposed formulation determines the optimal type and location of each center according to the system costs, the capacity of each center and the demand for blood. The present study is designed with two five-day periods and two coronary state scenarios of equal probability. However, due to the large bulk of the data as well as the duplication of cases, the performance of the model is examined only for one period and one scenario. In this case, the hospitals in each province are specified as demand nodes. Also, the blood supply is calculated due to certain parameters such as the population of each province, the percentage of blood donation, and the capacity and attractiveness of the blood centers. Besides, transportation costs are calculated based on the distance between the blood centers, and the values of the other parameters are extracted from the blood transfusion organization.

In general, if we discuss and analyze the above practical example, we can conclude the main managerial-practical insights as follows:

• The performance and attractiveness of a BSC can be enhanced significantly if the number of the collection centers and the amount of blood sent from the receiving centers to the demand nodes are increased. Also, the possibility of COVID-19 transmission will be improved significantly.

• On the other hand, as the dimensions of the problem grow, especially the number of blood products, the solution time of the proposed mathematical formulation increases.

• As the attractiveness and the possibility of COVID-19 transmission improve, the fixed and operating costs of the blood supply chain also increase. This represents the conflict between the three objective functions and emphasizes the necessity of establishing a reasonable balance between attractiveness and costs. Accordingly, the influential decision makers of the supply chain should choose the attractiveness and cost of the chain with a smart look and consider all hidden and visible aspects.

• Choosing an equilibrium point between three objective functions is not difficult and improves the overall utility of the supply chain to a significant extent.

The aspect of the generalizability of the present study compared to other similar blood supply chains worldwide is that the proposed approach can be used in an efficient and generalizable way in blood transfusion organizations of different countries in the world. The level of the possibility of COVID-19 transmission in the second objective function, and the attractiveness in the third objective function and are one of the most vital decision variables, which is determined by the proposed mathematical model depending on the input parameters and conditions of each country. It depends on parameters such as types of transportation operating costs, capacity of facilities and mobile centers, distance between centers, maximum coverage radius, procurement costs, advertising budget, staff experience, and donor sensitivity. Accordingly, all the mentioned parameters have been comprehensively included in the proposed mathematical modeling so that the generalizability aspect of the present study can be adequately met concerning other similar blood supply chains worldwide.

5.3 Sensitivity analysis

According to the above practical examples, a sensitivity analyses have been done and described as follows. The sensitivity of the objective functions is examined by the changing of the critical parameters, including the capacities of blood facilities, advertising, experience and blood donation time, along with the donor influence parameters related to individual factors. It should be mentioned that, for the involvement of both objectives, the sensitivity analysis of the parameters is performed by the ε of 0.5.

5.3.1 Blood facility capacity ${({\varvec{S}}{\varvec{a}}}_{{\varvec{l}}{{\varvec{p}}}_{1}{\varvec{t}}}{\boldsymbol{ },\boldsymbol{ }{\varvec{S}}{\varvec{b}}}_{{\varvec{p}}{\varvec{t}}}{\boldsymbol{ },\boldsymbol{ }{\varvec{S}}{\varvec{c}}}_{{\varvec{r}}{\varvec{p}}{\varvec{a}}{\varvec{t}}}{\boldsymbol{ },{\varvec{S}}{\varvec{e}}}_{{\varvec{r}}{\varvec{p}}{\varvec{a}}{\varvec{t}}}{\boldsymbol{ },\boldsymbol{ }{\varvec{S}}{\varvec{k}}}_{{\varvec{h}}{\varvec{p}}{\varvec{a}}{\varvec{t}}})$

The effects of 10% and 20% changes in the capacities of blood centers (i.e., all of ${{\varvec{S}}{\varvec{a}}}_{{\varvec{l}}{{\varvec{p}}}_{1}{\varvec{t}}}{\boldsymbol{ },\boldsymbol{ }{\varvec{S}}{\varvec{b}}}_{{\varvec{p}}{\varvec{t}}}{\boldsymbol{ },\boldsymbol{ }{\varvec{S}}{\varvec{c}}}_{{\varvec{r}}{\varvec{p}}{\varvec{a}}{\varvec{t}}}{\boldsymbol{ },{\varvec{S}}{\varvec{e}}}_{{\varvec{r}}{\varvec{p}}{\varvec{a}}{\varvec{t}}}{\boldsymbol{ },\boldsymbol{ }{\varvec{S}}{\varvec{k}}}_{{\varvec{h}}{\varvec{p}}{\varvec{a}}{\varvec{t}}})$ on the objectives were done. Unexpectedly, the total attractiveness of all the blood centers and, consequently, the cost of the entire network remain constant as the capacities of blood facilities increase. This indicates that the blood centers generally have a sufficient capacity and the increase in blood donation depends on other influential factors, including incentive policies. On the other hand, it is evident that, with the reduction of capacity, the blood centers will not be able to respond to all donors. Accordingly, the amount of donated blood and, subsequently, the operating costs will be reduced. This is because donors are not directly attracted to blood centers as the capacity of those centers increases. Some influential parameters in this regard are analyzed in the following.

5.3.2 Advertising and its effect on the rate of blood donation$({{\varvec{\sigma}}}_{{\varvec{w}}}\boldsymbol{ },\boldsymbol{ }{\varvec{S}}{{\varvec{\sigma}}}_{{\varvec{w}}}$)

The effects of 10% and 20% changes in the amount of advertisement on the objectives were considered. Advertisement can promote the attractiveness of the centers, which also leads to more blood donation and costs. After the establishment of centers, the rate of blood donation increases if the spatial attractiveness is improved. In this case, the operating costs rise too.

The cost parameter shows the same behavior. Increased advertisements result in more attractive blood centers, which, in turn, increase the blood donation and the operating cost. In contrast, with low advertisements, the number of clients cannot be expected to rise, and the operating costs decrease.

5.3.3 Donor experience and effectiveness $({\boldsymbol{\vartheta }}_{{\varvec{w}}}\boldsymbol{ },\boldsymbol{ }{{\varvec{S}}\boldsymbol{\vartheta }}_{{\varvec{w}}})$

The effects of 10% and 20% changes in the experience rate on the objectives were analyzed. After the desired changes are made in the experience parameter, similar impacts are observed on individual donors.

5.3.4 Donor time and sensitivity ${({\varvec{\tau}}}_{{\varvec{w}}}\boldsymbol{ },\boldsymbol{ }{{\varvec{S}}{\varvec{\tau}}}_{{\varvec{w}}})$

First, the effects of 10% and 20% changes in the time spent for blood donation on the objective functions were done.

A longer blood donation time and, as a result, a longer waiting time lead to the reduced attraction of the donation centers. This hurts the amount of donated blood and the operation costs. Conversely, given the prevalence of coronavirus, the faster the blood donation process, the more attractive the centers will be for donors. Consequently, the number of donors, the amount of blood donation and, ultimately, the total costs of the network are all positively affected. Assuming that the time required for blood donation is constant, the donor’s sensitivity to time and the effects of its change on the objectives were considered.

Since the donor’s reaction to time has an exponential effect on attractiveness, a decrease and an increase in the donor’s sensitivity to waiting time, respectively, reduce and increase the attractiveness of the centers, the amount of blood donation and, ultimately, the total costs of the network. The changes in both cases are significant.

According to the above sensitivity analyses, the following managerial insights can be concluded:

• Growing the capacity of mobile facilities up to a certain amount (for example, up to 20% of the original capacity) can lead to a growth in the attractiveness of donating blood and reduction in the possibility of COVID-19 transmission, and spending more in this field will not improve the attractiveness and the possibility of COVID-19 transmission.

• The role of the experience and expertise of the employees of different blood donation centers cannot be ignored and can have a significant impact on the attractiveness of the centers, the possibility of COVID-19 transmission, and the blood donation process.

• In the COVID-19 conditions, because of infectious diseases, it is very critical for blood donors not to be delayed in blood donation centers and to donate blood quickly. Therefore, there is a very significant relationship between the reduction of blood donation time, the possibility of COVID-19 transmission, and the attractiveness of the centers and, accordingly, the amount of blood donated.

6 Conclusion

A critical challenge of BSCs is the existence of several uncertainties in the blood supply and its products, transportation, cost, processing, time and demand. Therefore, deterministic assumptions for the parameters of optimization problems can lead to infeasible SCN designs or nonoptimal solutions.

Since the amount of demand and supply for blood and its products is not certain during crucial situations, such as the outbreak of Coronavirus, the corresponding managerial decisions may be affected. The supply chain dealt with in this study was considered dynamic, and its parameters were classified into different categories of uncertainty according to their nature. Moreover, after the main structure of the mathematical model was designed, two “Scenario-based robust optimization” and “Hybrid heuristic robust optimization” approaches that could face different types of uncertainty were suggested.

The proposed mathematical model was solved in a non-deterministic mode with a combination of scenarios, intervals and fuzzy robust programming. In this model, a hybrid robust optimization approach was developed. The GAMS software was used to solve the mathematical model with improved weighted Chebyshev. The proposed formulation facilitates strategic decisions on facility location, capacity, and technology type as well as tactical decisions on inventory levels, resource allocation, production quantities, and transportation across the network. In addition, uncertainty was dealt with in the parameters of the SCN of blood and its products, and the possible factors that may cause it were discussed. An updated review was also performed of the literature on the blood SCNs beset with uncertainty. The performance of deterministic models and the proposed robust approaches were represented by solving example problems of different sizes. The computational results showed that the proposed robust approaches outperform deterministic models due to performance criteria. As also found, once the attractiveness of blood donation is increased for the donor, the demand for the blood SCN increases too, which, in turn, increases the costs and the unmet demands. In this case, managers can control the costs and keep the shortage at an acceptable level.

Considering the importance of costs and the level of service for hospitals, managers can balance the costs and the number of unmet demands in the network. Meeting hospital demands in a timely and sufficient manner is a significant factor in the efficiency of the blood SCN. The network may incur higher costs if the manager sets the service level to the demand at an undue low rate. With an increase in the service level, the network costs rise due to the cost of the blood collection system, such as the cost of establishing mobile or fixed blood centers. However, increasing the level of service to hospitals and donation centers leads to a drastic reduction in the unmet demand in the chain. As the maintenance costs rise in regional centers, the costs of the entire network rise too. This gives those regional centers a greater desire to keep a smaller inventory, which causes untimely and inappropriate supply of hospital demands. Therefore, keeping both the maintenance and network costs low can lead to a higher service level and the better satisfaction of hospitals demands.

The results show that robust optimization approaches, as used in the present research, make it possible to provide suitable solutions to uncertain parameters. Indeed, they allow responding as well as possible to those who need the plasma of survivors. For future research, it is suggested to use new algorithms such as the red deer algorithm and social spider optimization algorithm, which provide more efficient solving methods.