1 Introduction

The inverse optimal control (IOC) problem is a framework used to determine the objective function optimized by a given control system. By optimizing the objective function obtained by IOC, a different system can imitate the given control system’s behavior. For example, several studies have been conducted on robots imitating human or animal movements [1,2,3]. To apply IOC, in these studies, the researchers assumed that human and animal movements are optimal for unknown criteria. Such an optimality assumption holds in some cases [4].

The first IOC problem, which assumes a single-input linear time-invariant system and quadratic objective function, was proposed by Kalman [5]. Anderson [6] generalized the IOC problem in [5] to the multi-input case. For this type of IOC problem, called the inverse linear quadratic regulator (ILQR) problem, Molinari [7] proposed a necessary and sufficient condition for a linear feedback input to optimize some objective functions. Moylan et al. [8] proposed and solved the IOC problem for nonlinear systems. IOC in [5,6,7,8] is based on control theory, whereas Ng et al. [9] proposed inverse reinforcement learning (IRL), which is IOC based on machine learning. Recently, IRL has become an important IOC framework, along with control theory methods [10].

There are many variations of data-driven ILQR problems depending on available information. For example, Zhang and Ringh [11] considered the case where the system is known, and the states can be observed, but the input cannot. In this paper, we consider the discrete-time case where the system is unknown, but the states and inputs can be observed. Such a case often occurs in biological system analysis, which is the main application target of IOC. The control theory approach solves the ILQR problem by solving a linear matrix inequality (LMI) that contains the algebraic Riccati equation (ARE) [12]. In [12], they discussed the method to numerically solve the ARE, assuming that the full knowledge of the system model is available. However, the system model is often unknown beforehand. In [12], they solved this problem by inserting the step of system identification. Suppose the system identification step can be bypassed. In that case, it will be beneficial in some cases, where we are not interested in the system itself, but only in the criterion for control. Recent studies [13,14,15] also consider the IOC problem with linear quadratic control over a finite-horizon. However, all the above-mentioned studies also assume that the system model is known. The IRL approach also has difficulty solving our problem. There is IRL with unknown systems [16], and IRL with continuous states and input spaces [17]; however, to the best of our knowledge, no IRL exists with both.

In the continuous-time case, we proposed a method to estimate the ARE from the observation data of the system state and input directly [18]. In the present paper, we estimate the ARE for a discrete-time system using a method that extends the result in [18]. Similarly to [18], our method transforms the ARE by multiplying the observed state and input on both sides. However, this technique alone cannot calculate ARE without the system model because the form of the ARE differs between continuous and discrete-time. We solve this problem using inputs from the system’s controller. Also, the use of such inputs enables us to estimate the ARE without knowing the system’s control gain. We prove that the equation obtained from this transformation is equivalent to the ARE if the dataset is appropriate. The advantage of our method is the economization of the observation data using prior information about the objective function. We conducted a numerical experiment to demonstrate that our method can estimate the ARE with fewer data than system identification if the prior information is sufficient.

The structure of the remainder of this paper is as follows: In Sect 2, we formulate the problem considered in this paper. In Sect 3, we propose our estimation method and prove that the estimated equation is equivalent to the ARE. In Sect 4, we describe numerical experiments that confirm our statement in Sect 3. Sect 5 concludes the paper.

2 Problem formulation

We consider the following discrete-time linear system:

$$\begin{aligned} x{\left( k+1\right) }=Ax{\left( k\right) }+Bu{\left( k\right) }, \end{aligned}$$
(1)

with an arbitrary initial state x(0), where \(A\in {{\mathbb {R}}}^{n\times n}\) and \(B\in {{\mathbb {R}}}^{n\times m}\) are constant matrices, and \(x{\left( k\right) }\in {{\mathbb {R}}}^n\) and \(u{\left( k\right) }\in {{\mathbb {R}}}^m\) are the state and the input at time \(k\in {\mathbb {Z}}\), respectively.

Let \({\mathbb {Z}}_+=\left\{ 0,1,2,\cdots \right\}\). We write the set of real-valued symmetric \(n\times n\) matrices as \({{\mathbb {R}}}^{n\times n}_{\textrm{sym}}\). In the LQR problem [19], we determine the input sequence \(u{\left( k\right) }\) \(\left( k\in {\mathbb {Z}}_+\right)\) that minimizes the following objective function:

$$\begin{aligned} J{\left( u\right) }=\sum _{k=0}^\infty \left[ x{\left( k\right) }^\top Qx{\left( k\right) }+u{\left( k\right) }^\top R u{\left( k\right) }\right] , \end{aligned}$$
(2)

where \(Q\in {{\mathbb {R}}}^{n\times n}_{\textrm{sym}}\) and \(R\in {{\mathbb {R}}}^{m\times m}_{\textrm{sym}}\).

We assume that the system (1) is controllable and matrices Q and R are positive definite. Then, for any \(x{\left( 0\right) }\), the LQR problem has a unique solution written as the following linear state feedback law [19]:

$$\begin{aligned} u{\left( k\right) }=-\left( R+B^\top PB\right) ^{-1}B^\top PAx{\left( k\right) }, \end{aligned}$$
(3)

where \(P\in {{\mathbb {R}}}^{n\times n}_{\textrm{sym}}\) is a unique positive definite solution of the ARE:

$$\begin{aligned} A^\top PA-P+Q-A^\top PB\left( R+B^\top PB\right) ^{-1}B^\top PA=0. \end{aligned}$$
(4)

For u defined in (3), \(J{\left( u\right) }=x{\left( 0\right) }^\top Px{\left( 0\right) }\) holds.

In the ILQR problem, we find positive definite matrices \(Q\in {{\mathbb {R}}}^{n\times n}_{\textrm{sym}}\) and \(R\in {{\mathbb {R}}}^{m\times m}_{\textrm{sym}}\) such that an input \(u{\left( k\right) }=-Kx{\left( k\right) }\) with the given gain \(K\in {{\mathbb {R}}}^{m\times n}\) is a solution of the LQR problem, that is, u minimizes (2).

We can solve the ILQR problem by solving an LMI. Let the system (1) be controllable. Then, \(u{\left( k\right) }=-Kx{\left( k\right) }\) minimizes (2) if and only if a positive definite matrix \(P\in {{\mathbb {R}}}^{n\times n}_{\textrm{sym}}\) exists that satisfies (4) and the following:

$$\begin{aligned} K=\left( R+B^\top PB\right) ^{-1}B^\top PA. \end{aligned}$$
(5)

By transforming (4) and (5), we obtain the following pair of equations equivalent to (4) and (5):

$$\begin{aligned} \begin{aligned} A^\top PA-P+Q-K^\top \left( R+B^\top PB\right) K=&0,\\ B^\top PA-\left( R+B^\top PB\right) K=&0. \end{aligned} \end{aligned}$$
(6)

Hence, we can solve the ILQR problem by determining P, \(Q\in {{\mathbb {R}}}^{n\times n}_{\textrm{sym}}\), and \(R\in {{\mathbb {R}}}^{m\times m}_{\textrm{sym}}\) that satisfy the following LMI:

$$\begin{aligned} P>0,\;Q>0,\;R>0\qquad \mathrm{s.t. ~Equation(6)}. \end{aligned}$$
(7)

In biological system analysis or reverse engineering, the system model and control gain is often unknown, and the ARE (6) is not readily available. Hence, we consider the following ARE estimation problem where we determine a linear equation equivalent to (6) using the system state and input observation:

Problem 1

Consider controllable system (1) and controller \(u{\left( k\right) }=-Kx{\left( k\right) }\) with unknown A, B, and K. Suppose \(N_d\) observation data \(\left( x_i{\left( 0\right) },u_i,x_i{\left( 1\right) }\right)\) \(\left( i\in \left\{ 1,\ldots ,N_d\right\} \right)\) of the system state and input are given, where

$$\begin{aligned} x_i{\left( 1\right) }=Ax_i{\left( 0\right) }+Bu_i\quad \left( i\in \left\{ 1,\ldots ,N_d\right\} \right) . \end{aligned}$$
(8)

Let \(N'_d\le N_d\). \(N'_d\) inputs in the data are obtained from the unknown controller as follows:

$$\begin{aligned} u_i=-Kx_i{\left( 0\right) }\quad \left( i\in \left\{ 1,\ldots ,N'_d\right\} \right) . \end{aligned}$$
(9)

Determine a linear equation of P, \(Q\in {{\mathbb {R}}}^{n\times n}_{\textrm{sym}}\), and \(R\in {{\mathbb {R}}}^{m\times m}_{\textrm{sym}}\) with the same solution space as (6).

We discuss without assuming that the data is sequential, that is, always satisfies \(x_{i+1}{\left( 0\right) }=x_i{\left( 1\right) }\). However, in an experiment, we show that our result can also be applied to one sequential data. The ARE has multiple solutions and we call the set of these solutions, which is a linear subspace, a solution space.

3 Data-driven estimation of ARE

The simplest solution to Problem 1 is to identify the control system, that is, matrices A, B and K. We define matrices \(X\in {\mathbb {R}}^{n\times N_d}\), \(X'\in {\mathbb {R}}^{n\times N'_d}\), \(U\in {\mathbb {R}}^{m\times N_d}\), \(U'\in {\mathbb {R}}^{m\times N'_d}\), and \(D\in {\mathbb {R}}^{(n+m)\times N_d}\) as follows:

$$\begin{aligned} \begin{aligned}&X{\left( k\right) }=\left[ x_1{\left( k\right) }\;\cdots \;x_{N_d}{\left( k\right) }\right] ,\quad X'{\left( k\right) }=\left[ x_1{\left( k\right) }\;\cdots \;x_{N'_d}{\left( k\right) }\right] \quad \left( k\in \left\{ 0,1\right\} \right) ,\\&U=\left[ u_1\;\cdots \;u_{N_d}\right] ,\quad U'=\left[ u_1\;\cdots \;u_{N'_d}\right] ,\quad D=\left[ X{\left( 0\right) }^\top \;U^\top \right] ^\top . \end{aligned} \end{aligned}$$
(10)

Let the matrices D and \(X'{\left( 0\right) }\) have row full rank. Then, matrices A, B, and K are identified using the least square method as follows:

$$\begin{aligned} \begin{aligned}&\left[ A\;B\right] =X{\left( 1\right) }D^\top \left[ DD^\top \right] ^{-1},\\&K=-U'X'{\left( 0\right) }^\top \left[ X'{\left( 0\right) }X'{\left( 0\right) }^\top \right] ^{-1}.\\ \end{aligned} \end{aligned}$$
(11)

In ILQR problems, prior information about matrices Q and R may be obtained. However, such information cannot be used for system identification. We propose a novel method that uses the prior information and estimates the ARE using less observation data than system identification.

The following theorem provides an estimation of the ARE:

Theorem 1

Consider Problem 1. Let F be an \(N'_d\times N_d\) matrix whose ith row jth column element \(f_{i,j}\) is defined as

$$\begin{aligned} f_{i,j}=x_i{\left( 1\right) }^\top Px_j{\left( 1\right) }+x_i{\left( 0\right) }^\top \left( Q-P\right) x_j{\left( 0\right) }+u_i^\top Ru_j. \end{aligned}$$
(12)

Then, the following condition is necessary for the ARE (6) to hold.

$$\begin{aligned} F=0. \end{aligned}$$
(13)

Proof

We define \(G_1\in {\mathbb {R}}^{n\times n}\) and \(G_2\in {\mathbb {R}}^{m\times n}\) as

$$\begin{aligned} \begin{aligned} G_1=&A^\top PA-P+Q-K^\top \left( R+B^\top PB\right) K,\\ G_2=&B^\top PA-\left( R+B^\top PB\right) K. \end{aligned} \end{aligned}$$
(14)

The ARE (6) is equivalent to the combination of \(G_1=0\) and \(G_2=0\). Let \(i\in \left\{ 1,\ldots ,N'_d\right\}\) and \(j\in \left\{ 1,\ldots ,N_d\right\}\) be arbitrary natural numbers. From the ARE, we obtain

$$\begin{aligned} \begin{aligned} \left[ \begin{array}{*{20}{c}} x_i{\left( 0\right) }\\ {u_i} \end{array}\right] ^\top \left[ \begin{array}{*{20}{c}} G_1&{}G_2^\top \\ G_2&{}0 \end{array}\right] \left[ \begin{array}{*{20}{c}} x_j{\left( 0\right) }\\ {u_j} \end{array}\right] =0. \end{aligned} \end{aligned}$$
(15)

Using the assumption (8) and (9), we can transform the left-hand side of (15) into the following:

$$\begin{aligned}{} & {} \begin{aligned}&\left[ \begin{array}{*{20}{c}} x_i{\left( 0\right) }\\ {u_i} \end{array}\right] ^\top \left[ \begin{array}{*{20}{c}} G_1&{}G_2^\top \\ G_2&{}0 \end{array}\right] \left[ \begin{array}{*{20}{l}} x_j{\left( 0\right) }\\ {u_j} \end{array}\right] \\& =x_i{\left( 0\right) }^\top \left( A^\top PA-P+Q-K^\top \left( R+B^\top PB\right) K\right) x_j{\left( 0\right) }\\&\quad +x_i{\left( 0\right) }^\top \left( A^\top PB-K^\top \left( R+B^\top PB\right) \right) u_j\\ {}& \quad +u_i^\top \left( B^\top PA-\left( R+B^\top PB\right) K\right) x_j{\left( 0\right) }\\ &=\left( Ax_i{\left( 0\right) }+Bu_i\right) ^\top P\left( Ax_j{\left( 0\right) }+Bu_j\right) -u_i^\top B^\top PBu_j\\&\quad -\left( Kx_i{\left( 0\right) }+u_i\right) ^\top \left( R+B^\top PB\right) \left( Kx_j{\left( 0\right) }+u_j\right) \\& \quad +u_i^\top \left( R+B^\top PB\right) u_j+x_i{\left( 0\right) }^\top \left( Q-P\right) x_j{\left( 0\right) }\\ &=f_{i,j}. \end{aligned} \end{aligned}$$
(16)

Therefore, we obtain \(f_{i,j}=0\) from (15) and (16), which proves Theorem 1. \(\square\)

Equation (13) is the estimated linear equation that we propose in this paper and it can be obtained directly from the observation data without system identification. Our method obtains one scalar linear equation of P, Q, and R from a pair of observation data. However, at least one of the paired data must be a transition by a linear feedback input with the given gain K. Equation (13) consists of \(N_dN'_d\) scalar equations obtained in such a manner. Therefore, it is expected that if \(N_d\) and \(N'_d\) are sufficiently large, (13) is equivalent to (6), which is also linear for the matrices P, Q, and R.

Equation (12) is similar to the Bellman equation [20]. Suppose that the ARE (6) holds, that is, \(u{\left( k\right) }=-Kx{\left( k\right) }\) minimizes \(J{\left( u\right) }\). Then, the following Bellman equation holds:

$$\begin{aligned}{} & {} x{\left( k\right) }^\top Px{\left( k\right) }=x{\left( k+1\right) }^\top Px{\left( k+1\right) }\nonumber \\{} & {} \quad +x{\left( k\right) }^\top Qx{\left( k\right) }+x{\left( k\right) }^\top K^\top RKx{\left( k\right) }. \end{aligned}$$
(17)

The equation \(f_{i,j}=0\) is equivalent to the Bellman equation if \(x_i{\left( 0\right) }=x_j{\left( 0\right) }\) and \(u_i=u_j=-Kx_i{\left( 0\right) }\). The novelty of Theorem 1 is that \(f_{i,j}=0\) holds under the weaker condition, that is, only \(u_i=-Kx_i{\left( 0\right) }\). As shown in Appendix, Theorem 1 is also proved from the Bellman equation (17).

The following theorem demonstrates that if the data satisfies the condition required for system identification, our estimation is equivalent to the ARE:

Theorem 2

Consider Problem 1. Suppose that matrices D and \(X'{\left( 0\right) }\) defined in (10) have row full rank. Then, the estimation (13) is equivalent to the ARE (6).

Proof

From Theorem 1, the ARE (6) implies the estimation (13), that is, \(F=0\). As shown in the proof of Theorem 1, matrix F is expressed as follows using the matrices defined in (10) and (14):

$$\begin{aligned} F=\left[ \begin{array}{*{20}{c}} X'{\left( 0\right) }\\ U' \end{array}\right] ^\top \left[ \begin{array}{*{20}{c}} G_1&{}G_2^\top \\ G_2&{}0 \end{array}\right] D, \end{aligned}$$
(18)

Because the matrix D has row full rank, \(F=0\) implies

$$\begin{aligned} \begin{aligned} X'{\left( 0\right) }^\top G_1+U'^\top G_2&=0,\\ X'{\left( 0\right) }^\top G_2^\top&=0. \end{aligned} \end{aligned}$$
(19)

Because \(X'{\left( 0\right) }\) has row full rank, we obtain \(G_1=0\) and \(G_2=0\) from (19), which proves Theorem 2. \(\square\)

The advantage of our method is the data economization that results from having prior information about Q and R. Suppose that some elements of Q and R are known to be zero in advance, and independent ones are fewer than the scalar equations in the ARE (6). Then, there is a possibility that our method can estimate the ARE with fewer data than \(m+n\) required for system identification.

For fixed \(N_d\), our method can provide the largest number of scalar equations when \(N'_d=\min \left\{ n,N_d\right\}\). We use the following lemma to explain the reason:

Lemma 1

Suppose that there exist \(k\in \left\{ 1,\ldots ,N'_d\right\}\) and \(c_i\in {\mathbb {R}}\) \(\left( i\in \left\{ 1,\ldots ,N'_d\right\} \backslash \left\{ k\right\} \right)\) that satisfy

$$\begin{aligned} d_k=\sum _{i=1,i\ne k}^{N'_d}c_id_i, \end{aligned}$$
(20)

where \(d_i=\left[ x_i{\left( 0\right) }^\top \;u_i^\top \right] ^\top\) for any \(i\in \left\{ 1,\ldots ,N_d\right\}\). Then, the following holds for any \(j\in \left\{ 1,\ldots ,N_d\right\}\):

$$\begin{aligned} f_{k,j}= {\left\{ \begin{array}{ll} \displaystyle {\sum _{i=1,i\ne k}^{N'_d}c_if_{i,j}} &{} \left( j\ne k\right) \\ \displaystyle {\sum _{i=1,i\ne k}^{N'_d} \,\, \sum _{j=1,j\ne k}^{N'_d}c_ic_jf_{i,j}} &{} \left( j=k\right) \end{array}\right. }. \end{aligned}$$
(21)

Proof

We can readily prove Lemma 1 using the following derived from (18)

$$\begin{aligned} f_{k,j}=d_k^\top \left[ \begin{array}{*{20}{c}} G_1 &{} G_2^\top \\ G_2 &{} 0 \end{array}\right] d_j\qquad \left( k\in \left\{ 1,\ldots ,N'_d\right\} ,j\in \left\{ 1,\ldots ,N_d\right\} \right) . \end{aligned}$$
(22)

\(\square\)

Lemma 1 means that if data \(d_k\) is the linear combination of other data, the equations obtained from \(d_k\) are also linear combinations of other equations not using \(d_k\). Hence, without noise, such a data as \(d_k\) is meaningless. If \(N'_d>n\), at least one of \(d_1,\ldots ,d_{N'_d}\) is the linear combination of other data because the inputs in those data are obtained from the same gain K. Therefore, \(N'_d\) larger than n reduces data efficiency. From the above and \(f_{i,j}=f_{j,i}\), our method can provide \(\frac{n\left( n+1\right) }{2}+n\left( N_d-n\right)\) equations if \(N_d\ge n\).

For an example of prior information, we consider diagonal Q and R. In this case, the number of the independent elements of P, Q, and R is \(\frac{n\left( n+1\right) }{2}+n+m\). Hence, if \(N_d\) is \(N_{d\mathrm min}{\left( n,m\right) }=n+1+\lceil \frac{m}{n}\rceil\) or larger, we have more equations than the independent elements. Figure 1 compares the numbers \(N_{d\mathrm min}\) and \(n+m\) of data required for our method and system identification, respectively, if Q and R are diagonal. From Fig. 1, our method may estimate the ARE with less data than system identification. Additionally, this tendency becomes stronger as the number m of inputs becomes larger than the number n of states.

Fig. 1
figure 1

Ratio \(\frac{N_{d\mathrm min}}{n+m}\) when \(5\le n\le 200\) and \(5\le m\le 200\). The contour lines are not smooth, but this is not a mistake

Full size image

Remark 1

If the number of data \(N_d\) satisfies \(N_d < n + m\), but the matrix D in (10) has column full rank, we have

$$\begin{aligned} \begin{bmatrix} A&B \end{bmatrix} = X(1) (D^{\top } D)^{-1} D^{\top } + W, \end{aligned}$$
(23)

where \(W \in {\mathbb {R}}^{n \times (n+m)}\) is any matrix that satisfies \(WD = 0\). Because our ARE estimation relies solely on the data D, this suggests that many systems result in the same ARE estimation, if there is some prior knowledge of R and Q. However, in Problem 1, we assume that \(1,\ldots ,N'_d\)th trajectories are optimal, but a system satisfying (23) does not always satisfy this assumption.

In the case of noisy data, we discuss the unbiasedness of the coefficients in (13). The coefficient of kth row lth column element \(q_{k,l}\) of Q in (12) is expressed as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{i,k}{\left( 0\right) }x_{j,l}{\left( 0\right) }+x_{i,l}{\left( 0\right) }x_{j,k}{\left( 0\right) }&{}\left( i\ne j\right) \\ x_{i,k}{\left( 0\right) }x_{i,l}{\left( 0\right) }&{}\left( i=j\right) \end{array}\right. }, \end{aligned}$$
(24)

where \(x_{i,k}{\left( 0\right) }\) is the kth element of \(x_i{\left( 0\right) }\). Suppose that the data is a sum of the true value and zero-mean noise distributed independently for each data. Then, we can readily confirm that if \(i\ne j\), the coefficient (24) of \(q_{k,l}\) in (12) is unbiased, and otherwise, it is biased. This result is also the same for the coefficients of the elements of P and R.

4 Numerical experiment

4.1 Distance between solution spaces

In our experiments, we evaluated the ARE estimation using a distance between the solution spaces of the ARE and estimation. Let \(s\in {\mathbb {R}}^{N_v}\) be a vector generated by independent elements in the matrices P, Q, and R in any fixed order, where \(N_v\) is defined according to the prior information. Because the ARE (6) is linear for s, we can transform (6) into the following equivalent form:

$$\begin{aligned} \Theta s=0, \end{aligned}$$
(25)

where \(\Theta \in {\mathbb {R}}^{N_{\textrm{ARE}}\times N_v}\) is the coefficient matrix and \(N_{\textrm{ARE}}=\frac{n\left( n+1\right) }{2}+mn\). Similarly, the estimation (13) is transformed into the following equivalent form:

$$\begin{aligned} {\hat{\Theta }} s=0, \end{aligned}$$
(26)

where \(\hat{\Theta} \in \mathbb R^{N_\textrm{est}\times N_v}\) is the coefficient matrix and \(N_{\textrm{est}}=N_dN'_d-N'_d\left( N'_d-1\right) /2\). We define the solution spaces S and \({\hat{S}}\) of the ARE (25) and estimation (26) as follows:

$$\begin{aligned} S=\left\{ s\in {\mathbb {R}}^{N_v}\left| \Theta s=0\right. \right\} ,\quad {\hat{S}}=\left\{ s\in {\mathbb {R}}^{N_v}\left| {\hat{\Theta }} s=0\right. \right\} . \end{aligned}$$
(27)

We define the distance between the solution spaces using the approach provided in [21]. Assume that \(\Theta\) and \({\hat{\Theta }}\) have the same rank. Let \(\Pi\), \(\hat{\Pi }\in \mathbb R^{N_v\times N_v}\) be the orthogonal projections to S and \({\hat{S}}\), respectively. The distance between S and \({\hat{S}}\) is defined as follows:

$$\begin{aligned} d{\left( S,\hat{S}\right) }=\left\| \Pi -\hat{\Pi }\right\| _2, \end{aligned}$$
(28)

where \(\left\| \cdot \right\| _2\) is the matrix norm induced by the 2-norm of vectors. Distance \(d{\left( S,\hat{S}\right) }\) is the maximum Euclidian distance between \(\hat{s}\in \hat{S}\) and \(\Pi \hat{s}\in S\) when \(\left\| \hat{s}\right\| _2=1\), as explained by the following equation:

$$\begin{aligned} \begin{aligned} \max _{\hat{s}\in \hat{S},\left\| \hat{s}\right\| _2=1}\left\| {\Pi }\hat{s}-\hat{s}\right\| _2=&\max _{\hat{s}\in \hat{S},\left\| \hat{s}\right\| _2=1}\left\| \left( {\Pi }-{\hat{\Pi }}\right) \hat{s}\right\| _2\\ =&d{\left( S,\hat{S}\right) }. \end{aligned} \end{aligned}$$
(29)

Hence, the distance satisfies \(0\le d{\left( S,{\hat{S}}\right) }\le 1\).

The orthogonal projections \(\Pi\) and \({\hat{\Pi }}\) are obtained from the orthogonal bases of S and \({\hat{S}}\). To obtain these orthogonal bases, we use singular value decompositions of \(\Theta\) and \({\hat{\Theta }}\). In our experiments, we performed the computation using MATLAB 2023a.

4.2 Experiment 1

In this experiment, we confirmed Theorem 2 by solving Problem 1. We set the controllable pair \(\left( A,B\right)\) as follows:

$$\begin{aligned} A=\left[ \begin{array}{*{20}{c}} -0.2&{}-0.4&{}-0.6\\ 0.4&{}-0.7&{}-0.3\\ -1.0&{}-0.8&{}-0.2 \end{array}\right] ,\; B=\left[ \begin{array}{*{20}{c}} 0.1&{}-0.6\\ -0.2&{}0.8\\ 0.4&{}-0.9 \end{array}\right] . \end{aligned}$$
(30)

The ground truth values of Q and R are defined as

$$\begin{aligned} Q=\left[ \begin{array}{*{20}{c}} 0.4&{}-0.2&{}0.7\\ -0.2&{}1.7&{}-0.7\\ 0.7&{}-0.7&{}1.9 \end{array}\right] ,\; R=\left[ \begin{array}{*{20}{c}} 1.7&{}0.4\\ 0.4&{}1.8 \end{array}\right] . \end{aligned}$$
(31)

The optimal gain \(K\in {\mathbb {R}}^{2\times 3}\) is the solution of the LQR problem for the above Q and R. We considered the following \(N_d=n+m\) observation data with \(N'_d=n\) that satisfy the condition of Theorem 2:

$$\begin{aligned} X{\left( 0\right) }=\left[ \begin{array}{*{20}{c}} 0.1&{}0.4&{}0.5&{}-0.4&{}-0.1\\ 0.4&{}0.7&{}1.0&{}0.6&{}0.8\\ -0.4&{}-1.0&{}0.5&{}-0.8&{}-0.4 \end{array}\right] , \end{aligned}$$
(32)
$$\begin{aligned} U=\left[ -K\left[ x_1{\left( 0\right) }\;\cdots \; x_3{\left( 0\right) }\right] \begin{array}{*{20}{c}} 0.0&{}0.1\\ -0.9&{}-0.7 \end{array}\right] . \end{aligned}$$
(33)

Using this setting, each of the ARE (6) and our estimation (13) contained 12 scalar equations for \(N_v=15\) variables, that is, independent elements in the symmetric matrices P, Q, and R.

Figure 2 shows the singular values of \(\Theta\) and \({\hat{\Theta }}\), in descending order, that we computed using the default significant digits. As shown in Fig. 2, there is no zero singular value of \(\Theta\), \(\hat{\Theta }\in \mathbb R^{12\times 15}\). Hence, the ranks of \(\Theta\) and \(\hat{\Theta }\) are 12, and the solution spaces S, \(\hat{S}\subset \mathbb R^{15}\) are three-dimensional subspaces. To investigate the influence of the computational error, we performed the same experiment with various numbers of significant digits. Figure 3 shows the relationship between the distance \(d{\left( S,{\hat{S}}\right) }\) and the number of significant digits. As shown in Fig. 3, the logarithm of the distance decreased in proportion to the number of significant digits. Therefore, we concluded that non-zero \(d{\left( S,{\hat{S}}\right) }\) was caused by the computational error and that our method correctly estimated the ARE.

Fig. 2
figure 2

Singular values of coefficient matrices \(\Theta\) and \({\hat{\Theta }}\) in Experiment 1

Full size image
Fig. 3
figure 3

Relationship between distance \(d{\left( S,{\hat{S}}\right) }\) and number of significant digits in the computation in Experiment 1

Full size image

4.3 Experiment 2

In this experiment, we confirmed that, if Q and R are diagonal, Theorem 1 can estimate the ARE with fewer observation data than system identification. We randomly set the matrices \(A\in {\mathbb {R}}^{100\times 100}\) and \(B\in {\mathbb {R}}^{100\times 50}\) by generating each element from the uniform distribution in \(\left[ -1,1\right]\). After the generation, we confirmed that \(\left( A,B\right)\) is controllable. The given \(K\in {\mathbb {R}}^{50\times 100}\) is the solution of the LQR problem for the diagonal matrices Q and R whose elements were generated from the uniform distribution in \(\left[ 0.01,1\right]\). We used \(N_d=N_{d\mathrm min}=102\) observation data that satisfy (9) for \(N'_d=n=100\). We generated the elements of \(x_{1}{\left( 0\right) },\ldots ,x_{102}{\left( 0\right) }\in {\mathbb {R}}^{100}\) and \(u_{101}\), \(u_{102}\in {\mathbb {R}}^{50}\) from the uniform distribution in \(\left[ -1,1\right]\). The number of used data, 102, is less than \(n+m=150\) required for system identification (11).

Using this setting, the ARE (6) and our estimation (13) contained \(N_{\textrm{ARE}}=\frac{n\left( n+1\right) }{2}+mn=10050\) and \(N_{\textrm{est}}=N_dN'_d-N'_d\left( N'_d-1\right) /2=5250\) scalar equations, respectively. The variables of these scalar equations were \(N_v=\frac{n\left( n+1\right) }{2}+n+m=5200\) independent elements in the symmetric matrix P and diagonal matrices Q and R.

Because the arbitrary-precision arithmetic was too slow to perform for the scale of this experiment, we performed the computation using the default significant digits. We indexed the singular values of \(\Theta \in \mathbb R^{10050\times 5200}\) and \(\hat{\Theta }\in \mathbb R^{5250\times 5200}\) in descending order; Fig. 4 shows the 5180–5200th singular values. From Fig. 4, we assumed that, without computational error, \(\Theta\) and \({\hat{\Theta }}\) each had a zero singular value. Then, the solution spaces S, \({\hat{S}}\subset {\mathbb {R}}^{5200}\) were one-dimensional subspaces, and the distance \(d{\left( S,{\hat{S}}\right) }\) was \(4.3\times 10^{-10}\).

Fig. 4
figure 4

Singular values of coefficient matrices \(\Theta\) and \({\hat{\Theta }}\) in Experiment 2

Full size image

We compared our method with system identification. For system identification, we generated additional data \(x_{103},\ldots ,x_{150}\) and \(u_{103},\ldots ,u_{150}\) in the same manner as \(x_{101}\) and \(u_{101}\). Using the same approach as that for S, we defined the solution space \({\hat{S}}_{\textrm{SI}}\subset {\mathbb {R}}^{N_v}\) of the ARE (6) using A, B, and K identified by (11). Then, the distance \(d{\left( S,{\hat{S}}_{\textrm{SI}}\right) }\) was \(2.8\times 10^{-10}\). Therefore, our method estimated the ARE with the same order of error as system identification using fewer observation data than system identification.

4.4 Experiment 3

In this experiment, we compared our method and system identification under practical conditions: a single noisy and sequential data and sparse but not diagonal Q and R. We set the matrices \(A\in {\mathbb {R}}^{40\times 40}\) and \(B\in {\mathbb {R}}^{40\times 20}\) in the same manner as Experiment 2. The control gain \(K\in {\mathbb {R}}^{20\times 40}\) is the solution of the LQR problem for the sparse matrices Q and R. We performed three operations to generate Q and R. First, we generated matrices \(M_Q\in {\mathbb {R}}^{40\times 40}\) and \(M_R\in {\mathbb {R}}^{20\times 20}\) in the same manner as A and set \(Q:=M_Q^\top M_Q\) and \(R:=M_R^\top M_R\). Second, we randomly set 800 non-diagonal elements of Q to 0 to make it sparse while maintaining symmetry. Similarly, we set 200 elements of R to 0. Finally, add the product of a constant and the identity matrix to Q and R so that the maximum eigenvalues are 10 times as large as the minimum ones, respectively.

To generate data, we used the following system:

$$\begin{aligned} \begin{aligned} x^*{\left( k+1\right) }=&Ax^*{\left( k\right) }+Bu^*{\left( k\right) },\\ u^*{\left( k\right) }=&-Kx^*{\left( k\right) }+v{\left( k\right) }, \end{aligned} \end{aligned}$$
(34)

where \(x^*{\left( k\right) }\in {{\mathbb {R}}}^n\) and \(u^*{\left( k\right) }\in {{\mathbb {R}}}^m\) are the state and input at time \(k\in {\mathbb {Z}}_+\), respectively. If \(\left\| x^*{\left( k\right) }\right\| _2\le 1\), the vector \(v{\left( k\right) }\in {{\mathbb {R}}}^n\) with norm 0.2 is the product of a scalar constant and a random vector whose elements follow a uniform distribution in \(\left[ -1,1\right]\). Otherwise, \(v{\left( k\right) }=0\). Note that v(k) is not a noise: it is an input signal to be added intentionally to make the trajectory data rich in information by making the input different from the optimal feedback input. We ran the system (34) through \(N_d=200\) time steps with a random initial state \(x^*{\left( 0\right) }\) with norm 1 and obtained data as

$$\begin{aligned} \begin{aligned} x_k{\left( 0\right) }=&x^*{\left( k-1\right) }+\varepsilon _{\textrm{state}}{\left( k-1\right) },\\ u_k=&u^*{\left( k-1\right) }+\varepsilon _{\textrm{input}}{\left( k-1\right) },\\ x_k{\left( 1\right) }=&x^*{\left( k\right) }+\varepsilon _{\textrm{state}}{\left( k\right) }, \end{aligned} \end{aligned}$$
(35)

where \(\varepsilon _{\textrm{state}}\in {{\mathbb {R}}}^n\) and \(\varepsilon _{\textrm{input}}\in {{\mathbb {R}}}^m\) are the observation noises whose elements follow a normal distribution with a mean 0 and variance \(\sigma ^2\). We explain the value of \(\sigma ^2\) later. Note that, although \(N_d\) can be arbitrary as long as \(N_d \ge n+m = 60\), we used a larger \(N_d\) because the data is contaminated with noise. Throughout the simulation, \(v{\left( k\right) }=0\) holds 121 times. Hence, \(N'_d=121\). We sorted the data \(\left( x_i{\left( 0\right) },u_i,x_i{\left( 1\right) }\right)\) \(\left( i\in \left\{ 1,\ldots ,N_d\right\} \right)\) so that (9) holds if noise does not exist.

Under the above condition, the ARE (6) and our estimation (13) contained \(N_{\textrm{ARE}}=\frac{n\left( n+1\right) }{2}+mn=1620\) and \(N_{\textrm{est}}=N_dN'_d-N'_d\left( N'_d-1\right) /2=16940\) scalar equations, respectively. The variables of these equations were \(N_v=n\left( n+1\right) +\frac{m\left( m+1\right) }{2}-500=1350\) independent elements in the symmetric matrix P and sparse matrices Q and R.

We indexed the singular values of \(\Theta \in \mathbb R^{1620\times 1350}\) and \(\hat{\Theta }\in \mathbb R^{16940\times 1350}\) in descending order. Figure 5 shows the 1330–1350th singular values when \(\sigma ^2=10^{-8}\). Although there is no zero singular value due to noise, the last singular value is noticeably small as shown in Fig. 5. Hence, we can conclude that the solution spaces S, \({\hat{S}}\subset {\mathbb {R}}^{1350}\) were one-dimensional subspaces.

Fig. 5
figure 5

Singular values of coefficient matrices \(\Theta\) and \({\hat{\Theta }}\) in Experiment 3

Full size image

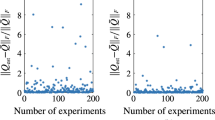
We conducted experiments with different noise variance \(\sigma ^2\) from \(10^{-6}\) to \(10^{-16}\). Also, the noise seed differs for each experiment, but the other seeds used to determine (A, B), the initial state, and (Q, R) are fixed. Figure 6 shows the relationship between the noise variance \(\sigma ^2\) and distances \(d{\left( S,{\hat{S}}\right) }\) and \(d{\left( S,{\hat{S}}_{\textrm{SI}}\right) }\). As shown in Fig. 6, our method outperformed system identification in almost all experiments. In the experiments of variances from \(10^{-8}\) to \(10^{-16}\), the ratio of \(d{\left( S,{\hat{S}}\right) }\) to \(d{\left( S,{\hat{S}}_{\textrm{SI}}\right) }\) is approximately constant, and the average ratio is 0.17. Because the distance is bounded from above by 1, as is clear from (29), we conclude that the estimations using both methods failed with a larger noise variance than \(10^{-8}\), which have distance values close to 1.

Fig. 6
figure 6

Relationship between the noise variance \(\sigma ^2\) and distances \(d{\left( S,{\hat{S}}\right) }\) (red “\(\times\)”) and \(d{\left( S,{\hat{S}}_{\textrm{SI}}\right) }\) (blue “\(+\)”) in Experiment 3

Full size image

4.5 Experiment 4

In the case where the discrete-time system is a discretization of a continuous-time system, our previous method [18] can also be used to solve the problem. In this experiment, we compare the performance of the proposed method and our previous method.

We set the controllable pair (A, B) as follows:

$$\begin{aligned} A = \begin{bmatrix} 1.0000 &{} 0.0010 &{} 0.0000 \\ 0.0000 &{} 1.0000 &{} 0.0010 \\ 0.0000 &{} -0.0001 &{} 0.9993 \end{bmatrix}, B = \begin{bmatrix} 0.0000 &{} 1.0000 \\ 0.0005 &{} 0.0000 \\ 0.9997 &{} 0.0000 \end{bmatrix} \times 10^{-3}, \end{aligned}$$
(36)

which is obtained by discretizing the following continuous-time system with a sampling period of \(10^{-3}\) s:

$$\begin{aligned} \dot{z} = \begin{bmatrix} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ -0.01 &{} -0.12 &{} -0.7 \end{bmatrix} z + \begin{bmatrix} 0 &{} 1 \\ 0 &{} 0 \\ 1 &{} 0 \end{bmatrix}u. \end{aligned}$$
(37)

The given gain \(K\in {\mathbb {R}}^{2\times 3}\) is the solution to the LQR problem for the following Q and R:

$$\begin{aligned} Q = \begin{bmatrix} 1.2 &{} 0.0 &{} 0.3 \\ 0.0 &{} 0.1 &{} 0.1 \\ 0.3 &{} 0.1 &{} 1.2 \end{bmatrix}, R = \begin{bmatrix} 2.1 &{} -0.9 \\ -0.9 &{} 0.5 \end{bmatrix}. \end{aligned}$$
(38)

The data was prepared in the same way as in Sect. 4.2 using the following \(N_d=n + m\) observation data with \(N'_d=n\) that satisfies the condition of Theorem 2:

$$\begin{aligned} X(0)&= \begin{bmatrix} -0.2 &{} -0.4 &{} -0.6 &{} 0.1 &{} -0.6 \\ 0.4 &{} -0.7 &{} -0.3 &{} -0.2 &{} 0.8 \\ -1.0 &{} -0.8 &{} -0.2 &{} 0.4 &{} -0.9 \end{bmatrix},\end{aligned}$$
(39)
$$\begin{aligned} U&= \left[ - K \begin{bmatrix} x_1(0)\;\cdots \; x_3(0) \end{bmatrix} \begin{array}{*{20}{c}} 0.9 &{} 0.4\\ -0.4 &{} -0.8 \end{array}\right] . \end{aligned}$$
(40)

Some integration needed to use the previous method [18] was performed by using the trapezoidal rule.

Let the solution space \(\hat{S}\) for the previous method be \(\hat{S}_{\text {prev}}\). The distances \(d\left( S, \hat{S} \right)\) and \(d \left( S, \hat{S}_{\text {previous}} \right)\) were \(1.36 \times 10^{-12}\) and \(4.85 \times 10^{-4}\), respectively. This result shows the superiority of the proposed method in the case where the data is discretized.

5 Discussion

The purpose of our method is to obtain the ARE from the state and the input trajectories without identifying the system model. The ARE is important to solve ILQR problems [5, 7, 11, 12]. From the result of Experiment 1, it is clear that this purpose is achieved. Moreover, Experiment 2 shows that, if there is some additional prior information other than the trajectory data, the estimation of ARE can be obtained with less data than is required for system identification. Also, Experiment 3 suggests that the estimate of the ARE by our method can be more accurate than that using the identified system model. Although most existing studies on ILQR assume that the system model is known in advance by system identification [5, 7, 11,12,13,14,15], our results suggest that the system identification is not essential and will better be avoided.

The present study is, in some sense, a discrete version of our previous study [18], in which we assume a continuous time system. In most cases where continuous systems are discretized because of the discrete observation, the method in [18] is also applicable by using the trapezoidal rule to approximate the integral. However, Experiment 4 clearly illustrates the superiority of the proposed method in the case where only the discrete-time observation is available. Because almost all systems only admit discrete-time observation, this result is essential in practice.

Although Experiment 3 shows that the proposed method is less sensitive to noise than the method using system identification, the effect of noise is still to be discussed. Especially, the question of whether it is unbiased and consistent is an important question to be discussed.

6 Conclusions

In this paper, we proposed a method to estimate the ARE with respect to an unknown discrete-time system from the input and state observation data. Our method transforms the ARE into a form calculated without the system model by multiplying the observation data on both sides. We proved that our estimated equation is equivalent to the ARE if the data are sufficient for system identification. The main feature of our method is the direct estimation of the ARE without identifying the system. This feature enables us to economize the observation data using prior information about the objective function. We conducted a numerical experiment that demonstrated that our method requires less data than system identification if the prior information is sufficient.