1 Introduction and motivation

Air pollution harms human health and the environment and represents the leading environmental risk factor, globally responsible for 6.7 million deaths in 2019 [1]. Despite the significant reduction in air pollutant emissions observed in Europe over the last 3 decades, around 300,000 premature deaths per year are still attributed to air pollution [2].

With the European Green Deal [3], the European Commission (EC) decided to update and improve the European Air Quality standards, set in the 2008 Air Quality Directive [4] aligning them to the new World Health Organization recommendations, revised in September 2021 [5], and the EC published in October 2022 the new proposal for the revision of the Air Quality Directive [6].

The evaluation of air quality is of great significance in the protection of both human health and the environment. Various resources are available, ranging from monitoring stations to complex models and satellite data, but also Machine Learning (ML) [7] and Data Assimilation (DA) [8] algorithms.

In our work, we used modelled and observed data combined with data assimilation methods to create a robust system capable of making more accurate and stable predictions about the levels of ambient air pollution. The air pollutant modelled data were elaborated with the Atmospheric Modelling System-Model to support the International Negotiation on atmospheric pollution on a National Italian level (AMS-MINNI) producing a data set of the observed and modelled concentrations of three air pollutants (nitrogen dioxide—NO\(_2\), ozone—O\(_3\) and particulate matter with a diameter of 10 \(\upmu\)m or less—PM10) in Italy from the years 2003–2010 [9,10,11].

AMS-MINNI has the limitation to be computationally very expensive when the spatial resolution becomes too fine. Then the necessity to develop a faster model which would be able to provide similar accuracy in the results but with shorter execution time.

To accurately replicate the air pollution tendencies in Italy elaborated by AMS-MINNI, the long short-term memory architecture neural networks were used, and our modelled values were assimilated with the observations using the Optimal Interpolation (OI) [8] data assimilation method. Because of the vast amount of data used (the data set has around 6 million instances), parallelism methods were tested and used.

An in-depth overview of the use of recurrent neural networks and data assimilation in air quality analysis is also provided as the basis of the theoretical knowledge needed for these fields. The main objective of our work was to build a data-driven modelling perspective to forecast more accurate air quality data from observed and simulated values by introducing a novel data assimilation algorithm called Dynamic Neural Assimilation (DyNA),, which is created using a single Long Short Term Memory (LSTM) network [12]. We then analysed the speed and accuracy advantages of DyNA over the other data assimilation methods. Furthermore, data parallelism on high-performance computing architectures was also tested to speed up our model training and efficiently search the hyperparameter space.

The aim of our paper is not to replace AMS-MINNI or to build a meta-model like the existing GAINS [13] and SHERPA [14]. The idea is to create a state-of-the-art system for air quality analysis using physics-informed recurrent neural networks to elaborate faster simulations than AMS-MINNI so that new perspectives could be explored and provided also for air pollution planning.

The final part of this work was devoted to a correlation analysis of air quality data and industrial air pollution data. Industrial air pollution is considered one of the main sources of outdoor air pollution [2] and the effects of heavy industries around human habitats have been associated with health problems such as decreased lung function [15]. We analysed the impact of industry on ambient air pollution in specific places where we can monitor pollution with sensors. We compared modelled and observed data with the number of industrial companies in the region.

The code implementing our DyNA system is available at https://github.com/DL-WG/Breathe-in-Breathe-out.

In this work, we have successfully created and tested a system for air quality analysis using a physics-informed recurrent neural network that can be used and validated in a different context and with different air pollutants. Future developments are foreseen to improve our system with the inclusion of physical equations into the loss functions. Moreover, if more computational resources are available, more sophisticated data parallelism and domain decomposition methods could be implemented.

This paper is structured as follows: Sect. 2 discusses similar work and explains our contribution, Sect. 3 provides a more detailed description of our main system called DyNA with fine tuning. In Sect. 4, we talk about the data used in our work and Sect. 5 describes the results we achieved during our experiments. The paper ends with Conclusions and future works.

2 Related work and contribution

Different studies have been conducted to analyse air pollution trends using machine learning methods, such as feed-forward Neural Network (NN), logistic regression, decision trees, and other models [16,17,18]. However, since predicting air pollution is usually a time series forecast problem, Recurrent Neural Network (RNN) and specifically LSTM [19] became quite popularly used architectures for this sort of task. Jiao et al. [20] proposed a multivariate LSTM model for predicting Air Quality Index (AQI) based on 9 different parameters which include the pollutants we are analysing in our work, PM10, NO\(_2\) and O\(_3\). Pardo et al. [21] successfully used LSTM to forecast hourly levels of NO\(_2\) from historical air quality and meteorological data, and Liu et al. [22] combined discrete wavelet transform with LSTM to predict NO\(_2\) concentration based on 5 other pollutants and meteorological data.

A way to make ML models more accurate and reliable is to ingest new data as soon as these data become available. An efficient method that can be coupled to ML models or any other dynamic system of this scope is DA [23,24,25,26,27] used not only for air pollution forecasts, but also for other air quality related tasks, such as sensor placement [28].

In our work, we integrated RNN [29] and DA methods to get the advantages of both fields and obtain accurate results. Approaches combining RNN and DA have been already explored in the literature. For example, Song et al. [30] analysed the possibility to combine LSTM and Kalman filter (KF) by predicting carbon monoxide (CO), benzene (C\(_6\)H\(_6\)) and NO\(_2\) concentrations in the air. More general ways of integrating DA and ML have been presented by Buizza et al. [31], where the authors introduced a data learning approach for several different real-world applications, including air pollution. To speed up the DA process, other approaches have been proposed by Arcucci et al. [32] where the authors implemented an integration of ML and DA via a coupled LSTM called Neural Assimilation (NA). The authors have tested the NA model on a one-dimensional test case for a medical application and it has been used only for the assimilation of existing historical data. When working with dynamic systems such as the ones used to predict air pollution tendencies, the main need is to make forecasting on future time steps. In this paper, we introduce DyNA, a system which is an extension of NA [32], able to ingest historical data while training an LSTM network and, able to make predictions of future time steps. Different studies emphasised the need to avoid the forecast/analysis cycle [8] used in statistical DA. As previously introduced in the NA method [32], our proposed DyNA does not follow the two-step forecast/analysis as it develops neural networks that can fully simulate the entire DA process. There is one very important novelty when comparing DyNA and NA methods. The DyNA model is created using a single recurrent neural network, which is a big difference compared to the NA model [32] that uses two coupled recurrent neural networks. This kind of modification requires less memory and computing power, as fewer neurons need to be trained and fewer parameters need to be used. For the same reasons, the training time is also significantly reduced.

Another issue with ML models is the computational cost when training the network. To face this problem, we have embraced data parallelism on high-performance computing architectures to speed up our model training and efficiently search the hyperparameter space.

We trained and tested the system on real data provided by air quality monitoring stations located in Italy from the European Environment Agency (EEA) and simulated results derived from the air quality modelling system AMS-MINNI (see Sect. 4).

Furthermore, we have implemented a comparison of the concentration of two air pollutants with the number of industries and analysed the correlation between these values in different Italian regions. We have combined all the components mentioned above into a single state-of-the-art system created on the basis of physics-informed RNNs and used it to link air quality and industrial data.

3 Dynamic Neural Assimilation with fine tuning

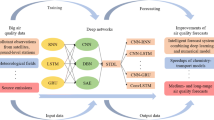
In this section, we give an overview of the full system that we developed and used for air quality analysis. The system, described in Fig. 1, consists of three main parts. The first part is the forecasting system based on a novel data-driven model called DyNA. DyNA not only assimilates the modelled and observed values from the past but also predicts into the future. DyNA is trained on simulated and observed data and forecasts values of air quality (see “Forecasting System” in Fig. 1). The forecast can be adjusted by a fine-tuning step based on data assimilation which ingests new observations in the system (see “Data Assimilation” in Fig. 1). Finally, the results can be compared with the number of industrial companies to analyse potential correlations (see “Analysis” in Fig. 1).

Fig. 1
figure 1

Scheme of the Dynamic Neural Assimilation system with fine tuning and correlation analysis

Full size image

3.1 Dynamic Neural Assimilation

Dynamic Neural Assimilation is a model that takes a window of modelled and observed values as input. It then forecasts the next value in time to ensure it falls between the modelled value at the next time step and the observed value at the next step.

Let us assume to have a set of states of a dynamic model \(x_k\), \(k \in \{1, 2, \dots , m\}\) at some subsequent time steps \(\{t_1,\,t_2,\dots ,t_m\}\). Let’s assume we also have the observed states at the same points in time \(\{{\bar{o}}_1, {\bar{o}}_2, \dots , {\bar{o}}_m\}\).

DyNA mainly consists of two steps: data pre-processing and model training.


Pre-processing


For the pre-processing, we standardise our data, but since we want to keep the initial gaps between observed and modelled values in our data, we cannot standardise these two features separately [32] but we standardise both modelled and observed values using the same parameters:

$$\begin{aligned} {\hat{x}}_k&= \frac{x_k - {\bar{x}}}{\sigma },\;\;for\; each\; k \in \{1, 2, \dots , m\} \end{aligned}$$
(1)
$$\begin{aligned} {\hat{o}}_k&= \frac{{\bar{o}}_k - {\bar{x}}}{\sigma },\;\;for\;each\; k \in \{1, 2, \dots , m\} \end{aligned}$$
(2)

where \({\bar{x}} = \frac{1}{m} \sum _{k=1}^m x_k\), \(\sigma = \sqrt{\frac{1}{m} \sum _{k=1}^m (x_k-{\bar{x}})^2}\), \(\{{\bar{o}}_1, {\bar{o}}_2, \dots , {\bar{o}}_m\}\) are initial observed values, \(\{{x}_1, {x}_2, \dots , {x}_m\}\) are inital modelled values, \(\{{\hat{o}}_1, {\hat{o}}_2, \dots , {\hat{o}}_m\}\) are the pre-processed observed values and \(\{{\hat{x}}_1, {\hat{x}}_2, \dots , {\hat{x}}_m\}\) are the pre-processed modelled values. After normalisation, data are ready to train our DyNA model based on RNN.


Model training


DyNA model can be seen as an extension of an LSTM neural network model to the case of multiple inputs since it takes observations as an input together with the modelled values. At each time step, DyNA cell takes three pieces of data – hidden state \(h_k\) responsible for the short-term memory, long-term memory state \(c_k\) and current inputs \({\hat{x}}_k\) and \({\hat{o}}_k\). This information then goes through three different gates [19] where it gets decided what information needs to be kept and passed further as described in Eqs. (3)–(8):

$$\begin{aligned} i_k&= \sigma (W_{xi}^T {\hat{x}}_k + W_{{\hat{o}}i}^T {\hat{o}}_k + W_{hi}^T h_{k} + b_i) \end{aligned}$$
(3)
$$\begin{aligned} f_k&= \sigma (W_{xf}^T {\hat{x}}_k + W_{{\hat{o}}f}^T {\hat{o}}_k + W_{hf}^T h_{k} + b_f) \end{aligned}$$
(4)
$$\begin{aligned} o_k &= \sigma (W_{xo}^T {\hat{x}}_k + W_{{\hat{o}}o}^T {\hat{o}}_k + W_{ho}^T h_{k} + b_o) \end{aligned}$$
(5)
$$\begin{aligned} g_k &= tanh(W_{xg}^T {\hat{x}}_k + W_{{\hat{o}}g}^T {\hat{o}}_k + W_{hg}^T h_{k} + b_g) \end{aligned}$$
(6)
$$\begin{aligned} c_{k+1} &= f_k c_{k} + i_k g_k \end{aligned}$$
(7)
$$\begin{aligned} h_{k+1} &= o_k tanh(c_{k+1}) \end{aligned}$$
(8)

where \(W_{xi}\), \(W_{xf}\), \(W_{xo}\), \(W_{{\bar{o}}g}\), \(W_{{\bar{o}}i}\), \(W_{{\bar{o}}f}\), \(W_{{\bar{o}}o}\) and \(W_{{\bar{o}}g}\) are weight matrices connecting current input with different gates, \(W_{hi}\), \(W_{hf}\), \(W_{ho}\) and \(W_{hg}\) are weight matrices connecting hidden state with different gates and \(b_i\), \(b_f\), \(b_o\) and \(b_g\) are bias vectors [19].

The DyNA model takes into account information from the modelled and observed values at once. Compared to a standard LSTM, in the DyNA loss function we are calculating the mean squared error metric, but our single output is weighted and compared to two different values at once. Our loss function J [12], takes into account both modelled and observed values as it is defined as follows:

$$\begin{aligned} J = \frac{1}{m}\sum _{k=1}^{m}(\alpha ({\hat{o}}_k - h_{k})^2 + (1-\alpha )({\hat{x}}_k - h_{k})^2) \end{aligned}$$
(9)

This way we force the model to learn how to predict the next value to be somewhere between modelled and observed values. We have added parameter \(\alpha\), such that \(0\le \alpha \le 1\), which denotes how confident we are in our observations: if we think that observations should be fully trusted, then we put \(\alpha = 1\) and our model will try to replicate the observed values. If we make \(\alpha\) to be equal to 0, then we say that we do not trust observations at all and we only try to model the simulated values [8].

As better detailed in Sect. 5.1, a hyperparameter search is needed for each model, which required a vast amount of resources. Although this component is not directly included in our air pollution analysis pipeline shown in Fig. 1, it is still an essential part of our work. We have implemented a hyperparameter search model using the Single-program-multiple-data paradigm [33] by running a separate process for the data of every monitoring station. To find the optimal set of hyperparameters, we have used the Hyperband [34] hyperparameter optimisation approach. After running such search for some specific amount of time or iterations based on the available resources, the hyperparameters that yielded the most accurate results were chosen for the final model. After the DyNA network is trained, the model is ready to use.

3.2 Fine tuning via Optimal Interpolation

When new observations become available, the DyNA system can be fine-tuned with these new observations by using OI. Given newly observed data \(y_{k+1}\), OI combines \(y_{k+1}\) and \(h_{k+1}\) to create a new state \(x^a_{k+1}\) and use it for the next forecast \(h_{k+2}\). In DA models, such as OI, we always assume data coming with an error: \(y_{k+1}=x^{TRUE}_{k+1}+e_y\) and \(h_{k+1}=x_{k+1}^{TRUE}+e_x\), where \(e_y\) and \(e_x\) represent the observation and the modelling errors respectively. They are assumed to be independent, white-noise processes with normal probability distributions [8]

$$\begin{aligned} e_y\sim {\mathcal {N}} (0,R), \quad e_x\sim {\mathcal {N}} (0,B) \end{aligned}$$

where R and B are the observation and model error covariance matrices respectively and I is the identity matrix:

$$\begin{aligned} { R}: =\sigma _0^2 { I}, \end{aligned}$$
(10)

with \(0\le \sigma _0^2\le 1\) (i.e. assuming high trust in the observations [8, 35]) and

$$\begin{aligned} { B}= { V} { V}^T \end{aligned}$$
(11)

The adjusted (or assimilated) state is computed via the normal equations [8]:

$$\begin{aligned} x^a_{k+1}=h_{k+1}+K_{k+1}(y_{k+1}-h_{k+1}) \end{aligned}$$
(12)

where \(K_{k+1}=B_{k+1}(B_{k+1}+R_{k+1})^{-1}\) is called the Kalman gain [8, 35].

3.3 Correlation analysis

As shown in the previous sections, the DyNA model can be used to predict levels of air pollution and it can be improved by assimilating observations as soon as they become available using OI. The air pollution concentrations are then compared to the number of industries in each region to find any relation between these two measurements. The correlation was computed by calculating the Pearson correlation coefficient [36].

$$\begin{aligned} r_{xy}&= \frac{\sum _{i=1}^n(h_i - {\bar{h}})(z_i - {\bar{z}})}{\sqrt{\sum _{i=1}^n(h_i - {\bar{h}})^2}\sqrt{\sum _{i=1}^n(z_i - {\bar{z}}})^2} \end{aligned}$$
(13)

where \(\{h_1, h_2, \dots , h_n\}\) still denotes the DyNA predicted and fine-tuned air quality concentrations and \(\{z_1, z_2, \dots , z_n\}\) denote the number of industries in selected regions, n denotes the number of instances in each of our data sets and \({\bar{h}}\) and \({\bar{z}}\) are the average values of each of these sets:

$$\begin{aligned} {\bar{h}} = \frac{1}{n} \sum _{i=1}^n h_i,\;\;\;\;{\bar{z}}&= \frac{1}{n} \sum _{i=1}^n z_i \end{aligned}$$

In Sect. 5.3, we analyse the correlation between the air pollution concentrations in 2007, 2010 and 2013 in Italy and the number of industries in particular Italian regions.

4 Data

As mentioned previously, we used hourly observed and modelled concentrations of different air pollutants in Italy. The concentrations analysed in our work were taken from D’Elia et al. [9] and are downloadable from the following link http://airqualitymodels.enea.it/.

The pollutants considered are NO2, PM10 and O3 due to their large monitoring coverage in the period of interest and their exceedances in limit values that are not observed for SO2. Particulate matter with diameter less than 2.5 \(\upmu\)m (PM2.5) could not be included in the analysis, as the data coverage from monitoring networks started in 2007.

4.1 Data structure

Both observed and modelled data were used. Observations derive from the European Environment Agency (EEA) that gathers hourly data about the ambient air pollution levels from each European country annually as required by the European Commission’s decision [37]. In our work, data from the years 2003 to 2010 and the year 2013 were collected. The air pollution data for the period 2003–2010 were elaborated by the air quality modelling system AMS-MINNI [38]. The choice of the period to investigate was determined by the availability of coherent model results that have the same model setup for the years 2003 to 2010. More specifically, in the following years, AMS-MINNI simulations adopted a different setup (spatial domain, chemical mechanism, boundary conditions), that clearly affects time series homogeneity. AMS-MINNI elaborates air quality fields based on the results of different models: an emission processor model, a meteorological prognostic model, a meteorological diagnostic processor, and a chemical transport model [9]. Each value of observed and modelled concentration was given at a specific station together with station coordinates and some other specific metadata, such as station altitude above sea level or the name of the Italian region the station belonged to. The use of data from AMS-MINNI, which is developed for country level simulations, brings in a spatial generality aspect. Observed data from monitoring stations, as described in the next section, will bring in specific details on area levels.

4.2 Air quality station selection

The air quality monitoring stations in our study were selected based on their type, zone, and percentage of valid data. Among the different stations, to test our model, we decided to choose an air quality monitoring station per region to cover different features (i.e. different orography, meteorology, emissions and population density). Moreover, only valid stations with both NO2 and O3 data were considered. PM10 data was collected as daily values, and could not be properly combined with our hourly predictions and therefore we decided to focus on the other two pollutants. The result of our selection is summarised in Table 1 and Fig. 2.

Fig. 2
figure 2

Map showing locations of the selected monitoring stations

Full size image
Table 1 Final list of valid air quality stations chosen from [9] for our analysis
Full size table

4.3 Industrial data

The Italian National Institute of Statistics (Istat) publishes yearly statistics about the size and structure of enterprise groups across Italy. Since we were searching for the relations between industry and the levels of air pollution, we have extracted the number of companies belonging to the industrial sector and the number of people working for them grouped by region. We have chosen to compare 3 years of data: 2007 [39], the year when the proposal for the Directive on industrial emissions was adopted by the EC, 2010 [40], the year when the Directive came into force, and 2013 [41], the year by which the Directive had to be transposed by all the Member States.

4.4 Data pre-processing

We filled in the missing values (about 8% of our data) with the mean value of the day. In case the data were missing for the full day and therefore the mean of the day could not be found, we then imputed the missing information with the value from the previous 24 h. Moreover, the problem of missing data was also mitigated with the data assimilation we implemented in our system. In fact, data assimilation integrates data from sensors in the predictive model and this helps to reduce the bias. It has been used for uncertainty minimization in several applications and we have seen it is very effective also for air quality applications [26, 27].

Fig. 3
figure 3

Fast Fourier transform (FFT) graph of the modelled concentrations of NO\(_2\) in Motta Visconti monitoring station

Full size image

We have also included a feature engineering step to our data pre-processing routine which would capture the periodicity in our data and which was shown to improve different machine learning model predictions [42]. The Fast Fourier Transform (FFT, [43]) allowed us to sensibly see the repetition intervals in our data (see Fig. 3 as an example) and therefore we have decided to add four features to each of our data points representing daily and yearly seasonality:

$$\begin{aligned} day\_cos&= \cos \left( \frac{hour\,of\,the\,point*2*\pi }{24}\right) , \\ day\_sin&= \sin \left( \frac{hour\,of\,the\,point*2*\pi }{24}\right) , \\ year\_cos&= \cos \left( \frac{timestamp\,of\,the\,point\,in\,seconds*2*\pi }{one\,year\,in\,seconds}\right) , \\ year\_sin&= \sin \left( \frac{timestamp\,of\,the\,point\,in\,seconds*2*\pi }{one\,year\,in\,seconds}\right) \end{aligned}$$

We have also standardised our data to tackle the saturation problem that LSTM often tends to suffer from [19].

5 Experiments and results

In this section, we analyse the performance of the system described in Sect. 3 on the air pollution data introduced in Sect. 4, i.e. simulations data from AMS-MINNI and observations from monitoring stations. In case historical data from monitoring stations are not available, DyNA can still be trained with AMS-MINNI data only, and fine tuned with OI after, as soon as new observations come available. In this case, DyNA is trained as a standard LSTM [19]. In the following sections, we will denote as LSTM a DyNA system where the historical observed data were not available. We test and compare DyNA with LSTM. We provide details about the training configuration, the accuracy of the DyNA model and the effect of the fine tuning via OI. We also show values of execution times and we discuss the analysis of the correlation with the number of industrial companies.

5.1 Model configuration

One of the first steps in the implementation of DyNA is the selection of \(\alpha\) in the loss function Eq. 9. Figure 4 demonstrates how DyNA predictions change based on different choices of \(\alpha\). In our work, we decided to trust observations and modelled values equally and therefore used \(\alpha = 0.5\).

Fig. 4
figure 4

Example of DyNA predictions with different \(\alpha\) parameter values. The x-axis denotes date and time and the y-axis denotes O\(_3\) air pollution concentration in \(\upmu\)g/m\(^3\)

Full size image

With the selection of \(\alpha\) settled, our focus shifted to the model training phase. Our air pollution data was sequential and for this reason, we did not shuffle them before training. We made the split into training, validation, and test data based on the date: years 2003–2008 were used for the training data (75% of the data), the year 2009 was used as the validation set (12.5% of the data), and the year 2010 was used for the testing (12.5% of the data).

In order to prevent our model from overfitting the training data and to control how many epochs are needed for our training, we have applied Early stopping and L2 Regularization [44]. We used Adam [45] as an optimisation algorithm for the training. It is an extended version of a stochastic gradient descent that uses adaptive learning rates: it assigns different learning rates to different weights of the neural network and then uses the first and second moments of the gradient to update these learning rates. Choices about the main hyperparameters were made based on extensive hyperparameter optimisation. Hyperparameter search was conducted using the KerasTuner framework: we trained possible models on our training set and evaluated their performance on our validation set. The final hyperparameter search space looked as follows:

  • input sequence length: \(\{1, 4, \dots , 25\}\) hours

  • number of neurons in the input layer and last hidden layer: \(\{5, 10, \dots , 60\}\)

  • number of hidden layers: \(\{1, 2, 3\}\)

  • number of neurons per hidden layer \(\{10, 15, \dots , 60\}\)

  • learning rate: \([10^{-4}, 10^{-2}]\)

We have mainly used Hyperband random search optimisation to find optimal hyperparameters. For each air quality station, we first chose the length of the input sequence and ran a search for the remaining hyperparameters. We ran 20 experiments for 20 epochs each to find the most accurate configuration for this station and input size combination. Since we had 9 options for the input sequence length (from \(\{1, 4, \dots , 25\}\) list), we had to create 180 models to search the parameter space of one station, which was already costly in terms of time and computational power. Having 9 monitoring stations in total (5 for NO\(_2\) and 4 for O\(_3\) as shown in Table 1) and needing two models (DyNA and regular LSTM) for each station made it impossible to search the parameter space in a sequential manner.

Table 2 Hyperparameter search durations
Full size table

We dealt with this challenge by parallelising our process on a high-performance computing architecture. Table 2 shows the speed-up achieved in the optimisation process. Running search processes in parallel was from 10.8 (O\(_3\) LSTM) to 20.6 (NO\(_2\) DyNA) times faster than what it would have taken to search the space sequentially. Since all four searches were independent as well, we were also able to execute them in parallel, and the whole search took only as long as the longest single search, 10.6 h, compared to the total of almost 550 h that it would have taken to search it one after another.

The hyperparameter search finished with the results that can be seen in Table 3.

Table 3 Optimal hyperparameters
Full size table

We can notice that DyNA required slightly more complex models, as it yielded better results when having more layers in the neural network than the respective models implemented to replicate AMS-MINNI modelled data. Hyperparameter optimisation showed that a longer input size results in better accuracy; only two models (LSTM model for Aosta Valley’s and DyNA for Lombardy’s NO\(_2\) level predictions with the input sizes of 7 and 4 h, respectively) reached the most accurate results when having an input sequence length of fewer than 10 h. However, the input size still could not be too large based on our search – only models for Lombardy’s O\(_3\) level predictions yielded the best results with a sequence length greater than 24 h.

5.2 Model evaluation: accuracy and execution time

In order to evaluate the accuracy with respect to the real available data, we used the mean squared assimilation error with respect to the observed values (MSE\(^{DyNA}\)) and compared it to the mean squared forecasting error with respect to the observed values (MSE\(^F\)) as defined in [32].

$$\begin{aligned}&MSE^{DyNA} = \frac{\sqrt{\sum _{i=1}^n(h_i-o_i)^2}}{\sqrt{\sum _{i=1}^no_i^2}} \end{aligned}$$
(14)
$$\begin{aligned}&MSE^F = \frac{\sqrt{\sum _{i=1}^n(x_i-o_i)^2}}{\sqrt{\sum _{i=1}^no_i^2}} \end{aligned}$$
(15)

where \(x_i\), \(i \in \{1, \dots , n\}\) denotes the AMS-MINNI forecasted value, \(o_i\) denotes the corresponding observed value and \(h_i\) is the DyNA assimilated value.

When comparing the mean squared assimilation error to the mean squared forecasting error with respect to the observed values, we can see great results—DyNA error is significantly lower with a minimum reduction of 38.0% (NO\(_2\) forecast in Aosta Valley) (see Table 4) to a maximum reduction of 47.5% (O\(_3\) forecast in Trentino-South Tyrol) (see Table 5).

Table 4 Comparisons of MSE\(^F\) and MSE\(^{DyNA}\) for values of NO\(_2\)
Full size table
Table 5 Comparisons of MSE\(^F\) and MSE\(^{DyNA}\) for values of O\(_3\)
Full size table

To test the accuracy of DyNA as predictive model, we used DyNA to predict levels of O\(_3\) and NO\(_2\) in 2010 as these data was not included in our training or validation. We used MSE\(^{DyNA}\) as a notation for this measure. We then again calculated the mean squared forecasting error between the observations from the year 2010 and the AMS-MINNI modelled values from the year 2010. After comparing these errors, we were able to confirm our assumption as the mean squared assimilation error was still lower than the mean squared forecasting error in all except one (Lombardy region, GAMBARA station, O\(_3\)) monitoring station.

In case we use simulations data from AMS-MINNI only, DyNA is trained as a standard LSTM and it acts as a surrogate of the predictive model AMS-MINNI. Below we will use LSTM to refer to a DyNA model trained to surrogate AMS-MINNI. We have trained LSTM models responsible for replicating the AMS-MINNI air pollution concentrations at each of our selected monitoring stations. We used hyperparameters derived from the hyperparameter optimisation shown in Table 3.

In order to keep track of our model improvements, we kept the results of two baseline models for comparison: one simple LSTM architecture network without any of our updates (such as the additional time variables chosen after FFT analysis or regularisation techniques) and one model which forecasted the next value to be the same as the one before which is called naive forecasting. In order to evaluate the accuracy with respect to the AMS-MINNI predictions, we used the Root Mean Square Error (RMSE) defined as:

$$\begin{aligned} RMSE&= \frac{\sqrt{\sum _{i=1}^n(h_i-x_i)^2}}{n} \end{aligned}$$
(16)

where \(x_i\), \(i \in \{1, \dots , n\}\) denotes the AMS-MINNI forecasted value and \(h_i\) is here the LSTM prediction.

With our updated model, we have managed to reach accurate results with RMSE ranging from 4.27 \(\upmu\)g/m\(^3\) (Lombardy O\(_3\) predictions) to 0.51 \(\upmu\)g/m\(^3\) (Aosta Valley NO\(_2\) forecast) and significantly improved over our baseline models (Table 6).

Table 6 RMSE of our LSTM model across different stations
Full size table

To be able to compare the results from different monitoring stations, we have also looked at the R\(^2\) score in Fig. 5: the results range from 0.879 to 0.989. The lowest results were found when predicting NO\(_2\) concentration in the Trentino-South Tyrol and Umbria regions. This can be explained by the zone and type of these stations: in selecting the air quality monitoring stations (see Sect. 4.2) we chose the background rural ones because of the better model performances of AMS-MINNI [9], a feature common in chemical transport model applications at a regional scale. In some regions the data with this combination of zone (rural) and type (background) were not available, so two stations were chosen having different type or zone (urban) and these are the stations that resulted in the lowest R\(^2\) score.

Fig. 5
figure 5

Graphs showing LSTM modelled values versus AMS-MINNI values in two monitoring stations

Full size image

5.2.1 Execution time

One of the important advantages of the DyNA is its improvement in the predictive time and assimilation time compared to AMS-MINNI and a standard DA algorithm. To forecast the levels of NO\(_2\) or O\(_3\) in a specific region in 1 year, AMS-MINNI takes approx \(1.21e+06\) s. DyNA takes approx 1320 s for the same forecasting, which gives us a speed up \(S=\frac{T_{AMS-MINNI}}{T_{DyNA}}=0.92e+03\). Another important aspect to underline its improvement in the assimilation time compared to standard DA model such as OI. Table 7 summarises results our our testing. For each DyNA and OI model, we have executed 7 runs of 50 loops of assimilation on the data from the year 2010 and calculated the average execution time of a single loop.

Table 7 Execution time comparisons between DyNA and OI
Full size table

During our experiments, DyNA showed to be from 18% (O\(_3\) assimilation in Aosta Valley) to even 46% (O\(_3\) assimilation in Lombardy) faster than the respective execution of the Optimal Interpolation algorithm. We can also notice that the execution time of the DyNA depends on the complexity of the RNN used in the structure of DyNA. Aosta Valley O\(_3\) level forecast model had the highest number of layers and this resulted in the slowest execution out of all DyNA models.

5.3 Correlation analysis: air pollution and number of industrial companies

Since we do not have AMS-MINNI modelled values for the year 2013, we will use the last available DyNA forecasts for the year 2013 as our modelled values. In Sect. 5.2, we evaluated the predictive accuracy of DyNA. We used the inherent seasonality of the data, noting that our air pollution dataset consistently exhibits identifiable patterns and periodic tendencies, as previously outlined in Sect. 4.4. After having all air pollution estimates, we have reached the stage where we could compare the air pollution tendencies with the changes of the industrial density in the regions.

We initially worked with the models based on two NO\(_2\) monitoring stations in Lombardy and Umbria and the results looked very promising as the correlation was high between these two measures. However, when we expanded our analysis to include all of our stations, we did not find a relationship between these two values in all of the regions. A moderate positive correlation was observed between the number of industries and NO\(_2\) concentration in the Lombardy and Trentino-Sud Tyrol regions (correlation coefficients of 0.70 and 0.51 respectively), and a high positive correlation was observed in the Umbria region (correlation coefficient of 0.99). The differences in the obtained results could be partially explained by the type (background or traffic) of the selected air quality monitoring stations. More accurate estimates of air quality could be derived by considering the distribution of industries, and their limitations could be established based on the air quality requirements defined in green policies. There are also other studies that analyse the correlation between air quality and meteorological data [46, 47], but our analysis serves as a first study toward the understanding of the impact of corporate emissions on air quality. Therefore, we decided to focus on industrial activities.

6 Conclusions and future work

In our work, we have successfully created a state-of-the-art system for air quality analysis using physics-informed recurrent neural networks. During this process, we have also derived a new data assimilation and forecasting method called Dynamic Neural Assimilation, analysed its accuracy and showed its execution time improvement over a popular statistical data assimilation Optimal Interpolation method. To deal with significant amounts of data and the high necessity of computing power under time constraints, we have also embraced parallel computing in our model training and hyperparameter optimisation. The flexible workflow we derived in this project could also be easily reapplied to other data to reach new conclusions.

We considered a few ways in which the presented system could be improved. Since we are solving a physics-informed task of air quality forecasting, our final system could be improved by including physical equations in the loss functions of our models if reliable computational fluid dynamics software becomes available. However, to our knowledge, currently there is no such software. Other interesting extensions could be to use our model for other air pollutants and analyse data from other air quality stations. This work demonstrates the flexibility and the replicability of our system to different pollutants, sources and fields.