1 Introduction

Investigation of fluid flow over a stretching surface is essential in various engineering processes, wire drawing, melt-spinning, including extrusion, hot rolling, and glass-fiber production. The analysis also extends to applications such as manufacturing rubber sheets and plastic, as well as cooling large metallic plates immersed in electrolytic baths. Understanding the dynamics of this flow is essential for optimizing and enhancing efficiency in industrial processes, highlighting its significance in diverse engineering applications. Kuznetsov and Nield [1] explored Brownian motion and thermophoresis in relation to the spontaneous flow of a nanofluid convective across a vertical plate at its boundary layer. It provided important insights into nanofluid dynamics within fluid mechanics by revealing variations in the decreased Nusselt number with buoyancy-ratio \(\left(\mathcal{N}\mathcalligra{r}\right)\), thermophoresis (\(\mathcal{N}\mathcalligra{t}\)) and Brownian motion (\(\mathcal{N}b\)) numbers using a similarity solution. Nield and Kuznetsov [2] employed the Darcy technique for a porous material and incorporating thermophoresis and Brownian motion into a nanofluid technique. These observations greatly advance our knowledge of the actions of nanofluids in permeable media. Rasool et al. [3] studied the intricate interplay of fluid flow, mass and heat transport, and entropy generation. Their study concluded with valuable insights into the influences of magnetic parameters on drag force, Brownian diffusion’s effects on heat transmission rates, and the various fluid parameters’ nuanced behavior throughout the domain. Khan et al. [4] examined nanofluid rheology through a comprehensive framework involving Radiation of heat, permeable medium, gyrotactic micro-organisms, and energy for activation. The meticulous examination of velocity distribution and critical flow parameters, guided by a renowned shooting method, added depth to our understanding of complex nanofluid systems. Shah et al. [5] focused on radiative heat and mass transport in a mechanism that revolves between parallel plates. Their findings were rigorously validated numerically, with graphical representations offering visual insights into the intricate interplay of influential factors. A Maxwell fluid in two dimensions: its Darcy-Forchheimer flow caused by a stretched exterior was examined by Hayat et al. [6], taking temperature-dependent thermal conductivity into account. According to their research, a higher Deborah number has the opposite impact on the temperature field and decreases the velocity field. Muhammad et al. [7] explored the imposition of thermal convection conditions at the border and zero mass flux of nanoparticles led to the formulation of normalized equations, analyzed through an optimal homotopic procedure. According to the study, skin-friction coefficients decrease with increasing porosity and Forchheimer parameters, which in turn causes the local Nusselt number to decrease at higher values. Hayat et al. [8] found that higher nanoparticle volume fractions improved skin friction and Nusselt numbers in their study of water-based carbon nanotube interactions in a porous medium. The complex dynamics of a second-grade nanofluid affected by EMHD mixed convective flow close to a vertical Riga plate evaluated by Rasool and Wakif [9]. Their research advances our knowledge of intricate fluid behaviors by providing insightful information on nanofluid dynamics. Mebarek-Oudina et al. [10] investigated free convection in a water-soluble composite nanoliquid-filled curved permeable environment, influenced through a magnetic field external to the object. Their findings, displayed as isotherms and streamlines, highlight the magnetic field's significant regulatory impact Regarding heat transmission and fluid movement in porous materials. The magnetohydrodynamic flow of a micropolar fluid over a permeable stretching sheet was investigated by Ramzan et al. [11], taking into account convective boundary circumstances, partial slip, joule heating, and heat radiation. Their findings provide valuable insights into the complex dynamics of this fluid flow scenario. Rasool et al. [12] examined mass transfer, heat generation, and formation of entropy in a nanofluid with Darcy-Forchheimer MHD flow near a surface that is expanding nonlinearly. They used advanced numerical techniques, including RK-45-based solutions, were employed to reveal nuanced details through graphical representations and tabulated results. Shah and Khan [13] examined an inferior fluid next to a vertical plate that oscillates. Their findings include the fractional parameter's enhancement of fluid flow. Muhammad et al. [14] explored the intricate dynamics of three-dimensional Darcy-Forchheimer flow in water-soluble nanomaterials made of carbon. Their study also analyzed coefficients for surface drag and heat transmission rates, contributing valuable insights to our understanding of nanofluid dynamics and the impact of carbon nanotubes on heat transmission in porous medium. Rasool et al. [15] delved into the intricacies of chemical reactions and bioconvection in an inclined magnetized cross nanofluid around a cylinder. Their findings reveal nuanced behaviors such as shear thinning, microorganism swimming speeds, and the impact of magnetic and thermal parameters, contributing significantly to our understanding of complex nanofluid dynamics. The intricacies of three-dimensional Magnetohydrodynamic (MHD) Maxwell Studying the flow of nanofluids, Hayat et al. [16], who took into account in which the surface that stretches in both directions two phenomena: thermophoresis and Brownian motion. Their study illustrates how several factors affect temperature and the concentration of nanoparticles by graphs and computes numerical Nusselt numbers. Khan et al. [17] employed a similarity solution to derive differential equations, numerically solving them using the 5th-order RK Fehlberg technique. Their study enhances our understanding of the complex interplay between bioconvection and MHD flow. In [18], researchers investigated how Newtonian heating affected three-dimensional MHD flow around a stretchable surface. A steady magnetic field that is parallel to the surface, and viscosity dissipation and Joule warming effects are taken into account together into the mathematical formulation. Shah et al. [19], investigated the mass and heat transmission complexities in a radiative electrically conducting Casson nanofluid. Their research uncovers insights into flow patterns, presenting computational results for velocity, heat flux, drag force and concentration gradient across various parameters. The dynamics of nano biomaterials were studied by Khan et al. [20], with particular attention on bioconvection in nanofluids over an oscillating stretched sheet. Their findings underscore the enhanced temperature of nanoparticles with increased buoyancy ratio and Rayleigh number. Ali et al. [21] examined unsteady hydro-magnetic convection of an electrically conducting liquid. Numerical calculations revealed highlighted stronger memory effects for smaller time values. Khan et al. [22] considering temperature-dependent viscosity, solar radiation, and viscous dissipation. Their study explores parameter effects on key variables and presents results graphically. A liquid metal's natural convection problem in the presence of a magnetic field has been the subject of numerous studies, according to Mebarek-Oudina and Bessaïh [23]. The significance of this can be attributed to its use in several industrial applications, including materials processing, nuclear engineering crystal growth, gas-cooled reactor safety, solar energy collectors, and welding. To discuss how a stretched sheet's varying viscosity and tilted Lorentz force effects affect Williamson nanofluid, Khan et al. [24] investigated the computer solution to the problem. The variable viscosity is thought to change linearly with temperature. The Oldroyd-B nanofluid flow in the presence of a combined convection impact and a slip mechanism was assessed in [25]. To examine the physical importance of flow characteristics, the zero-mass boundary assumptions were employed. In their study, Ramzan et al. [26] examined third-grade incompressible, two-dimensional fluid flow that included homogeneous-heterogeneous responses and Cattaneo-Christov flow of heat. Convective boundary conditions and the effects of MHD are also considered. Shah et al. [27] study examined the effects on an infinite vertical plate, of the recently created fractional integral on suspension of ternary nanoparticles and second-grade fluid. A study by Hayat et al. [28] offered an analytical examination of the MHD 3D-flow of Oldroyd-B nanoparticles when convective surface boundary conditions and heat generation/absorption are present. Shah et al. [29] examined third-grade fluid between parallel plates with a rotational structure in order to study the mass and heat transmission consequences of non-Newtonian electric-conducting nanofluid fluxes. Mebarek-oudina and Bessaïh [30] have explored numerically a low-Prandtl number fluid movement in a cylinder-shaped containment that is either axially or radially exposed to an exterior magnetic field. Muhammad et al. [31] examined the CCHF model, non-linear thermal radiation, and melting heat transfer in their study of the magnetized transport of a nanofluid containing CNTs across a quadrilateral stretched sheet. While Khan et al. [32] investigated the influence of temperature-sensitive viscosity on Williamson nanofluid circulation across a nonlinear stretching sheet, Waseem et al. [33] investigated the effects of MHD on the flow attributes and heat transmission of the metal copper, titanium, and water-based nanofluids throughout a bidirectional covering. Ali et al. [34] research demonstrates more inquiry towards non-Newtonian fluids and varied nanoparticle characteristics for improved comprehension of complex fluid mechanics. Wakif et al. [35] looked into the unpredictability of naturally occurring convection MHD Couette nanofluid flow caused by heat radiation and a transverse magnet, concentrating on copper–water nanofluids. Ali et al. [36] studied the flow patterns of a fluid carrying microparticles across a rotating surface, taking into account the Coriolis force, the Arrhenius stimulation energy, and the Cattaneo-Christov heat exchange. By suspending single and multiwalled carbon nanotubes in a salt-water solution, Ellahi et al. [37] studied the effects of natural convection MHD nanofluid. Computed values of Nusselt number and skin friction offer a comprehensive assessment of the intricate interactions in MHD nanofluid natural convection. Wakif et al. [38] explored the dynamics over an elastic sheet with nonuniform thickness, considering thermal conductivity and temperature-dependent viscosity. Their research addresses the impact of an external magnetic field, space-dependent strength, and linear thermal radiation. Ellahi et al. [39] considered temperature-dependent viscosity models, converting nonlinear partial differential equations into dimensionless form and solving them analytically using the Homotopy Analysis Method.

Acharya [42,43,44,45,46,47,48,49] examined the impact of thermal modes, concentrations of nanoparticles, and magnetic fields on heat transfer while investigating hydrothermal behavior in diverse nanofluidic flows inside distinct geometric enclosures. Understanding fluid dynamics and thermal processes was made possible by computational simulations and experimental validation, which also brought attention to the better heat transport properties of hybrid nanofluids. These results have important ramifications for engineering uses such as heat exchangers and thermal storage devices. It is recommended that future studies look into different fin forms and unique nanofluid compositions. Giri [51,52,53,54,55,56] explored various aspects of nanofluid dynamics and heat transfer, spanning bioconvection to melting heat transmission. Analyses covered complex scenarios like hydro-magnetic bioconvection and MHD nanofluid dynamics with rotational effects. Utilizing numerical simulations, the studies revealed how different parameters impacted temperature, concentration, and velocity profiles. Overall, findings highlighted nanofluids' potential in optimizing heat transfer processes across biomedical and industrial applications. Das et al. [57] investigated non-axisymmetric Homann stagnation-point flow of nanofluid over a stretched flat plate, contributing to fluid dynamics and heat transfer understanding. Incorporating a melting condition for enhanced heat transfer, the study transformed partial into ordinary differential equations via similarity analysis for numerical analysis, yielding innovative insights with industrial applicability.

The previously mentioned articles examined the concentration, temperature, and velocity profiles of nanoliquids under various circumstances. Motivated by the information and debates presented in these articles, we want to examine heat transfer in boundary-layer flow of nanofluids over a stretchable sheet by utilizing a comprehensive model that includes thermophoresis, Brownian motion, radiation effects, Cattaneo-Christov heat flux, and magnetohydrodynamics (MHD). We will also analyze important parameters such as radiation parameter, stretching sheet velocity, and nanoparticle volume fraction. Thus far, no studies on nanofluid flow under these circumstances have been conducted. The equations are initially presented as partial differential equations (PDEs) that are transformed into ordinary differential equations (ODEs) through the application of similarity notions, and are subsequently solved numerically. The influence of these attributes is presented graphically and quantitatively using the HAM technique. To the best of our knowledge, this paper's results are brand-new and have never been published previously.

2 Problem formation

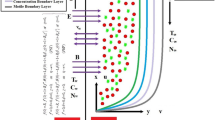
We study the continuous boundary layer flow in two dimensions of a nanofluid at a linear velocity past an expanding surface profile\({\mathcalligra{u}}_{\mathcalligra{w}}\left(x\right)=\mathcalligra{a}x\), where x is the point with respect to the expanding surface, and a is fixed (Fig. 1). With y serving as the stretching surface's coordinate normal, this flow happens at\(y\ge 0\). The sheet stretches as a result of an even, continuous stress that produces opposing, equal pressures maintaining the origin's stationary position along the x-axis. It is assumed that the nanoparticle fraction \((\mathcal{C})\) and temperature \((\mathcal{T})\) stay constant at the stretching surface (\({\mathcal{C}}_{\mathcal{W}}\) and\({\mathcal{T}}_{\mathcal{W}}\), respectively). As y approaches infinite, the surrounding values of \(\mathcal{C}\) and \(\mathcal{T}\) are represented as \({\mathcal{C}}_{\mathcal{W}}\) and \({\mathcal{T}}_{\mathcal{W}}\), respectively. As explained in detail by Kuznetsov and Nield [21, 22], the fundamental steady-state conservation equations for mass, thermal energy, momentum, and nanoparticles in nanofluids are provided in dimensions of Cartesian x and y.

$$\frac{{\partial \mathop u\limits^{ \ldots } }}{\partial x}\, + \,\frac{{\partial \mathop v\limits^{ \ldots } }}{\partial y}\, = \,0,$$
(1)
$$\mathop u\limits^{ \ldots } \,\frac{{\partial \mathop u\limits^{ \ldots } }}{\partial x}\, + \,\mathop v\limits^{ \ldots } \,\frac{{\partial \mathop v\limits^{ \ldots } }}{\partial y}\, = \, - \frac{1}{pf}\,\frac{\partial p}{{\partial x}}\, + \,v\left( {\frac{{\partial^{2} \mathop u\limits^{ \ldots } }}{{\partial x^{2} }}\, + \,\frac{{\partial^{2} \mathop v\limits^{ \ldots } }}{{\partial y^{2} }}} \right)\, - \,\frac{{\sigma B^{2} }}{pf}\,\mathop u\limits^{ \ldots } ,$$
(2)
$$\mathop u\limits^{ \ldots } \frac{{\partial {\mathcal{T}}}}{\partial x} + \mathop v\limits^{ \ldots } \frac{{\partial {\mathcal{T}}}}{\partial y} + \lambda_{{\mathbb{E}}} \varphi_{{\mathbb{E}}} = \alpha \left( {\frac{{\partial^{2} {\mathcal{T}}}}{{\partial x^{2} }} + \frac{{\partial^{2} {\mathcal{T}}}}{{\partial y^{2} }}} \right) + \tau \left\{ {{\mathcal{D}}_{{\mathcal{B}}} \left( {\frac{{\partial {\mathcal{C}}}}{\partial x}\frac{{\partial {\mathcal{T}}}}{\partial x} + \frac{{\partial {\mathcal{C}}}}{\partial y}\frac{{\partial {\mathcal{T}}}}{\partial y}} \right) + \frac{{{\mathcal{D}}_{{\mathcal{T}}} }}{{{\mathcal{T}}_{\infty } }}\left[ {\left( {\frac{{\partial {\mathcal{T}}}}{\partial x}} \right)^{2} + \left( {\frac{{\partial {\mathcal{T}}}}{\partial y}} \right)^{2} } \right]} \right\} + \frac{16}{3}\frac{1}{{{\uprho }{\mathcal{C}}_{f} }}\frac{{{\upsigma }^{*} {\mathcal{T}}_{\infty }^{3} }}{{{\mathcal{K}}^{*} }}\frac{{\partial^{2} {\mathcal{T}}}}{{\partial {\text{y}}^{2} }},$$
(3)
$$\mathop u\limits^{ \ldots } \frac{{\partial {\mathcal{C}}}}{\partial x} + \mathop v\limits^{ \ldots } \frac{{\partial {\mathcal{C}}}}{\partial y} + \lambda_{{\mathbb{C}}} \varphi_{{\mathbb{C}}} = {\mathcal{D}}_{{\mathcal{B}}} \left( {\frac{{\partial^{2} {\mathcal{C}}}}{{\partial x^{2} }} + \frac{{\partial^{2} {\mathcal{C}}}}{{\partial y^{2} }}} \right) + \frac{{{\mathcal{D}}_{{\mathcal{T}}} }}{{{\mathcal{T}}_{\infty } }}\left( {\frac{{\partial^{2} {\mathcal{T}}}}{{\partial x^{2} }} + \frac{{\partial^{2} {\mathcal{T}}}}{{\partial y^{2} }}} \right)$$
(4)
Fig. 1
figure 1

Coordinate system and physical model

Full size image

According to the boundary conditions.

$$\mathop u^{\dots}={\mathop u^{\dots}}_{w}\left(x\right)=\mathop {a} x, \mathop v^{\dots}=0, \mathcal{T}={\mathcal{T}}_{w},\mathcal{C}={\mathcal{C}}_{w},\quad \text{at}\, y=0,$$
(5)
$$\mathop u^{\ldots}=\mathop v^{\ldots}=0, \mathcal{T}={\mathcal{T}}_{\infty },\mathcal{C}={\mathcal{C}}_{\infty }\,as\,y\to \infty .$$
(6)

We seek a congruence resolution for Eqs. (1, 2, 3, 4 and 5) in conjunction with the stipulated boundary conditions (6), formulated in the subsequent manner by [40, 41]

$$\psi = \left( {\alpha \nu } \right)^{\frac{1}{2}} xf\left( \eta \right), \theta \left( \eta \right) = \frac{{{\mathcal{T}} - {\mathcal{T}}_{\infty } }}{{{\mathcal{T}}_{{\mathfrak{w}}} - {\mathcal{T}}_{\infty } }},$$
$$\varphi \left( \eta \right) = \frac{{{\mathcal{C}} - {\mathcal{C}}_{\infty } }}{{{\mathcal{C}}_{{\mathfrak{w}}} - {\mathcal{C}}_{\infty } }}, \eta = \left( {\frac{\alpha }{\nu }} \right)^{\frac{1}{2}} y$$
(7)

Generally, the stream function ψ is stated as \(\mathop u^{\ldots}=\frac{\partial \psi }{\partial y}\) ​ and \(\mathop {v}^{\ldots}=-\frac{\partial \psi }{\partial x}\)​. In the pursuit of the similarity solution denoted as (7), due consideration has been given to the fact because the external, inviscid flow's internal pressure is \(\mathcal{P}={\mathcal{P}}_{0}\) (constant). This results the subsequent ODEs when (7) is substituted into Eqs. (2, 3, 4 and 5).

$$f^{{\prime \prime \prime }} + ff^{{\prime \prime }} - f^{{\prime 2}} \, - \,Mf^{\prime } {\mkern 1mu} = {\mkern 1mu} 0,$$
(8)
$$\frac{1}{pr}\theta^{\prime\prime} + f\theta^{\prime} + {\mathcal{N}}b\varphi^{\prime}\theta^{\prime} + Nt\left( {\theta^{\prime}} \right)^{2} - \delta_{{\mathfrak{e}}} \left( {\theta^{\prime}ff^{\prime} + f^{2} \theta^{\prime\prime}} \right) + {\mathcal{R}}\theta^{\prime\prime} = 0,$$
(9)
$$\varphi ^{{\prime \prime }} + {\mathcal{L}\mathfrak{e}}\delta \varphi ^{\prime } + \,\frac{{Nt}}{{{\mathcalligra{N}}b}}\theta ^{{\prime \prime }} - {\mathcal{L}\mathfrak{e}}\delta _{c} \,\left( {\varphi ^{\prime } ff^{\prime } + f^{2} \varphi ^{{\prime \prime }} } \right)\, = \,0.$$
(10)

Moreover, the boundary conditions manifest in the subsequent manners:

$$f = 0,f^{\prime } = 1,\theta = 1,\varphi = 1at\eta = 0,$$
(11)
$${{f}}{^\prime}=0, \theta =0, \varphi =0, as \eta =\infty .$$
(12)

The parameters that are specified are expressed as follows:

$$\mathcal{P}\mathcalligra{r}=\frac{\nu }{\alpha }, \mathcal{L}\mathfrak{e}=\frac{\nu }{{\mathcal{D}}_{\mathcal{B}}},\mathcal{N}\mathcalligra{t}=\frac{\tau {\mathcal{D}}_{\mathcal{T}}\left({\mathcal{T}}_{\mathfrak{w}}-{\mathcal{T}}_{\infty }\right)}{{\mathcal{T}}_{\infty }\nu },\mathcal{N}b=\frac{\tau {\mathcal{D}}_{\mathcal{B}}\left({\mathcal{C}}_{\mathfrak{w}}-{\mathcal{C}}_{\infty }\right)}{\nu },$$
(13)
$${\delta }_{\mathfrak{c}}={\mathcalligra{a}\lambda }_{\mathbb{C}}, \mathcal{R}=\frac{16}{3}\frac{1}{\mu {\mathcal{C}}_{{f}}}\frac{{\sigma }^{*}{\mathcal{T}}_{\infty }^{3}}{{\mathcal{K}}^{*}},\mathcal{M}=\frac{\sigma {\mathcal{B}}_{^\circ }^{2}}{\mathcalligra{a}{\rho }_{{f}}},{ \delta }_{\mathfrak{e}}=\mathcalligra{a}{\lambda }_{\mathbb{E}}.$$
(14)

The symbols Lewis, Prandtl, thermophoresis, and Brownian motion reflect the parameters in question. \(\mathcal{L}\mathfrak{e}\), \(\mathcal{P}\mathcalligra{r}\), \(\mathcal{N}\mathcalligra{t}\), and \(\mathcal{N}b\) in this instance.

$$\mathcal{R}{\mathcalligra{e}}_{x}^{-\frac{1}{2}}{\mathcal{C}}_{{f}}={{f}}^{{\prime}{\prime}}\left(0\right),$$
(15)
$${\mathcal{R}}{\text{ mathcal}}e_{x}^{{ - \frac{1}{2}}} {\mathcal{N}}\mathop {{\text{ }}u}\limits^{ \ldots } _{x} = - (1 + {\mathcal{R}})\theta ^{\prime } \,\left( 0 \right),$$
(16)
$$\mathcal{R}{\mathcalligra{e}}_{x}^{-\frac{1}{2}}{\mathcal{S}\mathcalligra{h}}_{x}=-{\varphi }{^\prime}\left(0\right).$$
(17)

where \(\mathcal{R}{\mathcalligra{e}}_{x}=\frac{{\mathcalligra{u}}_{\mathcalligra{w}\left(x\right)x }}{\nu }\) is determined by the stretching velocity \({\mathcalligra{u}}_{\mathcalligra{w}\left(x\right) }.\mathcal{R}{\mathcalligra{e}}_{x}^{-\frac{1}{2}}{\mathcal{S}\mathcalligra{h}}_{x}\) and \(\mathcal{R}{\mathcalligra{e}}_{x}^{-\frac{1}{2}}{\mathcal{N}\mathop u^{\ldots}}_{x}\) are referred to as the reduced Sherwood number \({\mathcal{S}\mathcalligra{h}}_{x}=-{\varphi }{\prime}\left(0\right)\) and the reduced Nusselt number\({\mathcal{N}}\mathop {{\text{ }}u}\limits^{ \ldots } _{x} = - (1 + {\mathcal{R}})\theta ^{\prime } \left( 0 \right)\), respectively, by Kuznetsov and Nield [21].

3 Methodology

Solution by Homotopy Analysis Method (OHAM) [58,59,60,61]

The nonlinear model equations have been solved using the OHAM, (8–12) coupled with formulated boundary conditions (13, 14). The subsequent statements delineate the chosen initial assumptions:

$${{f}}_{^\circ }\left(\eta \right)=1-{\mathcalligra{e}}^{-\eta }, {\theta }_{^\circ }\left(\eta \right)={\mathcalligra{e}}^{-\eta }, {\varphi }_{^\circ }\left(\eta \right)={\mathcalligra{e}}^{-\eta },$$
(18)

It is postulated that the linear operators denoted as \({\mathcal{L}}_{f}\), \({\mathcal{L}}_{\theta }\) and \({\mathcal{L}}_{\varphi }\):

$${\mathcal{L}}_{f} \left( f \right) = \frac{{d^{3} }}{{d\eta ^{3} }} - \frac{d}{{d\eta }},{\mathcal{L}}_{\theta } \left( \theta \right) = \frac{{d^{2} \theta }}{{d\eta ^{2} }} - \theta ,{\mathcal{L}}_{\varphi } \left( \varphi \right) = \frac{{d^{2} \varphi }}{{d\eta ^{2} }} - \varphi .$$
(19)

They exhibit the following equalities:

$$\left.\begin{array}{c}{\mathcal{L}}_{{f}}\left[\stackrel{\smile}{{B}_{1}^{*}}+\stackrel{\smile}{{B}_{2}^{*}}{\mathcalligra{e}}^{\eta }+\stackrel{\smile}{{B}_{3}^{*}}{\mathcalligra{e}}^{-\eta }\right]=0, \\ {\mathcal{L}}_{\theta }\left[\stackrel{\smile}{{B}_{4}^{*}}{\mathcalligra{e}}^{\eta }+\stackrel{\smile}{{B}_{5}^{*}}{\mathcalligra{e}}^{-\eta }\right]=0,\\ {\mathcal{L}}_{\varphi }\left[\stackrel{\smile}{{B}_{6}^{*}}{\mathcalligra{e}}^{\eta }+\stackrel{\smile}{{B}_{7}^{*}}{\mathcalligra{e}}^{-\eta }\right]=0.\end{array}\right\}.$$
(20)

where the constant coefficients are \(\stackrel{\smile}{{B}_{1}^{*}},\stackrel{\smile}{{B}_{2}^{*}},\stackrel{\smile}{{B}_{3}^{*}},\stackrel{\smile}{{B}_{4}^{*}},\stackrel{\smile}{{B}_{5}^{*}},\stackrel{\smile}{{B}_{6}^{*}}\) and \(\stackrel{\smile}{{B}_{7}^{*}}\).

4 Entropy generation

The following is a model for the generation of volume entropy based on the second law of thermodynamics. In the context of the Cattaneo-Christov nanofluid.

$${\mathcal{S}}_{G}=\frac{\mathbb{k}}{{\mathcal{T}}_{\infty }^{2}}\left(1+\frac{16{\sigma }^{*}{\mathcal{T}}_{\infty }^{3}}{3{\mathbb{k}}^{*}}\right){\left(\frac{\partial \mathcal{T}}{\partial y}\right)}^{2}+\frac{\sigma {\mathcal{B}}_{^\circ }^{2}\ddot{{\mathcalligra{u}}^{2}}}{{\mathcal{T}}_{\infty }}+\frac{\mathcal{R}{\mathcal{D}}_{\mathcal{B}}}{{\mathcal{C}}_{\infty }}{\left(\frac{\partial c}{\partial y}\right)}^{2}+\frac{\mathcal{R}{\mathcal{D}}_{\mathcal{B}}}{{\mathcal{T}}_{\infty }}\left(\frac{\partial \mathcal{T}}{\partial y}\right)\left(\frac{\partial c}{\partial y}\right),$$
(21)
$$\mathcal{N}G=\frac{{\nu \mathcal{T}}_{\infty }{\mathcal{S}}_{G}}{{\mathbb{k}}\mathcalligra{a}\left({\mathcal{T}}_{\mathcal{W}}-{\mathcal{T}}_{\infty }\right)}.$$
(22)

One can obtain the entropy generation number \(\mathcal{N}G\) as

$${\mathcal{N}}G = \tau _{1} \left( {1 + {\mathcal{R}}} \right)\theta ^{{\prime 2}} + {\mathcal{M}\mathcal{B} }{\text{r}}f^{{\prime 2}} + \frac{{\tau _{2} }}{{\tau _{1} }}{\mathcal{L}\mathfrak{e}}\varphi ^{{\prime 2}} + \theta ^{\prime } \varphi ^{\prime } {\mathcal{L}\mathfrak{e}}.$$
(23)

The dimensionless temperature gradient and Brinkman's number are denoted as follows, embodying their respective manifestations in the context of academic discourse.

$${\mathcal{B}}{\mathcalligra{r}}=\frac{{\mu }_{{f}}{\mathbb{U}}^{2}}{{\mathbb{k}}_{{f}}\left({\mathcal{T}}_{\mathcal{W}}-{\mathcal{T}}_{\infty }\right)}, { \tau }_{1}=\frac{{\mathcal{T}}_{\mathcal{W}}-{\mathcal{T}}_{\infty }}{{\mathcal{T}}_{\infty }}, { \tau }_{2}=\frac{{\mathcal{C}}_{\mathcal{W}}-{\mathcal{C}}_{\infty }}{{\mathcal{C}}_{\infty }}.$$
(24)

4.1 Bejan number

The dimensionless form of the Bejan number is expressed as

$$\mathcal{B}\mathcalligra{e}=\frac{Entropy \,due \,to \,heat \,and \,mass \,trasfer}{total \,entropy \,generation}.$$

where \(\mathcal{B}\mathcalligra{e}\) is given by

$${\mathcal{B}}{\mathcalligra{e}} = \frac{{\tau _{1} \left( {1 + {\mathcal{R}}} \right)\theta ^{{\prime 2}} + \frac{{\tau _{2} }}{{\tau _{1} }}{\mathcal{L}}{\mathfrak{e}}\varphi ^{{\prime 2}} + \theta ^{\prime } \varphi ^{\prime } {\mathcal{L}}{\mathfrak{e}}}}{{\tau _{1} \left( {1 + {\mathcal{R}}} \right)\theta ^{{\prime 2}} + {\mathcal{M}}{\mathcal{B}}{\mathcalligra{rf}}^{{\prime 2}} + \frac{{\tau _{2} }}{{\tau _{1} }}{\mathcal{L}}{\mathfrak{e}}\varphi ^{{\prime 2}} + \theta ^{\prime } \varphi ^{\prime } {\mathcal{L}}{\mathfrak{e}} }}.$$
(25)

5 Results and discussion

An outline of the implications of new parameters has been given in this section. On velocities profiles \({{f}}{\prime}\left(\eta \right)\), temperature distribution \(\theta \left(\eta \right)\), concentration distribution \(\varphi \left(\eta \right)\) and entropy generation \(\mathcal{N}G\), the effects of thermal radiation parameter \(\mathcal{R}\), Brownian number \(\mathcal{N}b\), thermophoresis number \(\mathcal{N}\mathcalligra{t}\), Prandtl component \(\mathcal{P}\mathcalligra{r}\), Lewis number \(\mathcal{L}\mathfrak{e}\), thermal relaxation parameter \({\delta }_{\mathfrak{c}}\), and magnetic parameter \(\mathcal{M}\) are graphically displayed. The range of nanofluid parameters that are being examined in this study includes the following \(0.1\le \mathcal{M}.\le 1.3, 0.5\le \mathcal{P}\mathcalligra{r} \le 2.4, 0.1\le \mathcal{N}b\le 2.4, 0.1\le {\delta }_{\mathfrak{e}}\le 4.9, 0.1\le \mathcal{R}\le 1.7, 0.1\le \mathcal{L}\mathfrak{e}\le 1.3, 0.10\le \mathcal{N}b \le 0.50.\)

The velocity profiles presented in Fig. 2 show a significant decline in transport rate when the magnetic parameter \(\mathcal{M}\) causes the Lorentz force to increase. This observation suggests that the transverse magnetic field acts as a hindrance to transport, possibly attributed to heightened resistance arising from alterations in the Lorentz force. Nevertheless, it is significant that the velocity gradient, indicative of surface shear stress, exhibits an augmentation with increasing \(\mathcal{M}\). The temperature profile's dependence on the Prandtl number \(\mathcal{P}\mathcalligra{r}\), while maintaining constants for the other parameters \(\mathcal{M}=0.5, \mathcal{N}\mathcalligra{t}=0.2,\mathcal{N}b=0.3,\mathcal{R}=0.3,\mathcal{L}\mathfrak{e}=0.4,\) \({\delta }_{\mathfrak{c}}=0.4,\) and \({\delta }_{\mathfrak{e}}=0.3,\) is illustrated in Fig. 3. When thermal conductivity with high Prandtl numbers \(\mathcal{P}\mathcalligra{r}\) fails, temperature drops. The temperature profile in Fig. 4 increases as Brownian motion \(\mathcal{N}b\) increases. While holding the other parameters constant (\(\mathcal{M}=0.5,\mathcal{N}b=0.3,\mathcal{P}\mathcalligra{r}=1.0,\mathcal{R}=0.3,\mathcal{L}\mathfrak{e}=0.4,{\delta }_{\mathfrak{c}}=0.4,\) and \({\delta }_{\mathfrak{e}}=0.3\)) the thermophoresis parameter \(\mathcal{N}\mathcalligra{t}\) exhibits an inverse connection with the temperature in Fig. 5. The temperature rises when the thermophoresis parameter \(\mathcal{N}{t}\) increases because more random movement of the nanoparticles occurs. The purpose of Fig. 6 is to methodically examine the impact of modifying the thermal relaxation parameter, represented by \({\delta }_{\mathfrak{e}}\) on \(\theta \left(\eta \right)\). Interestingly, the temperature field \(\theta \left(\eta \right)\) shows a distinct declining pattern as the value of \({\delta }_{\mathfrak{e}}\) rises. Figure 7 shows how temperature profile \(\theta \left(\eta \right)\) is influenced by thermal radiation parameter \(\mathcal{R}\) while other parameters remain constant. We have values of \(\mathcal{M}=0.5,\mathcal{N}b=0.3,\mathcal{P}\mathcalligra{r}=1.0,\mathcal{N}\mathcalligra{t}=0.2,\mathcal{L}\mathfrak{e}=0.4,{\delta }_{\mathfrak{c}}=0.4,\) and \({\delta }_{\mathfrak{e}}=0.3.\) The graph indicates that a rise in \(\theta (\eta )\) results from an intensification in \(\mathcal{R}\). When conducting heat transport, \(\mathcal{R}\) is a crucial variable. As heat radiation increases, so does the flow's temperature inside the boundary layer. Figure 8 illustrates how \(\mathcal{L}\mathfrak{e}\) numbers affect the concentration profiles. It is evident that when the \(\mathcal{L}\mathfrak{e}\) numbers rise, the concentration falls. Keeping other parameters fixed (\(\mathcal{M}=0.5,\mathcal{N}b=0.3,\mathcal{P}\mathcal{r}=1.0,\mathcal{R}=0.3,\mathcal{L}\mathfrak{e}=0.4,{\delta }_{\mathfrak{c}}=0.4,\) and \({\delta }_{\mathfrak{e}}=0.3\)) the thermophoresis parameter \(\mathcal{N}\mathcalligra{t}\) exhibits an increase in Fig. 9. The concentration distribution rises as the thermophoresis parameter \(\mathcal{N}\mathcalligra{t}\) causes the concentration profile to climb. As shown in Fig. 10, while other parameters remain constant, the concentration profile is affected by the Brownian motion parameter \(\mathcal{N}b\). A rise in \(\mathcal{N}b\) results in a decrease in the nanoparticle fraction profile. Parallel to this, Fig. 11 provides a graphic representation of how changing the concentration relaxation parameter, represented by \({\delta }_{\mathfrak{c}}\), affects \(\varphi \left(\eta \right)\). A reduction in concentration within the \(\varphi \left(\eta \right)\) field is correlated with increasing \({\delta }_{\mathfrak{c}}\). The interaction between the Reynolds number and the entropy generation number is shown in Fig. 12. There is a major effect on the entropy formation number when the Reynolds number becomes closer to the sheet, as this results in an increasing entropy generation number. This illustrates the connection between the Lewis number and the entropy generation number. Figure 13 illustrates how the Lewis number close to the sheet boosts the entropy generation number, and Fig. 14 illustrates how the magnetic field close to the sheet affects the entropy generation number, expanding the resistance to fluid movement and reducing heat transfer rates. On the other hand, outside of the sheet area, the impact of the magnetic parameter is minimal. The impact of the \(\mathcal{B}\mathcalligra{r}\) on the \(\mathcal{B}\mathcalligra{e}\) is evident from the analysis presented in Fig. 15. It is observed that as the Brinkmann number increases, there is a notable decrease in the \(\mathcal{B}\mathcalligra{e}\). This phenomenon can be attributed to the Brinkmann number's association with the heat conduction process occurring between the fluid and the surface. With higher Brinkmann numbers, enhanced heat transport to the fluid is observed, consequently leading to an increase in the rate of entropy generation. This observation underscores the intricate relationship between the Brinkmann and \(\mathcal{B}\mathcalligra{e}\) in the context of heat transfer phenomena. Furthermore, Fig. 16 illustrates the impact of the Magnetic parameter on the \(\mathcal{B}\mathcalligra{e}\). Notably, there exists a decreasing trend in the \(\mathcal{B}\mathcalligra{e}\) as the Mach number increases. This trend suggests that larger \(\mathcal{M}\) are associated with a reduction in the \(\mathcal{B}\mathcalligra{e}\), indicating a decrease in the rate of convective heat transfer relative to other mechanisms. Additionally, Fig. 17 elucidates the influence of the \(\mathcal{R}\) on the \(\mathcal{B}\mathcalligra{e}\). It is observed that the \(\mathcal{B}\mathcalligra{e}\) exhibits an increasing trend with larger \(\mathcal{R}\). This behavior implies that as the \(\mathcal{R}\) increases, there is a corresponding increase in the Bejan number, indicative of enhanced convective heat transfer relative to other contributing factors. These findings provide valuable insights into the interplay between various dimensionless parameters and their impact on heat transfer processes, thus contributing to the broader understanding of thermal transport phenomena in engineering applications. Figure 18 demonstrates the parameter's noticeable impact \(\mathcal{P}\mathcalligra{r}\) on the system, proving beyond uncertainty that an increase in the value of \(\mathcal{P}\mathcalligra{r}\) corresponds to a proportional increase in the temperature profile. In Fig. 19, the augmentation of Brownian motion denoted as \(\mathcal{N}\mathcalligra{b}\) is observed to correlate with a concurrent escalation in the concentration profile.

Fig. 2
figure 2

Curves of velocity \({f}^{\prime}\left(\eta \right)\) for \(\mathcal{M}\)

Full size image
Fig. 3
figure 3

Curves of thermal \(\theta \left(\eta \right)\) for \(\mathcal{P}\mathcalligra{r}\)

Full size image
Fig. 4
figure 4

Curves of thermal \(\theta \left(\eta \right)\) for \(\mathcal{N}b\)

Full size image
Fig. 5
figure 5

Curves of thermal \(\theta \left(\eta \right)\) for \(\mathcal{N}\mathcalligra{t}\)

Full size image
Fig. 6
figure 6

Curves of thermal \(\theta \left(\eta \right)\) for \({\delta }_{\mathfrak{e}}\)

Full size image
Fig. 7
figure 7

Curves of thermal \(\theta \left(\eta \right)\) for \(\mathcal{R}\)

Full size image
Fig. 8
figure 8

Curves of solutal \(\varphi \left(\eta \right)\) for \(\mathcal{L}\mathfrak{e}\)

Full size image
Fig. 9
figure 9

Curves of solutal \(\varphi \left(\eta \right)\) for \(\mathcal{N}\mathcalligra{t}\)

Full size image
Fig. 10
figure 10

Curves of solutal \(\varphi \left(\eta \right)\) for \(\mathcal{N}b\)

Full size image
Fig. 11
figure 11

Curves of solutal \(\varphi \left(\eta \right)\) for \({\delta }_{\mathfrak{c}}\)

Full size image
Fig. 12
figure 12

Alteration of entropy generation with \(\mathcal{R}\)

Full size image
Fig. 13
figure 13

Alteration of entropy generation with \(\mathcal{L}\mathfrak{e}\)

Full size image
Fig. 14
figure 14

Alteration of entropy generation with \(\mathcal{M}\)

Full size image
Fig. 15
figure 15

Alteration of \(\mathcal{B}\mathcalligra{e}\) with \(\mathcal{M}\)

Full size image
Fig. 16
figure 16

Alteration of \(\mathcal{B}\mathcalligra{e}\) with \(\mathcal{B}\mathcalligra{r}\)

Full size image
Fig. 17
figure 17

Alteration of \(\mathcal{B}\mathcalligra{e}\) with \(\mathcal{R}\)

Full size image
Fig. 18
figure 18

Effect of Nusselt Number on \(\mathcal{P}\mathcalligra{r}\)

Full size image
Fig. 19
figure 19

Effect of Sherwood Number on \(\mathcal{N}b\)

Full size image

Table 1 displays, using the ideal values from additional parameters, each unique average squared residual error at various approximation orders. The effect of Magnetic Parameter \(\mathcal{M}\) on Skin Friction is displayed in Table 2. when \(\mathcal{P}\mathcalligra{r}=1.0, \mathcal{N}\mathcalligra{t}=0.2,{\delta }_{\mathfrak{e}}=0.3,\mathcal{N}b=0.3,\mathcal{L}\mathfrak{e}=0.4 and \mathcal{R}=0.3\). Table 3 shows how lowered Nusselt number is affected by \(\mathcal{P}\mathcalligra{r}\), \(\mathcal{N}\mathcalligra{t}\),\({\delta }_{\mathfrak{e}}\) and \(\mathcal{N}b\). This shows that by increasing \(\mathcal{P}\mathcalligra{r}\) and \({\delta }_{\mathfrak{e}}\) Nusselt number increases but opposite behavior occurred, as there is increase in \(\mathcal{N}\mathcalligra{t}\) and \(\mathcal{N}b\). Comparison of performed investigation with the results reported in [50] are established. An excellent agreement is shown in Table 4. Table 5 shows how the parameters have an impact \(\mathcal{N}b\) and \(\mathcal{N}\mathcalligra{t}\) in relation to the Sherwood number. The mass transfer rate decreases with the values of \(\mathcal{N}\mathcalligra{t}\) and parameters increase, whereas the mass transfer rate increases when the value of \(\mathcal{N}b\) increases. The values of Sherwood number upsurges against \({\delta }_{c}.\)

Table 1 Using the best values from auxiliary parameters to get the individual averaged squared residual errors
Full size table
Table 2 The skin friction coefficient \(- f^{{\prime \prime }} \left( 0 \right)\) can be estimated by the values of \(\mathcal{M}\)
Full size table
Table 3 \(\mathcal{P}\mathcalligra{r}\),\(\mathcal{N}\mathcalligra{t},\mathcal{N}b,\) and \({\delta }_{\mathfrak{e}}\) have an impact on the local Nusselt number when \(\mathcal{M}=0.5,\mathcal{L}\mathfrak{e}=0.4,\mathcal{R}=0.3,\) and \({\delta }_{\mathfrak{c}}=0.4,\) respectively
Full size table
Table 4 Comparative study of present investigation Present result when \(\mathcal{N}b=\mathcal{N}\mathcalligra{t}={\delta }_{\mathfrak{e}}=\mathcal{R}=0\) against \(\mathcal{P}\mathcalligra{r}\)
Full size table
Table 5 When \(\mathcal{M}=0.5,\mathcal{L}\mathfrak{e}=0.4,\mathcal{R}=0.3,\mathcal{P}\mathcalligra{r}=1.0,{\delta }_{\mathfrak{e}}=0.3,\) and the effects of \(\mathcal{N}\mathcalligra{t},\mathcal{N}b\) on the reduced Sherwood number are examined
Full size table

6 Conclusion

The current investigation deals the phenomena of modified heat flux and mass flux with radiation effect past over a linear stretched sheet by considering the Buongiorno model. The arising complex transformed equation are solved via OHAM.

The core findings are listed as:

  • A holistic model is constructed, encompassing thermophoresis, Brownian motion, Cattaneo-Christov heat flux, radiation, and Magnetohydrodynamics (MHD) to comprehensively capture the underlying physical phenomena;

  • Comprising a base fluid hosting suspended nanoparticles, the nanofluid exhibits distinctive thermophysical properties pivotal for governing heat and mass transfer dynamics;

  • Employing rigorous numerical analysis, key parameters such as nanoparticle volume fraction, stretching sheet velocity, Cattaneo-Christov parameter, radiation parameter, and magnetic field strength are systematically examined;

  • The outcomes unravel intricate interdependencies among these parameters, furnishing an exhaustive comprehension of their collective influence on velocity and temperature profiles within the boundary layer;

  • This research significantly advances fundamental knowledge in nanofluid dynamics and imparts practical insights for optimizing heat transfer processes over stretching surfaces, particularly in the context of advanced heat transfer mechanisms;

  • The far-reaching implications extend across diverse engineering disciplines and materials science, offering invaluable guidance for the refinement and design of processes involving nanofluid flows over stretching sheets;

  • The augmentation of the parameter \({\delta }_{\mathfrak{e}}\) leads to a decrease in the temperature distribution field;

  • The increase in the parameters \({\delta }_{\mathfrak{c}},\mathcal{N}b\) and the Lewis Number results in a reduction of the concentration distribution field;

  • Higher \(\mathcal{R}\) values cause the temperature function to increase, whereas higher \(\mathcal{P}\mathcalligra{r}\) values cause it to decrease.

7 Future recommendation

This study uses OHAM Analysis to examine the contribution of boundary-layer flow of a nanofluid past over a stretched sheet, taking into account radiation effect, MHD, Cattaneo-Chritov heat flux, and variable diffusion coefficient. It is possible to examine the conducted investigation further by taking into consideration the flow over parallel discs, a stretched cylinder, and the Riga plate.