1 Introduction

Seeking clean-energy technology for fast heating is one of our resent research topics. Magnetic heating, based on magnetic eddy current, was our primary choice (the physical nature of this heating technology is namely the “skin effect”). Moreover, particle-based magnetic heating is chosen in our fresh study [1]. In the study of particulate system, the particles are spherical-shape modeled in most time. Adopting this shape, I start an initial basic study on the thermal consumption power of a single conductive metal ball. I surveyed a huge batch of literatures. Most related work on the mathematical analysis of the “skin effect” on a metal ball can be traced back to 1950s: William R. Smythe, in his book [2], derived a power equation for the eddy current on the surface of conductive metal ball; however, a minor error was clearly shown as asymmetry on the denominator of his power equation. Today, similar ambiguous power equation [3] is still adopted to analyze magnetic heating process. As one cannot figure out which equation is the correct, I revisited the route of William R. Smythe for the derivation of this power equation. A clarified heating power equation as well as more important results are provided and discussed in this paper.

2 Derivation of the power equation

William R. Smythe is a great scientist that I respect. Even his derivation has a minor error in reference [2], I should also give thanks to his contribution. The route directing to derive the equation is right. Following his route, I start the derivation with Maxwell equations. Neglecting displacement current, one has:

$$\nabla \times \vec{E} = - \frac{{\partial \vec{B}}}{\partial t}$$
(1)
$$\nabla \times \vec{B} = \mu \vec{i}$$
(2)

where \(\vec{E}\) is the induced electric field vector, \(\vec{B}\),\(\mu\) and \(\vec{i}\) are respectively, magnetic flux density vector, magnetic permeability, and induced electrical current. Let \(\vec{B} = \nabla \times \vec{A}\), and insert this into Eq. (1): \(\Rightarrow \nabla \times \vec{E} = - \frac{{\partial \left( {\nabla \times \vec{A}} \right)}}{\partial t} = - \nabla \times \frac{{\partial \vec{A}}}{\partial t}\), one can get:

$$\vec{E} = - \frac{{\partial \vec{A}}}{\partial t}\;{\text{or}}\;\vec{i} = - \sigma \frac{{\partial \vec{A}}}{\partial t}$$
(3)

where \(\sigma\) and \(\vec{A}\) are, respectively, electrical conductivity and magnetic vector potential. Next, when inserting \(\vec{B} = \nabla \times \vec{A}\) into Eq. (2), and let \(\nabla \cdot \vec{A} = 0\), one can get:

$$\nabla \times \left( {\nabla \times \vec{A}} \right) = \nabla \left( {\nabla \cdot \vec{A}} \right) - \nabla^{2} \vec{A} = - \nabla^{2} \vec{A}$$

or:

$$\nabla^{2} \vec{A} = - \mu \vec{i}$$
(4)

Combining Eq. (3) and Eq. (4), the magnetic vector potential equation inside a metal sphere is obtained as:

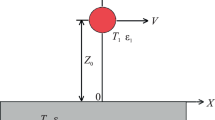
$$\nabla^{2} \vec{A} = \mu \sigma \frac{{\partial \vec{A}}}{\partial t}$$
(5)

Taking spherical coordinate system \(\left( {r,\phi ,\theta } \right)\), assuming that a metal sphere (located at zero point, with a radius of \(r = a\), the solid ball in Fig. 1) has uniform \(\sigma\) and \(\mu\), and is placed in a uniform oscillating magnetic field \(\vec{B}\). The direction of \(\vec{B}\) parallels \(\vec{z}\) axis. With these assumptions, the distribution of induced current inside the metal sphere should be symmetric around the \(\vec{z}\) axis. So, the value of the induced current is nothing to do with \(\phi\). Since, magnetic vector potential is located in \(\left( {x,y} \right)\) plane, it has \(\phi\) component as:

$$\vec{A} = \hat{\phi }A_{\phi } \left( {r,\theta ,t} \right)$$
(6)

where \(\hat{\phi }\) is a unit vector in the \(\phi\) direction. In \(\left( {x,y} \right)\) plane, it is expressed as:

$$\hat{\phi } = - \hat{x}\sin \phi + \hat{y}\cos \phi$$
(7)
Fig. 1
figure 1

Spherical coordinate system \(\left( {r,\theta ,\phi } \right)\), the direction of \(\vec{B}\) parallels \(\vec{z}\) axis. The solid sphere in the figure also represents a spherical metal particle with a radius of \(r = a\)

Full size image

Taking Eqs. (6–7) back into Eq. (5), and apply Laplace operator to \(\hat{\phi }\) \(\left( {\nabla^{2} \hat{\phi } = \frac{1}{{r^{2} \sin^{2} \theta }}\frac{{\partial^{2} }}{{\partial \phi^{2} }}\left( {\hat{\phi }} \right) = - \frac{1}{{r^{2} \sin^{2} \theta }}\hat{\phi }} \right)\), one can get:

$$\mu \sigma \hat{\phi }\frac{{\partial A_{\phi } }}{\partial t} = \nabla^{2} \left( {\hat{\phi }A_{\phi } } \right) = \hat{\phi }\nabla^{2} A_{\phi } + A_{\phi } \nabla^{2} \hat{\phi } = \hat{\phi }\left[ {\nabla^{2} A_{\phi } - \frac{{A_{\phi } }}{{r^{2} \sin^{2} \theta }}} \right]$$

Removing \(\hat{\phi }\) on both sides of above equation, one can get:

$$\mu \sigma \frac{{\partial A_{\phi } }}{\partial t} = \nabla^{2} A_{\phi } - \frac{{A_{\phi } }}{{r^{2} \sin^{2} \theta }}$$
(8)

Expanding \(\nabla^{2} A_{\phi }\) by using symmetric property \(\frac{{\partial A_{\phi } }}{\partial \phi } = 0\), gives:

$$\mu \sigma \frac{{\partial A_{\phi } }}{\partial t} = \frac{1}{{r^{2} }}\frac{\partial }{\partial r}\left( {r^{2} \frac{{\partial A_{\phi } }}{\partial r}} \right) + \frac{1}{{r^{2} \sin \theta }}\frac{\partial }{\partial \theta }\left( {sin\theta \frac{{\partial A_{\phi } }}{\partial \theta }} \right) - \frac{{A_{\phi } }}{{r^{2} \sin^{2} \theta }}$$
(9)

Let \(u = \cos \theta\), then:

$$\mu \sigma \frac{{\partial A_{\phi } }}{\partial t} = \frac{1}{{r^{2} }}\frac{\partial }{\partial r}\left( {r^{2} \frac{{\partial A_{\phi } }}{\partial r}} \right) + \frac{{\left( {1 - u^{2} } \right)^{\frac{1}{2}} }}{{r^{2} }}\frac{{\partial^{2} }}{{\partial u^{2} }}\left( {\left( {1 - u^{2} } \right)^{\frac{1}{2}} A_{\phi } } \right)$$
(10)

Assuming the angular frequency is \(\omega\), let \(A_{\phi } = real\left( {{\Theta }\left( \theta \right)r^{{ - \frac{1}{2}}} R\left( r \right)e^{j\omega t} } \right)\) (“real” means the real part of a complex number); substituting this in Eq. (10), dividing through by \({\Theta }\left( \theta \right)r^{{ - \frac{1}{2}}} R\left( r \right)e^{j\omega t}\), and using the method of variable separation, the above equation is transferred to:

$$\frac{{r^{2} }}{R}\frac{{d^{2} R}}{{dr^{2} }} + \frac{r}{R}\frac{dR}{{dr}} - \frac{1}{4} - j\mu \sigma \omega r^{2} = - \frac{{\left( {1 - u^{2} } \right)^{\frac{1}{2}} }}{{\Theta }}\frac{{d^{2} }}{{du^{2} }}\left[ {\left( {1 - u^{2} } \right)^{\frac{1}{2}} {\Theta }} \right] = n\left( {n + 1} \right)$$
(11)

Separate the above equation, one can get:

$$\left( {1 - u^{2} } \right)\frac{{d^{2} {\Theta }_{n} }}{{du^{2} }} - 2u\frac{{d{\Theta }_{n} }}{du} + \left( {n\left( {n + 1} \right) - \frac{1}{{\left( {1 - u^{2} } \right)}}} \right){\Theta }_{n} = 0$$
(12)

and:

$$\frac{{d^{2} R_{n} }}{{dr^{2} }} + \frac{1}{r}\frac{{dR_{n} }}{dr} - \left( {jp + \frac{{n\left( {n + 1} \right) + \frac{1}{4}}}{{r^{2} }}} \right)R_{n} = 0\quad p = \mu \sigma \omega$$
(13)

or:

$$\frac{{d^{2} R_{n} }}{{dy^{2} }} + \frac{1}{y}\frac{{dR_{n} }}{dy} - \left( {1 + \frac{{\left( {n + \frac{1}{2}} \right)^{2} }}{{y^{2} }}} \right)R_{n} = 0 \quad y = \left( {jp} \right)^{\frac{1}{2}} r$$
(14)

where Eq. (12) is associated Legendre differential equation with \(m = 1\), Eq. (14) is the modified Bessel equation written in \(y = \left( {jp} \right)^{\frac{1}{2}} r\). Combining Eqs. (12) and (14), the general solution of \(A_{\phi }\) is obtained as:

$$A_{\phi } = real\left( {\left( {F_{n} P_{n}^{1} \left( u \right) + C_{n} Q_{n}^{1} \left( u \right)} \right)\left( {D_{n} I_{{n + \frac{1}{2}}} \left( {\left( {jp} \right)^{\frac{1}{2}} r} \right) + E_{n} K_{{n + \frac{1}{2}}} \left( {\left( {jp} \right)^{\frac{1}{2}} r} \right)} \right)r^{{ - \frac{1}{2}}} e^{j\omega t} } \right)$$
(15)

In the above equation, \(\left( {F_{n} P_{n}^{1} \left( u \right) + C_{n} Q_{n}^{1} \left( u \right)} \right)\) is the general solution of associated Legendre differential equation, and \(\left( {D_{n} I_{{n + \frac{1}{2}}} \left( {\left( {jp} \right)^{\frac{1}{2}} r} \right) + E_{n} K_{{n + \frac{1}{2}}} \left( {\left( {jp} \right)^{\frac{1}{2}} r} \right)} \right)\) is the general solution of modified Bessel equation. \(F_{n}\), \(C_{n}\), \(D_{n}\), and \(E_{n}\) are constants which can be arbitrarily chosen. \(P_{n}^{1}\) and \(Q_{n}^{1}\) are, respectively, the associated Legendre functions of the first and second kind with \(m = 1\). \(I_{{n + \frac{1}{2}}}\) and \(K_{{n + \frac{1}{2}}}\) are, respectively, modified Bessel functions of first and second kind with the order of \(n + \frac{1}{2}\).

Outside the metal sphere, induced current is zero. The left side of Eq. (10) is zero. Let \(A_{\phi } = real\left( {{\Theta }\left( \theta \right)R^{\prime}\left( r \right)e^{j\omega t} } \right)\), again, taking it into Eq. (10), dividing through by \({\Theta }\left( \theta \right)R^{\prime}\left( r \right)e^{j\omega t}\) give:

$$\frac{d}{dr}\left( {r^{2} \frac{{dR^{\prime}}}{dr}} \right) - n\left( {n + 1} \right)R^{\prime} = 0$$
(16)

The general solution for Eq. (16) is:

$$R^{\prime} = Fr^{n} + Cr^{ - n - 1}$$
(17)

Holding above derivations, initially, the order of \(n\) should be determined. To obtain this value, let’s see the relationship between the projection of the field vector \(\vec{B}\) on \(\vec{r}\) (\(= B\cos \theta \vec{r}\)) and its phasor component \(A_{\phi }\):

\(\left( {\nabla \times \vec{A}} \right)_{{\vec{r}}} = \left( {\frac{1}{r\sin \theta }\left( {\frac{\partial }{\partial \theta }\left( {\sin \theta A_{\phi } } \right)} \right)} \right)\vec{r} = B\cos \theta \vec{r}\) or

$$d\left( {\sin \theta A_{\phi } } \right) = \left( {Br\sin \theta \cos \theta } \right)d\theta$$
(18)

Integrate both sides of Eq. (18), it clearly holds:

\(\sin \theta A_{\phi } = \mathop \int \nolimits_{{}}^{\theta } \left( {Br\sin \theta \cos \theta } \right)d\theta = Br\mathop \int \nolimits_{{}}^{\theta } \sin \theta d\left( {\sin \theta } \right) = \frac{1}{2}Br \sin^{2} \theta\), \(\Rightarrow\)

$$A_{\phi } = \frac{1}{2}Br\sin \theta \Rightarrow A_{\phi } = \frac{1}{2}BrP_{1}^{1} \left( u \right)$$
(19)

From above equation, the order of \(n\) in both Eq. (15) and (17) should be “1”. So, Eq. (17) is simplified as:

$$\vec{A} = \vec{A}_{o} = \hat{\phi }\frac{1}{2}B\left( {r + Cr^{ - 2} } \right)\sin \theta , a < r < \infty$$
(20)

Taking \(n = 1\) into Eq. (15), since inside a sphere, at the zero point, \(K_{{n + \frac{1}{2}}} \to \infty\), so, \(E_{n}\) must \(= 0\); when \(\theta = 0, 2\pi , 4\pi \ldots\), \(Q_{1}^{1} \left( {u = \cos \theta } \right) = \infty\), so, \(C_{n}\) should also be zero. Thus, Eq. (15) is simplified as:

$$\vec{A} = \vec{A}_{i} = \hat{\phi }\frac{1}{2}Br^{{ - \frac{1}{2}}} DI_{\frac{3}{2}} \left( {\left( {jp} \right)^{\frac{1}{2}} r} \right)\sin \theta , 0 < r < a$$
(21)

Now, there still has two unknow values: \(C\) and \(D\) (note: \(C\) and \(D\) are complex numbers). These values can be determined by boundary conditions at \(r = a\):

$$\vec{A}_{o} = \vec{A}_{i} \;{\text{and}}\; \mu_{0} \frac{\partial }{\partial r}\left( {r\sin \theta A_{i} } \right) = \mu \frac{\partial }{\partial r}\left( {r\sin \theta A_{o} } \right)$$
(22)

From above conditions, one can get (\(v = \left( {jp} \right)^{\frac{1}{2}} a\)):

$$D = \frac{{3\mu va^{\frac{3}{2}} }}{{\left( {\mu - \mu_{0} } \right)vI_{{ - \frac{1}{2}}} + \left[ {\mu_{0} \left( {1 + v^{2} } \right) - \mu } \right]I_{\frac{1}{2}} }}$$
(23)
$$C = \frac{{\left( {2\mu + \mu_{0} } \right)vI_{{ - \frac{1}{2}}} - \left[ {\mu_{0} \left( {1 + v^{2} } \right) + 2\mu } \right]I_{\frac{1}{2}} }}{{\left( {\mu - \mu_{0} } \right)vI_{{ - \frac{1}{2}}} + \left[ {\mu_{0} \left( {1 + v^{2} } \right) - \mu } \right]I_{\frac{1}{2}} }}a^{3}$$
(24)

when \(C\) and \(D\) are fixed with Eqs. (24) and (23) respectively, \(\vec{A}\) is obtained. So, the value of current \(\vec{i}\) distributed inside the metal ball is determined by:

$$\vec{i} = - jp\mu^{ - 1} \vec{A}_{i}$$
(25)

The power of the induced current is (in the following, \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{i}\) vs. \(\hat{i}\), \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D}\) vs. \(\hat{D}\), \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A}_{i}\) vs. \(\hat{A}_{i}\) are complex conjugate numbers):

$$P\left( r \right) = \int\limits_{0}^{r} {dP} = \int\limits\int\limits\int\limits_{0}^{r} {\frac{1}{2}\sigma^{ - 1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{i} \hat{i}dV} = \int\limits\int\limits_{{\left( {0,0} \right)}}^{{\left( {r,\pi } \right)}} {\sigma^{ - 1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{i} \hat{i}\pi r^{2} \sin \theta drd\theta }$$
$$= \sigma^{ - 1} \pi \left( {p\mu^{ - 1} } \right)^{2} \int\limits\int\limits_{{\left( {0,0} \right)}}^{{\left( {r,\pi } \right)}} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A}_{i} \hat{A}_{i} r^{2} \sin \theta drd\theta }$$
$$= \frac{1}{4}\sigma^{ - 1} \pi \left( {p\mu^{ - 1} } \right)^{2} B^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} \hat{D}\left( {\mathop \int \limits_{0}^{r} I_{\frac{3}{2}} \left( {\left( {jp} \right)^{\frac{1}{2}} r} \right)I_{\frac{3}{2}} \left( {\left( { - jp} \right)^{\frac{1}{2}} r} \right)rdr} \right)\mathop \int \limits_{0}^{\pi } \sin^{3} \theta d\theta$$
(26)

Since \(\mathop \int \limits_{0}^{\pi } \sin^{3} \theta d\theta = \frac{4}{3}\), Eq. (26) is modified as:

$$P\left( r \right) = \frac{1}{3}\pi \sigma \omega^{2} B^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} \hat{D}\mathop \int \limits_{0}^{r} I_{\frac{3}{2}} \left( {\left( {jp} \right)^{\frac{1}{2}} r} \right)I_{\frac{3}{2}} \left( {\left( { - jp} \right)^{\frac{1}{2}} r} \right)rdr$$
(27)

Next, one still needs to simplify the integration term of Eq. (27). Let \(k_{q} = \left( {jp} \right)^{\frac{1}{2}}\), and \(k_{p} = \left( { - jp} \right)^{\frac{1}{2}}\):

$$\mathop \int \limits_{0}^{r} I_{\frac{3}{2}} \left( {\left( {jp} \right)^{\frac{1}{2}} r} \right)I_{\frac{3}{2}} \left( {\left( { - jp} \right)^{\frac{1}{2}} r} \right)rdr$$
$$= \left( {2p} \right)^{ - 1} \left[ {k_{p} rI_{{ - \frac{1}{2}}} \left( {k_{p} r} \right)I_{\frac{1}{2}} \left( {k_{q} r} \right) + k_{q} rI_{{ - \frac{1}{2}}} \left( {k_{q} r} \right)I_{\frac{1}{2}} \left( {k_{p} r} \right) - 2I_{{ - \frac{1}{2}}} \left( {k_{q} r} \right)I_{\frac{1}{2}} \left( {k_{p} r} \right)} \right]$$
$$= \left( {2\pi rp^{\frac{3}{2}} } \right)^{ - 1} \left[ {\begin{array}{*{20}c} { - j\left( {jp} \right)^{\frac{1}{2}} r\left( {\sinh \left( {\left( {2p} \right)^{\frac{1}{2}} r} \right) + j\sin \left( {\left( {2p} \right)^{\frac{1}{2}} r} \right)} \right)} \\ { + \left( {jp} \right)^{\frac{1}{2}} r\left( {\sinh \left( {\left( {2p} \right)^{\frac{1}{2}} r} \right) - j\sin \left( {\left( {2p} \right)^{\frac{1}{2}} r} \right)} \right)} \\ { - 2\left( {\cosh \left( {\left( {2p} \right)^{\frac{1}{2}} r} \right) - \cos \left( {\left( {2p} \right)^{\frac{1}{2}} r} \right)} \right)} \\ \end{array} } \right]$$
$$= \left( {2\pi rp^{\frac{3}{2}} } \right)^{ - 1} \left( {\begin{array}{*{20}c} {\left( {1 - j} \right)j^{\frac{1}{2}} p^{\frac{1}{2}} r\left( {\sinh \left( {\left( {2p} \right)^{\frac{1}{2}} r} \right) + \sin \left( {\left( {2p} \right)^{\frac{1}{2}} r} \right)} \right)} \\ { - 2\left( {\cosh \left( {\left( {2p} \right)^{\frac{1}{2}} r} \right) - \cos \left( {\left( {2p} \right)^{\frac{1}{2}} r} \right)} \right)} \\ \end{array} } \right)$$

Since \(\left( {1 - j} \right)j^{\frac{1}{2}} = \sqrt {\left( {1 - j} \right)^{2} j} = \sqrt {\left( {1 + j^{2} - 2j} \right)j} = \sqrt 2\), so:

$$\int\limits_{0}^{r} {I_{{\frac{3}{2}}} \left( {\left( {jp} \right)^{{\frac{1}{2}}} r} \right)I_{{\frac{3}{2}}} \left( {\left( { - jp} \right)^{{\frac{1}{2}}} r} \right)rdr} = \left( {\pi rp^{{\frac{3}{2}}} } \right)^{{ - 1}} \left( {\begin{array}{*{20}c} {\frac{1}{2}\left( {2pr^{2} } \right)^{{\frac{1}{2}}} \left( {\sinh \left( {\left( {2pr^{2} } \right)^{{\frac{1}{2}}} } \right) + \sin \left( {\left( {2pr^{2} } \right)^{{\frac{1}{2}}} } \right)} \right)} \\ { - \cosh \left( {\left( {2pr^{2} } \right)^{{\frac{1}{2}}} } \right) + \cos \left( {\left( {2pr^{2} } \right)^{{\frac{1}{2}}} } \right)} \\ \end{array} } \right)$$
(28)

\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} \hat{D}\) is expanded as (the details for the derivation of \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} \hat{D}\) can be seen in Appendix 1):

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} \hat{D} & = \frac{{3\mu \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{v} a^{\frac{3}{2}} }}{{\left( {\mu - \mu_{0} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{v} I_{{ - \frac{1}{2}}} \left( {\left( {jp} \right)^{\frac{1}{2}} a} \right) + \left[ {\mu_{0} \left( {1 + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{v}^{2} } \right) - \mu } \right]I_{\frac{1}{2}} \left( {\left( {jp} \right)^{\frac{1}{2}} a} \right)}} \cdot \frac{{3\mu \hat{v}a^{\frac{3}{2}} }}{{\left( {\mu - \mu_{0} } \right)\hat{v}I_{{ - \frac{1}{2}}} \left( {\left( { - jp} \right)^{\frac{1}{2}} a} \right) + \left[ {\mu_{0} \left( {1 + \hat{v}^{2} } \right) - \mu } \right]I_{\frac{1}{2}} \left( {\left( { - jp} \right)^{\frac{1}{2}} a} \right)}} \\ & = \frac{{9\pi \mu^{2} a^{6} p^{\frac{3}{2}} }}{{\left( {\mu - \mu_{0} } \right)^{2} \left[ {\left( {pa^{2} + 1} \right)O + \left( {pa^{2} - 1} \right)o - m\left( {S + s} \right)} \right] + \left( {\mu - \mu_{0} } \right)\mu_{0} pa^{2} m\left( {S - s} \right) + \mu_{0}^{2} p^{2} a^{4} \left( {O - o} \right)}} \\ \end{aligned}$$
(29)

where \(m = \left( {2p} \right)^{\frac{1}{2}} a\), \(O = \cosh m\), \(o = \cos m\), \(S = \sinh m\), and \(s = \sin m\). Next, taking Eqs. (28), (29) into (27), one has:

$$P\left( {r \le a} \right) = \frac{{3\pi \sigma \omega^{2} B^{2} \mu^{2} a^{6} G\left( r \right)}}{{\left( {\mu - \mu_{0} } \right)^{2} \left[ {\left( {pa^{2} + 1} \right)O + \left( {pa^{2} - 1} \right)o - m\left( {S + s} \right)} \right] + \left( {\mu - \mu_{0} } \right)\mu_{0} pa^{2} m\left( {S - s} \right) + \mu_{0}^{2} p^{2} a^{4} \left( {O - o} \right)}}$$
(30)

where:

$$G\left( r \right) = \frac{1}{r}\left( {\begin{array}{*{20}c} {\frac{1}{2}\left( {2pr^{2} } \right)^{\frac{1}{2}} \left( {\sinh \left( {\left( {2pr^{2} } \right)^{\frac{1}{2}} } \right) + \sin \left( {\left( {2pr^{2} } \right)^{\frac{1}{2}} } \right)} \right)} \\ { - \cosh \left( {\left( {2pr^{2} } \right)^{\frac{1}{2}} } \right) + \cos \left( {\left( {2pr^{2} } \right)^{\frac{1}{2}} } \right)} \\ \end{array} } \right)$$

Note that \(pr^{2}\) is dimensionless, when \(r = a\), the numerator of the power equation listed in reference [2] is same with Eq. (30). However, errors are clearly located on the denominator. In this paper, the derivation of \(G\left( r \right)\) is innovative. Its importance can be shown in the following discussions.

3 Discussions

Now, let \(\mu_{r} = \frac{\mu }{{\mu_{0} }}\), Eq. (30) is transferred as:

$$P\left( {r \le a} \right) = \frac{{3\pi \sigma \omega^{2} B^{2} a^{6} \mu_{r}^{2} G\left( r \right)}}{{\left[ {\begin{array}{*{20}c} {\left( {\mu_{r} - 1} \right)^{2} \left[ {\left( {pa^{2} + 1} \right)O + \left( {pa^{2} - 1} \right)o - m\left( {S + s} \right)} \right]} \\ { + \left( {\mu_{r} - 1} \right)pa^{2} m\left( {S - s} \right) + p^{2} a^{4} \left( {O - o} \right)} \\ \end{array} } \right]}}$$
(31)

Obviously, for pure conductive metal (such as copper), \(\mu_{r} = 1\), so:

$$P\left( {r \le a} \right) = \frac{{3\pi \sigma \omega^{2} B^{2} a^{2} G\left( r \right)}}{{p^{2} \left( {O - o} \right)}}$$
(32)

Our objective to derive \(P\left( {r \le a} \right)\) and \(G\left( r \right)\) is to study the relationship between the wave penetration depth (\(\delta = \sqrt{\frac{2}{p}}\)) and the radius of a metal sphere. The importance of this study will direct the design of magnetic heating material (such as, saving their mass etc.). The discussions on the power equation (Eq. (31)) are separated in the following two parts.

3.1 When \({\varvec{r}} = {\varvec{a}}\)

Apparently, when \(r = a\), \(P\left( a \right)\) is the total power obtained by a metal sphere. Take \(r = a\) into \(G\left( r \right)\), one can find that,

$$P\left( a \right) = \frac{{3\pi \sigma \omega^{2} B^{2} a^{5} \mu_{r}^{2} \left( {\frac{1}{2}m\left( {S + s} \right) - O + o} \right)}}{{\left[ {\left( {\mu_{r} - 1} \right)^{2} \left[ {\left( {pa^{2} + 1} \right)O + \left( {pa^{2} - 1} \right)o - m\left( {S + s} \right)} \right] + \left( {\mu_{r} - 1} \right)pa^{2} m\left( {S - s} \right) + p^{2} a^{4} \left( {O - o} \right)} \right]}}$$
(33)

Now, let \(x = \frac{1}{2}\left( {2pa^{2} } \right)^{\frac{1}{2}}\) or \(x = \frac{a}{\delta }\), also notice that \(m = 2x\), get:

$$P\left( a \right) = \frac{{3\pi \sigma \omega^{2} B^{2} a^{5} \mu_{r}^{2} \left( {x\left( {S + s} \right) - O + {\text{o}}} \right)}}{{\left[ {\left( {\mu_{r} - 1} \right)^{2} \left[ {\left( {2x^{2} + 1} \right)O + \left( {2x^{2} - 1} \right)o - 2x\left( {S + s} \right)} \right] + 4\left( {\mu_{r} - 1} \right)x^{3} \left( {S - s} \right) + 4x^{4} \left( {O - o} \right)} \right]}}$$
(34)

When \(a \gg \delta\), \(x \to \infty\), and:

$$P\left( a \right) \approx \frac{{3\pi \sigma \omega^{2} B^{2} a^{5} \mu_{r}^{2} x\frac{{e^{2x} }}{2}}}{{\left[ {\left( {\mu_{r} - 1} \right)^{2} \left[ {2x^{2} \frac{{e^{2x} }}{2} - 2x\frac{{e^{2x} }}{2}} \right] + 4\left( {\mu_{r} - 1} \right)x^{3} \frac{{e^{2x} }}{2} + 4x^{4} \frac{{e^{2x} }}{2}} \right]}} \approx \frac{{3\pi \sigma \omega^{2} B^{2} a^{5} \mu_{r}^{2} }}{{4x^{3} }}$$
(35)

Take \(x = \frac{a}{\delta }\), \(p = \mu \sigma \omega\) and \(\delta = \sqrt{\frac{2}{p}}\) into above equation, a nice form of \(P\left( a \right)\) looks like:

$$P\left( a \right) \approx \frac{{3\pi \mu_{r}^{2} B^{2} }}{2\mu }\delta \omega a^{2} = \frac{{3\pi \mu_{r}^{2} B^{2} }}{2\mu }\sqrt {\frac{2}{\mu \sigma \omega }} \omega a^{2} = \frac{{3\pi \mu_{r}^{2} B^{2} }}{{\mu \sqrt {2\mu \sigma } }}\sqrt \omega a^{2}$$
(36)

So, when \(a \gg \delta\), or \(\omega \to \infty\), \(P\left( a \right) \propto a^{2}\) and \(P\left( a \right) \propto \sqrt \omega\).

For pure conductive metal, taking \(\mu_{r} = 1\) into Eq. (34), one has:

$$P\left( a \right) = \frac{{3\pi \omega B^{2} \delta^{2} a}}{2\mu }\left[ {\frac{a}{\delta }\frac{{\sinh \left( {2a/\delta } \right) + \sin \left( {2a/\delta } \right)}}{{\cosh \left( {2a/\delta } \right) - \cos \left( {2a/\delta } \right)}} - 1} \right]$$
(37)

When \(a \ll \delta\),

$$P\left( a \right) = \frac{{3\pi \omega B^{2} \delta^{2} a}}{2\mu }\left[ {\frac{{x\left( {S + {\text{s}}} \right) - \left( {O - {\text{o}}} \right)}}{{\left( {O - {\text{o}}} \right)}}} \right]$$
(38)

Let \(F\left( x \right) = \frac{{x\left( {S + {\text{s}}} \right) - \left( {O - {\text{o}}} \right)}}{{\left( {O - {\text{o}}} \right)}}\), \(F\left( x \right)\) can be evaluated as (the details for the derivation of \(F\left( x \right)\) can be seen in Appendix 2):

$$F\left( x \right) \approx \frac{4}{45}x^{4}$$
(39)

Taking this value back in to Eq. (38):

$$P\left( a \right) \approx \frac{{3\pi \omega B^{2} \delta^{2} a}}{2\mu }\frac{4}{45}x^{4} = \frac{{3\pi \omega B^{2} \delta^{2} a}}{2\mu }\frac{4}{45}\left( {\frac{a}{\delta }} \right)^{4} = \frac{1}{15}\pi B^{2} a^{5} \omega^{2} \sigma$$
(40)

Equation (40) tells that, when \(a \ll \delta\), \(P\left( a \right)\) is nothing related with magnetic permeability \(\mu\); \(P\left( a \right) \propto a^{5}\) and \(P\left( a \right) \propto \omega^{2}\).

Above, I have discussed the situations of \(a \ll \delta\) and \(a \gg \delta\). Next, let’s talk about \(a = \delta\). When \(a = \delta\), then \(x = 1\), from Eq. (34):

$$\begin{aligned} P\left( a \right) = P\left( \delta \right) & = \frac{{3\pi \sigma \omega^{2} \mu_{r}^{2} B^{2} \delta^{5} \left( {\left( {S + s} \right) - O + {\text{o}}} \right)}}{{\left[ {\left( {\mu_{r} - 1} \right)^{2} \left[ {3O + o - 2\left( {S + s} \right)} \right] + 4\left( {\mu_{r} - 1} \right)\left( {S - s} \right) + 4\left( {O - o} \right)} \right]}} \\ & = \frac{{3\pi \sigma \omega^{2} \mu_{r}^{2} B^{2} \delta^{5} \left( {0.3578} \right)}}{{1.7981\left( {\mu_{r} - 1} \right)^{2} + 4\left( {\mu_{r} - 1} \right)\left( {2.7176} \right) + 4\left( {4.1783} \right)}} \\ \end{aligned}$$
(41)

For pure conductive metal (\(\mu_{r} = 1\)):

$$P\left( a \right) = P\left( \delta \right) = \frac{{3\pi \sigma \omega^{2} B^{2} \delta^{5} \left( {0.3578} \right)}}{{4\left( {4.1783} \right)}} = 0.06422\pi \sigma \omega^{2} B^{2} \delta^{5} = 0.06422\pi \sigma \omega^{2} B^{2} a^{5}$$
(42)

Equation (41) and (42) show that, when \(a = \delta\), \(P\left( a \right) \propto \omega^{2}\) and \(\propto \delta^{5}\) or \(a^{5}\).

3.2 When \({\varvec{r}} \le {\varvec{a}}\), power distribution inside a metal sphere

The objective of Eq. (31) ( \(P\left( {r \le a} \right)\)) is to clarify the power obtained below a volume area of \(r \le a\) for a metal sphere, so the power obtained in the \(\delta\)-shell can be estimated. Now, let’s define a relative power ratio \(P_{\delta }\), such that (\(a \ge \delta\)):

$$P_{\delta } = 1 - \frac{{P\left( {r \le a - \delta } \right)}}{P\left( a \right)}$$
(43)

For a metal sphere (\(\mu_{r} \ge 1\)), when \(\omega \to 0\), apparently, \(P_{\delta } \to 1\); however, when \(\omega \to \infty\), let \(r_{\delta } = a - \delta\), \(x_{\delta } = \left( {2pr_{\delta }^{2} } \right)^{\frac{1}{2}}\), and \(x_{a} = \left( {2pa^{2} } \right)^{\frac{1}{2}}\), meanwhile, \(x_{\delta } ,x_{a} \to \infty\), and then:

$$P_{\delta } = 1 - \mathop {\lim }\limits_{\omega \to \infty } \frac{{G\left( {r_{\delta } } \right)}}{G\left( a \right)} = 1 - \mathop {\lim }\limits_{\omega \to \infty } \frac{{\frac{1}{{r_{\delta } }}\left( {\frac{1}{2}x_{\delta } \left( {\sinh x_{\delta } + \sin x_{\delta } } \right) - \cosh x_{\delta } + \cos x_{\delta } } \right)}}{{\frac{1}{a}\left( {\frac{1}{2}x_{a} \left( {\sinh x_{a} + \sin x_{a} } \right) - \cosh x_{a} + \cos x_{a} } \right)}}$$
$$= 1 - \mathop {\lim }\limits_{\omega \to \infty } \frac{{\frac{1}{{r_{\delta } }}\left( {\frac{1}{2}x_{\delta } \frac{{e^{{x_{\delta } }} }}{2}} \right)}}{{\frac{1}{a}\left( {\frac{1}{2}x_{a} \frac{{e^{{x_{a} }} }}{2}} \right)}} = 1 - \mathop {\lim }\limits_{\omega \to \infty } \frac{{ax_{\delta } e^{{x_{\delta } }} }}{{r_{\delta } x_{a} e^{{x_{a} }} }} = 1 - \mathop {\lim }\limits_{\omega \to \infty } e^{{x_{\delta } - x_{a} }}$$
$$= 1 - \mathop {\lim }\limits_{\omega \to \infty } e^{{ - \left( {2p} \right)^{\frac{1}{2}} \delta }} = 1 - e^{ - 2}$$

Or, simply:

$$P_{\delta } = 1 - e^{ - 2} \approx 86.5\%$$
(44)

Above equation is a very important conclusion. It tells that when the frequency of the magnetic field is high, the value of \(P_{\delta }\), or the power ratio obtained inside the surface shell with a depth of \(\delta\) (penetration depth), is nothing related to the radius of the sphere (\(a\)), and angular frequency (\(\omega\)) of the magnetic field. It is a constant value: \(1 - e^{ - 2}\). Bellow, I will show a few examples of Eq. (43).

Figure 2 gives the first example. Using copper sphere (\(\sigma = 5.7 \times 10^{7} {\text{S}}/{\text{M}}\), \(\mu_{r} = 1\)), let \(a = 1\;{\text{mm}}\), \(B = 16\;{\text{mT}}\) with a frequency of \(f = 100\;{\text{kHz}}\), thus, \(\delta = 0.21\;{\text{mm}}\). From the figure, the power obtained near the center (\(r \le 0.5\;{\text{mm}}\)) of the sphere is nearly vacant. Below \(r \le a - \delta = 0.78\;{\text{mm}}\), the obtained power is only:

$$\frac{{P\left( {r \le a - \delta } \right)}}{P\left( a \right)} = 12.59\%$$
(45)
Fig. 2
figure 2

Power distribution inside copper sphere: \(a = 1\;{\text{mm}}\), \(\mu_{r} = 1\), \(B = 16\;{\text{mT}}\), \(f = 100\;{\text{kHz}}\), \(\sigma = 5.7 \times 10^{7} \;{\text{S}}/{\text{M}}\)

Full size image

This means that above 87% power is located in the surface shell with a thickness of \(\delta\).

Again, let \(a = 1\;{\text{mm}}\), \(f\) has a range from \(10\;{\text{kHz}}\) to \(1000\;{\text{kHz}}\), a distribution of \(P_{\delta }\) for a copper sphere is outlined in Fig. 3. From this figure, one can find the curve of \(P_{\delta }\) is above 86%, and the limit of \(P_{\delta }\) is approaching \(1 - e^{ - 2}\). When the frequency is relatively lower, the penetration depth (\(\delta\)) is higher, and \(P_{\delta }\) approaches its limit (\(\approx 1\)). Moreover, “\(P_{\delta } \approx 1\)” also means best power efficiency without wasting of metal mass. Because, at this point, \(a \approx \delta\), the metal sphere is fully loaded with induced current and there is no vacant power area as located in Fig. 2.

Fig. 3
figure 3

\(P_{\delta }\) vs. frequencies: \(B = 16\;{\text{mT}}\), copper sphere with \(a = 1\;{\text{mm}}\), \(\mu_{r} = 1\), and \(\sigma = 5.7 \times 10^{7}\; {\text{S}}/{\text{M}}\)

Full size image

Figure 4 shows 5 cases (\(f = 30,50,100,200,500\;{\text{kHz}}\)) of \(P_{\delta }\) according to radius change (from \(a = \delta\) to \(a = 1\;{\text{mm}}\)) of a copper sphere. Apparently, their max value, which is “1”, all start from \(a = \delta\). Also, one can see that the initial slope of the power curve gets steeper when the frequency comes higher. In other words, the decreasing rate of \(P_{\delta }\) becomes faster with the increase of frequency. Moreover, the bottom limit, which is “\(1 - e^{ - 2}\)”, finally arrives on the right site of the figure.

Fig. 4
figure 4

\(P_{\delta }\) vs. radius (from \(a = \delta\) to \(a = 1\;{\text{mm}}\)): \(B = 16\;{\text{mT}}\), copper sphere with \(\mu_{r} = 1\) and \(\sigma = 5.7 \times 10^{7} \;{\text{S}}/{\text{M}}\)

Full size image

4 Conclusion

Following William R. Smythe’s route, in this paper, I re-derived the power equation “\(P\left( {r \le a} \right)\)” for the eddy current distribution inside a metal sphere under the action of uniform oscillating magnetic field. The ambiguous errors of the equation shown in reference [2, 3] are clarified. Based on \(P\left( {r \le a} \right)\), I discussed the following important results:

  • For a conductive metal sphere (\(\mu_{r} \ge 1\)):

    • The value of \(P\left( a \right)\) is proportional to \(\sqrt \omega\) when \(\omega\) is very high or \(a \gg \delta\) (Eq. (36)).

    • \(P_{\delta }\) is defined, and its limit is calculated: \(1 - e^{ - 2}\). And, the most efficient \(P\) comes from \(a = \delta\) (Eq. 44).

    • When \(a = \delta\), \(P\left( a \right)\) is proportional both to \(\omega^{2}\) and to \(a^{5}\) (Eq. (41)).

  • For a pure conductive metal sphere (\(\mu_{r} = 1\)): when \(a \ll \delta\), \(P\left( a \right)\) is nothing related with magnetic permeability \(\mu\), and is proportional both to \(\omega^{2}\) and to \(a^{5}\) (Eq. (40)).

At the end of this paper, I provided three examples to detail the physical meanings of \(P_{\delta }\).