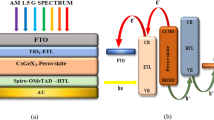
Abstract
Here, the first-principle calculations with the density functional theory calculations with PBE exchange–correlation functional were employed in investigating the effect of Cesium in the properties and optoelectronic performance of MAPb0.5Sn0.5I3 perovskite using A-site cation engineering technique. The control and Cesium based perovskites were generated and computed through CASTEP analysis from Material studio to determine their properties as well as optoelectronic performance. The findings revealed an improved properties of Cesium added perovskite compared to control ones. However, above 15%Cesium, phase separation was seen which declined the quality of the perovskite films. Moreover, simulation results of perovskites added with Cesium to 15% have demonstrated to have an improved optoelectronic performance as well as thermal stability by maintaining about 76% compared to the control which can retain about 39% of their initial power conversion efficiency after 15 days of aging at 85 °C in the ambient condition. This research presents a viable approach to investigate the impact of cation composition tuning on band gap, which can be extended to other perovskites. Additionally, it offers a broad set of design guidelines prior experiments for attaining a targeted band gap and modifying perovskite crystallization to enhance the characteristics, thermal stability, and optoelectronic performance of perovskite solar cells.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Comparative to other solar cells types on material costs being cheap, simple production, and their solar capabilities on generating high power conversion efficiency (PCE) [1], organometal halide perovskites, which are at the center of the next-generation photovoltaic technologies, have gained significant attention [2, 3]. Perovskite solar cells’ (PSCs) photovoltaic performance has undergone significant improvements. In comparison to traditional solar technology based on crystalline silicon, the PCE has increased from 3.8% [4] to roughly 26.1% [5, 6]. However, the device instability due to heat effect continue to be a major obstacle towards commercialization [7, 8]. It is understood that low formation energy halide perovskites are inherently unstable, making them susceptible to degradation from a variety of outside influences such as temperature and humidity [9]. Therefore, the main challenge is to improve the properties of the perovskite to obtain a thermally stable structure with improved optoelectronic performance.
Recently, a number of theoretical investigations have been used to improve the properties of perovskites which resulted into devices with increased thermal stability [5, 10, 11]. 1,3,7-trimethylxanthine was employed as an additive to boost the activation energy of perovskite films creating an improved optoelectronic performance caused by molecular lock between carboxyl group and the Pb/Sn ions [12]. Lin et al. [13] demonstrated that the breakdown of the perovskite layer when exposed to continuous illumination may be slowed down by adding a piperidinium salt to the perovskites. Hexyl trimethyl ammonium bromide was additionally deposited on top of the perovskite film to produce a thin layer of wide-bandgap halide perovskites. With one sun's light and 85% relative humidity, the in-situ reaction produced an excellent stability and PCE of 22.7% [14]. Either, investigations have been done on distinct phases of the MA(Pb: Sn)I3 perovskites [15, 16].
Many experimental and theoretical data show that the Pb: Sn phase transitions occur from around 110 to 330K [17]–[19]. Due to the perovskite's ability to undergo phase changes under varied temperature conditions, the features of each phase are crucial [20]. However, just a few studies on the properties and optoelectronic performance of MAPb0.5Sn0.5I3 perovskites have been published concurrently, leaving their properties unknown.
In this study, the first-principle analytical approach through CASTEP analysis using Materials Studio was used to investigate the effect of Cesium (Cs) on raising the properties and optoelectronic performances of halide Pb-Sn perovskite using A-site cation engineering technique. This offers a broad set of design guidelines prior experiments for attaining a targeted band gap and modifying perovskite crystallization to enhance the characteristics, thermal stability, and optoelectronic performance of perovskite solar cells. The obtained structures have shown the perovskite crystal’s formation was slowed down after addition of up to 15%Cs due to strong chemical bonding between the ions. Additionally, the structures were found to have a slower rate of crystallization, enhancing the homogeneity of the film shape, a low defect density, and a decreased rate of Sn2+ oxidation by lattice contraction achieved by its small ionic radius, all of which contributed to the improved optical and thermodynamic properties as well as optoelectronic performance of Cs-added perovskite materials. To put off the phase separation of the perovskite brought on by the high concentration of Cs+ in the perovskite, an optimum amount of Cs+ was used to the control sample [21]. This optimum amount was achieved by DFT theoretical approach using the CASTEP analysis in the Materials Studio software.
2 Methodology and simulation
The perovskite materials were computed using the DFT method and the CASTEP analysis from the Materials Studio simulation package was used to complete the calculations [22, 23]. The Crystallographic Information Files were obtained from the Materials Project and the Crystallography Open Database[24]–[27]. The ultrasoft pseudopotential corresponding to a Perdew, Burke and Ernzerhof (PBE) exchange–correlation (XC) functional was employed. An energy cutoff of 500 eV, which have been adopted in the previous theoretical work in the similar systems, is employed and the atomic positions are optimized using XC functional until the maximum force less than 0.02 eV Å−1 which was enough to obtain a relaxed structure [19]. The compounds were modeled using 4 × 3 × 4 Γ-centered grids k-points. Tests were made for the 4 × 3 × 4 grid in the similar systems in previous theoretical work demonstrating that the k-point grids are satisfactory for the calculations [28]. Cell relaxing was carried out in accordance with the CASTEP analysis documentation [29]. The optical properties such as dielectric functions, refractive index, absorption coefficient were calculated using the following formulas [23, 30]. Either the optoelectronic performance were mathematically computed using formulas 14–18 [31] and thermal stability analysis was computed using the kinetic modeling offered by Myong and Lim in 2006 [32] utilizing formulas 19–24 respectively adopted from previous studies.
where ε1 (ω) and ε2 (ω)- the real and imaginary parts, ω—phonon frequency, P- integral's principal value, e—electronic charge, Ω -unit cell volume, u—polarization of the incident electric field unit vector, and \({\Psi }_{k}^{c}\) and \({\Psi }_{k}^{v}\)—conduction and valence band (VB) electrons’ wave function at a specific k, n- refractive index, α-absorption coefficient,—\({E}_{photon}\)energy of the photon, h- Planck's constant, c- speed of light in vacuum, λ-frequency, I-light intensity, KB—Boltzmann constant, T-temperature and q-elementary charge.
3 Results and discussions
3.1 Structure parameters
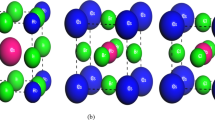
Figure 1 is the intended A-cation perovskites with typical compounds CsxMA1-xSn0.5Pb0.5I3, where x = 0, 0.1, 0.15 and 0.2. To determine whether optimizing structures before simulation is still relevant, the structures were simulated using the same values for the energy cut-off (ecutwfc). The compounds adopt a perovskite-type structure that consists of a network of [Pb0.5Sn0.5I6]−4 octahedra with corner-sharing Sn or Pb atoms occupying the metal site at random [33]. The members crystallize in orthorhombic at room temperature as indicated in the previous works [34]–[36]. To obtain the stable phase structures of the compounds as shown in Table 1, the lattice parameters were optimized by performing precise calculations for the energy as a function of volume. The stresses on the atoms are minimized at a specific cell volume where the ratios of the unit cell vectors are maintained at experimental values using initial estimates of experimental lattice characteristics. Except for the control sample which converted to an isostructure at a temperature of 60 °C, all Cesium added perovskites were found to contain an orthorhombic phase as in Table 2. This is consistent with earlier related research on the control sample [18]. Upon Cs addition, the lattice volume gradually decreased due to the partial substitution of larger MA+ cations with smaller Cs+ cations [21]. The energy-volume curve in Fig. 2 illustrates the relationship between the energy and volume of the perovskite cells. It was discovered that the perovskite with 15% Cs added had the lowest energy at a volume of about 980.32 Å3. These results agree with the previous experimental and theoretical results as shown in Table 1 [18, 21, 35, 37].
3.2 Electronic properties
Given that the Pb–Sn perovskites would be exploited as a substrate for light harvesting, it is essential to investigate the electrical structures of these materials. As can be seen in Fig. 3-56a, the band gap of the MAPb0.5Sn0.5I3 perovskite was adjusted because of the partial substitution of Cesium for the A-cation. The valence band shifting to a little lower energy and the octahedral tilting, which reduces metal-halide orbital overlap and moves the bands to deeper energies along with the band gap bending within a Pb–Sn compositional range, have accelerated this increase. This study's observation is consistent with theoretical and experimental results from earlier research that demonstrated an increase in band gap as a result of partial cesium substitution for A-cations [21, 39]–[42].
Total Density of States (TDOS) of the perovskite states depicted in Fig. 3, 4, 5, 6b were estimated using the CASTEP analysis from the Materials Studio and the GGA-PBE approximation. The Cs, N, H, C, Pb, Sn, and I atoms intermingle to form perovskites, and the TDOS profile shows the locations of characteristic peaks as well as the participation of certain electronic states. The perovskite's valence band exhibits a higher density of states, which suggests that the material is a member of the semiconductor family. The approach gives a clearer picture of how the electronic states of the Pb, Sn, and I atoms affect bandgap changes. The research helps to clarify how the electronic states of the Pb, Sn, and I atoms affect fluctuations in the bandgap. The I atoms' 5p-states, which somewhat overlap with the 5 s-states of Sn and Pb, are the main contributors to the valence band maxima. The 5p-states of Sn and Pb atoms, nonetheless, are what populate the conduction band and are responsible for the creation of the conduction band minima. The location of the Fermi level in a perovskite between the valence band and conduction band is typically determined by the electron density of the Pb, Sn, and iodine atoms p-states.
3.3 Optical properties
The suitability of the materials for use as light-harvesters is determined by this attribute. In this study, the dielectric functions, absorbance, and optical conductivity are investigated to explore the optical properties of the materials.
It is crucial to understand the dielectric function when evaluating data on the charge-recombination rate and the efficiency of optoelectronic devices because literature claims that a high dielectric constant increases overall device performance and lowers charge carrier recombination [43]. The optical properties of materials can be explained by the complex dielectric function ε (ω), which shows a system's linear response to an external electromagnetic field. The imaginary portion of the dielectric constant indicates a material's capacity to indefinitely absorb energy from an electric field, whereas the real portion describes the material's electronic polarizability. The static value of the dielectric constant of a 10%–15% mol Cs addition to the device at 0 eV is higher than that of the control device which agrees with the results from other studies [44], and it started to decline when the ratio is above 15% due to phase segregation in the compound. This is revealed by the real portion of the dielectric function, as shown in Fig. 7. The dielectric coefficient is found to be bigger in the low area than in the high energy region. This discovery points to a connection between the device's better performance in the visible region and the low charge-carrier recombination rate in the low energy zone.
Understanding the imaginary section in Fig. 8 which is likewise related to the band structure is necessary to comprehend the absorption behavior [30]. A noticeable peak is observed for both the control and the Cs added devices. The device's peaks with 15% mol Cs added were more displaced to the lower energy area, showing the substantial visible-range absorption [45]. In the high-energy area, it is discovered that the Cs added device's dielectric function is significantly reduced when compared to the control device. This suggests that there is little absorption at higher energies. The results show that the Cs-added device has substantial absorption in the low energy region, which makes it more appropriate for use in optoelectronic applications [46].
The amount of light that can pass through the material before it is absorbed, and the optimal solar energy conversion efficiency are both determined by its absorbance. Different frequencies of light photons are released by the sun. If a photon's energy is lower than the band gap, it cannot be absorbed; if it is equal to or higher than the band gap, it can be absorbed by the semiconductor [23]. The width of the band gap (Eg) of the materials influences whether a photon can be absorbed [47]. Moreover, the bands relax toward the electronic states near to the band gap when the photon energy exceeds the width of the gap, which results in energy loss. The resulting Eg of the control, as shown in Fig. 9, is not significantly changed by the addition of Cs; however, the Cs addition was responsible for slowing the crystallization rate, which was brought on by the presence of 50%mol Sn in the control; as a result, the material's morphology was poor due to their associated rapid crystallization [21].
The relationship between the amplitude of the inducing electric field and the current density generated in the material at any frequency is given by the optical conductivity of the materials [48]. Fig. 10 shows the optical conductivity of perovskites, which has improved photoconductivity in the lower energy area. It is evident that the increased photoconductivity in the visible region is caused by the higher absorption there. The samples' peak locations and shape changed toward the lower energy region. The Cs augmented sample shifted more than the control sample. Because of this, the Cs sample exhibits considerable optical conductivity over the whole visible light spectrum. As a result, the optimal Cs addition would be more suited for use in optoelectronic systems like solar cells.
3.4 Mechanical properties
Perovskite-based solar cells are susceptible to several factors that impact their stability, including cell degradation, stress and strain, design, fabrication, age and industrial processing [49]. As a result, the current density is lowered, which shortens the cell's lifespan and efficiency [50]. Since solar cells have recently been considerably thinner and more portable, there is growing concern about the mechanical stability of a solar cell under varied conditions. Hence a certain mechanical stability must be possessed by the perovskite solar cells to function properly. The mechanical properties of materials are controlled during manufacture and usage by use of the elastic constants (Cij), which are quantities that show a material's resistance to deformation in different directions when subjected to shearing, volumetric, and uniaxial stresses.
In this study, the six independent elastic constants exhibited in Table 3 were obtained using the CASTEP stress–strain method [51]. There exists a correlation between the control structure's estimated Cij values and the existing theoretical values [49]. Since, the structures employed in this study possess orthorhombic phases, the mechanical stability is determined by C22 + C33-2C23 > 0 and C11 + C22 + C33 + C12 + 2C13 + 2C23 > 0 criteria [51]. The results show that perovskites are mechanically stable and meet the orthorhombic crystal Born stability requirement due to the positive elastic constants. Table 4 further displays the results of the Voigt-Reuss-Hill (VRH) estimation for the young's modulus (E), bulk modulus (B), shear modulus (G), and Poisson's ratio (τ). The Debye temperature and the sound velocities in the crystal are directly correlated with the elastic characteristics by relations 8–10:

Where h- Planck constant, k- Boltzmann constant, NA—Avogadro’s number, n – molecular atomic number, M—molecular mass, ρ – density, \({\text{v}}_{\text{l}}\) and \({\text{v}}_{\text{t}}\) -longitudinal and transverse, vm – average sound velocities, and  —Debye temperature.
—Debye temperature.
The largest independent parameter for the halide perovskites is the C11 elastic constant. Furthermore, 1.75 is a common critical value for determining a material's ductility [52]. The computations' findings revealed that the B/G values are substantially greater than 2.0, meaning that even with deformation, they will yet have properties that are sensitive to bending, tensile, and compression. They are also useful for the large-scale deformation needed to create room-temperature thin film absorber layers due to the low shear modulus of perovskites. Poisson's ratio (τ), which measures ductility, is frequently higher than 0.26 [53]. The Poisson's ratio for each of the perovskites in this study was found to be more than 0.3, indicating that the elasticity of the materials allows for the adjustment of their band gaps. This is caused by the weak chemical bonds that result in element-dependent perovskite molecules (Table 6).
3.5 Thermodynamic properties
The stability of materials during moisture, light, and heat exposure is primarily determined by energy of the breakdown reaction and the enthalpy of synthesis of the perovskite solar cell materials [5, 54]. Under high temperature settings, the Pb–Sn halide perovskites rapidly transform into the halides [55, 56].
To determine the perovskites' thermodynamic stability, the formation energies of those materials must be computed. The general formula for the perovskite formation process is MAI + PbI2 → MAPbI3, and the formation energy can be calculated as follows [57, 58].
For the mixed perovskites CsxMA1-xSn0.5Pb0.5I3 perovskites, the formation energies (ΔH) are estimated by the following expression:
where x is the percentage of Cs atoms, and ΔHf is the enthalpy of formation for formula unit of CsxMA1-xSn0.5Pb0.5I3. When ΔH is negative, the decomposition reactions become endothermic and indicates a perovskite structure is stable [58].
According to Table 5, the formation energies of CsxMA1-xSn0.5Pb0.5I3 perovskites tend to decrease with the addition of 15% mol Cs, indicating a more thermally stable structure than the control. This might be brought on by the presence of Cs, which slows down crystallization. The film shape degrades once more when the Cs concentration surpasses 20 mol%, presumably due to phase separation caused by the immiscibility of the perovskites [33], which resulted in an increase in energy. These findings are equivalent to Pb–Sn halide perovskite experimental and theoretical data[57, 59]–[61].
3.6 Optoelectronic performance
The effect of binding interactions on device optoelectronic performance was highlighted by the simulation of perovskite. The effectiveness of the device’s photovoltaic capability was assessed using formulas 14–18 and led to generation of the J-V curves in Fig. 11 and External Quantum Efficiency (EQE) spectra in Fig. 12.
Where VOC-open circuit voltage, JSC-short circuit current density, FF-fill factor, Jph-photocurrent density, VMP & JMP- voltage and current at the maximum power point and I- Intensity of light, area (A) of the cell was taken to be 0.1225cm2 and the incident power (P) considered was 1000W/m2. Consistent with the morphological trends, Cs1.5MA8.5Pb0.5Sn0.5I3 perovskite delivered the improved optoelectronic performance parameters compared with the control device as shown in Table 6. As the Cs concentration rose from 15 mol% to 20 mol%, a noticeable decrease in performance parameters was observed, respectively. This may due to phase segregation of the perovskite caused by high concentrations of Cs which impedes the light absorption [33].
The integrated values from the EQE spectrum in Fig. 12 and these simulated values from the J-V curve in Fig. 11 were in excellent agreement. To enhance the long-term stability of Sn-based perovskites, the results demonstrate the effectiveness of adding Cs. This work used a 15 mol% partial replacement of Cs to examine the approach of this technique on improving the properties and optoelectronic performance of Pb-Sn perovskites which may led into increasing the thermal stability of the MAPb0.5Sn0.5I3 perovskite. The study's results demonstrate optoelectronic which are comparable to previous theoretical and experimental Pb-Sn based perovskite solar cells [62–67].
4 Thermal stability
To explore the devices’ thermal stability while being ambiently stored at 85°C, both the control and the Cs added devices were simulated at temperature of 85℃ as shown in Fig. 13. The loss in device parameters has been computed for the aging period after which the corresponding parameter either ceases to degrade, becomes stable, or begins to recover. The degradation and or recovery of FF and JSC were computed as they have been proven to be accountable for the decline in perovskite devices' efficiency[31]. To investigate the thermal stability of the control, and Cs based perovskites, the kinetic modeling offered by Myong and Lim in 2006 [32] was applied utilizing formulas 19-24.
Where α and β—ratio of photo-created fast and slow metastable defect density, NA-Avogadro’s number, τs and τf- time constants for the slow and fast metastable defects to return to stable state, N0 & Nd- defect density in perovskite layer before and after aging, and γ—defect annealing rate. The Cs added device retained 76% of its original PCE after 15 days while a control device’s PCE only kept around 39% of its initial value. The control data from this investigation agree well with those from experimental and theoretical studies [21].The notable improvement in thermal stability is attributed to either the impact of modifying the crystallization kinetics of perovskites or the production of high-quality films with large grain sizes and stable crystal structures because of bond interactions between the Cs and the perovskite.
5 Conclusions
The purpose of the study was to evaluate the effect of cesium partial substitution on the properties and optoelectronic performance of MAPb0.5Sn0.5I3 perovskite using A-site cation engineering technique. The study observed partial substitution of A-cation with Cesium provided a way to adjust band gaps due to the opposing effects of octahedral tilt and lattice contraction, along with the band gap bowing within a Pb–Sn compositional range. Additionally, the results showed that perovskites with up to 15% cesium added have enhanced characteristics and optoelectronic capabilities. Furthermore, after 15 days of aging at 85 °C in ambient conditions, the data show that perovskites with 15% cesium added have better thermal stability, preserving almost 76% of their initial power conversion efficiency, compared to the control sample, which may preserve about 39%. It is discovered that an ideal thermal stable perovskite material may be produced even at high temperatures by considering the characteristics and optoelectronic performance outcomes of the Cs added device.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Ghimire N, Bobba RS, Gurung A, Reza KM, Laskar MAR, Lamsal BS, Emshadi K, Pathak R, Afroz MA, Chowdhury AH, Chen K (2021) Mitigating open-circuit voltage loss in Pb-Sn low-bandgap perovskite solar cells via additive engineering. ACS Appl Energy Mater 4(2):1731–1742. https://doi.org/10.1021/acsaem.0c02895
Mbumba MT, Malouangou DM, Tsiba JM, Akram MW, Bai L, Yang Y, Guli M (2021) Compositional engineering solutions for decreasing trap state density and improving thermal stability in perovskite solar cells. J Mater Chem C 9(40):14047–14064. https://doi.org/10.1039/d1tc02315b
Junhui Y, Hao R, Wen W, Haipeng D, Yongli X, Yongbo G, Yingguo Y, Zhijun Y, Bin N (2022) Ionic liquid-tuned crystallization for stable and efficient perovskite solar cells. Sol RRL 6:1–9
Wu T, Qin Z, Wang Y, Wu Y, Chen W, Zhang S, Cai M, Dai S, Zhang J, Liu J, Zhou Z (2021) The main progress of perovskite solar cells in 2020–2021. Nano Micro Lett 13(1):1–18. https://doi.org/10.1007/s40820-021-00672-w
Mbumba MT, Malouangou DM, Tsiba JM, Bai L, Yang Y, Guli M (2021) Degradation mechanism and addressing techniques of thermal instability in halide perovskite solar cells. Sol Energy 230:954–978. https://doi.org/10.1016/j.solener.2021.10.070
Shaoshen C, Weiyin L, Chenxin G, Deli R, Lingfeng L, Xiaobo C, Lin W, Zongqiong S, Li L, Yonghua F (2021) Antisolvent-free fabrication of efficient and stable Sn Pb perovskite solar cells. Sol RRL 5:1–8
Marí-Guaita J, Bouich A, Shafi MA, Bouich A, Marí B (2022) Investigation on the stability and efficiency of MAPbI3 and MASnI3 thin films for solar cells. Phys Status Solidi Appl Mater Sci 219(5):1–7. https://doi.org/10.1002/pssa.202100664
Meggiolaro D, Ricciarelli D, Alasmari AA, Alasmary FAS, De Angelis F (2020) Tin versus lead redox chemistry modulates charge trapping and self-doping in tin/lead iodide perovskites. J Phys Chem Lett. https://doi.org/10.1021/acs.jpclett.0c00725
Matondo JT, Malouangou MD, Wu J, Bai L, Yang Y, Zhang Y, Pan J, Cai M, Mbumba MT, Akram MW, Guli M (2021) Lead acetate (PbAc2)-derived and chloride-doped MAPbI3 solar cells with high fill factor resulting from optimized charge transport and trap state properties. Sol Energy 228(August):129–139. https://doi.org/10.1016/j.solener.2021.09.010
Li B, Zhang X, Wang T, He Z, Lu B, Liang S, Zhou J (2022) Interfacial engineering strategy for high-performance Zn metal anodes, vol 14, no 1. Springer, Singapore. https://doi.org/10.1007/s40820-021-00764-7.
Zhu J, Chen C, Zhao D (2022) Low-bandgap mixed Tin–Lead perovskite solar cells. Solar 2:334–340. https://doi.org/10.3390/solar2030019
Leung TL, Ahmad I, Syed AA, Man A, Ng C (2022) Stability of 2D and quasi-2D perovskite materials and devices. Commun Chem 3(63):1–10. https://doi.org/10.1038/s43246-022-00285-9
Lin YH, Sakai N, Da P, Wu J, Sansom HC, Ramadan AJ, Mahesh S, Liu J, Oliver RD, Lim J, Aspitarte L (2020) A piperidinium salt stabilizes efficient metal-halide perovskite solar cells. Science 102:96–102
Jung EH, Jeon NJ, Park EY, Moon CS, Shin TJ, Yang TY, Noh JH, Seo J (2019) Efficient, stable and scalable perovskite solar cells using poly(3-hexylthiophene). Nature 567(7749):511–515. https://doi.org/10.1038/s41586-019-1036-3
Liu H, Xiang L, Gao P, Wang D, Yang J, Chen X, Li S, Shi Y, Gao F, Zhang Y (2022) Improvement strategies for stability and efficiency of perovskite solar cells halide perovskites usually possess a 3D structure [10], as chemical composition of ABX3, where A represents large-sized and cesium B refers denotes anion To power solve thes. Nanomaterials 12(19):1–8
Xu C, Liu Z, Lee EC (2020) Crystallization management for high-performance perovskite solar cells by introducing an antisolvent into the perovskite precursor. J Mater Chem C 8(44):15860–15867. https://doi.org/10.1039/d0tc04056h
Qin C, Matsushima T, Klotz D, Fujihara T (2019) The relation of phase-transition effects and thermal stability of planar perovskite solar cells. Adv Sci 6:1801079. https://doi.org/10.1002/advs.201801079
Ju MG, Sun G, Zhao Y, Liang WZ (2015) A computational view of the change in the geometric and electronic properties of perovskites caused by the partial substitution of Pb by Sn. Phys Chem Chem Phys 17(27):17679–17687. https://doi.org/10.1039/c5cp01991e
Liu Q, Li A, Chu W, Prezhdo OV, Liang WZ (2022) Influence of intrinsic defects on the structure and dynamics of the mixed Pb-Sn perovskite: first-principles DFT and NAMD simulations. J Mater Chem A 10(1):234–244. https://doi.org/10.1039/d1ta09027e
Paschal C, Pogrebnoi A, Pogrebnaya T, Seriani N (2020) Methylammonium tin iodide perovskite: structural, electronic and thermodynamic properties by a DFT study with different exchange–correlation functionals. SN Appl Sci 2(4):2549. https://doi.org/10.1007/s42452-020-2549-y
Liu X, Yang Z, Chueh C, Rajagopal A (2016) Improved efficiency and stability of Pb–Sn binary perovskite solar cells by Cs substitution. J Mater Chem A Mater energy Sustain 4:17939–17945. https://doi.org/10.1039/C6TA07712A
Diao X, Tang Y, Xiong D, Wang P, Gao L (2020) Study on the properties of perovskite materials under light and different temperatures and electric fields based on DFT. R Soc Chem 39:20960–20971. https://doi.org/10.1039/d0ra02841j
Lhouceine M, Omar B, Abdelhafid N, Khalid R (2022) The study of electronic and optical properties of perovskites CH3NH3PbCl3 and CH3NH3PbBr3 using first-principle. E3S Web Conf 336:00015.https://doi.org/10.1051/e3sconf/202233600015
Soe CMM, Nagabhushana GP, Shivaramaiah R, Tsai H, Nie W, Blancon JC, Melkonyan F, Cao DH, Traoré B, Pedesseau L, Kepenekian M (2019) Structural and thermodynamic limits of layer thickness in 2D halide perovskites. Proc Natl Acad Sci U S A 116(1):58–66. https://doi.org/10.1073/pnas.1811006115
Travis W, Glover ENK, Bronstein H, Scanlon DO, Palgrave RG (2016) On the application of the tolerance factor to inorganic and hybrid halide perovskites: a revised system. Chem Sci 7(7):4548–4556. https://doi.org/10.1039/c5sc04845a
Stoumpos CC, Malliakas CD, Kanatzidis MG (2013) Semiconducting tin and lead iodide perovskites with organic cations: Phase transitions, high mobilities, and near-infrared photoluminescent properties. Inorg Chem 52(15):9019–9038. https://doi.org/10.1021/ic401215x
Baikie T, Fang Y, Kadro JM, Schreyer M, Wei F, Mhaisalkar SG, Graetzel M, White TJ (2013) Synthesis and crystal chemistry of the hybrid perovskite (CH3NH3)PbI3 for solid-state sensitised solar cell applications. J Mater Chem A 1(18):5628–5641. https://doi.org/10.1039/c3ta10518k
Huang J, Yuan Y, Shao Y, Yan Y (2017) Understanding the physical properties of hybrid perovskites for photovoltaic applications. Nat Rev Mater 2:42. https://doi.org/10.1038/natrevmats.2017.42
Enkovaara J, Rostgaard C, Mortensen JJ (2017) Advanced capabilities for materials modelling with Quantum ESPRESSO. J Phys 29:79. https://doi.org/10.1088/1361-648X/aa8f79
Kholil MI, Bhuiyan MTH, Rahman MA, Ali MS, Aftabuzzaman M (2021) Effects of Fe doping on the visible light absorption and bandgap tuning of lead-free (CsSnCl3) and lead halide (CsPbCl3) perovskites for optoelectronic applications. AIP Adv 11(3):42847. https://doi.org/10.1063/5.0042847
Darvishzadeh P, Redzwan G, Ahmadi R, Gorji NE (2017) Modeling the degradation/recovery of short-circuit current density in perovskite and thin film photovoltaics. Org Electron 43:247–252. https://doi.org/10.1016/j.orgel.2017.01.034
Sohrabpoor H, Puccetti G, Gorji NE (2016) Modeling the degradation and recovery of perovskite solar cells. RSC Adv 6(55):49328–49334. https://doi.org/10.1039/c6ra06635f
Ašmontas S, Cerškus A (2022) Impact of cesium concentration on optoelectronic properties of metal halide perovskites. Materials (Basel) 15(5):1936. https://doi.org/10.3390/ma15051936
Hao F, Stoumpos CC, Chang RPH, Kanatzidis MG (2014) Anomalous band gap behavior in mixed Sn and Pb perovskites enables broadening of absorption spectrum in solar cells. J Am Chem Soc 136(22):8094–8099. https://doi.org/10.1021/ja5033259
Wang G, Wei J, Peng Y (2020) Electronic and optical properties of mixed perovskites CsSnxPb(1–x)I3. AIP Publ 065213:1–8. https://doi.org/10.1063/1.4954183
Evarestov RK, Kotomin RA, Senocrate EA, Kremerb A, Maier J (2020) First-principles comparative study of perfect and defective CsPbX3 (X = Br, I) crystals. R Soc Chem 22:3914–3920. https://doi.org/10.1039/c9cp06322f
Giorgi G, Fujisawa J, Segawa H, Yamashita K (2014) Cation role in structural and electronic properties of 3d organic—inorganic halide perovskites: a DFT analysis. J Phys Chem C. https://doi.org/10.1021/jp504479c
Mbumba MT (2023) Ionic liquid addition to the MAPb0.5Sn0.5I3 perovskites: the properties and optoelectronic performance analysis using DFT calculations. Mater Technol 38(1):12. https://doi.org/10.1080/10667857.2023.2254137
Prasanna R, Gold-Parker A, Leijtens T, Conings B, Babayigit A, Boyen HG, Toney MF, McGehee MD (2017) Band gap tuning via lattice contraction and octahedral tilting in perovskite materials for photovoltaics. J Am Chem Soc 139(32):11117–11124. https://doi.org/10.1021/jacs.7b04981
Rajagopal A, Yang Z, Jo SB, Braly IL, Liang PW, Hillhouse HW, Jen AKY (2016) Highly efficient perovskite-perovskite tandem solar cells reaching 80% of the theoretical limit in photovoltage. Adv Mater 28(40):8990–8997. https://doi.org/10.1002/adma.201602696
Filip MR, Eperon GE, Snaith HJ, Giustino F (2014) Steric engineering of metal-halide perovskites with tunable optical band gaps. Nat Commun 5:6757. https://doi.org/10.1038/ncomms6757
McMeekin DP et al (2016) A mixed-cation lead mixed-halide perovskite absorber for tandem solar cells. Science 351(6269):151–155. https://doi.org/10.1126/science.aad5845
Johnson A, Gbaorun F, Ikyo BA (2022) First-principles study of (CsMA)NaSbX6 (MA= methylammonium; X = Cl, Br, I) organic–inorganic hybrid double perovskites for optoelectronic applications. J Comput Electron 21(1):34–39. https://doi.org/10.1007/s10825-021-01832-2
Joshi TK, Sharma PG, Verma AS (2020) Investigation of structural, electronic, optical and thermoelectric properties of Ethylammonium tin iodide (CH3CH2NH3SnI3): an appropriate hybrid material for photovoltaic application. Mater Sci Semicond Process 115. https://doi.org/10.1016/j.mssp.2020.105111
Tumusange MS, Subedi B, Chen C, Junda MM, Song Z, Podraza NJ (2021) Impact of humidity and temperature on the stability of the optical properties and structure of MAPbI3, MA0.7FA0.3PbI3 and (FAPbI3)0.95(MAPbBr3)0.05 perovskite thin films. Materials (Basel) 95:11
Ghaithan HM, Alahmed ZA, Qaid SMH, Aldwayyan AS (2021) Density functional theory analysis of structural, electronic, and optical properties of mixed-halide orthorhombic inorganic perovskites. ACS Omega 6(45):30752–30761. https://doi.org/10.1021/acsomega.1c04806
Pazoki M, Jacobsson TJ, Cruz SH, Johansson MB, Imani R, Kullgren J, Hagfeldt A, Johansson EM, Edvinsson T, Boschloo G (2017) Photon energy-dependent hysteresis effects in lead halide perovskite materials. J Phys Chem C 121(47):26180–26187. https://doi.org/10.1021/acs.jpcc.7b06775
Ostrikov KK, Wang H, Du A (2017) Towards lead-free perovskite photovoltaics and optoelectronics by ab-initio simulations. Sci Rep 7(1):1–9. https://doi.org/10.1038/s41598-017-13172-y
Laamari ME, Cheknane A, Benghia A, Hilal HS (2019) Optimized opto-electronic and mechanical properties of orthorhombic methylamunium lead halides (MAPbX3) (X = I, Br and Cl) for photovoltaic applications. Sol Energy 182:9–15. https://doi.org/10.1016/j.solener.2019.02.035
Mayengbam R, Tripathy SK, Palai G (2020) Structural, electronic, optical and mechanical properties of Zn-doped MAPbI3 perovskites and absorber layer efficiencies: an ab-initio investigation. Mater Today Commun 24. https://doi.org/10.1016/j.mtcomm.2020.101216
Feng J (2014) Mechanical properties of hybrid organic-inorganic CH3NH3BX3 (B = Sn, Pb; X = Br, I) perovskites for solar cell absorbers. APL Mater 2(8):56. https://doi.org/10.1063/1.4885256
Sa R, Liu D, Chen Y, Ying S (2020) Mixed-cation mixed-metal halide perovskites for photovoltaic applications: a theoretical study. ACS Omega 5(8):4347–4351. https://doi.org/10.1021/acsomega.9b04484
Mohd Zaki NH, Ali AMM, Mohamad Taib MF, Wan Ismail WIN, Sepeai S, Ramli A (2023) Dispersion-correction density functional theory (DFT+D) and spin-orbit coupling (SOC) method into the structural, electronic, optical and mechanical properties of CH3NH3PbI3. Comput Condens Matter 34:e00777. https://doi.org/10.1016/j.cocom.2022.e00777
Mazumdar S, Zhao Y, Zhang X (2021) Stability of perovskite solar cells: degradation mechanisms and remedies 2:1–34. https://doi.org/10.3389/felec.2021.712785
Ha M, Karmakar A, Bernard GM, Basilio E, Krishnamurthy A, Askar AM, Shankar K, Kroeker S, Michaelis VK (2020) Phase evolution in methylaamonium tin halide perovskites with variable temperature solid-state Sn NMR spectroscopy. J Phys Chem C. https://doi.org/10.1021/acs.jpcc.0c03589
Savill KJ, Ulatowski AM, Herz LM (2021) Optoelectronic properties of Tin−Lead halide perovskites. ACS Energy Lett 6:2413–2426. https://doi.org/10.1021/acsenergylett.1c00776
Liu H, Li X, Zeng Y, Meng L (2020) Effects of halogen substitutions on the properties of CH3NH3Sn0.5Pb0.5I3 perovskites. Comput Mater Sci 177:109576. https://doi.org/10.1016/j.commatsci.2020.109576
Zhu S, Ye J, Zhao Y, Qiu Y (2019) Structural, electronic, stability, and optical properties of cspb1-xsnxibr2 perovskites: a first-principles investigation. J Phys Chem C 123(33):20476–20487. https://doi.org/10.1021/acs.jpcc.9b04841
Niu G, Li W, Li J, Liang X, Wang L (2017) Enhancement of thermal stability for perovskite solar cells through cesium doping. RSC Adv 7(28):17473–17479. https://doi.org/10.1039/c6ra28501e
You Q, Gu S, Gou X (2023) The highly accurate interatomic potential of CsPbBr3 perovskite with temperature dependence on the structure and thermal properties. Materials (Basel) 16(5):2043
Ciccioli A, Latini A (2018) Thermodynamics and the intrinsic stability of lead halide perovskites CH3NH3PbX3. J Phys Chem Lett 9(13):3756–3765. https://doi.org/10.1021/acs.jpclett.8b00463
González-Juárez E, Espinosa-Roa A, Cadillo-Martínez AT, Garay-Tapia AM, Amado-Briseño MA, Vázquez-García RA, Valdez-Calderon A, Velusamy J, Sanchez EM (2023) Enhancing the stability and efficiency of MAPbI3 perovskite solar cells by theophylline-BF4− alkaloid derivatives, a theoretical-experimental approach”. RSC Adv 13(8):5070–5080. https://doi.org/10.1039/d2ra07580f
Chandel A, Bin Ke Q, Chiang SE, Chang SH (2022) Improving device performance of MAPbI3 photovoltaic cells by manipulating the crystal orientation of tetragonal perovskites. Nanotechnology 33:41. https://doi.org/10.1088/1361-6528/ac7474
Raoui Y, Ez-Zahraouy H, Tahiri N, El Bounagui O, Ahmad S, Kazim S (2019) Performance analysis of MAPbI3 based perovskite solar cells employing diverse charge selective contacts: Simulation study. Sol Energy 193(February):948–955. https://doi.org/10.1016/j.solener.2019.10.009
Ashrafi SS, Hossain MK, Islam MM, Hossain MU, Fahad SM, Kamrujjaman M, Masum MMI, Ahmed F, Hossain MA, Rahman MO (2020) Characterization and fabrication of Pb-based perovskites solar cells under atmospheric condition and stability enhancement. Adv Mater Phys Chem 10(11):282–296. https://doi.org/10.4236/ampc.2020.1011022
Prasanna JL, Goel E, Kumar A (2023) Numerical investigation of MAPbI3 perovskite solar cells for performance limiting parameters. Opt Quantum Electron 55(7):1–21. https://doi.org/10.1007/s11082-023-04876-9
Wang Y, Liang Y, Zhang Y, Yang W, Sun L, Xu D (2018) Pushing the envelope: achieving an open-circuit voltage of 1.18V for unalloyed MAPbI3 perovskite solar cells of a planar architecture. Adv Funct Mate 28:30. https://doi.org/10.1002/adfm.201801237
Acknowledgements
This work was supported by the National Institute of Transport.
Author information
Authors and Affiliations
Contributions
M.T wrote the main manuscript and carried out the simulation works G.J & S.K.C guided the whole manuscript process J.K & J.M contributed on model preparations, preparation of the methods for simulations
Corresponding author
Ethics declarations
Conflict of interest
There are no conflicts to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mbumba, M.T., Mahona, J., Kihedu, J. et al. A-site cation engineering of cesium and MAPb0.5Sn0.5I3 perovskite: the properties and optoelectronic performance analysis using DFT calculations. SN Appl. Sci. 5, 363 (2023). https://doi.org/10.1007/s42452-023-05596-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-023-05596-1