1 Introduction

Preliminaries of structural dynamics and vibrations: In order to devise suitable electro-mechanical elements applicable in various fields of engineering, including energy harvesters, vibration controllers, atomic force microscopes, sensors, actuators, and resonators, a fundamental understanding of the anticipated oscillatory response of the device is of primary importance. For example, in the design of a generation of self-powered RFID components, a piezoelectric element might be employed and integrated with the RFID hardware system to provide the energy required to power the coupling of the antenna and tag without the need for an external power source. Incentives to integrate efficient small-size electromechanical subsystems arise from the expected benefits, including: low cost, longer lifespan, and robustness to ambient noises and vibrations. Consequently, investigations of micro and nano-electro-mechanical-systems (M-NEMS) are highly attractive to both research communities and such industrial sectors as automotive, bio-medical and electronics. Scholars generally utilize three primary methods to investigate electro-mechanical-systems from the perspective of efficacy. These methods include experimentation, numerical simulations, and analytical modeling. Experimentation using M-NEMS encounters the challenges of scale and size. While accurate simulations are mostly achievable via molecular dynamics, extremely high computational costs are generally unavoidable. Thus, well-posed analytical modeling is the most cost-efficient method of these three. Moreover, results from analytical investigations of modeling improvements are a reasonable input to serve as an underpinning of experimental study and validation prior to final manufacturing. Accordingly, several scholars have endeavored to improve electro-mechanical-systems via novel modeling (e.g., [1, 2]). Of primary interest in the modeling and analysis of these systems is understanding mechanical frequency response functions (transmissibility) and electrical frequency response functions, examining resonance frequency shifts, mode shape functions, and the impact of subsystems integrated within the main system from a behavioral aspect. Considered systems all have a well-defined geometry and boundary conditions play a significant role in both transient and steady-state responses. Integrating a subsystem (e.g., a tip mass or oscillator) to the base system (e.g., cantilever, plate) yields new boundary conditions. In the vibratory response analysis, the characteristic equation is obtained by applying the boundary conditions to the proposed solution of the ordinary equation of motion, which yields the eigenvalues (resonance frequency) of the system. Slight changes to the boundary conditions may impact the resonance frequency significantly. It is noteworthy that the integration of a new subsystem may generate coupled equations of motion. In short, it is crucial to study and analyze the system integrations and the subsequent changes as they yield different structural and modal behaviors of the system. Investigating the modal and vibratory behavior is vital. As an example, in the design of MEMS sensors, modal analysis reveals crucial information about the sensitivity and functionality of the system. In the case of piezoelectric energy harvesters, attuning the resonance frequency with the of driving frequency is the ultimate goal to maximize the energy generated by the harvester. A concise literature review of relevant prior work includes:

1.1 Vibrations of microbeams

Following the preliminaries provided in the above, understanding the vibratory behavior of a system is very important to understand the system behavior and response to an excitation. Such understanding usually falls in the category of modal analysis which can be carried out both numerically and experimentally. One of the most widely-known techniques in numerical modal analysis is: Finite Element Analysis (FEA). On the other hand, using external accelerometers and shaker or hammer can be adopted for Experimental Modal Analysis (EMA). Modal analysis of a system is even more important in small-size structures due to the size dependency. However, as mentioned in the above section, modeling and simulations, FEA, and numerical investigations are a better fit for microbeams and structures to avoid the curse of extremely expensive experimentations adding to the potential impossibility. Here a brief literature of vibration analysis of: microbeams, tubes and reinforced composites is provided: Ebrahimi et al. [3] investigated vibration and static response of nano-composites made up of GNPs. Temperature effects is a parameter widely studied in this domain: Babaei et al. [4] reported the oscillatory response of micro-sensors undergoing temperature shocks. Several methods to capture the small-size dependency is also considered. Gao et al. [5] carried out research regarding nonlinear vibrations of tubes modeled based on nonlocal strain gradient theory and the perturbation method.

1.2 Vibrations of reinforced composites

Graphene composites are advanced materials that combine graphene with other substances to improve their mechanical, thermal, and electrical properties. Vibration analysis in this field is of paramount importance as it enables the understanding of the materials' dynamic behavior, aids in optimizing their design for specific applications, and ensures their reliability and performance in various engineering fields. This analysis is vital for developing cutting-edge technologies, such as sensors, actuators, and energy harvesting devices, which rely on the precise control of vibrations for efficient functionality and enhanced performance [6]. Yee et al. [7] studied the imperfections and functionally graded impacts of the plates in terms of vibrations. They studied the reinforcement of plates in modal analysis to understand how the system deviations and reinforcement improves the response. Sibtain et al. [8] studied the effects of a lumped mass at the tip end of a beam. They analyzed how the cumulative layers in a non-uniform structure with elastic support can clatter the dynamics of the system. Babaei et al. [9] carried out a research to understand the effect of a lumped mass at the tip end of a cantilever over the dynamics. They considered a rigid support for the lumped mass at the tip end.

1.3 Vibrations of micro-rods

Micro-rods has a slightly different configuration and geometry than a beam or plate. While beams and plate undergo perpendicular cross sections in spatial domain, rods take circular cross sections. This means that in rods, usually the axial (longitudinal) vibrations are dominant and studied. Similarly, several research investigations cover the size effect of rods to better understand the vibration behavior and response of the system: The forced oscillatory response of rods based on the nonlocal strain gradient theory was reported by Babaei [10]. Babaei [11] analyzed the oscillatory response of micro-sensor rods under deterministic excitations of impulse, step and ramp.

1.4 Vibrations and energy harvesting

For vibration-based energy harvesting, matching the resonance frequency with the excitation frequency results in harvestable voltage if piezoelectric material is used for the conversion of energy. In this field, several scholars across the globe have investigated novel methods to improve the conversion and make the applications more widespread. Erturk and Inman [12] reported a microbeam-wise energy harvester under harmonic base excitations. External inertia effects have been one of the most interesting and conducive case studies for MEMS sensors, energy harvesters and vibration suppressers: Locally resonant microbeams under an attached mass inertia has been reported by Wu et al. [13]. Impact of secondary oscillators upon dynamic responses of vibration suppressors was conducted by Ma et al. [14]. Nonlinear effects of an oscillator upon dynamic responses of a vibration absorber has been published by Abundis et al. [15]. Paunovic et al. [16] studied the vibration analysis of viscoelastic microbeams with attached tip mass under base excitations. Liu et al. [17] reported nonlinearity effects over vibration analysis of an energy harvester coupled to an oscillator.

Contributions of current study: In the investigation presented in this paper, the additional equation of motion emerges due to an elastic lumped oscillator added to the free end of the base system (cantilever). This results in a system of equations of motion, where the first equation explains the motion of the main system and the second explains the oscillations of the tip mass. This case specifically occurs if the inertia of the oscillator is active (e.g., in case of base excitations). In prior works and literature, there is not a well-known investigation which considers the inertia effects of a lumped oscillator held by an elastic support, as is presented in this paper. Considering the effects of oscillator inertia is important from two aspects: the new boundary condition and the coupled system of governing equations. The new type of the boundary condition is expected to alter the modal and vibratory response of the system which is the key analysis platform for the design of efficient electro-mechanical subsystems. The system of coupled equations is also important as the mechanical transmissibility function is expected to shift. Such factors imply underpinning information about the system behavior which is essential to design adjustable and efficient subsystems. In this paper, free and forced vibration analysis of a micro-microbeam with an elastically hung oscillator at the free end is studied to determine the stiffness effect of the spring in rendering inertial effects of the oscillator over the oscillatory response of the cantilever. Such combined effects of stiffness and inertia are obtained and compared with the reference system (of the cantilever-oscillator). It is noted that the proposed research will be further studied in future work to generate an analytical model with electrical couplings and the ultimate model for a passive RFID system will be augmented as a case study to use an energy harvester to power the communication of an internet of things (IOT) device. The comprehensive model will build upon the investigations in [18, 19], and will further complement the research in [20] to suggest a system which does not require an external power source for tag communication. It is also noteworthy to express that this paper particularly focuses on the pure mechanical response of a cantilever with oscillator system, while the energy harvesting aspects are covered in [21], where authors have extensively studied the optimization techniques to maximize the harvestable amount of energy in the configuration of cantilever-oscillator.

2 Governing equations of motion and boundary conditions

2.1 Kinematics of cantilever-oscillator-spring

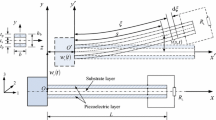
To study the continuous system vibratory response, we first derive the governing equation of motion for the proposed model. The kinematics of the proposed model are defined initially, using the schematic configuration of the elastically hung oscillator and cantilever microbeam system presented in Fig. 1. An oscillator with mass \({m}_{0}\) is attached to the cantilever via a linear spring with constant of \({k}_{s}\).

Fig. 1
figure 1

Schematic of cantilever-oscillator-spring system

Full size image

Where \(\rho\) is microbeam density, \(A\) is the cross-section area, \(E\) represents Yung’s modulus, \(I\) is second moment of inertia, microbeam has length of \(L\), thickness of \(h\), width of \(b\). \(x-y\) represents the Lagrangian cartesian coordinates, and \(X-Y\) is the fixed Eulerian cartesian coordinates. \({w}_{b}\left(x,t\right)\) is the base excitation in forced vibrations case study, and \({w}_{rel}\left(x,t\right)\) and \({w}_{s}\left(t\right)\) represent the relative lateral displacement of the microbeam and the oscillator with respect to the Lagrangian coordinates, respectively. According to Euler–Bernoulli microbeam models, displacement fields are defined as follows:

$${\mathrm{u}}_{\mathrm{x}}\left(\mathrm{x},\mathrm{z},\mathrm{t}\right)=-\mathrm{y}\frac{\partial {\mathrm{w}}_{rel}}{\partial \mathrm{x}}\left(\mathrm{x},\mathrm{t}\right)$$
(1a)
$${\mathrm{u}}_{\mathrm{y}}\left(\mathrm{x},\mathrm{z},\mathrm{t}\right)={\mathrm{w}}_{rel}\left(x,t\right)$$
(1b)
$${\mathrm{u}}_{\mathrm{z}}\left(\mathrm{x},\mathrm{z},\mathrm{t}\right)=0$$
(1c)

2.2 Variational terms and extended Hamilton’s principle

After finding the displacement fields of the system, dynamic principles are used to obtain the governing equations. Extended Hamilton is an efficient variational approach which is specifically suitable for complex, continuous systems. According to the modified couple stress theory [22], variations of strain energy terms due to deformation (\({U}_{s-1}\)), spring (\({U}_{s-2}\)) and kinetic energy terms \(({U}_{k}\)) are as follows:

$$\delta {U}_{s-1}=\left(EI+G{l}^{2}A\right)\frac{{\partial }^{2}{w}_{rel}}{\partial {x}^{2}}{\left.\delta \frac{\partial {w}_{rel}}{\partial x}\right|}_{0}^{L}-\left(EI+G{l}^{2}A\right)\frac{{\partial }^{3}{w}_{rel}}{\partial {x}^{3}}{\left.\delta {w}_{rel}\right|}_{0}^{L}+{\int }_{0}^{L}\left(EI+G{l}^{2}A\right)\frac{{\partial }^{4}{w}_{rel}}{\partial {x}^{4}}\delta {w}_{rel}dx$$
(2a)
$$\delta {U}_{s-2}={k}_{s}{w}_{s}\delta {w}_{s}$$
(2b)
$$\delta {U}_{k}={\int }_{o}^{L}\rho A\left({\ddot{w}}_{rel}\left(x,t\right)+{\ddot{w}}_{b}\left(x,t\right)\right)\delta {w}_{rel}dx+{m}_{s}\left({\ddot{w}}_{rel}\left(L,t\right)+{\ddot{w}}_{b}\left(L,t\right)+{\ddot{w}}_{s}\left(t\right)\right)\delta {w}_{s}+{m}_{s}\left({\ddot{w}}_{rel}\left(L,t\right)+{\ddot{w}}_{s}\left(t\right)\right)\delta {w}_{rel}+{\int }_{o}^{L}{m}_{s}{\ddot{w}}_{b}\left(x,t\right)\delta (x-L)\delta {w}_{rel}dx$$
(2c)

Variations of nonconservative dissipating terms (\({W}_{nc}\)) are expressed in Eq. (3):

$$\delta {W}_{nc}=-{\int }_{0}^{L}{c}_{a}\left({\dot{w}}_{rel}+{\dot{w}}_{b}\right)\delta {w}_{rel}dx-{\int }_{0}^{L}{c}_{s}I\frac{{\partial }^{4}{\dot{w}}_{rel}}{\partial {x}^{4}}\delta {w}_{rel}dx$$
(3)

where, \(G\) represents the rigidity modulus of microbeam, \(l\) is the material length scale parameter, \(\delta\) is the Dirac delta function, \({c}_{a}\) is the viscous air damping coefficient, and \({c}_{s}\) represents the equivalent coefficient of strain rate damping (Kelvin-Voigt damping). Using the Extended Hamilton’s variational approach, the governing system of equations is obtained:

$$\rho A{\ddot{w}}_{rel}\left(x,t\right)+\left(EI+G{l}^{2}A\right)\frac{{\partial }^{4}{w}_{rel}}{\partial {x}^{4}}+{c}_{s}I\frac{{\partial }^{4}{\dot{w}}_{rel}}{\partial {x}^{4}}+{\dot{{c}_{a}w}}_{rel}=-\left(\rho A+{m}_{s}\delta \left(x-L\right)\right){\ddot{w}}_{b}\left(x,t\right)-{\dot{{c}_{a}w}}_{b}$$
(4a)
$${m}_{s}\left({\ddot{w}}_{rel}\left(L,t\right)+{\ddot{w}}_{b}\left(L,t\right)+{\ddot{w}}_{s}\left(t\right)\right)+{k}_{s}{w}_{s}=0$$
(4b)

Corresponding boundary conditions are shown in Eq. (5):

$${w}_{rel}\left(0,t\right)=0$$
(5a)
$${\frac{\partial }{\partial x}w}_{rel}\left(0,t\right)=0$$
(5b)
$${\frac{{\partial }^{2}}{\partial {x}^{2}}w}_{rel}\left(0,t\right)=0$$
(5c)
$$\left(EI+G{l}^{2}A\right){\frac{{\partial }^{3}}{\partial {x}^{3}}w}_{rel}\left(0,t\right)-{m}_{s}\left({\ddot{w}}_{rel}\left(L,t\right)+{\ddot{w}}_{s}\left(t\right)\right)=0$$
(5d)

3 Solution procedure

3.1 Free vibrations: natural frequencies, mode shape functions

Finding the resonant frequencies of the system is necessary for further analysis. This is particularly important for energy harvester and micro-sensor systems, as the understanding of the natural frequency is essential. In this regard, equating all damping terms as well as forcing term to zero, and using the method of separation of variables (where \({w}_{rel}={\varphi }_{n}(x){e}^{j{\omega }_{n}t}\), \({\varphi }_{n}\left(x\right)\) is eigenfunctions, \(j\) is unit imaginary number, \({\omega }_{n}\) represents natural frequency, and \(t\) is time variable), yields the following form of Eq. (4):

$$\left(EI+G{l}^{2}A\right)\frac{{\partial }^{4}{\varphi }_{n}(x)}{\partial {x}^{4}}-\rho A{\varphi }_{n}\left(x\right){{\omega }_{n}}^{2}=0$$
(6a)
$${\ddot{w}}_{s}\left(t\right)+{{\omega }_{n-o}}^{2}w\left(t\right)={{\omega }_{n}}^{2}{\varphi }_{n}\left(L\right){e}^{-j{\omega }_{n}t}$$
(6b)

where, \({\omega }_{n-o}\) represents the natural frequency of the oscillator (\({\omega }_{n-o}=\sqrt{{k}_{s}/{m}_{0}}\)). The general solution to Eq. (6a) is a combination of trigonometric and hyperbolic functions with eigenvalue \({\lambda }_{n}\) where (\({{\lambda }_{n}}^{4}=\rho A{{\omega }_{n}}^{2}/ (EI+G{l}^{2}A)\)).

$${\varphi }_{n}\left(x\right)={A}_{1}\mathrm{cosh}({\lambda }_{n}x)+{A}_{2}\mathrm{cos}({\lambda }_{n}x)+{A}_{3}\mathrm{sinh}({\lambda }_{n}x)+{A}_{4}\mathrm{sin}{(\lambda }_{n}x)$$
(7)

The corresponding boundary conditions to the undamped, free vibration case study are as follows:

$${\varphi }_{n}\left(0\right)=0$$
(8a)
$$\frac{\partial }{\partial x}{\varphi }_{n}\left(0\right)=0$$
(8b)
$$\frac{{\partial }^{2}}{\partial {x}^{2}}{\varphi }_{n}\left(L\right)=0$$
(8c)
$$\left(EI+G{l}^{2}A\right)\frac{{\partial }^{3}}{\partial {x}^{3}}{\varphi }_{n}\left(L\right)-{m}_{s}\left(-{{\omega }_{n}}^{2}{\varphi }_{n}\left(L\right)+{\ddot{w}}_{s}\left(t\right)\right)=0$$
(8d)

The shearing force boundary condition is dependent on the motions and inertia of the oscillator. Thus, solving Eq. (6b) is a proceeding step. Considering beating conditions (\({w}_{s}\left(0\right)=\dot{{w}_{s}}\left(0\right)=0\)), the solution to Eq. (6b) is:

$${w}_{s}\left(t\right)=\frac{{{\omega }_{n}}^{2}}{{{\omega }_{n-o}}^{2}-{{\omega }_{n}}^{2}}{\varphi }_{n}\left(L\right)$$
(9)

Inserting the expression found in Eq. (9) into Eq. (8d) and applying the boundary conditions of Eq. (8) into the general solution presented in Eq. (7) yields the following nonlinear transcendental equation as the characteristic equation:

$$(EI+GA{l}^{2}){{\lambda }_{n}}^{3}\left(1+\mathrm{cosh}\left({\lambda }_{n}L\right)\mathrm{cos}\left({\lambda }_{n}L\right)\right)+\frac{{{\omega }_{n-o}}^{2}{{\omega }_{n}}^{2}{m}_{0}}{{{\omega }_{n-o}}^{2}-{{\omega }_{n}}^{2}}\left(\mathrm{sinh}\left({\lambda }_{n}L\right)\mathrm{cos}\left({\lambda }_{n}L\right)-\mathrm{cosh}\left({\lambda }_{n}L\right)\mathrm{sin}{(\lambda }_{n}L)\right)=0$$
(10)

It is very important to note the differences between the obtained characteristic equation and that of the reference system (cantilever-oscillator). In the reference system, a rigid support is assumed instead of a spring support with changeable stiffness. In the base case study (a single cantilever without the oscillator) the characteristic equation is simply the first part of Eq. 10 (\(1+\mathrm{cosh}\left({\lambda }_{n}L\right)\mathrm{cos}\left({\lambda }_{n}L\right)\)). It is clear that including an elastic support renders a more complex transcendental characteristic equation. Introducing the mass ratio (\({r}_{m}=\frac{{m}_{0}}{\rho AL}\)) and the stiffness ratio (\({r}_{s}=\frac{{k}_{s}}{(EI/{L}^{3})}\)), and ignoring nonclassical effects (as having either \(EI\) or \(EI+GA{l}^{2}\) as the coefficient of \(1+\mathrm{cosh}\left({\lambda }_{n}L\right)\mathrm{cos}\left({\lambda }_{n}L\right)\) does not alter function graph remarkably), Eq. (10) can be re-written as expressed in Eq. (11):

$$f\left({\lambda }_{n}L\right)=\left({r}_{s}-{r}_{m}{{(\lambda }_{n}L)}^{4}\right)\left(1+\mathrm{cosh}\left({\lambda }_{n}L\right)\mathrm{cos}\left({\lambda }_{n}L\right)\right)+({r}_{s}{r}_{m}({(\lambda }_{n}L))(\mathrm{sinh}({\lambda }_{n}L)\mathrm{cos}({\lambda }_{n}L)-\mathrm{cosh}({\lambda }_{n}L)\mathrm{sin}{(\lambda }_{n}L))$$
(11)

Equation (11) as a nonlinear transcendental equation does not have a closed-form (exact) solution. Consequently, numerical solvers are proposed. Among root-finding algorithms available, VPASOLVE is an efficient solver included within MATLAB software package. However, as is similar to most numerical solvers, VPASOLVE precision is extremely sensitive to the accuracy of initial guess. To reach the most feasibly precise numerical values of the eigenvalues of Eq. (11), the plot of the nonlinear transcendental equation in Fig. 2 was used to suggest an initial guess.

Fig. 2
figure 2

Characteristic eqautions graphs for differenet values of mass ratio and stiffness ratio

Full size image

Based upon Fig. 2, adding an oscillator attached to the free end of the microbeam via a spring result in roots smaller than 1.875. 1.875 is the first eigenvalue of a clamped free microbeam with an attached oscillator or a single cantilever. This conveys that, if the oscillator is attached via a spring support with an elastic feature, the restoring force in the spring accompanied with the mass of the oscillator yields another root (eigenvalue) smaller than 1.875. The second root of the cantilever-oscillator-spring system is almost coincident with the first root of the reference system (\(i.e., {r}_{s}\to \infty\)). This key point is highly important through the analysis of such systems. Accordingly, eigenvalues of the nonlinear transcendental equation are numerically obtainable. In Eq. (12), the dimensionless undamped natural frequency of the considered system is defined based upon both classical and modified couple stress theories, respectively.

$${\Omega }_{n}={{\omega }_{n}L}^{2}\sqrt{\rho A/EI}={{(\lambda }_{n}L)}^{2}, {\omega }_{n}=\sqrt{EI/\rho A} {{\lambda }_{n}}^{2}$$
(12a)
$${\Omega }_{n-MCST}=\sqrt{(EI+GA{l}^{2})/EI}{{(\lambda }_{n}L)}^{2}, {\omega }_{n-MCST}=\sqrt{(EI+GA{l}^{2})/\rho A} {{\lambda }_{n}}^{2}$$
(12b)

Despite the transition from Eqs. (10) and (11) in which nonclassical effects were ignored, such effects emerge more strongly within the definition of natural frequencies. Thus, in Eq. (12b), \(GA{l}^{2}\) is weighted. Correspondingly, mass-normalized mode shape functions (eigenfunctions) are expressible in the following format:

$$\varphi_{n} \left( x \right) = \frac{1}{{\sqrt {\rho AL} }}\left( {\cosh \left( {\lambda_{n} x} \right) - \cos \left( {\lambda_{n} x} \right) - \left( {\frac{{\cosh \left( {\lambda_{n} L} \right) + \cos \left( {\lambda_{n} L} \right)}}{{\sinh \left( {\lambda_{n} L} \right) + \sin \left( {\lambda_{n} L} \right)}}} \right)\left( {\sinh \left( {\lambda_{n} x} \right) + \sin (\lambda_{n} x)} \right)} \right)$$
(13)

3.2 Forced vibrations: harmonic base excitations

Considering harmonic base excitations (\({w}_{b}={Y}_{0}{e}^{j{\omega }_{e}t}\)) with excitation frequency and amplitude of\({\omega }_{e}\), \({Y}_{0}\), the mechanical frequency response functions along with temporal modal response of the system are to be examined. Using the Galerkin modal decomposition, the displacement function is assumed as:

$${w}_{rel}\left(x,t\right)=\sum_{n=1}^{\infty }{\varphi }_{n}\left(x\right){\eta }_{n}(t)$$
(14)

Due to the proportional damping criteria, \({\varphi }_{n}\left(x\right)\) is the same mode shape functions of the undamped, free system. \({\eta }_{n}(t)\) is the modal coordinate of the microbeam at the \(n{\prime}th\) mode. Multiplying Eq. (6a) by \({\varphi }_{m}\left(x\right)\), and using the orthogonality in integration over microbeam length \(L\), one obtains the following relationship:

$$\mathop \int \limits_{0}^{L} \rho A\varphi_{n} \left( x \right)^{2} dx = B_{n} \cong 1$$
(15a)
$$\mathop \int \limits_{0}^{L} \left( {EI + Gl^{2} A} \right)\varphi_{n} \left( x \right)\frac{{d^{4} }}{{dx^{4} }}\varphi_{n} \left( x \right)dx = B_{n} \omega_{n - MCST}^{2}$$
(15b)

Duplicating same process for the Eq. (4a) and using Eqs. (15); the following time-domain ordinary differential equation is obtained:

$$B_{n} \left( {\mathop \eta \limits^{ \cdot \cdot }_{n} \left( t \right) + 2\omega_{n} \zeta_{n} \dot{\eta }_{n} \left( t \right) + \omega_{n - MCST}^{2} \eta_{n} \left( t \right)} \right) = \left( {\rho A\gamma_{n} + m_{0} \mathop \gamma \limits{\prime}_{n} } \right)Y_{0} \omega_{e}^{2} e^{{j\omega_{e} t}}$$
(16a)
$${\zeta }_{n}=\frac{{c}_{a}}{2\rho A{\omega }_{n-MCST}}+\frac{{{c}_{s}I\omega }_{n-MCST}}{2EI}$$
(16b)
$${\gamma }_{n}={\int }_{0}^{L}{\varphi }_{n}(x)dx$$
(16cCA)
$$\mathop \gamma \limits{\prime}_{n} = \mathop \int \limits_{0}^{L} \varphi_{n} \left( x \right)\delta \left( {x - L} \right)dx$$
(16d)

\(\zeta_{n}\) is the mechanical damping ratio including both Kelvin-Voigt and air viscous damping. According to the beating conditions, steady-state temporal modal response of the system is the single solution of Eq. (16a) which is expressed as:

$$\eta_{n} \left( t \right) = \frac{{\left( {\rho A\gamma_{n} + m_{0} \mathop \gamma \limits{\prime}_{n} } \right)Y_{0} \omega_{e}^{2} }}{{B_{n} (\omega_{n - MCST}^{2} - \omega_{e}^{2} + j2\omega_{n} \omega_{n - MCST} \zeta_{n} )}}e^{{j\omega_{e} t}}$$
(17)

4 Results and discussion

In this section, numerical results pertaining to the natural frequency, modal response, and mechanical frequency response functions (FRFs) are presented and discussed. The geometrical, and mechanical properties utilized in reference [12], are also used in this study (and summarized in Table 1) for comparison:

Table 1 Geometrical, and mechanical parameters of the cantilever-oscillator-spring [6]
Full size table

According to the plots of the characteristic equation, it is observed that the new system has significantly different roots than presented in [6] and it is necessary to find eigenvalues and frequencies of the system of cantilever-oscillator-spring as a function of the oscillator mass and spring constant. A study of typical ranges of these parameters is necessary, as such values directly affect the resulting eigenvalues.

In the above table, current model and solution is compared against the benchmark [23]. It is considered to compare the results of current modeling with the case of infinite stiffness and zero mass ratio to mimic the rigidity of the rigid support foe the lumped oscillator. It is observed that the eigenvalues are closely aligned proving a good level of accuracy of current modeling and solutions (Table 2).

Table 2 Comparison of current results versus benchmark
Full size table

4.1 Minimal (new) eigenvalues generated due to restoring force of the spring

Table 3 is provided to numerically evaluate the effects of the restoring force of the spring and the resulting effects of the oscillator inertia over fundamental natural frequency of the system. Four representative cases: light oscillator-soft spring (\({r}_{m}=0.01,{r}_{s}=0.01\)); light oscillator-stiff spring (\({r}_{m}=0.01,{r}_{s}=100\)); heavy oscillator-soft spring (\({r}_{m}=10,{r}_{s}=0.01\)); heavy oscillator-stiff spring (\({r}_{m}=10,{r}_{s}=100\)) are shown and considered. Results show that, if the oscillator is hung with a soft spring, the first eigenvalue (fundamental natural frequency) of the cantilever-spring-oscillator is significantly less than the reference one (1.875104). Remarkably, increasing the mass of the oscillator, attempts to further deviations from the reference system. On the other hand, increasing the spring constant, drags the first eigenvalue towards the first eigenvalue of the reference system, meaning that stiffer spring is inclined to suppress the inertial effects of the oscillator.

Table 3 First eigenvalue and dimensionless resonant frequency of cantilever-oscillator-spring system
Full size table

Table 4 is generated similarly to Table 2 to provide the second vibration mode. Comparatively to the first mode gradations, a light oscillator-stiff spring pair has almost same second eigenvalue (\({\lambda }_{2}L\)) as a rigidly hung oscillator (\({r}_{s}=\infty\)). With the strong restoring forces (\({r}_{s}=100\)), the oscillator inertial effect is tangible only if the mass ratio is strikingly high (\({r}_{m}=10\)). Conversely, with weak restoring forces (\({r}_{s}=0.01\)) inertial effects of the oscillator significantly deduces the second eigenvalue. Interestingly, the inertial effect drags the second eigenvalue of the new system towards the first eigenvalue of the rigidly hung oscillator (\({\lambda }_{2}L\to {\lambda }_{1}L\)). Eventually, if a very stiff spring is used with heavy oscillator, moderate variations are observable as restoring forces tend to make the system behave like the reference system, yet the inertial effects make the system deviate from the reference system.

Table 4 Second eigenvalue and dimensionless resonant frequency of cantilever-oscillator-spring system
Full size table

Table 5 pertains to the third vibration mode. Similar patterns to the first and second vibration modes are found here. The main finding for the first three vibration modes of the new system is that the most remarkable deviation refers to the heavy oscillator with weak spring. In this case, the oscillator has relative motions which impact the microbeams behavior substantially. Clearly, the least sensitive effects of the oscillator inertia occur with stiff or hard spring and yield the least overshoot from the reference system. It is also good to note that dimensionless frequency of classical theory and Modified Couple Stress theory (MCST) have good agreement, with very little (0.22% shift (off-set)).

Table 5 Third eigenvalue and dimensionless resonant frequency of cantilever-oscillator-spring system
Full size table

4.2 Effect of mass and stiffness ratios over natural frequencies

Figure 3 demonstrates variations of dimensionless frequency of the first three modes with respect to mass ratio for a soft spring. As expected in the first mode, increasing the mass ratio (increasing the mass of the oscillator) decreases the frequency. In the second mode, such a decrement is barely discernible, while in the third mode, mass ratio has almost no effect on the frequency. Even for the first mode with more tangible variations, frequency decrements take place at very small values of the mass ratio only.

Fig. 3
figure 3

Variations of dimesnsionless frequencies versus mass ratio with soft spring (\({r}_{s}=0.01\); a. first mode, b. second mode, c. third mode)

Full size image

Figure 4 shows the variations of first three frequency modes with respect to the mass ratio with a stiff (hard) spring. It is evident that, versus the case of soft spring, oscillator mass suppresses frequencies significantly as it increases. In other words, the mass ratio effects as a function of frequency are more perceptible if the spring is stiffer. In addition to the impact of the spring stiffness, the heavier oscillator yields smaller natural frequencies. Finally, the modified couple stress theory predicts the resonance frequency slightly higher than the classical theory.

Fig. 4
figure 4

Variations of dimesnsionless frequencies versus mass ratio with stiff spring (\({r}_{s}=100\); a. first mode, b. second mode, c. third mode)

Full size image

To illustrate the effect of the spring stiffness (spring constant) on the natural frequency, Fig. 5 is presented. In this figure, a light mass oscillator (\({r}_{m}=0.01\)) is considered. It is evident that the frequencies of all three modes increase with increasing spring stiffness. Such variations seem to be larger in the higher vibration modes.

Fig. 5
figure 5

Variations of dimesnsionless frequencies versus stiffness ratio with light oscillator (\({r}_{m}=0.01\); a. first mode, b. second mode, c. third mode)

Full size image

Figure 6 illustrates variations of the frequencies with respect to the stiffness ratio in case of a heavy-mass oscillator. Similar profiles to the case of light-mass oscillator are repeated here, confirming that a stiffer spring yields increases in frequencies. Other finding discloses the fact that light oscillator yields smaller frequencies in comparison to the heavy oscillator with identical spring stiffness. Finally, the comparison between the modified couple stress and the classical theory reveals that, the difference in the first and second mode frequencies is minimal and barely tangible. In the third mode frequency, the modified couple stress theory shows slightly higher frequencies which holds for both Figs. 5 and 6.

Fig. 6
figure 6

Variations of dimensionless frequencies versus stiffness ratio with heavy oscillator (\({r}_{m}=10\); a. first mode, b. second mode, c. third mode)

Full size image

Mode shape functions are plotted in Fig. 7 to signify the effect of the minimum (new) resonant frequencies generated due to the inertial effects of the oscillator accompanied with the stiffness effects (restoring force) of the spring. It is evident that, if the oscillator is heavy, mode shape functions of all three first modes deviate significantly from than those of the reference system (mentioned as free in the figure legend). To focus on small-scale systems, only the results of the modified couple stress theory are presented. Moreover, it is observed in the frequency section, that the deviation between the classical and the modified couple stress theory is minimal and would not change the mode shapes tangibly. Current results of the proposed modeling and solution is verified against the benchmark study cited as: [24].

Fig. 7
figure 7

Mode shape functions of reference system and extreme cases of mass and stiffness ratios (a. mode one; b. mode two; c. mode three)

Full size image

4.3 Mechanical frequency response of microbeam vibrations

In this section, the relative tip motion frequency response function (FRF) (also known as the relative motion transmissibility function) is presented and discussed. Such a study is important to better understand the system oscillation amplitudes when it is excited. The relative motion transmissibility function is the ratio of the vibration amplitudes at the free end (tip of the microbeam) to the amplitude of the base displacement producing the vibrations.

$$\frac{{w_{rel} }}{{Y_{0} e^{{j\omega_{e} t}} }} = \mathop \sum \limits_{n = 1}^{\infty } \varphi_{n} \left( L \right)\left[ {\frac{{\left( {\rho A\gamma_{n} + m_{0} \mathop \gamma \limits{\prime}_{n} } \right)\omega_{e}^{2} }}{{B_{n} (\omega_{n - MCST}^{2} - \omega_{e}^{2} + j2\omega_{n} \omega_{n - MCST} \zeta_{n} )}}} \right]$$
(18)

Relative motion transmissibility (tip motion FRF) is of primary interest, especially for the design of cantilever energy harvesters or vibration isolators. With relative motion transmissibility FRF, valuable information about the level of the tip displacement of a harvester or isolator and structural dynamics of the system is demonstrated.

In Fig. 8, the modulus of the relative tip motion FRF against dimensionless excitation frequency is plotted for the four extreme cases presented in Sect. 4.2 as well as the reference case (\({r}_{s}\to \infty\)). To validate the current model and solution method (VPA solver), results are compared against the reference data derived from [12]. Comparison shows a good level of accuracy. According to this plot, vibration amplitudes at the tip (free end) is increased substantially with a heavy oscillator (\({r}_{m}=10\)). Regarding the frequency bandwidth, the comparison depends on the bandwidth between the first (resulted from the minimal eigenvalue) and the second or the third frequencies. The spring stiffness constant does not affect the oscillation amplitudes, but such restoring force drags the FRF towards the reference case (\({r}_{m}=0 or {r}_{s}\to \infty\)). It means that a weak (soft) spring yields a shortened (narrowed) frequency bandwidth, as shown in the red and blue lines. Such a finding is also seen by comparison between red line and cyan lines, where both pertain to identical mass ratios but different restoring forces. The soft spring (red line) has significantly shorter bandwidth between the first and second or third resonant frequencies than hard (stiff) spring (shown in cyan) between the first and second resonant frequencies. If the frequency bandwidth refers to the first (minimal) and the third frequencies, it is observable that in all extreme case studies, the bandwidth is wider than that of the reference system. Concisely, vibration amplitudes are mutable with only mass ratios and the frequency bandwidth is highly dependent on the amount of restoring forces. In summary, dominant inertial effects (heavy oscillator) generate a minimal resonant frequency close to zero, while the second resonant frequency is overlaid on the first resonant frequency of the reference system. Finally, it is understandable that the inertial effects strongly impact the oscillation amplitudes, but the frequency bandwidth is varying based on both the inertial effects and the spring stiffness with spring constant as the dominant factor. It is also good to note that, with a heavy oscillator and soft spring, the system’s behavior deviates most significantly from the reference system, and with the light oscillator and stiff spring, the system’s behavior is most similar to the reference system. Such findings can be crucial for the design of energy harvesters or vibration controllers using piezoelectricity.

Fig. 8
figure 8

Relative tip motion FRF versus dimensionless excitation frequency (reference system and extreme cases of mass and stiffness ratios)

Full size image

5 Conclusion

In this paper, vibration analysis of a microbeam with a lumped mass (oscillator) hanging elastically from the tip end is studied. Extended Hamilton’s principle was used to derive the governing equations of the beam restrained via the lumped oscillator using a spring, resulting in a set of coupled differential equations and new boundary conditions. Galerkin’s modal decomposition technique is adopted to obtain the mode shapes and transmissibility. It is found that, for such a system with applications in energy harvesters integrable with RFID components, vibration controllers, or M-NEMS sensors, replacing a rigid support with an elastic support via a spring will shift the system’s response drastically. Such modification is very important, as the resonance frequency is generatable at smaller frequency values which significantly increases the efficiency of the harvesters. The corresponding new nonlinear transcendental characteristic equation has been numerically solved using the MATLAB root-solver algorithm. Due to the relative motions of the oscillator with respect to the cantilever, small generated frequencies between zero and the first natural frequency of the cantilever-oscillator system (reference system) are detected. Through our investigation, we found that increasing the stiffness of the spring results in a response similar to the response of the reference system which is valid for all three vibration modes. Contrarily, the inertial effects derived from the oscillations of the lumped oscillator serve to substantially deviate system response by means of dragging the minimal (new) frequency to the left and far from the first frequency of the reference system. For the case of forced vibrations with harmonic base excitations, the relative tip motion FRF (transmissibility function) is presented and current results and solution procedure is validated against the bench mark. Results demonstrate that significant inertial effects resulted from a heavier oscillator, alter the system’s response and yield big amplitudes and significantly increased transmissibility. On the other hand, the spring stiffness cannot neutralize the inertial effects regarding the vibration amplitudes and transmissibility. However, such parameters can stretch the FRFprofile, meaning that stiffer springs result in a wider bandwidth. The new multisystem of cantilever-oscillator-spring, with values of oscillator inertia and spring restoring force, leads to the generation of minimal frequencies which can be at the vicinity of the first frequency of the reference system. In any case, such new frequencies yield widened bandwidth and one more resonance, particularly at the small excitations. In short, it is inferable that, depending on the specific desires of a given application, selecting the appropriate oscillator mass and spring stiffness as the design parameters can alter the system’s response as required.

The primary contributions of this study can be summarized as follows:

  1. (1)

    The cantilever system, joined with an oscillator-spring leads to the generation of new characteristic equations and eigenvalues. This presents the opportunity for an augmented resonance particularly at low frequencies, which can be helpful, as the external excitations are mostly small and generation of more resonances in a given bandwidth.

  2. (2)

    The increment in mass ratio causes intensified oscillation amplitudes, but the impact over the bandwidth is suppressed by the rigidity level of the spring.

  3. (3)

    The increment in rigidity of the support (spring constant) yields a wider bandwidth and stretched profile of transmissibility FRF. The spring constant is the more dominant influential factor rather than the inertia in terms of bandwidth mutations and gradations.

  4. (4)

    To tune an energy harvester, a system such as the one proposed in this paper overcomes the lack of coincidence and overlap between the excitation and natural frequencies since the location of the resonant frequencies can be significantly manipulated and altered by means of different values of oscillator mass and spring constant.