1 Introduction

Recently, researchers have been greatly interested in investigating nanofluids due to their importance in biological and medical applications such as genes, drug delivery, and specific targeting [1,2,3]. For instance, cancer cells can be treated by localised heat using NPs injected into the tumour, which reduces the treatment side effects [4]. Patel et al. [5] used a non-surgical technique to kill the tumour cells using NPs. McCarroll et al. [6] investigated different modern nanotechnology techniques that can potentially be used to treat and diagnose pancreatic cancer. To improve cancer treatment, magnetic polymer properties have been studied and evaluated. Purushotham et al. [7] investigated the thermal properties of magnetic NPs with a diameter of 13 nm. It was shown that the composite particles had excellent heating properties for simultaneous drug release, recommending them as active targeting and hyperthermic agents. A theoretical model was introduced by Abbasi et al. [8] for a peristaltic flow of a non-Newtonian silver nanofluid in a porous medium in a magnetic field incorporating heat and mass transfer. It was found that increasing the velocity slip coefficient reduces the nanofluid maximum velocity but increases the maximum fluid temperature. Kothandapani et al. [9] injected magnetic NPs into the tumour tissue in the presence of a magnet close to the tumour under the influence of peristaltic waves. This type of nanofluid flow contributed significantly to the treatment of cancer tissue. According to the data, the pressure rose as the number of Hartmann and the thermal separation coefficient increased. Zaman et al. [10] compared hybrid NPs and silver NPs, showing that hybrid NPs have an essential role in mitigating hemodynamic factors compared to silver particles. Hayat and Nadeem [11] discussed a new three-dimensional model incorporating the chemical reaction, the effect of heat radiation, and heat generation. It was concluded that the heat transfer rate of the hybrid nanofluid is higher than that of the simple nanofluid. Hayat et al. [12] compared water to a hybrid nanofluid and noted that thermal radiation increased the temperature in the nanofluid. Nadeem et al. [13], Nadeem and Abbas [14] discussed the properties of a three-dimensional hybrid nanofluid flow past a circular cylinder and concluded that the hybrid fluid heat transfer rate had been enhanced compared to the normal nanofluid. Abbas et al. [15] investigated the hydrodynamics and magnetism of hybrid nanofluids with two types of NPs suspended in water. Abbas et al. [16] examined the transport of NPs, within a magnetic field, on the curved surface of Riga. The magnetic nanofluids (micropolar) heat transfer rate was studied and investigated. Ghalambaz et al. [17] examined the hybrid nanofluids inside a cavity and studied the effect of the main factors on heat distribution. The results showed that the heat transfer rates increased due to adding the hybrid NPs, which is consistent with other studies in the literature [18]. Chamkha [19] discussed the generation of entropy and heat transport in a magnetic field inside a square enclosure filled with water equipped with a hollow cylinder. The results demonstrated that the presence of the hollow cylinder played an essential role in controlling the fluid flow and enhancing heat transfer. Khan et al. [20] studied the viscous hybrid nanofluids between two parallel plates and examined thermal radiation and heat generation. The chemical reactions with a novel aspect of activation energy have been explored. Furthermore, thermal radiation, heat generation, and Joule heating have been investigated. According to their findings, when the Eckert and Prandtl numbers were increased, the temperature reduced considerably.

Numerical simulation and computational modelling are widely used to solve mathematical problems in biological applications to reduce the cost and time of studying the problem parameters [21]. Sefidgar et al. [22] introduced three methods to simulate drug transport using advanced mathematical tools to study the effect of a static or dynamic blood vessel network. The results revealed that using the avascular approach with a large drug concentration enhanced drug delivery more than the vascular approach. حفظ الترجمة.

Hady et al. [23] employed a single-phase model to examine the flow of nanofluids past a horizontal plate, which generated a boundary layer consisting of heat transfer. The results indicated that the heat transfer rate increased when the expansion plate parameter and the power law index were increased. Perarasu et al. [24] discussed the heat transfer properties of nanofluids for a helical fluid and found that the heat transfer properties of the nanofluid improved significantly compared to water. Naik et al. [25] investigated the problem of heat transfer in three different nanofluids using thermal analysis to determine the total heat transfer coefficient and Nusselt number. The results showed that the concentration of the nanofluid increased with the increase in the Nusselt number.

Selectively delivering drugs to target tumours could improve the therapeutic efficiency of cancer treatment and reduce side effects in normal tissues. Hady et al. [26] introduced a study to investigate the issue of natural convection across a porous plate saturated with a nanofluid. The findings demonstrated that adding NPs to the base fluid changes the flow pattern. Nourazar et al. [27] examined the effect of heat transport through a horizontal porous cylinder in the presence of a magnetic field using the Optimal Collocation Method to solve this problem. The effects of different NP types on temperature, velocity, boundary layer thickness and Nusselt number were discussed.

According to Liaqat Ali et al. [28], who discussed the effects of NP diameter and transport on the temperature gradient of the nanofluid, a significant reduction in the thermal distribution occurred as NP diameter was increased. It was also discovered that the nanofluid viscosity significantly decreased due to the concentration gradient, which raised the fluid velocity. Sadia Hina et al. [29] investigated the fluid flow and heat transfer outside of a hollow rubber cylinder suspended in a Newtonian fluid. It was concluded that the increase in the power law index contributed effectively to the axial flow but reduced the wall shear resistance. Recently, Ahmed et al. [30] investigated theoretically tumour irradiation using an alternative magnetic field in the presence of NPs. According to this study, the efficacy of the thermal therapy depended on the accumulation of NPs within the tumour in addition to the tumour tissue thermal properties. On the other hand, the NP extravasation from the blood vessel into the surrounding hot tissue has been investigated theoretically by Mansour et al. [31]. Thermophoresis was found to elevate the blood temperature in the blood vessel.

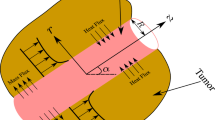
This research investigates the problem of heat transfer and NP mass transport within the interstitial fluid (the fluid which fills the gaps between the cells in the tissue [32]) in the extracellular matrix. In particular, the blood vessel segment is represented by a vertical cylinder, as shown in Fig. 1. The NPs were assumed to be injected into the blood vessel, which extravasated into the surrounding tissue. It is considered that the tissue surrounding the blood vessel is exposed to an external heat source (alternating magnetic field). In light of the accumulation of NPs within the tumour and the temperature of the tumour, this study investigates the heat transfer in the tissue to examine the efficacy of thermal therapy application. In order to address the problem in three dimensions, it is assumed that the tumour is homogeneous in the circumference direction. This study simulates thermal therapy for treating tumours by heating NPs using an external alternating magnetic field. Hence, the research question of this study would be: What are the optimal properties of the tissue and NPs which enhance the thermal therapy for cancers?

Fig. 1
figure 1

Geometry of the problem

Full size image

The structure of the manuscript is as follows: The introduction introduces the magnetohydrodynamic nanofluids, the intrinsic thermal properties of nanofluids, and the biomedical uses of nanofluids. In Sect. 2, both the physical problem and its mathematical model are described. The following section (Sect. 3) is a description of the numerical solution method. The results and explanation of the mathematical model are presented in Sect. 4, while the conclusion of the manuscript is presented in Sect. 5.

2 Description of the physical model

This study discusses the heat transfer in incompressible Newtonian fluids past a vertical cylinder (a blood vessel segment) surrounded by a tumour. Here \(r\) is the radial direction in the cylindrical coordinates, while z is the axial coordinate, as shown in Fig. 1. The NPs concentration in the blood vessel is denoted by \({C}_{b}\), while \({T}_{b}\) refers to the blood temperature. The mathematical model incorporates an external heat source, an alternating magnetic field with strength \({B}_{0}\) acts in the radial direction, which heats up the tissue surrounding the vessel assuming to be far from the blood vessel, as depicted in Fig. 1. Hence, the governing equations for the problem and the corresponding boundary conditions are given by [33]

$$\frac{\partial w}{{\partial z}}\, + \,\frac{\partial u}{{\partial r}}\, + \,\frac{u}{r}\, = \,0,$$
(1)
$$\frac{1}{{\varepsilon^{2} }}\,\left( {w\,\frac{\partial w}{{\partial z}}\, + \,u\frac{\partial w}{{\partial r}}} \right)\, = \,\frac{{\nu_{eff} }}{\varepsilon }\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }}\, + \,\frac{1}{r}\frac{\partial w}{{\partial r}}} \right)\, - \,\frac{{\nu_{eff} }}{K}\,W\, + \,\frac{1}{{\rho_{f} }}[\left( {1\, - \,C_{\infty } } \right)\rho_{f\infty } \beta g(T\, - \,T_{\infty } )\, - \,\left( {\rho_{p} \, - \,\rho_{f\infty } } \right)\left( {C\, - \,C_{\infty } } \right)g]\, - \,\frac{{\sigma_{0 } B_{0}^{2} }}{\rho }\,w,$$
(2)
$$w\,\frac{\partial T}{{\partial z}}\, + \,u\frac{\partial T}{{\partial r}}\, = \,\left( {\alpha_{eff} \, + \,\frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} \left( {\rho c_{p} } \right)_{eff} }}} \right)\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }}\, + \,\frac{1}{r}\frac{\partial T}{{\partial r}}} \right)\, + \,\tau \left( {\frac{{D_{B} }}{{\rho_{p} }}\left( {\frac{\partial T}{{\partial r}}\frac{\partial C}{{\partial r}}} \right)\, + \,\frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial r}}} \right)^{2} } \right)\, + \,\frac{SAR}{{\rho c_{p} }} \left( {C\, - \,C_{\infty } } \right),$$
(3)
$$\frac{1}{\varepsilon }\left( {w\frac{\partial C}{{\partial z}}\, + \,u\frac{\partial C}{{\partial r}}} \right)\, = \,D_{B} \left( {\frac{{\partial^{2} C}}{{\partial r^{2} }}\, + \,\frac{1}{r}\frac{\partial C}{{\partial r}}} \right)\, + \,\frac{{\rho_{p} D_{T} }}{{T_{\infty } }}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }}\, + \,\frac{1}{r}\frac{\partial T}{{\partial r}}} \right)\,r\, = \,a\,:\, u\, = \,U,\, w\, = \,0,\,T\, = \,T_{b} ,\,C\, = \,C_{b}$$
(4)
$$r \to \infty :\,\frac{1}{r} \left( {ru} \right)\, \to \,0,\,uT\, - \,\left( {\alpha_{eff} \, + \,\frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} \left( {\rho c_{p} } \right)_{eff} }}} \right) \frac{\partial T}{{\partial r}}\, \to \,Q_{H} ,\,\frac{1}{\varepsilon }\,uC\, - \,D_{B} \frac{\partial C}{{\partial r}}\, - \,\frac{{D_{T} }}{{T_{\infty } }}\frac{\partial T}{{\partial r}}\, \to \,k$$
(5)

where \((u,\mathrm{w}\)) are the components of the fluid velocity, \(U =ca\gamma\) is the radial velocity at the vessel wall, \(a\) is the radius of the cylinder, \({T}_{b}\) is the blood temperature of the interstitial fluid, \(C\) represents the concentration of NPs and \({C}_{b}\) is the NP concentration at the surface of the cylinder. The parameter \(g\) is the gravitational acceleration,\({k}^{*}\) is the mean thermal coefficient, \(\sigma\) is the electric conductivity,\({\sigma }^{*}\) is Stefan Boltzmann constant, \({D}_{B}\) is the Brownian coefficient, \({D}_{T}\) is the thermophoresis coefficient, α is thermal diffusivity, \(\beta\) is the thermal expansion coefficient, \(K\) is the tissue permeability, \(k\) is the NP extravasation coefficient,\(\rho\) is the density, \({\left(\rho {c}_{p}\right)}_{eff}\) is the effective heat capacity of the NP material, \({\alpha }_{eff}\) is the effective thermal diffusivity, \({\nu }_{eff}\) is the effective kinematic viscosity and \(\varepsilon\) is the tissue porosity. The specific absorption rate \(SAR\) is introduced into the energy equation, which represents the amount of absorbed non-ionising radiation power (or rate of absorbed energy) by the unit mass of the biological tissue. The model boundary conditions at the tissue far-field limits impose zero fluid flux and constant heat and mass fluxes, see Eq. (5).

When the tumour is exposed to an external heat source (such as an alternative magnetic field or laser beam), the tumour vasculature absorbs the heat generated in the tissue [34]. Hence, one can calculate the heat flux into the blood vessel in the form [33]:

$$\left. {Q_{H} } \right|_{r = a} = \left( {uT - \left( {\alpha_{eff} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} \left( {\rho c_{p} } \right)_{eff} }}} \right) \frac{\partial T}{{\partial r}}} \right)_{r = a}$$
(6)

We reduce the system of PDEs, Eqs. (2–4), into ODEs using the following similarity transformations [33]:

$$\eta = \left( \frac{r}{a} \right)^{2} , u = - ca\left[ {\frac{f\left( \eta \right)}{{\sqrt \eta }}} \right], w = 2czf^{\prime}\left( \eta \right), \theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{b} - T_{\infty } }}, \phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{b} - C_{\infty } }}$$
(7)

Substituting Eq. (7) into Eqs. (2–4), the following ordinary differential equations can be obtained:

$$\varepsilon R_{v} (\eta f^{?} + f^{?} ) - \frac{{\varepsilon^{2} R_{v} }}{4Da}f^{\prime}\, + \,R_{e} (ff^{\prime\prime} - f^{{\prime}{2}} ) + \varepsilon^{2} R_{e} G_{r} (\theta - N_{r} \phi ) + \varepsilon^{2} R_{e} M_{0} f^{\prime} = 0,$$
(8)
$${R}_{k}(1+{R}_{d})\left(\eta {\theta }^{{\prime}{\prime}}+{\theta }{\prime}\right)+{R}_{e}{ P}_{r}f{\theta }{\prime}+{ P}_{r} \eta \left({N}_{b}{\phi }{\prime}{\theta }{\prime}+{N}_{t}\theta {^{\prime}}^{2}\right)+\lambda Pe \frac{{N}_{b}}{{N}_{t}}\phi =0,$$
(9)
$$\frac{\varepsilon }{Sc}\left( {\eta \phi^{\prime\prime} + \phi^{\prime}} \right) + R_{e} f\phi^{\prime} + \varepsilon \left( {\frac{{N_{t} }}{{N_{b} }}} \right)\left( {\eta \theta^{\prime\prime} + \theta^{\prime}} \right) = 0,$$
(10)

where;

$$R_{k} = \frac{{k_{eff} }}{{k_{f} }},\,R_{v} = \frac{{\nu_{eff} }}{{\nu_{f} }}$$
(11)

Here \(f\) is the dimensionless velocity, \(\eta\) similarity variable, \({M}_{0}=\frac{{\sigma }_{0}{B}_{0}^{2}}{2\rho c}\) is the magnetic field parameter, \({R}_{e}=\frac{c{a}^{2}}{2{\upsilon }_{f}}\) is the Reynolds number, \(\mathit{Da}=\frac{K}{{a}^{2}}\) is the Darcy number, \({P}_{r}=\frac{{\upsilon }_{f}}{{\alpha }_{f}}\) is the Prandtl number and \(Sc={\upsilon }_{f}{D}_{B}^{-1}\) is the Schmidt number. In addition, \({N}_{b}=\frac{{\tau D}_{B}({C}_{b}-{C}_{\infty })}{{\upsilon }_{f}{C}_{\infty }}\) is the Brownian motion parameter, \({N}_{t}=\frac{\tau {D}_{T}({T}_{b}-{T}_{\infty })}{{\upsilon }_{f}{T}_{\infty }{C}_{\infty }}\) is the thermophoresis parameter, \({G}_{r}=\frac{(1-{\phi }_{\infty }){\rho }_{f\infty \beta g({T}_{b}-{T}_{\infty })z}}{{\rho }_{f}{U}^{2}}\) is the Grashof number and \({R}_{d}=\frac{16{\sigma }^{*}{T}_{\infty }^{3}}{3{k}^{*}{k}_{eff}}\) is the radiation parameter, \({N}_{r}=\frac{\left({\rho }_{p}-{\rho }_{{f}_{\infty }}\right)\left(C-{C}_{\infty }\right)}{\left(1-{C}_{\infty }\right){\rho }_{{f}_{\infty }} \beta \left({T}_{b}-{T}_{\infty }\right)}\) is the buoyancy ratio parameter,\(Pe={P}_{r}{R}_{e}\), is the Peclet number and \(\lambda =\frac{{\rho }_{p}{D}_{T} SAR}{{2c D}_{B} {T}_{\infty } \rho {c}_{p}}\) is the heat source coefficient.

Using the transformations (7), the dimensionless boundary conditions can be written in the form:

$$\eta = 1:f = - \gamma , f{\prime} = 0, \theta = 1, \phi = 1,$$
$$\eta \to \infty :f^{\prime} \to 0, - \eta_{\infty }^{ - 0.5} f\left( {\theta + \xi_{1} } \right) - B\left( {1 + R_{d} } \right)\eta_{\infty }^{0.5} \theta^{\prime} \to Q_{H}^{*} \,f\left( {\phi + \xi_{2} } \right) + A\eta_{\infty } \left( {\phi^{\prime} + \frac{{N_{t} }}{{N_{b} }}\theta^{\prime}} \right) = - \eta_{\infty }^{0.5} K^{*}$$
(12)

And the heat flux dimensionless at the vessel wall is given by

$${\left.{Q}_{H}^{*}\right|}_{\eta =1}=\gamma \left(1+{\xi }_{1}\right)-B\left(1+{R}_{d}\right){\theta }{\prime}$$
(13)

Where \(A=\frac{2\varepsilon {D}_{B}}{c{a}^{2}}\), \({K}^{*}=\frac{\varepsilon k}{ca\left({C}_{b}-{C}_{\infty }\right)}, B=\frac{2{\alpha }_{eff}}{c{a}^{2}} , {Q}_{H}^{*}=\frac{{Q}_{H}}{ca({T}_{b}-{T}_{\infty })}, {\xi }_{1}=\frac{{T}_{\infty }}{{T}_{b}-{T}_{\infty }}\) and\({\xi }_{2}=\frac{{C}_{\infty }}{{C}_{b}-{C}_{\infty }}\). Where,\({K}^{*}\), and \({Q}_{H}^{*}\) are dimensionless constants.

However, the local Nusselt number is given by:

$$Nu=\frac{-a}{\Delta T} {\left[\frac{\partial T}{\partial r}\right]}_{r=a}$$
(14)

Subistituting the dimensionless transformations [Eqs. (7)] into Eq. (14) one can get

$$Nu = - 2\theta^{\prime}\left( 1 \right)$$
(15)

The baseline parameter values are listed in Table 1.

Table 1 The baseline parameter value
Full size table

3 The numerical method of solution

The system of equations (ODE) was reduced into a system of first-order differential equations [33], using the following new variables:

$$s_{1} {\mkern 1mu} = {\mkern 1mu} f{\mkern 1mu} ,s_{2} {\mkern 1mu} = {\mkern 1mu} f^{\prime},s_{3} {\mkern 1mu} = {\mkern 1mu} f^{\prime\prime},{\mkern 1mu} s_{4} = \theta ,s_{5} = \theta ^{\prime},s_{6} = \phi ,s_{7} = \phi ^{\prime}$$

So, the system of Eqs. (8–10) and (12) can be written in the form:

$$s^{\prime}{\mkern 1mu} = {\mkern 1mu} s_{2} ,{\mkern 1mu} s_{2}^{\prime } {\mkern 1mu} = {\mkern 1mu} s_{3} ,$$
$$s_{3} ^{\prime } = \frac{{ - 1}}{{\eta \left( {\varepsilon R_{v} } \right)}}[\varepsilon R_{v} s_{3} - \frac{{\varepsilon ^{2} R_{v} }}{{4Da}}s_{2} + R_{e} \left( {s_{1} s_{3} - s_{2}^{2} } \right) + \varepsilon ^{2} R_{e} G_{r} \left( {s_{4} - N_{r} s_{6} } \right) + M_{0} \varepsilon ^{2} R_{e} s_{2} ]$$
$$s_{4}{\prime} = s_{5}$$
$$s_{5} ^{\prime } = \frac{{ - 1}}{\eta }[s_{5} + \frac{{R_{e} P_{r} }}{{R_{k} \left( {1 + R_{d} } \right)}}s_{1} s_{5} + \frac{{P_{r} }}{{R_{k} \left( {1 + R_{d} } \right)}}\left( {N_{b} s_{7} s_{5} - N_{t} s_{5}^{2} } \right) + \frac{{\lambda Pe}}{{R_{k} \left( {1 + R_{d} } \right)}}\left( {\frac{{N_{b} }}{{N_{t} }}} \right)s_{6} ]$$
(16)
$$s_{6}{\prime} = s_{7} { }$$
$$s_{7}{\prime} = \frac{ - 1}{\eta } [s_{7} + \frac{{N_{t} }}{{N_{b} }} \left( {\eta s_{5}{\prime} - s_{5} } \right) + \frac{{R_{e} Sc}}{\varepsilon } s_{1} s_{7} ]$$

The boundary conditions (12 & 13) can be written in the form.

$$\eta = 1:\,s_{1} = - \gamma ,s_{2} = 0,s_{4} = 1, s_{6} = 1,$$
$$\eta \to \infty :\,s_{2} = 0, - \eta_{\infty }^{ - 0.5} s_{1} \left( {s_{4} + \xi_{1} } \right) - B\left( {1 + R_{d} } \right) \eta_{\infty }^{0.5} s_{5} \to Q_{H}^{*} ,\, s_{1} \left( { s_{6} + \xi_{2} } \right) + A\eta_{\infty } \left( { s_{7} + \frac{{N_{t} }}{{N_{b} }} s_{5} } \right) = - \eta_{\infty }^{1/2} K^{*}$$
(17)

The initial solutions are given as \({s}_{1}={s}_{2}={s}_{3}={s}_{4}={s}_{5}={s}_{6}={s}_{7}=0\). Then, the system of Eqs. (8–10) and (12) was solved numerically using the subroutine bvp4c in MATLAB with a relative error tolerance of O(\({10}^{-5}\)).

4 Results and discussion

This study investigated the nanofluid flow in a tumour surrounding a vertical blood vessel exposed to a suitable magnetic field. In particular, the system of Eqs. (8–10) and (12) have been solved numerically, as shown in the previous section, where it was considered a spatial grid consisting of 100 mesh points, with relative error \(O({10}^{-5})\). The numerical solution has been validated against a previous work in the literature [35], as shown in Table 2. The numerical results of this problem are presented graphically in Figs. (2, 3, 4, 5).

Table 2 Comparison showing values of the local Nusselt number for different values of \({G}_{r}\) and \(\gamma\) at \({R}_{e}=2 , {N}_{b}={N}_{t}={N}_{r}=n=0.1 , {P}_{r}=7, Le=2 , {M}_{0}=0, \lambda =0.\) Note that the boundary conditions have been adjusted for model comparison
Full size table

The effect of \(\gamma , {K}^{*}\) on the velocity of the interstitial fluid and temperature, in addition to the NP concentration have been evaluated, as shown in Figs. 2. The results indicate that the most significant value of the interstitial fluid velocity occurs at the vessel wall, which is significantly reduced in the extracellular, see (Fig. 2A). Also, when the values of the interstitial fluid velocity at the vessel wall increased, the temperature of the interstitial fluid increased dramatically, see (Fig. 2B), which could improve the outcomes of the thermal therapy. Moreover, the fluid flux at the vessel wall increased the NP concentration significantly, improving the heat transfer in the interstitium, as shown in (Fig. 2C). Also, the increase in the values of the mass flow coefficient \({K}^{*}\) led to a significant decrease in the concentration of the NPs in the nearby tissues see (Fig. 2D), which reduced the accumulation of NPs inside the tumour and adjacent tissues. On the other hand, Figs. 3 describe the influence of the heat transfer, \({Q}_{H}^{*},\) and the Brownian motion coefficient, \({N}_{b}\), on the temperature and concentration of NPs in the interstitial fluid. The results showed that the increase in the heat transfer coefficient \({Q}_{H}^{*}\) led to a decrease in the temperature of the nanofluid, see (Fig. 3A) as a result of the cooling of the tissues due to heat dissipation at the tumour surface. In addition, the increase in the heat transfer coefficient \({Q}_{H}^{*}\) increased the concentration of NPs in the tumour, which contributed to the delivery of NPs into deep tissues, which enhanced the tumour ablation during the heating process using the alternative magnetic field, see (Fig. 3B). It was also observed that the increase in the Brownian motion coefficient (\({N}_{b})\) decreased the concentration of NPs inside the tumour (Fig. 3C); however, this corresponded to a noticeable rise in the temperature of the nanofluid (Fig. 3D), which enhanced the therapeutic process.

Fig. 2
figure 2

Numerical results for different dimensionless parameters: A The interstitial fluid velocity in the radial direction for different values of \(\gamma\). B The interstitial fluid temperature for different values of \(\gamma\). C NP concentration for different values of \(\gamma\). D NP concentration for different values of \({K}^{*}\)

Full size image
Fig. 3
figure 3

Numerical results for different dimensionless parameters: A The interstitial fluid temperature for different values of \({Q}_{H}^{*}\). B NP concentration for different values of \({Q}_{H}^{*}\). C NP concentration for different values of \({N}_{b}\). D The interstitial fluid temperature for different values of \({N}_{b}\).

Full size image

Figures 4 depict the influence of the thermal conductivity coefficient, \({N}_{t}\), and the radiation coefficient, \({R}_{d}\), on the temperature and concentration of the NPs in the interstitial fluid. The results indicated that the increase in the thermal conductivity coefficient \({N}_{t}\) value led to a decrease in the temperature of the nanofluid (Fig. 4A), while the concentration of the NPs increased. Therefore, increasing \({N}_{t}\) value reduced the induced tumour temperature during heating, corresponding to increasing the NP penetration into the deep tumour tissue (Fig. 4B). Similarly, the increase of radiation coefficient parameter, \({R}_{d}\), reduced the tumour temperature (Fig. 4C), but elevated the concentration of NPs (Fig. 4D).

Fig. 4
figure 4

Numerical results for different dimensionless parameters: A The interstitial fluid temperature for different values of \({N}_{t}\). B NP concentration for different values of \({N}_{t}\). C The interstitial fluid temperature for different values of \({R}_{d}\). D NP concentration for different values of \({R}_{d}\)

Full size image

Finally, the effect of the heat source coefficient \(\lambda\) on the temperature and the (NPs) concentration has been shown in Fig. 5. The results showed that the increase in the parameter \(\lambda\) value led to a significant increase in the tumour interstitium temperature, see Fig. 5A. The temperature elevation in the tumour showed that the alternating magnetic field might induce tumour cell death without need for medical surgery. Furthermore, the increase in \(\lambda\) enhanced the NP penetration into the tumour (Fig. 5B). Hence, increasing the value of the parameter \(\lambda\) enhanced the accumulation of NPs within the tumour and elevated the tumour temperature, which is required for successful hyperthermia. Figure 5C shows the increase in Nusselt number due to the increase in the heat source coefficient. Here the Nusselt number is negative, which refers to the direction of the heat transfer is from the tissue into the blood vessel. On the other hand, the Nusselt number decreased slightly against the increase in \({Q}_{H}^{*}\), see Fig. 5D. This small change in Nusselt number against \({Q}_{H}^{*}\) is due to the small variation of the tissue temperature adjacent to the blood vessel for different values of \({Q}_{H}^{*}\), as shown in Fig. 3A.

Fig. 5
figure 5

Numerical results for different dimensionless parameters: A The interstitial fluid temperature for different values of \(\lambda\). B NP concentration for different values of \(\lambda\). C The Nusselt number against \(\lambda\). D Nusselt number against \({Q}_{H}^{*}\)

Full size image

5 Conclusion

88In this work, a numerical analysis of a Newtonian nanofluid around a horizontal cylindrical vessel in the presence of a magnetic field was conducted. In addition, the effect of nanofluid interstitial fluid velocity, tissue heat absorption coefficient, heat radiation, and heat transfer within tumour tissue was explored. A system of partial differential equations (PDEs) was designed to mimic fluid movement, NP transport, and heat transfer in the interstitial space. The mathematical model was closed with appropriate boundary conditions to determine the heat and mass flux across tissue boundaries. The system of PDEs was transformed into a system of ODEs using similarity transformations, which was solved numerically by MATLAB.

The results showed that the maximum value of the velocity of the interstitial fluid is at the wall of the blood vessel, which decreased across the tumour, and the velocity of the interstitial fluid was inversely proportional to the temperature of the fluid. An increase in the mass flux coefficient \({K}^{*}\) lead to a near-homogeneous accumulation of NPs within the tumour. In addition, an increase in the heat transfer coefficient \({Q}_{H}^{*}\) enhanced the delivery of NPs to deep tissues, and an increase in the coefficient of Brownian motion \({N}_{b}\) lead to a decrease in the thickness of the boundary layer of fluid that resisted the NP transport in the tumour, increasing the temperature of the interstitial fluid adjacent to the blood vessels. Furthermore, increasing the value of the thermal displacement coefficient \({N}_{t}\) and the thermal radiation coefficient \({R}_{d}\) lead to an increase in the concentration of NPs in the interstitial tissue. The NPs spread throughout the tumour and raised the temperature of the tumour as the heat absorption \(\lambda\) was increased.

According to this study, the ability of NPs to absorb heat in tissue impacts the efficacy of thermal treatment for treating tumours. In the future work this study should be generalised to incorporate NP removal from the blood circulation in the body caused by the immune system, which requires extending this model using transient concentration and heat equations.