1 Introduction

Asphalt pavement is a popular road surface made of aggregate and asphalt binder. However, traditional asphalt pavement has low water permeability, which can cause safety issues like hydroplaning. Researchers have studied asphalt pavement distresses like fatigue, aging, and moisture sensitivity, leading to the development of high-strength asphalt using additives to improve crash resistance [1, 2].In areas with high precipitation, water, ice, and snow can cause asphalt pavement distress. To address this issue, researchers have investigated porous asphalt as a new type of asphalt mixture that can drain surface water and prevent moisture damage by providing a free water pavement surface. Porous asphalt, widely used since the 1980s, consists of a graded asphalt mixture with high air voids (around 20%). It is primarily used as a layer to drain surface water in areas with high moisture and precipitation [3]. Porous asphalt offers numerous benefits, including reducing traffic noise, reducing light reflection during rainy nights, preventing hydroplaning, reducing water sprays during rain, increasing slip resistance, and increasing traffic flow during rain [4,5,6,7]. Additionally, it is used as a stress absorber layer to reduce the expansion of reflective cracks [3]. However, there are some disadvantages to consider, such as high construction costs, low mechanical performance due to void space filling and inadequate surface drainage, and winter maintenance issues [3, 8]. The high percentage of interconnected spaces can accelerate the oxidation aging of the thin film thickness of the bitumen, leading to weak adhesion between the mastic and the aggregate, which can cause raveling [9]. Despite its drawbacks, porous asphalt has gained popularity in the United States and many European countries due to its increased pavement safety [10,11,12,13]. Siliceous and limestone aggregates have been widely studied in the literature for their utilization in conventional and porous asphalt mixtures. These aggregates have demonstrated significant effects on the performance and properties of asphalt pavements. Siliceous aggregates, such as silica sand and quartzite, are known for their high silica content. They have been extensively investigated for their influence on the engineering properties of asphalt mixtures. Silica sand, a naturally occurring siliceous aggregate, has been used in conventional asphalt mixtures to enhance the stability, durability, and skid resistance of pavements [14, 15]. Quartzite, another type of siliceous aggregate, has been explored for its potential to improve the resistance to rutting and moisture damage in asphalt mixtures [16, 17]. Various studies have examined the effects of different gradations and percentages of siliceous aggregates on the performance of asphalt pavements [18,19,20].

Limestone aggregates, including crushed limestone and limestone fines, have also received significant attention in the field of asphalt engineering. Crushed limestone, commonly used as a coarse aggregate, has been investigated for its impact on the mechanical properties and resistance to permanent deformation in asphalt mixtures [21, 22]. Limestone fines, a by-product of limestone quarrying and processing, have been studied as a filler material to improve the workability, stiffness, and resistance to moisture damage of asphalt mixtures [23, 24]. Several studies have explored the effects of different proportions and particle sizes of limestone aggregates on the performance of asphalt pavements [25, 26].

The use of siliceous and limestone aggregates in porous asphalt mixtures has also been examined. Porous asphalt, renowned for its ability to drain water and reduce storm water runoff, can benefit from the inclusion of these aggregates. Siliceous aggregates have been investigated for their impact on the porosity, permeability, and mechanical properties of porous asphalt mixtures [27, 28]. Limestone aggregates, particularly limestone fines, have been studied as fillers to enhance the stability, void content, and resistance to water sensitivity of porous asphalt [29, 30].

Different countries and research institutes have presented various aggregates for porous asphalt based on their expectations and limitations related to the specifications of this type of asphalt mixture. The most widely used approach is the granularity provided by the National Asphalt Pavement Association (NAPA) [31]. The mix design procedure and type of material used in porous asphalt pavement are critical for achieving satisfactory performance and quality. Therefore, different aggregate gradations and sources can significantly affect the results of experiments and provide an optimal mixing plan [32, 33]. Among the most important methods for porous asphalt mixing are Spanish Regulations, National Center for Asphalt Technology (NCAT), Hanson, and Federal Highway Administration (FHWA). NCAT Regulation is the most acceptable due to the limitations of functional tests [10, 34].

The type of aggregate material used in porous asphalt mixture is an essential variable that should be considered in its design due to its chemical characteristics. studying the effect of siliceous and limestone aggregates in porous asphalt is crucial for optimizing performance, enhancing durability, promoting sustainability, evaluating cost-effectiveness, and providing practical implementation guidelines. This research can contribute to the advancement and widespread adoption of porous asphalt as a reliable and effective pavement solution. This study aims to examine the impact of different types of aggregates and gradations on the functional and mechanical properties of porous asphalt mixes with two bituminous contents of 5% and 6%.

2 Material and method

2.1 Aggregate and gradation

In this study, materials were sourced from two different suppliers: the Stone Mining Company of Asb Charan, produced by Kandovan Pars Company, and the Kan River in Tehran Province. Lime filler was chosen for its high resistance to stripping. Table 1 presents the conventional properties of the aggregates. The aggregates used in this study were obtained from NAPA (Grade 2) and Spanish sources (Grades No. 1 and 3), and their ranges are shown in Table 2.

Table 1 Properties of aggregates used in this research
Full size table
Table 2 The range of aggregates
Full size table

In selecting the appropriate asphalt binder for porous asphalt mixtures, various factors such as the local environment, traffic volume, and desired performance characteristics should be taken into consideration. For this study, a bitumen with a penetration grade of 60/70, which was produced by Pasargad Oil Company, was utilized. Classical experiments were conducted to determine the properties of the bitumen, and the results are presented in Table 3.

Table 3 Properties of bitumen used in this research
Full size table

2.2 Marshall samples

To ensure the accuracy of the testing results, a strict three-stage production process was followed for the porous asphalt samples. The first stage involved heat treatment of the aggregate and bitumen, with the aggregates placed in an oven set at 150 °C for 24 h, and the bitumen heated in the oven for 1.5 h at the mixing temperature. The second stage involved mixing the heated bitumen with the aggregates in a mixer until the aggregate was uniformly coated with the bitumen. The mixture was then placed in the oven for 30 min at 138 °C to simulate compact temperature during construction. It should be noted that the Marshall molds were also heated for at least 2 h at the selected temperature.

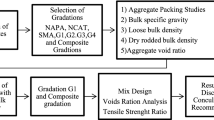
The third and final stage involved the compaction of the mixture using the Marshall apparatus with 50 hits on each side of the specimens. To ensure uniformity in sample height, 1050-g samples were used. After compaction, the asphalt samples were allowed to cool to room temperature for 24 h before being removed from the Marshall molds. This research focused on evaluating several properties of the porous asphalt samples, including percent effective void, unaged cantabro, permeability, moisture sensitivity, and drain down. Figure 1 illustrates the general overview of the research process conducted.

Fig. 1
figure 1

Research process flowchart

Full size image

2.3 Experiments

In order to evaluate and compare the performance of different asphalt mixtures with various gradations and types of aggregate materials, functional tests are conducted on the samples. These tests are designed to assess the overall performance characteristics of the asphalt mixtures.

2.3.1 Porosity

In this study, the Mantis et al. [35] method was used to determine the percentage of interconnected voids in the porous asphalt samples. The effective void content was calculated using Eq. (1) in this method. The percentage of porosity indicates the amount of voids that can hold water. To calculate the percentage of voids in the asphalt sample, the total volume (VT) of the sample was measured by determining its height and diameter. The dry mass (Mdry) of each sample was then determined and placed at 25 °C for 30 min. After 30 min, the samples were rotated 180° and tapped five times on the sample container to release any trapped air bubbles. The weight of the samples was measured in the saturated state (Msub). The percentage of voids in the porous asphalt samples was then calculated using Eq. (1) below, where ρw represents the density of water.

$$Porosity\left( \% \right) = \left[ {1 - \frac{{\frac{{\left( {M_{dry} - M_{sub} } \right)}}{\rho_w }}}{V_T }} \right] \times 100$$
(1)

2.3.2 Unaged Cantabro test

In this study, the Cantabro test was used to indirectly evaluate the adhesion, cohesion, wear and fatigue effects of aggregates and bitumen in porous asphalt mixtures. To ensure the accuracy of the test results, at least three replicas of the porous asphalt were prepared for each asphalt content, and their weights were carefully measured before the test (indicated as P1). After storing the samples at 25 °C for 4 h, they were placed in a Los Angeles abrasive machine with rotation speeds of 30 to 33 rpm. The machine was then set to rotate at a speed of 300 rpm, and after 300 rotations, the specimens were removed, and their weights were re-measured (indicated as P2). The weight loss (indicated as P) in the Cantabro test was calculated using Eq. (2) [36].

$$p = \frac{P_1 - P_2 }{{P_1 }} \times 100$$
(2)

2.3.3 Permeability test

In this study, the permeability of the porous asphalt samples was determined using a method developed by Soroush et al. (2008) [32]. Firstly, the samples were covered with a paraffin membrane to prevent water from passing through the wall between the tube and the specimen. The samples were then placed in a graduated transparent tube, and the top of the tube was filled with water. After saturating the samples in water for one hour, the time taken for the water level to drop from 70 to 30 mm was measured in seconds. This process was repeated three times to obtain an average time. The hydraulic conductivity coefficient k (m/day) was computed using Eq. (3), which takes into account the sample height values and the average time calculated. This method provides a reliable and accurate measurement of permeability, which is an important factor in determining the effectiveness of porous asphalt as a drainage material. The results of the permeability test can be used to assess the suitability of the porous asphalt samples for specific applications, such as parking lots, driveways, and roadways.

$$K = \frac{aL}{{At_m }}\log_{10} \left( {\frac{L + h_1 }{{L + h_2 }}} \right)T_c$$
(3)

In this relation, L is sample height (mm), tm is the average calculated time (sec), Tc is the temperature correction coefficient for water viscosity, a is pipe area (cm2) and A is sample area (cm2) [32, 36].

2.3.4 Evaluation of moisture sensitivity of porous asphalt mixtures

To evaluate the moisture sensitivity of porous asphalt mixtures, the AASHTO T283 standard was used with modifications since this test was initially developed for high-grade asphalt mixes. The modifications consisted of punching the porous asphalt samples with 50 hits of a Marshall hammer and subjecting them to a vacuum of 87.8 kPa (660 mm Hg) for 10 min to flood the punched samples and achieve a saturation level of 55–80%. The residual tensile strength was then calculated by dividing the indirect tensile strength of three wet specimens by the indirect tensile strength of three dry specimens. The resulting tensile strength ratio was obtained using Eq. (4), which serves as an indicator of the moisture sensitivity of porous asphalt mixes.

$${\text{Tensile}}\;{\text{Strength}}\;{\text{Ratio = }}TSR = \frac{S_2 }{{S_1 }} \times 100$$
(4)

S2 = Indirect tensile strength of the sample under wet conditions (after a period of melting and freezing) (kPa), S1 = Indirect tensile strength of sample in dry condition (kPa).

The stress applied to the sample is calculated using Eq. (5).

$$st = \frac{2000P}{{\pi tD}}$$
(5)

In this relation, St is tensile strength (kPa), P is the maximum load (N), t is sample thickness (mm) and D is sample diameter (mm).

2.3.5 Drain down test

The purpose of this test is to evaluate the quality of bitumen and its ability to be absorbed by the material without causing excessive precipitation in the mixture, which can lead to faster pore filling and slower water flow, eventually causing damage to the pavement. Additionally, if the bitumen drains and deposits around the grains, it can reduce the adhesion between the grains, resulting in rapid separation and pavement deterioration. The maximum allowable precipitation is 0.3%, and the test is conducted following the AASHTO T305-97 standard. To perform the test, a non-dense asphalt mixture is placed in a lace basket on a known weight tray. The sample is then heated in an oven at 165 °C with the basket and metal tray for one hour. After one hour, the amount of drainage from the basket is expressed as a percentage of the total weight of the mixture, and this value is calculated using Eq. (6).

Where D represents the percentage of drain down, A is the weight of the empty basket (g), B is the sample weight with the basket (g), C is the empty plate weight (g) and D is the weight of the plate and its contents after an hour (g) in oven.

$$D\% = \frac{D - C}{{B - A}}$$
(6)

3 Results and discussion

The following figures present the results of experiments conducted on porous asphalt samples. the letter A uses subscripts 1 and 2 to represent limestone and siliceous aggregates, respectively. For letter G uses subscripts 1, 2, and 3 to indicate different particle size gradations, while letter B uses subscripts 5 and 6 to represent binder percentages.

Figure 2 illustrates the percentage of voids in porous asphalt mixtures for different gradations and binder percentages of 5% and 6%. By comparing Figs. 2a and b, it is evident that asphalt samples made with limestone aggregates have lower percentages of voids compared to those with siliceous aggregates. Additionally, Figs. 2a and b indicate that, for both types of aggregates, gradation number 2 exhibits the highest percentage of voids, followed by numbers 1 and 3, when considering a fixed binder percentage. In other words, coarser gradations display higher percentages of voids with a fixed binder percentage. Figure 2 demonstrates that increasing the binder percentage leads to a decrease in the percentage of voids for both types of aggregates and all three gradations.

Fig. 2
figure 2

Average porosity of the porous asphalt mixtures

Full size image

The Cantabro abrasion test measures the adhesive properties between binder and aggregate materials. It is observed that an increase in the binder percentage reduces the weight loss of compacted samples [32]. Figures 3a and b show that, at a fixed binder percentage, gradation number 3 demonstrates the highest resistance to abrasion for both types of aggregates, followed by numbers 1 and 2. When comparing the Cantabro abrasion test results for both types of aggregates, siliceous aggregates exhibit higher resistance to mixture abrasion. The percentage of voids in the samples is another influential factor in this regard. Asphalt samples made with limestone aggregates, due to their lower percentage of voids, form a more continuous and cohesive mixture, which effectively reduces the level of abrasion.

Fig. 3
figure 3

Average Cantabro loss for unaged porous asphalt mixtures

Full size image

Figures 4a and b reveal that, at a fixed binder percentage, gradation number 2 demonstrates the highest permeability for both types of aggregates, followed by numbers 1 and 3. Comparing the permeability test results for both types of aggregates, siliceous aggregates exhibit higher permeability. Various factors contribute to the permeability of porous asphalt mixtures, such as the percentage of voids, particle shape, material arrangement, and void space connectivity. Among these factors, the percentage of voids significantly affects the permeability of porous asphalt and is easily measurable [36]. The experiments demonstrate that limestone samples, due to their lower percentage of voids, form a more continuous and cohesive mixture, resulting in fewer pathways for water passage. Furthermore, previous studies indicate that water-friendly materials possess higher permeability. Therefore, siliceous aggregates exhibit higher permeability in the asphalt mixture in this study.

Fig. 4
figure 4

Average permeability of porous asphalt mixtures

Full size image

Figures 5a and b demonstrate that, for both types of aggregate materials, when considering a fixed asphalt percentage, gradation No. 3 initially exhibits the highest level of indirect tensile strength in the dry state, followed by gradations No. 1 and 2. By comparing the results of the indirect tensile strength experiments in the dry state for both types of aggregate materials, it is evident that siliceous-based materials demonstrate a higher level of indirect tensile strength in this condition (as shown in Fig. 5). The increase in the asphalt percentage leads to a thicker asphalt film, reducing the likelihood of water penetration between the asphalt and aggregate materials [17, 23].

Fig. 5
figure 5

Average indirect tensile strength (ITS) of dry and conditioned specimens

Full size image

Figures 6a and b reveal that, for both types of aggregate materials, when considering a fixed asphalt percentage, gradation No. 1 initially exhibits the highest level of resistance to moisture sensitivity, followed by gradations No. 3 and 2. This observation aligns with the results of the percentage of voids experiments. By comparing the moisture sensitivity percentage results for both types of aggregate materials, it is observed that limestone materials exhibit higher resistance to moisture sensitivity (as shown in Fig. 6). The percentage of voids in the samples significantly contributes to this behavior. Limestone samples, due to their lower percentage of voids, form a more continuous and compact mixture, which enhances the level of resistance to moisture. Additionally, the type of aggregate material can impact the level of resistance to moisture-induced damage. This damage occurs when the bond between the asphalt and aggregate materials at their connection points deteriorates due to water. Siliceous-based materials, being hydrophilic and prone to water absorption, demonstrate lower resistance to moisture-induced damage. The increase in the asphalt percentage results in a larger volume of asphalt materials and a higher likelihood of asphalt bleeding. Figures 7a and b illustrate that, for both types of aggregate materials, when considering a fixed asphalt percentage, gradation No. 2 initially exhibits the highest level of asphalt bleeding, followed by gradations No. 3 and 1. Comparing the results of the asphalt bleeding percentage for both types of aggregate materials, it is observed that limestone materials have a lower level of asphalt bleeding. In other words, limestone samples, due to their better adhesion to asphalt, exhibit reduced asphalt bleeding (as shown in Fig. 7).

Fig. 6
figure 6

Tensile strength ratio (TSR) of porous asphalt mixtures

Full size image
Fig. 7
figure 7

Drain down test results of porous asphalt mixtures

Full size image

3.1 Analyzing data using the response surface method

The Response Surface Methodology (RSM) is a mathematical and statistical approach used to develop an analytical model that determines the influence of a set of independent variables on each response variable (dependent variable). This method allows for the assessment of individual factors and their interactions on each response variable. The most commonly used design in RSM is the central composite design (CCD) [37]. In this study, we used Design Expert 6.0 (Stat-Ease Inc., Minneapolis, USA) to analyze the data and establish the relationship between the functional characteristics of the response variables (percentage of the void, unaged cantabero, permeability, moisture sensitivity, and drain down) and the independent variables (bitumen and type of aggregate) as described in the previous section.

The RSM model equation is determined, and its coefficients are predicted. The model used is generally a complete quadratic equation or reduced form. A second-order model can be expressed as follows [38, 39]:

$$Y = C_{k0} + \sum_{i = 1}^4 {C_{ki} } x_i + \sum_{i = 1}^4 {C_{kii} } x_i^2 + \sum_{i < j = 2}^4 {C_{kij} } x_i x_j$$
(7)

To obtain the coefficients of Eq. (7), the least squares method was utilized. The resulting coefficients were then used to predict the response values. RSM models demonstrate the relationship between responses and independent variables [37]. To assess the statistical significance of each variable in the developed models, the P-value parameter was utilized. P-values range from 0 to 1, and any variable with a P-value greater than 0.05 should not be included in the regression model at the current significance level of 0.05 [40,41,42]. Additionally, the analysis of variance must have a P-value of less than 0.05 to be considered significant.

To evaluate the model's fitness, the coefficient R2 was employed. R2 indicates the proportion of variability in the response variable that is explained by the model. A higher value of R2 indicates a better fit between the observed and predicted values [43, 44]. However, R2 alone cannot determine the accuracy of the model since it represents changes around the average response. Therefore, the adjusted coefficient of determination (R2adj) is also used. This coefficient employs the mean square sum rather than the sum of squares and takes into account the number of terms in the model. The R2adj value should be as close to 1 as possible, indicating a good model fit. The calculations for these two coefficients are presented in the equations below [37]:

$$R^2 = 1 - \frac{{SS_{residual} }}{{SS_{total} }}$$
(8)
$$R_{adj}^2 = 1 - \frac{{SS_{residual} /DF_{residual} }}{{SS_{total} /(DF_{model} + DF_{residual} )}}$$
(9)

To make the statistical analysis possible, the samples' variables need to be represented in a numerical format. This process is known as encoding. In this study, three variables were encoded, namely, the percentage of bitumen (A), type of material (B), and different aggregates (C). The numerical code was used to represent each variable. The encoding of each variable is detailed in Table 4.To analyze the data using the Design Expert software, the variables were properly encoded. The encoding used in the software is presented in Table 4. To obtain each of the response variables, the encoded values were inputted into the models according to Table 5. One crucial encoding used in this study is related to aggregate gradation. The values of C[1] and C[2] for the variable-response models for aggregate 1 were 1 and 0, respectively. For aggregate 2, the values were 0 and 1, and for aggregate 3, the values were − 1 and − 1. This encoding was used to account for the different sizes of the aggregates and their impact on the response variables.

Table 4 Matrix coding of samples using design expert software
Full size table
Table 5 Encoding the variables in the design expert software
Full size table

After identifying the independent variables, ANOVA analysis was performed for each response variable. The results, shown in Table 6, reveal that the P-values for the effective factors in the models of all response variables are less than 0.05. The models for the permeability and Cantabro tests include variables A, B, C, and the interaction between aggregate and bitumen percentages (AC), as their P-values are less than 0.05. This interaction is evident in these tests, and the response variable changes accordingly, as discussed in Sect. 3.

Table 6 ANOVA analysis for response variables
Full size table

The high values of R2 and R2adj for each response variable indicate that the estimated model fits well with the experimental results. Figure 8 illustrates the actual values compared to the predicted values, and it is evident that the predicted values fit well with the real values, indicating the proper estimation of the model.

Fig. 8
figure 8

Design-expert plots; predicted versus actual values plots

Full size image

Table 6 demonstrates that the values of R2 and R2adj for all functional attributes are higher than 0.97, which confirms the results shown in Fig. 8. The permeability test has the highest value of R2adj, which is 0.9962, while the lowest value is 0.9726 for the moisture sensitivity results. Based on the relationships obtained in the encoded state, the following results were obtained:

$${\text{void}} = + 15.44 - 1.61 \times {\text{A}} + 1.03 \times {\text{B}} - 1.29 \times {\text{C}}[1] + 5.00 \times {\text{C}}[2]$$
(10)
$$\begin{aligned} {\text{CANTABERO}} & = + 10.49 - 1.45 \times {\text{A}} + 1.57 \times {\text{ B}} - 3.61 \times {\text{C}}[1] \\ & \quad + 9.43 \times {\text{C}}[2] + 0.23 \times {\text{AC}}[1] - 1.28 \times {\text{AC}}[2] \\ \end{aligned}$$
(11)
$$\begin{aligned} {\text{permeability}} & = + 91.24 - 13.21 \times {\text{A}} + 7.52 \times {\text{B}} - 15.10 \times {\text{C}}[1] \\ & \quad + 48.88 \times {\text{C}}[2] + 8.78 \times {\text{AC}}[1] - 14.02 \times {\text{AC}}[2] \\ \end{aligned}$$
(12)
$${\text{TSR}} = + 80.26 + 1.57 \times {\text{A}} - 2.66 \times {\text{B}} + 4.27 \times {\text{C}}[1] - 5.91 \times {\text{C}}[2]$$
(13)
$${\text{drain}}\;{\text{down}} = + 0.29 + 0.042 \times {\text{A}} - 0.018 \times {\text{B}} - 0.026 \times {\text{C}}[1] + 0.016 \times {\text{C}}[2]$$
(14)

3.2 Determine the optimum bitumen content

To determine the optimal mixing plan, the researchers utilized the DESIGN EXPERT software, incorporating functional limitations that align with both NCAT and Spanish regulations [10, 45]. The optimization process produced the ideal bitumen content for each aggregate and aggregate material. As shown in Table 7, Grade 2 limestone aggregate has an optimum bitumen content of 5.2% according to the NCAT limitation and 5% according to the Spanish regulation. In contrast, siliceous materials have an optimal bitumen content of 5.72% as per Spanish regulations, which is higher than that for limestone materials. However, it should be noted that adhering to the NCAT regulation may not be economically viable, as the optimal bitumen content for siliceous materials cannot be achieved within the 5–6% range.

Table 7 Optimum bitumen percentage values obtained using DESIGN EXPERT software for different conditions
Full size table

4 Conclusion

The present study aimed to investigate the impact of aggregate type and gradation on the functional and mechanical properties of porous asphalt mixtures with varying bitumen percentages (5% and 6%). Two types of aggregates, Grade 1 and Grade 2 limestone, and siliceous, were utilized. The findings of the experiments conducted are as follows:

  • The results showed that, when keeping the bitumen percentage consistent, both types of aggregates exhibited the highest void percentage with gradation number 2, followed by gradation numbers 1 and 3. This suggests that coarser gradations lead to higher void percentages at a fixed bitumen percentage. Additionally, siliceous aggregates demonstrated higher permeability compared to limestone aggregates.

  • BiIncreasing the bitumen percentage resulted in a decrease in void percentage, permeability, and weight loss in the unaged Cantabro test. However, it led to an increase in moisture susceptibility. This indicates that higher bitumen percentages contribute to a more compact mixture, reducing voids and improving the resistance to water penetration.

  • The study revealed that limestone aggregates exhibited better performance in the unaged Cantabro tests and demonstrated improved moisture susceptibility in porous asphalt mixtures compared to siliceous aggregates.

  • The data obtained from the tests were analyzed using DESIGN EXPERT software. The analysis showed that the bitumen content, aggregate material type, and gradation type significantly influenced the performance characteristics of the mixtures, as evidenced by high R2 and adj R2 values (above 0.97) for all tested properties.

  • For limestone aggregate materials with gradation No. 2, the optimal bitumen content was determined based on both NCAT and Spanish regulations for porous asphalt mixtures. The optimal content was found to be 2.5% for NCAT and 5% for Spanish regulations.

  • To achieve desirable results in porous asphalt mixtures, it is recommended to avoid the direct use of siliceous materials and instead explore the use of suitable additives that can enhance the performance and overcome the inherent limitations of siliceous-based mixtures.