1 Introduction

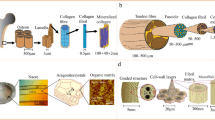
Bamboo as a bio-material has gained significant interest in a broad range of sectors including buildings [1, 2], renewable energy and many others [3]. Their light weight and fast-growing feature (3–4 years) while retaining stiffness and thermal properties comparable to those of structural wood products [4, 5] allow them to spread globally [6]. Additionally, bamboo specific strength-to-weight ratio can be compared to low-carbon steel and glass fibre reinforced polymer [4]. The culm, the part of bamboo plant above ground, is a wood-like material that contains two major components, the internodes and the nodes [7] (see Fig. 1a). The part of the culm right above the ground (of about 2.1 m height) has the largest diameter and wall thickness and lowest average internodal length in comparison to the upper segments of the bamboo culm [9,8,10].

Fig. 1
figure 1

Processing overview of bamboo strips with a bottom part of culm, b bamboo cross-section wall, c strips cutting, d short bamboo strips and e vascular bundles and parenchyma matrix. Microscopic image (e) is taken from Ref. [15]

Full size image

Several bamboo species including Phyllostachys pubescens or P. edulis referred herein as ‘Moso bamboo’, in particular, have been researched extensively. Moso bamboo has a ring-like cross-section with a natural functionally graded microstructure [10] (see Fig. 1b). This structure is considered as a natural composite material consisting of two major components: the vascular bundles and the parenchyma matrix. The culm wall is composed of spongy tissue-like material called parenchyma cells (matrix) (around 52% gross volume fraction, as a representative value) [11], stiff sclerenchyma-cells (fibre bundles) (about 40%) and conductive tissues (tube of vessels) (about 8%) [9], see Fig. 1e. The vascular bundles are distributed densely in the outer region of the wall and sparsely in the inner region [10, 12]. It has been shown that the strength of the outer wall layers is higher than that of the inner layers [12] due to the radial increase of the amount of fibres from the inside to the outside of the culm wall, whilst parenchyma matrix content increases reversibly from the outer towards the inner part [10, 13, 14].

The general manufacturing process starts with a standardised cutting of bamboo strips from the middle part of a ring like culm wall after the removal of the skin at the outer part and the pith ring at the inner part. The resulting end-product is the engineered bamboo product (EBP) with cross-section dimensions of 20 mm width and 6 mm thickness, see Fig. 1d. Even though EBP provides good performance characteristics for bio-composite design, utilising the outer layers of bamboo is more beneficial due to their high stiffness and strength compared to other layers as it will be seen in the next sections.

During the last three decades since 1995, several experimental investigations sought to determine through-culm gradient fibre content of Moso bamboo with their related stiffness and strength properties in tension parallel to the fibres. Nogata and Takahashi [16], and Amada et al. [17] investigated the radial distribution of bamboo fibres at different locations from the inside to the outside of the culm cross-section wall. The axial stiffness and axial tensile strength were found to be within the range of 5–25 GPa and 100–400 MPa, respectively. Huaqiang Yu et al. [18] investigated the radial variation in tensile stiffness and strength at three height locations along the culm. They observed that longitudinal stiffness and strength had a curvilinear regression from the inner layer towards the outer layer, the obtained values were within the range of 8.49–32.49 GPa and 115.94–328.15 MPa, respectively, at the top height segment of the culm. Shao et al. [14] quantitatively analysed the variation of tensile properties at two scale levels: macro-level across the radial thickness of the internodes and micro-level along the vascular bundles. At the macro-level, they observed a linear relationship between fibre volume fractions and tensile stiffness and strength properties. Also, they reported the tensile strength and elastic modulus to be within the range of 4.5–20 GPa and 79.24–294.75 MPa, respectively. Li and Shen [19] studied the elastic modulus parallel to the fibres at different locations along the bamboo culm. They proposed empirical equations to correlate stiffness and strength to fibre volume fractions. Liu et al. [20] applied advanced optical imaging, namely, confocal laser scanning microscopy to measure accurately the elastic modulus, strength and volume fraction for the vascular bundles of bamboo strips across the culm wall. They reported the tensile strength and the elastic modulus of bamboo strips taken from the inner part of the culm to be 101.85 MPa and 6.65 GPa, respectively, and those at the outer layer to be 294.26 MPa and 30.3 GPa, respectively. Long et al. [21] studied the dependence of the elastic modulus and tensile strength parallel to the fibres on the radial direction within the culm. They reported the tensile strength and the elastic modulus of bamboo strips taken from the inner part of the culm to be 37.5 MPa and 6.87 GPa, respectively, and those at the outer layer to be 262.26 MPa and 27.34 GPa, respectively. Recently, Akinbade et al. [22] conducted a modified flat-ring flexural test to obtain the stiffness properties in tension parallel to the fibres. Additionally, they analysed microscopically the culm radial wall tissue. The dependence of stiffness on moisture content was also investigated by Amaral et al. [23].

To conclude, the above investigations were focused on the tensile strength and elastic modulus parallel and perpendicular to the fibres. The longitudinal behaviour is combined with the assumption of uniform distribution of bamboo fibres through the thickness of the culm wall is typically modelled as a fibre reinforced polymer (FRP) material following the polymeric composite materials analogy of randomly oriented long fibres. Hence, the rule of mixture (RoM) approach can be considered applicable to predict the longitudinal stiffness and strength properties. However, recent evidence by [24] suggested that RoM works well in the axial direction, but seems not to be able to capture adequately the bamboo behaviour in transversal directions as it cannot easily be measured in experiment [25]. Also, they highlighted the need to extensively modelling the orthotropic behaviour of bamboo fibre and parenchyma matrix. This observation was already highlighted in the authors previous research on an anatomy-based numerical modelling of bamboo microstructure using Easy PBC, a plugin tool in ABAQUS, which accurately predicted the anisotropic material properties of Moso bamboo [26].

The failure mechanisms and modes of bamboo in tension parallel to fibres have been documented and investigated. Richard and Harries [27] reported that bamboo tensile test specimens exhibited six groups of failure modes: Mode A: specimen failure within the tabbed grip length, Mode B: failures at the interface of the grip and gauge length sample, Mode C: a tensile rupture across the gauge length of specimen, Mode D: a single bamboo splitting, Mode E: a "brooming" failure which affects the entire cross section, and Mode F: a combined failure of modes B and D. Shao et al. [14] obtained three distinct failures from samples at inner, middle and outer layers corresponding to bamboo fibres content. Samples from inner layers showed a brittle characteristic, indicating failure within the parenchyma matrix. Samples from middle layers show uneven combined fracture surface of parenchyma matrix and fibres. Outer layer samples showed a single bamboo splitting. The same fracture pattern was also investigated by Liu et al. [20], where samples from the higher fibre content outer layer predominantly fractured at parenchyma matrix and fibres surfaces, whereas samples with smaller fibre content from the inner layer failed within the parenchyma matrix.

In the literature cited above, there has been little quantitative analysis to understand the relative importance of the non-uniform distribution of bamboo fibres through the thickness of the culm wall. In order to consider the distribution pattern effect of bamboo vascular bundles on the performance of the culm itself, it is beneficial to divide the culm wall into many parts or thin layers in the radial direction. Therefore, there are two primary aims of this study:

  1. 1.

    To critically examine a through-thickness distribution of bamboo fibre volume fraction and to investigate the axial strength and elastic stiffness properties parallel to the fibres. This is achieved by physically testing thin layers of about 1 mm average thickness at four different layers from the inner towards the outer positions of the bamboo culm wall.

  2. 2.

    To ascertain the variation of the distribution pattern of bamboo vascular bundles in correlation to the mechanical performance of each layer through the radial direction. This objective can be attained by analysing microscopically the thin layers using image analysis software to count the gradient fibre content at each layer. This paper shows that the non-uniform radial distribution of fibres is in correlation to the variation of stiffness and strength properties of bamboo layers.

  3. 3.

    To determine a specific composite property by the Rule of Mixture (RoM) theory, an analytical homogenisation analysis. This is verified by the validity of Eqs. (9) and (10), to estimate the elastic stiffness and strength of Moso bamboo constituents parallel to the fibres.

The remainder of this paper is divided into the following sections. Section 2 gives a brief overview of the materials used and the coupon preparation for tensile test parallel to bamboo fibres. Then, the measurement of oven-dry density and moisture content of the specimens are briefly described. Experimental uniaxial tensile test results and measured bamboo fibre volume fractions are also reported in Sect. 2. The measured elastic properties, including stiffness modulus and tensile strength, are compared to previous experimental results, and the failure mechanisms of bamboo samples were presented in Sect. 3. Section 4 presents the analytical homogenisation analysis using RoM to estimate the elastic stiffness and strength for Moso bamboo parallel to fibres. Finally, the main conclusions and areas for further research are identified in Sect. 5.

2 Experimental programme

2.1 Materials and tensile specimen preparation

The bamboo strips were commercially supplied and obtained by Dasso Group, supplier of bamboo products. The strips, taken from the lower section of four-year-old Moso bamboo (Phyllostachys pubescens). First, the bamboo culms were harvested and collected from Fuyang bamboo plantation which is in North China’s subtropical zone in Zhejiang province. The culm diameter at chest height was between 100 and 120 mm and the average cross-section thickness of the culm wall was about 10 mm. A cylindrical segment of the culm from the ground level up to 2.1 m was cut. Then, the culm segments of 2.1 m length were pushed onto a spike machine, which had 8 sharp fins around it, hence the bamboo was split into 8 wedges with an arc of 45 degrees each. Then, to stabilise the moisture content of these strips between 8 and 12%, they were subjected to a preservation process with two rounds of carbonisation and air drying. The final strips had a dimension of 2.1 m length, 30–40 mm arched width and 10 mm thickness. Finally, the strips were packaged and shipped to Budapest, Hungary.

For tensile specimen preparation, 15 bamboo strips of 200 mm length were taken from the internodal region parallel to the fibres (longitudinal axis x). The peeling process starts with the removal of the outer skin and inner pith surfaces, see Fig. 2a. Strips are then machined on each side to achieve a rectangular section. The rectangular strips are then machined to required thickness using a manual layering tool, in which the required thickness is achieved by bolts adjusting the threaded gears in order to cut layers, see Fig. 2b. The original rectangular strips had 8 mm thickness, after the removal of the outer and inner layers, the layer from the strong outer layer had about 1 mm thickness, the next layers of moderate strength named Middle-2 and Middle-1 had about 1 mm thickness each, and the softer remaining layer had 1 mm thickness, see Fig. 2a. The final strips had a length of 200 mm (along the longitudinal axis x), a width of 20 mm (along the tangential axis z), and a thickness of 1 mm (along the radial axis y), see Table 1.

Fig. 2
figure 2

Steps of manufacturing tensile specimens with a bamboo strip selection, b bamboo strip layering, c tensile coupon specimen preparation and, d 75 tensile coupon specimens (out of which 60 was tested)

Full size image
Table 1 Geometrical dimensions of the uniaxial tensile specimen (unit: mm)
Full size table

Coupon tension specimens were categorised into four groups: specimens from the outer layer were denoted as Bo, those from the inner layer as Bi whereas the middle layers are BM1 and BM2 for specimens from the middle-1 and middle-2 layers, respectively. Each group of the uniaxial tensile coupon specimens were manufactured from 4 tabs glued to a single bamboo strip, two on each end. The tabs are acrylic clamping sheets made of glass fibre composite materials, see Fig. 2c. The tabs of size 1050 mm × 2050 mm and 5 mm thickness are Üveto-I sheets supplied by the Hungarian company R-VILL PLUSZ Kft. The epoxy adhesive is Araldite 2011, a two-component paste of 300 g supplied from the Hungarian company Neosil Kft. The tabs prepared for the test specimens were of 50 mm length, 20 mm width and 5 mm thickness, see Table 1. Thus, the specimens had an affective length of 100 mm. All dimensions were measured using Caliper, a precision device having an accuracy of at least 0.1 mm. The tension specimens’ dimensions shown in Table 2 were prepared conforming to the national bamboo standard ISO 22157: 2019 [28].

Table 2 Physical determination of the oven-dry density and moisture content for tensile specimens
Full size table

2.2 Oven-dry density analysis

In order to determine the density of the uniaxial tensile specimens, the dimensions were measured of four samples chosen at four layers at a precision of at least 0.1 mm to calculate their volume V0 following the national bamboo standard ISO 22157: 2019 [28]. Then, to measure the dry density \(\rho\), the specimens were dried out to a constant oven-dry mass, and the weighing were carried out immediately afterward. The mass mdry of the oven-dry test specimens were determined to a precision of 0.5% of the original specimen mass m0. The drying is considered complete when the difference between subsequent mass measurements (mi) do not exceed 0.5% of the pre-drying mass mo, see Table 3. The dry density \(\rho\) can be obtained from the formula:

$$\rho = \frac{{m_{{{\text{dry}}}} }}{{V_{o} }}$$
(1)
Table 3 Statistical analysis of the radial distribution of Moso bamboo strength and stiffness
Full size table

The equilibrium moisture content of the uniaxial tensile specimen was determined after the tension tests for four samples, one from each group, as listed in Table 3. Following the national bamboo standard ISO 22157: 2019 [28], the samples were placed in the oven at a temperature of 103 ℃ for 24 h, recording the mass at regular intervals. The equilibrium moisture content (EMC) can be calculated from the formula

$$EMC\left( \% \right) = \frac{{m_{0} - m_{{{\text{dry}}}} }}{{m_{0} }} \times 100$$
(2)

2.3 Tension test parallel to fibres

Coupon tension specimens were categorised into four groups: specimens from the outer layer were denoted as Bo, those from the inner layer as Bi whereas the middle layers are BM1 and BM2 for specimens from the middle-1 and middle-2 layers, respectively. For each group, 15 specimens were tested. All tension test specimens were prepared according to the procedure described in the national bamboo standard ISO 22157: 2019 [28]. As described above, the specimens had dimensions 200 mm length (axis x), 20 mm width (axis z) and 1 mm thickness (axis y). The gauge (effective) length l1 was 100 mm, as shown in Fig. 3b. All test specimens were conditioned and stored at a climate-room environment at a temperature of 20 ± 2 ℃ and relative humidity of 65 ± 5% for 24 h. The moisture content EMC of the samples was measured to be approximately 8% in average.

Fig. 3
figure 3

Schematic overview of the DIC system and the tension test specimen. a DIC system, b Coupon tension test specimen and c Schematic representation of tension stress–strain curves

Full size image

For the tensile test, the German universal material testing machine Zwick Z250, equipped with 20 KN capacity load head was applied, see Fig. 3a. Prior to commencing the test, the specimen was placed inside the two tensile grip jaws and the gauge area was marked with 4 points using a glow marker. Once the positions had been fixed, a digital image correlation (DIC) system including a camera (Mercury Monet, Sobriety, Kurim, Czech Republic assisted with LED lights) and a computer desktop were set up to monitor the field view of the gauge area and to record the data in form of individual images during the test. The DIC was used as the optical strain measurement system, its resolution and acquisition frequency are 5 Megapixel and 60 Hz, respectively. The distance of the DIC system and the camera from the testing machine apparatus was about 500 mm. The specimens were loaded at a constant displacement rate of 1 mm/min up to fracture when tensile strain reached less than 2%. Figure 3c shows the schematic tension stress–strain curves of the four different specimen groups. The elastic modulus was calculated as

$$E_{L} = \frac{{l_{1} \left( {F_{40} - F_{10} } \right)}}{{b_{o}{\cdot}{ }t_{1} { }\left( {{\Delta }_{40} - {\Delta }_{10} } \right)}},$$
(3)

where \({l}_{1}\) is the gauge length,\({F}_{40}\) is 40% of the ultimate load, \({F}_{10}\) is 10% of the ultimate load, \({\Delta }_{40}\) is the displacement at load \({F}_{40}\), \({\Delta }_{10}\) is the displacement at load \({F}_{10}\), \({b}_{o}\) is the width and \({t}_{1}\) is the thickness of the specimen. The tensile strength, also known as the modulus of rupture, was also calculated as

$$TS = \frac{F}{{b_{o} {\cdot}t_{1} }},$$
(4)

where F is the ultimate load.

2.4 Image processing analysis

This paragraph describes the procedure to determine the distribution pattern of bamboo vascular bundles based on Liu et al. [20], also explained in [13]. The distribution pattern of bamboo vascular bundles was determined at each thin strip and the fibre volume fraction Vf along the radial direction. This is achieved by polishing the surface of the samples and then taking photographs of the transverse sections by a compact digital camera Canon SX432 IS in a room with ceiling light. The resolution of the camera is 20 Megapixel with 45 × optical zoom, and the distance of images was about 21.60 cm. Eight thin slices, excluding the pith part at the inner side and the skin at the outer side of the culm, were photographed. The fibre volume fraction Vf at each thin slice was measured by analysing the images with the imageJ/FIJI processing software, see Fig. 4a–c. The digital images were converted to binary format to obtain black and white images. This is shown in Fig. 4c, with black background and white fibre vascular bundles. Then fibre surface areas Af were traced and measured as well as the total surface area Ac of each thin slice. The volume fraction Vf at each thin slice was calculated as

$$V_{f} \left[ \% \right] = \frac{{A_{f} }}{{A_{c} }} \times 100$$
(5)
Fig. 4
figure 4

Image processing analysis of the radial distribution of Moso bamboo fibre volume fractions

Full size image

3 Results and discussion

3.1 Oven-dry density analysis

The results of the physical determination of the oven-dry density and moisture content for tensile specimens along the fibre direction are summarised in Table 2. The moisture content EMC of the samples was measured to be approximately 8% in average.

3.2 Fibre volume fraction measurements

The correlation between the fibre volume fractions Vf and the normalised distance was analysed, which is the radial distance of the layer from the innermost point of the culm wall divided by the thickness of the culm wall (that is, it is 0 inside and 1 outside). Figure 5 shows the resulting correlation, we see a continuous increase of Vf along the radial direction from the innermost to the outermost regions. A second order regression polynomial function was found to describe the volume fraction Vf as a function of the normalised radial distance from the innermost layer with a fit having a coefficient of determination R2 around 0.9825. The regression function is

$$V_{f} = 0.3144 x^{2} + 0.1916 x + 0.0172$$
(6)

where \(x\) is the normalised distance from the inner to the outer layer. The volume fraction Vf in the four main layers was as follows: Bi: 0.1, BM1: 0.19, BM2: 0.28 and Bo: 0.44. These findings are consistent with those of [18,19,20,22] and support the authors’ previous research [26].

Fig. 5
figure 5

Distribution of fibre volume fractions of Moso bamboo from the innermost to outermost regions

Full size image

3.3 Statistical analysis of tensile properties of Moso bamboo samples

The results of the statistical analysis of the radial distribution of Moso bamboo strength and stiffness in tension along the fibre direction are summarised in Table 3. The coefficient of variation (COV.) at each thin coupon test group is equal to the ratio of the standard deviation (STD.) to the mean of n = 15 samples. It can be seen from Table 4 that the ultimate tensile loads change monotonically along the radial direction of the bamboo cross-section, it is the lowest at Bi (inner layer) and gradually increased up to the largest value at Bo (outer layer). The maximum tension loads at the four tested layers of bamboo were: Bi: 1924 N, BM1: 2489 N, BM2: 3389 N and Bo: 4503 N. Also, the ratio of the maximum break force of Bo is 2.3 higher than that of Bi, 1.9 higher than that in BM1, and 1.3 higher than that in BM2. It is worth mentioning that all layers’ properties have shown a pronounced dispersion reflected in a high value of variation coefficient COV. This is caused by the variation in material details of bamboo strips as a natural material as well as their thickness.

Table 4 Summary of gradient fibre volumes of Moso bamboo with their stiffness properties in tension, adopted from [22]
Full size table

3.4 Elastic modulus and tensile strength

Figure 6 illustrates the load–displacement relationship curves during the stretching of bamboo strips from the inner (Bi), middle-1 (BM1), middle-2 (BM2) and outer (Bo) layers of the culm. From the graphs, one can see a clear trend: the ultimate tensile load increases monotonically along the radial direction of the bamboo cross-section with the largest ultimate loads in the outer, and with the smallest ultimate loads in the inner layer. The load–displacement relationship is remarkably linear practically up to the significant peak at the ultimate load (fu), the load is proportional to the displacement almost along the whole tension test. Finally, a stage of brittle fracture is reached with a relatively small fluctuation of the ultimate load. At this load, the load–displacement curves exhibit a drastic reduction in tensile load reaching zero. Despite the marked differences in the break force across the four investigated layers, interestingly, there is quite small variation in the ultimate displacement at failure for all samples. The ultimate displacement values reached about 1.4 mm for the middle layers BM1 and BM2, whereas they were around 1.6 mm for Bi and Bo samples. The difference between the break force for the samples taken from the different layers is mainly attributed to the gradient density of bamboo fibres along the radial direction. In particular, higher fibre density in the outer layer results in higher tensile strength, whereas lower fibre density in the inner layer leads to lower tensile strength. This finding matches those observed in earlier studies [18,19,20,22] shown in Table 4.

Fig. 6
figure 6

Load–displacement curves from the tensile experiments of bamboo strips taken from various layers of the culm: a outer (Bo), b inner (Bi), c middle-2 (BM2), and d middle-1 (BM1) and layer

Full size image

After obtaining the stiffness related parameters of the samples, a regression analysis was used to compare the gradient of the stiffness properties along the radial direction of the bamboo cross-section with the variation of the fibre volume fraction Vf. The tensile strength and elastic modulus of Moso bamboo in the four layers are shown in Fig. 7a and b, respectively. There was a significant positive correlation between bamboo stiffness properties and relative positions with a trend of continuously increasing tensile strength and elastic modulus from the inner to the outer layers. The relative distance from the inner edge of the ring-like cross-section to the investigated layers is 0.2, 0.4, 0.6 and 0.8, see Fig. 7a and b. The outer layer Bo shows significantly higher tensile strength than the other three layers by the ratio of 3 for layer Bi, of 1.8 for BM1 and of 1.4 for BM2. Similarly, the outer layer Bo showed significantly higher elastic modulus than the other three layers by the ratio of 3.6 for Bi, of 2.4 for BM1 and of 1.7 for BM2. These observed trends are consistent with those found by [14, 18, 20, 21] see Table 4, and in authors previous research about the anatomy based microstructure of Moso bamboo, see [26].

Fig. 7
figure 7

Gradient stiffness properties along the radius of the culm with a tensile strength parallel to fibres versus distance from inner to outer locations, b elastic modulus parallel to fibres versus distance from inner to outer locations, c tensile strength versus fibre volume fraction, and d elastic modulus versus fibre volume fraction

Full size image

The regression analysis of tensile strength and modulus with respect to the fibre volume fractions Vf is shown in Fig. 7c and d, respectively. It can be observed in Fig. 7a and b that the increase of tension strength and elastic modulus is correlated to the increase in fiber volume fraction Vf, shown in Fig. 5. Based on this observation, one could expect a linear regression between the stiffness properties and the fiber volume fraction, which is validated by fitting straight lines in Fig. 7c and d. The obtained linear regression function for the tension strength TS, with a coefficient of determination R2 around 0.8766 is

$$TS = 544.46 V_{f} + 44.077$$
(7)

The elastic modulus \(E_{L}\) was also found to follow a linear regression function with respect to the fiber volume fraction with a coefficient of determination of R2 around 0.9069 as

$$EL = 55.544 V_{f} + 0.8257$$
(8)

As it can be seen that the stiffness depends essentially linearly on the amount of fibres, hence, the major part of the stiffness of the bamboo samples is attributed to the fibres with a relatively small part coming from the stiffness of the matrix.

3.5 Typical failure mode mechanisms of bamboo samples

The ultimate load capacity of bamboo strips depends on the failure mode and the amount of fibres present in the specific failure location. Now the tensile failure of bamboo in the various layers are examined. As outlined in the national bamboo standard ISO 22157: 2019 [28], there are six general groups of tensile coupon failures. The tensile coupons of bamboo applied in this study exhibited five distinct mechanisms of failure, as depicted in Fig. 8 and Table 5. These failure mechanisms are as follows. Mode A, which entails specimen failure within the tabbed grip length, was not observed because strong glass fibre reinforced polymer tabs were applied rather than wooden ones. Mode B pertains to failures at the interface of the grip and sample. Mode C constitutes a tensile rupture across the specimen. Modes D and E both involve longitudinal splitting failures along the length of the specimen, with Mode D comprising a single bamboo splitting, and Mode E refers to a "brooming" failure which affects the entire cross section. Mode F represents a combination of failure modes B and D.

Fig. 8
figure 8

Failure modes of bamboo samples parallel to fibres direction as observed in the experiments

Full size image
Table 5 Representative failure modes of the radial distribution of Moso bamboo slices
Full size table

From the 60 investigated tensile coupons (Table 5), regardless of the radial position of bamboo, 25 samples (42%) exhibited a mixed mode failure, mode F. This is a composite failure consisting of a mode B rupture failure and a mode D splitting failure. Seven specimens (11%) exhibited a mode D longitudinal splitting failure alone. Fifteen specimens (26%) experienced failures in mode B rupture near the tab area. Ten specimens (16%) were observed to have mode C tensile rupture, and only 3 specimens (5%) exhibited mode E fibre splitting explosion at the mid-region. It was discovered that samples with a higher fibre content, that is, from the outer layer of the culm, predominantly failed via mode F failure, whereas samples with a lower fibre content, that is, from the inner layer, failed within the parenchyma matrix, as evidenced by mode B failure. This observation is consistent with the findings reported by [27] and [20].

4 Estimate of the elastic modulus and strength for Moso bamboo parallel to fibres

In a previous study [26], the authors proposed an anatomy-based representative volume element (RVE) model utilising the EasyPBC homogenisation tool in ABAQUS FEA software [29] to estimate the stiffness properties of the modelled gradient volume fractions of RVEs. The vascular bundles and parenchyma matrix can be homogenized into a fibre/matrix region, whose properties can be conveniently determined by the implementation of the well-established rule of mixture (RoM) theory. Based on the linear Eq. (8) and [18] established between the elastic modulus \({E}_{L}\) and the fibre volume fraction Vf of the bamboo samples, it is found

$$E_{L} = 55.544 V_{f} + 0.8257 = 56.369 V_{f} + 0.8257 \left( {1 - V_{f} } \right)$$
(9)

from this, the elastic modulus of the fibre \({E}_{f}\) and parenchyma matrix \({E}_{p}\) can be approximated as \({E}_{f}\) = 56.369 GPa and \({E}_{p}\) = 0.825 GPa. These values are consistent with those reported elsewhere [14, 18, 20, 21]. It is evident that the fibre serves as the primary load-bearing component, which exerts a significant influence on the tensile properties of bamboo. Additionally, the findings lend support to the hypothesis that bamboo is a unidirectional fibre-reinforced composite material.

Analogously, a correlation (7) has been established between the measured tensile strength TS and the fibre volume fraction Vf of the bamboo samples. Applying the RoM theory, the formula can be written as follows:

$$TS = 544.46 V_{f} + 44.077 = {588}.{53}V_{f} + {44}.0{77}\left( {1 - V_{f} } \right)$$
(10)

That is, the tensile strength of fibre and parenchyma matrix are calculated as \({\sigma }_{f}\) = 588.53 MPa and \({\sigma }_{p}\)= 44.077 MPa, respectively. These numerical values are also consistent with those reported previously [20, 21].

It can be found that the RoM theory and the measured correlation between the stiffness and strength properties and the fibre volume fraction are consistent, and allow for a simple estimation of the properties of the individual components (fibre and matrix).

5 Conclusions and future work

This study critically examined the radial distribution of the stiffness properties of bamboo by dividing the culm wall into thin strips at different radial layers and uniaxially testing the specimens in tension. The tension test programme was performed on sixty coupon samples of Moso bamboo (Phyllostachys pubescens) parallel to fibres. The samples were prepared by dividing the bamboo culm wall into thin layers of about 1 mm average thickness at four different positions from the inner towards the outer layers. The main aim of this study was to critically examine a through-thickness distribution of stiffness and strength properties of bamboo (like elastic modulus and axial tensile strength). From the experimental programme, the elastic stiffness and strength properties can be obtained in four layers of the culm. In addition, the oven-dry density and moisture content of the specimens were determined. The relation between the distribution of the vascular bundles and the mechanical performance of each layer were investigated. The layers have been analysed microscopically using image analysis software to count the distribution of fibre content at each layer. The failure mechanisms of bamboo samples were further discussed and presented. Finally, an analytical homogenisation analysis, using rule of mixture theory was reviewed to estimate the elastic stiffness and strength of Moso bamboo constituents parallel to the fibres.

Based on the results obtained from this study, the following can be concluded:

  1. 1.

    The tension strength in the four layers are correlated to their radial positions from the inner towards the outer layer as follows: Bi: 84 MPa, BM1: 140 MPa, BM2: 181 MPa, and Bo: 249 MPa. This implies that the outer layer Bo has significantly higher tensile strength than the other three layers by the ratio of about 3.0 at Bi, of 1.8 at BM1, and of 1.4 at BM2.The elastic modulus \({E}_{L}\), in the four layers are also correlated to their radial positions from the inner towards the outer layer as follows: Bi: 6.4 GPa, BM1: 9.6 GPa, BM2: 13.3 GPa, and Bo: 22.8 GPa. The outer layer Bo has significantly higher elastic modulus than that of the other three layers by the ratio of about 3.6 at Bi, of 2.4 at BM1, and of 1.7 at BM2.

  2. 2.

    As a result of image analysis of bamboo cross-sections, distribution of fibre volume fraction Vf in the radial direction of the culm wall was determined and described by a second order regression polynomial function. The fibre volume fractions in the radial direction varied as follows: Bi: 0.1, BM1: 0.19, BM2: 0.28, and Bo: 0.44.

  3. 3.

    It was observed that samples with a higher fibre content predominantly failed via mode F failure (combined failure due to failure at grip and delamination of a single fibre), whereas samples with a lower fibre content by mode B failure (failure near grip).

  4. 4.

    It is found that the application of the Rule of Mixture theory was applicable to estimate the tensile strength and the elastic modulus of the individual components of bamboo, that is, of the fibres and the parenchyma matrix, from our experimental data. This was achieved by comparing the measured dependence of the elastic modulus and the axial strength on the radial direction to that of the fibre volume fraction using regression analysis.

We note that the similarity of the failure modes observed in our experiments are very similar to those observed for polymer and composite materials. This leads to the conjecture that bamboo can be looked at as a natural fibre reinforced polymer matrix composite.

As a possible next step, the authors expect to develop a reliability-based analysis of outer layer bamboo for wind turbine applications to assess their mechanical reliability considering a wide range of uncertainties at the laminate scale including lamina ply thickness (t), ply orientation (theta) and loadings. Another interesting direction could be to correlate not only the fibre density but also the fibre thickness to the strength. In general, thinner fibres can be associated with higher mechanical performance, but its precise role in bamboo is to be investigated further.