1 Introduction

Alumina or aluminum oxide is used as an amorphous ceramic material in different industries, including the pharmaceutical industry, to produce dental implants and various types of composites. Due to the lower price of alumina, in comparison to nanotubes, it can be used in the fabrication of nanocomposite specimens [1]. In addition, alumina demonstrates its preferred mechanical and superficial properties, and it can be produced in the granular form at an industrial scale. Given the practical reasons mentioned above, it is necessary to create this ceramic granular material in the laboratory and study its mechanical properties.

Primarily, it is essential to understand that alumina is a porous material. Researchers use the scanning electron microscope (SEM) to examine the porosity [2] and mechanical properties [3] of materials. Atomic force microscopy (AFM) is used as a significant device to study the properties of materials at the nanoscale [4]. The mechanical behavior of the material, especially ceramic material, is essential for engineering applications. The mechanical properties of ceramic materials, which include hardness, elasticity modulus, stiffness, roughness [5], scratch resistance, friction coefficient, and pile-up [6], have been widely studied. In doing so, researchers have used Nano indentation [7] and Nano scratch [8] tests.

Nanoindentation indicates the value of surface variation, and it was used as a standard and specific device for identifying the mechanical properties of ceramic materials, including the hardness and modulus of elasticity based on a small specimen [9]. By obtaining the load–displacement curve, it is possible to determine the mechanical properties of a specimen[10]. Every specimen has its own universal figure of the load–displacement curve, and these differences between various materials usually indicate different mechanical properties[11]. The scratch test was also used to study the resistance and tribological behavior of materials [12]. The scratch morphology on the surface presents a picture of the material's deformation mechanisms in the scratch test, including friction coefficient [13], scratch resistance, pile-up, and scratch hardness [14].

Shokrieh et al. [15] investigated the effect of graphene nanoparticles (GNPs) on the mechanical properties of polymeric nanocomposites by using nanoindentation and nano scratch tests. By implementing the indentation tests, both the elastic and hardness modules were amplified by adding 0.005 mass percent of GNP. Moreover, the scratch test revealed that the pile-ups decreased, and wear resistance increased. According to [18], the mechanical properties of a pure polymer matrix increase with the amplification of a small amount of GNP. Molazemhosseini et al. [16] carried out a study on the mechanical properties of hybrid composites based on polyether ether ketone (PEEK) reinforced by short carbon fibers and SiO2 nanoparticles using the Nano indentation and Nano scratch tests. The results represented a significant increase in the hardness and elastic modulus, which was due to the reinforcing agents.

Ahangari et al. [17] investigated the use of poly(urea–formaldehyde) (PUF) microcapsules containing dicyclopentadiene (DCPD) as self-healing agents for microcracks in polymeric matrices. The elastic modulus and hardness of the microcapsules with and without a nanocomposite shell wall reinforced with carbon nanotubes and nanoalumina were measured using the nanoindentation method. The addition of reinforcement nanoparticles led to significant increases in the elastic modulus and hardness of the microcapsules. The microcapsules with nanoalumina in the shell wall were found to be stiffer and harder than those without, and the surface roughness was smoother in the presence of nanoalumina nanoparticles. Ahangari and Fereidoon [18] studied the mechanical properties and morphology of self-healing nanocomposite epoxy using healing microcapsules and reported actual results. They investigated the mechanical properties of microcapsules using the nanoindentation test under three different loads before and after the healing and monitored the topography of the softened surface using AFM. They also showed the effects of healing using AFM after the scratch test on the composite surfaces. Using SEM, they characterized the microstructures of intact and healed composites using self-healing.

Yahyaei and Mohseni [19] focused on exploring the impact of precursor concentration and the inorganic to organic weight ratio on the mechanical properties of sol–gel based UV cured hybrid coatings. The coatings were prepared by combining different silanes with urethane acrylate monomers, and their performance was assessed using a range of testing methods. The results demonstrated that coatings with lower acrylic silane content and higher inorganic to organic weight ratios exhibited enhanced hardness, elastic modulus, and scratch resistance, while increasing the inorganic phase improved the elastic modulus and hardness, leading to enhanced elastic recovery and scratch resistance. Fereidoon et al. [20] investigated the effect of multi-walled carbon nanotubes (MWCNTs) on the nanoscratch resistance of polystyrene/poly(methyl methacrylate) (PS/PMMA) coatings using the nanoindentation procedure. The nanocomposite coatings were prepared using the solution spin coating technique. The results showed that the introduction of MWCNTs increased the elastic modulus and hardness of the nanocomposites by 7.5% and 32%, respectively, and improved their resistance to the nanoscratch phenomenon, as evidenced by the increased scratch hardness and decreased coefficient of friction. Liu et al. [21] utilized AFM for estimating the scratch at the nanoscale and the frictional behavior of polycarbonate (PC). They performed a Nano scratch test under various normal loads with a probe with a tip radius of 20 nm. Furthermore, AFM was employed to display the surface morphology after scratching. The results of this paper can be used as a useful guide for understanding the mechanical mechanisms for Nano scratch polymeric materials; therefore, it can improve the scratch performance on the nanoscale.

Various composite materials and ceramics, with most studies focusing on comparing their properties to those of raw materials of the same kind. Additionally, research has primarily focused on the mechanical properties of alumina in nanoparticle powders and their composites, with very little research in the literature review, extensive research has been conducted on the mechanical properties of conducted on the mechanical properties of γ-alumina granules synthesized with a specific diameter. Moreover, most previous activities in studying the mechanical properties of materials have resulted in material loss during testing. Consequently, the lack of a method to test the properties of materials that minimizes material loss while being cost-effective and accessible is evident. Thus, this highlights the need for systematic and precise approaches to research on the mechanical properties of materials. There is a requirement for a method with low-cost and accessible equipment that can reduce material loss during testing. In this regard, conducting new research on the mechanical properties of γ-alumina granules synthesized with a specific diameter and developing improved methods for testing the mechanical properties of materials can help expand the knowledge in this field.

The present study addresses a gap in the existing literature by synthesizing γ-alumina granules with a specific diameter of 1–2 mm. To obtain a comprehensive understanding of the material's morphology, scanning electron microscopy (SEM) and field-emission scanning electron microscopy (FESEM) are employed. The objective is to determine the pore size and nanoparticle characteristics of the specimens. To ensure minimal material loss during testing and to observe the material's surface under various loads, nanoindentation and nanoscratch tests are conducted to investigate the mechanical properties of the material. Additionally, atomic force microscopy (AFM) is utilized to examine surface topography before and after the aforementioned tests, and the correlations between the results of nanoindentation, nanoscratch, and AFM are analyzed in detail. The findings suggest that the proposed synthesis method resulted in a twofold increase in the Young's modulus of the material and a consequent significant improvement in its mechanical strength. These results provide valuable insights into the development of γ-alumina granules with enhanced mechanical properties.

The manuscript is organized as follows: Sect. 1 provides an introduction to the importance of γ-alumina and the motivation for this study. Section 2 describes the materials and methods used in the synthesis and characterization of the granules, including details on the instrumentation used for nanoindentation and nano scratch testing. Section 3 is divided into three subsections, with Sect. 3 of the paper is subdivided into three parts, which cover the results of the nanoindentation and nanoscratch experiments, as well as the validation of these findings. Finally, in Sect. 4, we draw our conclusions and suggest future directions for research in this area. Overall, this study sheds light on the mechanical properties of γ-alumina granules and highlights their potential applications in various fields.

2 Materials and methods

2.1 Materials

The granulation process incorporated a range of chemical compounds, such as aluminum isopropoxide which served as a precursor to achieve a nanoscale pseudo-boehmite sol. Nitric acid was employed as a peptizing and gelation agent for the sol, while ammonium hydroxide solution acted as a precipitating agent. Paraffin oil was utilized to produce spherical particles, and ethanol was used for washing the resultant granules. It should be noted that all chemical compounds utilized were of a superior quality and procured from Merck.

2.2 Synthesis of γ-alumina granules

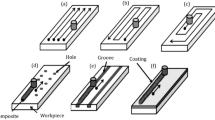
The synthesis procedure commenced with the gradual addition of 20 g of aluminium isopropoxide to 50 ml of deionized water. The addition was carefully monitored at an initial temperature of 80 °C and added at a rate of 30 g/hr to ensure appropriate control. The slurry obtained after one hour of maximum power stirring contained AlOOH precipitates, which were then dispersed by the addition of 7 ml of 1 M HNO3 (HNO3:AlOOH = 0.07 mol/mol). To complete the hydrolysis and condensation reactions, the peptized sol underwent refluxing for 20 h at a temperature of 90 °C. The method of shaping millimetric γ-alumina granules using the oil-drop granulation process has been extensively outlined by [22]. In summary, a small quantity of 1 M HNO3 was added to the stable boehmite sol and the temperature was maintained at 70 °C for a duration of 1 h, leading to partial gel formation due to a significant increase in viscosity. The partially gelled sol was then introduced into the hot paraffin oil through a syringe pump to form droplets, with temperature control achieved through a feedback loop from a thermocouple. Subsequently, the spherical wet gels were aged in a 10 wt.% ammonia solution for 2 h. After separating the granules from the ammonia solution, they underwent multiple washings with cold water, ethanol, and hot water, respectively. Finally, the granules were dried at 40 °C for 24 h, followed by calcination at 450 °C for a period of 3 h, with a heating rate of 2 °C/min. A schematic representation of the oil-drop granulation method is depicted in Fig. 1. Also, it is worth mentioning that following a series of experimental endeavors, various process parameters which are mentioned above were optimized and determined for the successful synthesis of millimetric γ-Al2O3 granules with controllable nanometer pores and high specific surface areas.

Fig. 1
figure 1

The schematic illustration of experimental device used for producing γ-alumina granules

Full size image

2.3 Instrumentation

Nanoindentation and nanoscrath tests were performed using the Triboscope® system that was armed with the Berkovich type indenter tip. The calibrated contact range function was derived from a nanoindentation test that had previously been performed on a fused quartz standard sample. A loading–unloading function with three various types of loads with maximum normal loads of 200 µN, 300 µN, and 400 µN was applied (Fig. 2). The full load was obtained in 5 s, and then the load was removed. The retention time was about 5 s. In each situation, three indentation tests were performed randomly to achieve reliable results. This system was accompanied by a Nanoscope E type AFM digital apparatus, which was used to study the topography of the surface of the samples under indentation and scratch tests. SEM imaging (Hitachi S-2300, Hitachi Scientific Ltd., Tokyo, Japan) at 10 kV was applied to examine the morphology of the samples, and FESEM analysis was carried out at Iran University of Science and Technology using a ZEISS SUPRA 55 high performance FESEM. The FESEM specifications for high-resolution imaging and analysis of non-conductive samples were acceleration voltage ranging from 0.1 to 30 kV, resolution of 1.0 nm at 15 kV, 1.7 nm at 1 kV, and 4.0 nm at 0.1 kV, and magnification between 12 and 900,000. Loose dust and debris on the sample surfaces were removed, and the samples were fixed onto sample mounts using conductive adhesive. Sputter-coating with gold was done for conductivity. The EDXS measurements were performed using a scanning Auger electron microscope JAMP 9500F (Jeol, Japan) equipped with a hemispherical electron energy analyzer, which enabled spectroscopic Auger electron measurements and an Arion sputter gun. The ion energies could be adjusted between 0 and 3 keV, allowing for sputter depth profiling or sputter cleaning of the samples.

Fig. 2
figure 2

The nanoindentation test loading–unloading function

Full size image

2.4 Nanoindentation

Nanoindentation is a sensor that can be used for applications such as controlled loads to the surface of a material to create a local superficial deformation. The general objective of the nanoindentation is to extract the elastic modulus and hardness of materials based on the determined load–displacement curves. This advanced characterizing technique has a normal workload range of about 1 µN to 500 MN, and its contact depth ranges from 1 nm to 20 µm [16]. During the test, the load and displacements were monitored continuously and recorded (Fig. 3). The maximum load (\({\mathrm{P}}_{\mathrm{max}}\)), maximum depth (\({\mathrm{h}}_{\mathrm{max}}\)), contact depth (\({\mathrm{h}}_{\mathrm{c}}\)), and final depth (\({\mathrm{h}}_{\mathrm{f}}\)) are important factors that should be obtained from the load–displacement diagram [15]. The interactions between the indenter tip and sample during the process are shown in Fig. 4.

Fig. 3
figure 3

The schematic illustration of load–displacement diagram in nanoindentation test

Full size image
Fig. 4
figure 4

The schematic of contact geometry during nanoindentation test

Full size image

The reduced elastic modulus was premeditated using the Oliver and Pharr method [23]. The contact stiffness (S) was introduced as the slope at the beginning of the unloading curve:

$$\mathrm{S}=\frac{\mathrm{dP}}{\mathrm{dh}}$$
(1)

where \(\mathrm{P}\) is the indentation load and \(\mathrm{h}\) is the indentation depth for calculating the slope. The power law sets the first part of the unloading curve [23]:

$$\mathrm{S}=\frac{2\upbeta }{\sqrt{\uppi }}{\left(\frac{1}{{\mathrm{E}}_{\mathrm{r}}}\right)}^{-1}\sqrt{{\mathrm{A}}_{\mathrm{c}}}$$
(2)

where \({\mathrm{E}}_{\mathrm{r}}\) is the reduced elastic modulus of the indentation surface of the indent contact, \({\mathrm{A}}_{\mathrm{c}}\) is the contact area of the indenter, and β is a constant for the indenter geometry. \({\mathrm{E}}_{\mathrm{r}}\) is related to the elastic modulus of the sample and the elastic modulus of the indenter is calculated by [23]:

$$\frac{1}{{\mathrm{E}}_{\mathrm{r}}}=\frac{1-{\upnu }^{2}}{\mathrm{E}}+\frac{1-{{\upnu }_{\mathrm{i}}}^{2}}{{\mathrm{E}}_{\mathrm{i}}}$$
(3)

where \(\mathrm{E}\) is the elastic modulus of the test sample, \({\mathrm{E}}_{\mathrm{i}}\) and \({\upnu }_{\mathrm{i}}\) are the elastic modulus, and Poisson’s ratio of the indenter and \(\upnu\) is the Poisson’s ratio of the test specimen. For the Berkovich indenter, \({\mathrm{E}}_{\mathrm{i}}\) and \({\upnu }_{\mathrm{i}}\) are 1140 GPa and 0.07, respectively [15]. As a result, the reduced elastic modulus \({\mathrm{E}}_{\mathrm{r}}\), is defined as follows:

$${\mathrm{E}}_{\mathrm{r}}=\frac{\sqrt{\uppi }}{2\upbeta }\frac{\mathrm{S}}{\sqrt{{\mathrm{A}}_{\mathrm{c}}}}$$
(4)

If the indenter is highly stiffer than the probe’s substance, the hardness is calculated by [15]:

$$\mathrm{H}=\frac{{\mathrm{P}}_{\mathrm{max}}}{{\mathrm{A}}_{\mathrm{c}}}$$
(5)

where \({\mathrm{P}}_{\mathrm{max}}\) is the achieved peak of the loading force. Furthermore, the plasticity index, \(\uppsi\), is usually used for describing the elastic–plastic reaction of material under applied stress and strain. In the nanoindentation test, the plasticity index of the specimen was obtained as [18]:

$$\uppsi =\frac{{\mathrm{A}}_{1}-{\mathrm{A}}_{2}}{{\mathrm{A}}_{1}}$$
(6)

where \({\mathrm{A}}_{1}\) and \({\mathrm{A}}_{2}\) denote the areas under the loading and unloading curves, respectively (Fig. 3).

2.5 Nano scratch

The Nano scratch test was performed by moving the indenter tip, which is in contact with the sample surface. Moreover, two different normal loads of 300 µN and 400 µN were applied. The load function for the scratch test was schematically shown in Fig. 5. As the experiments were performed, the standard and tangential displacements of the indenter tip and regular and tangential loads were simultaneously recorded. In a Nano scratch test, the friction coefficient (\(\upmu\)) was determined from the fraction of the lateral load, \({\mathrm{F}}_{\mathrm{L}}\) (tangent force) to the average load, \({\mathrm{F}}_{\mathrm{N}}\). The surface topography of the sample after the nano scratch and nanoindentation tests could be directly determined using the AFM. Friction coefficient, µ, could be easily calculated following [15]:

Fig. 5
figure 5

The Nano scratching test loading–unloading function

Full size image
$$\upmu =\frac{{\mathrm{F}}_{\mathrm{L}}}{{\mathrm{F}}_{\mathrm{N}}}$$
(7)

Moreover, the scratch hardness is a useful method for assessing the relative scratch resistance. The scratch hardness (\({\mathrm{H}}_{\mathrm{s}}\)) was defined by analyzing the indentation hardness. With regards to using the Berkovich indenter, the scratch hardness could be obtained as [15]:

$${\mathrm{H}}_{\mathrm{s}}=\frac{{\mathrm{F}}_{\mathrm{N}}}{\mathrm{A}}=2.31\frac{{\mathrm{F}}_{\mathrm{N}}}{{\mathrm{d}}^{2}}$$
(8)

where \({\mathrm{F}}_{\mathrm{N}}\) is the maximum applied average load on the indenter during the Nano scratch test, \(\mathrm{A}\) is the residual scratch groove area, and \(\mathrm{d}\) is the extra scratch width.

3 Result and discussion

3.1 Nanoindentation

SEM and FESEM were used to observe the surface of the particle and its properties. Figure 6 shows the topography of the surface of the produced granular alumina, its nanoparticles, and the holes on the covers. Figure 6a demonstrates the body of this material with a magnification of 37, and a diameter of 1.7 mm. FESEM images were taken with the enhancement of 1 μm and 200 nm (Fig. 6b–d) to see a better view of the surface of their holes. Additionally, Fig. 6b, d delineates the pores with diameters of 264.17 nm and 551.59 nm, which are abundant on the surface. Thus, this material contains porosity in the range of micrometers and even nanometers. Also, Fig. 6c shows the nanoparticles of this granular material, which are about 17 nm on average. It should be noted that the nanoparticles are firmly attached.

Fig. 6
figure 6

SEM topography of the surface of the produced alumina at different resolutions a 1 mm, b 1 μm, c and d 200 nm

Full size image

Figure 7 delineates the energy-dispersive X-ray spectroscopy analysis of this particle (EDX diagram), which was taken from the SEM test. This figure shows the volume of elements in the particle. As can be seen from the picture, this substance is almost pure and consists only of aluminum and oxygen elements, which form the parts of alumina. The other peaks in the figure represent the gold element, which is also visible in the EDX diagram as the material is gold-coated for the SEM test.

Fig. 7
figure 7

EDX analysis from SEM test of produced alumina

Full size image

To find the roughness of the nanoscale granules of alumina, AFM was used to observe the surface morphology in a state where there was no indentation or scratch on the material. The surface shown in the image is the surface of the produced specimen. Figure 8a demonstrates the morphology of the alumina surface. There are many ups and downs on the surface due to porosity. As seen in Fig. 8b, the roughness of the material is about 31.524 nm on average, and as expected, granular nanoparticles of alumina have a high hardness. One reason for this is the porosity of the specimen.

Fig. 8
figure 8

a Morphology and b Roughness of the produced pure alumina surface

Full size image

As stated above, the mechanical properties of the nanoparticles were obtained from the load–displacement curves. Therefore, the nanoindentation testing was done to achieve these results. Figure 9 displays the nanoindentation test of alumina nanoparticles under three different normal loads of 200 μN, 300 μN, and 400 μN. Consistently, Fig. 9b illustrates the morphology of the surface of the alumina nanoparticle in the indentation area under 400 μN using an AFM. Figure 9a represents the load–displacement diagram for these three normal loads. Conducting these tests is hard, which is due to the excessive porosity of the material, i.e., the lack of a smooth and uniform surface. However, three different types of nanoindentation testing were conducted using each force to improve the chance of obtaining mechanical properties. The reason for the fact that under each power, the depth of penetration in the particle is very different at each indentation, and suddenly a significant change in intensity is observed is the nature of the sample which is very porous. The tip begins to indent and then encounters the porous space, and suddenly the underneath is emptied, followed by a notable change in the specimen. The laboratory results support such behavior.

Fig. 9
figure 9

a Load–displacement curves for three different normal loads of 200 μN, 300 μN, and 400 μN; b Morphology of the surface of the alumina nanoparticle in the indentation area under the force of 400 μN

Full size image

The load–displacement curve also demonstrates reduced elastic modulus. So that the slope of the curve in the unload region expresses the reduced elastic modulus. Consequently, and having the reduced modulus of elasticity and modulus of elasticity of the indenter’s tip, the modulus of elasticity of alumina nanoparticles is obtained from Eq. (3). Figure 10a illustrates the reduced elastic modulus under three forces of 200 μN, 300 μN, and 400 μN for granules of alumina nanoparticles. The reduced elastic modulus does not follow a particular process with an increase in force. That is, with the rise of the load, the reduced elastic modulus increases at first and then decreases. It should be noted that three types of indentation were conducted under all three different forces. The figure illustrates each of these indentations under each force with an error value of less than 5%. Moreover, the values of the modulus of elasticity do not differ significantly under all three forces. With an error value of less than 5%, this difference is within a specific range. Consequently, by taking the average value into account, the reduced elastic modulus is equal to 12.6 GPa. In other words, under these three different forces (200 μN, 300 μN, and 400 μN), the reduced elastic modulus of alumina nanoparticles reached 12.3 GPa, 12.9 GPa, and 12.6 GPa, respectively. In addition, this process is uncharacteristic due to the number of holes and pores in the produced material, which is justified. Meanwhile, to find the reduced elastic modulus, the hardness of the nanoparticles can also be calculated from the load–displacement curve. Figure 9 and Eq. (5) were used to obtain these results, and the obtained values are shown in Fig. 10b. This shape is irregular, and as the force increases, the hardness decreases at first and then increases, which means that the mechanical properties of the material do not depend on the load. In other words, with an error approximation of about 16%, the hardness value for granules of alumina nanoparticles is 0.433 GPa. Moreover, the hardness under the forces 200 μN, 300 μN, and 400 μN is 0.43 GPa, 0.4 GPa, and 0.47 GPa, respectively.

Fig. 10
figure 10

a Reduced elastic modulus; b Hardness; for three different normal loads of 200 μN, 300 μN, and 400 μN

Full size image

Due to the reasons given above and to determine whether plastic or elastic deformations are more evident in the material under study, the plasticity index was obtained using Eq. (6) and Fig. 9, under three different forces of 200 μN, 300 μN, and 400 μN (Fig. 11). This figure shows that the plasticity index increases and then decreases with an increase in the force and does not follow the incremental and declining trend like the elastic modulus and hardness. It is also due to the number of holes and pores in the material. Moreover, as shown in the chart, the plasticity index has the same trend as the modulus of elasticity. The plasticity coefficients under these three different forces are equal to 0.8, 0.88, and 0.81, respectively, with an error of less than 10%. As a result, the magnitude of the plasticity index of the produced granular alumina nanoparticles is 0.83, which indicates that this material has a higher plasticity property than its elastic property. Therefore, this specimen is a relatively plastic material.

Fig. 11
figure 11

Plasticity index for three different normal loads of 200 μN, 300 μN, and 400 μN

Full size image

3.2 Nano scratch

The scratch process involves the introduction of an indenter to the surface, which moves laterally. There have been many efforts to determine this trend in the past years. A Nano scratch test can present a qualitative assessment of the tribological specifications of the surface layer of the materials. This method was used by Hodzic et al. [24]. The Nano scratch test on the material surface was performed under two different normal loads. Then, surface morphology was characterized using the AFM to extract typical longitudinal and cross-sectional profiles. It was also used to obtain the grooves and pile-up areas that were determined using the integration method. Many useful things can be observed from scratch tests in two different normal loads 300 μN and 400 μN, as it is seen in the following figures. However, none of the attempts achieved a scratch test at 200 μN, which is only due to the high porosity of the surface, which is not a smooth and uniform surface. Figure 12 represents the three-dimensional (3D) images of the surface morphology of two different normal loads. With the increase in average load, the scratch grooves become more visible. As seen in this figure, there are several ups and downs in the surface of the specimens. Figure 13 delineates the typical longitudinal section profiles of these visible scratch grooves. It was demonstrated that the scratch depths increase from 300 μN to 400 μN.

Fig. 12
figure 12

Scratched surface morphology at a 300 μN and b 400 μN average load

Full size image
Fig. 13
figure 13

Typical longitudinal section profile of the scratch grooves at normal loads of a 300 μN and b 400 μN

Full size image

Figure 14 demonstrates a specific cross-section profile of the scratch groove at average loads of 300 µN and 400 µN. Pile-ups and scratch widths are critical factors that can be used for understanding the mechanisms related to nano scratch behavior. Clearly, as the scratch test proceeds, the scratch depth becomes more profound due to the average load increase. Also, the material pile-up exists on both sides and at the two ends of the scratch. Pile-ups form and their height is identical for both parties. Furthermore, the scratch viewpoint shows the initial resistance. It is due to the light scatter from the surface. The scratch depth, scratch width, and pile-ups are considered the signs of scratch resistance obtained from AFM images that are calculated according to Figs. 12 and 14. These parameters are listed in Table 1. As listed, with an increase in the average scratch load, the pile-ups of the scratch depth grow. Thereby, high plasticity could be observed, as could many ripples on the surface of both sides and the pile-up height. Furthermore, we know that pile-ups are due to plastic deformation; therefore, more pile-ups are related to more plastic deformation. Consequently, the scratch width increases. About the scratch width, it is notable that the specimens or forces with more plastic deformation (or more pile-up) have a larger scratch width. These results are consistent with the findings of Liu et al. [21] for various normal loads on polycarbonate (PC).

Fig. 14
figure 14

Scratch cross-section profiles at normal loads of a 300 μN and b 400  μN

Full size image
Table 1 Parameters deduced from a cross-section of the scratch test
Full size table

Figure 15 illustrates the coefficient of friction on the surface of the produced granular alumina nanoparticles under 300 μN and 400 μN at the surface of the scratches. As shown, the friction coefficient grows with an increase in the force. More specifically, the point of the friction coefficient is the same as the scratch resistance under various effects, which increases with the induced effect. Clearly, by increasing the force, the tip of the indenter goes further inside the material, and the contact surface of the material improves. It improves the scratch resistance, so the coefficient of friction can also be enhanced. The precise numerical value of the friction coefficient was calculated from the diagram where the graph is almost flat or fluctuates within a given range. In other words, under 300 μN and 400 μN, coefficients of friction are equal to 0.72 and 0.9, respectively. Moreover, this excessive oscillation in the diagram happens due to the holes and pores of the material.

Fig. 15
figure 15

Friction coefficients across the scratch area for normal loads of 300  μN and 400  μN

Full size image

Finally, Fig. 16 indicates the scratch hardness of the granular alumina nanoparticles compared with the average hardness of this material obtained from the nanoindentation test, between 300 μN and 400 μN. Typical and scratch hardness were defined based on the capacity of the material to resist deformation. However, there are several differences in the mechanism. Despite mainly having dynamic scratch hardness, the typical indentation hardness is usually quasi-static. In the nanoindentation test, a stiff and rigid indenter penetrates the specimen surface and slides. Therefore, the frictional resistance between the indenter, the substance, and the side-force is inevitable. Such parameters are not seen in the nanoindentation test, which explains the difference between the average and scratch hardness. As shown in the figure, by increasing the reasonable force from 300 μN to 400 μN, both scratch hardness and typical hardness demonstrate the same rising trend, so that the increase in typical hardness is more intense than the enhancement of scratch hardness. It is also illustrated that the scratch hardness is always greater than the typical hardness. It is because scratching hardness is a dynamic process that includes frictional forces. Thus, the indenter requires more load to overcome these obstructions. Therefore, the scratch hardness increases significantly more than typical hardness.

Fig. 16
figure 16

Standard indentation and scratch hardness as functions of different normal loads of 300  μN and 400  μN

Full size image

3.3 Validation

The present work was evaluated for its validity and credibility by comparing it with a relevant article by Muller et al. [25]. In their work, the Young's modulus of granular γ-alumina with different diameters was measured and the results were reported in Table 2. In the present study, γ-alumina with an average diameter of 1.7 mm was synthesized, and its Young's modulus was measured. The results showed that the γ-alumina produced in the present study had a higher Young's modulus compared to Muller et al.'s work. Therefore, the proposed synthesis method in the present study has been successful in increasing the Young's modulus by more than 107%.

Table 2 Comparison of current work with previous studies on validity
Full size table

4 Conclusion

The granular γ-alumina ceramic nanoparticles were synthesized. The nanoindentation and nano scratch tests were utilized for determining the mechanical properties. Furthermore, to obtain the topography and surface morphology, SEM, FESEM, and AFM were used. So, the following results were obtained:

  1. 1.

    The SEM, FESEM, and AFM images were indicative of high material strength so that its roughness was significantly elevated and equal to 31.52 nm. Also, it is showed the nanoparticles of this granular material, which is about 17 nm on average. Plus, the nanoparticles are attached due to having muscular strength.

  2. 2.

    According to the load–displacement curves under three different loads of 200 µN, 300 µN, and 400 µN, none of the elastic modulus, hardness, and plasticity index followed a specific trend when the load increased. Still, their values remained at a particular range. Application of the interpolation, elastic modulus, hardness, and plasticity index was obtained equal to about 12.6 GPa, 0.433 GPa, and 0.83, respectively. These figures are indicative of a plastic material.

  3. 3.

    Using the scratch test under two different loads of 300 µN and 400 µN, it was clear that the scratch depth, scratch width, and pile-ups increased with loading. Moreover, with the increase of load, scratch resistance, which is a representative of the friction coefficient, increased from 0.72 to 0.9. Finally, the scratch hardness increased with the load, and it was higher than the indentation hardness.

However, this study has some limitations. For example, we only tested two different loads in the nanoscratch test, and future studies could explore a wider range of loads to gain a more complete understanding of the material's behavior. Additionally, our study only investigated the mechanical properties of the γ-alumina granules and did not explore their potential applications in various fields. Therefore, we recommend that future research focuses on further characterizing the γ-alumina granules and exploring their potential uses in fields such as catalysis, adsorption, and drug delivery. Overall, our study provides important insights into the mechanical properties of γ-alumina granules and opens up avenues for future research in this area.