1 Introduction

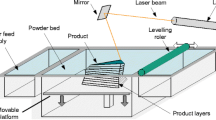
Selective laser melting (SLM) is an additive manufacturing (AM) process used in different industrial sectors to produce metallic parts directly from powder materials. The SLM process allows product developers to design and improve parts with high degree of geometrical freedom. AM facilitates the production of lightweight components in the aerospace sector and allows designers to create parts that would not be possible with traditional manufacturing technologies [1]. SLM is an AM process that uses laser melting to produce metallic components from thin layers of powdered material. The high melting point of metals requires a significant amount of power, but components produced through SLM have comparable mechanical properties to those of bulk materials. The process involves depositing layers of metal powder on a build platform, which are melted by a laser and then coated with new powder layers until the object is complete. A support structure is necessary to hold the object and enable heat transfer, and a low oxygen environment is required to minimize thermal stresses and prevent deformations [2].

Freedom of complex design geometries impacts the final part weight, the lifecycle cost, the material cost and energy consumption during the manufacturing process [3]. Nowadays, AM productivity using metals still needs to be improved compared to traditional manufacturing, especially when fabricating large parts. To get an overview of the costs of AM processes, it is usual to represent the cost level using a cost-to-mass index such as €/kg [4]. The costs of metal parts manufactured by an AM process seem very high compared to those of traditionally fabricated parts. Thus, current researchers are still investigating the cost modelling that appropriately covers all economic aspects to extend the AM technology's use in industrial applications by implementing different approaches [5,6,7].

When analysing costs in AM processes, current studies show that the most relevant factors are the machine, material, post-processing, preparation, and building time costs. Estimating the building time is one of the most challenging tasks since its influence on the building cost is significant [8]. Several cost methods have been developed in the past, but not all of them calculate the cost for a single part. A cost model developed by Cicconi et al. [9] considered a breakdown of material, machine, labour, equipment, consumables and energy costs. Other studies state that the cost of an AM part is the addition of five contributions: material, machining, heat treatment, post-processing, and human work [10]. The material cost depends on the part volume, the volume of supports, the powder recovery rate, powder density and powder. Other researchers have focused on the following factors: preparation of geometry data, the build job assembly, the machine set-up, building up the part, removing the part from the SLM machine, the part separation from its substrate plate, and post-processing [11]. Compared to other approaches, this analysis model does not consider energy costs as a separate input since these factors are included in the machine costs. In addition, Rickenbacher et al. did not specify any cost for heat treatment or a HIP process in their model. In this work, their approach was used and extended considering a detailed heat treatment post-processing since, nowadays, producing complex geometries with SLM requires advanced heat treatments such as the HIP process.

During the post-processing of manufactured AM components, it is usual to apply techniques to improve the quality of the final part, such as hot isostatic pressing (HIP). The laser powder bed fusion technique leads to tensile residual stresses near the top and compressive near the bottom of the part. The scope of the heat treatment is to relax stresses and reduce them while fixing the part displacements [12]. The heat-treatment costs are allocated to the parts produced per job [13], which can be estimated at a fixed cost of 100 €/job [10]. For critical applications requiring high elongation, the hot isostatic pressing (HIP) treatment is a reliable approach for improving ductility and allows the optimisation of SLM parameters [14]. The HIP is used to eliminate pores in the material and to release residual stresses [15], as well as to densify materials due to the degree of homogenisation of the alloy composition that can be achieved. However, there is no general scheme for implementing a HIP treatment since it depends highly on the application [16]. The cost of a HIP process depends on the system characteristics, like furnace size and type, and critical HIP cycle characteristics parameters, such as material and payload weight. In addition, consumption costs play an essential role comprising electricity, gas, maintenance and labour, including the local price for utilities, like person-hours. For large parts processed using HIP, Ahlfors et al. considered 183 € as the fixed operation cost per cycle and 0.19 € as the operation cost per part [17]. This technology has been further developed, and the combined costs have been drastically reduced to approximately 0.33 €/kg [18].

Considering the existing research, the total manufacturing costs may be calculated as follows [11]:

$$C_{tot} \left( {P_{i} } \right) = C_{prep} \left( {P_{i} } \right) + C_{buildjob} \left( {P_{i} } \right) + C_{set\;up} \left( {P_{i} } \right) + C_{build} \left( {P_{i} } \right) + C_{removal} \left( {P_{i} } \right) + C_{substrate} \left( {P_{i} } \right) + C_{postp} \left( {P_{i} } \right)$$
(1)

where \(P_{i}\) is the part with the ith geometry, \(C_{prep}\) is the cost for preparing geometry data, \(C_{buildjob}\) is the cost for build job assembly, \(C_{set\;up}\) is the machine set up cost, \(C_{build}\) is the cost for building up the part, \(C_{removal}\) is the cost for removing the part from the SLM machine, \(C_{substrate}\) is the cost to separate parts from their substrate plates, and \(C_{postp}\) is the cost for post-processing. Each cost quantity in Eq. (1) can be broken down to calculate the actual value of the contribution of each term. This equation will be split up and adapted to the case study of this work.

Cost of preparing geometry data

$$C_{prep} \left( {P_{i} } \right) = \frac{{C_{oper} + C_{pc} }}{{N_{i} }} \cdot t_{prep}$$
(2)

where \({C}_{oper}\) is the operator's hourly rate in euros per hour (€/h), \({C}_{pc}\) is the hourly rate of the workstation including costs of required software and tools in €/h, \({t}_{prep}\) is the time required for preparing CAD data in hours (h), and \({N}_{i}\) is the quantity of parts with ith geometry.

Cost for build job assembly

$$C_{buildjob} \left( {P_{i} } \right) = \frac{{C_{oper} + C_{pc} }}{{N_{i} }} \cdot t_{ba}$$
(3)

where \({t}_{ba}\) is the time required for build job assembly in h.

Machine set up cost

$$C_{set\;up} \left( {P_{i} } \right) = \frac{{C_{oper} + C_{machine} }}{{N_{i} }} \cdot t_{set\;up}$$
(4)

where \({C}_{machine}\) is the machine's cost per hour in €/h, and \(t_{set\;up}\) is the time required for machine set up in h.

Cost of building up the part

$$C_{build} \left( {P_{i} } \right) = C_{machine} \cdot t_{build} + C_{material} \cdot m_{part}$$
(5)

where \({t}_{build}\) is the building time in h, \({C}_{material}\) is the material cost in €/kg, and \({m}_{part}\) is the part mass in kg.

Cost of removing the part from the SLM machine

$$C_{removal} \left( {P_{i} } \right) = \frac{{C_{oper} + C_{machine} }}{{N_{i} }} \cdot t_{removal}$$
(6)

where \({t}_{removal}\) is the time required for removing parts from the SLM machine in h.

Cost to separate parts from their substrate plates

$${C}_{substrate} \left({P}_{i}\right)=\frac{{C}_{EDM}}{{N}_{i plate}}$$
(7)

where \({C}_{EDM}\) is the cost for the electrical discharge machining (EDM) process to separate parts from their substrate plates in €, and \({N}_{i}\) is the number of parts with ith geometry that can be built in one job and that fit on one base plate.

Cost for post-processing

$$C_{postp} \left( {P_{i} } \right) = C_{T} + C_{tools} \cdot t_{tools}$$
(8)

where \({C}_{T}\) is the cost of post-processing treatment in €, \({C}_{tools}\) is the cost per hour for a workplace, including all required tools for post-processing in €/h, and \({t}_{tools}\) is the time required for all tools during post-processing in h. Equation 8 differentiates whether \({C}_{T}\) is just a standard heat treatment or a HIP process. Table 1 summarises the parameter values used in this work.

Table 1 Parameter values used in the case study
Full size table

The material cost of AA7050 was estimated to be 75 €/kg considering that it belongs to the same aluminium alloy series as AA7050 [20]. The costs \({C}_{oper}\), \({C}_{pc}\) and \({C}_{machine}\) were estimated according to Company A, which provided a quotation for printing the parts, while the building times \(t_{build\;rib}\) and \(t_{build\;cover}\) were previously estimated through simulations with Simufact Additive™ and confirmed by Company B, which provided a quotation for printing the parts. Companies A and B were contacted to get the prototype printed in aluminium. Company A is based in the United Kingdom, and Company B is in Spain. Both companies are suppliers of AM services such as 3D printing. In [11], the relationship between the operator's hourly rate and the costs of tools for post-processing was \(\frac{{C_{oper} }}{{C_{tools} }} = \frac{{90\frac{\euro }{h}}}{{40\frac{\euro }{h}}}\). This ratio was considered to be acceptable, and it was used in this paper to obtain \({C}_{tools}\). Taxes and transportations costs for delivering printed parts were not considered.

There are ongoing studies on cost modelling methods for wing ribs using additive manufacturing processes that focus on cost estimation accuracy. In [21] a wing rib made of carbon-fibre-reinforced polymer (CFRP) using single-line-injection (SLI) had a direct manufacturing cost of about 584 €/kg, where the labour costs comprised 49%. At the same time, the fibre and matrix were about 35%. Other researchers manufactured wing rib geometries using a specific technique known as wire arc additive manufacturing (WAAM) with a deposited stiffening web (WAAM 1). They are then also machined from a thicker substance (WAAM 2). Their manufacturing costs were compared to traditional machining considering two different material removal rates (MRR) to produce an aluminium wing rib of 15 kg. For a MRR of 65 kg/h, the part cost was 5684 € when machined from solid material, 1972 € with WAAM 1 and 2320 € with WAAM 2. For a MRR of 323 kg/h, the part machined from solid material was 5104 €. Using WAAM 1, the cost was 1972 €, while manufacturing using WAAM 2 was 2204 € [22]. A summary of the current literature review is given in Table 2.

Table 2 Costs of additive and traditional manufactured wing ribs (converted to euros)
Full size table

When comparing those manufacturing methods, the most cost-effective technique seems to have been WAAM 1 since the costs for fabricating one part result in 131.47 €/kg for both MRRs.

This paper examines an extended cost analysis for the SLM manufacturing process. The aim is to answer the following research question: How does the metal powder feedstock impact the overall cost of SLM processes, including heat treatment and HIP process? An existing SLM cost model was extended through a detailed heat treatment cost breakdown concerning aircraft components, and a case study is presented to answer this question.

This work is structured into the following sections: the introduction, extended cost analysis method, results and discussion, conclusions and further work, and references.

2 Cost analysis method

The total material cost for manufacturing parts using the powder bed fusion process depends on the volume and the price of the material. In AM processes, the volume of the material used is not completely limited to the geometry of the final part. To produce geometrical shapes like holes, an amount of support structure is required. This depends on the complexity of the part and its orientation in the build chamber. In MPBF, the build chamber is filled with powder to the maximum height of the final part based on its position. Most of the powder is not used for producing the part but can be reused in subsequent printing activities.

For this research, AA7050 aluminium alloy powder was selected since it was used at the part design stage [23]. This alloy is heat treatable and is used in various aerospace applications, including wing skin, bulkheads and fuselage frames, and it is a popular commercial alloy in the aerospace industry [24]. In order to specify AA7050 powder in Simufact Additive™, its powder material characteristics were introduced. The relevant properties of this material are listed in Tables 3 and 4 [25].

Table 3 Properties for AA7050 powder
Full size table
Table 4 Chemical composition of AA7050 powder (percentage mass proportion)
Full size table

2.1 The 3D aircraft wing rib

The simulation of the AM process for the wing rib was carried out in the Simufact Additive™ software that was used to achieve an optimal cost-effective part orientation and to evaluate the build quality in terms of strain and stresses due to thermal effects. This paper's additive manufacturing technique used to generate samples includes the powder bed fusion process since it is the most appropriate process for fabricating aluminium parts in the aerospace industry. The part was simulated with aluminium alloy (AA7050), and the part's geometry had already been optimised for the AM process.

The wing rib is an aircraft component that withstands wing torsion, skin, and spars. Figure 1 shows a virtual 3D model of the wing rib and the sensory cover. The wing rib has a maximum length of 1000 mm, a maximum height of 180 mm and a 3 mm web thickness with 6 mm upper and lower caps. Each cover is 34.7 mm in diameter and 15 mm in length.

Fig. 1
figure 1

Wing rib

Full size image

The brief data related to this wing rib part is described in Table 5.

Table 5 Details of the wing rib part
Full size table

2.2 Extended cost analysis

This section presents the cost analysis of an aircraft wing rib with three sensory covers that have been virtually manufactured using a selective laser melting process with Simufact Additive™. The methodology introduced by Rickenbacher et al. [11] has been applied and extended in this work to facilitate the computation of costs linked with SLM processes. The approach has been extended to consider the integration of cutting-edge heat treatments, such as the hot isostatic pressing (HIP) process, in the comprehensive cost evaluation. The manufacturing cost for the wing rib was calculated according to the cost model previously described in the state-of-the-art section. To calculate the total manufacturing costs, the build and post-processing costs must be split up for the wing rib and sensory covers. Equation 9 was used to calculate the cost of building up the wing rib:

$$C_{build\;rib} = C_{machine} \cdot t_{build\;rib} + C_{material\;rib}$$
(9)

where:

$$C_{material\;rib} = C_{part\;rib} + C_{support\;rib} = m_{rib} \cdot C_{material} + m_{support\;rib} \cdot C_{material}$$
(10)

In order to calculate the cost of building up one sensory cover, the following equation was used:

$$C_{build\;cover} = C_{machine} \cdot t_{build\;cover} + C_{material\;cover}$$
(11)

where:

$$C_{material\;cover} = C_{part\;cover} + C_{support\;cover} = m_{cover} \cdot C_{material} + m_{support\;cover} \cdot C_{material}$$
(12)

According to Eq. 8, the cost for the post-processing for the wing rib considered the HIP, and for the sensory covers a standard heat treatment:

$$C_{postp\;rib} = C_{HIP} + C_{tools} \cdot t_{tools}$$
(13)
$$C_{postp\;cover} = C_{HT} + C_{tools} \cdot t_{tools}$$
(14)

where \({C}_{HIP}\) is the cost of the HIP in €, and \({C}_{HT}\) is the cost of heat treatment in €. The cost of the HIP is also split up in two terms: the fixed operation cost per cycle, \(C_{HIP\;cycle}\), and the fixed operation cost per part, \(C_{HIP\;part}\). Thus:

$$C_{HIP} = C_{HIP\;cycle} + C_{HIP\;part} \cdot N_{i}$$
(15)

It is estimated that four ribs can be built on one base plate to calculate the costs of separating parts from their substrate plate. In addition, for the sensory covers, the number of pieces is estimated to be 30.

3 Results and discussion

In the previous sections, an existing cost model given by Rickenbacher et al. [11] was extended due to its lack of a detailed heat treatment cost breakdown and HIP process consideration. A cost analysis has been performed considering a wing rib with sensory covers as a case study, and the use of the SLM process with material AA7050 powder. The results prove a significant cost reduction for both the wing rib and the sensory cover production volume, starting from manufacturing 100 pieces, Fig. 2. To manufacture 100 wing ribs, it is necessary to fabricate three sensory covers, so the necessary production volume for those is 300 pieces (Fig. 3). Thus, for each wing rib, the cost would be 812.80 € considering a production volume of 100 parts, and the cost for each sensory cover would be 20.83 € when the production volume is 300 pieces. Figure 4 shows that manufacturing one single wing rib with three sensory covers would cost 879.26 €.

Fig. 2
figure 2

Total cost per part in €—Wing rib

Full size image
Fig. 3
figure 3

Total cost per part in €—Sensory cover

Full size image
Fig. 4
figure 4

Total cost per part in €— Wing rib with three sensory covers

Full size image

Figure 5 shows the total costs per kg for one rib and three sensory covers. For a production volume of 100 wing ribs, each with three sensory covers, the cost would be 1362.75 €/kg. Compared to the current literature, the cost per kg seems to be much higher than for other AM manufacturing processes, such as WAAM, by around ten times. However, in this work, the cost estimation was performed considering a lighter part: the weight was around 96% less than the components shown in the above literature.

Fig. 5
figure 5

Total cost per part in €/kg—Wing rib with three sensory covers

Full size image

The cost variation within the production volume of up to 300 parts was calculated to get an overview of the cost reduction. Table 6 shows the results.

Table 6 Total cost variation against piece number
Full size table

As mentioned before, the significant cost variation for the wing rib is when manufacturing 100 components. At the same time, the sensory cover is 200 parts, although a production volume of 300 sensory covers is required for 100 wing ribs. Figure 6 shows the total cost variation per part concerning the production volume.

Fig. 6
figure 6

Total cost variation per part for the production volume

Full size image

A cost breakdown was performed to understand the cost contribution during the AM manufacturing process, considering each contributor to the total cost. The building cost remains constant, independent of the production volume and always represents the major contributor to the total cost, which was validated by the previous cost model [11]. The other cost contributors decreased when the number of parts increased. Supposing one part was manufactured, the building cost would be 818.06 €, which represents 52.17% of the total cost. The second contributor to the total cost was the cost of post-processing, 19.48%. This is shown in Table 7.

Table 7 Cost breakdown for one wing rib with three sensory covers
Full size table

Figure 7 shows the detailed cost breakdown for each cost contributor.

Fig. 7
figure 7

Cost breakdown for one wing rib with three sensory covers

Full size image

The building cost for one wing rib and three sensory covers would be as follows:

$$\begin{aligned} C_{build\;wing\;rib} & = C_{build\;rib} + 3 \cdot C_{build\;cover} \\ & = \left( {C_{machine} \cdot t_{build\;rib} + C_{material\;rib} \cdot m_{part\;rib} } \right) \\ & \quad + 3 \cdot \left( {C_{machine} \cdot t_{build\;cover} + C_{material\;cover} \cdot m_{part\;cover} } \right) \\ \end{aligned}$$
(16)

Within the building cost, the main contributor was the machine cost. For one wing rib, it can be calculated considering the machine costs and the building times for the parts:

$$\begin{aligned} C_{machine\;wing\;rib} & = C_{machine} \cdot t_{build\;rib} + 3 \cdot C_{machine} \cdot t_{build\;cover} \\ & = 28\frac{\euro }{h} \cdot 23.5 h + 3 \cdot 28\frac{\euro }{h} \cdot 0.5 h = 700 \euro \\ \end{aligned}$$

The AA7050 powder cost is the other contributor to the building cost. The mass of the rib (mpart rib) is 631.96 g, while the mass of the support (msupport rib) is 895.59 g. The AA7050 powder cost for fabricating the wing rib, including the support, is 114.57 €, and the wing rib itself represents 41.37% of the total AA7050 powder costs, while the support is 58.63%. In the case of the sensory cover, the mass of the cover (mpart cover) is 4.42 g, and its support (msupport cover) is 11.10 g. The AA7050 powder cost percentage for the cover is 28.46%, while its support percentage represents 71.54%. The total mass for one rib with three sensory covers is \(m_{part} = m_{part rib} + 3 \cdot m_{part cover} = 631.96 g + 3 \cdot 4.42 g = 645.22 g\), and the AA7050 powder costs for one rib are \(C_{material\;wing\;rib} = \left( {C_{part\;rib} + C_{support\;rib} } \right) + 3 \cdot \left( {C_{part\;cover} + C_{support\;cover} } \right) = \left( {47.40 \euro + 67.17 \euro } \right) + 3 \cdot \left( {0.33 \euro + 0.83} \right) = 114.57 \euro + 3 \cdot 1.16 \euro = 118.06 \euro\). Table 8 shows a cost summary of the AA7050 powder costs.

Table 8 Estimation of the AA7050 powder costs for the wing rib and the sensory cover considering the support
Full size table

The contribution of the AA7050 powder cost for one single rib to the total cost is given by Eq. 17:

$$\frac{{C_{material\;wing\;rib} }}{{C_{tot} }} = \frac{118.06 \euro }{{1568.04 \euro }} \cdot 100 \% = 7.53 \%$$
(17)

The building cost highly depends on the printed geometries and whether different geometries are built up in separate build jobs [11]. In their study, Rickenbacher et al. estimated the building for three different geometries, resulting between around 33% and 78% of the total costs when separating the printing of each geometry. Compared to their study, in this work the building cost represented around 52% of the total costs for one single wing rib with three sensory covers. This value is within their estimated range.

Compared to the research conducted by Cicconi et al., who obtained a material share of 0.8% concerning the total manufacturing costs, this case study gives a metal powder contribution of around ten times higher. This is explained by the fact that their part weight is around 34% of the wing rib with sensory covers. Besides, their geometry is quite different, and the manufacturing costs thus vary [9].

Abattouy et al. estimated a cost model of the SLM process printing a cubic crane of 8 cm3 and 64 g. Their model results in a contribution of the powder metal cost of 1.8% to the total costs, around four times less than the study analysed in this work. Again, the geometry is a relevant factor in analysing the SLM costs. When manufacturing one single rib with sensory covers, the machine cost is considered within the building (52.17%), set-up (10.71%) and removal costs (7.14%), which make up 70% of the total costs. This value is slightly higher than the SLM machine costs (62%) presented by Abattouy et al. since they separate the operator’s hourly rate. The post-processing (9%) and build planning (4%) costs in their study are also less compared to this work, 19.5% and 7.14%, respectively [26].

4 Conclusions and future work

The scope of this work was to extend a previous cost analysis method of SLM process considering a detailed heat treatment cost breakdown and HIP process in complex lightweight components. A metallic aircraft wing rib, produced with SLM and AA7050 powder weighing around 96% less than the ribs shown in the current research, was used as a case study. The main results are as follows:

  • Data from one 3D printing supplier was used to validate the operator's hourly rate, the hourly rate of the workstation, including costs of required software and tools, and the machine's cost per hour.

  • The data from a second supplier was used to verify the building times for the wing rib and the sensory cover, which had been previously calculated through simulations in Simufact Additive™.

  • The results gave an optimal production volume of 100 wing rib parts and 200 for the sensory cover parts. The cost of one wing rib with three sensory covers was estimated to be 879.26 € for a production volume of 100 manufactured parts, while the price per kg was 1362.75 €/kg for 100 manufactured parts.

  • The results also showed that the main cost driver was the building costs, and within these, the major contributor was the machine cost, followed by the metal powder costs.

  • The support contributed 58.63% to the material cost for the wing rib, while the sensory cover contribution to the support was 71.54%.

This research's main contribution and novel findings entail an expanded cost analysis of the SLM process, comprehensively incorporating a detailed cost breakdown of heat treatment processes for manufacturing lightweight aircraft components. Two industrial 3D printing companies validated this work, and the main cost drivers in aircraft components manufactured with SLM and HIP processes were identified. The study also estimates the optimal volume parts of wing rib mass production with sensory covers.

Future work will estimate the wing rib cost, including the IoT implementation.