Effect of CO₂ tax on energy use in oil production: waterflooding optimization under different emission costs

Abstract

Tackling emissions from hydrocarbon production is a necessity because hydrocarbon production will last for a prolonged time. As a popular hydrocarbon production method, waterflooding operation is energy-intensive and accounts for significant CO₂ emissions. This article investigates the effect of CO₂ tax level on recovery process of already producing fields with waterflooding. Our methodology is waterflooding optimization in reservoir simulation models, specifically optimizing well-controls. Unlike traditional studies, our optimization objective comprises two components: the profitability of hydrocarbon production and an additional tax proportional to CO₂ emissions. The associated CO₂ emissions is estimated using a scheme developed upon an integrated model of reservoir, surface network, and topside facility. We examine our methodology on two cases with heterogeneous reservoir models. In each case, we optimize multi-scenarios enforcing different CO₂ tax rates. The solutions indicate that imposing a higher CO₂ tax rate reduces both emissions and hydrocarbon production. The fractional reduction of oil produced is however smaller than the emission reduction. While an increased tax rate drives the topside equipment to operate at higher efficiencies, the main effects of a higher tax rate are reduced water injection and more efficient subsurface drainage. There is a non-linear relationship between the reduced production and emissions. For increasing tax levels there are diminishing returns on lower emissions, reflecting reduced opportunities for emission reduction by changes in the drainage strategy. Some increments on the tax rate will therefore have negligible impacts on the optimal drainage strategy, and hence an adverse effect on the profitability with negligible emission reduction.

Article highlights

• A methodology for reducing carbon emissions from water injection via well-control optimization is introduced.

• Higher CO₂ tax rates result in optimal injection strategies that lower emissions with small reduction in production.

• The main effects of a higher CO₂ tax rate are reduced water injection and more efficient subsurface drainage.

1 Introduction

We are in the middle of an energy transition away from fossil fuels. For decades hydrocarbons have been a principal energy source. In 2018, oil contributed 31.6% of the total energy supply globally, higher than any other energy source [1]. Natural gas had the third largest portion of the global energy mix that year by supplying 22.8% [1]. The shares of oil and natural gas in the total energy supply did not change much from 1990 to 2018 [2], and are likely to remain high in the near future [3]. Despite a slight drop in 2020 due to the pandemic, the Stated Policies Scenario defined by the International Energy Agency projects that the global energy demand will continue to grow, reaching about 10% higher than the 2019’s energy need by 2030 [3]. The upward trend of the total energy need implies that substantial amounts of oil and natural gas will be produced in the coming years.

Exploitation of hydrocarbon resources has severe environmental impacts, and emissions from hydrocarbon extraction activities may constitute a substantial portion of domestic emissions [4]. Norway is such an example, where the petroleum sector accounted for 31% of the nationwide CO₂ emissions in 2018 (see Fig. 1a), despite its CO₂ emission intensity from oil and gas production is among the lowest in the world [4]. CO₂ emissions from petroleum activities on the Norwegian Continental Shelf (NCS) stem primarily from the combustion of natural gas when running gas turbines. According to [5], gas turbines used for power generation in offshore platforms made up 84% of the 13.65 million ton CO₂ emitted by petroleum activities on the NCS in 2018 (see Fig. 1b). Electric power generated by gas turbines is mainly used for pumping, compression, and separation operations [6, 7]. The Sustainable Development Goals #13 outlines that the global net CO₂ emissions must decrease by 45% between 2010 and 2030, and reach net zero around 2050 in order to limit the global temperature increase below $1.5^{\mathrm{o}}\hbox {C}$ [8]. To support this emission reduction target, it is urgent to develop and deploy economically viable low-emission technologies for hydrocarbon extraction processes.

Fig. 1

Norway’s CO₂ emissions in 2018, by source [$10^{9}$ kg CO₂]. Extracted from [5]

Except for an indirect penalty for emissions through the cost of energy use, emissions have traditionally received little focus in optimization of hydrocarbon production. However, with increasing CO₂ tax on emissions, cost of emissions has to become an integral part of the optimization of hydrocarbon production. The natural reservoir energy can initially drive the hydrocarbons through the reservoir and the well to surface, and this is a common first stage of hydrocarbon production, typically denoted primary recovery [9, 10]. However, only a fraction of the oil in place can be extracted by primary recovery, thus additional energy has to be provided to increase the hydrocarbon production, i.e., secondary recovery. Water injection has been one of the most popular secondary recovery methods for increased production [9, 11, 12]. Water injection entails an introduction of external energy into the reservoir through the injection of water, aiming to (i) maintain reservoir pressure and (ii) displace mobile oil left in the pore space towards production wells [9, 13]. Water injection or any other methods providing additional energy to the reservoir to support production come with associated emissions. In this article we will present how the inclusion of different levels of CO₂ tax will yield different optimal solutions for the drainage of existing fields with limited opportunities for changing the production facilities. We will limit our focus to fields with water injection as this recovery method is the most widely used [14,15,16].

Water injection is attractive for several reasons; (i) pressure maintenance to sustain high field production rates, (ii) a fairly high sweep efficiency, indicating a large the portion of the reservoir volume is being swept by the injected water and this leads to a substantial increase in recovery, (iii) cost efficiency when water is in abundant supply, e.g., in offshore fields, and (iv) a relatively simple injection operation that can be scaled to large field cases [9,10,11,12,13]. Secondary recovery by injection of fluids into a reservoir is a very energy-intensive activity [17]. Water injection typically requires about one third of the electric power available on an offshore platform [18]. In some offshore platforms operating on the NCS, the energy allocation for water injection system could be higher than 50% [19]. Furthermore, energy use per unit oil produced and consequently CO₂ emission intensity increase significantly as the field production declines and the water cut rises above 90% [4, 11, 20]. Considering its vast number of applications worldwide and its high energy consumption, water injection is responsible for a considerable amount of CO₂ emissions. Therefore, improvements in the water injection process might offer a notable global CO₂ emission reduction.

Optimization is an important tool to improve a waterflooding strategy. Multiple studies related to optimization of water injection process have been carried out. From a reservoir management perspective, we organize studies considering waterflooding optimization into four categories depending on their decision variables: (i) well-placement and -trajectory [21,22,23,24,25], (ii) well-control [26,27,28,29,30,31,32,33], (iii) coupled well-placement and well-control [34,35,36,37,38], and (iv) well with inflow control valves [39,40,41]. Moreover, the various studies employ different types of reservoir models, including numerical reservoir simulation models [25, 29, 34], physics-based data-driven models [28, 32, 33], “pure” data-driven models [26, 27, 31], and streamline-based models [21, 30, 38]. Finally, geological uncertainty is typically taken into account by involving an ensemble of equiprobable realizations of the reservoir [23,24,25, 29]. A detailed review of water injection operation and optimization is provided by [42].

Improvements to water injection can also be made at the surface or topside part. For instance, [43,44,45] optimize the structural design of centrifugal pumps (commonly used for water injection), whereas [46,47,48] optimize the pumping operational parameters, such as pump flow rate, speed, activation (on/off), and valve opening. A methodology for designing energy-efficient offshore platforms is presented by [49]. This methodology optimizes both process plant configuration and utility plant operation. Furthermore, several works target optimizing subsea layout, in terms of pipeline routing and diameter, manifolds and riser locations, and well rate allocation [50, 51]. Finally, to more accurately represent production and injection systems, some optimization studies utilize integrated models that couple both subsurface and surface parts [52,53,54,55,56].

Most water injection optimization studies (especially if they model the subsurface reservoir) aim to maximize the profitability or oil recovery. These traditional optimization studies do not provide estimates for the CO₂ emissions, and consequently will not include tax on CO₂ emissions into the objective function. This requires a model for both the subsurface and surface parts, as the energy-intensive injection is dictated by the subsurface flow, while the emissions occur at the surface facilities. Before attempting to assess the impact of CO₂ tax on emissions from water injection process, we need methods for quantifying the CO₂ emissions associated with a certain water injection strategy. In the literature there are some relevant approaches.

One approach is based on exergy analysis which enables us to locate and quantify the thermodynamic imperfections of a system [57]. An exergy-based life-cycle assessment of a water injection operation is proposed by [11]. The authors took into account several components that are directly influenced by the water injection process, such as water treatment, injection pump, oil transport, artificial lift, and oil heating. They pointed out that water pumping and treatment are the two most significant contributors to exergy loss. For the estimation of exergy destruction in injection pumps, the authors assume that the pressure boost, mechanical efficiency, hydraulic efficiency, and power plant efficiency are constant. This is notably different from the methods that will be introduced in this paper. Generic exergy analyses have also been performed for offshore oil and gas platforms in Brazil and the North Sea [6, 58, 59].

CO₂ emissions due to water injection process can also be estimated using empirical models. Such an empirical model can be based on several inputs, e.g., field production, original reserves, reservoir and water depths, oil price, CO₂ tax rate, time, and other variables, as presented by [4]. In that work the authors employed yearly CO₂ emission data for all Norwegian oil and gas fields between 1997 and 2012. The model, however, did not consider water injection volume which is expected to impact significantly on the CO₂ emission intensity. Nevertheless, the authors did note that there is a correlation between CO₂ tax rate and emission intensity, where a higher CO₂ tax rate reduces emission intensity.

Alternatively, CO₂ emissions due to water injection can be estimated using the open-source software OPGEE (Oil Production Greenhouse Gas Emissions Estimator) proposed by [60]. OPGEE enables a rapid assessment of greenhouse gas emissions from crude oil production and includes an extensive number of processes in the O&G value chain that emit CO₂ gas. Important simplifications are however made in the software, e.g., fluid production and injection rates are explicitly computed from the well productivity index and the water injection ratio provided by users. This work, in contrast, computes all fluid production rates using full physics reservoir simulations. Moreover, optimization is enabled by determining various well-control settings to manage injection and improve overall production.

In [20], the authors investigated three well-control optimizations implementing distinct objective functions: (i) maximizing the net present value, NPV, (ii) maximizing a net cumulative exergy which is defined as the difference between total exergy gained and invested, and (iii) maximizing a modified NPV with CO₂ emission cost. The authors reported similar optimal solutions for these optimization scenarios. This contradicts observation which will be presented in this article, where we find different optimal solutions for different CO₂ tax rates.

This paper presents a methodology to optimize water injection process with inclusion of the CO₂ emission cost into the optimization objective. In particular, this study optimizes well-control setting, i.e., well rates and/or bottom-hole pressures, in a reservoir simulation model. The distinctive characteristics and contributions of this study are as follows:

• We propose a scheme that integrates a subsurface reservoir simulation model, a surface network model, and a topside facility model. This scheme is developed for estimating the amount of CO₂ gas emitted for a particular set of well-controls using simulation results of the corresponding production scenario. The integrated model considers the energy use for both pumping and water treatment systems, as these two systems contribute significantly to the overall energy use for water injection.

• The scheme calculating CO₂ emissions includes generic and typical performance characteristics for pumps and gas turbines. These performance attributes encompass the pump’s head and hydraulic efficiency curves, as well as the gas turbine’s part-load efficiency profile. The inclusion of these performance characteristics will help us identifying a more efficient strategy for operating the pumps and gas turbines. Furthermore, part of the calculation scheme involves solving sub-optimization problems to determine the optimal setting for the pumping system.

• The well-control optimization problem in this work has an objective function consisting of two components, i.e., the traditional part of the net present value consisting of production revenue and operating costs, and an additional CO₂ tax that depends on the amount of CO₂ emissions. In this study, the well-control optimization is solved for different CO₂ tax rates, and the optimal solutions for the different tax rates are compared and analysed. The methodology is tested using two heterogeneous reservoir models.

With this methodology we are able to assess the effect of different CO₂ tax levels on the energy use of the oil fields investigated in this article.

The article is structured as follows: Sect. 2 explains the developed methodology covering the formulation of the optimization problem, the calculations of the objective function components and its underlying assumptions, the software implementation, as well as the optimization algorithm. Section 3 provides descriptions of two reservoir simulation models employed for evaluating the presented methodology. Optimization results for two case studies are discussed in Sects. 4 and 5. Concluding remarks are given in Sect. 6, including suggestions on how to reduce CO₂ emissions from the petroleum sector.

2 Methodology

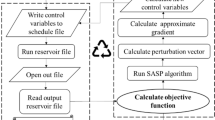
To assess the effect of emission cost on water injection, we seek a methodology for finding the optimal well-control settings under different CO₂ tax levels. Figure 2 outlines the optimization workflow to find the optimal well-control setting for a given tax rate. An algorithm in the optimization loop chooses well-controls before letting the simulator run the reservoir model. The simulation is the most computational costly part of the optimization loop. The simulation results are then used to compute the optimization’s objective function.

Fig. 2

A flow chart of the optimization loop. The blue box contains the traditional net present value terms, $NPV_{t}$, while the red box indicate the additional emission term, $E_T$, extending the traditional net present value to $NPV= NPV_t - E_T$

Traditionally, either a net present value, NPV, or oil production objective function formulation is used for well-control optimization. As we want to infer the effect of emission cost, we will use an NPV approach, however, our NPV will be extended from the traditional formulation to also include a term accounting for the cost of the CO₂ emissions, hereby referred to as the emission term, $E_T$. The augmented NPV formulation is used as objective during the optimization. The optimization algorithm systematically modifies the well-controls to improve the given objective. The optimization loop continues until optimality criteria for the objective or controls are met or other termination conditions, e.g., a maximal number of cost function evaluations, are reached.

The augmented objective is expressed as follows:

$$\begin{aligned} \mathop {\text {max}}_{\vec {u}} \; \bigg ( NPV(\vec {u}) \bigg ) = \mathop {\text {max}}_{\vec {u}} \; \bigg ( NPV_t(\vec {u}) - E_{T}(\vec {u}) \bigg ) \quad \text {s.t.} \quad \vec {u}_{lb} \le \vec {u} \le \vec {u}_{ub} \end{aligned}$$

(1)

where $\vec {u}$ is a vector of well-control variables, $NPV_{t}$ is the traditional net present value accounting for earnings from hydrocarbon sales and operational costs, while NPV is the augmented net present value that also includes cost for the emissions (see Fig. 2). In this study, the well-control variables $\vec {u}$ are (i) bottom-hole pressure (BHP) targets for the producers, $\bar{p}_{wf, p}^{\;c}$, and (ii) water injection rate targets for the injectors, $\bar{q}_{wi, i}^{\;c}$:

$$\begin{aligned} \vec {u} = \bigg [ \bar{p}_{wf, p}^{\;c}, \;\bar{q}_{wi, i}^{\;c} \in \mathbb {R} \bigg ] \end{aligned}$$

(2)

where

$$\begin{aligned}&p \in \{1, \dots , M_p\}, \\&i \in \{1, \dots , M_i\}, \\&c \in \{1, \dots , M_c\}, \\ \end{aligned}$$

and $M_p$, $M_i$, and $M_c$ are the numbers of producers, injectors, and control periods, respectively. The well-control variables are restricted to be within their lower and upper limits, $\vec {u}_{lb}$ and $\vec {u}_{ub}$. The $E_T$ and $NPV_{t}$ terms in Eq. (1) will be formulated in the next two subsections, while the software and optimization algorithm employed are discussed in Sects. 2.3 and 2.4.

2.1 Calculation of emission term, $E_T$

In contrast to traditional optimization of reservoir simulation models, a prediction of the emission term $E_T$ in the extended NPV requires a model of the surface facilities. The objective function calculation is therefore derived based on an integrated model that couples subsurface reservoir simulation, surface network, and topside facility models (see Fig. 3). The model considers two systems that consume most of the energy for water injection process, i.e., pumping and water treatment systems [11]. The energy consumption for these two systems greatly influences the amount of CO₂ emitted. Even though simplified, the integrated model is sufficient to efficiently relate an injection strategy with its CO₂ emissions. The simplifications and assumptions adopted for the model (as well as their implications) are thoroughly discussed later in this subsection.

Fig. 3

Integration of subsurface reservoir model, surface network, and topside facility models

As illustrated in Fig. 3, fluids from the producer flows to a separator on the platform. There, the oil is segregated from the produced water before it is transported or stored, while the produced water is re-injected into the reservoir. The volume of water being injected is typically larger than the volume of produced water. Therefore, some additional water will be taken from the sea. Before being injected into the reservoir, the water goes through a water treatment system. The treatment system removes large suspended particles or oil droplets that could clog near-wellbore pores and hence diminish well injectivity. A pumping system that is made up of several pumps is responsible for providing sufficient injection pressure and rate. From the pumping system, the injected water flows to an injection manifold located at the seafloor. From there, the injected water is distributed to the injectors. Each injector is equipped with a well-head valve. This valve adjusts the injection rate for an injector to its desired rate. Electricity for operating the pumping and water treatment system is generated from gas turbines. Natural gas is combusted when running the gas turbines, and CO₂ gas is emitted as a byproduct of the combustion process. Note that the integrated model is scalable. It can be made more complex by capturing more details in the production system, energy consumption, and CO₂ emissions.

In this study, the reservoir and surface network models are weakly coupled, in the sense that the surface network model is not involved when performing reservoir simulations. The surface network is only applied once the reservoir simulation is complete. The network model utilizes the reservoir simulation results to estimate pressures and rates required from the pumping system. This coupling strategy is adequate for the present study as the well BHPs or injection rates are the only decision variables in the optimization. If also, e.g., pressures at the injection manifold or at the pumping system outlet are considered as the decision variables, then a "strong" coupling between the reservoir and surface network models would be needed to capture the inter-dependencies between the systems. In contrast to the weaker coupling used in this work, a strong coupling requires solving both the reservoir and surface network models simultaneously at every simulation timestep. Some studies which implemented such strong coupling strategies are [53, 61, 62]. The main benefits of using a weakly-coupled system are a simpler implementation and a shorter simulation runtime. However, one consequence is that we need to assume each injector has a well-head valve. The well-head valve opening is regulated so that we have pressure continuity across the injection network. If not fully-opened, the well-head valve is a source of energy loss in the injection system.

Figure 4 outlines the procedure for calculating the emission term, $E_T$. The calculation scheme is divided into seven steps (shown with the boxes in Fig. 4). The blue notations in the figure are the inputs for or outputs from each step. To compute the emission term, the scheme takes the reservoir simulation results as its inputs, namely, the injector’s BHP, $p_{wf, i}^{t}$, and the injector’s water rate, $q_{wi, i}^{t}$. As the calculation of the emission term $E_T$ through a coupled model of the reservoir and surface is novel, it will be described in detail in the next subsections.

Fig. 4

Calculation scheme for the emission term

2.1.1 Calculating required head and flow rate from the pumping system

The first step in the emission term calculation is to estimate head and flow rate that need to be provided by the water pumping system, $h_{req}^{t}$ and $q_{req}^{t}$, respectively (t indicates the timestep). To estimate the required head from the pumping system, we first compute the injector’s well-head pressure, $p_{wh, i}^{t}$, using the injector’s BHP, $p_{wf, i}^{t}$, data:

$$\begin{aligned} p_{wh, i}^{t} = p_{wf, i}^{t} - \rho _{wi} \cdot g \cdot D_{tv, i} \end{aligned}$$

(3)

where $\rho _{wi}$ is the density of the injected water, g is the acceleration of gravity, and $D_{tv, i}$ is the true vertical depth between the well-head and bottom-hole. The values for $\rho _{wi}$ and g are provided in Appendix A. The subtracting term in Eq. (3) represents a hydrostatic pressure loss due to water column in the injector. In this study, the frictional pressure loss is assumed insignificant compared to the hydrostatic pressure loss, and therefore disregarded in Eq. (3).

Next, we determine pressure needed at the injection manifold so that each injector can operate at its required well-head pressure. Since the injected water is distributed from one injection manifold to all the injectors, the injection manifold’s pressure, $p_{im}^{t}$, is determined as:

$$\begin{aligned} p_{im}^{t} = \text {max} \bigg ( \left( p_{wh,i}^{t} \right) _{i = 1, 2, \dots , M_{i}} \bigg ) \end{aligned}$$

(4)

Again, the frictions along the injection flowlines from the manifold to the well-heads are neglected.

After evaluating the required pressure at the injection manifold, we estimate the required head from the pumping system, $h_{req}^{t}$. In this study we neglect the frictional pressure losses in the injection pipeline that connects the pumping system with the injection manifold. With this assumption, the required pressure at the pumping system’s outlet is equal to the required pressure at the injection manifold minus a hydrostatic pressure proportional to the water depth, $h_{w}$. The required pressure at the pumping system’s outlet is then converted to $h_{req}^{t}$:

$$\begin{aligned} h_{req}^{t} = \frac{ p_{im}^{t} - p_{ps, in}}{\rho _{wi} \cdot g} - h_{w} \end{aligned}$$

(5)

where $p_{ps, in}$ is the inlet pressure for the pumping system (given in Appendix A). The zero friction assumption is invalid if the injection pipeline is long. In the following we will also omit the effect of water depth.

The consequence of neglecting frictional pressure drops along the injection pipeline, flowlines, and wells is that the required pressure at the pumping system’s outlet might be slightly underestimated, and so does the power consumption and CO₂ emissions. In contrast, omitting the hydrostatic pressure from platform to seafloor works in the opposite direction.

The required flow rate from the pumping system, $q_{req}^{t}$, is calculated as the total water rate for all the injectors:

$$\begin{aligned} q_{req}^{t} = \sum _{i = 1}^{M_{i}} q_{wi, i}^{t} \end{aligned}$$

(6)

2.1.2 Determining optimal pumping system configuration

After evaluating the required head and flow rate from the pumping system, the next step in the emission term calculation is to determine the optimal setting for the pumping system. As illustrated in Fig. 5, this study assumes that the pumping system is composed of several water injection pumps. These pumps are installed in parallel and series, where $M_{pp}^{t}$ and $M_{ps}^{t}$ indicate the numbers of pumps running in parallel and in series, respectively, at time t. We assume that all the pumps running at a given time have a uniform operating point. This means that every running pump delivers the same head and flow rate.

Fig. 5

Illustration of the pumping system

Generic pump performance curves are defined and used for optimizing the pumping system configuration. The solid blue line in Fig. 6a shows how the head provided by a pump decreases as the pump runs at a higher flow rate. The solid blue line in Fig. 6b indicates the relationship between the pump’s flow rate and its hydraulic efficiency. Calculations for the pump’s head and hydraulic efficiency are provided in Appendix B. We assume that (i) all the pumps installed in the pumping system have identical performance characteristics, (ii) the pumps are operated with a fixed pump speed, and (iii) the pumps can deliver any rate that is less than or equal to the pumps’ maximum flow rate. These assumptions do influence the power consumption of the pumping system and thus affect the amount of CO₂ emitted, as more degrees of freedom in the optimization, e.g., operating the pumps independently, can reduce the power consumption further.

Fig. 6

Pump performance curves that are employed to decide the optimal pumping system setting for given head and flow rate values

Variables $h_{ps}^{t}$ and $q_{ps}^{t}$ denote the head and flow rate, respectively, provided by the pumping system. With the assumption that all the running pumps have a uniform operating point, we can define $h_{ps}^{t}$ as a product of the pumps’ head and $M_{ps}^{t}$, whereas $q_{ps}^{t}$ as a product of the pumps’ flow rate and $M_{pp}^{t}$. Since (i) the pumps’ head depends on the pumps’ flow rate and (ii) the pumps’ flow rate itself is computed as $q_{ps}^{t} / M_{pp}^{t}$, the head $h_{ps}^{t}$ can be calculated using a head function, $f_{h}$:

$$\begin{aligned} h_{ps}^{t} = f_{h} \bigg ( q_{ps}^{t}, M_{pp}^{t}, M_{ps}^{t} \bigg ) \end{aligned}$$

(7)

where the quantities within the parentheses indicate the function’s inputs. Curves in Fig. 6a represent the relationship between $q_{ps}^{t}$ and $h_{ps}^{t}$ for nine combinations of $M_{pp}^{t}$ and $M_{ps}^{t}$.

Hydraulic efficiency of the pumping system, $\eta _{ps}^{t}$, is determined by only the pumps’ hydraulic efficiency, which is a function of the pumps’ flow rate. As the flow rate is given by $q_{ps}^{t} / M_{pp}^{t}$, the efficiency $\eta _{ps}^{t}$ can be computed using an efficiency function, $f_{\eta }$:

$$\begin{aligned} \eta _{ps}^{t} = f_{\eta } \bigg ( q_{ps}^{t}, M_{pp}^{t} \bigg ) \end{aligned}$$

(8)

The $q_{ps}^{t}$ - $\eta _{ps}^{t}$ curves for different values of $M_{pp}^{t}$ are provided in Fig. 6b.

The pumping system has to provide head and flow rate in excess of what are required from it. The excessive flow rate will be disposed, while the excessive head will be lowered using a control valve. As visualized in Fig. 6a, the red circle denotes the head and flow rate required from the pumping system while the purple rectangle indicates the head and flow rate provided by the pumping system. The purple rectangle theoretically can be placed on any curves in Fig. 6a as long as it is on the upper right side of the red circle. The choice of the pumping system’s operating point however affects the pumping system’s power consumption, $P_{ps}^{t}$, that is calculated as:

$$\begin{aligned} P_{ps}^{t} = \frac{q_{ps}^{t} \cdot \rho _{wi} \cdot g \cdot h_{ps}^{t}}{\eta _{m} \cdot \eta _{ps}^{t}} \end{aligned}$$

(9)

where $\eta _{ps}^{t}$ is the pumping system’s efficiency as plotted in Fig. 6b, while $\eta _{m}$ is the pumps’ mechanical efficiency. The mechanical efficiency used in this study is listed in Appendix A.

In this study, the pumping system’s operating points are optimized using a sequential approach. The approach implies that, for a given set of well-controls, we determine an optimal setting for the pumping system that is best-suited to the corresponding reservoir simulation results. To find the optimal pumping setting, we solve multiple subproblems, where each subproblem is an optimization for one particular simulation timestep. The pumping system configuration to optimize comprises of $q_{ps}^{t}$, $M_{pp}^{t}$, and $M_{ps}^{t}$. Furthermore, the subproblem takes $h_{req}^{t}$ and $q_{req}^{t}$ as the inputs.

Every subproblem aims to minimize the power consumption for the pumping system. The subproblem’s objective function is thus formulated as follows:

$$\begin{aligned} \mathop {\text {min}}_{q_{ps}^{t},\; M_{pp}^{t},\; M_{ps}^{t}}\; P_{ps}^{t} \end{aligned}$$

(10)

The search space for the decision variables is bounded as follows:

$$\begin{aligned}&0 \le q_{ps}^{t} \le q_{pm}^{max} \cdot M_{pp}^{max} \end{aligned}$$

(11)

$$\begin{aligned}&1 \le M_{pp}^{t} \le M_{pp}^{max}; \quad M_{pp}^{t} \in \mathbb {Z} \end{aligned}$$

(12)

$$\begin{aligned}&1 \le M_{ps}^{t} \le M_{ps}^{max}; \quad M_{ps}^{t} \in \mathbb {Z} \end{aligned}$$

(13)

where $q_{pm}^{max}$ is the pumps’ maximum flow rate, $M_{pp}^{max}$ is the maximum number of pumps running in parallel, and $M_{ps}^{max}$ is the maximum number of pumps running in series. The values for $q_{pm}^{max}$, $M_{pp}^{max}$, and $M_{ps}^{max}$ are provided in Appendix A. There are some operational constraints considered for the optimization. First, the pumping system must provide head and flow rate higher than or equal to what are required:

$$\begin{aligned}&h_{req}^{t} \le h_{ps}^{t} \end{aligned}$$

(14)

$$\begin{aligned}&q_{req}^{t} \le q_{ps}^{t} \end{aligned}$$

(15)

Second, the pumps’ flow rate, $q_{pm}^{t}$, must not exceed their maximum flow rate:

$$\begin{aligned} 0 \le q_{pm}^{t} \le q_{pm}^{max} \end{aligned}$$

(16)

In addition, pump manufactures often recommend to operate the pumps within a preferable range of flow rate, aiming to prolong the pumps’ lifetime. Even though not being considered in this study, supplementary constraints associated with the preferred range could be easily appended to the existing set of constraints given by Eqs. (11) to (16).

Optimization of the pumping system configuration is a computationally demanding task because the optimization is performed for every simulation timestep in thousands of simulation cases, where each simulation case itself has hundreds of simulation timesteps. For this reason, we populate a lookup table for optimal pumping system configuration by performing an exhaustive search for $141 \times 526$ combinations of $h_{req}^{t}$ and $q_{req}^{t}$. Figure 7 presents a visualization of the optimal solutions.

For every pair of $h_{req}^{t}$ and $q_{req}^{t}$, we optimize the pumping system setting using a population-based stochastic optimization technique, specifically the Particle Swarm Optimization (PSO) algorithm [63, 64]. A Python package called pyswarm [65] is employed for the optimizations, and the PSO’s parameters used are given in Appendix D. One subproblem optimization needs around 4 s to complete. Moreover, every optimization is run twice to ensure the consistency of the optimization results because of the stochastic nature of the search algorithm.

Fig. 7

Optimal pumping system configuration for various $(h_{req}^{t}, \; q_{req}^{t})$ combinations

2.1.3 Ensuring that the injection operation is feasible

The gray-colored area in Fig. 8 indicates a region for which there is no combination of $q_{ps}^{t}$, $M_{pp}^{t}$, and $M_{ps}^{t}$ that will honor all the constraints given in Eqs. (11) to (16). The infeasible region for the operation of the pumping system will be denoted by $I_R$. To ensure that the pumping system is always viable to operate, we introduce a simple penalty function as follows:

$$\begin{aligned} V_{p} \left( h_{req}^{t}, \; q_{req}^{t} \right) = {\left\{ \begin{array}{ll} 0 &{} ,\text {if} \left( h_{req}^{t}, \; q_{req}^{t} \right) \notin I_{R}\\ L &{} ,\text {if} \left( h_{req}^{t}, \; q_{req}^{t} \right) \in I_{R} \end{array}\right. } \end{aligned}$$

(17)

where $V_{p}$ is the penalty value, and L is an arbitrary large number (given in Appendix A). Later, the penalty value will be incorporated into the emission term, $E_{T}$. If an injection strategy requires an infeasible operation of the pumping system, the corresponding objective function value will deteriorate, and consequently will not be selected by the optimization algorithm.

Fig. 8

Infeasible region for the pumping system’s operation

2.1.4 Calculating total power consumption for the water injection process

After the optimal setting for the pumping system has been decided, the fourth step in the emission term calculation is to estimate power demand of the pumping and water treatment systems. The power consumption of these two systems is directly controlled by the injection strategy. Injection at a higher rate typically requires more power to run the pumping system and treat the injected water.

The pumping system’s power consumption is determined using Eq. (9), while the power demand of the water treatment system, $P_{wt}^{t}$, is estimated as:

$$\begin{aligned} P_{wt}^{t} = E_{wt} \cdot \left( \sum _{i = 1}^{M_{i}} q_{wi, i}^{t} \right) \end{aligned}$$

(18)

where $E_{wt}$ is the energy used for treating a unit volume of injected water. In this study we use the value provided in Appendix A. The injector’s water rate, $q_{wi, i}^{t}$, is retrieved from the reservoir simulation results. The total power consumption, $P_{tot}^{t}$, for operating both the pumping and water treatment systems is then given as:

$$\begin{aligned} P_{tot}^{t} = P_{ps}^{t} + P_{wt}^{t} \end{aligned}$$

(19)

2.1.5 Configuring power generation system

The fifth step in the emission term calculation is to configure power generation system that produces all the electric power needed to operate both the pumping and water treatment systems. The power generation system is made up of several gas turbines. The gas turbines convert thermal energy of a combusted fuel, in particular the natural gas, into mechanical work. Generators then turn the mechanical energy into electric energy.

We assume that (i) all the installed gas turbines have identical designs, specifications, and properties, (ii) the electrical load for the water injection process is split evenly between the running turbines, and (iii) the gas turbine’s operation can be started or stopped immediately. With these assumptions, the number of gas turbines $M_{gt}^{t}$ running at time t is determined as:

$$M_{{gt}}^{t} = \left\lceil {\frac{{P_{{tot}}^{t} }}{{P_{{gt,fl}} }}} \right\rceil$$

(20)

where $P_{gt, fl}$ is the power output of a gas turbine at full-load operation, and the bracket indicates a ceiling function. The value for $P_{gt, fl}$ used in this study is provided in Appendix A.

As the electricity demand frequently varies, the gas turbines often run at part-load conditions, at which conditions they generate less power than their maximum capability [66]. The power output of a gas turbine at part-load operation, $P_{gt, pl}^{t}$, is regulated as:

$$\begin{aligned} P_{gt, pl}^{t} = \frac{P_{tot}^{t}}{M_{gt}^{t}} \end{aligned}$$

(21)

The gas turbines’ performance degrades when they run at part-load conditions, so efficiency of the gas turbines worsens as they are requested to deliver a lower power output [67,68,69]. We embed this gas turbines’ characteristic for the emission term calculation. In this study we use a relationship depicted in Fig. 9 to estimate the gas turbines’ efficiency at part-load operation, $\eta _{gt, pl}^{t}$. Calculation for $\eta _{gt, pl}^{t}$ is detailed in Appendix C.

Fig. 9

Gas turbine performance curve. Adopted from [68]

There are potential strategies for improving $\eta _{gt, pl}^{t}$ and hence reducing the amount of CO₂ emissions. Installing several gas turbines of different sizes could enable the gas turbines to operate at higher power outputs and thus have higher part-load efficiencies [67]. Also installing a bottoming cycle for the power generation system, where the bottoming cycle will utilize the gas turbines’ heat waste, could improve the net efficiency of the power generation system up to 50% [67, 70]. As we consider the effect of emission cost on producing fields where larger changes to the infrastructure are often unfeasible, e.g., due to space or weight limitations on platform, such potential strategies are not studied in this work.

2.1.6 Estimating total mass of CO₂ emissions

After configuring the power generation system, the next step in the emission term calculation is to estimate total mass of CO₂ emissions for a particular set of well-controls. For that, we first estimate mass flow rate of fuel combusted in the gas turbines, $\dot{m}_{f}^{t}$, as:

$$\begin{aligned} \dot{m}_{f}^{t} = \frac{M_{gt}^{t} \cdot P_{gt, pl}^{t}}{S_{e} \cdot \eta _{gt, pl}^{t}} \end{aligned}$$

(22)

Thereafter, mass flow rate of CO₂ emitted from the gas turbines, $\dot{m}_{CO_{2}}^{t}$, is approximated with the following linear function:

$$\begin{aligned} \dot{m}_{CO_{2}}^{t} = S_{CO_{2}} \cdot \dot{m}_{f}^{t} \end{aligned}$$

(23)

Here $S_{e}$ and $S_{CO_{2}}$ are the specific energy content and CO₂ emissions of the fuel, respectively. These two quantities reflect the amount of thermal energy released and CO₂ gas emitted, respectively, from the combustion of a unit mass of the fuel. The values for $S_{e}$ and $S_{CO_{2}}$ vary for different types of fuel. For natural gas, representative values used in this study are given in Appendix A. The total mass of CO₂ emissions at the end of the field lifetime, $m_{CO_{2}}^{t_{end}}$, is eventually computed as follows:

$$\begin{aligned} m_{CO_{2}}^{t_{end}} = \int _{0}^{t_{end}} \dot{m}_{CO_{2}}^{t} \; dt \end{aligned}$$

(24)

2.1.7 Calculating emission term, $E_{T}$

After the total mass of CO₂ emissions has been estimated, the emission term, $E_{T}$, is finally computed as follows:

$$\begin{aligned} E_{T} = r_{CO_{2}} \cdot m_{CO_{2}}^{t_{end}} + V_{p} \end{aligned}$$

(25)

The first right-hand side term in the above equation represents the CO₂ tax that operating companies are subject to. Here, $r_{CO_{2}}$ indicates the applied CO₂ tax rate. The last term, $V_p$, is the penalty value from Eq. (17) ensuring the injection is feasible.

For the well-control optimization discussed in Sect. 2, $r_{CO_{2}}$ can be viewed as a weighting factor that determines the level of importance between increasing the traditional net present value $NPV_{t}$, dominated by the hydrocarbon production, or reducing CO₂ emissions. Specifying a higher $r_{CO_{2}}$ will emphasize lowering CO₂ emissions compared to increasing the $NPV_{t}$, and vice versa. In this study, we compare the solutions of three optimization scenarios with different values for $r_{CO_{2}}$, i.e., 0.0, 0.0525, and 0.525 USD/kg CO₂. The middle value of $r_{CO_{2}} = 0.0525$ USD/kg CO₂ reflects the current tax rate for O&G operators in Norway, i.e., around 500 NOK/ton CO₂ [4, 71].

2.2 Calculation of the traditional net present value, $NPV_{t}$

The traditional $NPV_{t}$ in Eq. (1) is calculated as a weighted sum of cumulative oil production, $N_{p,f}^{t_{end}}$, cumulative water injection, $W_{i,f}^{t_{end}}$, and cumulative fuel combusted in the gas turbines, $m_{f}^{t_{end}}$, at the end of the field lifetime:

$$\begin{aligned} NPV_t(\vec {u}) = P_o \cdot N_{p,f}^{t_{end}}(\vec {u}) - C_{wi} \cdot W_{i,f}^{t_{end}}(\vec {u}) - C_{f} \cdot S_{e} \cdot m_{f}^{t_{end}}(\vec {u}) \end{aligned}$$

(26)

The weighting factors comprise oil price, $P_o$, operating cost for treating the injected water, $C_{wi}$, and fuel cost, $C_{f}$. Values for these weighting factors are provided in Appendix A. The total fuel consumption for running the gas turbines, $m_{f}^{t_{end}}$, is obtained by taking an integral of $\dot{m}_{f}^{t}$ in Eq. (22) over the field lifetime. As discussed in Sect. 2.1, $\dot{m}_{f}^{t}$ reflects the energy use for both the pumping and water treatment operations. Note that the $NPV_{t}$ calculation used in this study is without a discount factor, however, the inclusion of a discount factor can easily be made without altering the overall methodology of this paper.

2.3 Software implementation

This study is conducted using the FieldOpt open-source optimization framework [72]. FieldOpt is supported by a modular architecture that enables quick prototyping and testing of optimization methodologies for field development problems [73]. To date, the framework facilitates optimization of well placement, completion design, and production schedule. In this study, the computation of CO₂ emission term is introduced as a new feature within the objective function computation in FieldOpt’s optimization module.

An industry standard reservoir simulator is used for simulations. When performing the simulations, the timestep size is kept below ten days to lessen the numerical dispersion effects on the objective function value. Besides the well-control search space given in Eq. (1), additional restrictions are imposed by the simulator on the well-controls during simulation. These extra constraints are (i) the producers’ maximum liquid rate which is dictated by the topside fluid processing capacity and (ii) the injectors’ maximum BHP to represent the formation fracture pressure. If the producer liquid rate reaches its maximum value, the producer will switch to liquid rate mode. In contrast, the injector control mode will switch to BHP mode if the injector BHP reaches its maximum value.

2.4 Optimization algorithm

As previously mentioned, three optimization problems using different $r_{CO_{2}}$ values are solved and compared in this study. Applying different tax rates implies that these problems have similar but different objective functions depending on the relative influence of the CO₂ emission term. In this study, we employ an extended PSO algorithm that solves concurrently for the three problems using separate swarms but with the ability to share underlying simulation results to compute corresponding objective functions. This new algorithm and its advantages will be described in detail in an upcoming paper. Parameters for the extended PSO algorithm are given in Appendix D. Twelve combinations of these parameters are examined, and the one providing the best performance is presented here. Finally, because PSO is fundamentally a stochastic optimization technique, multiple runs are made to ensure consistency.

3 Reservoir models

The presented methodology is tested on two numerical reservoir simulation models: a 5-spot model and a cropped version of the Olympus model. This section provides descriptions on these two reservoir simulation models.

3.1 5-spot model

The 5-spot model is a synthetic 2D reservoir model with $60 \times 60$ grid blocks. The reservoir top extends horizontally at a depth of 1700 m below the seafloor, covering an area of $1.44 \times 1.44\hbox { km}^{2}$. The initial reservoir pressure at the datum depth (specified at the reservoir top in this model) is $1.7 \times 10^{7}$ Pa. The reservoir fluid properties are modeled using black oil correlations. No free gas is initially present in the reservoir model, and the oil contains a very small amount of dissolved gas. The oil has a very low bubble point pressure and remains at undersaturated conditions during simulations (dead oil). Thus only two immiscible phases are present throughout the simulations.

The 5-spot reservoir model has substantial heterogeneity in terms of porosity and permeability. These rock properties are cropped from a horizontal cross-section of the SPE 10 model [74], specifically Layer #21. As shown in Fig. 10, a highly permeable sand body extends diagonally from the northwest to southeast part of the reservoir model. To allow for higher injection rates, and thus more representative power consumption for an offshore platform, we scale the original permeability retrieved from the SPE 10 model by a factor of ten, resulting in a permeability variation between 10 mD and 10 D. With uniform initial water saturation of 0.1 and clean-sand thickness of 100 m, the reservoir model has original oil-in-place of $2.167 \times 10^{7}\hbox { m}^{3}$. Supplementary fluid and rock properties are available in Appendix E.

Fig. 10

Permeability distribution in the 5-spot model

There are five wells in the model: one producer located at the center and four injectors placed near the corners (see Fig. 10). The producer is drilled horizontally, penetrating three grid blocks with a total horizontal length of 72 m. In contrast, all the injectors have a vertical well path with an identical true vertical depth from well-head to bottom-hole of 1700 m. The producer and injectors are primarily controlled with the BHP and water rate mode, respectively. The internal simulation constraints ensure that the producer’s liquid rate and injectors’ BHPs do not exceed $5.787 \times 10^{-1} \hbox { m}^{3}/\hbox {s}$ and $3.5 \times 10^{7}$ Pa, respectively. The production period is defined to last for 15 years. This model is computationally light; one reservoir simulation needs approximately 4 s to finish on a single processor on a standard workstation.

3.2 Cropped Olympus model

The Olympus model is a synthetic 3D reservoir model that is built for benchmarking studies of optimization methods applied for field development [75]. The reservoir consists of two zones (the upper and lower zones) that are separated by an impermeable shale layer. The Olympus model has 50 realizations with different reservoir properties, such as facies, porosity, permeability, net-to-gross ratio, initial water saturation, and transmissibility across the faults [75]. As this study is not about optimization under geological uncertainty, we only employ one of the realizations, namely Realization #1. This model realization is also cropped (see Fig. 11) to reduce the computational cost for optimization. Even though only considering the upper reservoir zone, the cropped model still possesses complex geological features, such as faults and channelized sands. The channelized sands introduce potential high-connectivity between wells, and thus possibly early water breakthrough. These challenges are particularly relevant when designing a waterflooding strategy.

Fig. 11

Distribution of horizontal permeability [mD] in the cropped Olympus model (Layer #1). The base figure is created using ResInsight [76]

The cropped Olympus model has 39155 active grid blocks, roughly 20% of the total number of active cells in the Olympus model. These active grid blocks are divided into seven layers representing the upper reservoir zone. The oil-water contact lies at 2092 m below the seafloor, and the initial reservoir pressure at the contact depth is $2.05 \times 10^{7}$ Pa. In terms of reservoir fluids, only oil and water exist in the reservoir model. The behaviors of both fluids are represented using a black oil model, again assuming the oil is undersaturated all the time. The presence of channel sand bodies is evident from the permeability distribution shown in Fig. 11 as well as from the distributions of porosity and initial water saturation provided in Appendix E. As in the 5-spot model, the original horizontal and vertical permeabilities are multiplied by a factor of ten. Moreover, the original grid block height is tripled, resulting in gross thickness of about 60 m for the cropped Olympus model. These modifications are intended to enhance water transmissibility between the grid blocks, allowing us to inject at higher rates and thus operate at typical power consumption values for an offshore platform. The cropped Olympus model has original oil-in-place of $5.215 \times 10^{7}$ m$^{3}$.

Six new vertical wells comprising two producers and four injectors are defined for the cropped Olympus model. The well-placement illustrated in Fig. 11 is predefined based on engineering judgment, considering the surrounding reservoir properties, connectivity with the adjacent wells, and well spacing. Each well is drilled penetrating all the seven layers of the reservoir model. True vertical depths of the injectors’ bottom-hole are 2050.64, 2050.78, 2047.49, and 2062.89 m, for Injector I1 to I4, respectively. Like the 5-spot model, the producers are primarily controlled by BHP, while the injectors are set to water rate control. Simulation-based constraints consist of a maximum liquid rate of $5.787 \times 10^{-1}\hbox { m}^{3}/\hbox {s}$ for the producers and a maximum BHP of $4 \times 10^{7}$ Pa for the injectors. Simulation time frame is set to 15 years. The wall-clock time of one simulation is roughly 12 min on a single processor.

4 Case study #1: optimization of 25 well-control variables on the 5-spot model

4.1 Description of optimization problems

In the first case study, we conduct numerical experiments of the well-control optimization described in Sect. 2 using the 5-spot reservoir simulation model. The well-control variables encompass all the wells defined in the reservoir model, i.e., one producer (P1) and four injectors (I1 to I4). The producer BHP target, $\bar{p}_{wf, p}^{\;c}$, and the injector water rate target, $\bar{q}_{wi, i}^{\;c}$, can be altered every three years, giving five control periods throughout the simulated field lifetime. Thus, this case study involves 25 variables. The search for optimal $\bar{p}_{wf, p}^{\;c}$ is limited within a range of $0.8 \cdot 10^{7}$ to $1.8 \times 10^{7}$ Pa, whereas the search space for $\bar{q}_{wi, i}^{\;c}$ is bounded between 0 and $2.315 \cdot 10^{-1}$ m$^{3}$/s. In this case study, three optimization scenarios are solved using different CO₂ tax rates, $r_{CO_{2}}$. The different scenarios are summarized in Table 1 (see Scenario 1 - 3). The main goals of this case study are to (i) investigate the effects of raising CO₂ tax rate on the optimal solution and (ii) explore the relation between the tax rate and emissions.

Table 1 Summary of all optimization scenarios

4.2 Assessment of optimization performance

Before comparing the solutions of the three optimization scenarios, we will first evaluate the performance of the optimization algorithm in this subsection. Since we employ a stochastic search technique, the optimization run is repeated five times. For each scenario, we pick the best run which provides the highest objective function value, NPV. Figure 12 illustrates the evolution of NPV for the three scenarios. As shown in the figure, the NPV graphs show relatively small increments from the 100^th iteration onward which indicates the solutions may have converged, possibly to local optima. Moreover, the NPV graphs are very similar in all five runs for Scenario 1 and 2. In contrast, for Scenario 3, the NPV graphs have larger variations between the runs. This indicates that Scenario 3 has perhaps a less smooth response surface than the other two scenarios. A single optimization run which involves 60000 reservoir simulations (3 optimization scenarios $\times$ 50 particles $\times$ 400 iterations) needs approximately 13 hours to finish using a 9-core workstation.

Fig. 12

Progression of objective function value, NPV, for the three different tax rate scenarios in case study #1

The optimal BHPs and injection rates for the three scenarios are presented in Fig. 13. In this figure we observe that the optimal well-control settings lie within the specified search space. For Injector I1 some injection rate targets are not achieved due to the enforcement of the BHP limit by the simulator. In Fig. 14, a sensitivity analysis is carried out on these optimal solutions with respect to the variation of CO₂ tax rate, $r_{CO_{2}}$. For instance, the solid red line in Fig. 14 indicates how the NPV changes if we impose a different $r_{CO_{2}}$ on the optimal solution for Scenario 1. From the figure, we notice that, at $r_{CO_{2}} = 0.0$ USD/kg CO₂, the optimal solution for Scenario 1 offers a higher NPV than the solutions for the other two scenarios. Likewise, the optimal solutions for Scenario 2 and 3 are better than the rest when $r_{CO_{2}}$ equals to 0.0525 and 0.525 USD/kg CO₂, respectively. Also note that the slope of the curves decreases with increasing CO₂ tax rate, as expected. Such type of plots could be instrumental for operational management when the CO₂ tax rate is uncertain.

Fig. 13

Optimal well BHPs and injection rates for case study #1. Top-to-bottom: Producer P1, Injector I1, Injector I2, Injector I3, and Injector I4

Fig. 14

Sensitivity of NPV versus CO₂ tax rate $r_{CO_2}$ for the optimal solutions in case study #1

4.3 Comparison of optimal solutions

Table 2 Metrics of the optimal solutions for the 5-spot case

Table 2 encapsulates main terms for comparing the optimal solutions for the three scenarios. These terms are NPV, $NPV_{t}$, cumulative oil produced, $N_{p, f}^{t_{end}}$, cumulative water injected, $W_{i, f}^{t_{end}}$, total fuel combusted, $m_{f}^{t_{end}}$, and total CO₂ gas emitted, $m_{CO_{2}}^{t_{end}}$, at the end of the field lifetime. We choose the solution for Scenario 1 as the baseline for comparison because it provides a higher $NPV_{t}$ while releasing more CO₂ than the solutions for the other two scenarios. Setting $r_{CO_{2}}$ to 0.0 USD/kg CO₂ makes Scenario 1 equivalent to traditional formulations that maximize $NPV_{t}$ only. As reflected in Table 2, the total volume of water injected is diminished by 4.2% and 37.8% in the solutions for Scenario 2 and 3, respectively. By cutting the total injection volume, the fuel consumption and CO₂ emissions are lowered, though this to a certain extent also lessens the oil production and consequently the $NPV_{t}$. Nevertheless, referring to Table 2, we observe that the reductions of oil production and $NPV_{t}$ are not as significant as the reductions of fuel consumption and CO₂ emissions. The optimal solution for Scenario 2, for example, emits approximately 6% less CO₂ while pruning the oil production and $NPV_{t}$ by only 0.2% and 0.1%, respectively. We also notice that the percentage of CO₂ emission reduction has roughly the same magnitude as the percentage of injection volume reduction. Furthermore, if applying a higher $r_{CO_{2}}$, the emissions are lowered like the solution for Scenario 3. From both economic and environmental perspectives (around 1% reduction in $NPV_{t}$ and 44% reduction in CO₂ emissions), the optimal well-control setting obtained in Scenario 3 is a very attractive option.

In this study, the calculation of $NPV_{t}$ in Eq. (26) leaves out the discount factor. If included, the discount factor is used for discounting the value of future cash flow to its present value. Since the discount factor grows over time, the cash flow in the near future is more valuable than the later one. Therefore, the inclusion of discount factor in the $NPV_{t}$ calculation will produce optimal solutions that might have higher production rates in the beginning of the field lifetime in order to boost the early cash flows. Even though the inclusion of discount factor will alter the optimal solutions, we could still derive the same conclusion, i.e., that the reductions of oil production and $NPV_{t}$ are not as significant as the reductions of fuel consumption and CO₂ emissions, because the inclusion of discount factor will mainly accelerate the field production and/or injection. We have also assumed constant oil price, $P_{o}$, operating cost of the injected water, $C_{wi}$, and fuel cost, $C_{f}$, in the $NPV_{t}$ calculation. Changes on these parameters will also change the optimal solution. For instance if the oil price, $P_{o}$, is specified higher than the value listed in Appendix A, the optimal solutions found are likely less energy-efficient because the revenue component in Eq. (26), i.e., $P_{o} \cdot N_{p,f}^{t_{end}}(\vec {u})$, will have dominance over the emission component, $E_{T}$, in the objective function given in Eq. (1).

Figure 15a portrays the total power requirement, $P_{tot}^{t}$, for running the water injection operation. As shown in the figure, the optimal injection strategy for Scenario 3 demands less power than the other two scenarios. Overall, the total power demand in Scenario 3 is, most of the time, below the maximum power output of a single gas turbine at full-load condition, $P_{gt, fl}$. This means that for almost the entire life span of the field (see Fig. 15b) only one gas turbine is used, and this gas turbine produces electrical power relatively close to its maximum capability. Consequently, with the correlation shown in Fig. 9, the gas turbine in Scenario 3 operates at higher efficiencies compared to the gas turbines in the other two injection strategies (see Fig. 15c). This is reflected by the different trends for oil-production $N_{p, f}^{t_{end}}$ and the traditional net-present-value $NPV_{t}$ versus tax rate (see Table 2); there is a smaller reduction in $NPV_{t}$ than $N_{p, f}^{t_{end}}$ due to a more efficient production of the oil. This production efficiency comes from two different sources; one is due to the lowered amount of water injection, the other is more efficient operations of the gas turbines. This shows the importance of our introduced methodology which embeds representative gas turbine characteristics within the optimization loop. Our introduced coupled model is required to obtain more energy-efficient gas turbine operations under higher tax regimes.

Fig. 15

Comparison on various aspects of the optimal solutions for the three tax rate scenarios

The flow rates of water provided by the pumping system, $q_{ps}^{t}$, are presented in Fig. 15d. This figure also gives an indication of the total rates of water being injected into the reservoir, $q_{req}^{t}$. We can see that less water is pressurized by the pumping system in the optimal injection scheme for Scenario 3. Figure 15e outlines the number of pumps running in parallel, $M_{pp}^{t}$. With lower injection rates, the injection scheme for Scenario 3 often runs fewer pumps in parallel compared to the injection schemes for the other two scenarios. In addition, all the optimal injection schemes operate only one pump in series, $M_{ps}^{t} = 1$, throughout the field lifespan (not exhibited in Fig. 15). This event is caused by the BHP limit enforcement for the injectors which maintains a low or not too high head requirement, $h_{req}^{t}$. If one embeds a higher BHP limit for the injectors or installs smaller injection pumps, the injection schemes might operate more than one pump in series.

Looking at Eqs. (7), (8), and (9), the electrical power needed for running the pumps in the pumping system, $P_{ps}^{t}$, is essentially a function of $q_{ps}^{t}$, $M_{pp}^{t}$, and $M_{ps}^{t}$. Figure 15f illustrates the profile of $P_{ps}^{t}$ over time for the scenarios’ optimal injection schemes. Due to the lower rate $q_{ps}^{t}$, the optimal injection strategy for Scenario 3 requires less power for pumping than the other two strategies. In addition, if we take a look at Fig. 13, particularly at the second and last control periods (year 3 - 6 and 12 - 15), we notice that the rates of Injector I1 in Scenario 3 are below the other two scenarios. Because Injector I1 is located in the less permeable area (see Fig. 10), decreasing the injection rates for this well could considerably lower the injection pressure and thus affect the required head, $h_{req}^{t}$. This then might influence not only the pumping system configuration ($q_{ps}^{t}$, $M_{pp}^{t}$, and $M_{ps}^{t}$) but also its power consumption, $P_{ps}^{t}$.

By combining Eqs. (21) and (22) into Eq. (23), the mass rate of CO₂ emissions, $\dot{m}_{CO_{2}}^{t}$, is in principle governed by the total power consumption, $P_{tot}^{t}$, and the gas turbine part-load efficiency, $\eta _{gt, pl}^{t}$. With $P_{tot}^{t}$ and $\eta _{gt, pl}^{t}$ shown in Figs. 15a and c, respectively, the plot for $\dot{m}_{CO_{2}}^{t}$ is given in Fig. 15g. Herein, we define the term emission intensity as the amount of CO₂ gas emitted for producing a unit volume of oil. This term can be used as an indicator of how energy-efficient the oil recovery process is. The emission intensity is calculated by simply dividing $\dot{m}_{CO_{2}}^{t}$ with the field oil production rate, $q_{o, f}^{t}$. Figure 15h shows the emission intensity profile over the field’s lifetime. This figure denotes the emission intensity for Scenario 3 being more or less half of the emission intensity for the other two scenarios. Moreover, we notice that the emission intensity has an overall ascending trend for all optimal scenarios. This trend is consistent with results from [4].

In Fig. 15i, we plot the emission intensity against the field water cut for all scenarios. The figure shows the curves follow nearly the same path with different endpoints (highest in Scenario 1 and lowest in Scenario 3). One could interpret these endpoints as the "environmental cost" for producing the "last" barrels of oil from the field. In agreement with studies conducted by [11, 20], Fig. 15i indicates that emission intensity rises rapidly with increasing water cut, especially when the water cut is above 90%. This behaviour could advise when emission mitigation efforts should be prioritized.

4.4 The influences of CO₂ tax rate

CO₂ tax rate, $r_{CO_{2}}$, plays an important role in the well-control optimization process. As mentioned, from the objective function formulation in Eq. (1), $r_{CO_{2}}$ can be regarded as a weighting factor that helps drive the optimization towards a less-profitable-but-more-sustainable solution. To investigate this proposition further, we refine the case study described in Sect. 4.1 to include eleven tax rates instead of three, which are uniformly sampled between 0.0 and 0.525 USD/kg CO₂.

Figure 16 shows the eleven optimization results (some of them are overlapping, e.g., the results for $r_{CO_{2}} = 0.2625$ to 0.525 USD/kg $\hbox {CO}_{2}$). Each point in this figure represents the total oil production, $N_{p, f}^{t_{end}}$, and the CO₂ emissions, $m_{CO_{2}}^{t_{end}}$, associated with a given scenario over the defined range of $r_{CO_{2}}$ (represented by the tax rate color bar). The figure shows a non-linear relationship between the total oil production and CO₂ emissions that is monotonically decreasing. As expected, this implies that there is a trade-off between these two quantities. In other words, the efforts to mitigate the CO₂ emissions will also reduce the oil production. We can also see in the figure that the curve tempers, especially when the optimal injection strategy becomes cleaner or greener. The tempering section indicates a diminishing return on CO₂ emission reduction when increasing tax rate. Further, while the use of a higher $r_{CO_{2}}$ generally yields a more energy-efficient injection scheme, we notice that some increments on the $r_{CO_{2}}$ do not alter the optimal solution significantly and hence do not provide a meaningful reduction on the CO₂ emissions (e.g., when doubling the $r_{CO_{2}}$ from 0.2625 to 0.525 USD/kg CO₂). We note that this relationship is case-dependent and might be influenced by particular reservoir characteristics, well-control configuration, the variable search space, etc.

Fig. 16

The influences of CO₂ tax rate on the emissions, $m_{CO_{2}}^{t_{end}}$, and oil production, $N_{p, f}^{t_{end}}$

In Fig. 17 the CO₂ emissions are plotted against NPV for different CO₂ tax rates. The NPV indicates the operator’s financial gain for a given $r_{CO_{2}}$ and the corresponding optimal injection scheme. The figure shows that some $r_{CO_{2}}$ escalations are not effective if the purpose of the tax is to lower emissions. For instance, raising the $r_{CO_{2}}$ from 0.2625 to 0.525 USD/kg CO₂ only deteriorates operator’s profit without providing a meaningful reduction in CO₂ emissions.

Fig. 17

The influences of CO₂ tax rate on the emissions, $m_{CO_{2}}^{t_{end}}$, and net-present-value, NPV

5 Case study #2: optimization of 30 well-control variables on the cropped Olympus model

Table 3 Metrics of the optimal solutions for the cropped Olympus case

5.1 Description of optimization problems

In contrast to the simple 2D model considered in the previous section, the second case study employs the more realistic cropped Olympus model. The iterative optimization process intends to maximize the objective function expressed in Eq. (1) by adjusting the BHPs or injection rates for the six wells defined in the reservoir simulation model. Similar to the earlier case study, we split the field lifespan into five uniform control periods, which gives 30 well-control variables for this problem. Search space for these variables is identical to the one reported in Sect. 4.1, except for the upper limit of BHP target, $\bar{p}_{wf, p}^{\;c}$, which is now set to $2.1 \cdot 10^{7}$ Pa. Again, three optimization scenarios are evaluated with different CO₂ tax rates (see Scenario 4 - 6 in Table 1). The primary goal of this case study is to examine the presented methodology on a more realistic reservoir model. Additionally, this case enables us to verify observations and interpretations from the earlier case study.

5.2 Comparison of optimal solutions

Evaluation of optimization performance is carried out as in Sect. 4.2. Due to the inclusion of a relatively complex reservoir model, performing optimization on this case study incurs substantial computational cost. Even with a 35-core machine, one optimization run entails around 16 days to finish. For this reason, the optimization scenarios have only been solved twice. Besides, due to this high computational cost, figures like Figs. 16 and 17 have not been produced for case study #2.

Several aspects of the optimal solutions are summarized in Table 3. The solution for Scenario 4 is used as reference for comparison. Similar to the previous case study, we observe that the injection strategy which consumes less fuel and emits less CO₂ also has lower oil production and $NPV_{t}$. The reductions of oil production and $NPV_{t}$ are, however, significantly smaller than the reductions of fuel consumption and CO₂ emissions. The table also indicates that (i) the CO₂ emissions are correlated with the volume of water injected, and (ii) the percentage of emission reduction is more or less the same as the percentage of injection volume reduction. As in case study #1, the equipment (pumps and gas turbines) in Scenario 6 runs at higher efficiencies than in the other two scenarios in consequence of lowering the total injection rates. However, the increased efficiency of the equipment has a smaller contribution to the emission reductions than the reduced volume of injected water. In other words, the subsurface drainage offers larger opportunities for efficiency improvements than the topside facilities.

Further, while the use of a higher CO₂ tax rate, $r_{CO_{2}}$, in the well-control optimization often promotes a more energy-efficient solution, an increment of $r_{CO_{2}}$ from 0 to 0.0525 USD/kg CO₂ in case study #2 does not substantially change the optimal solution and therefore does not reduce the emissions, oil production, and $NPV_{t}$ much. The current tax rate of 0.0525 USD/kg CO₂ is hence deemed not effective to reduce emissions for this particular case study. This is different to what we observe in case study #1 (see Table 2), where raising $r_{CO_{2}}$ from 0 to 0.0525 USD/kg CO₂ results in a solution with $5.9\%$ reduced emissions. This does not mean that our presented methodology only works in case study #1, but this rather strengthens our earlier statement in Sect. 4.4, i.e., the effect of changing $r_{CO_{2}}$ is dependent on the case being evaluated. Referring to the reductions of production, $NPV_{t}$, and emissions in Table 3, operators could consider implementing the optimal well-control setting for Scenario 6. We observe that producing the "last" barrels of oil (to increase the production by about 0.6%) is a very energy-intensive effort which yields an increase in CO₂ emissions of roughly 17%. This observation is also valid for the preceding case study (see Table 2). The optimal injection strategies for the three scenarios in case study #2 are given in Appendix F.

6 Conclusions

In this paper, we focus presenting a methodology for coupling models of surface facilities and subsurface reservoir simulation to enable the inclusion of CO₂ tax into optimization of field operations. This work therefore employs an objective function consisting of two components, i.e., the traditional net-present-value, $NPV_{t}$, accounting for the earnings from hydrocarbon sales and the operating costs, and an additional emission term $E_T$ accounting for the tax on the CO₂ gas emitted. The basis of the developed methodology is an optimization of waterflooding in a reservoir simulation model. The methodology is focused on optimizing well-controls (well rates and/or bottom-hole pressures). When increasing the CO₂ tax rate, the optimization procedure will design water injection strategies that emit less CO₂ while sustaining the field production and economics.

To estimate the amount of CO₂ emissions for a given set of well-controls, we present a calculation scheme that uses reservoir simulation results as its inputs. The calculation scheme integrates reservoir, surface network, and topside facility models and enables the evaluation of energy use for pumping and water treatment. Furthermore, the calculation scheme (i) applies typical performance characteristics for the pumps and gas turbines, and (ii) involves a step for optimizing the pumping system configuration.

The methodology has been tested using two heterogeneous reservoir models in a couple of case studies. For each case study, several optimization scenarios are solved using different CO₂ tax rates. Comparisons of the optimal solutions lead to the following conclusions:

• While topside equipment efficiency improves with increased CO₂ tax, the main contribution to reduced emissions is associated to lower water injection, i.e., a more energy-efficient drainage of the subsurface reservoir.

• Efforts to diminish CO₂ emissions will lower both oil production and traditional $NPV_{t}$. However, reductions in oil produced and $NPV_{t}$ are small compared to the corresponding reduction in emissions, as optimization of our introduced coupled model obtains more energy-efficient operations under higher tax regimes.

• A non-linear relationship between CO₂ emissions and oil production (see Fig. 16) indicates a diminishing decrease in emissions with decreasing oil production. This reflects reduced opportunities for emission reductions by changes in the drainage strategy. Consequently, the $NPV_{t}$ will stabilize while the $E_t$ will grow linearly with tax rate, thus lead to lower NPV without any associated reduction in emissions (see Fig. 17).

• In any optimal solution, emission intensity generally increases throughout the field lifetime (see Fig. 15h). The emission intensity also rises rapidly with the growth of water cut, especially when the water cut is above 90% (see Fig. 15i).

In early 2021, the Norwegian government communicated an upcoming tax increase for CO₂ emissions from the NCS production [77, 78]. Our work herein is relevant to assess the impact of such policy changes on a project’s CO₂ footprint, oil production, and operator profit for producing fields. Typically, government policies aim at retaining operators’ interests in exploiting hydrocarbon resources in a region, while at the same time promoting significant CO₂ emission reductions. Given such policy targets, from the presented case studies we infer an opportunity to reduce CO₂ emissions while having relatively small reductions in oil production and the traditional $NPV_{t}$. The non-linear relationship between tax rate, production profit, and emission reduction discussed in this paper implies that CO₂ tax rates can be set to levels that effectively lower emissions with limited reduction in production. As a lower NPV is expected to hurt overall production, a small production reduction with a significant emission reduction can be obtained by relocating taxes from traditional taxes to CO₂ taxes, thus maintaining NPV and production at lower emissions. In the context of reducing CO₂ emissions and planing for future CO₂ tax rates, both O&G operators and government bodies could consider performing evaluations similar to those presented in this paper. An in-depth discussion on policy implications is beyond the scope of this paper and left out for future studies.

Appendices

Appendix A: Constants

See Table 4.

Table 4 Summary of all constants

Appendix B. Pump performance characteristics

The pumps’ head, $h_{pm}^{t}$, and hydraulic efficiency, $\eta _{pm}^{t}$, are calculated as follows:

$$\begin{aligned} \begin{aligned} h_{pm}^{t}&= a_{0} + a_{1} \cdot \left( \frac{ q_{pm}^{t} - \bar{q} }{\sigma _{q}} \right) \\&\quad + a_{2} \cdot \left( \frac{\omega _{pm} \cdot q_{pm}^{t} - \bar{\omega _{q}}}{\sigma _{\omega q}} \right) + a_{3} \cdot \left( \frac{ \left( \omega _{pm} \right) ^2 - \bar{\omega _{2}}}{\sigma _{\omega 2}} \right) \\&\quad + a_{4} \cdot \left( \frac{ \left( \omega _{pm} \right) ^3 - \bar{\omega _{3}}}{\sigma _{\omega 3}} \right) + a_{5} \cdot \left( \frac{ \left( q_{pm}^{t} \right) ^3 - \bar{q_{3}} }{\sigma _{q 3}} \right) \end{aligned} \end{aligned}$$

(27)

$$\begin{aligned} \begin{aligned} \eta _{pm}^{t}&= b_{0} + b_{1} \cdot q_{pm}^{t} + b_{2} \cdot \left( q_{pm}^{t} \right) ^2 \\&\quad + b_{3} \cdot \omega _{pm} \cdot \left( q_{pm}^{t} \right) ^2 + b_{4} \cdot \left( \omega _{pm} \right) ^2 \cdot q_{pm}^{t} \end{aligned} \end{aligned}$$

(28)

where $q_{pm}^{t}$ and $\omega _{pm}$ are the pumps’ flow rate and speed, respectively. The values for $\omega _{pm}$ and other constants in Eqs. (27) and (28) are given in Table 5.

Table 5 Summary of all constants for the pumps’ head and hydraulic efficiency calculations.

Appendix C. Gas turbine performance characteristic

The gas turbines’ efficiency at part-load operation, $\eta _{gt, pl}^{t}$, is calculated as follows:

$$\begin{aligned} \eta _{gt, pl}^{t} = \eta _{gt, fl} \cdot \eta _{gt, r}^{t} \end{aligned}$$

(29)

where $\eta _{gt, r}^{t}$ is defined as follows:

$$\begin{aligned} \begin{aligned} \eta _{gt, r}^{t} =&\; c_{0} + c_{1} \cdot \Bigg ( \frac{P_{gt, pl}^{t}}{P_{gt, fl}} \Bigg ) + c_{2} \cdot \Bigg ( \frac{P_{gt, pl}^{t}}{P_{gt, fl}} \Bigg )^2 \\&+ c_{3} \cdot \Bigg ( \frac{P_{gt, pl}^{t}}{P_{gt, fl}} \Bigg )^3 + c_{4} \cdot \Bigg ( \frac{P_{gt, pl}^{t}}{P_{gt, fl}} \Bigg )^4 + c_{5} \cdot \Bigg ( \frac{P_{gt, pl}^{t}}{P_{gt, fl}} \Bigg )^5 \end{aligned} \end{aligned}$$

(30)

The values for $P_{gt, fl}$ and $\eta _{gt, fl}$ are provided in Appendix A, while the values for other constants in Eq. (30) are given in Table 6.

Table 6 Summary of all constants for the gas turbines’ part-load efficiency calculation.

Appendix D. Parameters for the optimization algorithms

Parameters for the PSO algorithm employed in solving the optimization of pumping system configuration are provided in Table 7. Parameters for the extended PSO algorithm involved in solving the well-control optimization are given in Table 8.

Table 7 Parameters for the PSO algorithm

Table 8 Parameters for the extended PSO algorithm

Appendix E. Supplementary reservoir properties

1.1 5-spot model

Densities of the oil and water at surface conditions are 786.51 and 1037.84 kg/m$^{3}$, respectively. Variations of the oil’s formation volume factor, $B_{o}$, and viscosity, $\mu _{o}$, with respect to the oil phase pressure, $p_{o}$, are depicted in Fig. 18. At a reference pressure of $2.732 \times 10^{7}$ Pa, the water’s formation volume factor, $B_{w}$, compressibility, $C_{w}$, and viscosity, $\mu _{w}$, are 1.029, $4.6 \times 10^{-10}$ Pa$^{-1}$, and $3.1 \times 10^{-4}$ Pa.s, respectively. Distribution of porosity in the 5-spot model is shown in Fig. 19. At a reference pressure of $1 \times 10^{5}$ Pa, the rock compressibility, $C_{r}$, is specified to be $4.409 \times 10^{-10}$ Pa$^{-1}$. Relative permeability curves used in the 5-spot model are provided in Fig. 20. Capillary pressure between the oil and water phases is neglected in this reservoir model.

Fig. 18

Oil properties in the 5-spot model

Fig. 19

Porosity distribution in the 5-spot model

Fig. 20

Relative permeability curves in the 5-spot model

1.2 Cropped Olympus model

Distributions of porosity and initial water saturation in the cropped Olympus model are depicted in Figs. 21 and 22, respectively.

Fig. 21

Distribution of porosity [fraction] in the cropped Olympus model (Layer #1). The base figure is created using ResInsight [76]

Fig. 22

Distribution of initial water saturation [fraction] in the cropped Olympus model (Layer #1). The base figure is created using ResInsight [76]

Appendix F. Optimal solutions for case study #2

See Fig. 23.

Fig. 23

Optimal well BHPs and injection rates for case study #2. Top-to-bottom: Producer P1, Producer P2, Injector I1, Injector I2, Injector I3, and Injector I4