Effects of axial loading on dynamic response of laterally loaded single piles in liquefiable layered soil of Kolkata city considering nonlinearity of soil

Abstract

In the present study, an advanced nonlinear finite-element based 3D numerical study has been carried out to investigate the effects of axial loading on dynamic response of soil-pile system in liquefiable layered soil deposits of Kolkata city. An advanced soil constitutive law based on multi-yield surface plasticity model implemented in fully-coupled u-p formulation is adopted for soil-fluid interaction and pore water pressure development reasonably. The present model is validated with the past experimental results. Then, a detailed systematic parametric study is performed for numerical simulation of pile failures in layered soil deposit under axial loading by taking into account various soil conditions, pile and ground motion parameters. It is seen that the depth of liquefaction (DL) is decreased from 11.5 to 1.5 m adjacent to the pile when the axial load on pile increases from 0 to 1327 kN. Parametric studies also reveal that the bending moment response of pile under axial loading can be higher in non-liquefiable condition, with reference to the liquefiable condition. The peak lateral displacement decreases by 83.2% in non-liquefiable condition and 60.71% in liquefiable condition due to decrease of axial load from 1327 to 0 kN. Also, peak bending moment developed in the pile decreases by 97.2% in non-liquefiable condition and 82.7% in liquefiable condition when the axial load reduces from 1327 to 0 kN. So, the designer should be considered both extreme scenarios for safe and economical design. Also, it is noticed that the buckling capacity of pile is improved significantly by using larger diameter pile and the bending capacity is increased by selecting higher grade of concrete. It is concluded that the bending and buckling failure mode may be avoided by selecting a suitable combination of material strength and pile geometry.

Article highlights

• This study shows the importance of the bending-buckling interaction in dynamic response of piles in liquefiable layered soil deposit.

• The effect of axial load is to be considered for evaluation of peak response of soil and pile in both liquefiable and non-liquefiable condition.

• The present study can be utilised for safe and economical seismic design of pile foundations in liquefiable layered soil deposit.

1 Introduction

Piles are a common form of deep foundation primarily used to transfer vertical load from superstructure to deep strong soil strata or rock when top soil is weak which causes bearing capacity and settlement problem. Pile foundations are extensively used to support high rise buildings, bridges, chimney, transmission towers, port and harbour structures in seismically liquefiable soil for support both vertical and lateral loads. The seismic analysis of pile foundations is a complicated soil-structure interaction (SSI) problem. The problem of soil-pile interaction gets further intricated in liquefiable soil because of degradation of strength and stiffness of soil over time due to soil nonlinearity and evolvement of excess pore water pressure. A significant number of damages and/or collapses of pile foundations and pile-supported structures are reported in liquefiable soil after past major earthquakes in spite of employing large factor of safety (FOS) in their design as per latest standard code of practices [1]. So, it is challenging job for geotechnical earthquake engineers to ensure safe and economical design of pile foundation and pile-supported high-rise structures on liquefiable soil of metropolitan city like Kolkata, where rapid growing of population and infrastructure makes it essential.

The effects of soil liquefaction on seismic response of pile foundations have been studied by several investigators using physical model test [2,3,4,5,6,7]. They showed that the pile response is strongly affected by type of soil, nature of input motions, inertial effects of superstructure and kinematic effects due to soil displacement. Also, simplified 1D, 2D [8,9,10,11,12,13] and 3D [14,15,16,17,18] numerical studies have been performed by several researchers using robust numerical codes and platforms due to spatial and economic limitations of physical model. 3D finite-element based dynamic study has been conducted by Oliaei et al. [19] for large diameter pile under clay layer to examine soil and pile response during liquefaction. Also, 3D numerical study for non-liquefiable [20] and liquefiable soil [21] has been conducted recently and showed that dynamic response of soil-pile system in liquefiable condition is significantly different from non-liquefiable condition. Mehdi et al. [22] performed 3D nonlinear time-history analysis for numerical assessment of soil-pile system in liquefiable soil and suggested to perform effective stress-based ground analysis for evaluation of pile response when there is a chance of liquefaction. Some of the latest numerical studies related to seismic response of pile foundations in liquefiable soil are summarized in Table 1. The constitutive model considered for most of these numerical studies are very simple and based on uncoupled formulation of soil-fluid interaction. This approach is incapable to simulate direct pore water pressure development and changing of shear strength due to shear deformation of soil.

Table 1 Brief of latest numerical studies of pile foundations in liquefiable soil

The systematic research into the failure mechanisms of pile foundation due to liquefaction and liquefaction-induced lateral spreading was first started after 1964 Niigata and Alaska earthquakes. However, this research was intensified using experimental, numerical and analytical approaches [38,39,40,41,42] after failure of several piles and pile-supported structures following the 1995 Kobe earthquake. A theory based on bending failure mechanism considering pile as laterally loaded beam is evolved. Japanese standard code JRA [43] advices design engineers to design the piles based on bending failure mechanism assuming that pile experienced passive earth pressure by non-liquefiable layer while the pressure on a pile due to liquefiable soil layer is equal to 30% of total over-burden pressure. The code also advices design engineers to check the bending failure of piles for kinematic forces and inertial forces individually. Eurocode [44], NEHRP code [45] and Indian standard seismic code [46] also advises to design pile based on bending strength. Eurocode emphasis to consider extra forces on the pile foundation in liquefiable soil due to lateral spreading, specifically in existence of non-liquefiable soil layer overlying liquefiable soil layer. IS 2911[47] recommends depth of fixity method which is based on bending failure mechanism for evaluating the flexural response of earthquake -induced laterally loaded pile foundations. The response of pile foundations in liquefiable soil considering both inertial and kinematic interaction effects have been studied by several investigators [48,49,50,51,52]. Recently, Bhattacharya [53], Knappett and Madabhusi [54] and Kimura and Tokimatsu [55] established an alternative theory of possible pile failure in liquefiable soil based on buckling mechanism. They showed that pile behaves as an unsupported column because of loss of lateral confinement during liquefaction. This axially-loaded column is prone to buckling failure in the direction of least bending stiffness even without lateral spreading loading. So, pile in liquefiable soil may be assumed as laterally loaded slender column and Euler’s buckling criteria must be satisfied for analysis of piles in liquefiable soil. Also, vulnerability of pile foundations due to bending-buckling interaction in liquefiable soil has been studied by several researchers [1, 56, 57]. They concluded that both bending and buckling failure mechanism must be considered for designing of pile foundations in liquefiable soil. Bhattacharya et al. [58] have recently introduced new procedure for evaluating buckling failure mechanism using two main parameters. The evaluation procedure includes determination of Critical depth on account of buckling as capacity and laterally unsupported length of pile as demand. Bhattacharya and Goda [59] have illustrated this method using probabilistic approach. Chatterjee et al. [60] conducted dynamic field testing and numerical study using FLAC3D at three different places of Kolkata city for determination of net pile displacement and ultimate pile capacity. Chatterjee and Choudhury [49] proposed an analytical procedure to evaluate the influence of combined loading on pile response considering typical soil profile of Kolkata city using pseudo-static approach. Chatterjee [61] performed pseudo-static analysis using results obtained from equivalent linear ground response analysis for seismic response of pile foundations in Kolkata city considering both inertial and kinematic effects. Sinha et al. [62] evaluated flexural response of pile foundation in liquefiable soil using case study of a site in Patna city of India using pseudo-static approach considering bending and buckling criteria. The depth of liquefaction and reduction of shear strength are evaluated using empirical equations by previous authors.

It is clearly understood from above discussions that the simplified methods based on pseudo-static approach needs various numerical assumptions and not able to simulate the complex dynamic response of piles during earthquake. Besides, due to large shear strain is likely to be developed during soil liquefaction, nonlinearity of soil needs to be considered for seismic analysis of pile foundations in liquefiable soil. Bending and buckling are two distinct approaches of structural design. Buckling criteria will not be fulfilled automatically by designing the pile against bending criteria. Bending is stable failure mode which depends on bending strength of material (Plastic moment capacity, Mp). Contrariwise, buckling is unstable failure mode which depends only on geometric characteristics of the member. Hence, in present study, seismic response of pile foundations in liquefiable layered soil of Kolkata city is carried out through numerical simulation of dynamic nonlinear soil-pile interaction under influence of axial loading to incorporate bending and buckling interaction. An advanced soil constitutive model, implemented in fully-coupled u-p formulation (where u and p are soil skeleton displacement and pore water pressure respectively) is adopted using nonlinear finite-element based computer program OpenSeesPL [63, 64] for soil-fluid interaction and pore water pressure development reasonably. The finite-element model is three dimensional with consideration of P-delta effect. There are others computer program also like FLAC or ABAQUS for numerical analysis of pile foundations. FLAC is finite volume-based software, whereas, ABAQUS and OpenSeesPL are finite element-based software. There are many advanced soil constitutive models in OpenSees framework for simulating dynamic nonlinear behaviour of soil. Also, the OpenSeesPL is an open-source software and the user interface is easier to use than ABAQUS and FLAC. Hence, in the present study OpenSeesPL based on finite element method is selected for dynamic analysis of soil-pile system.

In the next section, we present a brief overview of the study area Kolkata city, Sect. 3 describes details of the present numerical model. In Sect. 4 and 5, we present methodology adopted for this study and validation of the present numerical model respectively. Section 6 discusses the important results obtained from numerical analysis and Sect. 7 summarises the key conclusions from this study.

2 Study area

The Kolkata metropolitan city, is a gateway to north-east India. It is third-most populated city in India. Originally, Kolkata city was developed towards the east side of the river Hooghly. But due to increasing population and scarcity of vacant land, infrastructures are often constructed without proper town planning on reclaimed lands in the Salt Lake and Rajarhat areas. More than 80% of the city area has covered with different types of important heritage building, school, hospital buildings in unplanned way. The altitude of the city above MSL is 5.8 to 6.1 m and GWT is located near surface level [65]. The soil of Kolkata city is mainly alluvial in nature having two different soil formations such as Normal Kolkata Deposit (NKD) and River Channel Deposit (RCD). NKD soil mainly compose with silty clay or clayey silt of soft to stiff consistency with sandy deposit at intermediate layer. NKD soil is existed in central Kolkata region like Sealdah, Beliaghata, Ultadanga and Park circus area. The RCD soil mainly composes with medium to dense compactness sand deposit up to significant depth along the existing old Adiganga channel [66]. RCD soil is predominant in south Kolkata region like Tollygunge, Alipore and Kasba area. In the present study, geotechnical bore hole data of Kolkata city has been selected from previous study [66]. The subsoil profile at Ultadanga site (Latitude 22.5948 °N, Longitude 88.3869 °E) having NKD soil and Tollygunge Metro site (Latitude 22.4986 °N, Longitude 88.3454 °E) having RCD soil have been chosen to replicate typical soil layers of Kolkata Metropolitan city. The depth of borehole is 50 m for both the sites. Friction angles (φ) for cohesionless soils and undrained shear strength (C_u) for cohesive soil are calculated using the co-relation of SPT-N with φ for cohesionless soil and SPT-N with C_u for cohesive soils [67]. The values of various soil properties of two typical soil are shown in Tables 2 and 3 [66].

Table 2 Typical soil properties of NKD soil of Ultadanga site (after Roy et al. 2018 [66])

Table 3 Typical soil properties of RCD soil of Tollygunge Metro site (after Roy et al. 2018 [66])

Kolkata city falls in the Zone III & IV according to zonation map of Indian standard design code IS:1893 [46]. The Kolkata city is located on the important regional basement fault Eocene Hinge Zone. The width of Eocene Hinge Zone is about 25 km and extended about 45 km below ground level [68]. Kolkata, in the past, has suffered tremendous damages due to near and far field earthquakes. The local soft, alluvial soil of Kolkata city magnify the earthquake ground motion. The input ground motions considered for present analysis are Imperial valley (IMV) and Bhuj (BHJ) earthquakes with significant variation in moment magnitude, maximum bedrock level acceleration (MBRA), strong motion duration and frequency content as tabulated in Table 4. The maximum bed rock level acceleration (MBRA) values of selected input motions are well within the reported range of 0.1 g to 0.34 g of Kolkata city [69]. Strong motion record of IMV earthquake is adopted from the database of OpenSeesPL, whereas the BHJ earthquake is adopted from strongmotioncenter.org. The input earthquake motions used in present analysis are shown in Fig. 1a, b. The various parameters of these input motions have been estimated using SEISMOSIGNAL [70] and are tabulated in Table 4.

Fig. 1

Acceleration time-history of a IMV and b BHJ earthquake

3 Descriptions of the present numerical model

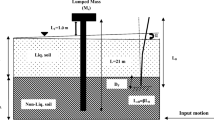
Full 3D numerical model is built using finite-element based program OpenSeesPL [63, 64] as shown in Fig. 2 to simulate coupled soil-pile system. All the simulations in OpenSeesPL are performed using open-source finite element-based computational platform OpenSees [71]. Due to symmetric condition, only half of the soil domain is modelled. A floating pile of Length L and diameter d is embedded in the layered soil. The soil domain is modelled with 8-node brick elements and elastic beam-column element is used to model the pile. Each soil and pile node has four and six degrees-of-freedom (DOF) respectively. The first three DOFs of soil node illustrate translation of soil skeleton and the fourth DOF represents pore water pressure. Rigid connecting element having similar material properties of the pile is used to implement the physical modelling of the pile. Each 3D brick element of soil domain is connected to the adjacent pile element at same elevation using outer nodes of these rigid links through equal DOF command and transfer the forces from pile to soil and vice versa. Fine mesh size is used for pile zone and mesh size becomes comparative larger near domain boundaries to prevent reflection of seismic waves. The total length of mesh in each horizontal direction considered is 40d from the middle of the pile. The total depth of the soil profile (50 m) is considered for the dimension of model in vertical direction. Also, the maximum size of element in dynamic analysis considered is less than λ/10 (λ = wave length) to prevent filtration of parts of the seismic waves [19].

Fig. 2

3D FE model used in the present study

All the soil nodes at the base of the model are considered as completely fixed in all directions. The pore water pressure DOF on ground surface is fixed for drain out water and is open in the rest of the nodes for free variation of pore water pressure (PWP). Side nodes orthogonal to the direction of base excitation are considered as fixed in this direction and are set free parallel to the direction of excitation. Nodes at the boundaries parallel to the base excitation are constrained orthogonal to the excitation direction and are set free to move in the excitation direction. Ground motions are applied at assumed bed rock level (50 m depth) in longitudinal direction (x-axis) and its amplification has been considered for dynamic analysis of soil-pile system.

The plasticity model used in the present study is based on pressure-dependent multi-yield surface approach to model the cyclic hysteretic response [72, 73] of frictional cohesionless soil. Yield function (f) is defined in the following form [74]:

$$f = \frac{3}{2}(s - \left( {p^{\prime} + p_{0}^{^{\prime}} } \right)\alpha :\left( {s - \left( {p^{\prime} + p_{0} ^{\prime}} \right)\alpha } \right) - m^{2} \left( {p^{\prime} + p_{0} ^{\prime}} \right) = 0$$

(1)

where, $s = \sigma^{\prime} - p^{\prime}\delta$ is the deviatoric stress tensor, $p^{\prime}$ is mean effective stress and $p_{0}^{^{\prime}}$ is the small positive constant for finite size of yield surface at ${p}^{^{\prime}}=0$. Parameters α and m are the second order kinematic deviatoric tensor and size of yield surface respectively [72].

Multi-yield surface plasticity constitutive model has several features. The yield surface is pressure-dependent and nested cone shape in principal stress space. The peak shear strength of soil is represented by the outermost surface. The hardening zone is formed by the nested yield surfaces with regards to multi-surface plasticity for simulating nonlinear soil response. Shear-induced dilatancy during liquefaction is modelled using this constitutive model. A new adequate flow rule is developed to incorporate the contractive, completely plastic and dilative stages. In this respect, effort is placed to the coupling of deviatoric volumetric strain under cyclic loading, which is responsible for cyclic mobility. Shear-induced dilation or contraction is defined by the volumetric component $\mathrm{P}"$ of the normal to the plastic potential. Along the phase transformation (PT) surface, the stress ratio η = τ/p' is indicated by η_PT. Clear contractive or dilative characteristics are simulated through the following equations of P" based on the value of η in comparison to η_PT and the sign of ͘ ή (time rate of η):

$$\mathrm{P}"=\frac{1-{(\upeta /{\upeta }_{PT})}^{2}}{1+{(\upeta /{\upeta }_{PT})}^{2}}c1 \,\,\,(\mathrm{for contraction})$$

(2)

where c1 = non-negative parameter indicating the rate of shear-induced volume contraction or pore-pressure build up and

$$\mathrm{P}"=\frac{1-{(\upeta /{\upeta }_{PT})}^{2}}{1+{(\upeta /{\upeta }_{PT})}^{2}}d1\mathrm{exp}(d2{\gamma }_{d}) \,\,\,(\mathrm{for dilation})$$

(3)

where d1 and d2 = non-negative parameters indicating the rate of shear-induced volume dilation and ${\gamma }_{d}$=octahedral shear strain build up throughout dilation cycle.

The principal component of this modelling approach is the prior calibration of the employed soil model under liquefaction and lateral spreading scenario. The Pressure dependent multi-yield02 (PDMY02) type material model [73] is used in the present study for modelling the liquefiable sands which is modified form of Pressure dependent multi-Yield material. Extra parameters (c3 and d3) are required to account for effect of overburden pressure (K_σ effect). Parameter c2 is required to include the effect of past dilation history on consequent dilation tendency. Mass density (ρ), Friction angles (φ) and reference mean effective confining pressure (P_ref), pressure dependent coefficient (d), reference low-strain shear modulus (G_r), reference low-strain bulk modulus (B_r), peak shear strain (y_max) at which highest shear strength is achieved and number of yield surfaces (NYS) are the principal input parameters for this material model.

Soil dilatancy is defined by specifying phase transformation angle (Φ_PT), contraction (c1_, c2 and c3) and dilation parameters (d1_, d2 and d3). These parameters monitor the rate of pore water pressure accumulation in soil during liquefaction.

Nonlinear hysteretic material model is used for modelling clay material using Von Mises multi-surface kinematic plasticity model [73, 75, 76]. Simulating the soil hysteretic elasto-plastic shear response is focused in this model. Plasticity develops only in the deviatoric stress–strain response for this material. The volumetric stress–strain response is linear-elastic and is free from the deviatoric response. This constitutive model simulates monotonic or cyclic response of materials having shear response is independent to the confinement variation. Multi-surface approach is used to formulate the plasticity with an associative flow rule based on Prevost approach. Pressure independent multi-yield (PIMY) type material [73] is used for modelling the cohesive soils.

Mass density (ρ), cohesion (c) and reference mean effective confining pressure (P_ref), pressure dependent coefficient (Co-eff), reference low-strain shear modulus (G_r), reference low-strain bulk modulus (B_r), peak shear strain (y_max) at which highest shear strength is achieved and number of yield surfaces (NYS) are the principal input parameters for this material model. The values of various input parameters for modelling each layer are considered from OpenSees user manual [64, 71] based on soil type of each layer of NKD and RCD soil and summarized in Tables 5 and 6 respectively. The values of fluid mass density, combined bulk modulus, permeability of clay and sandy soil considered are 1.0 Mg/m³, 2.2 × 10⁶ kN/m², 1 × 10^–09 and 6.6 × 10^–05 m/s respectively [64].

Table 4 Ground motion parameters of the considered earthquake

Table 5 Values of model parameters for NKD soil of Ultadanga site

Table 6 Values of model parameters for RCD soil of Tollygunge Metro site

An advanced soil constitutive model implemented in fully-coupled u-p formulation is adopted for soil-fluid interaction and pore water pressure development reasonably. The matrix form of fully-coupled u-p formulation for dynamic problem is given by:

$$M\"U + \mathop \smallint \limits_{v} B^{T} \sigma ^{\prime}dV - QP - f^{\left( s \right)} = 0$$

(4)

$${Q}^{T}\dot{U}+HP+S\dot{P}-{f}^{\left(p\right)}=0$$

(5)

where M, B, Q, S and H are mass, strain–displacement, coupling, compressibility and permeability matrices respectively. The vectors f^(s) and f^(p) represent body and surface forces in soil and fluid respectively. The above equations are solved numerically using Newmark’s algorithm which is implemented in OpenSees.

4 Methodology

The effects of axial loading in addition to the input earthquake motion on dynamic response of laterally loaded single piles in liquefiable layered soil of Kolkata city considering nonlinearity of soil is evaluated in the present study using finite-element based program OpenSeesPL. The properties of pile section [49, 77] considered in this study are presented in Table 7. A circular pile of total length 21 m with free head length of 1 m and embedded length of 20 m is selected for the study. Pile head is pinned and linear elastic material behaviour is considered. The geometric configuration along with the boundary conditions of the soil-pile system adopted in this study is shown in Fig. 3. The modulus of elasticity (E) of the pile is calculated from IS:456 [77] using following equation:

$$E=5000\sqrt{{f}_{ck}}$$

(6)

where f_ck is the characteristic strength of concrete.

Table 7 Pile properties considered in the present numerical study [49, 77]

Fig. 3

Schematic diagram of soil-pile system considered in the present study

The value of M_p is calculated using the following expressions based on recommendations of IS 456–2000:

$${M}_{p}={Z}_{p} x {\sigma }_{y}$$

(7)

where, Z_p = Plastic section modulus = d³/6 and ${\sigma }_{y}=$ yield stress = 0.446f_ck.

The allowable load carrying capacity (P_all) of 20 m embedded piles of various diameters in NKD and RCD soil are computed by dividing the ultimate capacity of pile with a factor of safety of 2.5 based on IS 2911 [47] and shown in Fig. 4. The three different masses, describing superstructure, equivalent of 30%, 50% and 100% of P_all are connected to the pile head to assess the effects of axial load on flexural response of pile foundation in liquefiable and non-liquefiable condition. The depth of liquefaction and reduction of shear strength are evaluated using finite-element simulation. The detailed depth and time-varying effects of kinematic and inertial forces on pile foundation are also assessed.

Fig. 4

Allowable load carrying capacity (P_all) of piles with various diameters in NKD and RCD soil

During ground shaking, the effective stress of saturated cohesionless soil decreases due to increase of pore water pressure. When the effective stress becomes zero, the soil loses its shear resistance and behaves like liquid. The pile becomes laterally unsupported during liquefaction stage and becomes prone to buckling failure under axial loads. Critical buckling load of concrete piles are computed using Euler’s buckling equation:

$${P}_{cr}=\frac{{\pi }^{2}EI}{{L}_{eff}^{2}}$$

(8)

where L_eff and EI are the effective length and flexural rigidity of the pile respectively. The effective length of pile depends on the end conditions and length of pile.

In the present study, the effective length of pile is estimated using the following expression:

$${L}_{eff}=\beta {L}_{0}$$

(9)

where β is the factor which depends on end conditions of pile and L₀ is the length of pile in buckling zone. According to Davisson and Robinson [78], laterally load pile foundations may be assumed to be fixed at depth of 1.8 T (D_F) below the interface between liquefiable and non-liquefiable layer, where T is the relative stiffness factor may be calculated using the following equation:

$$T=(EI/{n}_{h})^0.2$$

(10)

where, n_h = coefficient of modulus of subgrade reaction of soil.

The value of n_h considered in this study is 4500 kN/m³ for non-liquefiable sand (N = 32) from IS 2911 [47].

The value of L₀ is the depth of liquefiable layer (D_L) plus depth of fixity (D_F). Also, the boundary condition of top end of pile is assumed to be restrained against rotation but not held in position. The bottom boundary condition is assumed to be effectively held in position but not restrained against rotation (i.e., pinned type) when depth of embedment of pile in bottom non-liquefiable layer is less than five times pile diameter and effectively held in position and restrained against rotation (i.e., fixed type) when depth of embedment of pile in bottom non-liquefiable layer is more than five times pile diameter [79]. The values of β considered from Table 8 of IS 456–2000 [77] depending on the boundary conditions of top and bottom ends of pile foundation.

Table 8 Checking against bending failure mechanism of various diameter pile of M-30 grade in RCD soil under scaled IMV motion

The effects of axial load on seismic response of pile foundations in liquefiable soils are next evaluated. Bhattacharya [53] suggested the following effects of axial load:

• (i) Increasing the possibility of buckling instability

Bhattacharya et al. [58] proposed buckling failure mechanism based on Euler’s and Rankine’s buckling criteria by investigating the seismic performance of pile foundations in liquefiable soil using dynamic centrifuge tests. They proposed slenderness ratio (λ) of pile is expressed by the following expression:

$$\lambda ={L}_{eff}/{r}_{min}$$

(11)

where L_eff is the effective length of the pile in liquefiable zone and r_min is the minimum radius of gyration which is the ratio between moment of inertia about weakest section (I_min) and cross-sectional area of pile (A).

The Euler’s buckling criteria which is applicable for long column is given by the following equation:

$${P}_{cb}=\frac{{\pi }^{2}E{I}_{min}}{{L}_{eff}^{2}}$$

(12)

$${\sigma }_{cb}=\frac{{P}_{cb}}{A}=\frac{{\pi }^{2}E}{{\uplambda }^{2}}$$

(13)

where P_cb is the critical buckling load and ${\sigma }_{cb}$ is the elastic critical buckling stress.

Rankine’s buckling criteria which is applicable for both short and long column is expressed by the following equation:

$$\frac{1}{{\sigma }_{f}}=\frac{1}{{\sigma }_{y}}+\frac{1}{{\sigma }_{cb}}$$

(14)

where ${\sigma }_{f}$ is the Rankine’s failure stress considering both crushing and buckling criteria, ${\sigma }_{y}$ is the yield stress of material.

Bhattacharya and Bhattacharya et al. [53, 58] reported that the possibility of buckling instability of pile in liquefiable layer is dependent on slenderness ratio of pile. Liquefaction-induced lateral spreading is not necessary for buckling instability.

• (ii) Reduction of plastic moment capacity of piles

A hinge may be formed within a pile section under the coupled action of axial load (P) and moment (M). The combined action of axial load and moment in plastic moment capacity of pile is governed by the following equation [62]

$$\left( {\frac{P}{{P_{y} }}} \right)^{n} + \left( {\frac{M}{{M_{p} }}} \right) = 1$$

(15)

where P_y is the squash load without bending; M_p is the plastic moment capacity without axial load and n = 1.5 for circular section.

The value of P_y is calculated using the following expressions based on recommendations of IS 456–2000:

$${P}_{y}={\sigma }_{c} x A$$

(16)

where ${\sigma }_{c}$= Compressive strength = 0.67f_ck.

P-M interaction curve can be plotted for any pile section having particular diameter and grade of concrete. The plastic moment capacity of any pile section decreases in presence of axial load in liquefiable soil layer.

5 Validation of the present numerical model

The suitability of the present FE model is carried out by comparing the results with the dynamic centrifuge tests conducted by Wilson [2] prior to conducting parametric study to evaluate the effects of various parameters on dynamic response of pile foundations. The model was consisted with two horizontal layers of saturated, fine and uniformly graded Nevada sand having 9.1 m thick upper medium dense sand (Dr = 55%) and 11.4 m thick lower dense sand (Dr = 80%) at the prototype scale. A single steel pile having diameter of 0.67 m and wall thickness of 19 mm was used to model the pile. The pile head was extended 3.8 m from the ground level and a superstructure load of 480 kN was applied on pile head. The embedded depth of pile was about 16.8 m. This model was excited to the Kobe (1995) earthquake motion [2] with peak acceleration value scaled to 0.22 g as shown in Fig. 5. The measured and calculated excess pore pressure (EPP) ratio and bending moment time history at 2.3 m depth are presented in Fig. 6a, b respectively. Also, Fig. 6c displays the measured and calculated acceleration time history of the superstructure. The pile displacement profile at 11.2 s after earthquake loading is shown in Fig. 7.

Fig. 5

Acceleration time-history of 1995 Kobe earthquake motion [2]

Fig. 6

Comparison of present study with dynamic centrifuge tests conducted by Wilson [2] a EPP time-history b bending moment time-history and c superstructure acceleration time-history

Fig. 7

Comparison of lateral displacement profile obtained from present study with dynamic centrifuge tests [2]

It is observed that the excess pore pressure ratio and bending moment time-history at 2.3 m depth obtained from the present numerical model are fairly matching with the results of centrifuge test. The difference of results may be attributed to the use of constant value of permeability in the present study, but in real case, it increases several times during liquefaction. The dilative response of soil is noticed in the present study for the first few cycles (prior to complete liquefaction) due to sharp reduction of EPP. The reduction of EPP due to soil dilation increases soil shear modulus and corresponding stiffness. As a result, big acceleration spikes are transmitted to the superstructure through the field during earthquake and higher acceleration response is observed. On the other hand, the maximum bending moment is generated in the pile with the softening of soil due to rise of EPP. Hence, the maximum bending moment is noticed at 6.1 s after applying of earthquake motion due to abrupt change of EPP. Also, Fig. 7 shows the comparison of the lateral displacement profile of pile at 11.2 s after applying of earthquake motion. The results are matching well. The slight deviation in results for the first few cycles may be reasonable due to the distinction between frequency content of the Kobe earthquake record originated for the centrifuge test and considered for the present study. Hence, the present model can be efficiently used to predict soil and pile response under seismic loading condition.

6 Results and discussions

A parametric study has been conducted using the present numerical model for evaluating the effects of axial load on flexural response of pile foundation in liquefiable and non-liquefiable soil of Kolkata city considering nonlinearity of soil using finite-element based computer program OpenSeesPL and the results are presented and discussed graphically.

6.1 Assessment of liquefaction potential and response of Soil

Flexural response of pile foundation is greatly dependent on adjacent soil conditions. The axially-loaded pile becomes unsupported during soil liquefaction due to significant reduction of shear strength of soil. The determination of unsupported length of pile is needed to calculate critical buckling load (P_cr). So, the assessment of liquefaction potential for the considered site is essential. The depth of liquefaction may alter depending upon the type of soil and input motion characteristics. In the present study, liquefaction assessment is conducted using a practical parameter excess pore pressure (EPP) ratio (R_u). R_u is defined as the ratio of EPP to the initial effective vertical stress. The soil is termed as liquefiable when R_u becomes unity. To evaluate the influence of various parameters on the generation and distribution of time and depth varying EPP ratio (R_u), different figures are plotted and discussed. The near-field and far-field soil response are also compared graphically.

The variation of R_u with depth for NKD and RCD soil at 0.25 m and 13.2 m horizontal distance from centre of pile representing near and far-field soil response for various input motions are shown in Figs. 8 and 9 respectively. It is seen that depths of liquefaction (D_L) are 10 m, 16 m and 16 m for NKD soil and 8.25 m, 11.5 m and 11.5 m for RCD soil under BHJ, scaled IMV and IMV motion respectively in case of near-field response. The same is observed as 1 m, 10 m and 13 m for NKD soil and 8.25 m, 9.87 m and 13.25 m for RCD soil in case of free-field response. The depth of liquefaction is dependent on both soil types and characteristics of input motions. From the Figs. 8 and 9, it is clear that R_u value decreases with increasing depth due to increasing soil stiffness. The relative density of soil for top portion of the model is relatively low which causes more vibrations of soil grains during seismic event. Accordingly, pore water pressure increases due to densification of soil’s structure. The rapid increase of R_u is observed near ground for all the cases because of presence of low permeability clay layer at the top of granular layer. During seismic excitation, top clay layer prevents to drain out the pore water from deeper layer.

Fig. 8

Profile of R_u in NKD soil a near field and b far field for various input motions

Fig. 9

Profile of R_u in RCD soil a near field and b far field for various input motions

The weight of the super structure on pile foundation has profound influence on depth of liquefaction. The near-field variation of R_u with depth for different pile head mass under scaled IMV input motion is presented in Fig. 10. It is noteworthy that the depth of liquefaction decreases significantly adjacent to the pile with an increase of pile head mass. The depth of liquefaction (D_L) decreases from 11.5 m to 1.5 m adjacent to the pile when the superstructure weight increases from 0 to 1327 kN. This is due to densification of soil adjacent to pile during earthquake with an increase of pile head mass or superstructure weight. Figure 11 shows the time-dependent near-field variation of R_u at 5 m, 9.87 m, 11.5 m and 20 m depth of RCD soil for the scaled IMV input motion. It is noteworthy that liquefaction begins at distinct times over depth, usually, from top to bottom layers. Liquefaction starts after 2.66 s, 5.05 s, 26.36 s of application of input motion for depth of 4.63 m, 9.53 m, 11.16 m respectively.

Fig. 10

Profile of R_u of RCD soil under scaled IMV motion for various superstructure weight

Fig. 11

Comparison of time history of R_u at various depths a NKD soil and b RCD soil using scaled IMV motion

Assessment of undrained residual strength (S_r) of liquefiable soil is a vital issue in earthquake geotechnical engineering. It involves the complicated nonlinear soil response during earthquake loading. Several empirical correlations are available in the literature based on SPT-N value for estimating S_r [80]. Cyclic shear stress vs shear strain plot of RCD soil under scaled IMV motion at various depths obtained from present finite element analysis are shown in Fig. 12. It is noteworthy that the S_r value at various depths tends to zero at liquefaction phase. Hence, it can be concluded that liquefiable soil loses its strength and consequently pile becomes laterally unsupported susceptible to buckling failure under axial load.

Fig. 12

Shear stress vs shear strain relationship for RCD soil under scaled IMV motion a 4.63 m b 9.53 m c 11.16 m and d 19.58 m depths

6.2 Response of pile

The lateral displacement (y) and bending moment (M) of pile obtained in the present dynamic analysis are normalized with pile diameter (d) and available plastic moment capacity (M_p') and plotted in the form of dimensionless lateral pile displacement coefficient (y/d) and bending moment coefficient (M/ M_p') against depth.

6.2.1 Response of pile displacement

Figures 13a and 14a presents the variation of kinematic peak lateral displacement co-efficient (y/d) of pile with depth in NKD and RCD soil respectively for 0.5 m diameter M-30 grade concrete pile when subjected to the BHJ, Scaled IMV and IMV earthquake motions. It is observed from Fig. 13a and 14a that kinematic peak lateral displacement co-efficient increases dramatically with an increase of PGA.

Fig. 13

Kinematic a peak lateral displacement and b peak bending moment of pile in NKD soil under various input motions

Fig. 14

Kinematic a peak lateral displacement and b peak bending moment of pile in RCD soil under various input motions

6.2.2 Response of pile bending moment

The variation of peak bending moment co-efficient (M_max/M_p') of pile with depth in NKD and RCD soil are represented by the Figs. 13b and 14b respectively. The kinematic peak bending moment co-efficient is maximum at 10 m depth of NKD soil which is near the boundary between liquefiable and non-liquefiable layer and its maximum values are 1.53, 1.06 and 0.32 for IMV, scaled IMV and BHJ earthquake motion respectively. However, for RCD soil the maximum kinematic bending moment co-efficients are 0.68 at 11.5 m depth, 0.41 at 9.87 m depth and 0.28 at 9.87 m depth under IMV, scaled IMV and BHJ earthquake motion respectively. The maximum kinematic bending moment developed in the pile exceeds the plastic moment capacity in NKD soil for IMV, scaled IMV earthquake motions. So, formation of plastic hinge is expected for 0.5 m diameter M-30 grade concrete piles in NKD soil under IMV, scaled IMV earthquake motion. However, the same pile when embedded in RCD soil is safe against kinematic bending failure under same earthquake motions. So, kinematic bending failure is dependent on both soil type and input motion characteristics. Also, due to increase of free length, large bending moment is developed for pile embedded in RCD soil when subjected to IMV and scaled IMV motion in comparison with the BHJ motion.

6.3 Effect of axial load on pile response

Response of pile Pile supports superstructure which are generally multi-degree of freedom (MDOF) systems. These MDOF systems are assumed as lumped mass at the pile head for simplification of analysis during design of pile foundations. During travelling of seismic waves from bedrock level to the ground, the inability of the embedded pile to follow the free field motion develops bending moment in the pile foundation even in absence of lumped mass and is termed as kinematic interaction. On the other hand, inertial force is generated due to the vibration of the lumped mass i.e., super-structure during seismic shaking. So, for accurate estimation of the maximum bending moment developed in the pile foundation for soil-pile system with lumped mass during earthquake event, the combined effect of kinematic and inertial interaction should be considered. Figure 15 shows the effect of axial load on dynamic response of pile foundation. The four different masses, describing superstructure, equivalent of 0%, 30%, 50% and 100% of P_all (0, 363, 635 and 1327 kN) are connected to the head of 0.5 m diameter M-30 grade concrete pile to assess the effects of axial load on flexural response of pile foundation in RCD soil using scaled IMV earthquake motion. The comparative lateral pile displacement and bending moment response along pile between kinematic and combined kinematic and inertial soil-pile interaction are provide in Fig. 15a, b respectively. It is observed that the maximum lateral displacement co-efficient under kinematic loading is significantly less than the combined kinematic and inertial loading. The lateral displacement co-efficient under combined loading increases by 29.5%, 102.3% and 154.5% with respect to kinematic lateral displacement co-efficient when the axial load increases from 0 kN to 363, 635 and 1327 kN respectively. Also, the peak value, position and incidence time of kinematic pile bending response in liquefiable soil is markedly dissimilar from combined response. In case of kinematic interaction, pile follows the imputed motion of liquefiable soil. Hence, the peak bending moment occurs at deeper depth during post-liquefaction stage. The maximum kinematic bending moment obtained is 115.4 kN-m (M/M_p = 0.41) at 9.87 m depth. The maximum bending moments due to combined loading obtained are 218.62 kN-m (M/M_p = 0.81) at 0.75 m depth, 326.81 kN-m (M/M_p = 1.25) at 0.75 m depth and 667.45 kN-m (M/M_p = 2.97) at 1.5 m depth when the axial loads are 363, 635 and 1327 kN respectively. The maximum pile bending moment increases by 89.4%, 184.2% and 478.4% with respect to kinematic bending moment when the axial load increases from 0 kN to 363, 635 and 1327 kN respectively. The increase of maximum bending moment in the pile due to inertial loading before liquefaction is dependent on the mass of the superstructure. The maximum bending moment at ground level increases significantly with an increase of the mass of superstructure as shown in Fig. 16a, b for NKD and RCD soil respectively. When, the maximum bending moment becomes doubled when superstructure mass doubles for both the soil profile.

Fig. 15

Variation of a peak lateral displacement and b peak bending moment of pile for different combinations of vertical loading in RCD soil when subjected to scaled IMV motion

Fig. 16

Comparison of peak bending moment time-history of pile at ground level for different combinations of vertical loading in a NKD soil and b RCD soil when subjected to scaled IMV motion

6.4 Comparison of pile response in liquefiable and non-liquefiable conditions

The effect of the axial load on dynamic response of pile foundation for different soil condition is evaluated in this study by comparing the peak lateral displacement and bending moment co-efficient profile in liquefiable and non-liquefiable condition of RCD soil. Figure 17a, b shows the profile of peak lateral displacement and bending moment co-efficient of pile founded in non-liquefiable condition of RCD soil for four distinct axial loads. It is seen that pattern of peak lateral displacement and bending moment co-efficient profile for kinematic loading is remarkably different from others. Kinematic force is induced due to deformation of ground, on the other hand, inertial force is developed by the vibration of superstructure. The peak lateral displacement co-efficient under various axial loads are shown in Fig. 18a, b in non-liquefiable and liquefiable condition respectively. Similarly, Fig. 19a, b shows the peak bending moment co-efficient of pile under various axial loads in non-liquefiable and liquefiable condition respectively. The peak lateral displacement decreases by 83.2% in non-liquefiable condition and 60.71% in liquefiable condition due to decrease of axial load from 1327 to 0 kN. Also, peak bending moment developed in the pile decreases by 97.2% in non-liquefiable condition and 82.7% in liquefiable condition when axial load reduces from 1327 to 0 kN. So, kinematic force is predominant in liquefiable soil condition and inertial force is prevalent in non-liquefiable condition and mainly accountable for peak bending moment in the vicinity of pile head.

Fig. 17

Variation of a peak lateral displacement and b peak bending moment co-efficient of pile for different combinations of vertical loading in non-liquefiable condition of RCD soil when subjected to scaled IMV motion

Fig. 18

Comparison of peak lateral displacement co-efficient of pile for a non-liquefiable and b liquefiable soil condition of RCD soil when subjected to scaled IMV motion

Fig. 19

Comparison of peak bending moment co-efficient of pile for a non-liquefiable and b liquefiable soil condition of RCD soil when subjected to scaled IMV motion

6.5 Bending and buckling interaction analysis

After reliable estimation of unsupported length of the pile, bending and buckling failure criteria can be checked using procedure discussed before. When the stress on pile due to axial load (σ) exceeds the Rankine’s failure stress (σ_f), buckling failure may be occurred and when the maximum bending moment (M) developed in the pile section exceeds the available plastic moment capacity (M_p), bending failure may be occurred. So, failure due to bending-buckling interaction may be occurred when both criteria exceeded. Pile may be considered as safe when both bending moment co-efficient (M/ M_p') and buckling co-efficient (σ/σ_f) are less than 1. Tables 8 and 9 shows the results obtained for analysis of bending and buckling failure criteria of 21 m long (free head length = 1 m) M-30 grade concrete pile with various diameters embedded in RCD soil of Kolkata city under scaled IMV earthquake motion and Fig. 20 presents bending-buckling interaction graph for the same. The bending-buckling interaction graph is the plot of σ/σ_f and M/M_p' for a particular analysis case. This graph is necessary for identifying a probable failure mode of pile foundation under combined vertical and lateral loads. It is noticed from Fig. 20 that the maximum bending moment of pile increases with an increase of axial load on pile for a particular diameter of pile because of buckling and P-delta effects. With an increase of pile diameter buckling co-efficient of pile reduces significantly and bending moment co-efficient changes slightly. Hence, it may be interpreted that larger diameter pile can be used in liquefiable soil to avoid buckling failure mode. The capacity against bending of a pile can be greatly improved by using high grade of concrete or steel having high flexural strength. However, buckling capacity of pile does not change significantly with the grade of concrete. Significant improvement of buckling capacity can be achieved by increasing the diameter as it is connected with the geometrical properties of pile section.

Table 9 Checking against buckling failure mechanism of various diameter pile of M-30 grade in RCD soil under scaled IMV motion

Fig. 20

Bending-buckling interaction graph of various diameter piles in RCD soil due to the scaled IMV motion

Similarly, Fig. 21 presents bending-buckling interaction graph for the 0.5 m diameter concrete pile under BHJ, scaled IMV and IMV earthquake motions having different PGA. It is observed that amplitude of the input motions has profound influence on seismic response of pile foundations. Higher amplitude of input motions enhances the inertial forces working on pile and develops higher bending moment in the pile. As the soil properties changes dramatically during liquefaction, the input motion characteristics have profound influence on bending and buckling failure criteria. Several dynamic forces may be developed within pile section based on the time period of pile-supported structures and the characteristics of liquefiable soil. Here, the 0.5 m diameter M-30 grade pile is safe against both bending and buckling for axial load equal to 50% of P_all under BHJ earthquake motion but the same pile is unsafe at same axial load when subjected to scaled IMV and IMV input motions having higher PGA.

Fig. 21

Bending-buckling interaction graph of 0.5 m diameter pile in RCD soil due to the BHJ, scaled IMV and IMV motions

Finally, Fig. 22 shows a bending-buckling interaction graph for the 0.5 m diameter concrete piles of various grade under scaled IMV earthquake motion. It is noticed that the buckling capacity is slightly improved by using higher grade of concrete but the bending capacity is increased significantly by selecting higher grade of concrete pile. Here, the 0.5 m diameter M-20 grade pile is unsafe against bending for axial load equal to 30% of P_all under scaled IMV earthquake motion but the same pile is safe against bending and buckling at 30% of P_all and 50% of P_all for M-30 grade and M-40 grade concrete pile respectively. So, bending and buckling failure mode can be avoided by selecting a suitable combination of material strength and pile geometry.

Fig. 22

Bending-buckling interaction graph of 0.5 m diameter pile of various grade of concrete in RCD soil due to the scaled IMV motion

6.6 Effect of liquefaction on natural time period of the soil-pile system

The natural frequency (f_n) of the soil-pile system is calculated using the following expression [81]:

$${f}_{n}=\frac{3.515}{8\pi }\frac{d}{{L}_{0}^{2}}\sqrt{\frac{E}{\rho }}$$

(17)

The total stiffness (k) of soil-pile system in liquefiable condition is contributed mainly by pile foundation due to negligible stiffness of liquefiable soil. The time period of the soil-pile system in liquefiable condition (T_Liq) can be calculated using the following equation [79]:

$${T}_{Liq}=2\pi \sqrt{\frac{M}{k}}$$

(18)

where, M is the lumped mass at the pile head and stiffness

$$k=\frac{12EI}{{L}_{0}^{2}}$$

(19)

The natural time period of soil-pile system obtained for 0.5, 0.75 and 1.0 m diameter M-30 grade concrete pile in RCD soil using Tables 7 and 9 are 3.37, 2.63 and 2.24 s respectively.

The time period of the soil-pile system in liquefiable condition are presented in Table 10 for various diameter M-30 grade concrete piles under different superstructure weight in RCD soil.

Table 10 Natural time period of soil-pile system in liquefiable condition for M-30 grade concrete pile of various configuration

It is observed from Tables 4 and 10 that predominant periods of the considered scenario earthquake motions are far away from the natural frequency of soil-pile system in liquefiable condition for 0.5, 0.75 and 1.0 m diameter M-30 grade concrete pile embedded in RCD soil. Hence, possibility of happening resonance in dynamic loading due to liquefaction for the considered case is not expected. However, proper assessment of natural frequency of soil-pile system in liquefiable condition depending on the pile properties and the superstructure weight is very much essential for safe design of pile foundation.

7 Summary and conclusions

In the present study, three-dimensional numerical study using an advanced nonlinear finite-element based computer program OpenSeesPL has been carried out to investigate the dynamic response of soil-pile system in liquefiable layered soil of Kolkata city under the influence of axial Loading. In this regard two soil formations have considered such as Normal Kolkata Deposit (NKD), and River Channel Deposit (RCD) to replicate typical soil layers of Kolkata metropolitan city. Two acceleration time histories, viz., Imperial Valley (1940) and Bhuj (2001), have been considered in the present analysis, and their PGA values are well within the reported range of Kolkata city. The present model is validated with the experimental results prior to carrying out parametric study. Then, a detailed systematic parametric study is performed for numerical simulation of pile failures in layered soil deposit of Kolkata city in liquefiable and non-liquefiable condition by taking into account various soil, pile parameters and ground motion characteristics. The major conclusions from the results of this study are as follows:

• 1. The weight of the super structure on pile foundation has profound influence on depth of liquefaction. It is noteworthy that the depth of liquefaction decreases significantly adjacent to the pile with an increase of superstructure weight. Hence, it is recommended to use effective ground improvement techniques like dynamic compaction for liquefiable soil adjacent to pile foundations instead of adopting heavy pile section.

• 2. The peak lateral displacement and bending moment decreases more in non-liquefiable condition with compared to the liquefiable condition due to decrease of axial load. So, kinematic force is predominant in liquefiable soil condition and inertial force is prevalent in non-liquefiable soil condition and mainly accountable for peak bending moment in the vicinity of pile head. Therefore, kinematic and inertial interaction should be carefully considered for safe and reliable design of pile foundations under different soil conditions.

• 3. The present results indicate that the laterally loaded slender end-bearing pile is prone to buckling failure mode in liquefiable soil when axial load on the pile exceeds certain percentage of P_all depending on the material and geometric properties of pile and input motion characteristics. Hence, it is recommended that larger diameter pile may be used in liquefiable soil to avoid buckling failure mode and thus is likely to fail because of bending also.

• 4. Parametric studies reveal that bending and buckling failure mode can be avoided by selecting a suitable combination of material strength and pile geometry for designing of piles under combined axial and lateral load in liquefiable soil.

• 5. It is observed that maximum kinematic bending moment is developed near the boundary between liquefiable and non-liquefiable layer due to stiffness contrast. Hence, extra care should be taken for designing of pile foundations in multi-layered soil profile as abrupt increase of bending moment may be occurred at the boundary due to change of soil stiffness.

It is worthy to consider various end conditions of pile, dynamic effects of superstructure on axial force, more ground motion records and performing cyclic simple shear or cyclic triaxial shear test to carefully calibrate the model instead of SPT correlation for future scope. Based on the parametric studies, the bending-buckling interaction analysis of slender piles is recommended for safe and reliable design of pile foundations in seismically liquefiable soil.