1 Introduction

A large number of coupling designs are available for torque transmission. For non-contact torque transmission, magnetic couplings are used, which use the force of a magnetic field. The use of magnetic couplings is effective in cable drums of cranes [1].

In cable drums, it is necessary to prevent cable breakage in case of unexpected cable snagging on objects while winding on the drum. This task is accomplished precisely because there is no rigid connection between the engine and the drum. This is the relevance of their use.

However, in addition to torque transfer, stopping when the equipment is turned off is also required. The non-contact transfer of stopping torque also prevents cable breakage in case of emergency. This paper deals with the method of calculating the parameters of a magnetic coupling with the presence of a stop and its experimental validation.

Many books and articles are devoted to the problems of modeling [2,3,4,5], designing [6,7,8] and heating [9,10,11] of magnetic couplings. In the rest of this section, we will consider some related works.

Many books and articles are devoted to the problems of optimizing magnetic couplings. A full mathematical model is described in [12]. The calculation method described in the article is difficult to use in engineering practice. Calculation methods based on FEM [13, 14] allow to achieve high accuracy of the results, but they are labor-intensive at the initial stages of the design procedure. To achieve a compromise between the complexity, accuracy, and difficulty of calculations, it is convenient to use approximate analytical methods.

A coupling consisting of a copper disk and a disk with permanent magnets were described in [15]. Its torque function was obtained and validated experimentally. Due to the presence of slip, the copper part heats up and loses its conductivity. The torque function takes these losses into account, however, it does not take into account the heating of the magnets and the losses in their magnetic properties.

The design and mathematical model of coupling cooling are presented in [16]. However, it does not take into account the real design features or the presence of radiant heat transfer and thermal conductivity of parts. In this paper, the cooling model is refined and experimentally validated. The resulting mathematical model is convenient for engineering use and requires no additional expensive software.

In [17], a mathematical model of the stop is proposed, but it does not take into account the different values of the torque at different polarities of the magnets.

All the above-mentioned articles ignore the cost of making the coupling and the actual operating conditions. The problem of large heating and efficient cooling significantly increases the cost of design. And it is necessary to revise existing calculation methods for practical application in mechanical engineering.

Moreover, there is a need to combine both the coupling and the stop inside one design. The mutual influence of the stop on the working part of the coupling is theoretically absent, but it is necessary to check when working in real operation. There are no articles on the study of the joint operation of the coupling and the stop.

The purpose of the work is an experimental study of the magnetic coupling combined with a stop in real working conditions, verification, and validation of the developed mathematical model of torque and cooling. The model developed model should be effective for engineering use at the design stage of magnet couplings, especially for cable drums of cranes.

The paper is organized as follows. First, we describe the design of the coupling, its working conditions, and technological limitations. Then we proceed to the description of the mathematical model of the coupling and stop operation, the model of convective cooling. The original model has been refined. In the next section, we describe the experimental setup and make a plan for the experimental validation. In the last part, we present the results of the experiment. The correlation between the model and the experiment and the correction factor are obtained.

2 Design and working conditions

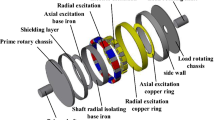
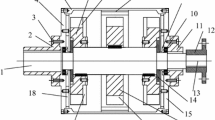
In this section we describe design and working conditions of the resulting coupling. Description of technical and technological problems and cooling problem are presented here. A sketch of the coupling combined with the stop is shown in Fig. 1. The coupling parameters are shown in Fig. 2. The coupling consists of a copper disk (1), an impeller (2), a stop consisting of two disks (5,6) with permanent magnets (3,4), a rotating housing with cooling fins (7).

Fig. 1
figure 1

Sketch of the coupling

Full size image
Fig. 2
figure 2

Side cut of the coupling

Full size image

The input shaft of the engine rotates the working part of the coupling with a copper disc, housing, and impeller, as well as with a stop disc. The rotating copper disc interacting with fixed permanent magnets creates a torque that exceeds the stop torque.

The flux linkage of the permanent magnets in the disks (5,6) creates a stopping torque. The stopping torque holds the cable drum when the equipment is not in operation.

The impeller and housing provide efficient cooling of the coupling at high slip. Its production is carried out on CNC machines. It is necessary to ensure a minimum radial run-out between the copper disc (1) and the disc with magnets (4). As it will be shown below, radial run out with a small gap significantly affects the torque.

3 Mathematical modeling

In this paper, we use a mathematical model based on Maxwell theory to design the coupling. Rotating permanent magnets create an eddy magnetic field that crosses the copper disk. At the same time, an induced EMF arises in the disk, which causes eddy currents in the copper plate. As a result, there is a conjugation of flows that leads to a system of partial differential equations, the solution of which can be performed in cylindrical coordinates using Bessel functions [5]. However, the articles [10, 18] state that the edge effects are insignificant and it is possible to reduce the problem to a linear three-dimensional one in Cartesian coordinates.

To find the coupling torque we use Eq. (1) proposed by [11]. The author [11] used Governing field equations and showed a detailed derivation of the coupling torque equation. Equation (1) reflects the dependencies on the geometric characteristics of the coupling and its parts, as well as on the properties of the material. The equations take into account the change in conductivity properties of copper and magnets when heated.

To calculate the torque, we introduced a number of assumptions. Both induced current losses and eddy losses at high slip values are not taken into account. During experimental study, a correction factor was obtained that takes into account the above losses.

$$ \begin{gathered} T_{e} = \frac{1}{2}\mu _{0} p^{2} \tau R_{3} \mathcal{R}\left( {\sum\limits_{{n = 1}}^{K} {\sum\limits_{{k = 1}}^{K} j } k\frac{{M_{{nk}}^{2} }}{{\alpha _{{nk}} }}{\mathbf{r}}\sinh \left( {\alpha _{{nk}} b} \right)} \right), \hfill \\ M_{{nk}} = \frac{{16B_{r} \left( \theta \right)}}{{\pi ^{2} \mu _{0} nk}}\sin \left( {k\alpha \frac{\pi }{2}} \right)\sin \left( {n\frac{\pi }{2}} \right)\left( {\frac{{R_{2} - R_{1} }}{{R_{3} }}} \right), \hfill \\ \tau = \frac{\pi }{2}R_{m} ,r = - \frac{{\cosh \left( {\alpha _{{nk}} c} \right)\sinh \left( {\gamma _{{nk}} } \right) + \frac{{\alpha _{{nk}} }}{{\gamma _{{nk}} }}\sinh \left( {\alpha _{{nk}} c} \right)\cosh \left( {\gamma _{{nk}} } \right)}}{{\cosh \left( {\alpha _{{nk}} \left( {b + c} \right)} \right)\sinh \left( {\gamma _{{nk}} d} \right) + \frac{{\alpha _{{nk}} }}{{\gamma _{{nk}} }}\sinh \left( {\alpha _{{nk}} \left( {b + c} \right)} \right)\cosh \left( {\gamma _{{nk}} d} \right)}}, \hfill \\ \alpha _{{nk}} = \sqrt {\left( {\frac{{n\pi }}{{R_{3} }}} \right)^{2} + \left( {\frac{{k\pi }}{\tau }} \right)^{2} } , \hfill \\ \gamma _{{nk}} = \sqrt {\left( {\frac{{n\pi }}{{R_{3} }}} \right)^{2} + \left( {\frac{{k\pi }}{\tau }} \right)^{2} + j\sigma \left( \theta \right)\mu _{0} \Omega R_{m} \frac{{k\pi }}{\tau }} , \hfill \\ \sigma \left( \theta \right) = \frac{{\sigma _{0} }}{{1 + \alpha _{t} \theta }}, \hfill \\ \end{gathered}$$
(1)

where p is number of poles, \(\sigma \) is electrical conductivity of the copper, \(B_r\) is remanence of the permanent magnets, \(\varOmega \) is the slip speed, and \({\varTheta }\) is the temperature of material.

The magnets of the stop are axially magnetized. Through magnetic interaction, the torque applied to one disc is transferred through an air-gap to the other disc. To find the stop torque we use the mathematical model proposed by [17]. The author [17] reduced 3-D problem to 2-D problem, which makes the axial magnetic coupling equivalent to a linear magnetic coupling. He developed simple formulas for the axial and tangential components of the flux density in the air gap. The stop torque for direct polarity is calculated by Eq. (2).

$$\begin{aligned} \begin{aligned}&T_b\,=\, \frac{16 B^2_r}{3 \pi \mu _0} R^2_3 \left( 1-\left( \frac{R_4}{R_6} \right) ^2 \right) \sin ^2 \left( \alpha \frac{\pi }{2} \right) \frac{\sinh ^2 (v)}{\sinh (2(1+v)f)},\\&f \,=\, p \frac{h}{R_5},\\&v\, =\, \frac{e}{2h}. \end{aligned} \end{aligned}$$
(2)

According to the Eq. (2), the main dimensions of the coupling are determined. The next task is the constructive provision of cooling.

As a result of a high slip during the operation of the coupling, a high thermal power occurs. The thermal power is assumed to be equal to \(P\,=\,T_e \varOmega \), the heat flow is distributed to the surface of the copper disk.

Convective and radiant heat transfer occurs during operation. Part of the heat is transferred to the housing and the engine through the contact of parts. Analytical calculation of the transient problem is impossible. Numerical calculation and accounting of all these factors are labor-intensive [19,20,21]. Therefore, we describe steady-state problem.

The surface temperature of the coupling is calculated according to Eq. (3) proposed by [22]. The thermal power is calculated according to the torque calculated equation by Eq. (1), that takes into account that there is no change of conductivity of copper and magnets during heating. Therefore, the torque calculation must be performed sequentially. According to the obtained temperature, the conductivity of copper and magnetization of magnets are recalculated as functions of slip.

$$\begin{aligned} \begin{aligned}&\theta \,=\, \theta _0+ \frac{P_J}{h_1S_1+H_2S_2},\\&P_J\,=\, T_e \omega ,\\&h_1 = \frac{\kappa Nu}{L}, \\&Nu\,=\, a_1 Re^{1/2} Pr^{1/3},\\&Pr \,=\, \frac{C_p \mu }{\kappa }. \end{aligned} \end{aligned}$$
(3)

In Eq. (3), \(P_J\) is the thermal power, \(a_1\) is coefficient of forced convection [22], \(c_p\) is specific heat capacity, \(\mu \) is dynamic viscosity, and \(\kappa \) is specific thermal conductivity.

We solved the problem by the iterative approach. At the first step we calculated the temperature of the copper disk and magnets for a higher torque without taking into account losses of the properties. At the second step we used Eq. (3) to find the temperature. At the third step the values of electrical conductivity of the copper and remanence of the permanent magnets due to higher temperature were obtained and substituted in Eq. (1)

The results of the analytical calculation of the surface temperature of the coupling are shown in Fig. 3.

Fig. 3
figure 3

Coupling surface temperature

Full size image

To calculate the temperature, it is necessary to take into account the cooling of the coupling surface by the airflow generated by the rotation of the impellers of the coupling itself, i.e. there is a process of forced convection. To determine the factors affecting the efficiency of convective heat transfer, we use the thermal similarity criterion. In this case, with convective heat transfer of the airflow and coupling surface with a guaranteed turbulent flow \((Re >10^4)\), the criterion of thermal similarity is Nusselt coefficients (Nu).

The torque function on the output shaft of the coupling without considering the heating effect (T) and considering the heating effect of the copper part and magnets (\(T^*\)) is shown in the Fig. 5. The stop torque is shown in Fig. 4. The temperature dependence on the slip is shown in Fig. 5. A temperature of 112 °C was calculated for slip \(\varOmega\, =\,2160\) rpm. According to the calculated convective heat transfer coefficient, a verification FEM temperature calculation and magnetostatic calculation was performed in ANSYS Mechanical. To provide the FEM temperature calculation, we use the following assumptions:

  1. 1.

    Steady-state conditions.

  2. 2.

    Radiant heat transfer is negligible compared to the convective and thermal conductivity of parts.

  3. 3.

    The temperature on the input shaft of the electric motor is constant.

  4. 4.

    The air temperature at the surface is constant.

Using the above formulas, we determine the main dimensions of the coupling. The next task was the constructive provision of cooling.

Fig. 4
figure 4

Stop torque

Full size image
Fig. 5
figure 5

Coupling output torque

Full size image

The calculation results are shown in Figs. 6 and 7. The surface temperature of the copper disk was 129 °C, i.e. the difference between numerical and analytical solutions is 15%. Figure 5 shows the comparison of torques without heating (T) and with heating (\(T^*\)). The maximum stop torque was 0.85 Nm, i.e. the difference between numerical and analytical solutions is 7%.

Fig. 6
figure 6

Results of the steady state heat transfer simulation, Temperature in °C

Full size image
Fig. 7
figure 7

Results of the magnetostatic simulation for gap 3 mm, Total magnetic flux density in mT. Maximum stop torque is 0.85 Nm

Full size image

4 Experiment plan

Two experiments were designed for the experimental study of magnetic coupling: a two-factor experiment and a one-factor experiment. The factors were assumed to be linear and independent. The variable factors were the gap in the working part of the coupling, the rotation speed of the electric motor, and the gap between the magnets in the stop. The controllable factor was the coupling torque. The test in real working conditions was also carried out. A sketch of the experimental setup is shown in Fig. 8.

Fig. 8
figure 8

Experimental setup

Full size image

The complex of laboratory setup included a magnetic coupling and a drive based on an asynchronous motor, controlled by frequency converter FC-301 P4K0T4E20H2 (Danfoss), the coupling was rigidly fixed on the motor shaft.

The converter was controlled from remote control on the stand, where rotation speed signals were generated using buttons that simulate various operating modes. Braking of the asynchronous motor was carried out by free run-out.

The frequency converter control module, connected to the USB 2.0 bus of the computer allows observing and registering the variable parameters of the electric drive (actual motor speed, preset value of the motor rotation speed, actual current, preset value of current, shaft load torque).

5 Results of the experimental study

To validate the developed methodology, we tested the designed coupling for three values of gaps. In all tests, we observed lower torques compared to the calculated ones. The average relative difference was 0.75, but the type of dependence corresponded to the theoretical one. The experiment showed that the accuracy of making the parts to ensure the constancy of the gap has a significant impact on the torque. According to the results of the calculations using a mathematical model, the difference in torque at 2100 rpm was 19%.

When the gap is small, the mathematical model shows greater sensitivity of the torque to the input parameters. At a gap of 2 mm or less, the coupling behavior be- comes less predictable.

Based on the results of the experiment, a regression equation was compiled for the coupling under study:

$$\begin{aligned} M\,=\,1.51\,-\,0.63c\,+\,0.27n, \end{aligned}$$
(4)

where c is the gap, n is the slip speed.

The graphs of the obtained dependencies are shown in Fig. 9. The obtained model correlation confirms the possibility of using the model with a correction factor of 0.75. The difference in torque does not depend on the gap, speed of rotation, assembly process and is is inherent in the design or materials. The stop has no effect on torque.

Fig. 9
figure 9

Comparison of mathematical models

Full size image

5.1 Checking the stop torque

The operation of the coupling was tested in the parking stop mode. The results are shown in Fig. 10. The stop torque was 10% higher than the calculated one. The mathematical model of the stop is adequate to the real one. The stop magnets do not affect the operation of the coupling.

Fig. 10
figure 10

Stop torque

Full size image

6 Discussions

It should be noted that the production cost of this type of magnetic coupling remains high. Ensuring manufacturing accuracy and reducing dimensional tolerances of parts significantly increases the cost of construction, however, it is necessary for providing the specified output torque and smooth running. So, additional cost-effectiveness studies of the design and manufacture of a magnetic coupling are required. In addition, it is necessary to study the work of magnetic couplings with high slip, because using asynchronous motors in mechanical engineering more is profitable.

Using copper discs for torque transmission is quite expensive. This fact requires the study of magnet couplings with discs made of other magnetic materials. Finding a trade-off between design efficiency and cost remains a major challenge for manufacturing.

7 Conclusions

The method and mathematical model for calculating the parameters of a magnetic coupling combined with a stop have been developed. The resulting mathematical model is convenient for engineering use and requires no additional expensive software. The developed model takes into account the decrease of properties of magnets and copper during heating, as well as the operation of the coupling when fixing the torque. The experiment showed the influence of manufacturing accuracy and eddy losses at a high slip speed on the torque.

In accordance with the developed method, the coupling was designed and tested experimentally. A correlation between the mathematical model of the coupling and the experiment was obtained. A correction factor of 0.75 was introduced into the mathematical model to account for torque reduction due to inaccuracies in coupling fabrication and eddy losses at high slip speed. The analytical calculation of convective heat transfer combined with numerical calculation using the FEM makes it possible to effectively solve the problem of the cooling design. At the same time, it is important to take into account the cost of its manufacturing.

7.1 Future works

Since the function of eddy losses is non-linear, and the magnetic coupling operates on a high slip, an additional study of the dependence of the correction factor on the slip value is required. It is also required to perform electromagnetic FEM simulation of the coupling.