1 Introduction

Wave energy, as a clean energy with a large reserve [1], is used worldwide, and its energy density increases significantly during autumn and winter [2,3,4]. Among the various types of wave energy generation devices, point absorption wave energy generators, which are wave energy conversion devices with a better comprehensive performance than other wave energy conversion devices, have attracted the attention of many scholars [5,6,7]. As the energy-capturing device of a point absorption wave energy generator, the float is directly stimulated by the wave and converts the wave energy into kinetic energy, which is the first-order energy conversion for the entire power-generation system. Therefore, researching and developing a wave energy conversion device is a necessary step when studying the energy-capturing characteristics of floats in order to achieve the maximum energy gain [8].

Scholars have conducted many research studies on the influencing factors of float energy capture characteristics. Liu [9], McCabe [10], Garcia-Teruel [11] and Dong [12] used finite element simulation analysis or algorithm optimization to analyze the influence of different float shapes on the float energy-capturing characteristics. Gao studied the wave absorption efficiencies and output powers of floats with different masses operating under the same conditions [13]. Based on these trends, Fang designed and proposed a quality-adjustable float to adapt to different sea conditions [14]. Marten Hollm studied the energy-capturing characteristics of floats with different tilt states [15]. Ma analyzed the influences of the float shape, the maximum width, and the centroid position on the hydrodynamic performance of a float to be used in a wave energy conversion device operating in the harsh environment of the South China Sea [16]. Gao [17], Zheng [18] and Huang [19] discussed the influence of the wave incidence angle and the float draft depth on the wave force using a cylindrical float model in a specific environment. Stansby found that different draft depths lead to different resonance frequencies [20]. Cai proposed the active resonance wave energy conversion technology using the concept of resonance in a wave energy system and optimized the float body according to the linearized vibration mode of the wave energy system [21]. The experimental verification showed that the conversion efficiency of the wave energy conversion device could be greatly improved using this method. Luan found that the power take-off (PTO) damping of the float can affect the motion response of the float, which in turn affects the resonant frequency of the float [22]. However, Alper Burgac studied the effect of the ratio of PTO damping and radiation damping on the energy-capturing characteristics of the float [23]. However, Zhi proposed a PTO damping control method and conducted a coupling study using floats with different bottom shapes to explore the variations in the energy-capturing characteristics of floats [24].

Many factors affecting the energy-capturing characteristics of floats have been analyzed by scholars. However, there are few studies that simultaneously investigated the resonance performance and the capture width ratio of a float, and changes in the energy-capturing characteristics of floats under the influence of multiple factors were seldom considered. In this study, four common types of floats (conical, frustum, spherical, and cylindrical) were selected. The factors affecting the energy-capturing characteristics of the floats were analyzed according to the mathematical model for float movement on a wave surface. Based on this analysis, an orthogonal level table was constructed, and orthogonal experiments were conducted using hydrodynamic simulation analysis tools, such as AQWA, to calculate the degree of influence each factor had on the energy-capturing characteristics of the floats [25]. Based on the frequency domain, the variation trends in the energy-capturing characteristics of the floats when influenced by multiple factors were summarized. The conclusions obtained from this study can provide a reference for the design and optimization of floats and further research into wave energy devices.

In Sect. 2, we derive the factors influencing the energy-capturing characteristics of a float based on a mathematical model of its motion in waves. In Sect. 3, we use AQWA to perform hydrodynamic simulation and orthogonal tests on four common floats. The results are discussed in Sect. 4. In Sect. 5, we present the conclusions of this study.

2 A mathematical model for float motion in waves

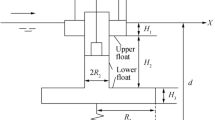
The motion of a float in a wave is shown in Fig. 1. The force exerted by the waves on the float was divided into a wave force, a hydrostatic restoring force, and a radiation force:

$$F_{{\text{w}}} = F_{{\text{v}}} + F_{{\text{s}}} + F_{{\text{c}}} + mg = (m_{1} + m_{{\text{a}}} ) \times a$$
(1)

In Eq. (1), Fv is the wave force (N), which is composed of the Froude-Krylov (F-K) and diffraction forces: \(F_{{\text{v}}} = F_{{{\text{F}} - {\text{K}}}} + F_{{\text{d}}}\). The calculation is based on the F–K assumption method, which assumes that the space occupied by the float is filled with fluid, this generates acceleration due to wave propagation. Then, there must be a pressure field around the fluid that is similar to the pressure field around the float. The wave force acting on the float can be calculated by integrating the pressure on the wet surface of the float. \(F_{{\text{s}}}\) is the hydrostatic restoring force (N), \(F_{{\text{s}}} = - \rho gA_{{{\text{wp}}}} x\), which represents the different forces exerted by the water on the float when it rises and falls in the water for different distances in order to return to its equilibrium position. \(\rho\) is the density of seawater (kg/m3). g is the acceleration due to gravity (N/kg). x is the distance between the float and its equilibrium position (m). \(A_{{{\text{wp}}}}\) is the cross-sectional area of the float on the water surface (\({\text{m}}^{{2}}\)). If the float is cylindrical with a radius r, then \(F_{{\text{s}}} = - \rho g\pi r^{2} x\). \(F_{{\text{c}}}\) is the radiation force (N), \(F_{{\text{c}}} = - i\omega xP_{{\text{c}}}\). \(\omega\) is the circular wave frequency (rad/s). \(P_{{\text{c}}}\) is the damping coefficient. \(m_{1}\) is the mass of the float (kg). \(m_{{\text{a}}}\) is the additional mass of the float (kg), which represents the mass of water excited by the float during its reciprocating motion. The additional masses of differently shaped floats are different. a is the acceleration of the float (N/kg).

Fig. 1
figure 1

The motion of a float in a wave

Full size image

The radiation force exerted by the wave on the float was assumed to be equivalent to the damping force of a damper, and the hydrostatic restoring force of the sea water was set equivalent to the elastic force of a spring. The motion of the float in the wave was then equivalent to a second-order damped forced vibration, with an equation of motion expressed as follows:

$$(m_{1} + m_{{\text{a}}} )\ddot{x} + c\dot{x} + \rho g\pi r^{2} x = F_{{\text{w}}}$$
(2)

In Eq. (2), c represents the equivalent damping coefficient. Then, the natural vibration frequency could be expressed as follows:

$$\omega^{\prime} = \sqrt{(\rho g \pi r^{2}/(m_1 +m_{\rm a})}$$
(3)

The mass of the float, m1, could be expressed by its draft depth h:

$$T^{\prime} = 2\pi \sqrt {\left(1 + \kappa \right)h/g}$$
(4)

In Eq. (4), \(T^{\prime}\) is the natural period of the float (s), and \(\kappa = m_{\text{a}}/m_{1}.\)

According to Yin [26], the wave force can be calculated as follows:

$$F_{{\text{v}}} = \left[ { - \left( {m_{1} + m_{{\text{a}}} } \right)\omega^{2} + \rho gA_{{{\text{wp}}}} - i\omega P_{{\text{c}}} } \right]x$$
(5)

Equation (6) expresses the average output power of the float:

$$N = \frac{1}{2}\omega^{2} F_{{\text{v}}}^{2} \frac{{P_{{\text{c}}} }}{{K^{2} + \omega^{2} P_{{\text{c}}}^{2} }}$$
(6)

K from Eq. (6) is defined as follows:

$$K = - \left( {m_{1} + m_{{\text{a}}} } \right)\omega^{2} + \rho gA_{{{\text{wp}}}}$$
(7)

The input wave power within the width of the float could be calculated as follows:

$$W = \left[ {1 + \frac{2Lk}{{\sinh (2Lk)}}} \right]\frac{{A^{2} \rho g\omega B}}{16k}$$
(8)

In Eq. (8), L represents the depth of the water where the float is located (m), k is the wave number (m−1), A is the wave height (m), and B is the width of the float (m).

The float capture width ratio, which is the ratio of its average output power to the input wave power within the float width, is an important indicator of a float’s ability to absorb wave energy:

$$\eta = \frac{N}{W}$$
(9)

The response amplitude operator (RAO) concept is also introduced here, and it is defined as the ratio between the displacement amplitude of the float and the amplitude of an incident wave. This value represents the motion of the float. A large RAO value represents intense float motion, indicating a situation that is conducive to the absorption of energy.

Based on the float motion analysis presented above, Eqs. (6), (7), and (8) indicate that the float shape and the maximum radius of the float affect the additional mass and the radiation damping, thus affecting the capture width ratio of the float. Meanwhile, Eq. (4) shows that changes in the draft depth and the additional mass of the float also cause changes in the float resonance frequency.

3 Orthogonal test for energy-capturing characteristics of floats

According to the mathematical model for float motion in waves, the float shape, the maximum float radius, and the float draft depth affect the capture width ratio, the amplitude response operator, and the resonance frequency of the float. Therefore, the orthogonal test principle could be used to solve this multi-factor problem.

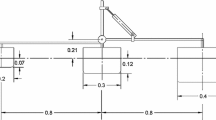
To study the influence of the factors mentioned above on the hydrodynamic performance of a float, the same float height should be used because of the control variables principle. Four common float shapes were initially selected in this study: conical, frustum, spherical, and cylindrical. The height of each float type, H, was constrained to 1.8 m, the bottom radius of the frustum float, r2, was greater than or equal to 0.1 m, the semi-apex angle, θ, of the frustum was 30°. The specific float configurations are shown in Fig. 2.

Fig. 2
figure 2

Float model shapes: a conical, b frustum, c spherical, and d cylindrical

Full size image

The range of the float maximum radius, r1, was selected to be 0.8–1.4 m, which was divided into four levels at 0.2 m intervals. The range of the float draft depth, h, was selected to be 0.6–1.5 m, which was divided into four levels with 0.3 m intervals. Table 1 presents specific information regarding the factors and levels. After determining the factors and levels, a horizontal orthogonal table, \(L_{16} (4^{3} ),\) with three factors and four levels was constructed using the software SPSSUA. The float capture width ratio, the float resonant frequency point, and the float amplitude response operator were selected as the optimization objects. AQWA simulation analyses were used to insert the corresponding simulation results into the horizontal orthogonal table, as shown in Table 2. To facilitate the presentation of the results, factor A represented the float shape, factor B represented the maximum float radius, and factor C represented the float draft depth.

Table 1 Factors and levels of optimization objects
Full size table
Table 2 Horizontal orthogonal table of experimental results
Full size table

Range analysis was conducted based on the data in Table 2. The range of a factor, R, reflected the variation range of the experimental target value when the factor level changed. An increase in the range of a factor indicated that, compared with other factors, the influence of this factor on the experimental target value is greater. The calculation method used for this analysis was relatively simple. For example, AI is the mean value of all experimental target values when the A-factor (float shape) was at level 1 (conical float):

$$AI = \frac{A1B1C1 + A1B2C2 + A1B3C3 + A1B4C4}{4}$$
(10)

In Eq. (10), Ai represents the A-factor at level i, Bi represents the B-factor at level i, and Ci represents the C-factor at level i.

The changing trend of the mean experimental target values for each factor at different levels reflected the changing trend of the experimental target values as the level changed under the action of a certain factor.

The range of a factor is the difference between the maximum and minimum mean values of all the experimental objective values for this factor at all the levels. Taking factor A (float shape) as an example, the range of this factor is expressed as follows:

$$R = \max (Aj) - \min (Aq)$$
(11)

In Eq. (11), Aj and Aq are the mean values of all the experimental target values for factor A (float shape) at levels j and q, respectively.

The results of these calculations are listed in Tables 3, 4 and 5, where the test target in Table 3 is the float capture width ratio, the test target in Table 4 is the float resonance frequency, and the test target in Table 5 is the float amplitude response operator.

Table 3 Range analysis table for the float capture width ratio from the orthogonal test
Full size table
Table 4 Range analysis table for the float resonance frequency from the orthogonal test
Full size table
Table 5 Range analysis table for the float amplitude response operator from the orthogonal test
Full size table

For example, R1A represents the A-factor range affecting the float capture width ratio, R2A represents the A-factor range affecting the float resonance frequency, and R3A represents the A-factor range affecting the float amplitude response operator. The range analysis results in Tables 3, 4 and 5 show that for the float capture width ratio, R1A > R1B > R1C, for the float resonance frequency, R2A > R2C > R2B, and for the float amplitude response operator, R3A > R3B > R3C. Comparisons of the mean experimental target values for all factors at different levels are presented next. For the float capture width ratio, AI < AII < AIII < AIV, BIV < BIII < BII < BI and CII < CI < CIII < CIV. For the float resonance frequency, AIV < AIII < AII < AI, BIV < BIII < BII < BI and CIV < CIII < CII < CI. For the float amplitude response operator, AI < A < AII < AV, BIV < BIII < BII < BI and CI < CII < CIII < CIV.

Table 3 and 5 show that, among the factors affecting the float capture width ratio and the float amplitude response operator, A (float shape) was the primary factor, B (maximum float radius) was the secondary factor, and C (float draft depth) had the least influence. The capture width ratio and the float amplitude response operator increased as the float shape changed from conical, frustum, and spherical to cylindrical. When the maximum radius of the float was larger, the capture width ratio and the amplitude response operator of the float were smaller. With the increase in the float draft depth, the float capture width ratio decreased and then increased, and the float amplitude response operator increased continuously.

Table 4 shows that, among the factors affecting the float resonant frequency, A (float shape) was again the primary factor, C (float draft depth) was the secondary factor, and B (maximum float radius) was again the least influential factor. Unlike the above results, the float resonance frequency decreased as the float shape changed from conical, frustum, and spherical to cylindrical. A large maximum float radius led to a low float resonant frequency. A high float draft depth led to a low float resonance frequency.

4 Results and discussion

According to the data presented in Sect. 3, to select the maximum capture width ratio for floats of various shapes, a horizontal combination for the maximum capture width ratio could be selected based on factor A (float shape), such as BI (the maximum float radius was 0.8 m) and CIV (the float draft depth was 1.5 m). To verify the correctness of the orthogonal test results and to reflect the significance of the influence of each factor on the float hydrodynamic performance, the minimum float capture width ratio for each shape of floats was selected and a corresponding degree of improvement in the float capture width ratio was calculated. The horizontal combination selected was BIV (the maximum float radius was 1.4 m) and CII (the float draft depth was 0.9 m). The horizontal combination of the selected factors is shown in Table 6, and the corresponding hydrodynamic characteristics of the float are shown in Figs. 3 and 4. To facilitate the presentation of the results, the symbols are defined, the meanings of which are provided in Table 7.

Table 6 Selection of various factors for different applicable conditions
Full size table
Fig. 3
figure 3

Hydrodynamic characteristics of floats with different shapes at the maximum capture width ratio: a capture width ratio, b wave force, and c RAO

Full size image
Fig. 4
figure 4

Hydrodynamic characteristics of floats with different shapes at the minimum capture width ratio: a capture width ratio, b wave force, and c RAO

Full size image
Table 7 The meaning of the float symbol
Full size table

Four main conclusions are obtained from Figs. 3(a) and 4(a). First, for both \({\text{Float}}_{{{{\max\eta }}}}\) and \({\text{Float}}_{{{{\min\eta }}}}\), the float capture width ratio was the largest for the cylindrical float, which decreased sequentially for the spherical float, the frustum float and the conical float. Second, for both \({\text{Float}}_{{{{\max\eta }}}}\) and \({\text{Float}}_{{{{\min\eta }}}}\), the dramatic changes in the float capture width ratio were the largest for the cylindrical float, which decreased sequentially for the spherical float, the frustum float and the conical float. Third, the frequency range of efficient energy-capturing for \({\text{Float}}_{{{{\max\eta }}}}\) was small, that is, the float resonance frequency range was small. However, the float resonance frequency range for \({\text{Float}}_{{{{\min\eta }}}}\) was large. Fourth, the maximum capture width ratio did not necessarily occur at the float resonance frequency because the capture width ratio was also affected by the additional mass, the radiation damping, and the wave force; these factors were also indirectly reflected in the float shape, the maximum float radius, and the float draft depth.

Two main conclusions are obtained from Figs. 3b and 4b. First, for both \({\text{Float}}_{{{{\max\eta }}}}\) and \({\text{Float}}_{{{{\min\eta }}}},\) the magnitude of the change in the wave force decreased sequentially from the cylindrical float to the spherical float, the frustum float and the conical float. Second, compared with \({\text{Float}}_{{{{\max\eta }}}}\), the float shape for \({\text{Float}}_{{{{\min\eta }}}}\) tended to be flatter, which caused it to be subject to a larger wave force, with a maximum value of 60,000 N. However, the float capture width ratio was not significantly correlated to the wave force received by the float, which can be determined by the float shape, as shown in Table 8. Therefore, the wave force acting on the float is not the most powerful basis to judge the energy-capturing characteristics of the float.

Table 8 Improvement rates for the wave forces and capture width ratios for floats of various shapes
Full size table

Two main conclusions are obtained from Figs. 3c and 4c. First, the performance of the float amplitude response operator was similar to that of the float capture width ratio, indicating a significant correlation between them. Second, for both \({\text{Float}}_{{{{\max\eta}}}}\) and \({\text{Float}}_{{{{\min\eta }}}},\) the steepness in the RAO changes decreased sequentially from the cylindrical float to the spherical float, the frustum float and the conical float.

Although some conclusions have been drawn from the research, some shortcomings and room for development remain. The orthogonal test method still has some limitations. This method cannot obtain the optimal combination of levels at a particular frequency. In this study, only four types of common float shapes were investigated, and other combined or special float shapes are still to be considered. In addition, this study only analyzed the maximum float radius and the float draft depth at four levels. These questions will be supplemented in future research.

5 Conclusion

In this study, based on different float shapes, different maximum radii, and different draft depths, the orthogonal test method was combined with AQWA hydrodynamic simulations to comprehensively analyze the hydrodynamic characteristics of floats in the frequency domain. According to the horizontal orthogonal table, the influence degrees of the different factors on the test target were obtained. Finally, the float with the maximum capture width ratio and the float with the minimum capture width ratio were selected for comparative study, and the capture width ratio, wave force, and amplitude operator curves were plotted.

Three primary conclusions were drawn from this research. The influence degree of each factor on the capture width ratio and resonance frequency of the float is in descending order: Float shape > Float draft depth > Maximum float radius. The influence degree of each factor on the amplitude response operator of the float is ranked from large to small: Float shape > Maximum float radius > Float draft depth. In addition, at a higher draft depth, a “slender” float shape had a larger capture width ratio and amplitude response operator but a smaller resonance frequency. Compared with a “slender” float shape, at a lower draft depth, a “flat” float shape had a smaller capture width ratio and amplitude response operator but a larger resonance frequency. The key point is that the float capture width ratio was significantly correlated with the float resonance frequency. However, the maximum float capture width ratio was not necessarily at the resonance frequency. The float capture width ratio was also affected by the additional mass, the radiation damping and the wave force. These factors were indirectly reflected in the float shape, the maximum float radius, and the float draft depth. The float capture width ratio had little correlation with the wave force received by the float, which could be determined by the float shape. Therefore, the wave force acting on the float is not the most powerful basis to judge the energy-capturing characteristics of the float.