1 Introduction

Concrete is the most widely used material in the construction of various infrastructures throughout the world. Various types of concrete have also been invented. Each type of concrete offers certain advantages to resolve specific problems related to the construction process and post-construction performance. One of the concrete types that was developed as a response to the problem of casting work, especially in congested reinforcements, is self-compacting concrete (SCC). This type of concrete can flow and fill narrow spaces between reinforcements independently, without requiring external energy intervention. The flowing properties of this concrete are possible due to a moderate level of viscosity. Viscosity at moderate levels can be met through a higher proportion of fine materials compared to conventional concrete [1]. However, the need for a large amount of fine materials should not be fulfilled solely by relying on high cement content, especially when considering environmental issues. Compared to other components, cement is a major contributor to carbon dioxide (e-CO2) emissions in concrete production. The amount of CO2 contained (embodied CO2) in cement (calculated in kg CO2 per kg of concrete) is around 0.83 [2]. Therefore, substituting some cement with other cementitious material becomes a practical way to reduce e-CO2. Fly ash is an example of cementitious material that may be used as cement substitution. This material is a waste and is abundantly available in a coal power plant. Thus, utilizing large amounts of fly ash as a partial replacement of cement is a way to realize environmental friendly concrete [3].

Research on the use of high-volume fly ash (HVFA) in concrete has been carried out for many years by various researchers, either investigating mechanical [4], structural element [5] or durability related performance [6]. With regard to structural performance, the ability of reinforced concrete beams to carry a load is a result of combining the strengths contributed by the concrete and reinforcement as a composite system. In this composite system, reinforcement must be firmly embedded into the concrete so that when it is subjected to tensile stress, the reinforcement can develop sufficient strength to resist the induced tensile stress. The strength development in the reinforcement is influenced by the bond between the concrete and the reinforcement [7]. This bond is provided via adhesion, friction and mechanical interlocking [8]. The magnitude of this bond strength will determine the needed length for the embedded reinforcement (development length) so that when receiving tensile loads, the stress on the reinforcement effectively reaches its yield stress [9].

In general, development length is fulfilled automatically in a reasonable beam span. However, in certain situations (for example in a very long span beam), the available reinforcement length may be limited so there is no other option except to use a lap splice for the connection. In this part of the connection, the transfer of stress from the spliced reinforcement to the concrete will be effective if the minimum splice length is fulfilled [10]. The splice length is related to the development length, which allows the reinforcement to develop a strength to reach its yield state. If the splice length is too short, splitting of concrete in the spilced zone can occur resulting in lower flexural capacity and brittle failure mode [11]. Another possible failure mode is a slippage of the embedded spliced reinforcement especially in beam reinforced with plain bar [12]. Slippage can occur at the connection even though the tensile stress on the reinforcement may be still below the yield stress. Consequently, the respective reinforced concrete beams are only able to carry flexural loads at a lower level than they should. In the opposite case, if the splice length is too long, there will be wasted reinforcement because the excess length of the splice length may not significantly increase the strength of the beam. Thus, it is very important to determine the splice length requirement for effective and efficient design [13].

Apart from the strength requirement, the performance of beams under flexural loading must also conform to other safety and serviceability requirements [14]. As an example, the designer must provide a ductile behavior for reinforced concrete beam [15]. This requirement will ensure that there are a noticeable warning and sufficient time for occupants to exit the building before collapse. Ductile behavior can be expected by applying an under-reinforced design concept. Over length of splices could increase the reinforcement ratio that may cause a change the ductile level of the respected reinforced concrete beam. On the other hand, insufficient splices length can induce splitting of concrete or slippage of the splice reinforcements with a consequence of brittle failure. Therefore, the minimum required splice length should be determined by considering the whole performance parameters of the respected reinforced concrete beam and not just the strength [16].

In the Code of Practices, the minimum splice length can be calculated using the specified formula [17, 18]. However, it should be noted that the formula was developed for normal (conventional) concrete. This formula must be modified if it will be applied to unconventional concrete, considering the differences in the nature of the concrete material to develop bonds to reinforcement. Chan et al. [19] observed the difference in the bond behaviour between OPC concrete and SCC by pullout testing of reinforcements embbeded in full-scale RC walls. They showed that the bond strength development of reinforcing bars in OPC concrete reaches a maximum value at 7 days while in SCC the bond strength continues to increase until 14 days. Additionally, SCC has greater bond strength and, to a lesser extent is affected by the top bar. Azizinamini et al. [20] suggested a difference mechanisme of mechanical interlock that contributes to the bond strength of deformed bar embedded in normal strength concrete (NSC) and high strength concrete (HSC). In the case of NSC, all lugs are assumed to carry uniform bond stress so that they can be considered to participate simultaneously in bearing the concrete under ultimate load. The failure that occurs at this load is depicted by a simultaneous concrete crushing at the vicinity of all the lugs. In the case of HSC, however, a different phenomenon occurs. It is known that the bearing strength of HSC is higher than that of NSC so that under the ultimate load the bond stress is not evenly distributed throughout the lugs. Additionally, considering the increase in the tensile strength of HSC is not the same as the bearing strength, it causes concrete crushing only occurs in the vicinity of a few lugs that bear higher stress. Hence, it can be concluded that not all lugs play an active role in bearing the concrete. Esfahani and Rangan [21] confirmed similar results and proposed different expression of cracking bond for the case of NSC and HSC in short length specimens. These expressions were further used in the analysis of bond between concrete and spliced reinforcing bars in beams [22].

Wolfe [23] noted that HVFA concrete has similar bond strength to the conventional concrete. However, the slippage that occurs after the crushing of concrete around the reinforcement is faster in HVFA concrete than conventional concrete. Alghazali and Myers [16] investigated bond performance of reinforcing bars in full scale HVFA-SCC beams. The inclusion of fly ash was in the range of 50–70%. The beams were designed using spliced reinforcing bars in such a way to fail by bond failure before the yielding of the reinforcing bars. The results were analyzed in terms of strength and ductility indices. The strength index is defined as the ratio of the ultimate load of beams with spliced reinforcement to those of reference beams without spliced reinforcement. The ductility index is defined similarly to the strength index, except that it is expressed in terms of maximum deflection at mid-span. Based on these two indices, an increase in bond strength can be shown when replacement cement by fly ash is increased from 50 to 70%. The bond strength of the HVFA-SCC tests were also compared with a database of the bond strength of various types of concrete from literature. The data were presented in the form of the relationship between normalized bond strength and the ratio of the splice length to the bar diameter. The normalized bond strength is expressed in term of ratio of bond strength to the square root of compressive strength. Based on the generated nonlinear regression curve it is shown that HVFA-SCC has a comparable bond strength with other types of concrete.

Reinforcement bond strength to concrete is also influenced by bar types. The presence of lugs on the surface of deformed bar provides an additional mechanism of bond via interlock where the lugs bear against concrete. In the case of plain bar, the bond rests solely on the adhesion and friction mechanisms. Hazan and Feldman [24] noted the splice specimens reinforced with plain bars only be able to resist 60% of those specimens with deformed bars having the same nominal diameter. Currently, most codes do not allow to use plain bars anymore. Therefore, the equations to determine the development and splice lengths in the codes are derived for deformed bars only. However, information on bond strength of plain bar will be valuable for assessing the development and splice lengths in existing reinforced concrete structures built in the time when the previous code provisions permitted the use of plain bars [25]. It can be useful as well for evaluating the contribution of adhesion by various concrete types on bond development to the reinforcing bar.

It has been shown in the preceeding paragraphs that reinforcement bond strength to concrete is influenced by concrete types. Among other concrete types, informations of reinforcement bond strength to HVFA-SCC are still limited, and none of them specifically addresses the bond strength of plain reinforcement embedded in HS-HVFA-SCC. This research aims to investigate the efficacy of bond development of HS-HVFA-SCC to plain reinforcing bar. The efficacy of the bond development is assessed on the basis of the flexural performance of HS-HVFA-SCC beam with spliced reinforcement in the tensile zone. The splice lengths are designed to be greater than the estimated minimum splice length (ls) according to Eq. (1).

$${l}_{s}=\frac{{f}_{y}}{4\mathrm{u}}{d}_{b}$$
(1)

where fy, db, and u is reinforcement yield strength, reinforcement diameter, and bond strength of concrete to reinforcement, respectively.Thus, it is expected that the designed splice lengths sufficiently induces a flexural failure, not a bond failure. Strength, stiffness, and ductility will be used to assess the efficacy of HS-HVFA-SCC to develop bond to plain reinforcement. Based on the evaluation, a minimum splice length for tensile plain reinforcement embedded in an HS-HVFA-SCC beam is suggested.

In the following section, we describe the materials and their properties for producing HS-HVFA-SCC beam specimens, the type of the beams for this purpose of investigation, and the testing method used. In Sect. 3, we discuss the experimental results in term of various flexural performance parameters in order to determine the required splice length, and subsequently compare the obtained splice length with that of other concrete types. Following discussion of the results, the main findings, limitations, and suggestions for future works are given in Sect. 4.

2 Methods

2.1 Materials and properties

The mixture proportion of HS-HVFA-SCC per m3 of concrete was as follows: 384.3 kg of cement and 384.3 kg of fly ash; 709.8 kg of coarse aggregate; 595.35 kg fine aggregate; 231 kg of water and 7,686 L of superplasticizer. As indicated in the proportion, about 50% of fly ash was used to compose the total binder (cement + fly ash). The chemical composition of fly ash is shown in Table 1. The physical properties of course and fine aggregates used in the production of concrete are given in Table 2. The superplasticizer intended to control the flow properties of the concrete mixture was Sika Viscocrete, obtained from PT SIKA Indonesia. This superplasticizer was mixed with water before added into the concrete mixes. The proportion of this mixture was determined by several trials to achieve the required characteristics of high strength, high volume fly ash, and self-compacting concrete.

Table 1 Chemical composition of fly ash
Full size table
Table 2 Properties of aggregates
Full size table

The fresh properties of HS-HVFA-SCC mixture were determined based on two tests, slump flow and L-Box test. The average slump flow was 730 mm, while the average for the L-Box test was 0.815. The hardened property of the concrete was determined by uniaxial compression test on cylinder specimens. The above proportion produced HS-HVFA-SCC with an average strength of 73 MPa after 90 days. Meanwhile, the bond strength of HS-HVFA-SCC to reinforcement was determined by pull out test on cylinder specimens with a bond length of 275 mm. The obtained bond strength corresponding to a maximum load to pull the embedded reinforcement was 2.99 MPa.

2.2 Beam specimens

Reinforced concrete beams having size of 100 × 250 × 2000 mm were cast. Only a single longitudinal reinforcement was embedded in the tensile zone of the beams. This reinforcement was a plain bar with a 10 mm diameter. Meanwhile, a single compression reinforcement was provided within the shear spans as well. In addition, shear reinforcements (6 mm diameter) were installed in the shear spans at 80 mm spacing to ensure sufficient shear strength so that the tested beam would rupture under a flexural failure mode. The splice length was designed within pure bending areas with various lengths (see Table 3). In Table 3, B0 indicates a normal beam without splice connection, while BS1–BS5 represent beams with a splice connection. The splice lengths are greater than the estimated minimum splice length according to Eq. (1). Given fy = 402 MPa, u = 2.99 MPa, and db = 10 mm, the estimated minimum splice length is 336 mm (33.6db). Figure 1 shows the beam specimens with their reinforcements.

Table 3 Variation of splice lengths
Full size table
Fig. 1
figure 1

Beam specimens with their reinforcements layout

Full size image

2.3 Loading test

A schematic of a reinforced concrete beam under loading is illustrated in Fig. 2. The span length of the beam was 1800 mm, and a four-point loading test was applied. The load was imposed incrementally at 1 kN. The mid-span deflection of the beam under incremental load was monitored by using a linear variable displacement transducer (LVDT). The beams were tested at the age of 90 days.

Fig. 2
figure 2

Overview of four-point loading test on beam specimen

Full size image

3 Results and discussion

3.1 Crack pattern

Figure 3 shows the crack patterns of the beams at rupture. The figure also illustrates the reinforcements layout in the setting of crack patterns. There may be noticed a slight difference of cracks between the photos and the sketches, for example cracks in B0. This can be clarified as follows: it was not possible to take a photo of the entirely beam length when the tested beam still laid on the loading test (see Fig. 2). We had to remove the beam after testing and took a photo outside the flexural loading frame. Unfortunately, the lifting and handling of the beam caused splitting of the beam across the primary cracks.

Fig. 3
figure 3

Final cracking pattern of beam with continuous reinforcement (B0) and spliced reinforcements (BS1–BS5)

Full size image

Figure 3 shows all cracks arise within the maximum bending moment, as anticipated [26], and form vertical patterns, typical for the flexural failure mode. No horizontal cracks along the spliced zone were observed indicating there was no splitting failure mode. Other possible failure mode i.e. slippage was not noticed. The findings are consistent with that found in the literature where beams with sufficient tensile splice length show a flexural failure mode. On the contrary, beams with short splice length demonstrate a splitting failure mode [27]. For the case of plain reinforcement, insufficent splice length more likely to cause a slippage (pull out) failure mode rather than splitting failure [24]. The intensity of cracks was approximately similar for all beams regardless of splice length [10] and no cracks were observed in the shear span. The similarity of crack intensities suggests that the presence of splice length gave a little effect on the distribution of stresses in the beams. This could be due to the use of a single reinforcement with a small diameter i.e. 10 mm resulting in no significant transformed section in the spliced zone.

It can be noticed as well that one of the cracks appeared to be a primary crack where there was significant propagation of crack both in length and width. The exception was those of cracks in B0 where two primary cracks were formed. At cracked cross-sections, the tensile stress of concrete dropped to zero and the stresses in the tensile zone of reinforced concrete were taken up by the reinforcement. Consequently, localized large tensile strains of reinforcement occured at the cracking zones as the load increased and this would be the source of large deformation behavior observed in the beams as discussed in the following section.

3.2 Load-deformation behavior

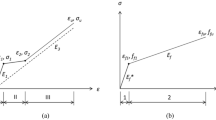
The global response of the beams under imposed flexural loading is presented in the form of load–deflection curves (Fig. 4). Generally, all beams appear to have a similar response, i.e. the load–deflection curve can be devided into three regions. At the beginning of loading up to a certain limit (about 4 kN), the curves form the first linear region of load and deflection. Above this load level, the curves are deflected and show the second linear relationship region up to loads ranging from 18 to 23 kN. At this range of loading, the beam seems to be able to maintain a relatively high stiffness. After the second limit of linearity, a non-linear region of was observed, where a small increase in load causes a considerable increase of deflection. This third region of the curves indicates that the beam has already reached its plastic state and lost its previous stiffness. This behavior can be traced from the fact that the beam is a composite element. Under imposed load, the stresses are initially distributed linearly across the section of the beam where the top and bottom fibre undergoes the highest compressive and tensile stress, respectively. At a certain limit of load, the maximum tensile stress at the bottom fibre attains a larger value than the tensile capacity of concrete. This situation generates a crack that develops both in length and width as the load increases [5]. As a result, a higher tensile stress is transferred to the tensile reinforcement in the cracked section. At first cracks, the stress in the reinforcement is small and far below the yield stress. Further increases in load will widen and lengthen the cracks and subsequently induce large localized strains in the reinforcement at the cracked sections that causes a large deformation of the beam due to the yielding of reinforcement. At this point, the load–deflection curve starts to deviate from the preceding linear relationship and the beam shows a plastic behavior. This plastic behavior suggests that the splice length is sufficient for the HS-HVFA-SCC to develop bond to the plain reinforcement; and so the embedded spliced reinforcement is capable to take a higher tensile load with no indication of pull out failure.

Fig. 4
figure 4

Comparison of load–deflection behavior of beam with continuous bar (B0) and spliced bars (BS1-BS5)

Full size image

3.3 Flexural performance parameters

In Fig. 4, the load–deflection curve of the beams with spliced reinforcement (BS1–BS5) is directly compared with the beam with non-spliced reinforcement (B0). A comparison between the curves will be further analysed and quantified in terms of stiffness index, maximum load, and ductility index. The parameters may be used as indicators to quantify the performance of beams. Table 4 summarises the flexural performance parameters of the investigated beams.

Table 4 Flexural performance parameters
Full size table

3.3.1 Stiffness index (SI)

Examining the curves of Fig. 4, there is a point within each of the curves where the elastic behavior of the beam ends and the curves start to show plastic deformation. The load corresponding to this limit is in the 18–23 kN range. At this load range, large strains of the tensile reinforcements commence. A small increase in load will produce a large increase in strain, which in turn, induces a large increase in deflection as well. This load limit (Py) and its corresponding deflection (∆y) are given in Table 4. The values will be further evaluated to determine the stiffness index of the beams. Stiffness index SI is defined as the ratio of Py to ∆y.

Stiffness is a property that characterizes how the beams resist deformation in response to an imposed load. In the case of beams under flexural loading, stiffness is a pertinent parameter to quantify, for examples, short-term and long-term deflection. As there is a requirement to limit the total deflection, beams with a higher stiffness will be better. Based on this consideration, it is implied that any attempts to modify a beam should satisfy the minimum stiffness of the original beam to meet the deflection limit.

The influence of splice length on the stiffness index of the reinforced HS-HVFA-SCC beams can be examined in Fig. 5. The stiffness index of the normal beam SI0 is set as a comparison. Figure 5 shows that the order of the stiffness follows the corresponding splice length. The longer the splice length, the higher the stiffness. However, not all beams with spliced reinforcement hold a superior stiffness compared to the normal beam. Only beams with splice length of at least 380 mm or 38db i.e. BS2–BS5 give a stiffness ratio higher than 1 (one). On the other hand, BS1 has stiffness ratio below 1 (one) indicating this beam does not satisfy the minimum stiffness requirement. The lower stiffness of BS1 in comparison to the stiffness of B0 is unexpected. Hypothetically, the presence of splice length should increase the stiffness of the beam for the following reasons. Within the splice length, the reinforcement area (As) of a beam with spliced reinforcement is greater than that of the original non-spliced reinforced beam. It is also known that the elastic modulus of steel reinforcement, Es, is far greater than the elastic modulus of concrete, Ec. Consequently, a greater reinforcement area within the splice length will make the stiffness of that beam be higher than a corresponding beam with non-spliced reinforcement. The findings of this research confirm the above presumption for BS2–BS5 but that is not the case for BS1.

Fig. 5
figure 5

Influence of splice length on beam stiffness

Full size image

Another factor that controls the deformation resistance of the beam is the occurrence of cracks. Cracks will reduce the depth or cross-section of the beam and cause high stresses transfer to the reinforcement within the cracks zone. A reduction of beam depth on the crack sections would decrease the overall stiffness of the respective beam [28]. Moreover, higher localized stresses of the reinforcement within the cracks zone would induce large deformation as well. Thus, the higher the crack intensity, the lower the stiffness. Nevertheless, this proposition cannot also explain the inferior stiffness of BS1 compared to B0 since the crack intensity of all beams is relatively comparable (see Fig. 3).

The BS1 beam with splice length that is a barely higher than the minimum requirement according to Eq. (1) may exhibit a little slippage of the reinforcement in the spliced zone. If this is true, this can be the source of the lower stiffness of BS1. However, the experiment did not measure the possibility of the slippage of the reinforcement in the spliced zone. What can simply be pointed out from the current experimental results is that there is a minimum splice length of tensile reinforcement to meet a comparable stiffness with the corresponding beam with non-spliced reinforcement [27].

3.3.2 Flexural capacity

The flexural capacity of the beam can be directly indicated by the maximum load (Pmax) that the beam can withstand. The flexural capacity of the spliced beams is shown in Fig. 6 in comparison to the BS0. All the beams with spliced reinforcement yield a higher capacity than the non-spliced reinforced beam. These results suggest that the given splice lengths of the tensile reinforcements satisfy the minimum requirement of strength. The spliced lengths sufficiently promote concrete bond strength to the reinforcements and so, adequate tensile stresses are developed in the tensile reinforcements to sustain a high flexural load. The tensile stress (fs) in the reinforcement at the tip of spliced zone may be estimated using Eq. (2). This equation is suggested by Hassan and Feldman [24] and applicable for plain reinforcement.

Fig. 6
figure 6

Influence of splice length on beam flexural capacity

Full size image
$${f}_{s}=\frac{{T}_{max}}{{A}_{s}}=1.29\times {10}^{-3}{l}_{s}{d}_{b}\sqrt{{f}_{c}^{^{\prime}}}$$
(2)

where Tmax, As, ls, db, and f’c is maximum load carried by reinforcement (kN), reinforcement area (mm2), splice length (mm), reinforcement diameter (mm), and compressive strength of concrete (MPa), respectively. The calculated stresses are presented in Table 5. The results indicate that most of the reinforcements already reach their yield stress with the exception of BS1. The non-yielding of BS1 reinforcement estimated by Eq. (2) is not inline with the expected flexural failure mode of this beam as discussed in Sect. 3.1. This may be due to the fact that Eq. (2) was developed on the basis of splicing reinforcement embedded in normal concrete beams, where its bond strength is different to HS-HVFA-SCC (see Sect. 3.4). Furthermore, the equation also takes into account the surface roughness of the reinforcement due to sandblasted. Despite the limitation, Eq. (2) confirms that the splice length of BS2-BS5 is sufficient for the HS-HVFA-SCC to develop bond to the plain reinforcement so that the reinforcement can withstand a yield load without experiencing pull out failure.

Table 5 Calculated reinforcement stress
Full size table

3.3.3 Ductility

The flexural performance of beams can be further characterized in term of their ductility. Ductility is a property that characterizes a beam’s ability to undergo significant plastic deformation before rupture. Several methods may be employed to determine the ductility index. Generally, the ductility index is used to show the deformation characteristic of the beam after the stage of linear behavior. Parameters that may be used to quantify such behavior are rotation (θ), curvature (φ), deflection (Δ), or absorbed energy (E). Therefore, ductility is usually expressed in term of ratio of these parameters at failure (peak load) to the corresponding parameter at the start of steel yielding [29]. For the sake of simplicity, the deflection ductility (D) i.e. ratio of deflection at failure (∆max) to deflection at yield load (∆y) was chosen in this investigation [30]. Additionally, the start of the third linear region of the load–deflection curve was assumed to be the start of reinforcement yielding or plastic deformation. Referring to Table 4, plastic deformation of the spliced beams take place at a lower deformation compared to the non-spliced beam, with the exception of BS1. On the other hand, the maximum deflection of the non-spliced beam is larger than the corresponding maximum deflection of the spliced beams. It means the calculated ductility of the spliced beams could be greater than the non-spliced beam even thought their maximum deflection is inferior compared to the non-spliced beam. Figure 7 shows the ductility ratio of the spliced beams (denoted as Di) to the non-spliced beam (denoted as D0). Beams with a spliced length of at least 380 mm or 38db i.e. BS2–BS5 give a higher ductility compared to the normal beam with non-spliced reinforcement (B0). On the other hand, BS1 do not attain the ductility level of B0. The results confirm that the minimum splice length of tensile plain reinforcement embedded in HS-HVFA-SCC is 380 mm or 38db to satisfy the ductility level.

Fig. 7
figure 7

Influence of spliced length on beam ductility

Full size image

3.4 Comparison to other concrete

In the preceeding section, the minimum splice length has been recommended for tensile plain reinforcement embedded in HS-HVFA-SCC based on the flexural performance parameters (stiffness, strength, and ductility). In this section, the recommended splice length will be compared with the splice length of other concrete types. For this purpose a database of splice length collected from several literatures will be used. Splice length data of concrete (C) are obtained from [23, 31]–[38]. The data encompass spliced beams with ratio of splice length to bar diameter (ls/db) ranging from 9.52 to 57.1 and concrete compressive strength ranging from 30 to 104 MPa. In addition, splice length data of special type of concretes (HVFA, SCC, HVFA-SCC) are included for this comparison. The following literatures provide the useful data: [23, 33, 39] for HVFA; [31, 32, 36, 37, 40]–[42] for SCC; and [43] for HVFA-SCC. The collected data is presented in Fig. 8 in term of normalized bond strength of concrete (μ/√f’c) versus ratio of splice length to bar diameter (ls/db). Given the bond strength u = 2.99 MPa, compressive strength f’c = 73 MPa, splice length ls = 380 mm, and db = 10 mm the coordinate point of HS-HVFA-SCC can be inserted into Fig. 8.

Fig. 8
figure 8

Comparison of beam splice length of HS-HVFA-SCC with other concrete types

Full size image

Equations that relate normalized bond strength and ratio of splice length to bar diamater for C and SCC type of concrete has been suggested, respectively, as follow:

$$\mu /\sqrt {f_{c}^{\prime } } = 10.701\left( {l_{s} /d_{b} } \right)^{{ - 0.914}}$$
(3)
$$\mu /\sqrt {f_{c}^{\prime } } = 10.36\left( {l_{s} /d_{b} } \right)^{{ - 0.883}}$$
(4)

The equations show that for a similar ls/db, the normalized bond strength of SCC is slightly more than that of C concrete type. For the other type of concrete, the database is not sufficient to generate such equation. However, their respected coordinate points within the figure can indicate whether the expected normalized bond strength follows the equation or not. For example, the coordinate points of HVFA and HFVA-SCC lay above the the equation curves. This means at the same ls/db the normalized bond strength of HVFA and HVFA-SCC will be more than those of C and SCC beam. The higher bond strength will result in a lesser requirement of splice length for a given bar diameter. Meanwhile, for the HS-HVFA-SCC the coordinate point lays very close to the equation curves even though the equations were originally determined for deformed bar. Feldman et al. [25] showed that a factor of 1.32–1.53 is needed to determine the development length for plain bar cast at the bottom beam compared to that of deformed bar; with an average value of 1.42 for round bar. Considering Feldman results, the required splice length of HS-HVFA-SCC may be less than that estimated by Eq. (3) or (4) if deformed bar is used. And so, an efficient splice length can be expected in the case of reinforced HS-HVFA-SCC structural elements.

4 Conclusions

Splice length of tensile plain reinforcement embedded in HS-HVFA-SCC beams has been determined in this research based on the flexural performance. The main conclusions can be summarized as follow:

  1. a.

    Crack pattern of all beams is typical of flexural failure mode. No other failure modes (splitting of concrete cover in the spliced zone and slippage of spliced reinforcement) were noticed. Furthermore, the region and intensity of cracks are practically similar for all beams.

  2. b.

    The global response of beams under incremental load can be characterized by three regions. The appearance of plastic deformation can be related to the large deformation of tensile reinforcement that already reach its yielding point. The large tensile strain (stress) can indicate that HS-HVFA-SCC developes sufficient bond to the plain reinforcement so that the reinforcement can withstand a yield load without experiencing pull out failure.

  3. c.

    From load–deflection curve, flexural parameters have been deduced to identify the influence of splice length on the stiffness, strength, and ductility of beams. These flexural parameters can be used to indicate the minimum splice length of plain tensile reinforcement embedded in HS-HVFA-SCC which yields comparable performance to the non-spliced beam.

  4. d.

    Splice lengths within a 342–570 mm range (or 34.2db–57.0db), as given in this research, provide sufficient flexural strength. However, in term of stiffness and ductility, only beams with a splice length of at least 380 mm (38db) are superior compared to the non-spliced beam. Based on the above consideration, the minimum splice length of plain tensile reinforcement for the investigated beams is 380 mm (38db). The validity of this finding should be verified by extending the current research to include other bar diameters.

  5. e.

    The splice length of plain tensile reinforcement embedded in HS-HVFA-SCC of this investigation has been compared to other type of concretes. The finding of this research lays within the expected correlation of normalized bond strength versus ratio of splice length to bar diameter even though the correlation was originally determined for deformed bar. The finding implies that an efficient splice length can be expected in the case of HS-HVFA-SCC structural element. To confirm the current finding, further research is suggested to cover a range of splice length to bar diameter ratio.

  6. f.

    This research is limited to the use of lap-spliced plain bar in unconfined HS-HVFA-SCC beam. To provide more comprehensive data of bond strength and its subsequent splice length requirement for a variety of cases, the research can be extended to cover the use of deformed bar and also the influence of confinement by stirrups.