1 Introduction

Ising model is considered the simplest model dealing with nearest neighbor interaction and has many applications in physics, such as lattice gas, alloys, and magnets. The Ising model has been studied in one, two, and three dimensions. In one dimension, magnetic nanotubes have gained much interest since these magnetic nanotubes have unique physical properties and wide applications [1,2,3]. These nano-sized magnetic particles can be used in spintronic devices [4], drug delivery [5], sensors [6], and bio-molecular motors [7]. Different methods such as the effective field theory (EFT) [8,9,10] and Monte Carlo (MC) simulations [11,12,13] are used to study the magnetic and thermodynamic properties of these nanosystems. The Ising model effectively predicts the magnetic properties and can predict some unusual behavior of several mixed spin structures [14, 15].

The two-dimensional structure is the most widely studied because of its wide range of high-density recording media applications. Various studies emphasize the effect of temperature, magnetic field, exchange coupling, and crystal field on the magnetic properties of the system [16,17,18]. Many shaped structures have been studied such as hexagonal core–shell [19,20,21], ladder-like boronene nanoribbon [22], square-octagon lattice [23], Blume-Capel system for square and simple cubic lattices [24,25,26], borophene core–shell structure [27], ladder-like graphene nanoribbon [28,29,30,31], triangular lattice [31, 32], diamond-like decorated square [33], rectangle Ising nanoribbon [34].

The mixed spin lattices have been a subject of theoretical and experimental research, such as ferrimagnetic-ferrimagnetic coupling in \({\text{Fe}}_{3} {\text{O}}_{4} /{\text{Mn}}_{3} {\text{O}}_{4}\) superlattice where such superlattice reveals unusual magnetic behavior [35]. Also, unusual magnetic behavior was found in a mixed spin compound of three source spins [36], where the magnetization reverses sign twice below the ordering temperature, which we reveal in our study using a honeycomb-hexagonal structure. Studying the magnetic properties of two sublattices with mixed spins reveals a significant effect on the magnetic properties because less translational symmetry exists in this case [37, 38]. Therefore, at least two relevant interactions of different natures must exist for compensation. These interactions will be shown when one constructs the Hamiltonian of the system under study [38, 39].

In order to investigate the existence of point compensations and look for different magnetic properties of layered systems, we adopt a honeycomb-hexagonal structure in this study. We will use the MC method in this study. A similar system to this structure can be found in the nano-graphene system [39] and be applicable for bimetallic layered compounds [40, 41]. Similar works were done by us using different crystal structures [18, 42, 43].

The following section defines our model and gives the related formulation. Results and discussions in Sect. 3. Finally, Sect. 4 is the conclusions.

2 Model and formalism

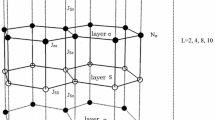
A schematic representation of one structure layer studied in this work is shown in Fig. 1. The structure layer consists of two sublattices, sublattice-A is centered-hexagonal with atoms of spin \(\sigma = 1/2\), and sublattice-B is hexagonal with atoms of spin \(S = \) 1.

Fig. 1
figure 1

Schematic representation of the centered honeycomb-hexagonal structure. The blue circles are atoms of spin 1/2 (sublattice-A). The red circles are atoms of spin 1 (sublattice-B). Different exchange interactions are shown in the mid-right of the figure

Full size image

The Hamiltonian terms of our structure can be written as

$$ H = - J_{1} \mathop \sum \limits_{ij} \sigma_{i} \sigma_{j} - J_{2} \mathop \sum \limits_{kl} S_{k} S_{l} - J_{12} \mathop \sum \limits_{ik} \sigma_{i} S_{k} - D\mathop \sum \limits_{k} S_{k}^{2} $$
(1)

The first two terms are the spin–spin interaction of each intralayer coupling strengths \(J_{1}\) and \(J_{2}\) where we consider \(J_{1}\) > 0 and \(J_{2} \) > 0 to have ferromagnetic interaction within the same type of atoms. The third term is the interlayer coupling \(J_{12}\) and is taken negative to have an antiferromagnetic interaction. The summations are over the nearest neighbor's spins. The fourth term is the single-ion anisotropy or crystal field interaction D of S spins.

The ferrimagnetic structure shown in Fig. 1 was simulated using the Monte Carlo simulation method based on the Metropolis algorithm [44], and periodic boundary conditions were applied. The procedure followed is similar to the procedure discussed in previously published papers from this group [18, 42, 43]. A 400,000 step was used to equilibrate the system, and then data was generated for 450,000 MC steps per spin. Each layer has 50 atoms of sublattice-A and 100 atoms of sublattice-B. We choose the number of layers to be \(L = 50\) layers. So \(N_{A} = 50 \times 50\) and \(N_{B} = 50 \times 100\). There is no significant effect on our results if we increase the number of layers by more than 50 layers. This will be confirmed using Binder cumulant. The magnetic properties were calculated as follows:

The average magnetization per site for the whole system is given by:

$$ M_{tot} = \frac{{N_{A} M_{A} + N_{B} M_{B} }}{{N_{A} + N_{B} }} $$
(2)

where \(M_{A} , M_{B}\) are the magnetizations per site for each sublattice, calculated as:

$$ M_{A} = \frac{1}{{N_{A} }}\mathop \sum \limits_{i = 1}^{{N_{A} }} \sigma_{i} $$
(3)
$$ M_{B} = \frac{1}{{N_{B} }}\mathop \sum \limits_{i = 1}^{{N_{B} }} S_{i} $$
(4)

The total susceptibility of the system is

$$ {\upchi }_{{{\text{tot}}}} = \frac{{N_{A} \chi_{A} + N_{B} \chi_{B} }}{{N_{A} + N_{B} }} $$
(5)

where \(\chi_{A} , \chi_{B}\) are the sublattices susceptibility, calculated as:

$$\chi_{\alpha } = \beta N_{\alpha } \left( \langle{M_{\alpha }^{2}\rangle - \langle M_{\alpha }\rangle^{2} } \right)$$
(6)

Here β = 1/kBT, where kB is Boltzmann constant, which is taken 1 for simplicity.

The compensation temperature, \(T_{comp}\), is the temperature at which the magnetization of the two sublattices are equal and opposite to each other to add up to zero-total magnetization. The crossing point of the magnetizations of the two sublattices must be determined under the following condition to determine \(T_{comp}\):

$$ \left| {N_{A} M_{A} \left( {T_{comp} } \right)} \right| = \left| {N_{B} M_{B} \left( {T_{comp} } \right)} \right| $$
(7)
$$ sign\left( {N_{A} M_{A} \left( {T_{comp} } \right)} \right) = - sign\left( {N_{B} M_{B} \left( {T_{comp} } \right)} \right) $$
(8)

with Tcomp < Tc, where Tc is the transition temperature \(T_{c}\). In this paper, Tc is determined from the maxima of the susceptibilities' curves and confirmed using Binder cumulant as a function of temperature T for various lattice sizes L [26].

3 Results and discussions

Figure 2 shows the effect of \(J_{1}\) parameter on the magnetization, total susceptibility, system’s compensation, and critical temperature at fixed \(J_{2} = 0.3, J_{12} = - 0.1,D = 0\). The behavior shown is due to the slow magnetization drop of sublattice-A as \(J_{1}\) increases. Meanwhile, the variation of \(J_{1}\) does not affect the magnetization of sublattice-B. Figure 2a shows N-type magnetization for all values of \(J_{1}\). Figure 2b shows the variation of magnetization with T. It shows that lattice A is more ordering than lattice B as T increases toward \(T_{c}\). Figure 2c shows the \(\left( {T, J_{1} } \right)\) phase diagram of the system, and it shows the appearance of the compensation at \(J_{1}\) = 1.1, which stays constant with increasing \(J_{1}\). This value of \(J_{1}\) can be predicted from the ground state energy where we set D = 0 in the Hamiltonian. The ground state energy can be found from the Hamiltonian and depends on the number of parameters included [38, 45, 46]. The ordering temperature \(T_{c}\) increases with \(J_{1}\) and it exists for all values of \(J_{1}\) seen in Fig. 2c.

Fig. 2
figure 2

Effect of \(J_{1}\) coupling constant on a total magnetization, b sublattices magnetization, c critical and compensation temperature, and d total susceptibility of the system at fixed \(J_{2} = 0.3, J_{12} = - 0.1, D = 0\)

Full size image

The magnetic susceptibility \(\chi_{tot}\) is shown in Fig. 2d. It shows double peaks where the peak at lower T corresponds to the compensation temperature \(T_{comp}\) and the second peak corresponds to the transition temperature \(T_{c}\). These values of \(T_{c}\) occurred at the higher peaks will be confirmed later when we plot Binder cumulant versus T.

The next step is to vary \(J_{2}\) which corresponds to the strength of S–S coupling and keep other parameters constants. Therefore, we set in Fig. 3, \(J_{1} =\) 1.8, \(J_{12}\) = − 0.1 and D = 0. Figure 3a shows the total magnetization versus T. It shows P-type magnetization for \(J_{2}\) > 0.75 and N-type behavior for \(J_{2}\) < 0.6. Figure 3b shows the magnetization of each sublattice. It shows that lattice A of small spins is kept ordered up to nearly \(T_{c}\) while lattice B starts without plateau for small values of \(J_{2}\). Therefore, this gives the linearity of \(T_{comp}\) with increasing T. \(T_{comp}\) vanishes at \(J_{2}\) > 0.75. Figure 3c also shows that \(T_{c}\) increases with \(J_{2}\). In Fig. 3d, we plot \(\chi_{tot}\) versus T, which shows double peaks where the peak at small T corresponds to \(T_{comp}\) and the second peak at a bigger value of each curve represents \(T_{c}\) as discussed for the previous figure above.

Fig. 3
figure 3

Effect of \(J_{2}\) coupling constant on a total magnetization, b sublattices magnetization, c critical and compensation temperature, and d total susceptibility of the system at fixed \(J_{1} = 1.8, J_{12} = - 0.1, D = 0\)

Full size image

As a final aspect of this part, we have to vary the interlayer antiferromagnetic coupling \(J_{12}\). Moreover, keep the other parameters fixed. Therefore, we use in Fig. 4, \(J_{1}\) = 1.8, \(J_{2}\) = 0.3 and D = 0. Figure 4a shows the total magnetization M versus T. It clearly shows the existence of compensations. In Fig. 4b, we are showing the magnetization of each sublattice versus T. It shows that \(J_{12}\) has more influence on the magnetization of sublattice B, consistent with the results in Figs. 2 and 3. It is worth reminding that atoms in lattice B have spin 1 with three projection states + 1, 0, and − 1.

Fig. 4
figure 4

Effect of \(J_{12}\) coupling constant on a total magnetization, b sublattices magnetization, c critical and compensation temperature, and d total susceptibility of the system at fixed \(J_{1} = 1.8, J_{2} = 0.3, D = 0\)

Full size image

Figure 4c shows the variation of \(T_{c}\) and \(T_{comp}\) with the absolute value of \(J_{12}\). It shows that the compensation temperature exists only for \(\left| {J_{12} } \right| < 0.3\) and the value of \(T_{comp}\) increases as \(\left| {J_{12} } \right|\) increases, while \(T_{c}\) stays almost constant in this range and increases with \(\left| {J_{12} } \right|\). It also shows N-type magnetization for \(J_{12} <\) − 0.3 The susceptibility versus T is shown in Fig. 4d. It has two peaks which can be explained as before.

Next, we will include the single-ion anisotropy D in our calculations to explore its effect on the different magnetic properties possessed by this layered honeycomb-hexagonal structure. The influence of the crystal field \(D\) on the total magnetization of the system is shown in Fig. 5. Here, we fix the parameters \(J_{1} = 1.8, J_{2} = 0.3, J_{12} = - 0.1\) for selected positive and negative values of \(D\). Our choice for these parameters is determined by the three previous figures where the system has an obvious compensation behavior. Figure 5a shows that the compensation temperature increases as the crystal field D increases. However, for \(D \le - 0.75,\) the system shows no compensation temperature. There are two points of compensation temperatures for \(D = - 0.7\), and there is one compensation temperature for \(D > - 0.6\). Therefore, two compensation points exist in a narrow range of D (i.e., − 0.7 to − 0.6). These results agree with the work done by A. Boubekri on ferrimagnetic mixed spin Ising trilayer nano-graphene structure [39]. This is important in the thermomagnetic recording, where small temperature changes reverse the magnetization [45]. In Fig. 5b, we show the magnetization of each sublattice with D. It shows that the crystal field has an insignificant effect on sublattice-A magnetization and stays constant to near \(T_{c}\) then goes up sharply to zero at \(T_{c}\), while for sublattice-B, the magnetization varies rapidly with increasing D. In Fig. 5c, we are showing the variations of \(T_{c}\) and \(T_{comp}\) with D. The figure shows \(T_{c}\) is constant while \(T_{comp}\) is increasing with D. The figure shows the two compensation points with different colors at \(D = - 0.7\). These results agree with the results presented in Figs. 3, 4, and 5, except for the existence of two compensation points in a narrow range of the crystal anisotropy of negative values. In fact, and according to previous studies in different layer structures effective field method was used and found that the effect of D influences the location of compensation temperature, but in our work, we include intralayer coupling \(J_{1}\) and \(J_{2}\) which is not included in the previous work [38, 39].

Fig. 5
figure 5

Effect of \(D\) on a total magnetization, b sublattices magnetization, c critical and compensation temperature, and d total susceptibility of the system at fixed \(J_{1} = 1.8, J_{2} = 0.3, J_{12} = - 0.1.\)

Full size image

In summary, the two compensation points do not exist, as shown in Figs. 2, 3, 4, unless we include the crystal anisotropy constant D. It appears in a narrow range of negative values D (− 0.5 to − 0.7). It is worth mentioning that the interlayer coupling \(J_{12}\) = − 0.1. Our calculations show that the appearance of the two points of compensation is sensitive to the value of interlayer coupling to get two points of compensation. Therefore, the single-ion anisotropy plays a significant factor in the foundation of the second compensation temperature [47].

Figure 5d shows the magnetic susceptibility versus T, which has the same behavior discussed in Figs. 3, 4, and 5.

Moreover, Further investigation is done for the range \(- 0.7 \ge D \ge - 0.5\). This is shown in Fig. 6. Where it shows the total magnetization of the system in this range. One compensation temperature is found for \(D \ge - 0.58\). Two compensation temperatures for \(D = - 0.6, - 0.62, - 0.65,\) and \(- 0.7\).

Fig. 6
figure 6

The total magnetization of the system versus temperature for different crystal field values at fixed \(J_{1} = 1.8, J_{2} = 0.3, J_{12} = - 0.1.\)

Full size image

Finally, for the completion of this study and to confirm the existence of transition temperature Tc we plot in Fig. 7 the Binder cumulant [48] versus T for different crystal sizes L. In this figure, we used the same values of J1, J2, and J12 used in Fig. 2. On the other hand, we varied the length until the Binder cumulant reached zero to avoid the finite size effect, and we found that the minimum length side at which the Binder cumulant reached zero was L = 50. For this reason, all our results are based on our estimated minimum length side of 50 to avoid the finite size effect [49].

Fig. 7
figure 7

Binder cumulant as a function of T for different crystal sizes L. The values \(J_{1} , J_{2} \) and \(J_{12}\) are the same as in Fig. 2

Full size image

4 Conclusions

The magnetic and thermodynamic properties of the ferrimagnetic honeycomb inside a hexagonal structure have been studied using Monte Carlo simulations based on the Metropolis update protocol.

For a honeycomb-hexagonal structure studied in this work, we found that with no single-ion anisotropy and fixing the intralayer exchange coupling of higher spin sublattice \(J_{2}\) and antiferromagnetic coupling between the two spin layers \(J_{12}\) the compensation starts for \(J_{1} \) ≥ 1.1 and stays constant with increasing \(J_{1}\) while the transition temperature exists for all values of \(J_{1}\) and increases with T, as shown in Fig. 2c. The magnetization M shows N-type Neel magnetization. Varying the exchange coupling \(J_{2}\) of higher spin sublattice and keeping the other parameters \(J_{1}\), \(J_{12}\) fixed and D = 0 compensation exists for small values of \(J_{2}\) and vanishes for all values of \(J_{12}\) > 0.75. Both P-type and N-type Neel magnetization behavior has been observed depending on the value of \(J_{2}\). The more interesting result is that when the single-ion anisotropy D was introduced in our calculations, we found two points of compensation for a narrow range of negative D (− 0.7 < D < − 0.6). Detailed calculations for this case are presented in Fig. 6. These results are applicable to the layered nano-graphene and bimetallic magnetic compounds [37, 38]. Therefore, the mixed spin lattices such as this honeycomb-hexagonal adopted here reveal two compensation points. It has been argued that such two compensation points exist when nearest neighbor interactions of spin 1/2 layer are considered [37, 39, 46]. Such finding is essential in the thermomagnetic recording where a slight temperature change reveres the magnetization [45]. Finally, we confirmed the existence of the transition temperature using the Binder cumulant and discussed the size system effect.