1 Introduction

Having been utilized since the 1940s and 1950s, the 1.7 million km of metallic pipelines exist in the oil industry worldwide, which plays a vital role in transporting oil and gas products. Therefore, every year between 2 and 3.3 billion dollars in the United States alone is lost due to corrosion in gas and petroleum pipelines, needing either repair or replacement [1]. During the lifetime of a pipeline, repairs would be necessary to reinstate it to the essential conditions and maintain its reliability. Therefore, the repair/maintenance of vast pipeline networks represents an essential part of oil and gas transportation [2]. A wide range of temperature variations (between − 50 °C and 130 °C), high pressure, and chemical erosion are the major factors that affect the internal/external corrosion on transmission pipelines [3].

In the oil and gas industry, the usage of fibre composite materials is continually growing, along with the development of new piping systems, pressure vessels, and other structural components [4]. Different commercial repair systems based on fibre reinforced composite materials can be found: (a) dry fibreglass fabric to be wrapped with impregnation of liquid resin, (b) ready pre-cured layers ready to wrap around the pipe, and (c) flexible resin pre-impregnated bandage to be wrapped with water [5]. The high tensile strength, lightweight, durability, and versatility of fibre composites makes them the material of choice for many repair and rehabilitation projects [6]. Industry research has shown that this type of repairs can be typically 24% cheaper than replacing the damaged pipe section or welded sleeve repairs. Most composite repairs are installed on land-based piping systems both aboveground and underground. Since the applications of such repair systems do not require shutdown, there has been increasing demand for the development of composite repair systems which can be applied in a variety of service conditions [7]. Nevertheless, multiple factors influence the strength of the systems used for these applications, such as properties and characteristics of the materials, design geometric specifications as the adhesive layer and the polymeric sleeve thickness, temperature, and applied load conditions [8].

Many researchers have studied the behavior of metallic pipes repaired by composite materials to optimize various parameters, such as the defect geometry [1], the material of repair system [9], the composite repair thickness [10], the filler material [11], etc. Similarly, some papers focused on the influence of temperature on the degradation of the composite material properties, such as the elasticity modulus and tensile strength [8, 12].

Last but not least, few studies investigated the mechanical analysis of the composite repair system. Sirimanna et al. [2] employing Lame’s solution, analyzed internally composite repaired steel pipes suffering from an axisymmetric defect, considering both pipe and composite repair as thick-walled isotropic cylinders. Mattos et al. [5] proposed an analytical method to calculate the pipe’s burst pressure considering pipe and composite reinforcement as thin-walled isotropic cylinders. Mattos et al. [13] calculated the optimized thickness of composite sleeves, where pipe and sleeve were modelled as the thin-walled isotropic and thick-walled orthotropic cylinders, respectively. Budhe et al. [11] developed the contributions of Mattos et al. [5, 13], considering the effect of polymer filler between the pipe and composite repair, with an analytical formula being proposed to obtain the failure pressure of the repaired pipe. In that study, the pipe and composite patch were modeled as thin-walled isotropic and thick-walled orthotropic cylinders, respectively. These analytical contributions, in turn, have been employed by researchers for the reliability analysis of composite repaired pipes [14]. Nevertheless, the effect of temperature and moisture need to be studied in the mechanical analysis of the composite repair system. Besides that, assuming the plane stress condition, the majority of recent studies [5, 9, 11, 13, 15] did not account for axial stress and strain, and in turn, put forward a plane problem.

To sum up, the literature suffers from a lack of an extensive study towards the thermo-mechanical analysis of composite repaired pipes. Hence, the main purpose of this study is to obtain the failure pressure of the metallic pipes repaired by composite sleeves. To this aim, the effects of temperature and moisture, which, to the best of our knowledge, were not comprehensively investigated in the previous studies, are focused. Moreover, various loading conditions (including proportional loading, plane stress, and plane strain), partial bonding conditions, and the stiffness of polymer filler are researched.

2 Methodology

In this section, some methodologies are introduced to achieve the failure pressure of a repaired pipe. For this purpose, assuming the pipe and sleeve as elastic isotropic and orthotropic cylinders, respectively, the novel idea is that the effects of temperature and moisture on the failure pressure are focused. Having obtained the radial displacements of the components, the radial displacement compatibility at the pipe and sleeve interface is applied, extracting the contact pressure as a fraction of the internal pressure subjected to the pipe. Then the burst pressure can be obtained with a procedure which will be expressed in Eqs. (32) to (35) in detail.

With the aim of investigating the effect of polymer filler between the pipe and sleeve, three concentric thick-walled cylinders are considered and the failure pressure is obtained (neglecting the filler effect); however, in this case, the damage factor is not applied. To consider the presence of the defect, the polymer filler is assumed to fill an axisymmetric defect, accounting for the same depth of the defect and the circumferential length of the pipe. It should be pointed out that the distinct idea for this case is that all of the components, including the pipe, filler, and sleeve, are thick-walled cylinders. By doing so, the contribution of repair components in bearing loads is found out more conveniently.

2.1 Basic equations

Having been prepared in the recent studies [13, 16], the required equations for the composite sleeve and the metallic pipe assumed as orthotropic and isotropic cylinders, in order, are only mentioned so that they are employed for the failure analysis in the next sections.

2.1.1 Composite sleeve

Herein, both plane stress and plane strain conditions, are presented. In the case of plane stress model, the radial stress, hoop stress, hoop strain and radial displacement can be written as follows:

$${\sigma }_{r}=\frac{1}{r}\frac{d\phi }{dr}=\left(1+k\right){c}_{1}{r}^{k-1}+\left(1-k\right){c}_{2}{r}^{-k-1}+2B$$
(1)
$${\sigma }_{\theta }=\frac{{d}^{2}\phi }{d{r}^{2}}=k\left(1+k\right){c}_{1}{r}^{k-1}-k\left(1-k\right){c}_{2}{r}^{-k-1}+2B$$
(2)
$${\varepsilon }_{\theta }=\left({\beta }_{r\theta }+k{\beta }_{\theta \theta }\right)\left(1+k\right){c}_{1}{r}^{k-1}+\left({\beta }_{r\theta }-k{\beta }_{\theta \theta }\right).\left(1-k\right){c}_{2}{r}^{-k-1}+2\mathrm{B}\left({\beta }_{r\theta }+{\beta }_{\theta \theta }\right)+{\alpha }_{\theta }T+{\beta }_{\theta }c$$
(3)
$${u}_{r}=\left({\beta }_{r\theta }+k{\beta }_{\theta \theta }\right)\left(1+k\right){c}_{1}{r}^{k}+\left({\beta }_{r\theta }-k{\beta }_{\theta \theta }\right)\left(1-k\right){c}_{2}{r}^{-k}+2\mathrm{Br}\left({\beta }_{r\theta }+{\beta }_{\theta \theta }\right)+{(\alpha }_{\theta }T+{\beta }_{\theta }c)r,$$
(4)

where

$${\beta }_{rr}=\frac{1}{E{}_{r}}, {\beta }_{r\theta }=-\frac{\upsilon {}_{r\theta }}{{E}_{r}}, {\beta }_{\theta \theta }=\frac{1}{{E}_{\theta }}k=\sqrt{\frac{{\beta }_{rr}}{{\beta }_{\theta \theta }}}$$
(5)
$$B=\frac{a+b}{2({\beta }_{\theta \theta }-{\beta }_{rr})}, a=\left({\alpha }_{r}-{\alpha }_{\theta }\right)Tb=\left({\beta }_{r}-{\beta }_{\theta }\right)c$$
(6)
$${c}_{1}=\frac{1}{1+k}\frac{-{p}_{1}{r}_{2}^{-k-1}+2B({{r}_{1}^{-k-1}-r}_{2}^{-k-1})}{{r}_{1}^{k-1}{r}_{2}^{-k-1}-{r}_{1}^{-k-1}{r}_{2}^{k-1}}$$
(7)
$${c}_{2}=\frac{1}{1-k}\frac{{p}_{1}{r}_{2}^{k-1}+2B(-{{r}_{1}^{k-1}+r}_{2}^{k-1})}{{r}_{1}^{k-1}{r}_{2}^{-k-1}-{r}_{1}^{-k-1}{r}_{2}^{k-1}},$$
(8)

where \({r}_{1}\) and \({r}_{2}\) are the internal and external radii of the cylinder, in order. \({E}_{r}\) and \({E}_{\theta }\) are the elasticity moduli in the circumferential, and radial directions, respectively. \(\upsilon {}_{r\theta }\) is the coefficient relating contraction in the circumferential direction to extension in the radial direction. \({\alpha }_{r}\), \({\alpha }_{\theta }\) and \({\beta }_{r}\), \({\beta }_{\theta }\) are the thermal and hygroscopic expansion coefficients in the radial and tangential directions, respectively; while c, denotes the moisture concentration. Substituting \({c}_{1} \mathrm{and} {c}_{2}\) from Eqs. (7) and (8) into Eq. (4), \({u}_{r}\) can be obtained. This procedure was done in appendix A (subchapter 5.1). Finally, \({u}_{r}\) can be written as:

$${u}_{r}={p}_{1}\left({E}_{5}{r}^{k}+{E}_{6}{r}^{-k}\right)+{E}_{7}{r}^{k}{+E}_{8}{r}^{-k}+{E}_{9}r$$
(9)

Equation (9) represents radial displacement of an orthotropic cylinder in plane stress condition, which is considered as the radial displacement of composite sleeve. Factors corresponding to Eq. (9) can be found in appendix A (subchapter 5.1).

Similarly, the stress and strain components in the case of plane strain condition are as follows:

$${\sigma }_{r}=\left(1+k\right){c}_{1}{r}^{k-1}+\left(1-k\right){c}_{2}{r}^{-k-1}+2\overline{B }$$
(10)
$${\sigma }_{\theta }=k\left(1+k\right){c}_{1}{r}^{k-1}-k\left(1-k\right){c}_{2}{r}^{-k-1}+2\overline{B }$$
(11)
$${\sigma }_{z}=-\frac{{a}_{rz}+k{a}_{\theta z}}{{a}_{zz}}\left(1+k\right){c}_{1}{r}^{k-1} +\frac{-{a}_{rz}+k{a}_{\theta z}}{{a}_{zz}}.\left(1-k\right){c}_{2}{r}^{-k-1}-\frac{2\overline{B}}{{a }_{zz}}\left({a}_{rz}+{a}_{\theta z}\right)-\frac{{\alpha }_{z}T+{\beta }_{z}c}{{a}_{zz}}$$
(12)
$${\varepsilon }_{\theta }=\left({\beta }_{r\theta }^{^{\prime}}+k{\beta }_{\theta \theta }^{^{\prime}}\right)\left(1+k\right){c}_{1}{r}^{k-1}+\left({\beta }_{r\theta }^{^{\prime}}-k{\beta }_{\theta \theta }^{^{\prime}}\right).\left(1-k\right){c}_{2}{r}^{-k-1}+2\overline{\mathrm{B} }\left({\beta }_{r\theta }^{^{\prime}}+{\beta }_{\theta \theta }^{^{\prime}}\right)+\overline{{\alpha }_{\theta }}T+\overline{{\beta }_{\theta }}c$$
(13)
$${u}_{r}=\left({\beta }_{r\theta }^{^{\prime}}+k{\beta }_{\theta \theta }^{^{\prime}}\right)\left(1+k\right){c}_{1}{r}^{k}+\left({\beta }_{r\theta }^{^{\prime}}-k{\beta }_{\theta \theta }^{^{\prime}}\right).\left(1-k\right){c}_{2}{r}^{-k}+2\overline{\mathrm{B}}\mathrm{r }\left({\beta }_{r\theta }^{^{\prime}}+{\beta }_{\theta \theta }^{^{\prime}}\right)+\left(\overline{{\alpha }_{\theta }}T+\overline{{\beta }_{\theta }}c\right)r,$$
(14)

where

$${a}_{rr}=\frac{1}{Er}, {a}_{r\theta }=-\frac{\upsilon {}_{r\theta }}{{E}_{r}}, {a}_{rz}=-\frac{\upsilon {}_{rz}}{{E}_{r}} {a}_{\theta \theta }=\frac{1}{{E}_{\theta }}, {a}_{\theta z}=-\frac{\upsilon {}_{\theta z}}{{E}_{\theta }}, {a}_{zz}=\frac{1}{{E}_{z}}$$
(15)
$${\beta }_{rr}^{^{\prime}}={a}_{rr}-\frac{{a}_{rz}^{2}}{{a}_{zz}}, {\beta }_{r\theta }^{^{\prime}}={a}_{r\theta }-\frac{{a}_{rz}{a}_{\theta z}}{{a}_{zz}}{\beta }_{\theta \theta }^{^{\prime}}={a}_{\theta \theta }-\frac{{{a}_{\theta z}}^{2}}{{a}_{zz}}, \overline{{\alpha }_{r}}={\alpha }_{r}-{\alpha }_{z}\frac{{a}_{rz}}{{a}_{zz}}\overline{{\beta }_{r}}={\beta }_{r}-{\beta }_{z}\frac{{a}_{rz}}{{a}_{zz}}, \overline{{\alpha }_{\theta }}={\alpha }_{\theta }-{\alpha }_{z}\frac{{a}_{\theta z}}{{a}_{zz}}\overline{{\beta }_{\theta }}={\beta }_{\theta }-{\beta }_{z}\frac{{a}_{\theta z}}{{a}_{zz}}$$
(16)
$$\overline{B }=\frac{\overline{a }+\overline{b} }{2({\beta }_{\theta \theta }^{^{\prime}}-{\beta }_{rr}^{^{\prime}})}, \overline{a }=(\overline{{\alpha }_{r}}-\overline{{\alpha }_{\theta }})T\overline{b }=(\overline{{\beta }_{r}}-\overline{{\beta }_{\theta }})c$$
(17)

2.1.2 Metallic pipe

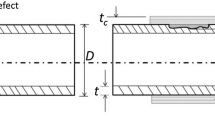
If the wall thickness of the metallic pipe is less than the 1/10th of internal radius, it can be assumed as thin walled, otherwise known as thick. In a thick walled cylinder, radial stresses cannot be neglected. For a thick walled isotropic cylinder (Fig. 1) the related equations are as follows [17]:

$${\sigma }_{r}=\frac{{p}_{i}{r}_{i}^{2}-{p}_{o}{r}_{o}^{2}}{{r}_{o}^{2}-{r}_{i}^{2}}-\frac{\left({p}_{i}-{p}_{o}\right){r}_{i}^{2}{r}_{o}^{2}}{{r}^{2}({r}_{o}^{2}-{r}_{i}^{2})}+E{\alpha }_{s}T$$
(18)
$${\sigma }_{\theta }=\frac{{p}_{i}{r}_{i}^{2}-{p}_{o}{r}_{o}^{2}}{{r}_{o}^{2}-{r}_{i}^{2}}+\frac{\left({p}_{i}-{p}_{o}\right){r}_{i}^{2}{r}_{o}^{2}}{{r}^{2}({r}_{o}^{2}-{r}_{i}^{2})}+E{\alpha }_{s}T$$
(19)
$${u}_{r}=\frac{1-\nu }{E}\left[\frac{{p}_{i}{r}_{i}^{2}-{p}_{o}{r}_{o}^{2}}{{r}_{o}^{2}-{r}_{i}^{2}}\right].r+\frac{1+\nu }{E}\left[\frac{\left({p}_{i}-{p}_{o}\right){r}_{i}^{2}{r}_{o}^{2}}{{r}_{o}^{2}-{r}_{i}^{2}}\right]\frac{1}{r}{+\alpha }_{s}rT,$$
(20)

where E, \({\alpha }_{s}\) and T are the elastic modulus, the expansion coefficient of the material and temperature, respectively.

Fig. 1
figure 1

Pipe subjected to internal and external pressure [11]

Full size image

Regarding a thin-walled pipe, the circumferential stress is only considered, with the radial and axial stress components being negligible compared to the hoop stress [11]. In this case, simplifying Eqs. (18)–(20), \({\sigma }_{\theta }\), \({\varepsilon }_{\theta }\), and \({u}_{r}\) are rewritten as follows:

$${\sigma }_{\theta }=\frac{{p}_{i}{r}_{i}-{p}_{o}{r}_{o}}{{r}_{o}-{r}_{i}}+E{\alpha }_{s}T$$
(21)
$${\varepsilon }_{\theta }=\frac{1}{E}\frac{{p}_{i}{r}_{i}-{p}_{o}{r}_{o}}{{r}_{o}-{r}_{i}}+{\alpha }_{s}T$$
(22)
$${u}_{r}={r}_{i}\frac{1}{E}\frac{{p}_{i}{r}_{i}-{p}_{o}{r}_{o}}{{r}_{o}-{r}_{i}}+{{r}_{i}\alpha }_{s}T$$
(23)

2.2 Failure analysis of pipe repaired by composite sleeve

The present subchapter is concerned with the failure pressure analysis of the corroded metallic pipe repaired by a composite sleeve undergoing an elastic deformation with localized metal loss defects. Under various conditions such as plane stress, proportional loading and plane strain, the burst pressure of the repaired pipe is obtained. The basic equations presented in the Sect. 2.1 are used in the case of pipe with wall loss defect being reinforced with a composite sleeve. Firstly, the failure pressure of the repaired pipe under the plane stress condition is obtained, followed by the proportional loading problem, and finally the plane stress condition.

The following assumptions have been done [11]:

  • The variation of wall thickness due to the pressure can be neglected.

  • Failure first occurs in the metallic pipe rather than the composite sleeve.

Having an inner radius \({r}_{i}\) and external radius \({r}_{o}\), the metallic pipe is reinforced by a composite sleeve with an inner radius \({r}_{o}\) and external radius \({r}_{e}\) (Fig. 2). It is assumed that the pipe is a thin cylinder, but the sleeve is thick:\(e=({r}_{o}-{r}_{i})<({r}_{i}/10)\) and \(({r}_{e}-{r}_{o})>({r}_{o}/10)\). Assuming that the radial displacement of the contact surface is the same for both cylinders and neglecting ovalization, it is possible to obtain analytical expressions for the stress, strain and displacement fields. The law of compatibility applies that:

Fig. 2
figure 2

Composite repair system applied to the corroded pipe

Full size image
$${\left[{\mathrm{u}}_{\mathrm{r}}\right]}_{\mathrm{pipe}}={\left[{\mathrm{u}}_{\mathrm{r}}(\mathrm{r}={\mathrm{r}}_{\mathrm{o}})\right]}_{\mathrm{sleeve}}$$
(24)

The adequate values with regard to Fig. 2 are taken as follows:

Sleeve:\({p}_{1}\Rightarrow {p}_{c}\)

Pipe:\({p}_{o}\Rightarrow {p}_{c}\)combining Eqs. (9) and (23), one can write as follows:

$${r}_{i}\frac{1}{E}\frac{{p}_{i}{r}_{i}-{p}_{c}{r}_{o}}{{r}_{o}-{r}_{i}}+{{r}_{i}\alpha }_{s}T{=p}_{c}\left({E}_{5}{r}_{o}^{k}+{E}_{6}{r}_{o}^{-k}\right)+{E}_{7}{r}_{o}^{k}{+E}_{8}{r}_{o}^{-k}+{E}_{9}{r}_{o}$$
(25)

To simplify equations, it is supposed that:

$${{F}_{1}=E}_{5}{r}_{o}^{k}+{E}_{6}{r}_{o}^{-k}$$
(26)
$${{F}_{2}=E}_{7}{r}_{o}^{k}{+E}_{8}{r}_{o}^{-k}+{E}_{9}{r}_{o}-{{r}_{i}\alpha }_{s}T$$
(27)
$${F}_{3}=\frac{1}{E}\frac{{r}_{i}}{{r}_{o}-{r}_{i}}$$
(28)
$${F}_{4}=\frac{{F}_{1}}{{F}_{3}}$$
(29)
$${F}_{5}=\frac{{F}_{2}}{{F}_{3}}$$
(30)

considering Eqs. (25)–( 30), \({p}_{c}\) is obtained as follows:

$${p}_{c}=\frac{{p}_{i}{r}_{i}-{F}_{5}}{{r}_{o}+{F}_{4}}$$
(31)

now that the contact pressure \({p}_{c}\) has been determined, the maximum admissible pressure \({p}_{i}\) (failure pressure) due to the localized corrosion defect can be approximated by one of the many effective area methods. Here, \({\alpha }_{\theta } \mathrm{and} {\sigma }_{flow}\) obtained from RSTRENG Criterion, because it suggests a failure pressure close to the experimental tests [5]. \({\alpha }_{\theta } \mathrm{and} {\sigma }_{flow}\) were introduced in appendix B (subchapter 5.2).

$${\alpha }_{\theta }\left\{\frac{{p}_{i}{r}_{i}-{p}_{c}{r}_{o}}{{r}_{o}-{r}_{i}}+E{\alpha }_{s}T\right\}<{\sigma }_{flow}$$
(32)

Combining Eqs. (31) and (32) it is possible to obtain the theoretical failure pressure \({P}_{max}^{th}\).

$${\alpha }_{\theta }\left\{\frac{{p}_{i}{r}_{i}-\frac{{p}_{i}{r}_{i}-{F}_{5}}{{r}_{o}+{F}_{4}}{r}_{o}}{{r}_{o}-{r}_{i}}+E{\alpha }_{s}T\right\}<{\sigma }_{flow}{\Rightarrow \alpha }_{\theta }\left\{\frac{{P}_{max}^{th}{r}_{i}-\frac{{P}_{max}^{th}{r}_{i}-{F}_{5}}{{r}_{o}+{F}_{4}}{r}_{o}}{{r}_{o}-{r}_{i}}+E{\alpha }_{s}T\right\}={\sigma }_{flow}$$
(33)

It’s more convenient to consider:

$${F}_{6}=\frac{{r}_{o}}{{r}_{o}+{F}_{4}}$$
(34)

If Eqs. (33) and (34) are combined, then \({P}_{max}^{th}\) can be obtained as follows:

$${P}_{max}^{th}=\frac{\left\{\left({r}_{o}-{r}_{i}\right)(\frac{{\sigma }_{flow}}{{\alpha }_{\theta }}-E{\alpha }_{s}T)-{F}_{5}{F}_{6}\right\}}{{r}_{i}(1-{F}_{6})}$$
(35)

Equation (35) presents the theoretical failure pressure of the pipe repaired by a composite sleeve in the plane stress condition. It should be noted that the effects of temperature, moisture, mechanical and geometrical properties of the pipe and the composite sleeve have been included.

The proportional loading is considered as a constant ratio of longitudinal to hoop strain which is applied to the pipe [18]. Also \({\varepsilon }_{r}\) can be neglected in the thin cylinder.

$$\frac{{\varepsilon }_{z}}{{\varepsilon }_{\theta }}=\alpha \Rightarrow {\varepsilon }_{z}=\alpha {\varepsilon }_{\theta }$$
(36)

The equivalent strain based on the Tresca criterion is applied:

$${\varepsilon }_{e}=\left|{\varepsilon }_{\theta }-{\varepsilon }_{z}\right|=\left|{\varepsilon }_{\theta }-\alpha {\varepsilon }_{\theta }\right|=\left|1-\alpha \right|{\varepsilon }_{\theta }$$
(37)

Assuming a linear isotropic elastic behavior, the constitutive equations can be expressed as follows:

$${\varepsilon }_{\theta }=\frac{1}{E}\left({\sigma }_{\theta }-\nu {\sigma }_{z}\right)+{\alpha }_{s}T$$
(38)
$${\varepsilon }_{z}=\frac{1}{E}({\sigma }_{z}-\nu {\sigma }_{\theta }){+\alpha }_{s}T$$
(39)

Substituting Eq. (36) in Eq. (39) becomes:

$${\sigma }_{z}=E\alpha {\varepsilon }_{\theta }+\nu {\sigma }_{\theta }-E{\alpha }_{s}T$$
(40)

combining Eqs. (38) and (40) becomes:

$${F}_{2}^{new}={{E}_{7}r}_{o}^{k}{+E}_{8}{r}_{o}^{-k}+{E}_{9}{r}_{o}-{r}_{i}(\nu {\alpha }_{s}T)$$
(41)
$${F}_{3}^{new}=\frac{1}{E}\frac{{r}_{i}}{{r}_{o}-{r}_{i}}(1-{\nu }^{2})$$
(42)
$${\varepsilon }_{\theta }=\frac{\left\{{\sigma }_{\theta }\left(1-{\nu }^{2}\right)+\nu E{\alpha }_{s}T\right\}}{E(1+\nu \alpha )}$$
(43)
$${\sigma }_{e}=E{\varepsilon }_{e}$$
(44)

Introducing Eqs. (37) and (43) into Eq. (44), it is possible to obtain:

$${C}_{p}=\frac{\left(1-{\nu }^{2}\right)\left|1-\alpha \right|}{(1+\nu \alpha )}{D}_{p}=\frac{\left(\nu E{\alpha }_{s}T\right)\left|1-\alpha \right|}{(1+\nu \alpha )}$$
(45)
$${\sigma }_{e}={C}_{p}{\sigma }_{\theta }+{D}_{p}$$
(46)

The remaining methodology is similar to that one proposed to obtain Eq. (31), however, these new factors are introduced:

$${F}_{2}^{new}={{E}_{7}r}_{o}^{k}{+E}_{8}{r}_{o}^{-k}+{E}_{9}{r}_{o}-\frac{{r}_{i}(\nu {\alpha }_{s}T)}{1+\nu \alpha }$$
(47)
$${F}_{3}^{new}=\frac{1-{\nu }^{2}}{1+\nu \alpha }\frac{1}{E}\frac{{r}_{i}}{{r}_{o}-{r}_{i}}$$
(48)

Thus, another parameters which depend on \({F}_{3}\) change. Finally \({P}_{max}^{th}\) is obtained similar to Eq. (35), however there are new parameters including \({C}_{p} and {D}_{p}\).

$${P}_{max}^{th}=\frac{\left\{\frac{\left({r}_{o}-{r}_{i}\right)({\sigma }_{flow}-{D}_{p})}{{C}_{p}{\alpha }_{\theta }}-{F}_{5}{F}_{6}\right\}}{{r}_{i}(1-{F}_{6})}$$
(49)

It should be noted that Eq. (49) accounts for the burst pressure of pipe reinforced by a composite wrap under proportional loading.

Plane strain condition is a specific case of proportional loading, by which Eq. (36) reduces to:

$${\varepsilon }_{z}=0\Rightarrow \alpha =0$$
(50)

In order to investigate the effect of filler between pipe and thick-walled composite sleeve a methodology based on [11] is employed, where the assumption is that all components including pipe, filler and composite sleeve are three concentric cylinders subjected to an internal pressure \({p}_{i}\), and the contact pressures, \({p}_{c1}\) and \({p}_{c2}\) between the pipe-filler and the filler-sleeve, respectively [11]. The main novel idea is that all of components including pipe, filler and sleeve are thick walled cylinders (Fig. 3).

Fig. 3
figure 3

Pipe-filler-composite repair system

Full size image

The unknown contact pressures, \({p}_{c1}\) and \({p}_{c2}\), can be found using the radial displacement compatibility at pipe-filler and filler-sleeve interfaces, respectively. In this method, first, \({p}_{c2}\) is calculated as a function of \({p}_{c1}\), then \({p}_{c1}\) is substituted in the equation related to the continuity of pipe-filler interface. It is assumed that pipe and filler as thick-walled isotropic cylinders and composite sleeve as thick walled orthotropic cylinder. This assumptions can help one to consider variation of stress and strain along radial centerline from inner layer of the pipe up to outer layer of the composite sleeve. For this purpose, using Eqs. (9) and (20), it can be written as follows:

$${u}_{r}^{P}={A}_{1}.({p}_{i}{r}_{i}^{2}-{p}_{c1}{r}_{p}^{2}).r+{{A}_{2}(p}_{i}-{p}_{c1})\frac{1}{r}$$
(51)
$${u}_{r}^{F}={A}_{3}.({p}_{c1}{r}_{p}^{2}-{p}_{c2}{r}_{o}^{2}).r+{{A}_{4}(p}_{c2}-{p}_{c1})\frac{1}{r}$$
(52)
$${u}_{r}^{S}={p}_{c2}({E}_{5}{r}^{k}+{E}_{6}{r}^{-k})+{E}_{7}{r}^{k}{+E}_{8}{r}^{-k}+{E}_{9}r$$
(53)

where \({u}_{r}^{P}, {u}_{r}^{F}, {u}_{r}^{S}\) are pipe, filler and sleeve radial displacements, respectively. Related factors have been presented in appendix C (subchapter 5.3). The other factors related to \({u}_{r}^{S}\) can be found in Subsect. 2.2. Applying continuity condition between filler and sleeve, one can write as follows:

$${\left.{u}_{r}^{F}\right|}_{r={r}_{o}}={\left.{u}_{r}^{S}\right|}_{r={r}_{o}}\Rightarrow {A}_{3}.\left({p}_{c1}{r}_{p}^{2}-{p}_{c2}{r}_{o}^{2}\right).{r}_{o}+{{A}_{4}(p}_{c2}-{p}_{c1})\frac{1}{{r}_{o}}{=p}_{c2}({E}_{5}{r}_{o}^{k}+{E}_{6}{r}_{o}^{-k})+{E}_{7}{r}_{o}^{k}{+E}_{8}{r}_{o}^{-k}+{E}_{9}{r}_{o}$$
(54)
$${\Rightarrow p}_{c2}={A}_{12}{p}_{c1}-{A}_{13}$$
(55)

Factors related to Eqs. (54) and (55) were introduced in appendix D (subchapter 5.4). Also, applied continuity condition between pipe and filler, one can write as follows:

$${\left.{u}_{r}^{F}\right|}_{r={r}_{p}}={\left.{u}_{r}^{P}\right|}_{r={r}_{p}}\Rightarrow {A}_{3}.\left({p}_{c1}{r}_{p}^{2}-{p}_{c2}{r}_{o}^{2}\right).{r}_{p}+{{A}_{4}(p}_{c2}-{p}_{c1})\frac{1}{{r}_{p}}{=A}_{1}.({p}_{i}{r}_{i}^{2}-{p}_{c1}{r}_{p}^{2}).{r}_{p}+{{A}_{2}(p}_{i}-{p}_{c1})\frac{1}{{r}_{p}}$$
(56)
$${\Rightarrow p}_{c1}={L}_{1}{p}_{i}+{L}_{2}$$
(57)

Factors related to Eqs. (56) and (57) were presented in appendix E (subchapter 5.4). Equivalent stress in the pipe can be presented as follows:

$${\sigma }_{e}={\sigma }_{\theta }-{\sigma }_{r}$$
(58)

If \({\sigma }_{\theta }\) and \({\sigma }_{r}\) are substituted from Eqs. (18) and (19), then the Eq. (58) changes to:

$${\sigma }_{e}=\frac{2\left({p}_{i}-{p}_{c1}\right){r}_{i}^{2}{r}_{p}^{2}}{{r}^{2}({r}_{p}^{2}-{r}_{i}^{2})}$$
(59)

Knowing that at the ultimate pressure, \({\sigma }_{e}={\sigma }_{flow}\) and replacing \({p}_{c1}\) from Eq. (57) into Eq. (59), one can write as follows:

$${P}_{failure}=\frac{{L}_{2}+{L}_{3}}{1-{L}_{2}},$$
(60)

where \({L}_{3}\) is as follows:

$${L}_{3}=\frac{{\sigma }_{flow}{r}^{2}({r}_{p}^{2}-{r}_{i}^{2})}{2{r}_{i}^{2}{r}_{p}^{2}}$$
(61)

Therefore, one can employ Eq. (60) to obtain burst pressure of repaired pipe and investigate effect of filler (such as its stiffness) between pipe and composite sleeve. Also, variation of stress and strain along the thickness of system can be characterized.

If the defect surface is not properly prepared before applying the composite repair system, the contact debonding between the pipe and composite sleeve would occur, and so sleeve will not be able to reinforce the damaged pipe anymore. To investigate this phenomenon, using methodology based on [2] one can write as follows:

$${\left.{u}_{r}^{F}\right|}_{r={r}_{p}}={\left.{{\mu }_{1}u}_{r}^{P}\right|}_{r={r}_{p}}$$
(62)
$${\left.{u}_{r}^{S}\right|}_{r={r}_{o}}={\mu }_{2}{\left.{u}_{r}^{F}\right|}_{r={r}_{o},}$$
(63)

where \({\mu }_{1}\) and \({\mu }_{2}\) are bond coefficients of pipe-filler and filler-sleeve, respectively, which have a value between 0 and 1. The burst pressure has a formula similar to Eq. (60), however some new factors are introduced as follows:

$${G}_{4}^{new}={\mu }_{1}{G}_{4}, {G}_{5}^{new}={\mu }_{1}{G}_{5}{G}_{6}^{new}={\mu }_{1}{G}_{6}, {A}_{7}^{new}={\mu }_{2}{A}_{7}, {A}_{8}^{new}={\mu }_{2}{A}_{8}, {A}_{9}^{new}={\mu }_{2}{A}_{9}$$
(64)

2.3 Temperature-dependent properties of Composite sleeve

The temperature dependent properties of two specific composite materials utilized for repairing metallic pipes are presented.

2.3.1 Thermo-Wrap composite

Thermo-Wrap is a bidirectional fiberglass which is used for repairing and reinforcing pipelines. The tensile strength and the tensile modulus of elasticity of Thermo-Wrap varying by temperature taken from [8] are as follows:

$${E}_{TW} =-0.0822.T+27.81$$
(65)
$${\sigma }_{TW}=-1.531.T+531.78,$$
(66)

where \({E}_{TW}\) \(\left(GPa\right)\), \({\sigma }_{TW} \left(MPa\right), \mathrm{and} T \left(^\circ{\rm C} \right)\) are tensile module of elasticity, tensile yield strength of Thermo-Wrap, and temperature, respectively.

2.3.2 Glass fibre reinforced polyurethane composite

Fibre-reinforced thermoplastic polymer composites are widely used to reinforce corroded metallic pipelines. It is observed that the impact of temperature on their elastic properties is negligible, and yet their ultimate strength is strongly temperature-dependent. The following expression in Eq. (67) provides a suitable correlation between ultimate strength and temperature [12].

$${\sigma }_{GFRP}=2557.{T}^{-0.78},$$
(67)

where \({\sigma }_{GFRP }\left(MPa\right)\) is the ultimate strength of the glass fibre reinforced polyurethane.

2.4 Finite element modelling

A plane stress condition has been employed to define 2-D Finite element behavior. The model consists of 3 concentric cylinders: the pipe, polymer filler, and composite sleeve, with the bonded condition being applied between them in order that a perfect contact would be simulated. An automatic mesh generated by ANSYS Workbench has been used. It applies Plane183 element which is suitable for plane elements (plane stress, plane strain). The element has 2 degree of freedom at each node: translations in the nodal x and y directions [19]. The internal pressure loading is applied to the inner edge of pipe. A linear elastic orthotropic model is used to define composite sleeve material, but an isotropic case, which only considers circumferential elasticity modulus, is also defined to compare isotropic and orthotropic composite material models. The FE model has been shown in Fig. 4.

Fig. 4
figure 4

Finite element model for plane stress condition

Full size image

3 Results and discussion

Firstly, the analytical results are compared to the FE simulations in a specific case, and the obtained theoretical outcomes are subsequently presented. The effect of moisture, temperature-dependent tensile elasticity modulus of composite sleeve, composite thermal expansion coefficients in the radial and circumferential directions, proportional loading of thin walled pipe, partially bonded sleeve and the presence of filler between pipe and sleeve are presented. The data for pipe, filler and composite sleeve extracted from [11, 16, 20, 21] are presented in Table 2.

3.1 FEM results

An automatic mesh convergence used by the ‘convergence’ command of the Ansys workbench shows that if the element figures increase from 476 to 1004, the safety factor only changes 0.49%, representing a good convergence. For finding the burst pressure of the FE model, the internal pressure increases up to a value, in which the factor of safety (using the von Mises criterion) is equal to 1. Such a pressure is supposed to be the failure pressure obtained from the FE analysis. Figure 5 indicates that the burst pressure, which is 19.8 MPa, is in good agreement with the analytical burst pressure (that was 19.94 MPa) obtained in subchapter (3.3.1) (the error percentage is 0.7). Assuming the composite sleeve having either isotropic or orthotropic material, the von Mises stress in the repaired pipe presented in Fig. 6 does not express a significant difference. Analytical and FE hoop stress and strain through the thickness of the pipe, filler, and composite sleeve (using the orthotropic model) were compared in Figs. 7 and 8, presenting a good agreement between the results. Additionally, the burst pressure obtained from the model with isotropic composite sleeve (considering only its hoop elasticity modulus) is 19.97 MPa, with a 0.15% error relative to the analytical one (that is 19.94 MPa). For comparing analytical and FE results, they have been presented in Table 1, where \({p}_{th}^{f}, {p}_{iso}^{f} \mathrm{and} {p}_{ort}^{f}\) are the theoretical, numerical with the isotropic sleeve case, and the numerical with the orthotropic case, respectively.

Fig. 5
figure 5

Investigation of the burst pressure of the 2-D Finite element model

Full size image
Fig. 6
figure 6

The von Mises stress in the burst pressure of the pipe repaired by a isotropic sleeve and b orthotropic sleeve

Full size image
Fig. 7
figure 7

Comparison of the analytical and FEM hoop stress in the burst pressure of the repaired pipe

Full size image
Fig. 8
figure 8

Comparison of the analytical and FEM hoop strain in the burst pressure of the repaired pipe

Full size image
Table 1 Theoretical and numerical burst pressures
Full size table

3.2 Pipe and composite repair as thin-walled cylinders

3.2.1 Moisture effect

For different fractions of the composite sleeve moisture concentration, the burst pressure of repaired pipe in various temperatures based on Eq. (35) has been shown in Fig. 9. It is observed that the higher moisture fraction, the higher burst pressure, since in higher moisture fractions, the effect of high temperatures decreases-in other words, the higher moisture is equal to composite sleeve cooling.

Fig. 9
figure 9

Burst pressure of repaired pipe in different moisture concentrations of composite sleeve

Full size image

3.2.2 Temperature dependent composite sleeve

Thermo-Wrap, which is used to repair a damaged pipe, is considered to investigate the effect of temperature in tensile elasticity reduction. To this aim, considering composite sleeve has either constant or temperature dependent tensile elasticity (Eq. 65), the failure pressures are compared in Fig. 10. This shows that the burst pressure of the repaired pipe, when elasticity modulus of the composite sleeve degrades with temperature, experiences more reduction than the constant elasticity modulus case, particularly in the higher temperatures. The same trend was reported by Ref. [8] in the case of a composite-metal joint under bending moment. Moreover, comparison of the hoop stress and tensile strength of the Thermo-wrap composite sleeve has been shown in Fig. 11, which evidently represents that failure will not occur in the composite sleeve even at severe temperatures. This is consonant with the fact that failure first occurs in the pipe, not in the composite repair [22].

Fig. 10
figure 10

Comparison of repaired pipe burst pressure constant and temperature dependent tensile elasticity

Full size image
Fig. 11
figure 11

Tensile stress and failure strength of sleeve vs temperature

Full size image

3.2.3 Effect of thermal expansion coefficients of composite

Here, the effect of different thermal expansion coefficients in the radial and circumferential directions are investigated. For this purpose, \({\alpha }_{\theta }\) and \({\alpha }_{r}\) are considered as \({\alpha }_{1}\) and \({\alpha }_{2}\), respectively. The effects of \({\alpha }_{1}\) and \({\alpha }_{2}\) on the burst pressure of repaired pipe are presented in Figs. 12 and 13. It is evident from Fig. 12 that the increase of \({\alpha }_{1}\) causes the burst pressure to decrease. It should be noted that this effect is significant in the low values of \({\alpha }_{2}\). By contrast, Fig. 13 indicates that the increase of \({\alpha }_{2}\) makes the failure pressure slightly go up. Also, the low values of \({\alpha }_{1}\) are desirable, bringing a higher pressure capacity.

Fig. 12
figure 12

Effect of different values of \({\mathrm{\alpha }}_{1}\) on the burst pressure of repaired pipe at: a low values of \({\mathrm{\alpha }}_{2}\), b high values of \({\mathrm{\alpha }}_{2}\)

Full size image
Fig. 13
figure 13

Effect of different values of \({{\varvec{\upalpha}}}_{2}\) on the burst pressure of repaired pipe at: a low values of \({{\varvec{\upalpha}}}_{1}\), b high values of \({{\varvec{\upalpha}}}_{1}\)

Full size image

3.2.4 Proportional loading of the thin-walled repaired pipe

In the case of proportional loading, the longitudinal strains should be involved. For various proportionality factors (\(\alpha \)), resulting from Eq. (49), Fig. 14 has been presented. Accounting for \(\alpha \)=0, the results are obtained in the case of plane strain, which is a particular state of proportional loading. As can be seen from Fig. 14, the higher positive values of \(\alpha ,\) the lower failure pressure. Besides that, the trend of burst pressure at negative and positive values of \(\alpha \) is dissimilar. On the other hand, if \(\alpha \) is less than − 3.1, then the hoop stresses in the sleeve will be higher than the tensile strength of the sleeve considered from Eq. (67), in the case of GFRP, presented in Fig. 15.

Fig. 14
figure 14

Burst pressure in the case of the pipe subjected to the proportional loading

Full size image
Fig. 15
figure 15

Comparison of hoop stress and ultimate tensile strength for GFRP sleeve at various proportionality factors

Full size image

It points out that in \(\alpha =-3.15,\) if the temperature is greater than 85 °C\(,\) the composite sleeve breaks down. Also, the failure pressure versus proportionality factor (\(\alpha \)) illustrated in Fig. 16 gives the idea that at significant positive values of \(\alpha \), the burst pressure levels off, but it dramatically declines at negative \(\alpha \) values. As presented by Ref. [18], the most substantial stresses appear in the pipe in the case of \(\alpha <0\) rather than positive, which in turn accounts for a critical state at the high compressive longitudinal strains.

Fig. 16
figure 16

The failure pressure versus the proportionality factor (α)

Full size image

3.2.5 Effect of axial stresses

Using the plane strain solution, one can consider the effect of axial stress on the failure pressure of the repaired pipe. Figure 17 indicates that in the low and high temperatures, the plane strain solution, in comparison with the plane stress one, makes the burst pressure of the repaired pipe higher and lower, respectively.

Fig. 17
figure 17

Effect of composite’s longitudinal modulus relative to neglect it

Full size image

The impact of longitudinal elasticity modulus of the composite patch, presented in Fig. 18, proves that in the larger values of \({E}_{z},\) there is an opposite trend between the temperature and the burst pressure.

Fig. 18
figure 18

Effect of longitudinal elasticity modulus of the composite patch on the burst pressure of the repaired pipe

Full size image

3.3 Results for thin-walled pipe-composite repair system

3.3.1 Effect of filler between pipe and sleeve

To investigate the effect of filler between pipe and composite patch, Eq. (60) is applied. Using the data of Table 2, the burst pressure of repaired pipe is equaled to 19.94 MPa. However, the elasticity modulus of infill material can be different. The influence of filler modulus on the burst pressure of the repaired pipe has been shown in Fig. 19. It is possible to observe that as the filler elasticity modulus changes from 0 to 3 GPa, the failure pressure increases dramatically; however, it goes up steadily in the higher elasticity moduli of the filler. Regarding Fig. 19, if the elasticity modulus of the infill material increases from 1 to 5 GPa (which are practical values), makes the failure pressure rise about 10%.

Table 2 Main parameters for the investigation of failure pressure [11, 16, 20, 21]
Full size table
Fig. 19
figure 19

Burst pressure versus elasticity modulus of filler

Full size image

The hoop stresses in the pipe, filler and sleeve in different elasticity modulus of the filler along the radial centerline from the inner layer of the pipe up to outer layer of the composite sleeve, illustrated in Fig. 20, indicate that the higher elasticity modulus of the filler, the lower and higher stresses in the pipe and composite sleeve, respectively. Therefore, a stiffer filler will be able to transfer the stresses from the pipe to the sleeve effectively, but high stiffness may cause the brittle failure of the filler. To avoid such kind of failure, a combination of experimental tests and analytical solutions for choosing optimized properties of infill material can be suitable. Moreover, Fig. 20 shows that the filler transfers the loads from the pipe to the composite but does not have a significant contribution in tolerating the loads. Likewise, the circumferential strains of the system have been presented in Fig. 21. As expected, the higher filler’s elasticity modulus, the higher hoop strains for the filler and sleeve; however, pipe strains do not vary substantially. On the other hand, the inner layers of the composite sleeve carry higher values of stress and strain than the outer ones. Thus, the inner layers of the composite should be considered with enough strength and stiffness to carry the loads properly.

Fig. 20
figure 20

Circumferential stress in the pipe, filler and sleeve at different elasticity modulus of the filler along radial centerline from inner layer of the pipe up to outer layer of the composite sleeve

Full size image
Fig. 21
figure 21

Circumferential strain in the pipe, filler and sleeve at different elasticity modulus of the filler along radial centerline from inner layer of the pipe up to outer layer of the composite sleeve

Full size image

Furthermore, the effect of partially bond factor presented in Fig. 22 indicates that bonded contact between pipe and filler is more important than between filler and sleeve. As a matter of fact, in the case of a partially bonded pipe-filler, the burst pressure has a lower value than in another case. Therefore, it is essential to clean the surface of the defect perfectly before applying a filler to prevent the contact debonding between the pipe and filler. Additionally, the burst pressure as a function of \({\mu }_{1}\) and \({\mu }_{2}\) is shown in Fig. 23. As expected, \({{\mu }_{1}=\mu }_{2}=1\) accounts for the highest burst pressure.

Fig. 22
figure 22

Effect of partially bond factor considering the effect of filler

Full size image
Fig. 23
figure 23

3-D diagram of the burst pressure versus \({\mu }_{1}\) and \({\mu }_{2}\)

Full size image

4 Conclusions

This study is concerned with the impacts of various parameters on the internal pressure capacity of the metallic pipe repaired by a composite sleeve. The most prominent findings are as follows:

  1. 1)

    The temperature-dependent properties of the composite repair, such as elasticity modulus and tensile strength, can substantially reduce the internal pressure capacity in elevated temperatures. Neglecting the effect of temperature, the strength of GFRP utilized to rehabilitate the metallic pipe would be greater than that of thermo-wrap composites. However, including the temperature-dependency of both materials would make the failure happen in the former at lower temperatures compared to the latter.

  2. 2)

    A partially-bonded composite repair system cannot reinforce the damaged pipe efficiently. A good surface preparation before applying the filler material would be able to enhance the composite repair effectiveness.

  3. 3)

    A stiffer filler can transfer loads from the pipe to the sleeve effectively, but a great deal of stiffness potentially leads to its brittle failure. It is recommended that further research should be conducted to determine an optimized elasticity modulus of the filler.