1 Introduction

Developing metal oxide-based transparent electronics in the rapidly expanding semiconductor industry is one of the priority research areas. In industrial applications, discovering the controllability of physical properties for materials is an essential fact and desired factor. A controllable multiferroic has been found with inherent geometric magnetic frustration [1,2,3,4]. CuCrO2 (delafossite oxide) is in the group of systems having an antiferromagnetic triangular sublattice and this trivalent cationed system possesses the space group of \(R\bar{3}m\) in the hexagonal setting. Due to the discovery of its multiferroic behavior, the magnetic behaviors of defalossite CuCrO2 receive detailed interest [5,6,7]. Further, CuCrO2 exhibits interesting magnetoelectric properties which are tunable by both a magnetic and an electric field [7,8,9]. In the optoelectronic device technology, n-type transparent conducting oxides (TCOs), such as Sn-doped In2O3 [10], Sb-doped SnO2 [11], and Al-doped ZnO [12] are some of the well-known and widely-used examples in touch panels, solar cells, and flat panels. However, the p-type of TCOs are relatively less developed and therefore less widely utilized. By achieving the first CuAlO2 film, a new highly conductive p-type TCO candidate has been found and this conducted research brought new Cu-incorporation oxides trials like CuFeO2 [13] and CuInO2 [14]. Intrinsically, the low hole mobility of p-type TCOs gives rise to low conductivity, and therefore the research, together with development efforts for p-type TCOs is still a worthwhile issue. So far, many methods have been carried out to synthesize n-type semiconductor nanoparticles through different methods such as titanium dioxide (TiO2) [15], zinc oxide (ZnO) [16], and tin dioxide (SnO2) [17] but the number of reports on p-type transparent oxide semiconductor (TOS) nanoparticles needs to be increased by conducting research and discoveries. As a p-type TCO, CuCrO2 is an interesting material of which elemental components are non-toxic, inexpensive, and considerable for industrial purposes. At room temperature, CuCrO2 has the property of varying a direct optical band gap as large as 2.95–3.30 eV in bulk shape, and this varying bandgap property of CuCrO2 is crucial in bandgap engineering [18,19,20].

In this presented study, the pressure effect on the physical properties of CuCrO2 is investigated. The samples are subjected to 10, 30, and 50 tons of pressure and coded as S1, S2, and S3, respectively. The technical measurement properties such as structure, optic, and magnetic properties are detailed in the experimental section. The results and discussion section exhibits and discusses the obtained results and correlates them with the literature. Finally, the conclusion section provides an overview of the conducted research with some important details.

2 Experimental

Cu2O and Cr2O3 chemicals provided by Sigma-Aldrich were subjected to thorough mixing of Redox reaction (Cu2O + Cr2O32CuCrO2). The mixture was sintered in a furnace by increasing the final temperature to 900 °C for 2.5 h. The furnace then was switched-off for self-cooling to room temperature. The samples were taken out and ground by an agate mortar and pressed for 10, 30, and 50 MPa pressures for 10 min with a thickness of 4 mm and a diameter of 10 mm. For better atomic packing, a second time sintering was applied for all samples by increasing the temperature by 4 °C/min. The sample was kept at the final temperature of 1100 °C for 3 h and taken out the samples after self-cooling to room temperature. The crystallinity of the synthesized powder was analyzed by Rigaku Automated Multipurpose X-ray Diffractometer (XRD) instrument using a monochromated Cu Kα (1.5418 Å) source in the 2θ scan range of 10° to 120°. The defined surface morphology and sample stoichiometry was provided by Jeol-6390-LV Scanning Electron Microscopy (SEM–EDX) tool. A special design X-ray Photoelectron Spectroscopy tool was used to measure the core levels of all species at the surface of the samples. The optical properties of the samples were clarified by Shimadzu 2600 UV-Spectrophotometer in the range of 200–900 nm. Photoluminescence properties were measured by using the Agilent Cary Eclipse Fluorescence Spectrophotometer. Quantum Design Model 6000Vibrating Sample Magnetometer (VSM) for Physical Property Measurement System (PPMS) was used to measure magnetic parameters.

3 Result and discussions

3.1 Structural study

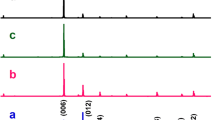
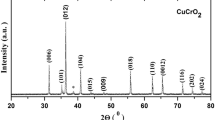
A detailed X-ray study was provided for the samples S1, S2, and S3 in a wide range of 10–110°. As seen in Fig. 1, all samples give almost the same structural phase properties without any secondary peaks. CuCrO2 system has the trigonal crystal structure with the space group of \(R\bar{3}m\). The lattice parameters were calculated by Cohen’s method for S1, S2, and S3 samples as (a = 2.976°A and c = 17.110°A), (a = 2.972°A and c = 17.107°A), and (a = 2.969°A and c = 17.109°A), respectively [21]. The results were also proofed by NIMS database. The effect of pressure on lattice parameters and unit cell volume was demonstrated in Fig. 1b and c respectively. The in-plane lattice parameters are in decrement tendency with increasing applied pressure but out of plane lattice parameters show a decrease up to 30 tons of pressure and an increase after 30 tons. The unit cell volume is in the decrement tendency with applied pressure, so this is an indication of increasing chemical pressure in the cell volume.

Fig. 1
figure 1

XRD patterns of pressure-dependent CuCrO2 samples in (a). The variation of pressure-dependent in-plane and out-of-plane lattice parameters and the unit cell variation with pressure was demonstrated

Full size image

Figure 2 depicts the SEM macro images in 5 µm, 1 µm, and 500 nm magnifications to figure out the granular behavior of the S1, S2, and S3 samples. As seen in all magnifications of SEM images, no melting was found and thus the annealing temperature of the samples was optimized.

Fig. 2
figure 2

SEM images at varying magnifications and EDX spectrums of S1, S2, and S3 samples. In the figure a, b, c, and d are belong to S1, e, f, g, and h are belong to S2, and k, l, m, and n are belong to S3 samples

Full size image

3.2 Photoluminescence (PL)

PL measurements of the CuCrO2 sample were induced in the range of 350 nm to 900 nm as shown in Fig. 3. Two main peaks were observed in Fig. 3 which are ultraviolet (UV) emission peak and broad visible emission band (DL). In the UV region, a sharp transition peak, attribute to near band edge (NBE) transitions, was observed at 362 and 378 nm for the CuCrO2 sample. NBE emission is caused by excitonic transitions between electrons and holes, the stronger the UV emission of the sample, the higher the crystallization quality, and fewer defects occurred. The second dominant and broad emission peak is Deep-level (DL) emission, consisting of violet, blue-green-yellow-orange, and red emission peaks. Deep-level emission is adjusted impurities or defects such as Cu-interstitial (Cui), Cu vacancies (Vcu), Cr vacancy (Vcr), oxygen vacancies (Vo), and oxygen interstitial (Oi) in the crystal structure. Therefore, the Gaussian decomposition of PL spectra was analyzed by “Fityk” software. To our knowledge, such PL emission has not been reported for CuCrO2 delafossit oxides in the literature.

Fig. 3
figure 3

PL spectra of the CuCrO2 sample

Full size image

The eight Gaussian decompositions of PL spectra versus emission wavelength were plotted as shown in Fig. 4. The peak labels with positions center, areas, and height of these curves varied according to the various pressure of CuCrO2 samples as indicated in Table 1. The eight peaks are suited to five emissions; two ultraviolet emissions (Peak 1 and Peak 2) from 360 to 390 nm can be ascribed to the NBE of CuCrO2 as an indication of the excitonic characteristic. Violet and blue emissions (Peak 3 and Peak 4) from 390 to 492 nm can be attributed to Cu-interstitial and Cu vacancies, respectively, and the red emission is divided into two parts; (Peak 5 and Peak 6) from 620 to 750 nm and (690–750 nm) might be attributed to oxygen interstitials (Oi) and oxygen vacancy (Vo), respectively. Two NIR (near-infrared) emissions (Peak 7 and Peak 8) from 750 to 768 nm were the results of oxygen vacancy depicted [22] and references in]. Moreover, it can be attributed to the second-order diffraction (a harmonic of the first peak of the near band-edge) [20].

Fig. 4
figure 4

Gaussian decomposition of PL spectra of CuCrO2 samples at various pressures a 10t, b 30t, and c 50t

Full size image
Table 1 The peak center, height, and area, values, emission range, the origin of PL emission of the CuCrO2 samples
Full size table

As seen in Fig. 4, the DL emission (visible region) band consists of violet, red, and NIR emission peaks for the CuCrO2 samples. It can be concluded that reactions in the solid-state reaction process may cause cooper and oxygen vacancies and affect the luminescence, and structural and magnetic properties of the CuCrO2 sample.

3.2.1 Band gap calculation

The values of Eg depended on several factors such as crystallite size, carrier concentration, lattice strain, and the size effect of the dopant metals in the CuCrO2 lattice. The optical band gap Eg can be found using the following equation for the absorption coefficient (α) and the photon energy (hν):

$$\alpha h\upsilon = k\left( {h\upsilon - E_{g} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n}}}$$
(1)

In Eq. (1), Eg and k is the optical band gap and energy-independent constants, respectively. Since F(Rα) is proportional to α and n is a constant that depends on the bandgap type 1/2 and 2 for direct and indirect bandgaps, respectively. Thus, for directly and indirectly allowed transitions, n is taken as 1/2 and 2 Eq. (1) can be transformed to Eq. (2):

$${\text{F}}\left( {{\text{R}}_{\alpha } } \right)h\upsilon = {\text{k}}\left( {h\upsilon - {\text{E}}_{{\text{g}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \quad {\text{and}}\quad {\text{F}}\left( {{\text{R}}_{\alpha } } \right)h\upsilon = {\text{k}}\left( {h\upsilon - {\text{E}}_{{\text{g}}} } \right)^{2}$$
(2)

in other words,\(\left( {F\left( {R_{\alpha } } \right)h\upsilon } \right)^{2} = k^{2} \left( {h\upsilon - E_{g} } \right).\;and\;\left( {F\left( {R_{\alpha } } \right)h\upsilon } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} = k^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \left( {h\upsilon - E_{g} } \right)\).

The slope of the graph of \({\left(F\left({R}_{\alpha }\right) h\upupsilon \right)}^{2}\) was approximated by using a linear fit \(y\left( {h\upsilon } \right) = A \times h\upsilon + B\) in the least-squares sense [23]. To do this, the following error formula given in Eq. (3)

$$E\left( {A,B} \right) = \mathop {\min }\limits_{A, B} \mathop \sum \limits_{i = 1}^{N} \left[ {A \times \left( {h\upsilon } \right)_{i} + B - \left( {\left( {F\left( {R_{\alpha } } \right) h\upsilon } \right)^{2} } \right)_{i} } \right]^{2}$$
(3)

was minimized for A and B where N is the number of data points. Tables 2 and 3 displays A, B, Eg-direct and indirect band gap energies and relative error values for these data set.

Table 2 Fitting the curve function y(hυ) = A × hυ + B, Eg-direct (eV) bandgap energies and relative errors for CuCrO2 samples
Full size table
Table 3 Fitting the curve function y(hυ) = A × hυ + B, Eg-indirect (eV) bandgap energies and relative errors for CuCrO2 samples
Full size table

As shown in Tables 2 and 3 and Fig. 5, the direct and indirect bandgap energy (Eg-direct and Eg-indirect) were calculated by the linear approximation of the graphical slope of (F(Rα)hυ)2 and (F(Rα)hυ)0.5 to the photon energy axis in which, F(Rα) = 0. In other words, the Eg value was obtained from the intersection between the linear fit and the photon energy axis. As shown in Fig. 5, the direct-I and direct-II bandgap energies of the CuCrO2 samples were observed as (1.86, 1.87, and 1.90 eV) and (2.41, 2.41, and 2.47 eV) respectively. The indirect-I and indirect-II bandgap energies of the CuCrO2 samples were observed as (1.50, 1.51, and 1.58 eV) and (1.65, 1.66, and 1.82 eV), respectively. It was found that the direct and indirect bandgap of CuCrO2 samples increased with the pressure. The values of Eg depended on the crystallite size, carrier concentration, lattice strain, the size effect of the dopant, and the effect of defects formed under pressure on CuCrO2 delafossite.

Fig. 5
figure 5

The plots of a, c, and e exhibit photon energy-dependent (F(Rα)hν)2 behavior, and b, d, and f for (F(Rα)hν)0.5

Full size image

3.3 Magnetic properties

We further investigated field-dependent magnetization for the samples S1, S2, and S3 under varying fixed temperatures (10, 50, 100, 180, 220, 300, and 400 K) separately. As seen in Fig. 6 except for the measurements at 10 and 50 K, all samples above 100 K show paramagnetic behavior. Below 100 K there might be antiferromagnetic behavior. Magnetic variations (Remanent Magnetisation and Coercivity Field) of S1, S2, and S3 samples at 10 and 50 K are shown in Table 4. In the delafossite structure, each linearly coordinated Cu by two oxygen atoms, forming O–Cu–O structures parallel to the c-axis. This is the form of a layered triangular lattice anti-ferromagnetic and oxygens in the O–Cu–O structure are each coordinated with three Cr atoms parallel to the ab plane.

Fig. 6
figure 6

Field-dependent moment variation in the magnetic field region ± 6 kOe

Full size image
Table 4 Magnetic variations of S1, S2, and S3 samples at 10 and 50 K
Full size table

However, due to the granular structure of the samples, magnetic behavior slightly to superparamagnetic behavior. This should be the reason for the pressure effect of each sample. The pressure effect much clearly seen in Fig. 7 which depicts the temperature-dependent moment behaviors of S1, S2, and S3 CuCrO2 samples. As seen in Fig. 7, below 100 K, inter-grain magnetization gets in antiferromagnetic order. Each grain has a net magnetic moment, such that in a plane, the spins are antiferromagnetically oriented while they have a magnetic moment component perpendicular to the plane. Therefore, each grain should be considered a weak magnet. After 100 K in Fig. 7, all 3 samples showed the same decrement behavior. Before 100 K all samples exhibited a slight variation in moment values. The reason behind this should be attributed to the grain size, related to the formation of grains by applied pressure. The observed exchange bias in Fig. 6 (M-H measurements) reveals interfaces of grains that are not identical but active in the formation of coercive fields.

Fig. 7
figure 7

Temperature-dependent moment variations of S1, S2, and S3 CuCrO2 samples

Full size image

4 Conclusion

Pressure-dependent delafossite CuCrO2 samples were synthesized by the solid-state reaction method. The effect of pressure was detailed in all samples revealing that almost all samples were at the same structural phase properties without any secondary peaks. Excitonic transitions between electrons and holes were revealed by near band emission of Photoluminescence measurements and using the stronger the UV emission of the sample, the higher the crystallization quality and fewer defects occurred. In PL measurements, the second dominant and broad emission peak was Deep-level (DL) emission adjusted impurities or defects such as Cu vacancies (Vcu), and oxygen vacancies (Vo), in the crystal structure. Below 100 K, inter-grain magnetization gets in antiferromagnetic order and at that temperature range, all samples exhibit a slight variation in moment values in Fig. 7. Magnetic field–dependent moment variations in Fig. 6 also supported the results of PL measurements due to the observed exchange bias shifts. The reason behind this should be attributed to the grain size related to the formation of grains by applied pressure, the vacancies revealed by PL measurements, and the sample synthesizing type affecting especially the physical properties.