Abstract
In this article, the problems studied are to optimize the life of the network of sensors covering mobile targets by minimizing the energy consumption of the network. Indeed, wireless sensor networks have received particular attention in recent years, as their applications are common today, such as vehicle tracking or battlefield monitoring. In a wireless sensor network, the sensor battery plays an important role. The function of the sensor depends on the battery life. Replacement of batteries becomes impossible once deployed in a remote or unattended location. A set of randomly placed sensors monitors targets moving in an area. Each sensor has a limited lifetime and two states: Active or Inactive. An active sensor can monitor targets in its monitoring sub-area at a necessary energy consumption cost. To model these problems, we use a mathematical model based on linear programming with mixed integer variables. AMPL is used to formulate the model and MINOS for its resolution and the numerical results allowed to obtain an adequate activation scheduling of the sensors by improving their lifetime.
Article Highlights
-
Wireless sensor networks Their applications are common today, such as vehicle tracking or battlefield monitoring. A set of randomly placed sensors monitors targets moving in an area.
-
Energy consumption Optimizing the life of the network of sensors covering mobile targets by minimizing the energy consumption of the network.
-
Mathematical model To model these problems, we use a mathematical model based on linear mixed-integer variable programming.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Technological advances in the production of electronic circuits, and to a lesser extent advances in batteries for the storage of electrical energy, have enabled the development of autonomous sensors, small and with a lower manufacturing cost. Sensors are devices capable of collecting different information within their range and communicating with other sensors. Wireless sensor networks are a very promising and coveted technology.
When monitoring mobile or fixed targets, maximizing the lifetime of the sensor network is one of the most studied research themes [1, 2]. In a wireless sensor network, the time during which all targets are covered defines the network’s lifespan. According to some authors as [3,4,5], the formulation of this problem is based on the notion of connectivity and coverage. Indeed, a subset of sensors can cover all targets. Therefore, at every moment of any mission, it is unnecessary to activate all the sensors, but only the faces containing the sensors to be activated. Energy consumption is a key factor in a wireless sensor network given that the sensors are equipped with batteries that are not rechargeable. Thus, several algorithms and protocols are developed to overcome this energy problem of a wireless sensor network [6,7,8].
The ability to monitor targets in a vast area at a lesser cost is one of the key advantages of wireless sensor networks. Wireless sensor networks are often made up of low-cost devices that may be dropped from an airplane or a helicopter in large numbers in areas where surveillance infrastructure is weak or non-existent. Typically, autonomous sensors are powered by a battery with a finite lifespan. Because many areas of the area to be watched are covered by many sensors, it is not practical to activate all sensors at the same time to monitor all targets. Assuming that the target trajectories are known ahead of time, our goal is to plan a sensor activity sequence. Such scheduling must preserve, as far as workable, the sensor network’s existing capacity to monitor later certain regions of interest to the sensor network’s operator. It is also envisaged that, by scheduling each monitoring expedition, the total amount of energy consumed will be reduced. The sensor network is now being used in a context with several missions, with the initial goal being to conserve the network for future monitoring operations while focusing on solutions that require the least amount of energy to complete the current task [9].
Energy consumption is one of the most important criteria since sensors are usually equipped with a non-rechargeable battery. It is also one of the most studied and the subject of very abundant literature. One of the flagship protocols is Dynamic Convoy Tree-based Collaboration (DCTC) [10, 11], which calculates successively minimum cost trees by tracking the movements of a target. Many protocols that meet this criterion rely on Low Energy Adaptive Clustering Hierarchy (LEACH) [12] or Hybrid Energy-Efficient Distributed (HEED) [13]. Better tracking accuracy can be achieved by activating more sensors or correctly predicting target behavior. A good target prediction technique can help to activate fewer sensors and save batteries. Authors Yang et al., and Xu et al. [14, 15] and [16] propose predictive-based protocols. Since sensor networks can have a very large number of nodes, protocols must be able to adapt to all network sizes. Scalability means the ability to adapt to all network sizes. This criterion is crucial in the design of protocols to avoid network overload. For example, the authors Kung et al. [17] looked at this aspect in particular. If the sensors suffer malfunctions or attacks from an enemy, it may be necessary to expect hazards. Robustness or tolerance to errors responds to this problem and is the subject of increasing interest in recent years [18, 19].
Given an interesting area within the surveillance zone, the first step will be to determine the minimum trajectory used by the different targets guaranteeing their coverage. The coverage guarantee is the minimum duration at the end of the current mission, during which the sensor network can monitor any point in an interesting area. Thus, knowing the optimal trajectory of the targets, the aim is now to minimize the total energy consumed by the sensors to accomplish the current monitoring mission. We first consider the case where the trajectory of the targets is established and known and then assume that they are subject to the uncertainty that their actual positions may deviate from their forecast positions by a certain distance.
The rest of this article is organized as follows. Section 2 presents the architecture of the sensor network. In Sect. 3, we have the discretization model allowing a localization schedule of targets. A discretization of target movement areas and time windows for each given mission will be established in this section. The linear programming model with mixed variables maximizing the life of the network is given in Sect. 4. We used AMPL for the numerical formulation of this mixed linear model and MINOS for its resolution and the numerical results are presented in Sect. 5. The conclusions and discussions are presented in Sect. 6.
2 Architecture of a sensor network
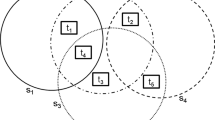
According to the authors [20, 21], in two dimensions, the monitoring of a service area of a sensor network, as shown in Fig. 1, can be modeled into a planar graph \(G(\mathcal{X}, \mathcal{U})\). Indeed, the intersections between the edges of the coverage areas represent the nodes. Along these edges, the edges connect the nodes. The face is the area bounded by the edges. All points on one face are covered by the same number of sensors. If multiple targets are in the same area, then a single sensor is enough to cover them all. For example, in Fig. 2, the Face geometric \(F_3\) is covered by all the sensors \( \{S_1, S_2 \}.\) So, as these sensors monitor the same points in this sub-zone, then the latter is the same Face. In three dimensions, the surveillance zone is divided into volumes, delimited by surfaces.
According to Berman et al. [20], when the coverage areas are \(|\mathcal{M}|\) discs, the number of faces is at most equal to \(|\mathcal{M}|(|\mathcal{M}| - 1) + 2.\) Two circles that can be cut at most twice. If we assume that each circle exactly cuts each of the other circles twice, then the number of peaks \(| \mathcal{X}|\) is at most \( | \mathcal{M}|(| \mathcal{M}| - 1),\) and the number of edges \(| \mathcal{U}|\) is at most \( 2| \mathcal{M}| (| \mathcal{M}| - 1).\) Thus, using Euler’s formula we have: \( | \mathcal{X}| - | \mathcal{U}| + | \mathcal{F}| = 2 \) with \(| \mathcal{F}|\) the number of faces, \( | \mathcal{F}| \) being at most \(| \mathcal{M}| (| \mathcal{M}| - 1) + 2,\) knowing that the undiscovered face is considered.
In three dimensions where the coverage areas are spheres, the number of volumes is at most \( \frac{1}{3}| \mathcal{M}|(| \mathcal{M}|^2 - 3| \mathcal{M}| + 8) \) according to the authors [22] if the external volume is included. For reasons of harmonization, the term face will be used for Face (in case of two dimensions) and Volume (in case of three dimensions). In the following, a Face is defined by a set of sensors covering the same sub-area. Thus, all disjointed geometric areas covered by the same set of sensors will be different Faces.
3 Sequencing the location of a target
The aim in this section is to plan the follow-up of the target by protecting the solution against advance or delay from the planned transit times. This is achieved by ensuring that the target is continuously monitored throughout the mission. More robust scheduling of monitoring activities without additional energy costs is designed. To comply with this last constraint, a single sensor can be activated.
A target at a t moment is represented by a point. We assume that the trajectory of a target is given. The trajectory of a target is noted by \(\mathcal{T}.\) It is modeled by a continuous vector function \(\mathcal{P}: {\mathbb {R}}^{+} \mapsto \mathbb {R}^n,\) defined by \(\mathcal{P} (t) \) where t is a time variable and \(n \in \mathbb {N}^{\star }\) is the space dimension.
Suppose a m surveillance mission lasts \( H_m\) time units and runs between instances \( t_1 = \)0 and \( t_m = H_m.\) The time interval \( \left[ 0, H_m \right] \) is called the time horizon of a mission m. Each target may enter or exit the surveillance zone at different times. Some may appear after \( t_1 = 0,\) as disappear before \( t_m = H_m.\) It will be assumed, without loss of generality, that any target is present in the surveillance zone for the entire mission time horizon. Indeed, a target that leaves the surveillance area can only be covered by a fictitious sensor whose life (energy) is infinite, and which only covers targets that are outside the sensor coverage area.
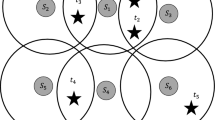
For the duration of a m mission, all targets must be monitored by at least one sensor. Therefore, it is necessary to ensure that, at all times, a single subset of sensors is available to cover all targets. Thus, this response to the target coverage constraint. The trajectory of a j target can be seen as a sequence of \((F_1, F_2, \ldots , F_f) \) where f is the index of the \(f^{th} \) face crossed. For example, in Fig. 3, the target successively crosses \(F_3,F_4,F_7,\) and \(F_6.\) Let \(\overline{ \mathcal{F}} \subseteq \mathcal{F}\) all the faces covered by the targets. All points on one side \( F_f \in \overline{ \mathcal{F}}\) are covered by the same set of candidate sensors. Thus, to cover a target, it is enough to know the \(F_f\) face in which it is in and to activate at least one sensor.
The exact positions of the sensors and targets are no longer necessary to solve the various monitoring problems. The key moments of a surveillance mission are when a target crosses the border on one side. When a j target changes sides, all the sensors candidates for its monitoring also change. These transition dates are called ticks. The ticks are got by calculating the moments when the targets cross the boundaries of the faces, which is possible as soon as their trajectories are known, including the beginning and the end of the time horizon. By definition, no target changes sides between two consecutive ticks, and therefore the candidate sensor sets for each target remain unchanged. Thus, each of the monitoring problems can be viewed as a sequence of set coverage problems.
For each j target, we get a sequence \( (t_j^1, t_j^2, \ldots , t_j^n) \) of associated ticks, where \(t_j^u\) is an entry or exit date of the coverage area of a sensor, with \(t_j^1\) and \(t_j^n\) respectively the entry and exit instances of the monitoring area. The \(t_j^u\) tick is the entry date in the \(u^{th}\) face, and \(t_j^1\) and \(t_j^n\) are respectively the target’s appearance and disappearance dates relative to the surveillance zone. Based on our initial assumptions, we consider \(t_j^1 = 0\) and \(t_j^n = H_m\). A target may come out of a \(z_i\) coverage area and enter another \(z'_i\) at the same time. Here, we consider two ticks of the same value. The face visited between these two ticks is a face that is not covered by \(z_i\), nor by \(z'_i\).
Figure 4 defines the different sub-procedures and variables allowing the ordering of the activation of the sensors in the area of interest. Thus, by initialization, all sensors are initially inactive while waiting for the appearance of a target in a face to activate it. This allows determining all the necessary variables and optimizing the duration of the sensor network covering the moving targets.
4 A mathematical model
4.1 Sets and parameters
A set of \(\mathcal{I}: = \{1 \ldots M \}\) static sensors are randomly dispersed within a region. Each \(i \in \mathcal{I}\) sensor is powered by a battery with an initial duration of \(V_i\) and can monitor targets in its coverage area. All points in the coverage area of a i sensor are noted as \(z_i\). Without loss of generality, we assume that the coverage area of each sensor is defined by a R radius disk. When a i sensor is active, it monitors all targets in the \(z_i\) coverage area and fires power on its battery regardless of the number of targets monitored. This reduces its life. When the sensor is idle, its battery capacity remains unchanged. The union of the coverage areas is called the surveillance area and is given by: \(Z \subseteq \bigcup z_i\). To ensure a m mission, the lifetime of each i sensor must be within the range of \(\left[ V_{m}^{min}, V_{m}^{max} \right] \).
Let \( \mathcal{J}: = \{1 \ldots J \}\) a set of targets whose number is noted by J. By convention, the index of a target is noted j. For each given time window, the minimum time considered monitoring the j target is given by: \(T_{m}^{min, k}\) during any m mission. \(P_j(t)\) Target position j at time t. When two ticks have the same value, only one is kept. Ticks are partitioned into two categories: incoming and outgoing ticks. The incoming ticks correspond to the date a target enters the coverage area of a sensor, while the outgoing ticks correspond to the time a target leaves the coverage area of a sensor. By convention, the first and last tick are respectively outgoing and incoming.
Let \( \mathcal{F}: = \{1 \ldots F \}\) all faces crossed by the targets. The number of faces is noted by F. If the clue of a face is f then that face is scored by \(F_f\). In order to have an adequate schedule, the time set to cover each f side is bounded by the values \( {\tilde{D}}_{m}^{min, k}\) and \( {\tilde{D}}_{m}^{max, k}\) in each k time window of each m mission. \( \mathcal{F}^\star \): All faces of interest \( \{F_1 \ldots F_q \}\). \( \mathcal{I}(f) \subseteq \mathcal{I}\): Candidate sensors covering face f.
All mission time windows are scored \( \mathcal{K}: = \{1 \ldots K\}\). The number of time windows and its corresponding index are respectively noted by K and k. Each m mission can then be partitioned into K time windows, where a time window is a period separated by two consecutive ticks. The underlying idea of this variant is to consider that target coverage is equivalent to face coverage. Indeed, activating a sensor to cover a target is equivalent to covering all the points of its coverage area, and therefore, all the points of the face in which the target is located. To cover all targets, it suffices to cover the faces where they are located. For each k time window, let’s define a set \( \mathcal{F}(k) \subseteq \mathcal{F}\) of the faces to cover. The set of targets is no longer necessary since the faces where they are located are known. Thus, one advantage of the discretization following the faces is to free oneself from the notion of a target. The scheduling parameter for each k time window during a m mission is given by: \(\Delta _{m}^{k}\).
Using a sensor network can be done on several missions. Thus, to optimize the use of the sensor network to fulfill the current mission, while considering that the network will have to fulfill subsequent monitoring missions [9].
A set of \(\mathcal{M}: = \{1 \ldots M\}\) missions. The total number of missions is M. The index of a mission is m. The life reduction rate for each i sensor after each m mission is equal to \( \alpha _{i, (m-1)}\). The total duration of all missions is H determined by:
4.2 Variables and bounds
The continuous, binary, and integer decision variables of the mixed-integer variable linear programming model are defined:
Let \(v_{i,m} \in [V_{m}^{min}, V_{m}^{max}]\) be the remaining lifetime of the \(i \in \mathcal{I}\) sensor after the mission \(m \in \mathcal{M}\).
Let \(y_{i,m}^{k,f} \in [Y_{m}^{min, k}, Y_{m}^{max, k}]\) the sensor activation time \(i \in \mathcal{I}\) to cover the face \(f \in \mathcal{F}\) belonging to the time window \(k \in \mathcal{K}\) during the mission \(m \in \mathcal{M}\).
The variable defining the activation or not of a sensor in a face during a mission is a binary variable established by:
Let \(d_{m}^{k,f} \in [D_{m}^{min, k}, +\infty )\) the duration of coverage of the face \(f \in \mathcal{F}\) during the time window \(k \in \mathcal{K}\) during the mission \(m \in \mathcal{M}\).
Let \({\tilde{v}}_{i,m} \in [V_{m}^{min, k}, +\infty )\) the minimum sensor lifetime \(i \in \mathcal{I}\) to ensure a mission \(m \in \mathcal{M}\).
Let \({t}_{j,m} \in [T_{m}^{min, k}, +\infty )\) the minimum monitoring time of the target \(j \in \mathcal{J}\) after the mission \(m \in \mathcal{M}\).
The variable defining an incoming tick, outgoing or not of a f face during a m mission, is an integer variable established by:
\({\tilde{d}}_{i,m}^{k} \in [{\tilde{D}}_{m}^{min, k}, {\tilde{D}}_{m}^{max, k}]\) the time required for a sensor \(i \in \mathcal{I}\) provide one-sided surveillance \(f \in \mathcal{F}\) during the mission \(m \in \mathcal{M}\).
4.3 Objective function and constraints
The mixed-integer variable linear programming aims to maximize the total remaining life of the network sensors, which is equivalent to minimizing the total energy consumption of all the sensors that make up the network. This maximizes the life of the sensor network by allowing multiple mobile target monitoring missions within the same network.
The lifetime of each i sensor is equal to the sum of its remaining duration after each m mission and the time spent on all active faces during all windows to which it is active. The 3 constraint that translates this equilibrium situation is given by:
Proposition 4.1
The 3 constraint is non-linear. Thus, to get a mixed-integer variable linear programming model, the continuous variable \(y_{i, m}^{k, f}\) is introduced by:
The linearization of the 3 constraint will thus allow us to get a linear model. To do this, the 1 proposal and the constraint 3 will get there. Thus, the following linear stress is got:
Proposition 4.2
To get a rapid convergence of the mixed variable linear programming model, the equation \(y_{i,m}^{k,f} = x_{i,m}^{k,f} \cdot d_{m}^{k,f}\) is replaced by linear constraints 5, 6 and 7 following :
Proof
-
(1)
\(y_{i,m}^{k,f} \le d_{m}^{k,f}\) : We have: \(y_{i,m}^{k,f} = x_{i,m}^{k,f} \cdot d_{m}^{k,f}\) however,
$$\begin{aligned} x_{i,m}^{k,f} = \left\{ \begin{array}{ll} 1 &{} \hbox {If the sensor } \; i \in \mathcal{I} \; \hbox { covers the face } \; f \in \mathcal{F} \; \hbox {belonging to} \\ &{} \hbox { the time window }k \in \mathcal{K}\hbox { during the mission }m \in \mathcal{M} \\ 0 &{} { Otherwise}. \\ \end{array}\right. \end{aligned}$$So we get: \(y_{i,m}^{k,f} \le d_{m}^{k,f}.\)
-
(2)
\(y_{i,m}^{k,f} \le V_{i,m} \cdot d_{m}^{k,f}\)
$$\begin{aligned} y_{i,m}^{k,f}&\le x_{i,m}^{k,f} \cdot d_{m}^{k,f} \\&\le d_{m}^{k,f} \\&\le V_{i,m} \cdot d_{m}^{k,f} \end{aligned}$$ -
(3)
\(y_{i,m}^{k,f} \ge \Delta _{k,m} \cdot (x_{i,m}^{k,f} - 1) + d_{m}^{k,f}\)
$$\begin{aligned} y_{i,m}^{k,f}&\ge x_{i,m}^{k,f} \cdot d_{m}^{k,f} \\&\ge (x_{i,m}^{k,f} - 1) + d_{m}^{k,f} \\&\ge \Delta _{k,m} \cdot (x_{i,m}^{k,f} - 1) + d_{m}^{k,f} \end{aligned}$$
\(\square \)
The remaining life of each i sensor becomes smaller and smaller at a given fixed rate, after each m mission, which is translated as:
The coverage time of the active faces is equal to the time allocated to each k time window covering the active faces. This is expressed as:
For each given m mission, the remaining life of the sensors must be greater than or equal to the time required to monitor the targets present in the areas of interest.
During each m mission, for each f face activated in each time window, there is at least one i sensor activated. Thus, it will allow putting all the other sensors on standby to save the energy of their battery, hence their life.
To help the MINOS solver converge faster, the 8 constraint below exploits the symmetry of the model. To do this, the solver runs in each active f face for each k time window of any m mission.
To carry out each m mission, each i sensor must have a lifetime allowing it. To meet this condition, the following constraint is established:
The time required for a i sensor to monitor the targets in each time window of each m mission which is equal to the sum of the time of that window and the time put by the targets between the ticks of that same time window is calculated by:
For each j target, the incoming tick is always the opposite of the outgoing tick for two successive time windows during each m mission. This constraint is given:
The origin of the time windows is considered being \(k_0 = 2\) at the time the sensors are initialized at \(i_0 = \)1, for each given m mission. This is expressed by:
Proposition 4.3
The sum of the time sequences for the use of the sensors cannot exceed their lifespan, which is subtracted from the mission time horizon. This top-up terminal rated \(\sup (V)\) is calculated:
This upper bound \( \sup (V) \) can be improved using coefficients \( \beta _{m} {k}\), representing the lower terminal of the minimum number of sensors to be activated during a k time window to cover all targets during all programmed missions.
Remark 4.1
The maximum value of \( \beta _{m}^{k}\) can be got by solving a defined coverage problem.
5 Computational results
Let us consider the situation of Fig. 3 with three sensors \(\mid \mathcal{I}\mid = 03,\) two targets \(\mid \mathcal{J}\mid = 02,\) seven windows of time \(\mid \mathcal{K}\mid = 07\) and three missions \(\mid \mathcal{M}\mid = 03.\)
Several numerical tests were carried out, which resulted in average results presented in the various tables below. These results were analyzed based on an optimal activation or inactivation schedule for each sensor in order to increase the lifetime of the sensor network. Thus, the optimal solutions got at the end of this schedule are mainly the remaining life of each sensor, the duration of each time window, the forecasts of activation or inaction of each sensor in a time window. An important optimal variable is the activation time of any sensor activated in a time window. Knowing that the sensors are in an inaccessible area, then the use of multiple missions in the same sensor network would be more cost-effective. In fact, compared to recent studies by researchers such [23, 24], our work involves multiple uses of the same sensor network. Thus, our resulting sequencing allows us to activate fewer sensors for a mission composed of three sensors, two targets and seven time windows. Therefore, this maximizes the remaining life of each and the life of the sensor network (Table 1).
For each k time window, the FACES[k] faces allowing the coverage of the target whose trajectory is visualized by Fig. 3 are: \(FACES[1] := \{F_1 \}\); \(FACES[2] := \{F_1, F_2\} \) ; \(FACES[3] := \{F_1, F_2, F_3 \}\); \(FACES[4] := \{F_1, F_3 \}\); \(FACES[5] := \{F_3 \}\); \(FACES[6] := \{F_2, F_3\}\) ; \(FACES[7] := \{F_2\} \). The coverage area of the k sensor is noted by: \(F_k\). We assume the coverage area is a three-dimensional space (Table 2).
It should be noted that in the sequencing of tracking all targets in a surveillance zone comprising three sensors with seven-time windows during three missions, not all sensors need to be activated at the same time. Thus, when a sensor is activated, its activation time is necessary to cover targets appearing in its area of action. The faces to which it belongs must be known. When no target appears in its radius of coverage, then its energy, otherwise its life is returned to infinity as recorded in the Table 5. As an example, during the 1 mission, in the \(F_1\) face and in the 1 time window, is activated at the average required time of 50 Units. What makes the other sensors belonging to the same side as the 1 sensor are put on standby and see their energy sent back to infinity. Therefore, in the \(F_2\) face, during all three missions and in all-time windows, the 1 sensor is activated ten times out of twenty or an activation rate of \( (\frac{1}{2}) \) as it should be. In short, this scheduling enables fewer sensors to monitor the entire area of interest, thus maximizing the life of the sensor network.
Knowing the activation time required for each sensor considered in each time window at each side \(F_k\) during a mission, then it is also important to determine the total time required to activate a sensor for an entire mission m. For example, the 1 sensor in the \(F_2\) face taken in the 2 time window is enabled in the scheduler scheme established at a required time of 77.5 Time units. Therefore, as recorded in Table 4, the time required to activate the 1 sensor during an entire mission for all seven-time windows is equal to \(140 + 77.5 + 1.70678 + 2 = 221.20678\). Thus, we notice that in the 3 sensor scenario, 7 time windows and faces \(F_1\), \(F_2\) and \(F_3\), a sensor is activated only four times in each face for the seven-time windows. If a sensor is not activated, its energy (its lifetime) is sent back to infinity. Another note in the sensor activation sequence is that for each given time window, either the sensor is activated or not. For example, in the 7 time window on the 1 side, no sensor is activated, but in the same time window on the 2 side, all sensors are activated (Table 6).
To help with scheduling that allows for better monitoring of targets in the areas of interest, it is imperative to establish all the ticks entering and exiting in each time window during a mission. For example, during the 3 mission, the 1 target started with a tick entering the 1 time window. This is mentioned in the Array 3 Knowing that ticks are alternatives for each target, then by knowing the first tick, we can deduce that of all other ticks in all time windows. Thus, knowing the trajectory of a target, then the role of ticks, is to determine at each time window whether the target enters a face or exits it. This allows knowing the exact movements of a target to facilitate a perfect sequencing of all the activities of the sensor network. This is when we need to mobilize several sensors and targets. This principle remains intact when the trajectory of a target is subject to a certain stochastic notion.
After each mission, the energy of the sensor batteries becomes increasingly low. Since the sensor battery reduction rate is initially fixed, it is possible to determine the remaining life of each sensor after each mission. Therefore, at the level of Fig. 5a, we see a decrease in the sensor life (energy) after each mission. Thus, this rate of battery decay is a major factor in the longevity of the sensor network. Therefore, the smaller the growth rate, the longer the sensor network lasts. In addition, it is necessary to know the duration of use of each sensor during each mission. This is then shown by Fig. 6b, (a) and (b). Therefore, when we know the time of use of the sensors in each time window, then we can deduce the total time of use of each sensor during an entire mission. For example, in Fig. 6a, during the first mission, the time window exceeds an average value of 120 units of time.
For a sensor to take part in a mission, its lifetime (energy) must be greater than or equal to the threshold of \(\alpha _{i, m}\) participation in a mission m. Otherwise, it is likely to cause a failure to monitor a target once it is in interest. Thus, before the start of a mission, we must check the life (energy) of each sensor to ensure that some sensors will not be running energy on a full mission. For example, Fig. 7b shows the different thresholds that a sensor must have before taking part in a mission. Thus, to begin the second mission, the 3 sensor must have a threshold allowing it to take part in this mission of 18-time units. In addition, each target must have a minimum coverage guarantee time for any sensor in interest. For example, for the second target, during the second mission, the average minimum time to properly monitor it without faults is in the [12, 13] time interval.
6 Conclusion
We have developed a mixed variable linear programming model to optimize the life of a network of sensors covering mobile targets. Thus, the timing of the target location is established by entering or exiting ticks for each time window during any mission. Therefore, scheduling of network sensor activation for each side during any mission is developed by obtaining the longevity of the sensor network life. This makes it possible to know the sensor that must be activated in the shower time window, at the time required for a fixed mission. In addition, we have also established the energy threshold that a sensor must have to take part in a mission to accomplish. Similarly, we calculated the minimum time to cover a moving target. The role of the threshold for a sensor’s participation in a mission and the role of the minimum monitoring time of a target, otherwise known as a guarantee of coverage, have made it possible to have clear visibility of any target of any mission. In short, we have found a schedule that allows us to have the maximum duration of a network of sensors that can be used in several missions. In fact, in contrast to current research, our approach employs numerous sensor networks. For a mission with three sensors, two targets, and seven-time windows, our resultant sequencing allows us to activate fewer sensors. As a result, the remaining life of each sensor and the sensor network are maximized.
In future work, we use a stochastic model to solve the same optimization problem. This will allow us to work with targets, including more complex trajectories.
References
Liang D, Shen H, Chen-L (2021) Maximum target coverage problem in mobile wireless sensor networks. Sensors 21(1):184
Amutha J, Sharma S, Nagar J (2020) WSN strategies based on sensors, deployment, sensing models, coverage and energy efficiency: review, approaches and open issues. Wirel Pers Commun 111(2):1089–1115
Boukerche A, Sun P (2018) Connectivity and coverage based protocols for wireless sensor networks. Ad Hoc Netw 80:54–69
Nguyen TN, Liu BH, Wang SY (2019) On new approaches of maximum weighted target coverage and sensor connectivity: hardness and approximation. IEEE Trans Netw Sci Eng 7(3):1736–1751
Li C, Bai J, Gu J, Yan X, Luo Y (2018) Clustering routing based on mixed integer programming for heterogeneous wireless sensor networks. Ad Hoc Netw 72:81–90
Farsi M, Elhosseini MA, Badawy M, Ali HA, Eldin HZ (2019) Deployment techniques in wireless sensor networks, coverage and connectivity: a survey. IEEE Access 7:28940–28954
Elhoseny M, Hassanien AE (2019) Dynamic wireless sensor networks. Studies in systems, decision and control. Springer, Cham, p 165
Elhabyan R, Shi W, St-Hilaire M (2019) Coverage protocols for wireless sensor networks: review and future directions. J Commun Netw 21(1):45–60
Jishy K (2011) Detection and tracking of maneuvering targets on passive radar by Gaussian particles filtering. Theses. Institut National des Telecommunications. https://tel.archives-ouvertes.fr/tel-00697130
Zhao Q, Gurusamy M (2008) Lifetime maximization for connected target coverage in wireless sensor networks. IEEE/ACM Trans Network 16(6):1378–1391
Torshizi ES, Yousefi S, Bagherzadeh J (2012) Life time maximization for connected target coverage in wireless sensor networks with sink mobility. In: 6th International symposium on telecommunications (IST). IEEE
Handy MJ, Haase H, Timmermann D (2002) Low energy adaptive clustering hierarchy with deterministic cluster-head selection. In: 4th International workshop on mobile and wireless communications network, pp 368–372
O. Younis and S. Fahmy. Heed: a hybrid, energy-efficient, distributed clustering approach for ad hoc sensor networks. n : IEEE Transactions on Mobile Computing 3.4, pages 366–379, 2004
Yang H, Sikdar B (2003) A protocol for tracking mobile targets using sensor networks. In: Proceedings of the first IEEE international workshop on sensor network protocols and applications, pp 71–78
Yang H, Li D, Chen H (2010) Coverage quality based target-oriented scheduling in directional sensor networks. In: 2010 IEEE international conference on communications, pp 395–410
Xu Y, Winter J, Lee W-C (2004) Prediction-based strategies for energy saving in object tracking sensor networks. In: IEEE international conference on mobile data management, Proceedings
Kung HT, Vlah D (2003) Efficient location tracking using sensor networks. In: IEEE wireless communications and networking (WCNC)
Mahmood MA, Seah WKG, Welch I (2015) Reliability in wireless sensor networks: a survey and challenges ahead. Comput Netw 79:166–187
Oracevic A, Ozdemir S (2014) A survey of secure target tracking algorithms for wireless sensor networks. In: 2014 World congress on computer applications and information systems (WCCAIS)
Berman P et al (2005) Power efficient monitoring management in sensor networks. In: 2004 IEEE wireless communications and networking conference (IEEE Cat. No. 04TH8733)
S. Slijepcevic and M. Potkonjak. Power efficient organization of wireless sensor networks. n : ICC 2001. IEEE International Conference on Communications. Conference Record (Cat. No.01CH37240)., 2001
Gordon B et al (1987) Challenging mathematical problems with elementary solutions. T. 1. Courier Corporation, pp 102–106
Elkamel R, Messouadi A, Cherif A (2019) Extending the lifetime of wireless sensor networks through mitigating the hot spot problem. J Parallel Distrib Comput 133:159–169
Srivastava V, Tripathi S, Singh K, Son LH (2020) Energy efficient optimized rate based congestion control routing in wireless sensor network. J Ambient Intell Human Comput 11(3):1325–1338
Acknowledgements
We are solemnly eager to thank all the members of the research team for the mathematical decision of Cheikh Anta Diop University for their collaboration, their critic and support to realize this project. We also thank all the mathematics teachers in the department of mathematics and computing at Cheikh Anta Diop University of Dakar for the realization of these scientific works.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have declared no conflict of interest.
Funding
No funding source available.
Ethical approval
As authors, we declare the manuscript is our original work. Thus, the arguments, ideas, points of view, innovations, and results presented in this manuscript are entirely ours, unless otherwise stated in the text.
Consent to participate
The works of other researchers, which are necessary for the demonstration of the arguments presented in this manuscript, are referenced in the text and thus enumerated with precision. Therefore, the authors declare their consent to the publication.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dione, D., Mbainaissem, T.C. & Ndekou, P.P. Optimizing lifetime of a wireless sensor network covering moving targets. SN Appl. Sci. 4, 192 (2022). https://doi.org/10.1007/s42452-022-05073-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-022-05073-1