1 Introduction

One of the nonlinear dynamic model that shows non-uniqueness is the Taylor vortex flow that swirls between cylinders. The pioneering study by Taylor [1] showed that the theoretical and experimental results for the instability of a Couette-Taylor flow between infinite length cylinders are in agreement. Grossmann et al. [2] reviewed the progress of recent Taylor-Couette turbulence at higher Reynolds numbers. Coles [3] first clarified the non-linear stability and discovered the critical value that bifurcates from a steady Taylor flow into a wavy Taylor flow. Since then, many studies of the stability of the Taylor flow have been reported. Most of these studies, for examples by Burlhalter et al. [4], Koschmieder [5], assumed that the annulus of the working fluid has infinite length and they identified a phenomenon where the flow bifurcates from a Couette flow to a Taylor flow, a wavy Taylor flow, a modulated wavy Taylor flow and finally to a turbulent Taylor flow as the rotating speed of the cylinder is increased. Jones [6] examined numerically the transition from the steady axisymmetric Taylor flow to the time-dependent wavy flow in the infinite-cylinder model. His investigation is the growth of the disturbances added to the two-dimensional fundamental flow and described the behavior of the transition to wavy Taylor flow.

Benjamin [7, 8] focused on the new flow states under the condition that the influence of the end walls of the annulus with the small aspect ratio was taken into account. He applied mathematical theory to the bifurcation of the Taylor flow. His work led to subsequent applications of chaos theory in the evaluation of the stability of nonlinear dynamical system phenomena. For the first time, Mullin and Benjamin [9] experimentally revealed the critical Reynolds number at which the Taylor flow bifurcates to the wavy Taylor flow, in the small aspect ratio which the end plates affect the bifurcation between the flows. As a similar visualization experiment with small aspect ratios, Nakamura et al. [10] clarified the instability of Taylor flows having two geometric conditions with axially symmetric and asymmetric systems. Cliffe et al. [11, 12] numerically simulated a Taylor flow with a small aspect ratio and compared their results with the experimental results. Watanabe et al. [13, 14] reported the mode formation process under the two boundary conditions of axially symmetric and asymmetric systems with small aspect ratios. Toya et al. [15, 16] numerically examined the fluctuation of the kinetic energy of vortices and showed the numerical result of the critical Reynolds number at which a steady Taylor flow bifurcates into a wavy Taylor flow. In this analysis, kinetic energy was used as the evaluation standard. However, it was difficult to distinguish whether the difference was due to a kinetic energy fluctuation or a numerical error of the computer. Because the fluctuation range of the kinetic energy was very small near the critical Reynolds number of the bifurcation, the comparison between experimental and numerical results was inadequate.

Several numerical methods have been proposed to determine the instability of the Taylor flow. Razzak et al. [17] used the variation of the magnitude of the averaged axial velocity component to distinguish among the Taylor flow, the transition flow, and the wavy Taylor flow. Martinand et al. [18] performed a weakly nonlinear analysis and examined the mechanism of transition to a wavy Taylor flow when the radius ratio was large. They added exponential developmental perturbations to the stationary solution and investigated the growth of the perturbations in the positive and negative parts of the exponent. Rudman et al. [19] used a new method based on Poincaré section and determined the perturbations of wave formation for the divergence-free interpolation of discrete velocity data. Crowley et al. [20] carried out the experimental visualization and the numerical simulation, and identified the subcritical laminar-turbulent transition in a system of counter-rotating cylinders. Though the flow is not the Taylor flow, Pasche et al. [21] used a bifurcation analysis and clarified the transition process from a helical vortex flow to a chaotic axisymmetric oscillation flow.

In this study, we focus on the attractor drawn from the axial velocity component of the vortex flow. We apply a theory from chaotic time series analysis to perform a numerical analysis on the instability of the Taylor flow. The time series axial velocity component of the vortex on the bottom end wall is converted into a three-dimensional vector by the embedded theorem, and an attractor orbit is drawn in the three-dimensional space. And the critical value at which the Taylor flow bifurcates into the wavy Taylor flow, which shows the Hopf bifurcation from a fixed point to a limit cycle, is determined.

In the rest of this paper, the governing equations and the calculation methods for Taylor flow and their problems of the study that is previously performed are denoted in Sects. 2 and 3, respectively. Section 4 presents details of the numerical calculation and our new analysis procedure to find the bifurcation Reynolds number. In Sect. 5, after explaining the new analysis method, the critical Reynolds number at each aspect ratio will be clarified while the analysis results of typical Taylor flows are exemplified. Also, the analytical result is compared with the experimental results. Finally, Sect. 6 gives some conclusions of the present study.

2 Flow region and governing equations

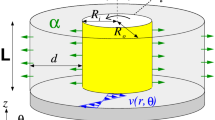
We focus on a circulating flow between concentric cylinders with finite length. The inner cylinder rotates and the outer cylinder and the end walls are stationary.

The governing equations are the continuity equation and the Navier–Stokes equations in the cylindrical coordinate system ( r, θ, z) as shown in Fig. 1:

$$ \nabla \cdot {\varvec{u}} = 0, $$
(1)
$$ \frac{{ \partial {\varvec{u}}}}{\partial t} + \left( {{\varvec{u}} \cdot \nabla } \right){\varvec{u}} = - \nabla p + \frac{1}{{{\text{Re}}}}\Delta {\varvec{u}}, $$
(2)

where t is the time, u is the velocity vector with its components of u, v and w, p is the pressure, and Re is the Reynolds number. These values are normalized by the reference velocity and the reference length defined by the circumferential velocity of the inner cylinder, the gap width between the inner and outer cylinders, respectively, and the kinematic viscosity of the fluid.

Fig. 1
figure 1

The Analytical model: The inner cylinder rotates and the outer cylinder and the end walls are stationary

Full size image

The main parameters are the Reynolds number Re and the aspect ratio \({\Gamma }\) defined by the fraction of the lengths of the cylinders to the gap between the inner and outer cylinders. In this analysis, the range of the aspect ratio is from 1.0 to 7.2 and the radius ratio is 0.667.

3 Previous analysis method utilizing kinetic energy amplitude

The authors have conducted numerical analysis on the stability of the Taylor flow, which is representative of nonlinear dynamical systems, and have been conducting research to compare it with the experimental results that have already been clarified. In the numerical calculation, the axial velocity component of the vortex was obtained, and the bifurcation phenomenon was clarified from the time series fluctuation of the spatially averaged kinetic energy. The kinetic energy fluctuation of the Taylor vortex is in the steady state, and that of the wave Taylor flow is in the fluctuation state. In the previous numerical analysis, it is decided to identify by the magnitude of the amplitude fluctuation of the spatially averaged kinetic energy.

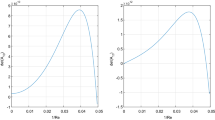
Figures 2a, b show time series signals of the spatially averaged kinetic energy of the vortex located at the bottom of the Taylor flow. The unit of energy value in perpendicular axis is the dimensionless spatial average kinetic energy due to the axial velocity component of the vortex. Figure 2a shows an unsteady state at Re = 630 with the difference between the maximum and minimum values of the amplitude fluctuation being approximately 5 × 10–7. Figure 2b also shows the unsteady state at Re = 635 with the difference between the maximum and minimum values of the amplitude fluctuation being approximately 2.5 × 10–6. Although not shown in the figure, the energy value of Re = 620 is 0.57, which is constant. As shown in Fig. 2a and b, the amplitude fluctuation is so small that it is not possible to determine whether this unsteady state is due to flow fluctuations or numerical errors of computer. Therefore, it is difficult to make a clear determination in Fig. 2a and b. Figure 3 shows the amplitude fluctuation of kinetic energy for each Reynolds number. This figure indicates that the amplitude fluctuation increases sharply from Re = 660. From this fact, we decided the threshold of the amplitude fluctuation in which the fluctuation of the kinetic energy of the flow becomes unsteady as 0.001.

Fig. 2
figure 2

Analytical results utilizing the kinetic energy at \({\Gamma }\) = 3.8. The unit of the energy value is the dimensionless spatial average kinetic energy due to the axial velocity component of the vortex

Full size image
Fig. 3
figure 3

Amplitude fluctuation of energy

Full size image

Figure 4 shows the critical Reynolds number between the Taylor flow and the wavy Taylor flow by comparing the amplitude fluctuation of the kinetic energy in the flow for each aspect ratio with the threshold value of 0.001. It can be seen that the results of the analytical result and the experimental result are qualitatively consistent. On the other hand, it can be seen that there are some variations in the curve of the analytical result. Though it is effective to increase the number of calculations in order to suppress the variation, the number of effective calculations differs depending on the conditions, and the procedure for.

Fig. 4
figure 4

Critical Reynolds number The open symbols denote the experimental results, and the filled symbols represent the numerical results. The square and circle symbols indicate the 2-vortex and the 4-vortex flows respectively

Full size image

setting the number of calculations is complicated and a large amount of work. This our previous analysis study utilizing kinetic energy amplitude is reported in reference [16]. From this result, another analysis method different from the method using the amplitude of kinetic energy is required.

4 Numerical calculation method and analysis procedure

The three-dimensional numerical calculation adopts the MAC method for the basic solution: the QUICK method for the convection terms, the central finite difference method for the spatial integration of other terms, and the fractional method for the time integration. The SOR method and the ILUCGS method are used for the Poisson's equation of the pressure. The grid is a staggered grid. The number of grid points in the three-dimensional space (r, θ, z) at \({\Gamma }\) = 1.0 is (41, 74, 41). The number of points in the axial direction z is determined to be proportional to the value of \({\Gamma }\). The step value of the dimensionless time is 2.5 × 10–3, and the maximum time step number is 10 million TS. The boundary condition is the no-slip condition for the velocity components and the Neuman condition for the pressure Poisson equation. Initially, the fluid is at rest and the inner cylinder is suddenly or linearly accelerated to the prescribed Reynolds number.

As, for example, pointed out by Burkhalter et al. [22], Benjamin [23] and Mullin et al. [24], the non-uniqueness indicates that there are multiple stable solutions on a fixed condition. The Taylor flow also has multiple solutions. One of them is called a primary mode that is generated as the Reynolds number is increased in a quasi-stationary manner, and it is unique at each aspect ratio. The others are the secondary modes generated due to the history of the increase in the Reynolds number [9, 10]. Figure 5 shows the azimuthal-section views of the flows in the normal 4-vortex mode, the anomalous 4-vortex mode in which the flow direction on the end wall(s) is radially outward and the normal 2-vortex modes at a fixed aspect ratio and a fixed Reynolds number. The normal 4-vortex mode is the primary mode, and the anomalous 4-vortex and the normal 2-vortex modes are the secondary modes at \({\Gamma }\) = 3.7 and Re = 660. This study focuses on only the instability of the normal mode and reveals the critical Reynolds number at which the Taylor flow bifurcates to the wavy Taylor flow.

Fig. 5
figure 5

Azimuthal-sectional view of the flow at \({\Gamma }\) = 3.7, Re = 660: in each panel, the right side shows outer cylinder and the left side is inner cylinder. a is the normal 4-vortex flow (primary mode), b the anomalous 4-vortex flow (secondary mode), and c is the normal 2-vortex flow (secondary mode)

Full size image

Figure 6 shows the process of the embedded analysis. The mode of a stable flow at each aspect ratio depends on the increase histories of the rotation speed and the final value of the Reynolds numbers as clarified by Toya et al. [25]. At first, a preliminary simulation is carried out to confirm the mode formed at each increasing rate of the rotation speed and each final value of the Reynolds number. In the next step, the time series of the axial velocity component near the outer cylinder side in the bottom vortex at each aspect ratio is sampled. Then the time series fluctuation of the axial velocity component is used to draw a three-dimensional attractor. The attractor requires the three-dimensional embedded process, and the embedded process requires a delay time (τ). The delay time can be obtained from the autocorrelation function r given by Eq. (3):

$$ r\left( { k } \right) = \frac{{\mathop \sum \nolimits_{i = 1}^{N - 1} (w_{i } - \overline{w})\left( {w_{i + k} - \overline{w}} \right)}}{{\mathop \sum \nolimits_{i = 1}^{N - 1} \left( { w_{i} - \overline{w} } \right)^{2} }}, $$
(3)

where \(w_{i}\) is a value of the axial velocity component, \(\overline{w}\) is an average of \(w_{i}\), and N is a sampling number. In this study, N is set at 1000, and k is a time step difference.

Fig. 6
figure 6

Analytical methods based on autocorrelations: a is the three-dimensional embedding, b is the orbit of the attractor and (c) is the autocorrelation function of the sine wave

Full size image

One way of determining the delay time is to adopt the time at which the autocorrelation function is 0. The Hopf bifurcation which bifurcates from the steady Taylor flow to the wavy Taylor flow corresponds to the T1 bifurcation in the Ruelle-Takens-Newhouse scenario [21]. In this analysis, under the assumption that the time series variation of the axial velocity component follows the sine wave, the delay time (τ) is defined as a quarter of one period, where the value of the autocorrelation function becomes 0. This is partly because Abarbanel et al. [26] stated that it may not be misleading to use the first zero crossing of the autocorrelation function as a useful delay time.

We identify the Taylor flow or the wavy Taylor flows from the orbit where the attractor converges. When the orbit of the attractor converges to a fixed point, it is determined to be a steady Taylor flow, and when it converges on a limit cycle, it is determined to be a wavy Taylor flow.

5 Results and discussion

5.1 Numerical calculation

Figure 7a shows typical sectional vector diagram of the Taylor flow at Re = 1350 and \({\Gamma }\) = 4.7. Figure 7b shows the first ten thousand variation of the axial velocity component in the time steps TS from 0 to 10 million. Figure 7c shows the autocorrelation function r given by Eq. (3) from the first 0 to 1000 time steps (TS) created by the axial velocity component.

Fig. 7
figure 7

Numerical results at Re = 1350, \({\Gamma }\) = 4.7

Full size image

The orbit of the attractor is superposed every 1 million TS up to 10 million TS. The orbit of the attractors shown in next section are made by selecting the last few sets of 1 million TS. The target Taylor flows are the normal 2-vortex mode, the normal 4-vortex mode, and the normal 6-vortex mode. The attractor converges on a limit cycle with the time step progress. In this analysis, the interval of the Reynolds number is set to 20 and the interval of the aspect ratio is 0.1. The maximum number of the calculation is 10 million time steps TS.

5.2 The attractors of the Taylor flow and the wavy Taylor flow

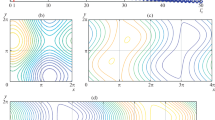
Figure 8 shows the orbit of the attractor of a 2-vortex Taylor flow numerically obtained from 7 to 10 million TS at \({\Gamma }\) = 2.1 and Re = 1660. In this figure, the three axes show the dimensionless velocities (w(t), w(t + τ), w(t + 2τ)) reconstructed by the embedding process. The calculated values for each axis have a large number of digits, therefore they are processed for easy viewing. For example, in Fig. 8, the number 4 indicates 4 in the 9th decimal place of 2.120160724 × 10–2 as the calculated value on each axis. In the figure, the red colored orbit shows an orbit from 7 to 8 million TS, the green color shows an orbit from 8 to 9 million TS, and the blue color shows an orbit from 9 to 10 million TS. As the time step increases, the orbit shrinks towards a fixed point. According to this result, this state represents a steady Taylor flow. Figure 9 shows the orbit of the attractor of a 2-vortex wavy Taylor flow from 7 to 10 million TS at \({\Gamma }\) = 2.1 and Re = 1680. The red, green and blue curves show the orbits from 7 to 8 million, from 8 to 9 million and from 9 to 10 million TS respectively. Pfister and Gerdts [27] measured the time dependence and the final amplitude of the lowest-order wavy Taylor flow. They noted that the slowing down of the time constant at the critical point was clearly seen. In our analysis, the attractor may not always show the final convergence to a fixed point or limit cycle with limited TS, however it is able to show a tendency to converge. A huge number of calculations are required to confirm the convergence point. The way to determine the attractor's convergence at up to 10 million TS is to check the orbit of the attractor with a Reynolds number that is 20 less or greater than the expected critical Reynolds numbers. Therefore, we investigate the orbit of the attractor at Re = 1640, which is 20 smaller than Re = 1660 in Fig. 8, and have confirmed that it clearly converged to a fixed point. Similarly, we check the orbit of the attractor at Re = 1700, which is 20 larger than Re = 1680 in Fig. 9, and have confirmed that it clearly converged on the limit cycle. For example, if we can confirm that the attractor at Re = 1640 which is 20 less than the expected critical Reynolds number Re = 1660, converges to a fixed point, we can estimate that the attractor at Re = 1660 converges at the fixed point as shown in Fig. 8. If we can confirm that the attractor at Re = 1700 which is 20 greater than the another expected critical Reynolds number Re = 1680, converges on the limit cycle, we can estimate that the attractor at Re = 1680 converges on the limit cycle as shown in Fig. 9. By this method, the critical Reynolds number Rec at \({\Gamma }\) = 2.1 is determined to be 1680. Therefore, the analysis with the maximum number of time step of 10 million TS, provides sufficient accuracy to detect critical values.

Fig. 8
figure 8

Attractor of 2-vortex mode at \({\Gamma }\) = 2.1, Re = 1660 (TS = 7 million to 10 million). The numerical dimensionless values 4 on the axes indicate 2.120160724 × 10–2

Full size image
Fig. 9
figure 9

Attractor of 2-vortex mode at \({\Gamma }\) = 2.1, Re = 1680 (TS = 7 million to 10 million). The numerical dimensionless values 6 on the axes indicate 2.1506 × 10–2

Full size image

Figure 10 shows the orbit of the attractor of a 2-vortex Taylor flow from 7 to 10 million TS at \({\Gamma }\) = 2.6 and Re = 960. The attractor does not have a circular orbit and continuously takes an irregular orbit in a quite small range of values. The small variation of these values is estimated as a numerical variation of computer. The size of the orbit indicates quite small like the size that converges at a fixed point. From this result, this state is a Taylor flow. Figure 11 shows the orbit of the attractor of a 2-vortex wavy Taylor flow from 7 to 10 million TS at \({\Gamma }\) = 2.6 and Re = 980. Since the attractor converges on a limit cycle, this state is a wavy Taylor flow. From these results of Figs. 10 and 11, the critical Reynolds number Rec at \({\Gamma }\) = 2.6 is decided to be 980.

Fig. 10
figure 10

Attractor of 2-vortex mode at \({\Gamma }\) = 2.6, Re = 960 (TS = 7 million to 10 million). The numerical dimensionless values 1.0 on the axes indicate 9.04137501541 × 10–3

Full size image
Fig. 11
figure 11

Attractor of 2-vortex mode at \({\Gamma }\) = 2.6, Re = 980 (TS = 7 million to 10 million). The numerical dimensionless values 8 on the axes indicate 9.28608 × 10–3

Full size image

Similar to the 2-vortex Taylor flow, we analyzes the attractors near the critical Reynolds number that bifurcated from the 4-vortex and 6-vortex Taylor flow to the wavy Taylor flow. For examples of the attractor orbits, the attractor of 4-vortex mode at \({\Gamma }\) = 4.9 and Re = 1320 converged at a fixed point and the attractor at \({\Gamma }\) = 4.9 and Re = 1340 shows a limit cycle. Therefore the critical Reynolds number Rec is determined to be 1340. The attractor of 6-vortex mode at \({\Gamma }\) = 5.9 and Re = 840 gradually shrinked into a fixed point and the attractor at \({\Gamma }\) = 5.9 and Re = 860 converged on a limit cycle. From these results, the critical Reynolds number Rec at \({\Gamma }\) = 5.9 is determined to be 860.

5.3 The bifurcation of the critical Reynolds number between the steady and wavy Taylor flows

Figure 12 shows the critical Reynolds number in each mode of the Taylor flow obtained by the present numerical analysis and that by the previous experiment by Nakamura et al. [10]. The experimental apparatus has the rotating inner cylinder and the stationary outer cylinder whose aspect ratio is from 1.0 to 7.2 and the radius ratio is 0.667. The numerical analysis and the experiment have the same geometrical condition. The critical value measured in the experiment was determined by the Reynolds number at which the boundary between the vortices began to oscillate. The oscillation of the boundary was observed by a microscope with its accuracy of 0.01 mm.

Fig. 12
figure 12

The critical Reynolds number at which the Taylor flow bifurcates into the wavy Taylor flow: the open symbols denote the numerical results and the filled symbols represent the experimental results [10]. The circle, square and triangle marks show the 2, 4 and 6-vortex modes, respectively

Full size image

The open symbols denote the numerical results, and the filled symbols represent the experimental results. The circle, square and triangle symbols indicate the 2-vortex, the 4-vortex and the 6-vortex modes, respectively. In the comparison between the numerical and the experimental results, they show an agreement in the smaller aspect ratio range than the aspect ratio at the each peak value of a critical Reynolds number. In the range of the larger aspect ratio than that at the peak value, however, the critical Reynolds number of the analytical result is larger than that of the experimental result. For the experimental values, the Reynolds number at which one of vortices started to oscillate in the Taylor flow was adopted as the critical value. The calculated critical Reynolds number was obtained by the embedding method for the axial velocity component of the vortex at the bottom of the Taylor flow. The reason why the analysis value and the experimental value match on the left side of the peak value of the critical Reynolds number is as follows. On the left side of the peak value, the boundary of vortices near the end walls firstly begins to oscillate, whose axial velocity component is sampled from the numerical results. However, on the right side of the peak value, the first fluctuation of the boundary between vortices firstly observed by the microscope tends to appear around the center of the flow region. While, in the numerical analysis, the determination is performed by the fluctuation of the bottom vortex in all range of the aspect ratio. Therefore difference of the measuring methods may make the higher numerical critical value at downward branches. Regarding this point, it is necessary to confirm by matching the judgment criteria. This will be considered in the future.

The authors have performed their numerical analysis by using the amplitude of the variation of the kinetic energy of the vortex of the Taylor flow to estimate the Reynolds number of the Hopf bifurcation [15, 16]. However, the accuracy of the method was insufficient when the kinetic energy was very small and it is near the critical value and the comparison between the numerical and experimental results was inadequate. Comparing Figs. 4 and 12, it can be said that the results of the new method in Fig. 12 are in good agreement with the results of experimental observations. Especially, the result at smaller aspect ratio gives better agreement. The values of the former method are more variation than the values obtained by the present new method. This study demonstrates that the numerical method using an attractor visualized in three-dimensional phase space gives more accurate results.

6 Conclusions

The instability of the Taylor flow between two cylinders with both fixed end walls with a small aspect ratio is clarified by a three-dimensional embedded analysis in a chaotic theory. The critical Reynolds number at which the Taylor flow with 2-vortex, the 4-vortex and the 6-vortex bifurcates to the wavy Taylor flow is determined by means of the attractor structure. The attractors are obtained in three-dimensional phase space by embedding the time series of the axial velocity component in the lowest vortex of the flow. The critical Reynolds number, which corresponds to the Hopf bifurcation point where the attractor structure changes from a fixed point to a limit cycle is estimated. The results of the numerical analysis are good agreement with the results of the experiment conducted under the same conditions in the smaller aspect ratio range than the aspect ratio at the each peak value of a critical Reynolds number. In the larger aspect ratio range than that at the each peak value, however, the analytical results are larger than the experimental results.

It is presumed the difference of the measured target boundary of vortices to explain why the analytical results differ from the experimental results in the larger aspect ratio range than the aspect ratio at the peak value of the critical Reynolds number. The numerical analysis uses the numerical result of the bottom vortex to determine the critical value, while the experimental method used the boundary of vortices, which firstly began to oscillate, and identified the critical Reynolds number. Regarding this point, it may be helpful to match the criteria to confirm the critical value.

This study shows that the instability of the Taylor flow is revealed by determining the structure of the attractor applied by the Hopf bifurcation. In addition, it is shown that a numerical approach using attractors can obtain more accurate results than those obtained by a numerical evaluation method using the amplitude fluctuation of the kinetic energy of the Taylor flow. Furthermore this study could be extended to the transition to turbulence which is much less well clarification for the instability of the Taylor flow by determining the structure of the attractor applied by the Hopf bifurcation.