1 Introduction

Reliable data on wetting characteristics are crucial for a large number of industrial applications and systematic investigation of naturally occurring phenomena. Efficiency of fluid separation processes in columns depends on the wetting of the packing surfaces [1]. Water condensation on the inner walls of gas pipelines and subsequent corrosion is triggered by low solid–liquid interfacial energies represented by low contact angles [2]. Good wetting of the inner surface of a pipeline results from favorable adhesion energies that help overcome the energetic barrier for (heterogeneous) nucleation of condensate droplets. Safe storage of gases like hydrogen and carbon dioxide in depleted oil and gas reservoirs as well as aquifers is only possible under favorable wetting conditions, i.e. a capillary pressure positively adding to the hydrostatic pressure for enabling mechanisms such as structural trapping. Migration of hydrocarbons in porous media is also closely related to the interaction of the respective fluid phases with the rock surfaces under prevailing reservoir conditions [3]. Last but not least, efficiency of enhanced hydrocarbon recovery techniques depends on favorable relative permeabilities of the fluids present in oil and gas reservoirs that on their turn are influenced by the competitive wetting of aqueous and hydrocarbon phases on the inner pore surface; the phase showing the higher rock-fluid interactions has lower contact angles (higher wetting), thereby displaying less mobility [4] and lower relative permeability [5]. In all of the aforementioned applications, experimental determination of the wetting behavior in terms of the three-phase contact angle has become an essential approach in order to quantify the multiple interactions between all present phases under real conditions.

Several methods are employed to assess wettability such as the Amott and the United States Bureau of Mines (USBM) tests which are somewhat qualitative in nature and only measure the average wettability [6]. Further, they are performed at atmospheric conditions and do not consider the presence of gases in the system. In recent years, the optical sessile drop or captive bubble method gained increasing interest, since this method best represents the situation within the formation and high-pressure optical cells that allow simple and easy performance of respective measurements are well developed [7,8,9,10]. In the context of carbon capture and storage (CCS), wettability is investigated in systems composed of three components, namely rock samples, brines and CO2. Mostly, the contact angle is determined by creating sessile brine drops on a surface of interest in compressed CO2 environment [11,12,13]. In analogy, the efficiency of methods of enhanced oil recovery (EOR) where gas is present also depends on the wetting behavior, but up to four phases (rock-brine-oil–gas) need to be considered depending on the recovery technique in question. To name a few: alternating gas–water flooding [14], carbonated water flooding [4],or a combination of these techniques, e.g. during foam flooding [15].

Contact angle measurements are usually studied at reservoir conditions, where brine salinity, oil composition, rock mineralogy as well as pressure and temperature are the most investigated parameters [16,17,18,19,20,21]. While the aforementioned indeed influence the wettability, there exist other factors that impact the measurements and their interpretation from a methodological perspective. Any experimentalist who is dedicated to determining the contact angle on a plane solid surface under real conditions faces a series of factors that influence the result, among those are impurities and surface roughness/porosity which are two of the most important. Alnoush et al. investigated the impact of surface roughness on the wettability of calcite and concluded that increasing the surface roughness increases water wetting [22]. Sari et al. investigated the impact of calcite surface roughness on contact angle in high and low salinity brines [23]. Similar to Alnoush et al., they reported that contact angle decreases with increasing surface roughness in both high and low salinity brines, where the surface roughness impacted the contact angle in a subtler manner in the low salinity brine. Other important aspects to be considered are preconditioning of the solid surface [24, 25] and ion interaction specifically with mineral surfaces [26]. Additionally, the drop size dependance of the contact angle needs to be considered. Sakai and Fujii investigated the influence of the drop size on the contact angle [27]. They state that the classical Young equation relating the participating interfacial energies must be corrected by the addition of a term that includes the contribution of the line tension as a characteristic value of the 3-phase system including the radius of the contact line (assuming an axi-symmetric drop) into an overall force balance. Sakai and Fujii include a gravity term in the definition of a relative free energy based on the interfacial energies of the contacting phases and calculate the deviation from a (virtual) case where gravitational forces are absent [28]. The conclusions seem somewhat confusing, as they refer to voids in the surface that are filled with adsorbed gas and these voids tend to “smoothen”, which—according to the authors-justifies the deviation from Wenzel´s law [29]. Ren et al. also try to describe the effect of gravity defining a “k-value” that represents an inverted Bond number and conclude that at k > 30 the effect of gravity on the drop shape is negligible [30]. Seo et al. reported that the contact angle of water drops on a superhydrophobic surface is not affected by the volume for a minimum drop size of 5 µl and above [31]. On the other hand, Cansoy did not find a clear tendency regarding the impact of drop volume on the contact angle on superhydrophobic surfaces [32]. Drelich et al. [33] tried to explain the drop size dependency with the help of a hypothetical quantity called line tension originally defined by Good and Koo [34] as the one-dimensional tension in analogy to the surface tension as a correction term in Young´s equation taking influence especially in case of small drops.

One basic question is whether the drop liquid is in direct contact with the solid surface at the moment of determining the contact angle [35]. It was found that droplets bounce off of a surface if the surface happens to be non-wetted by the droplet phase, however, it has also been reported that there exists a fluid cushion which appears also when the surface is wetted by the droplet [36]. This is confirmed by Fig. 1b where a water film separates the hydrocarbon drop phase and the solid surface during the first contact while a direct contact exists between the wetting oil droplet and the surface after the drop stabilizes (f).

Fig. 1
figure 1

Procedure of dispensing an oil drop on a steel surface in water: a–e bouncing of the drop due to a water film and posterior deposition with a contact angle signifying good wetting by the hydrocarbon phase (f)

Full size image

Based on several years of laboratory and industrial experience, this work serves as a concise guide that summarizes the main aspects to be considered during contact angle measurement from a methodological point of view, especially when non-atmospheric conditions are applied. These considerations should be accounted for in order to obtain meaningful and objective interpretation of the results, isolate any artefacts that are likely to impact the measurement and facilitate the derivation of generalized statements regarding wettability especially in terms of underground gas storage and enhanced oil recovery.

2 Materials and methods

2.1 Solids

Shale rock samples originating from Al-Sultani deposit located south of Amman, Jordan have been utilized for the captive bubble test. The samples were subject to supercritical carbon dioxide extraction to remove any hydrocarbons. Full details on the extraction procedure are reported in detail elsewhere [37]. No surface treatment was performed on the shale samples to preserve the native characteristics of the natural rock. Moreover, a limestone sample in addition to a calcite crystal -described in [38]- representing a quasi ideal smooth surface were used. X-ray Diffraction (XRD) was performed using an X-ray diffractometer (Empyrean – Malvern Panalytical, UK) to verify the mineralogical composition of the Sultani shale and limestone samples. Powdered samples were loaded into the diffractometer with Cu Kα radiation and a nickel filter, in a 2θ range of ≈ 10°–80°. Figure 2 shows the XRD pattern for both rocks.

Fig. 2
figure 2

X-ray diffraction plots of Sultani shale and Limestone

Full size image

2.2 Fluids

Alkanes {n-hexadecane (C16), eicosane (C20) and tetracosane (C24)} were purchased from Fischer Scientific, GmbH, Germany at analytical grade. A model oil composed of 45 wt% C16, 45 wt% C20 and 10 wt% C24 was synthesized based on gas chromatography analysis of oil extracted from the shale using supercritical carbon dioxide as described in [37]. The complete analysis of the extracted oil can be found in [17]. West Texas sour crude oil was also used. The characteristics of the aforementioned crude oil are listed in details in reference [38]. Deionized water as well as brine resembling sea water were used. Sea water composition is shown in Table 1. Carbon dioxide with 99.99% purity was supplied by Westfalen AG, Germany.

Table 1 Brine composition
Full size table

2.3 Methods

For determining the contact angle, the sessile drop and captive bubble methods were performed in a high-pressure drop analysis system. The system is composed of a high-pressure (HP) view cell (Pmax 70 MPa, Tmax 200 °C, Eurotechnica GmbH, Germany) coupled with a drop shape analyzer (Kruss GmbH, Germany). The view cell has two high pressure-resistant sapphire windows opposing each other. One window faces a light source that illuminates the back of the view cell and the other faces a charge-coupled device (CCD) camera for measurement observation. A heating jacket is used to heat the view cell to the desired temperature. Within the view cell, a movable capillary extends from either the bottom of the view cell or the top depending on the measurement configuration.

2.3.1 Sessile drop

The capillary extends from the top for a sessile drop configuration. The capillary is connected to a drop dispensing device that is used to dispense the drop of liquid through the capillary and onto the solid surface. A thermocouple with an accuracy of ± 0.1 °C is located 10 mm away from the capillary and is connected to a digital readout device for temperature observation. A pressure transducer with an accuracy of ± 0.1 bar is used to measure the pressure inside the view cell. The CCD camera is connected to a computer to record high quality images in a timely manner. Using a drop shape analysis software (Advance- Kruss GmbH, Germany) the axisymmetric drop shape analysis (ADSA) technique is employed for the evaluation of the contact angle. The software fits a baseline to the solid where the drop meets the surface, detects the drop profile as well as the 3-phase contact point where the contact angle is evaluated. Further information about this technique can be found elsewhere [39]. A syringe pump (D100, Teledyne ISCO, USA) is used to pressurize the CO2 and charge it into the view cell at designated pressure conditions. The schematic diagram of the sessile drop method is depicted in Fig. 3a.

Fig. 3
figure 3

Schematic diagram of experimental setup: a Sessile drop configuration and b Captive bubble configuration

Full size image

2.3.2 Captive bubble

In the captive bubble configuration, the capillary extends from the bottom. This configuration is prevalent in systems where the drop forming fluid has a lower density than the surrounding fluid. As the name implies, the drop forming liquid is trapped between the surrounding fluid and the rock surface. The experimental setup for the captive bubble is otherwise identical to that mentioned in the previous section (see Sect. 2.3.1 Sessile drop). The schematic diagram of the captive bubble configurations is depicted in Fig. 3b.

2.3.3 Dual-drop dual-crystal

Although the previous methods are also used to measure the advancing and receding contact angle, another way to measure the latter in a well-defined way is called the dual-drop dual-crystal (DDDC) method [40]. Basically, a drop is captured between two plates where one is moved laterally to stretch the drop and produce advancing and receding contact angles at the three-phase contact of both plates. In order to guarantee similar starting conditions at both solid surfaces, the final oil drop -of which advancing and receding contact angles are of interest- is created following the procedure presented in Fig. 4: two small oil drops are deposited on two identical plates in a captive bubble configuration where a drop of oil is surround by an aqueous phase. Due to buoyancy forces, the oil drops are pushed towards the surface and in this way the aging of the two surfaces is ensured to be identical. By tilting the lower plate 180°, both drops are brought to coalesce, and the new single larger drop is captured between the plates. Afterwards, the composition of the surrounding aqueous phase may be changed by replacing the originally used aqueous phase with a new solution that either contains surfactants or dissolved gas. So far, measurements have only been carried out in liquid–liquid–solid systems containing either dead oils or live oils above the bubble point pressure [41]. One advantage of this method is that the horizontal movement can be carried out in a precise and defined way for adjusting the velocity to a reproducible value.

Fig. 4
figure 4

Schematic diagram of the dual-drop dual-crystal method

Full size image

2.4 Experimental procedure

Prior to measurement, the entire setup is cleaned to ensure an environment free of contamination. The rock sample is introduced into the view cell and is supported by means of a sample holder. The glass windows are closed and tightened to seal the system against any leakage and the heating of the view cells is initiated. The syringe pump is pre-pressurized to reduce the time required for the CO2 to reach the designated pressure. The valve connecting the view cell to the syringe pump is opened and CO2 is pumped into the view cell until the designated pressure is reached. After the desired temperature is also reached, the drop dispensing device is used to form a drop of brine on the solid surface for contact angle measurement in a rock-brine-CO2 system using the sessile drop configuration. For measurements in a system composed of rock-brine-oil-CO2 using the captive bubble configuration, after the placement of the rock sample, the view cell is filled with brine that is pumped from the brine reservoir as seen in Fig. 3B. A waiting time of 30 min is sufficient for heating the newly introduced brine until it reaches the desired temperature. Once this is achieved, a drop of oil is placed on the sample surface via the moveable capillary. After a drop is created, the valve connecting the view cell to the syringe pump is opened and CO2 is pumped into the view cell until the designated pressure is achieved. The ADSA software evaluates and records the contact angle as a function of time.

3 Results and discussion

Below the factors impacting contact angle measurements are presented and discussed based on experimental data.

3.1 Drop size

Different opinions exist in literature regarding the influence of the drop size on experimental values of the contact angle. As a drop becomes bigger, the influence by gravity on the drop shape increases. This fact is accounted for by the Young Laplace equation of axi-symmetric drop shapes regardless of whether they are attached to a needle or resting on a solid surface. From the Young–Laplace relation, the interfacial tension may be deduced based on the balance between gravitational and interfacial forces. In terms of the contact angle at the three-phase contact of a drop resting on a solid surface, the gravity may distort the macroscopic (optically detectable) value. While a spherical drop is rather unfavorable for measuring the interfacial tension because the interfacial forces dominate over the gravitational forces, it may be preferable for measuring the contact angle. The ratio of gravitational to interfacial forces is given by the so-called Eötvos or Bond number as per Eq. (1):

$$B_{o} = g\Delta \rho d^{2} /\sigma$$
(1)

where g is the gravity constant in m/s2, Δρ is the density difference between two adjacent phases in kg/m3, d is the drop diameter in m and σ is the interfacial tension in mN/m. In case of very small drops and relatively high interfacial tension, Bo is smaller than unity leading to rather spherical drops. As a consequence, small drops are preferred because the impact of gravity on the contact angle itself is reduced. A threshold value of Bo is rather arbitrarily set to unity. In our experiments, a moderate dependency of the contact angle is found in a system comprising model oil drops on an extracted and cleaned shale surface in deionized water where the system is pressurized with CO2 at 10 MPa and 60 °C. This tendency is depicted in Fig. 5.

Fig. 5
figure 5

Contact angle as a function of the bond number as calculated based on the baseline diameter at 10 MPa and 60 °C

Full size image

In Fig. 5, the contact angle is measured using the captive bubble method (Sect. 2.3.2 Captive bubble) and the contact angle values are depicted as a function of the bond number. The principal findings of previous authors could be confirmed, i.e. a diminishing dependence of contact angle on the drop size as volume increases. For heptane—water—quartz and tetradecane—water—quartz systems, Drelich found contact angle variations in a range of 2–3 degrees, especially for drops of baseline diameters beyond 2 mm [33]. Only in case of heterogeneous and rough surfaces some model approaches are presented in order to describe the influence that becomes apparent for small drop volumes and for explaining the influence on the contact angle hysteresis, but the lack of a consistent theory must indeed be acknowledged. In general, it is recommended to apply sessile or captive bubble drops with base diameters of no less than 5 mm.

3.2 Drop deposition velocity

Lyklema states that the proper (advancing) contact angle for determining the interfacial energies is the one at zero velocity of the three-phase contact line [42]. In order to meet both requirements—a stationary interface yet an advancing angle—the contact angle may be determined at different sessile drop (Sect. 2.3.1 Sessile drop) deposition rates on a solid surface as shown in Fig. 6.

Fig. 6
figure 6

A sea water drop on a calcite crystal in West Texas crude at different rates of drop deposition at 5.5 MPa and 50 °C

Full size image

The corresponding contact angle is depicted as a function of the velocity of three-phase contact moving across the solid surface in Fig. 7.

Fig. 7
figure 7

Contact angle as a function of velocity of the three-phase contact across a solid surface. Sea water – calcite in crude oil at 5.5 MPa and 50 °C. Extrapolation towards u = 0 mm/s is indicated by the dashed line

Full size image

According to Lyklema [42] and based on the values in Fig. 7, the designated contact angle is determined by extrapolating the line towards u = 0 mm/s, i.e. where the resultant CAu→0 = 78°. The application of the DDDC method (Sect. 2.3.3 Dual-drop dual-crystal) to a system composed of crude oil–water-calcite at elevated pressure is presented in Fig. 8.

Fig. 8
figure 8

Dual-drop dual-crystal method for a system comprising crude oil—brine and a calcite crystal, P = 49.4 MPa, T = 60 °C

Full size image

In Fig. 8a, the drop is already extended but the interface has not moved yet whereas in the next image (b) the contact line has “shifted”, i.e. it moved away from the area originally exposed to the oil during the aging process due to which erroneous results may be obtained. Hence the decisive contact angle will be retrieved from the image just before this happens (a). In (c) the drop is divided into the two drops again that originally had been aged separately and brought to coalesce for the experiment. From the experiments on the DDDC as illustrated in Fig. 8, adhesive forces may be estimated based on the information on cohesion: As seen in Fig. 8c, the adhesive forces appear to be stronger than the cohesion which on its turn can be determined through the interfacial tension and geometrical considerations. From the geometrical situation in Fig. 8b, a minimum force of adhesion can be deduced from Eq. 2 where σ oil–water is the interfacial tension between water and oil in mN/m, d is the diameter in m and F is the adhesive force in mN:

$$\sigma_{oil - water} \pi d_{bridge} \cos \alpha \le F_{adhesion}$$
(2)

Based on an interfacial tension of around 20 mN/m between the water and the oil [38], the adhesion force between the oil and rock results in a value of at least 0.15 mN on a surface area of 32 mm2. This force can be translated directly to the flow force in the pore required to displace the oil (Fig. 9).

Fig. 9
figure 9

Ahesion and cohesion forces

Full size image

3.3 Preconditioning of solid surface

Especially for applications related to oil/gas reservoirs as well as subsurface gas storage, relevance of laboratory experiments depends on the extent to which the solid surface under investigation resembles the real situation. In case of shales, the impact by preparing the sample is minimal, because it is laminated and fissile, i.e. it breaks easily leaving smooth surfaces on which the measurement can be directly performed without the need for surface preconditioning. Calcite crystals, which are representative of ideal and clean carbonates, also possess naturally smooth surfaces that are useful for obtaining reproducible results. When using core samples from real carbonate or sandstone reservoirs, the situation becomes more complicated: First, these rock samples are exposed to a cutting process that induces unnatural thermal and chemical conditions. Secondly, the rock samples undergo a cleaning procedure after which the original reservoir conditions shall be restored as much as possible prior to further investigation of the wetting behavior. Based on many years of experience, both industrial and academic, research laboratories developed standard procedures so at least internally comparable results from wetting tests are guaranteed. Hoeiland et al. propose to age the rock samples in acids extracted from crude oil, since these compounds are assumed to be decisive for changing wettability [43]. For this reason, Jaeger et al. applied naphthenic acid for aging carbonate surfaces prior to measuring the contact angle under reservoir conditions [38]. Other labs suggest the following procedure:

  1. 1.

    Vigorous cleaning renders the core water-wet.

  2. 2.

    Saturate in simulated formation brine and age.

  3. 3.

    Flood with crude oil (dead oil).

  4. 4.

    Age for 40 days at reservoir temperature and pressure.

This procedure can also be varied with help of an Amott-type equipment [44]:

  1. 1.

    Expose the rock to vacuum.

  2. 2.

    Saturate rock with crude oil.

  3. 3.

    Place the oil-saturated rock in brine.

  4. 4.

    The release of oil will occur spontaneously until original conditions are restored.

In Fig. 10, the contact between an oil drop and the rock surface is schematically depicted depending on the preconditioning of the rock.

Fig. 10
figure 10

Oil drop on an unaged rock surface immersed in water (left) and oil drop on an aged rock immersed in water (right)

Full size image

3.4 Surface roughness

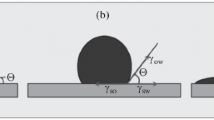
Particularly for investigation of wettability effects in reservoirs, one has to deal with rough or porous surfaces. Wenzel’s statement shown in Eq. 3 is commonly used as the starting point for describing the effect of surface roughness on the macro contact angle [29] where θr is the micro contact angle of the rough surface and θ is the macro contact angle:

$$\cos \left( {\theta_{r} } \right) = \frac{area\;of\;the\;rough\;surface}{{area\;of\;an\;assumed\;perfectly\;smooth\;surface}} = \cos \left( \theta \right)$$
(3)

implying that for \(\theta > 90^\circ\) the contact angle increases for increasing roughness while the inverse happens for \(\theta < 90^\circ\). This effect is made use of for technical “self-cleaning” surfaces by increasing hydrophobicity through enhanced roughness under the condition of extremely small adherence forces, also known as Cassie´s state [45]. In spite of high contact angles, adherence can still be high which is associated with large contact angle hysteresis, i.e. large differences between the advancing and receding contact angle [46]. Figure 11 shows the effect of a porous surface on the dynamics of the contact angle of a water drop on calcium carbonate surfaces in a CO2 environment measured using the sessile drop method (Sect. 2.3.1 Sessile drop) where the calcite crystal represents a smooth surface, and the limestone represents a rougher surface.

Fig. 11
figure 11

Contact angle of a water drop on porous and non-porous calcium carbonate surfaces at atmospheric conditions and in compressed carbon dioxide, T = 40 °C

Full size image

Comparing the values at 0.1 and 5 MPa it can be seen that the initial contact angle increases as the pressure is increased due to competitive wetting between the water and the compressed CO2-phase. An initial contact angle of just below 90° (water wet) as seen for the limestone sample at 0.1 MPa results in a rapidly decreasing contact angle over time due to the permeation of the droplet inside the sample pores, while the initial value on the smooth crystal surface only results in a slightly diminishing value over time at the same pressure. Increasing the contact angle (due to increasing the pressure) to slightly above 90° leads to fairly stable values in both samples as seen at 5 MPa. This is in line with the findings of Ge et al. [47] who stated that at contact angles larger than 90°, i.e. lower surface wetting, the permeation is inhibited. These results indicate that the contact angle may be measured on smooth surfaces as a first indication and for comparison but when transferring the results to real (porous) systems the effect strongly depends on whether the contact angle is below or above 90°.

3.5 Zeta potential and pH

The pH itself is only a measure of free H+ ions that on their turn reflect the degree of dissociation of acids being present in the solution. Dissolved minerals can buffer the acidity as demonstrated in reference [26] for carbonic acid in the presence of carbonate rocks. Due to the existence and nature of ionized sites on rock surfaces, the effect of pH on the wettability is different for carbonates and sandstones. Silica surfaces are negatively charged above a pH of about 2, so positively charged ions (base chemical species) can adsorb. Conversely, calcite surfaces are commonly positively charged, especially below pH 9.5 [48] so negatively charged ions (acidic species) can adsorb. In case anions like SO42− are present in the brine, these may compete with carboxylic acids in crude oils rendering the surface more water wet [49]. Carbonate wettability is also influenced by the reactivity of carbonate minerals. Starting out from a chemical thermodynamic equilibrium initially existing in the reservoir at a pH of 5–6, clay minerals act as ion exchange materials on which acidic and protonated basic components from the crude oil are adsorbed as well as cations from formation water especially those that are divalent like Ca2+, which are known as potentially determining ions (PDI) [50]. The subsequent low pH environment enhances the adsorption of both acidic and basic components of the oil on the surface of the clay. However, the proton H+ has the strongest affinity towards the clay surface (negatively charged), leading to an increase in pH in the bulk. This increase in pH helps release more of the organic material and renders the system more water wet. In other terms, an increase in pH impacts the surface charge of the rock and consequently the overall zeta potential at a rock-brine interface.

The zeta potential is used to measure the electrical potential in the shear plane separating the stern layer (inner layer of the so-called electric double layer (EDL)) and diffusive layer (outer layer of the EDL that forms at the rock-water interface) [51], and will therefore determine the electrostatic forces acting between the rock-water and oil–water interfaces in an oil reservoir. When the zeta potential at each interface has the same polarity, repulsive electrostatic forces act between the two interfaces and stabilize the water film on the mineral surface promoting higher water wetting. The more negative the surface charge in the case of the sandstone, the higher the repulsive forces towards the negative component of the crude oil (carboxylic acid). When the repulsive forces are dominant, the EDL expands and the water film surrounding the rock is said to be stabilized [52].

The zeta potential at the rock-water interface is highly dependent on the concentration and the type of ion (monovalent or divalent). The absolute value of Zeta potential is reported to increase with decrease in salinity and increase in pH [53]. The so-called low salinity water flooding is believed to be favored as an EOR method over high salinity water injection because the presence of high salt concentrations shields the surface charges leading to a reduced repulsion at the solid-oil interfaces [54]. As a conclusion for the experimentalist it may be stated that investigation on wettability in oil reservoirs shall be carried out using model systems not only comprising model brines but also contain carboxylic and other surface active compounds such as asphaltenes [55, 56] in the organic phase in order to gain significant conclusions on the ion interactions that govern wettability [18].

4 Conclusions

The wetting behavior is crucial for a number of applications under reservoir conditions. Quantifying wettability using sessile drop and captive bubble methods has shown great potential. Whether or not the resulting contact angles are significant depends on the correct interpretation for which a number of influencing factors need to be considered, especially in order to exclude artefacts. In this regard, standard operating procedures that lead to formation of uniform drop sizes may support the reproducibility of the experiments. Especially with respect to the drop size, neither too small nor too large drops shall be considered. According to the findings of this study:

  • The drop base diameter is advised to be no less than 5 mm.

  • Sophisticated techniques like the dual-drop dual-crystal method give valuable insight especially into the adhesion-cohesion phenomena but due to the complex experimental setup, measurements under reservoir conditions, especially at elevated pressures, are very time-consuming resulting in a relatively small number of comparable experiments.

  • The impact of the drop deposition speed shall be accounted for. It was found that performing the measurements at different velocities of the three-phase contact across a solid surface yields different results, however, the extrapolation towards zero velocity can yield a meaningful outcome.

  • The wetting behavior changes depending on surface roughness. For rough surfaces such as limestone, it is found that the contact angle decreases over time due to drop permeation into the rock pores when the contact angle is less than 90°, however, as water wetting decreases (contact angle just above 90°), the permeation process is inhibited. This is represented by a stable value of water contact angle on limestone at 5 MPa.

  • The pH and zeta potential should be accounted for during contact angle measurement as they impact the adsorption of brine ions on the rock surface and the polarity of rock- brine and oil-brine interfaces which ultimately influences electrostatic forces.

In general, it is advisable to investigate the multiple factors of influence separately making use of model systems and draw conclusions regarding the original system based on the dominating mechanisms.